保险精算练习题
寿险精算习题及答案
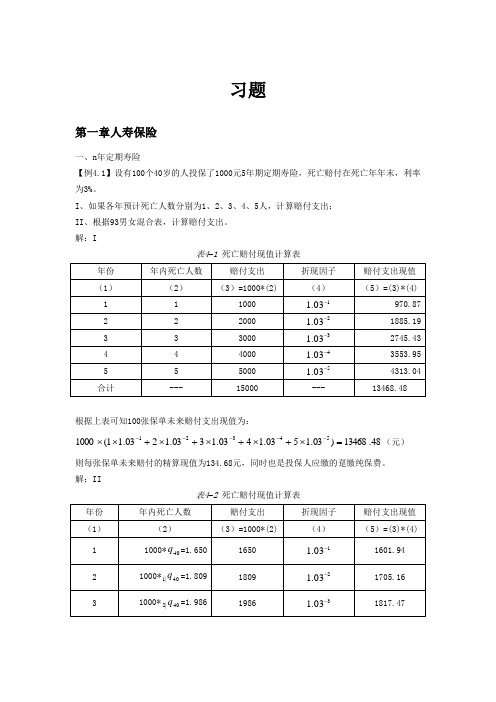
习题第一章人寿保险一、n 年定期寿险【例4.1】设有100个40岁的人投保了1000元5年期定期寿险，死亡赔付在死亡年年末，利率为3%。
I 、如果各年预计死亡人数分别为1、2、3、4、5人，计算赔付支出； II 、根据93男女混合表，计算赔付支出。
解：I表4–1 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为：48.13468)03.1503.1403.1303.1203.11(100054321=⨯+⨯+⨯+⨯+⨯⨯-----（元）则每张保单未来赔付的精算现值为134.68元，同时也是投保人应缴的趸缴纯保费。
解：II表4–2 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为：86.9124)03.103.103.103.103.1(1000540|4440|3340|2240|11402=⨯+⨯+⨯+⨯+⨯⨯-----q q q q q （元）则每张保单未来赔付的精算现值为91.25元，同时也是投保人应缴的趸缴纯保费。
【例4.2】某人在40岁时投保了10000元3年期定期寿险，死亡赔付在死亡年年末，利率为5%。
根据93男女混合表计算：I 、单位趸缴纯保费；II 、单位赔付现值期望的方差；III 、（总）趸缴纯保费； 解：I 、单位趸缴纯保费为，)()(424023414024040|2340|1240240|11|3:40q p v q p v vq q v q v vq q v Ak k k ++=++=⨯=∑=+]05.1001993.0)001812.01()00165.01(05.1001812.0)00165.01(05.100165.0[32⨯-⨯-+⨯-+=00492793.0=（元）。
II 、单位赔付现值期望的方差为，00444265.0)()()()(21|3:4040|2640|1440221|3:40240|)1(221|3:401|3:402=-++=-⨯=-∑=+A q v q v q v A q v AAk k k III 、趸缴纯保费为，28.49100001|3:40=⨯A （元） 【例4.3】某人在50岁时投保了100000元30年期定期寿险，利率为8%。
精算数学练习题
精算数学练习题1. 计算以下年金的现值：- 年金每年末支付1000元，连续支付10年，年利率为5%。
- 年金每年末支付1200元，连续支付15年，年利率为4%。
2. 假设一个保险公司签发一份保额为100万元的定期寿险保单，保险期限为5年，年利率为3%，求该保单的精算现值。
3. 计算以下生存年金的精算现值：- 年金每年初支付1500元，连续支付20年，生存者的年龄为30岁，年利率为6%。
- 年金每年末支付2000元，连续支付25年，生存者的年龄为45岁，年利率为5%。
4. 某保险公司提供一种终身年金，每年初支付1000元，购买者年龄为50岁，年利率为4%，求该年金的精算现值。
5. 计算以下联合生存年金的精算现值：- 年金每年末支付1500元，只要两个生存者中至少有一个存活，连续支付20年，两个生存者的年龄分别为60岁和55岁，年利率为5%。
- 年金每年初支付2000元，只要两个生存者都存活，连续支付25年，两个生存者的年龄分别为40岁和35岁，年利率为4%。
6. 假设一个保险公司签发一份保额为50万元的终身寿险保单，购买者年龄为40岁，年利率为3%，求该保单的精算现值。
7. 计算以下递增年金的精算现值：- 年金每年末支付1000元，连续支付10年，每年支付额递增5%，年利率为6%。
- 年金每年初支付1200元，连续支付15年，每年支付额递增3%，年利率为5%。
8. 某保险公司提供一种递减定期寿险，保险期限为10年，每年初支付保费1000元，购买者年龄为30岁，年利率为4%，求该保单的精算现值。
9. 计算以下年金的精算现值，其中包含一个保证期：- 年金每年末支付1000元，连续支付10年，保证期为5年，年利率为5%。
- 年金每年初支付1200元，连续支付15年，保证期为8年，年利率为4%。
10. 假设一个保险公司签发一份保额为200万元的终身寿险保单，购买者年龄为50岁，年利率为3%，求该保单的精算现值。
保险精算例题
10
=4405.216554（元）
在职工 30 岁至 49 岁间，个人账户在 20 岁的现值为： 480
（n）
n
）n
（2） 12% -12 d （1+ 12 ） =（1— ）2 2
d
（2）
12% =2×[1—（1+ 12 ）-6]=11.59%
【例 2.7】某人从银行借款 4000 元，这笔借款的利息每年结算 4 次， 年利率为 16%。那么，他在借款 21 个月后欠银行的歀为多少？ 解：年利率为 16%，每年结算 4 次，也就是每 3 个月结算一次，每次 结算的利息率为 4%（16%/4=4%） ，21 个月共结算 7 次（21/7=7） 。这 样，4000 元本金在结算 7 次后的本利和为： 4000×（1+4%）7=5263.73（元） 值得注意的是，在单利下，由于利率只在本金上计量，故没有名 义利率和实际利率的区别。 【例 2.8】 某人在 1998 年 7 月 22 日贷款 4000 元， 如果利息力是 14%，
X=
200000i 1 v
30
=13010.29（元）
【例 2.14】某人用 2000 元一次性购买了 15 年确定年金，假设年利 率为 6%，第一次年金额领取从购买时开始，试计算每年可以领取的 数额。 解：X X= 由于 i d=1+i =0.0566 故 X=194.27（元） 【例 2.15】某人在 30 岁时计划每年初存入 300 元建立个人账户，如 果他 60 岁退休，存款年利率假设恒定为 3%。 （1） 求退休时个人账户的累积额。 （2） 如果个人账户累积额在退休后以固定年金的方式在 20 年内每 年领取一次，求每年可以领取的数额。 解： （1）退休时个人账户累积额是 30 年定期的年金终值： 300 s 30 =X a 240
保险精算考试题及答案
保险精算考试题及答案1. 保险精算中，用于计算未来现金流的现值的公式是：A. 未来值 = 现值× (1 + 利率)^期数B. 现值 = 未来值÷ (1 + 利率)^期数C. 未来值 = 现值× (1 - 利率)^期数D. 现值 = 未来值× (1 - 利率)^期数答案：B2. 在非寿险精算中，用于计算纯保费的公式是：A. 纯保费 = 预期损失 + 预期费用B. 纯保费 = 预期损失 - 预期费用C. 纯保费 = 预期损失× 预期费用D. 纯保费 = 预期损失÷ 预期费用答案：A3. 以下哪项是寿险精算中的生命表的主要组成部分？A. 死亡率表B. 疾病率表C. 残疾率表D. 以上都是答案：A4. 寿险精算中，计算年金现值的公式是：A. 年金现值 = 年金支付额× 利率× (1 - 1/(1 + 利率)^期数)B. 年金现值 = 年金支付额÷ 利率× (1 - 1/(1 + 利率)^期数)C. 年金现值 = 年金支付额× 利率÷ (1 - 1/(1 + 利率)^期数)D. 年金现值 = 年金支付额÷ 利率÷ (1 - 1/(1 + 利率)^期数) 答案：A5. 保险精算中，用于评估保险公司财务稳定性的指标是：A. 偿付能力比率B. 资产负债比率C. 投资回报率D. 以上都是答案：A6. 在精算评估中，用于计算保单持有人未来利益的现值的贴现率是：A. 预定利率B. 市场利率C. 法定利率D. 以上都不是答案：A7. 以下哪项是精算师在评估寿险保单的死亡率风险时常用的方法？A. 蒙特卡洛模拟B. 敏感性分析C. 精算表分析D. 以上都是答案：C8. 保险精算中，用于计算保单持有人未来利益的现值的公式是：A. 未来利益现值 = 未来利益× 利率× (1 - 1/(1 + 利率)^期数)B. 未来利益现值 = 未来利益÷ 利率× (1 - 1/(1 + 利率)^期数)C. 未来利益现值 = 未来利益× 利率÷ (1 - 1/(1 + 利率)^期数)D. 未来利益现值 = 未来利益÷ 利率÷ (1 - 1/(1 + 利率)^期数) 答案：B9. 在保险精算中，用于计算保单的准备金的公式是：A. 准备金 = 未来利益现值 - 已收保费B. 准备金 = 未来利益现值 + 已收保费C. 准备金 = 未来利益现值× 已收保费D. 准备金 = 未来利益现值÷ 已收保费答案：A10. 以下哪项是保险精算中用于评估保单持有人未来利益的不确定性的方法？A. 精算评估B. 风险评估C. 敏感性分析D. 以上都是答案：C。
保险精算习题
1．确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
(2)名义贴现率为每4年计息一次的年名义贴现率6%。
2．已知第1年的实际利率为10%，第2年的实际贴现率为8%，第3年的每季度计息的年名义利率为6%，第4年的每半年计息的年名义贴现率为5%，求一常数实际利率，使它等价于这4年的投资利率。
3．基金A 以每月计息一次的年名义利率12%积累，基金B 以利息强度6t tδ=积累，在时刻t (t=0)，两笔基金存入的款项相同，试确定两基金金额相等的下一时刻。
4. 基金X 中的投资以利息强度0.010.1t t δ=+(0≤t ≤20), 基金Y 中的投资以年实际利率i 积累；现分别投资1元，则基金X 和基金Y 在第20年年末的积累值相等，求第3年年末基金Y 的积累值。
5.某银行推出2年期存单，年利率为9%，存款者若提前支取则面临两种可供选择的惩罚方式：变为活期存款，年利率为7%；损失3个月的利息。
某存款人拥有这种存单但要在第18个月末时支取，试问该人该选择哪种惩罚方式？第二章：年金练习题1．证明()n m m n v v i a a -=-。
√2．某人购买一处住宅，价值16万元，首期付款额为A ，余下的部分自下月起每月月初付1000元，共付10年。
年计息12次的年名义利率为8.7% 。
计算购房首期付款额A 。
√3. 已知7 5.153a = , 117.036a =, 189.180a =, 计算 i 。
√4．某人从50岁时起，每年年初在银行存入5000元，共存10年，自60岁起，每年年初从银行提出一笔款作为生活费用，拟提取10年。
年利率为10%，计算其每年生活费用。
√5．年金A 的给付情况是：1～10年，每年年末给付1000元；11～20年，每年年末给付2000元；21～30年，每年年末给付1000元。
年金B 在1～10年，每年给付额为K 元；11～20年给付额为0；21～30年，每年年末给付K 元，若A 与B 的现值相等，已知1012v =，计算K 。
保险精算习题及答案
第一章：利息的基本概念练习题1．已知()2a t at b =+，如果在0时投资100元，能在时刻5积累到180元，试确定在时刻5投资300元，在时刻8的积累值。
(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+=∵2．(1)假设A(t)=100+10t,试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A −−−======(2)假设()()100 1.1nA n =×，试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A −−−======3．已知投资500元，3年后得到120元的利息，试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。
11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4．已知某笔投资在3年后的积累值为1000元，第1年的利率为110%i =，第2年的利率为28%i =，第3年的利率为36%i =，求该笔投资的原始金额。
123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5．确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
(2)名义贴现率为每4年计息一次的年名义贴现率6%。
(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎞⎜⎟=+=⎜⎟⎜⎟⎝⎠6．设m ＞1，按从大到小的次序排列()()m m d d i i δ<<<<。
保险精算习题及答案
1 an = v n a∞ 2 1 − vn 1 = 2v n i i 1 vn = 3
11. 延期 5 年连续变化的年金共付款 6 年，在时刻 t 时的年付款率为 ( t + 1) ,t 时刻的利息强度为 1/(1+t), 该年金的现值为（ A.52
5| 2
） B.5411C. Nhomakorabea6D.58
a6 = ∫ v(t)(t + 1) 2 dt
8．已知第 1 年的实际利率为 10%，第 2 年的实际贴现率为 8%，第 3 年的每季度计息的年名义利率为 6%， 第 4 年的每半年计息的年名义贴现率为 5%，求一常数实际利率，使它等价于这 4 年的投资利率。
i (4) 4 i (2) 2 ) (1 + ) 4 2 = 1.1*1.086956522 *1.061363551*1.050625 = 1.333265858 ⇒ i = 0.74556336
a1 (t ) = (1 + i )
t
t
0.01t 2 +0.1t 2
δ t dt a2 (t ) = e ∫0 = e
⇒ (1 + i ) = e
20
0.01*202 + 0.1*20 2
= e4
(1 + i )3 = 1.8221
11. 某人 1999 年初借款 3 万元，按每年计息 3 次的年名义利率 6%投资，到 2004 年末的积累值为（ 万元。 A. 7.19 B. 4.04 C. 3.31 D. 5.21 ）
1 − v120 = 79962.96(i = 8.7% /12) i ∴160000 − 79962.96 = 80037.04 1000a120 = 1000
保险精算第二版习题及答案
保险精算（第二版）第一章：利息的基本概念练 习 题1．已知()2a t at b =+，如果在0时投资100元，能在时刻5积累到180元，试确定在时刻5投资300元，在时刻8的积累值。
(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+= 2．(1)假设A(t)=100+10t, 试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =⨯，试确定 135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3．已知投资500元，3年后得到120元的利息，试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。
11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4．已知某笔投资在3年后的积累值为1000元，第1年的利率为 110%i =，第2年的利率为28%i =，第3年的利率为 36%i =，求该笔投资的原始金额。
123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5．确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
(2)名义贴现率为每4年计息一次的年名义贴现率6%。
(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎫ ⎪=+= ⎪ ⎪⎝⎭6．设m ＞1，按从大到小的次序排列()()m m d di i δ<<<<。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1．李华1990年1月1日在银行帐户上有5000元存款，（1）在每年10%的单利下，求1994年1月1日的存款额。
（2）在年利率8%的复利下，求1994年5月1日的存款额。
解：（1）5000×（1+4×10%）=7000（元）4.33=7556.8（元） 5000×（1+10%）（2）2．把5000元存入银行，前5年的银行利率为8%，后5年年利率为11%，求10年末的存款累计额。
55=12385（元）×（1+11%解：5000（1+8%））3．李美1994年1月1日在银行帐户上有10000元存款。
（1）求在复利11%下1990年1月1日的现值。
（2）在11%的折现率下计算1990年1月1日的现值。
-4=5934.51（元）1+11%）（1）10000×（解：4=6274.22（元）） 2）10000×（1-11%（4．假设1000元在半年后成为1200元，求(2)(3)id。
⑴ i, ⑶，⑵(2)i(2)1000?(1?)?12004.??i0；所以解：⑴2(2)i2)1?i?(1?44?0.i⑵；所以2(n)(m)di?1?mn(1?)?1?i?(1?d)?(1?)⑶；mn(3)d3?1(1?)?(1?i))(3?0.34335d；所以，3 (n)(n)???id?id?。
时，证明：5．当1?n(n)dd?证明：①，为因(n)(n)(n)(n)dddd012n323))(C)C1CC(1d(1?????????????d1??nnnn nnnn(n))(n dd?所以得到，；(n)??d②?????????423423?)??1C?1??C?()?C?()??(e m?)(n)e(1?d?m m；??i③nnn mmmmm?)n(??)](1?d?m[1?所以，m(n)(n)i)(n i n[1?]?1?i??)1?iln(1?)?ln(n?即，，n n??????(n)i?n?(e?1)n所以，?434232?1??)C?e?1?C?()??()?C?(n?nnn mmmmm?(n)??])?1?n[(i1?n(n)?ii④(n)(n)(n)iii)(n i)n22(n01[1?]?C?1?C??C?()???1?i n[1?]?1?i nnn，nnn n)(n ii?所以， 6．证明下列等式成立，并进行直观解释：m aav?a?⑴；nnm?m m v?1n?nmm v1?vv?n?m v1?a?mm?va?v a?i m ii n，，解：i n?m n?mmm v?1?v?v m a?ava??i mnnm?所以，m sva?a?nm?nm⑵；m v1?n?m v?1nmm?v?v?a a?m??vsi m i n?m，解：，i n nmm?m vv??1?v m a??a?vsi mnm?n所以，m as?s?(1?i)nmm?n⑶；m1?i)(1?mnnm?)?i)?(11(1?i)?1(?i?s mm?)1(?i(1?i)s?i，解：)1?i)1?(1?i?()(1?i?m s??(1?i)as?m ii n mnmm?i mm?nn所以，m ai)1s?s?(?nnm?m。
⑷解：（同上题）略。
岁退元，7．某人今年30岁，其计划每年初存300共存30年建立个人存款能从6020休开始每年年末得到固定金额，共能领取20年。
假设存款利率在前十年为6%，后年为12%，求每年能取的养老金额。
10101(1?i)(?11?i)?202021???(si)?1?i)ss??(1?5?s59759.300?30 60所以22解：ii10302021岁时存款有（元）sX?a?X=7774.122020由此知，（元），可得从存入最后一笔款后的元建立职工奖励基金。
年内每年存入银行5000208．某单位在年起，每年提取固定金额奖励一名有突出贡献的职工，这种奖励形式将永远持续2第 8%，求每次能够提取的最大金额。
下去。
假设存款的利率为182??.?2288095000?sX?A?X7918304.X?解：。
所以（元）i20?．证明：9i a?a?a?s1n；⑴?nn nn ivi1?v1???a???a???i nn证明：i)?(1i?1a?as??s?1nn??1，所以?n?e1??a n?；⑵．??nn??n?n e)1?v?1(1?i1?)1?(e?a???n?????n1e??s n?⑶。
??nnn1i)e?(e)1??1(1????s n???证明：1000增加到一次收付假设每年第一年收付200元，以后每隔一年增加收付100元，10．，求这一12%元时不在增加，并一直保持每年1000元的水平连续收付。
假设年利率为年金的现值。
a?100a?100(Ia)?1000a?91?8a)(1?i?8??18解：91??1000??v?4362)(?1001?i?100.94ii1．依据生命表的基础填充下表：xlqpd xxxx0.1 0.9 0 1000 100(1/6) 1 (5/6) (900) (150)(0.2) 0.8 2 750 (150)(0.5) (600) (0.5) (300) 30.6 (180) 4 (0.4) 300(1) 5 (0) (120) (120)6x)l?1000(1?已知3. ，计算：x120q dl pl；，⑴，，，20303303020120⑵25岁的人至少再活20，最多活25年的概率；岁的概率。
80岁的人均存活到25⑶三个1200)?0l?1000(1?1000?l?1000(1?)1200120解：⑴；120251?1000?d?l?l?3433333120ll?l750203?0.q?50?p?2030l3020；9l 2030ll?15045??q25520⑵19l25l83380074646449.p?()?(?0)255519l⑶44000?l)100000(l?35x，求：， 4．若x?c 25x?cc的值；⑴⑵生命表中的最大年龄；岁的概率；⑶从出生存活到50 岁之间死亡的概率。
⑷15岁的人在40～5035c?44000)??l100000(c=9035。
所以，解：⑴35?c x?900l?100000()?x?90?，所以，⑵x?90l450?p?05013l⑶0ll?25040?q?15 10253l⑷。
155．证明并作直观解释：q?p?p xmxnnx?mn；⑴l?lll x?n?x?x?nnmx?n?m q????p?pq?p?q xn?xnxn；⑵xx?xmnn mn lll证明：xxxl?llll x?nn?11x?nx?nx?x?n?q?????p?qp?p?p。
⑶x?xxnn n llll证明：nxxxx?nnxx?n?mmx lll x?n?mx?nmx?n????p?pp?x?mx?nnxmn lll证明：x?nxx6．证明：??x??dt?ll xx?x?tt0；⑴?x???dt?p1ttxx?；⑵0???)(?p?p?txtxxx?t?x；⑶?????pp x?xxttt?t⑷。
??x??dt?l?l?ll?l?l??xx?x?t?t?xx0?xx证明：⑴0⑵．l1?1?1????x??x?x???t?x?1?pldt?)??(dl??1dll??x??x?tttxxx?tx?x llll000x?txxx；llDl?Dl?l???tx?tx?xxx?t??p()xt2lx?x?)l(xx DllDlDlDl xttxx?t?x?x?t??⑶)(??(?)?p??? txxx?t lllll xxxx?xt lDlDll??t?x?txx?tx?t????p?)????p(xtx?ttx llll?t?x。
⑷t?xxxx 给出的生命表计．分别在死亡均匀分布，死亡力恒定和鲍德希假设下，用课本附表17 算：?q q125140150⑴；⑵；⑶。
5342d98021.11625???q0??.00030575t1q??p??251t25x解：⑴1595650.44l?254略。
?17746l?7681l?40：，计算，8．若40414⑴死亡均匀分布假设；⑵鲍德希假设；l?1000100?x⑶假设x q40??0.008409068??11?t?q解：⑴；40404． ???1404???t e?p?xt l??41e?p?可令t?1,⑵q x???0.008444573x l40??0.?00842683411?(1?t)q40。
⑶x4q与n．证明在鲍德希规律下，无关。
9x n x?1x)??s(?s(x?n)?s(x?n?1)1证明：q??x n??xx)s(q x n与n所以，无关。
1某人10岁买了定期生存保险，这一保险使其从18岁到25岁每年得到2000元生存保险金，以附表2转换函数值计算这一年金现值。
N?N10?8?810?8?1?12000?a?2000?2000?0.22775?455.51088（元）解：N102．证明下列等式成立，并解释其含义。
??a?vpa xxx?1；⑴NN?D x?1xx????a???vpa?a?1xx?1xx DD证明：xx????a?vpa1?1xx?x；⑵．????avpa?1?1xx?x证aa?1?vp1xx?x所以，明：??????)E1??a?(a xn n:nxx:；⑶)?N?D(N?DN?ND nx?1?1x?nX?xx?1?x?n?1nX?)?a?(1?)?(1?Exn DDD nx:xxx NN?证明：nxx?a????D nx:x n aa?v?p?nxxx?n n；⑷NNN nn1??n?1nx?n?1?xx a?v?pa??E??v?p??xxnnxxnx?n n DDD xnxx?证明：E xn m ap?a?a?v?xm n:x:n?m:mx?mx；⑸证明：N?N x?n?m?x?11?a D m?x:nx N?N x?1m?1x??aD mx:x N?NN?N m1?m?1?n?1x1x?m?n??x?mx?m?p?a?v?E?xxmm DD nm:x?xx?m NN?N?NNN?m1n??xm?11x?m?n?1x?x?1?x?m1?xm??a?v?p?????aa???(1?i)ap?a1xx?x1?⑹xm DDD x?:xn?mmm:nx:xxxNp?Np?N xx1x?x1x????p?p?a???(1?i)ax?1xx?x1?1DE?Dv?p?D证明：x1?x1x1x?1x??1元的生存年金。
假设购k．某人在50岁时以50000元的趸缴净保费购买了每月给付3 值。