均值极差(标准差)控制图练习数据
极差、方差及标准差典型例题及习题(2)

典型例题例1计算下列一组数据的极差、方差及标准差(精确到0.01);50,55,96,98,65,100,70,90,85,100.解极差为100-50=50.平均数为.方差为:标准差为.于是,这组数据的极差、方差和标准差分别为50,334.69,18.29.例2若样本,,…,的平均数为10,方差为2,则对于样本,,…,,下列结论正确的是()(A)平均数为10,方差为2 (B)平均数为11,方差为3(C)平均数为11,方差为2 (D)平均数为12,方差为4解由已知条件,得故应选(C)说明此题充分应用了已知条件来进行整体计算,使运算十分简捷.例3 如图,公园里有两条石级路,哪条石级走起来更舒适?(图中数字表示每一级的高度,单位:厘米)解由于15+14+14+16+16+15=90,19+10+17+18+15+11=90,所以两条石级路总高度一样,都是90厘米;由于都是6个台阶,所以台阶的平均高度也一样,都15厘米.上台阶是否舒适,就看台阶的高低起伏情况如何,因此,需要计算两条石级路台阶高度的极差、方差和标准差.左边石级路台阶高度的极差为16-14=2,方差为:,标准差为;右边石级路台阶高度的极差为19-10=9,方差为:,标准差为.由以上计算可见,左边石级路的极差、方差和标准差都比右边小,所以左边石级路起伏小,走起来舒服些.例4要从甲、乙、丙三位射击运动员中选拔一名参加比赛,在预选赛中,他们每人各打10发子弹,命中的环数如下:甲:10 10 9 10 9 9 9 9 9 9 ;乙:10 10 10 9 10 8 8 10 10 8;丙:10 9 8 10 8 9 10 9 9 9 .根据这次成绩,应该选拔谁去参加比赛?分析本题着重考查对方差的意义及实际运用.解经计算,甲、乙、丙三人命中的总环数分别为93,93,91.所以丙应先遭淘汰.设甲、乙的命中环数分别为和,方差分别是和,则:.∵∴在总成绩相同的条件下,应选择水平发挥较稳定的运动员甲参加比赛.说明丙的总成绩显著,应先遭淘汰,然后利用方差的含义,来考查甲、乙二人成绩的稳定性.例5 小明和小华假期到工厂体验生活,加工直径为100毫米的零件,为了检验他们的产品的质量.从中各随机抽出6件进行测量,测得数据如下:(单位:毫米)小明:99 10 98 100 100 103小华:99 100 102 99 100 100(1)分别计算小明和小华这6件产品的极差、平均数与方差.(2)根据你的计算结果,说明他们两人谁加工的零件更符合要求.解(1)小明:极差=5,平均数=100,方差,小华:极差=3,平均数=100,方差=1.(2)计算结果说明,小明加工的零件极差大,方差也大,小华加工的零件极差小,方差小,所以小华加工的零件更符合要求。
均值极差控制图制作步骤

均值极差控制图制作步骤序号1 选择子组样本容量、频率和数量1.1子组容量: 原则:子组内的样本之间出现变差的机会要尽量小。
一般为4~5次(连续测量)1.2分组频率是指子组之间的间隔时间原则:要能反映出潜在的变化。
它与研究的目的有关,如想暴露短时间存在的问题,则组间的间隔要短。
反之可以加长。
可以每小时、每班、每周,视目的而异。
1.3 子组数量原则:收集数据的时间足够长、确保变差原因有机会出现。
一般25组或更多些,数量的增加可使置信度提高。
2 建立控制图及作好原始数据的记录(按所列序列号进行) 2.1 把原始数据记录在控制图原始数据记录栏内2.2计算和R 值式中:xi —子组容量中每个观测值 n ——子组容量个数 R=Xmax-Xmin式中:Xmax —子组容量中最大观测值; Xmin —子组容量中最小观测值。
2.3选择控制图的分度图:分度值max-分度值min≥2(子组max-子组min );R 图:分度值≥2(X 图的分度值) 2.4将和R 值对应描点画在控制图上3 标明控制图的用途—初始研究用或控制用4 计算控制限(按所列序列号进行) 4.1式中:k 为子组数量 4.24.3计算控制限 R 图控制限,图控制限 ,式中:A 、D 是系数,其中n 为子组内测量次数。
n23 4 5 6 7 8 9 10 A2 1.88 1.02 0.73 0.58 0.48 0.42 0.37 0.34 0.31 D3 —— —— —— —— —— 0.08 0.14 0.18 0.22 D4 3.27 2.57 2.28 2.11 2.00 1.92 1.86 1.82 1.785把控制限画在控制图上。
质量管理与质量控制论述题 题库

论述题1、某工件在生产过程中出现缺陷的项目及其频数如下表所示,根据表中的数据画出排列图,并指出影响通行质量的主要因素。
缺陷项目统计表项目断裂擦伤污染弯曲裂纹砂眼其他频数10 42 6 90 18 20 14解:由图表可知影响通行质量的主要因素(A类因素)是:弯曲、擦伤、砂眼2、某厂生产电路板元件,其中一关键电阻生产过程的计量数据如下:(抽样数据每五个为一组)0.5 0.8 1.0 1.6 0.9 ;0.4 0.7 1.0 1.1 0.8 ;0.7 1.3 1.0 0.6 1.5 ;0.9 0.8 0.9 1.3 1.1作X-R均值极差控制图,并判断过程是否处于稳定状态。
n4 0.729 2.266 0 2.2825 0.577 2.089 0 2.114解:由上述图表可知X =0.945,R =0.8 每组大小n=5由题目表中可知,n=5时,2A =0.577,4D =2.114 平均值X 控制图:CL=X =0.945UCL=X +2A R =0.945+0.8*0.577=1.4066 LCL=X -2A R =0.945-0.8*0.577=0.4834 R 控制图:CL=R =0.8UCL=4D R =2.114*0.8=1.6912 LCL=3D R (n ≤6,忽略)由上图可知,过程处于稳定状态。
3、某厂建筑型材QC小组,统计了某月生产线上的废品,其结果如下:磕伤78件,弯曲198件,裂纹252件,气泡30件,其他42件。
请画出排列图,并指明主要质量问题是什么?解:由图表可知,主要质量问题是裂痕、弯曲。
4、已知某问题的发生原因,作排列图问题原因累计频数原因1 106 106原因2 46 152原因3 18 170原因4 12 182原因5 10 192原因6 6 198原因7 2 200解:做法同第一题。
五计算与综述1、从大小N=5000的批中随机抽取n=20的样本,进行合格判定数为AC=2的一次抽样检验,试计算其不合格品率为5%的批的接受概率(已知0.9518=0.397,结果保留一位小数)。
均值-极差控制图(x-R)

X匀值:是通过每组样本的平均值得出的,然后把每组的平均值相加除以组数,得到总的平均值。
R 匀值:是通过每组两个极端值得到的,就是每组的最大值-最小值,等于每组的极差,再通过每组的极差值来计算总的极差平均值平均极差分布及控制图常数表2 用EXCEL软件绘均值一极差控制图(rR图)2.1 绘图方法2.1.1 EXCEL软件的作用随着计算机技术的不断发展,尤其是计算速度的不断加快,使其在办公领域得以充分应用.一些软件不但能制表,还能绘图,使质量管理工作也上了一个新水平。
近来,笔者尝试用EXCEL 绘均值一极差控制图( R 图),以使质量管理工作更方便、更快捷。
2.1.2 应用示例现以齿条总高为例,用EXCEL软件绘a—R 图.设共有25组数据,样本大小为5,其操作过程如下。
2.1.2.1 打开EXCEL软件中的一个工作薄,选择其中一个工作表.2.1.2.2 在第1行输入表头。
2.1_2.3 在第l列单元格输入样本编号:选定要填充的第1个单元格A2,输入1,A3格输入2,选择A2、A3格将鼠标移到A3格右下角的填充柄上,当鼠标指针变成小黑十字时,按鼠标左键在要填充的区域上拖动(即从A4到A26),松开鼠标左键,填充自动完成。
2.1.2.4 在第2列单元格输入标准值:选定单元格B2,输入2.8,将鼠标移到B2格右下角的填充柄上,当鼠标指针变成小黑十字时,按鼠标左键在B3到B26格上拖动,松开鼠标左键填充自动完成. 2.1.2.5 将收集到的数据输入表中。
2.1.2.6 计算均值:选定H2,选“常用”工具栏中的“粘贴函数"(即厂 ),出现“粘贴函数”对话框,在函数分类栏中选“常用函数”,在函数名栏中选“AV—ERAGE”,点“确定”,在“Number1"栏中输入“C2:G2”,点“确定”,即求得一个均值,选定H2格,点常用工具栏中的“复制”,再选定H3到H26,选“常用”工具栏中的“粘贴”,即求出其余24个均值. 2.1.2.7 计算极差的方法与计算均值大致相同,其公式为:R=max(B2:F2)~min(B2:F2)并将单元格的位置作相应变化。
(整理)均值极差控制图与均值标准差控制图的选用0411

-------------
------------- 均值极差控制图与均值标准差控制图的选用
时间:2014-4-11
关键词:均值极差控制图,均值标准差控制图
对计量值控制图,在确定选用均值标准差或者均值极差控制图时应考虑以下几个因素:
对每批数据计算极差要比计算标准偏差简单得多,因此使用均值极差控制图比使用均值标准差控制图简单方便。
这一优点在计算机和计算机未广泛采用之前,对控制图的推广使用有很大影响。
但是在计算机已很普及的今天,特别是使用控制图软件的情况下,这一优点就无关紧要了。
计算标准偏差时要使用一批样本中的每个数据,而极差只涉及一批样本中最大和最小两个数据,未能考虑该批中的其他数据信息,因此均值标准差控制图提供的信息比均值极差控制图更丰富。
通过分析可得,对不同的样本数据个数n,均值极差控制图与均值标准差控制图的相对效率之比如下表所示:
均值标准差控制图与均值极差控制图相对效率与样本量的关系总之,在每批样本数据量较小时,使用均值极差控制图或者均值标准差控制图差别不大。
如果每批样本量大于10,则应该使用均值标准差控制图,而不要使用均值极差控制图。
若每批样本只有一个数据,则应选用单值-移动极差控制图。
常规计量值控制图

1 均值-极差控制图
• 控制图对大波动灵敏,对小波动不灵敏
当n=4时
ARL=1 图对大波动监测效果显著,平均只需1个值就可以 发出失控信号。
而当θ=0.5σ时
ARL=44
对均值小漂移不敏感,平均需要44个值才能发 出失控信号。
1 均值-极差控制图
当过程稳态时,ARL值越大越好;说明控制图是稳 健的。 但过程已经发生异常波动,ARL值越小越好,说明 控制图是灵敏的
2 判稳判异准则
控制用控制图
控制用控制图由分析控制图转化而成,它用 于对生产过程进行连续监控。
按照确定的抽样间隔和样本大小抽取样本, 计算统计量数值并在控制图上描点,判断生产过 程是否异常。
控制用控制图在使用一般时间以后,应根据 实际情况对中心线和控制界限进行修改。
2 判稳判异准则
控制图判稳准则
4.1 均值-极差控制图
4.当R图受控时,认为过程的波动是稳定的,再分析 图,类似于对R图的分析,对任意失控情况及异常模式 分析原因。也可能要经过反复的“识别-纠正-重新计算 ”这一过程。
5.当两个图都显示稳定时,并且满足过程能力的要求, 可以用于实际的过程控制。一旦发现失控或出现异常模 式的信号时,应该及时分析原因,并采取行动。
9 80.69 80.49 82.16 84.29
10 81.72 81.12 80.77 80.60
11 80.98 81.33 81.60 80.70 12 80.42 82.20 80.13 80.24
13 81.11 81.13 82.22 81.17
14 82.40 81.41 82.93 83.13
21 81.06 82.06 82.76 82.46
22 82.55 83.53 82.94 81.89
均值 标准差X-s图-例题
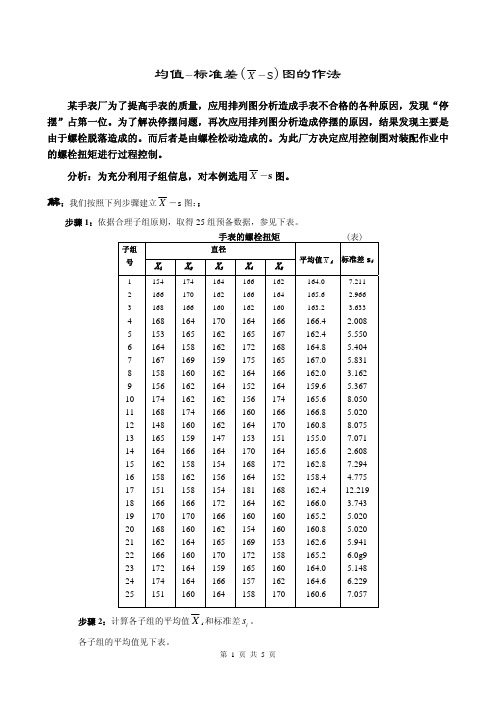
X3
164 162 160
X4
166 166 162
X5
162 164 160
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
168 153 164 167 158 156 174 168 148 165 164 162 158 151 166 170 168 162 166 172 174 151
x
j 1
5
ij
Xi
(6) (7) 164.0 165.6 163.2 166.4 162,4 164.8 167.0 162.0 159.6 165.6 166.8 160.8 155.0 165.6 162.8 158.4 162.4 166.0 165.2 160.8 162.6 165.2 164.0 164.6 160.6
第 2 页 共 5 页
25 个子组的标准差控制图 可见,5 图在第 17 点超出了上控制限,应查找异常的原因,采取措施加以纠正。为了简单起见,我们 将第 17 子组剔除掉。利用剩下的 24 个子组来重新计算 X - s 控制图的控制限。得到:
X =163.292; s =5.370;B4=2.089;B3=0,代人 s 图的控制限公式,得到:
ˆ
T TL 180 140 s 5.265 = = 5.601; Cp= U = =1.19 c4 0.940 6 6 5.601
由于 X =163.652 与容差中心 M=( TL+TU)/2=160 不重合,所以,有必要计算有偏移的过程能力指数, K=
ˆ 160 163.652 3.652 M = = = 0.18 T /2 (TU TL ) / 2 20
均值-标准差控制图

作图步骤: 作图步骤 组以上, (1)收集数据,收集近期生产数据(一般在 组以上,每组 个样本 )收集数据,收集近期生产数据(一般在25组以上 每组5个样本 (2)计算各组样本的平均值 与标准差 ) (3)计算 均值的均值与标准差的均值 ) (4)计算控制界限 ) (5)绘制控制图 ) (6)控制图的分析 ) 例:某轧钢厂生产的6±0.4(mm)厚度的钢板 ,绘制其控制图。 某轧钢厂生产的 ( 厚度的钢板 绘制其控制图。 解:(1)收集数据 组,每组 个样本。如下表。 个样本。 :( )收集数据20组 每组5个样本 如下表。
UCLs 0.3378 0.3378 0.3378 0.3378 0.3378 0.3378 0.3378 0.3378 0.3378 0.3378 0.3378 0.3378 0.3378 0.3378 0.3378
5.74733 5.74733 5.74733 5.74733 5.74733 5.74733 5.74733 5.74733 5.74733 5.74733
均值控制图 6.30 6.20 6.10 均值 6.00 5.90 5.80 5.70 1 11 组号
标准差控制图 0.40 0.35 0.30
21
31
0.30 0.25 0.20 0.15 0.10 0.05 0.00 1 6 11 16 组号 21 26 31
标准差n=5 A1Fra bibliotek B3:个样本) 个样本)
UCL LCLs CLs(标准差的均值) 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16 6.2088 0 0.16
