高考复习:三视图专题精编版
高考三视图(含解析)理试题汇总(精编文档).doc

【最新整理,下载后即可编辑】专题21 三视图1.某几何体的三视图如图所示,则其表面积为()A.2π B.3π C.4π D.5π【答案】B点睛:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.2.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )A.B.C.D.【答案】B【解析】由正视图和俯视图还原几何体如图所示,由正视图和俯视图对应线段可得2⊥平面时,BC=2,===,当BC ABDAB BD AD∆的边AB上的高为3,只有B选项符合,当BC不垂直平面ABD ABD时,没有符合条件的选项,故选B.点睛:1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.2.三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据3.某个长方体被一个平面所截,得到几何体的三视图如图所示,则这个几何体的体积为( )A . 4B . 22C .203 D . 8【答案】D4.如图,正三棱柱111ABC A B C 的主视图是边长为4的正方形,则此正三棱柱的左视图的面积为( )A . 16B . 23C . 43D . 83【答案】D点睛:三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合. (3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.5.某几何体的三视图如图所示,则该几何体的体积为 ( )(A) 168π+ (B) 88π+ (C) 1616π+(D) 816π+【答案】A【解析】将三视图还原为原来的几何体,再利用体积公式求解.原几何体为组合体;上面是长方体,下面是圆柱的一半(如图所示), 其体积为21422241682V ππ=⨯⨯+⨯⨯=+.故选A;6.如图5,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的几条棱中,最长的棱的长度为( )(A) 62 (B) 42 (C) 6 (D)4【答案】C【解析】如图所示点睛:对于小方格中的三视图,可以放到长方体,或者正方体里面去找到原图,这样比较好找;7.某几何体的三视图如图所示,则该几何体的表面积为( )A.24π-B.24π+C.20π-D.20π+【答案】A8.已知某空间几何体的三视图如图所示,则该几何体的表面积是()A.B.C.D.【答案】A【解析】由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,如图,平面,,,,,经计算,,,,∴,∴, ,,,∴,故选A .9.一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )A .1π+B .2π+C .21π+D .3522π++【答案】A【解析】考点:由三视图求体积.10.如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )A .263π+B .83π+ C .243π+ D .43π+ 【答案】C【解析】试题分析:相当于一个圆锥和一个长方体,故体积为122221433ππ⋅+⋅⋅=+.考点:三视图.11.一个几何体的三视图如图所示,则该几何体的体积为( )A . 143B . 5C . 163D .6【答案】A【解析】考点:三视图.12.一个几何体的三视图如图所示,则该几何体的体积为____.【答案】13【解析】本题考查三视图、四棱锥的体积计算等知识,难度中等.由三视图可知该几何体是底面为长和高均为1的平行四边形,高为1的四棱锥,故其体积为11111V=⨯⨯⨯=.33。
三视图(高三)

三视图(⾼三)三视图⼀、简单⼏何体型【知识点1.1】三视图还原⽅法(1)画长⽅体;(2)只画俯视图,交点处并画上圆圈,因为这些点同时竞争,竞争可能垂直上拉;(3)看正视图和侧视图,看他有没有直⾓;若有直⾓,直⾓点垂直上拉,若没有,什么都不动;若不能够往上拉的点直接划掉;能够拉点与下⾯的圆圈点直接连起来;这样就还原出来了。
【知识点1.2】空间⼏何体的表⾯积与体积⑴圆柱侧⾯积;l r S ??=π2侧⾯;⑵圆锥侧⾯积:l r S ??=π侧⾯;⑶圆台侧⾯积:l R l r S ??+??=ππ侧⾯⑷体积公式:h S V =柱体;h S V ?=31锥体;()h S S S S V 下下上上台体+?+=31⑸球的表⾯积和体积:32344R V R S ππ==球球,.【例1.1】(2012·北京⾼考⽂、理科·T7)某三棱锥的三视图如图所⽰,该三棱锥的表⾯积是()(A )28+(B )30+(C )56+(D )60+【解题指南】由三视图还原直观图,再求表⾯积.【解析】选B.直观图如图所⽰,底⾯是边长AC=5,BC=4的直⾓三⾓形,且过顶点P 向底⾯作垂线PH ,垂⾜在AC 上,AH=2,HC=3,侧(左)视图俯视图PH=4.145102ABC S ?==,154102PAC S ?=??=.因为PH ⊥⾯平ABC ⊥⾯,所以PH BC ⊥.⼜因为所以BC PC ⊥,所以145102PBC S ?==.在PAB ?中,PA PB AB ===PA 中点E ,连结BE ,则6BE =,所以162PAB S ?=?=因此三棱锥的表⾯积为10101030+++=+【变式1】(2013·⼴东⾼考⽂科·T6)某三棱锥的三视图如图所⽰,则该三棱锥的体积是()A .16 B .13 C .23D .1 【解题指南】本题考查空间想象能⼒,要能由三视图还原出⼏何体的形状. 【解析】选B. 由三视图判断底⾯为等腰直⾓三⾓形,三棱锥的⾼为2,则111=112=323V .【变式2】(2013·浙江⾼考⽂科·T5)已知某⼏何体的三视图(单位:cm)如图所⽰,则该⼏何体的体积是 ( )A.108cm 3B.100cm 3C.92cm 3D.84cm 3 【解题指南】根据⼏何体的三视图,还原成⼏何体,再求体积. 【解析】选B.由三视图可知原⼏何体如图所⽰,所以111111ABCD A B C D M A D N V V V --=-1166334410032=??-?=. 【变式3】(2013·浙江⾼考理科·T12)若某⼏何体的三视图(单位:cm )如图所⽰,则此⼏何体的体积等于 cm 3 .【解题指南】先由三视图,画出⼏何体,再根据⼏何体求解. 【解析】由三视图可知原⼏何体如图所⽰,所以111ABC A B C M ABC V V V --=-111153345343306243232ABC ABC S S =?-=-=-= . 【答案】24 【变式4】(2011·新课标全国⾼考理科·T6)在⼀个⼏何体的三视图中,正视图和俯视图如图所⽰,则相应的侧视图可以为()(A )(B )(C )(D )【思路点拨】由正视图和俯视图可联想到⼏何体的直观图,然后再推出侧视图.【精讲精析】选D. 由正视图和俯视图可以推测⼏何体为半圆锥和三棱锥的组合体(如图所⽰),且顶点BCA在底⾯的射影恰是底⾯半圆的圆⼼,可知侧视图为等腰三⾓形,且轮廓线为实线,故选D【变式5】(2014·四川⾼考⽂科·T4)某三棱锥的侧视图、俯视图如图所⽰,则该三棱锥的体积是()(锥体体积公式:13V Sh=,其中S 为底⾯⾯积,h 为⾼)A .3 B .2 C D .1【解题提⽰】由三视图得到该三棱锥的直观图是解决本题的关键.【解析】选D.根据所给的侧视图和俯视图,该三棱锥的直观图如下图所⽰.从俯视图可知,三棱锥的顶点A 在底⾯内的投影O 为边BD 的中点,所以AO 即为三棱锥的⾼,其体积为21213V ==.【变式6】(2014·湖南⾼考理科·T7)7.⼀块⽯材表⽰的⼏何何的三视图如图2所⽰,将该⽯材切削、打磨,加⼯成球,则能得到的最⼤球的半径等于 ( )A .1B .2C .3D .4【解题提⽰】先由三视图画出直观图,判断这个⼏何体是底⾯是边长为6,8,10的直⾓三⾓形,⾼为12的躺下的直三棱柱,底⾯的内切圆的半径就是做成的最⼤球的半径。
高考三视图复习

(3)已知图形中平行于x轴的线段,在直观图中保持原长度不 变;平行于y轴的线段,长度为原来的一半.
小结:“横同,竖半 ,平行性不变”
已知正△ABC 的边长为 a,那么正△ABC 的直观图△
A′B′C′的面积是( )
几何体
主视图
左视图
俯视图
空间想象力2
主视图 左视图
三视图
主视图 左视图
宽
宽
俯视图
俯视图
w老师提示:不见部分的轮廓线通常画成虚线.
w画三视图要认真准确,特别是宽相等.
画物体的三视图时,要符合如下原则:
A:大小:长对正(主视图与俯视图),高平 齐(主视图与左视图),宽相等(左视图与俯 视图).
3、 探照灯、手电筒、路灯和台灯 的光线可以看成是从一点出发的,
像这样的光线所形成的投影称为
中心投影(central projection).
两条光线是平行,因此 它们是太阳光下形成的.
两光线相交于一点,因 此它们是灯光下形成的.
一个物体在三个投影面内同时进行 正投影,
在正面得到的由前向后观察物体 的视图,叫做主视图;
A. 43a2
B. 83a2
C. 86a2
• [答案] D
D. 166a2
[解析] 如图(1)为 实际图形,建立 如图所示的平面 直角坐标系xOy.
小结 :
▪ 三视图
▪ 主视图——从正面看到的图
▪ 左视图——从左面看到的图
▪ 俯视图——从上面看到的图
▪ 画物体的三视图时,要符合如下原则:
▪ 位置: 主视图 左视图
在水平面内得到的由上向下观察物 体的视图,叫做俯视图 ;
高中数学立体几何三视图专题
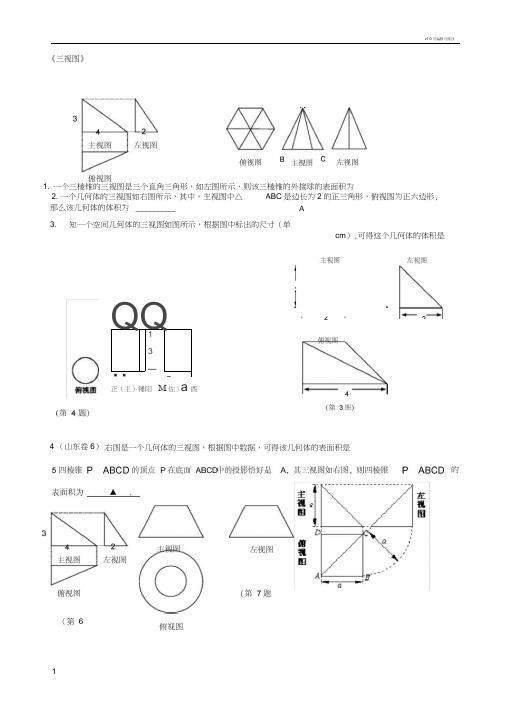
1 3—■ 一 ■r ----《三视图》1. 一个三棱锥的三视图是三个直角三角形,如左图所示,则该三棱锥的外接球的表面积为2. 一个几何体的三视图如右图所示,其中,主视图中△ABC 是边长为2的正三角形,俯视图为正六边形, 那么该几何体的体积为 __________ 3. 知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是A 正(主)锤阳M 佐)a酉QQ右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是4 (山东卷6) 的(第 6 题)俯视图6一个三棱锥的三视图是三个直角三角形,如图所示则该三棱锥的外接球的表面积为7 一个几何体的三视图如图所示,其中主视图、左视图均为上底为2,下底为4,腰为.5的等腰梯形,俯视图为一圆环,则该几何体的体积为____________ •8.(课本改编题,新增内容)右图为一个几何体的三视图,尺寸如图所示,则该几何体的体积为______ 9据图中尺寸(单位:cm),可知这个几何体的表面积是10图是一个空间几何体的三视图,其主视图、左视图均为正三角形,俯视图为圆,则该几何体的侧面积为▲.1.下列四个几何体中,每个几何体的三视图中有且仅有两个视图相同的是( )•(第 6 题)(第 7 题)A .①② •①③C.③④D .②④(第 8 题)2 一 r俯视图v1.0可编辑可修改7. 一个多面体的三视图分别为正方形、等腰三角形和矩形,如图所示,则该多面体的体积为 2.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是 3. 一个几何体的三视图如图所示 (主)视图和俯视图如图所示,则相应的侧 (左)视图可以为5.如图,直观图所示的原平面图形是(A.任意四边形等腰梯形6•将正三棱柱截去三个角(如图1所示A ,B ,C 分别是A GHI 三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为()4.在一个几何体的三视图中,正,则该几何体的直观图可以是 ()正(主)视图俯视图D.图1 图23 3 3A. 24 cm B . 48 cm C . 32 cm8.若正四棱锥的正(主)视图和俯视图如图所示,则该几何体的表面积是( ).10.已知某个几何体的三视图如上,根据图中标出的尺寸 (单位: cm ),可得这个几何体的体积是()A.4000cm 3 B. 8000 3cmC .2000cm 33D. 4000cm3311.如图,一个空间几何体的正视图、 侧视图都是面积为 二3,且一个内角为60;的菱形,俯视图为正方形,2那么这个几何体的表面积为( )A2.3B.4.3 C . 4D . 8A . 4B . 4 + 4 10 C8 D . 4+ 4 119.如下图是某几何体的三视图, 其中正(主)视图是腰长为2的等腰三角形,侧(左)视图是半径为1的半圆,则该几何体的体积是().nA .nB . . — C3.'3n 3D.正(主)视图慚左底图15. 一个五面体的三视图如下,正视图与侧视图是等腰直角三角形,俯视图为直角梯形,部分边长如图所示,则此五面体的体积为 第12题12. 一空间几何体的三视图如图所示,则该几何体的体积为A. 2 2 3B.4 23 C.D.13.如果一个几何体的三视图如图所示 (单位长度:cm ),则此几何体的表面积是A. (20 4」2)cm 2B.21 cmC.(24 4.2) cm 2D. 24 cm14. 若一个螺栓的底面是正六边形,它的正(主)视图和俯视图如图所示,则它的体积是B . 9 ;3 + 12nC . 27 .'3 + 3nD . 54 '3 + 3n第14题 第15题正丘)杷區俐n 團).A . 27 .'3+ 12 n 7正(主)视图俯视图1 12 1正初!图侧视團僻视图图为直角三角形,尺寸如图所示 ).(1)求四棱锥P - ABCD 勺体积;⑵若G 为BC 的中点,求证:AEL PG.4鮒左}视图第16题16.如图是一个几何体的三视图,若它的体积是 3 3,则a 17.设某几何体的三视图如下(尺寸的长度单位为m ) o 则该几何体的体积为18. 一块边长为10 cm 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作 侧面,以它们的公共顶点P 为顶点,加工成一个如图所示的正四棱锥容器,当是一个矩形,则这个矩形的面积是20. 如图是一个空间几何体的三视图, 若直角三角形的直角边长均为 1,则这个几何体的外接球的表面积为 21.如图,在四棱锥 P -ABCD^,底面为正方形,PC 与底面ABCDi 直,图为该四棱锥的主视图和左视图,(1)根据图所给的主视图、左视图,画出相应的俯视图,并求出该俯视图的面积;(2)求PA第17题x = 6 cm 时,该容器的容积19. 一个正三棱柱的侧棱长和底面边长相等,体积为2」:3,它的三视图中的俯视图如图所示,侧 (左)视图它们是腰长为6 cm 的全等的等腰直角三角形.22.下图是一个几何体的直观图及它的三视图 (其中正(主)视图为直角梯形,俯视图为正方形,侧第18题第19题 第20题侧视图 俯视图俯视图A俯观图5.。
高考三视图(含解析)理试题汇总

专题21 三视图1.某几何体的三视图如图所示,则其表面积为()A.2πB.3πC.4πD.5π【答案】B点睛:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.2.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )A .B .C .D .【答案】B【解析】由正视图和俯视图还原几何体如图所示,由正视图和俯视图对应线段可得2AB BD AD ===,当BC ABD ⊥平面时, BC=2, ABD ∆的边AB ,只有B 选项符合,当BC 不垂直平面ABD 时,没有符合条件的选项,故选B .点睛:1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图. 2.三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据 3.某个长方体被一个平面所截,得到几何体的三视图如图所示,则这个几何体的体积为( )A . 4B .C . 203D . 8 【答案】D4.如图,正三棱柱111ABC A B C 的主视图是边长为4的正方形,则此正三棱柱的左视图的面积为( )A . 16B .C .D . 【答案】D点睛:三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.5.某几何体的三视图如图所示,则该几何体的体积为 ( )(A) 168π+ (B) 88π+ (C) 1616π+ (D) 816π+ 【答案】A【解析】将三视图还原为原来的几何体,再利用体积公式求解.原几何体为组合体;上面是长方体,下面是圆柱的一半(如图所示), 其体积为21422241682V ππ=⨯⨯+⨯⨯=+.故选A; 6.如图5,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的几条棱中,最长的棱的长度为( )(A) (B) (C) 6 (D)4 【答案】C 【解析】如图所示点睛:对于小方格中的三视图,可以放到长方体,或者正方体里面去找到原图,这样比较好找;7.某几何体的三视图如图所示,则该几何体的表面积为( )A . 24π-B . 24π+C . 20π-D . 20π+ 【答案】A8.已知某空间几何体的三视图如图所示,则该几何体的表面积是( )A.B.C.D.【答案】A【解析】由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,如图,平面,,,,,经计算,,,,∴,∴,,,,∴,故选A.9.一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是()A .1π+B .2π+C .21π+D .35π++【答案】A 【解析】考点:由三视图求体积.10.如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )A .263π+B .83π+C .243π+ D .43π+【答案】C 【解析】试题分析:相当于一个圆锥和一个长方体,故体积为122221433ππ⋅+⋅⋅=+.考点:三视图.11.一个几何体的三视图如图所示,则该几何体的体积为()A.143B.5 C.163D.6【答案】A【解析】考点:三视图.12.一个几何体的三视图如图所示,则该几何体的体积为____.【答案】1 3【解析】本题考查三视图、四棱锥的体积计算等知识,难度中等.由三视图可知该几何体是底面为长和高均为1的平行四边形,高为1的四棱锥,故其体积为1111133V=⨯⨯⨯=.。
高考复习:三视图专题
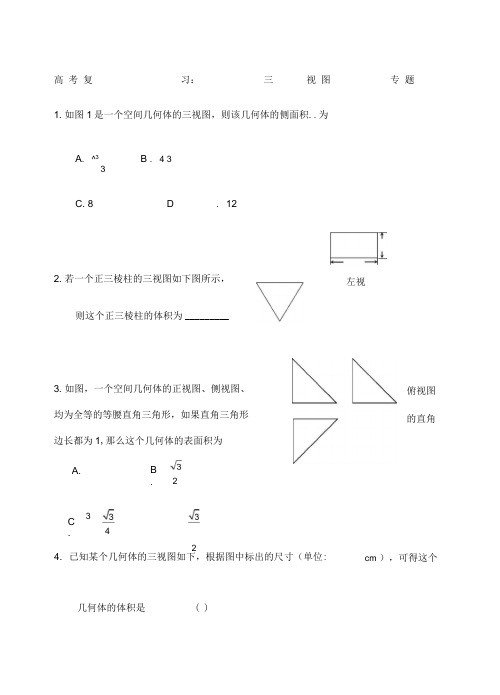
2几何体的体积是 ( )高 考 复 习: 三 视 图 专 题1. 如图1是一个空间几何体的三视图,则该几何体的侧面积..为A . ^3B . 4 33C. 8 D . 122. 若一个正三棱柱的三视图如下图所示,则这个正三棱柱的体积为 _________3. 如图,一个空间几何体的正视图、侧视图、 均为全等的等腰直角三角形,如果直角三角形 边长都为1,那么这个几何体的表面积为4. 已知某个几何体的三视图如下,根据图中标出的尺寸(单位:A.B .2C .34cm ),可得这个左视俯视图 的直角BD(寸 D A iCDBBl4、5 CA B D 2 2 54 5得 DC A B D视B iC i.MC 2A . 8cm 33 4 3 -cm 3 4AA . 4 cm 3B . 8 cm 3C . 2cm 3D . 4cm 333C i 截去两个角后所得的几何体,6.如图是一正方体被过棱的中点M N 和顶点A 、 9 .一个长方体被一个平面截去一部分后所剩几何体的正视图和俯则该几何体的主视图(或称正视图)为(称主视图)是2 3C•一 cm35.已知某几何体的三视图如右, 根据图中标出的尺 位:cm ),可得这个几何体的体积是(7 •如图,在三棱柱 ABC AiBC i 中,AAi 平面ABC ,BC 1,AB . 5,则此三棱柱的侧(左)视图的面积为8 .如图1,将一个正三棱柱截去一个三棱锥, 何体到几F FBC DEF ,则该几何体的正视图(或1 3 -cm 3,\:A如图所示,贝y 该几何体的侧视图可以为10 .一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( )A.1B.2C.3D.4部分,则截面的面积为A . - B4 9 C. 9D . 4412. 一个几何体的三视图如图所示,则该几何体的体积为13 .如图所示,一个空间几何体的主视图和俯视图都是边长为 1的正方形,侧视图是一个直径为1的圆,那么这个几何体的表面积为(A. 4A.B. C.Da 3C.a 312D.3a_ 1832B.C. 214 .已知某几何体的三视图如右图所示,则该几 体积是15. 一个简单几何体的正视图、侧视图如图所 视图不可能为①长方形;②正方形;③圆;④椭圆.其中正确A.①②B.②③A .-B16.3C. 1D.J2• 2示,则其俯C.③④D.①④16.如图,是一个几何体的正视图、侧视图、俯视图,A. 3B.且正视图、侧视图都是矩形,则该几何体的体积是 _________ 17. 一个空间几何体的三视图及部分数据如上图所示,则这个几何体的体积是( )聽视图 218.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是3 3 3 3A. 4 cm B . 5 cm C . 6 cm D . 7 cm19.如图为一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的全面积为A. 6 3 2 .3B. 2 2 4,2B.C. 8 5 2、3 D. 2 3 4 •、220 .如图是某几何体的三视图,其中正视图是腰长为等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是__________ .。
高考复习空间几何体三视图试题汇编(含答案)
空间几何体三视图题库一、单选题(共31题;共62分)1.甲、乙几何体的三视图分别如图•图 所示,分别记它们的表面积为S甲,S乙,体积为V甲,V乙,则()A. S甲>S乙, V甲>V乙B. S甲>S乙, V甲<V乙C. S甲<S乙, V甲>V乙D. S甲<S乙, V甲<V乙2.一个四棱锥的三视图如图所示,关于这个四棱锥,下列说法正确的是()A. 最长的棱长为√7B. 该四棱锥的体积为√3C. 侧面四个三角形都是直角三角形D. 侧面三角形中有且仅有一个等腰三角形3.某四棱锥的三视图如图所示,则该四棱锥的外接球半径为()A. 1B. √32C. √22D. 124.已知一个几何体的正视图和俯视图如图所示,正视图是边长为2a的正三角形, 俯视图是边长为a的正六边形,则该几何体侧视图的面积为()A. √3a2B. √32a2 C. 3 a2 D. 32a25.若某几何体的三视图如图所示,则此几何体的体积等于()A. 30B. 12C. 24D. 46.某几何体的三视图如图所示,则这个几何体的体积为()A. 4B. 203C. 263D. 87.已知一个几何体的三视图如图所示(单位:cm),那么这个几何体的表面积是( )A. (1+√2)cm2B. (3+√2)cm2C. (7+√2)cm2D. (8+√2)cm28.某三棱柱的三视图如图粗线所示,每个单元格的长度为1,则该三棱柱外接球的表面积为()A. 4πB. 8πC. 12πD. 16π9.某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的表面积为()A. (4+4√2)πB. (6+4√2)πC. (8+4√2)πD. (12+4√2)π10.某三棱锥的三视图如图所示,则该三棱锥最长的棱的棱长为()A. 2B. √5C. 2√2D. 311.某几何体的三视图如图所示(单位:cm)则该几何体的体积(单位:cm3)是()A. √212B. √26C. √23D. √212.已知某几何体的三视图如图所示,则该几何体的体积为( )A. 13+π4B. 1+π4C. 13+π12D. 1+π1213.某四面体的三视图如图所示,该四面体四个面的面积中最大的是( )A. 8B. 6√22C. 10D. 8√214.一个长方体被一个平面截去一部分后所剩几何体的三视图如图所示(单位:cm),则该几何体的体积为( )A. 120 cm3B. 100 cm3C. 80 cm3D. 60 cm315.(2017•北京卷)某三棱锥的三视图如图所示,则该三棱锥的体积为()A. 60B. 30C. 20D. 1016.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是()A. 4 √2B. 2 √5C. 6D. 4 √317.四棱锥P﹣ABCD的三视图如图所示,四棱锥P﹣ABCD的五个顶点都在一个球面上,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为2√2,则该球表面积为()A. 12πB. 24πC. 36πD. 48π18.祖冲之之子祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图如图所示,用一个与该几何体的下底面平行相距为h(0<h<2) 的平面截该几何体,则截面面积为()A. 4πB. πℎ2C. π(2−ℎ)2D. π(4-h²)19.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )A. 4B. 6+4√2C. 4+4√2D. 220.如图所示为一个简单几何体的三视图,则其对应的几何体是( )A. B. C. D. 21.一个几何体的三视图及尺寸如图所示,则该几何体的外接球半径为( )A. 12B. √316C. 174 D. √17422.一个几何体的三视图如图所示,则该几何体的体积(单位:cm 3)为( )A. π+√33B. 2π+√33C. 2π+√3D. π+√3 23.三视图如图的几何体是( )A. 三棱锥B. 四棱锥C. 四棱台D. 三棱台24.若一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )A. 1B. 2C. 3D. 425.某三棱锥的主视图与俯视图如图所示,则其左视图的面积为A. 2B. 3C. 4D. 626.把边长为的正方形ABCD 沿对角线BD 折起,形成的三棱锥A-BCD 的正视图与俯视图如图所示,则其侧视图的面积为( )A. √22B. 12C. √24D. 14 27.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的 ( )A. 外接球的半径为√33B. 表面积为√7+√3+1C. 体积为√3D. 外接球的表面积为4π 28.某几何体的三视图如图所示,则该几何体的体积为( )A. √2πB. 2√2πC. π3D. 2π329.一个几何体按比例绘制的三视图如图所示(单位:m ),则该几何体的体积为( )m 3 .A. 73B. 92C. 72D. 9430.某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( )A. 203B. 43C. 6D. 4 31.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的锲体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知1丈为10尺,该锲体的三视图如图所示,则该锲体的体积为( )A. 10000立方尺B. 11000立方尺C. 12000立方尺D. 13000立方尺二、填空题(共8题;共10分)32.如图为某几何体的三视图,则该几何体的体积为________.33.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是________.34.一个四棱锥的三视图如图所示,那么在这个四棱锥的四个侧面三角形中,有________个直角三角形.35.如图是由大小相同的长方体木块堆成的几何体的三视图,则此几何体共由________ 块木块堆成.36.已知某几何体的三视图如图所示(单位:cm),则此几何体的体积为________,表面积为________.37.一简单组合体的三视图如图,则该组合体的体积为________.38.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某三棱锥的三视图,则该三棱锥的体积为________.39.某几何体的三视图如图所示,若俯视图是边长为2的等边三角形,则这个几何体的体积等于________;表面积等于________.三、解答题(共3题;共20分)40.已知四棱锥P-ABCD的体积为√2,其三视图如图所示,其中正视图为等腰三角形,侧视图为直2角三角形,俯视图是直角梯形.(1)求正视图的面积;(2)求四棱锥P-ABCD的侧面积.41.一个空间几何体的三视图如图所示,其中正视图与左视图上方均为等边三角形,根据图中数据:(1)求三棱锥外接球表面积(2)求该几何体的表面积(3)求该几何体的体积.42.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,求这个多面体最长的一条棱的长.答案解析部分一、单选题1.【答案】B【考点】由三视图求面积、体积,由三视图还原实物图【解析】【解答】甲几何体是棱长为2a的下方体去掉一个棱长为a的小正方体后的几何体,则其体积V甲=8a3−a3=7a3,表面积S甲=24a2;乙几何体是一个棱长为2a的正方体去掉一个底面为直角边为a的等腰直角三角形,高为a的三棱柱后的几何体,其体积V乙=8a3−12a3=152a3,表面积S乙=24a2−a2+√2a2=(23+√2)a2;则S甲> S乙, V甲< V乙.故答案为:B.【分析】分别由三视图还原出几何体的形状和数据,甲是一个棱长为2a的正方体去掉一个棱长为a的小正方体后的几何体,求出表面积和体积;乙是一个棱长为2a的正方体去掉一个底面为直角边为a的等腰直角三角形,高为a的三棱柱后的几何体,求出表面积和体积,再比较大小.2.【答案】B【考点】由三视图还原实物图【解析】【解答】还原四棱锥,如图所示,由主视图可知,PA⊥底面ABCD, AB⊥AD, AD⊥DC, PA=2, AB=1, BC=CD=2, AD=√3, 计算可知B正确,故答案为:B.【分析】由三视图还原出四棱锥,P A ⊥底面ABCD,计算可知B正确.3.【答案】B【考点】球面距离及相关计算,由三视图还原实物图,球内接多面体【解析】【解答】由三视图可知,该四棱锥是底面为边长为1的正方形,一条长为1的侧棱与底面垂直,将该棱锥补成棱长为1的正方体,则棱锥的外接球就是正方体的外接球,正方体外接球的直径就是正方体的对角线,即2R=√3,R=√32,故答案为:B.【分析】结合三视图,将几何体还原为棱锥,将棱锥补成棱长为 1 的正方体,则棱锥的外接球就是正方体的外接球,由正方体外接球的直径就是正方体的对角线求解.4.【答案】D【考点】由三视图求面积、体积,由三视图还原实物图,棱柱、棱锥、棱台的体积【解析】【解答】由题图可知该几何体为正六棱锥,侧视图为等腰三角形,其中底边长为√3a,高与正视图的高相同,为√3a,所以面积为12×√3a×√3a=32a2.故答案为:D.【分析】结合三视图还原出几何体为正六棱锥,由公式求体积.5.【答案】C【考点】由三视图求面积、体积,由三视图还原实物图,棱柱、棱锥、棱台的体积【解析】【解答】由三视图可知,原几何体是一个三棱柱被截去了一个小三棱锥得到的,如图,V=1 2×3×4×5−13×(12×3×4)×3=24.故答案为:C.【分析】由三视图还出原几何体是一个三棱柱被截去了一个小三棱锥得到的,再由公式求体积.6.【答案】B【考点】由三视图求面积、体积,由三视图还原实物图,棱柱、棱锥、棱台的体积【解析】【解答】由三视图可得到几何体的直观图如图所示,该几何体是由一个四棱锥A-CDEF和一个三棱锥F-ABC组成,四棱锥A-CDEF的底面面积为4,高为4,所以体积是V=13×4×4=163;三棱锥F-ABC的底面积为2,高为2,故体积是43,所以该几何体的体积为203.故答案为:B.【分析】由三视图还出原几何体是由一个四棱锥A-CDEF和一个三棱锥F-ABC组成的,再由公式求体积. 7.【答案】C【考点】简单空间图形的三视图,由三视图还原实物图【解析】【解答】由题可知,三视图复原的几何体是一个放倒的底面是直角梯形的四棱柱,所以几何体的表面积S=(1+1+2+√2)×1+1×1+2×1=7+√2(cm2),故答案为:C.【分析】根据三视图将空间几何体还原后计算可得出答案。
三视图高考试题集锦
立体几何——三视图高考真题集锦1.〔14X 卷〕某空间几何体的正视图是三角形,则该几何体不可能是 〔 A 〕 A .圆柱 B.圆锥 C.四面体 D.三棱柱2.〔10年X 卷〕正视图是一个三角形的几何体可以是_______〔写出三种〕 3〔11X 卷〕右图是长和宽分别相等的两个矩形,给定以下三个命题: ①存在三棱柱,其正〔主〕视图、俯视图如右图; ②存在四棱柱,其正〔主〕视图、俯视图如右图;③存在圆柱,其正〔主〕视图、俯视图如右图。
其中真命题的个数是 (A) 3 (B) 2 (C) 1 (D) 0 4.(14X)7.某几何体三视图如下图,则该几何体的体积 为〔 〕A .82π- B .8π- C .82π-D .84π-5.〔12X 卷〕如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为〔 〕()A 6 ()B 9 ()C 12 ()D 186.〔14X 卷〕已知一个几何体的三视图如下图〔单位:m 〕,则该几何体的体积为____3m .〔第4题〕 〔第5题〕 〔第6题〕7.〔13X 卷〕一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分 别是〔1,0,1〕,〔1,1,0〕,〔0,1,1〕,〔0,0,0〕,画该四 面体三视图中的正视图时,以zOx 平面为投影面,则得到正视 图可以为〔 〕244242俯视图侧视图正视图俯视图正〔主〕视图(A) (B)(C)(D)8.〔14X 卷〕在如下图的空间直角坐标系xyz O 中,一个四面体的顶点坐标分别是〔0,0,2〕,〔2,2,0〕,〔1,2,1〕,〔2,2,2〕,给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为〔 〕A.①和②B.③和①C. ④和③D.④和②9.〔202X •X 〕某几何体的三视图〔单位:cm 〕如下图,则此几何体的外表积是〔 〕 A . 90cm 2 B . 129cm 2 C . 132cm 2 D . 138cm 2 10.〔07X 文理〕已知某个几何体的三视图如下图,依据图中标出的尺寸〔单位:cm 〕,可得这个几何体的体积是〔 〕A .334000cmB .338000cm C .202X 3cm D .40003cm〔第9题〕 〔第10题〕201010202020正视图侧视图俯视图11.〔07X 文理〕以下几何体各自的三视图中,有且仅有两个视图相同的是 〔 〕A .①②B .①③C .①④D .②④12.〔08X 理〕某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 的b 的线段,则b a +的最大值为〔 〕A .22B .32C .4D .5213.〔09X 文理〕一个棱锥的三视图如图,则该棱锥的全面积〔单位:2cm 〕为〔 〕A .21248+ B .22448+ C .21236+ D .22436+ 14.〔09X 文理〕一空间几何体的三视图如下图,则该几何体的体积为〔 〕 A .223π+ B .423π+ C .2323π+ D .2343π+〔第13题〕 〔第14题〕15.〔11X 文理〕在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为〔 〕15.〔10X 文理〕一个几个何体的三视图如图,该几何体的外表积为〔 〕A .280B .292C .360D .372 16.〔11X 文理〕如图是某几何体的三视图,则该几何体的体积为〔 〕A .9122π+B .9182π+ C .942π+ D .3618π+〔第15题〕 〔第16题〕 20.〔09X 文理〕设某几何体的三视图如下〔尺寸的长度单位为m 〕。
高考数学三视图汇编.doc
高考立体几何三视图1( 2017 全国卷二理数)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为A .90B.63C.42D.36【答案】 B【解析】该几何体可视为一个完整的圆柱减去一个高为 6 的圆柱的一半.2( 2017 北京文数)某三棱锥的三视图如图所示,则该三棱锥的体积为A 60B 30C 20D 10【答案】 D【解析】该几何体是如图所示的三棱锥P-ABC ,由图中数据可得该几何体的体积为V 115 3 4 10 3 23( 2017 北京理数)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为A 3 2B 2 3C 2 2D 2【答案】 B【解析】如下图所示,在四棱锥P ABCD 中,最长的棱为PA,所以 PA= PC2AC 222(2 2) 2 2 3 ,故选B.4( 2017 山东理数)由一个长方体和两个何体的三视图如图,则该几何体的体积为1圆柱构成的几4。
【答案】2+ 【解析】由三视图可知,长方体的长、宽、2高分别是2、 1、 1,圆柱的高为1,底面半径为1,所以V 2 1 1 2 121=2+4 25( 2017 全国卷一理数)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A .10B .12C.14 D .16【答案】 B【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成,如下图,则该几何体各面内只有两个相同的梯形,则这些梯形的面积之和为2(2 4) 2 112 ,故选 B. 26( 2017 浙江文数)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A. π+1 πB. +32 2C. 3 3π+1 D. +3 2 2【答案】 A 【解析】由三视图可知该几何体由一个三棱锥和半个圆锥组合而成,圆锥的体积为 V1 1 1 12 3 π,三棱锥的体积为 V2 112 13 1 ,2 3 2 3 2 2所以它的体积为V V1 V2π 1 2 27.( 2016 全国卷 1 文数)如图所示,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π,则它的表面积3是().A .17πB.18πC.20π D .28π【答案】 B 【解析】由三视图可知该几何体是7个球(如图所示),设球的半径为 R ,则8V 7 4π 3 28πS表7 2 3 28R 得 R=2 ,所以它的表面积是84π 2 +42 173 38.( 2016 全国卷 2 文数)右图是圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为().A.20πB.24C.28D.32【答案】 C【解析】由题意可知,圆柱的侧面积为S12π 2 4 16圆锥的侧面积为S212π 2 48 2圆柱的底面积为S3π 22 4该几何体的表面积为S S1+S2 +S3289.( 2016 全国卷 3 文数)如图所示,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为() .A. 18 36 5B. 54 18 5C. 90D. 81【答案】 B 【解析】(1)由题意知,几何体为平行六面体,边长分别为3,3,45,几何体的表面积S=3×6×2+3×3×2+ 3× 45×2= 54+ 18 5. 10.( 2016 北京文数)某四棱柱的三视图如图所示,则该四棱柱的体积为___________.【答案】3【解析】由已知中的三视图可知,该几何体是一个以俯视图为底面的四棱柱,2棱柱的底面积为 S 1(1+2) 1 3 棱柱的高为1,故体积为3 2 2 211.(2016 山东文数)一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为() .A . 1 2 πB . 1 2 π3 3 3 3C. 1 2 πD.1 2 π3 6 6 11 1正(主)视图侧(左)视图俯视图【答案】 C【解析】由题意可知,该几何体上部是一个半球,下部是一个四棱锥,半球的直径为棱锥的底面对角线,由棱锥底面棱长为1,可得2R 22,故 R2半球的体积为,2 23 2(g )=326棱锥的面积为1,高为 1,故体积为1故几何体的体积为1 +23 3 612.( 2016 天津文数3)将一个长方形沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为() .【答案】 B【解析】由正视图和俯视图可知该几何体的直观图如图所示,故该几何体的侧视图为选项 B.13( 2016 四川文数)已知某三棱锥的三视图如图所示,则该三棱锥的体积等于. 【答案】 C【解析】由题意可知,该几何体为三棱锥,底面为俯视图所示的三角形,底面积 S 13 1 3 ,高为 h1 1 32 1 棱锥的体积为VSh g 3g1=3 2 3 314.( 2016 浙江文数)某几何体的三视图如图所示(单位:cm),则该几何体的表2 3面积是 ______cm ,体积是 ______cm .【答案】 C 【解析】由题意可知,该几何体为长方体上面放置一个小的正方体,其表面积为 S 6 22 2 42 4 2 4 2 22 80其体积为 V 23 4 4 2 40。
高考三视图复习
第三十三页,共57页。
微专题 2:由三视图还原直观图
(1)(2018·福州质检)如图,网格纸上小正方形的边长为 1, 粗线画出的是某几何体的三视图,则此几何体的所有面中直角三 角形的个数是( )
A.2 C.4
B.3 D.5
第三十四页,共57页。
【解析】 由三视图知,可将该几何体还原在正方体中, 为如图所示的四棱锥P-ABCD,易知四棱锥P-ABCD的四个侧 面都是直角三角形,所以该几何体的所在面中直角三角形的个 数是4,故选C.
④“拼”:指的是将小几何体嵌入一个大几何体中,如有 时将一个三棱锥复原成一个三棱柱,将一个三棱柱复原成一个 四棱柱,还台为锥,这些都是拼补的方法.
第二十五页,共57页。
思考题1 (1)在正五棱柱中,不同在任何侧面且不同在
任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱
对角线的条数共有( )
A.20
第三十页,共57页。
思考题 2 (1)如图所示,下列四个几何体中,它们各自的 三视图(正视图、侧视图、俯视图)中有且仅有两个相同的是( )
A.①② C.②③ 【答案】 C
B.①③ D.①④
第三十一页,共57页。
(2)(2018·衡水调研卷)如图,在正方体 ABCD-A1B1C1D1 中, 点 P 是线段 A1C1 上的动点,则三棱锥 P-BCD 的俯视图与正视 图面积之比的最大值为( )
第四十页,共57页。
思考题 3 (1)(2017·温州模拟)若某几何体的三视图如图 所示,则此几何体的直观图是( )
【解析】 利用排除法求解.B 的侧视图不对,C 的俯视图
不对,D 的正视图不对,排除 B,C,D.A 正确,故选 A.
【答案】 A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考复习:三视图专题
精编版
MQS system office room 【MQS16H-TTMS2A-MQSS8Q8-MQSH16898】
N
M
A
B
C D
B 1
C 1
高
考复习:三视图专题
1.如图1是一个空间几何体的三视图,则该几何体的侧面积...
为 A .
43
B .43
C .8
D .12
2.若一个正三棱柱的三视图如下图所示,
则这个正三棱柱的体积为_______.
3.如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的直角边长都为
1,那么这个几何体的表面积为
A .6
1
B .2
3
C .3324+
D .33
22+
4.已知某个几何体的三视图如下,根据图中标出的尺寸
(单位:cm ),可得这个几何体的体积是() A .383
cm B .34
3cm
C .323cm
D .31
3
cm
5.已知某几何体的三视图如右,根据图中标出的尺寸(单位:
cm ),可得这个几何体的体积是( )
A .343cm
B .38
3
cm C .32cm D .34cm
6.如图是一正方体被过棱的中点M 、N 和顶点A 、D 、
1C 截去两
个角后所得的几何体,则该几何体的主视图(或称
正视图)
为()
7.如图,在三棱柱111ABC A B C -中,1AA ⊥平面ABC ,12,A A AC ==
1,5BC AB ==,则此三棱柱的侧(左)视图的面积为
A .2
B .4
C .
45
D .25 8.如图1,将一个正三棱柱截去一个三棱锥,得到几何体
主视图
俯视图
2
左视图
正视图 俯视图
正视图
俯视图
2
2
侧视图
2
1
1 2 第5题图
第7题
DEF BC -,则该几何体的正视图(或称主视图)是
A .
B .
C .
D .
9.一个长方体被一个平面截去一部分后所剩几何体的正视图和俯视图
如图所示,则该几何体的侧视图可以为
A .
B .
C .
D .
10.一个四棱锥的底面为正方形,其三视图如图所示,
则这个四棱锥的体积是() .2
11.一个圆锥的正(主)视图及其尺寸如图2所示.若一个平行于 圆锥底面的平面将此圆锥截成体积之比为1﹕7的上、下两 部分,则截面的面积为
A .1
4πB .π
C .94π
D .4π 12.一个几何体的三视图如图所示,则该几何体的体积为
32a 36a 312a 3
18
a 如图所示,一个空间几何体的主视图和俯视图都是边长为1的正方形,侧视图
是一个直径为1的圆,那么这个几何体的表面积为()
A .π4
B .π3
C .π2
D .π2
3
14.已知某几何体的三视图如右图所示,则该几何体
的体积是
A .16
B .13
C .1
2D 2
15.一个简单几何体的正视图、侧视图如图所示,则其俯视图
不可能为....
①长方形;②正方形;③圆;④椭圆.其中正确的
是
A .①②
B .②③
C .③④
D .①④
16.如图,是一个几何体的正视图、侧视图、俯视图,
且正视图、侧视图都是矩形,则该几何体的体积是.
17.一个空间几何体的三视图及部分数据如上图所示,则这个几何体的体积是( )
A .3
B .
C .2
D .
18.已知一个空间几何体的三视图如图所示,根据
图中标出的尺寸(单位:cm),可得这个几何体的体
4
6 图
1
1
1
主视图
侧视图
1
1
俯视图
积是
A.4 cm3B.5 cm3 C.6 cm3D.7 cm3
19.如图为一个几何体的三视图,正视图和侧视图均为
矩形,俯视图中曲线部分为半圆,尺寸如图,则该几
何体的全面积为
A.3
2
3
6+
+π B.2
4
2
2+
+π
B.C.3
2
5
8+
+π D.2
4
3
2+
+π
20.如图是某几何体的三视图,其中正视图是腰长为2的
等腰三角形,俯视图是半径为1的半圆,则该几何体
的体积是.正视
图
俯视
图侧视图。
