平行线与相交线经典例题汇总3
_第5章平行线与相交线 解答专项练习(三) 2020-2021学年七年级人教版下册

2020-2021学年七年级人教版下册第5章平行线与相交线总复习之解答专项练习(三)1.如图,AE平分∠BAC,∠CAE=∠CEA.(1)如图1,求证:AB∥CD;(2)如图2,点F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°;(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数.2.已知:如图,∠DAE=∠E,∠B=∠D.直线AD与BE平行吗?直线AB与DC平行吗?说明理由(请在下面的解答过程的空格内填空或在括号内填写理由).解:直线AD与BE平行,直线AB与DC.理由如下:∵∠DAE=∠E,(已知)∴∥,(内错角相等,两条直线平行)∴∠D=∠DCE.(两条直线平行,内错角相等)又∵∠B=∠D,(已知)∴∠B=,(等量代换)∴∥.(同位角相等,两条直线平行)3.已知点A在射线CE上,∠BDA=∠C.(1)如图1,若AC∥BD,求证:AD∥BC;(2)如图2,若BD⊥BC,请证明∠DAE+2∠C=90°;(3)如图3,在(2)的条件下,∠BAC=∠BAD,过点D作DF∥BC交射线CE于点F,当∠DFE=8∠DAE时,求∠BAD的度数.(直接写出结果)4.如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,(1)问直线EF与AB有怎样的位置关系?加以证明;(2)若∠CEF=70°,求∠ACB的度数.5.完成下列推理,并填写完理由.已知,如图,∠BAE+∠AED=180°,∠M=∠N,试说明:∠1=∠2.解:∵∠BAE+∠AED=180°(已知)∴∥()∴∠BAE=又∵∠M=∠N(已知)∴∥()∴∠NAE=()∴∠BAE﹣∠NAE=﹣()即∠1=∠26.如图,已知,AB∥PF,∠FPB=∠C,∠FED=30°,∠AGF=80°,FH平分∠EFG.(1)证明:AB∥CD;(2)求∠PFH的度数.7.已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.(1)如图1,求证:AB∥CD;(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.8.如图,已知在△ABC中,点D、E、F分别在边BC、AB、AC上,且DF∥AB,∠1=∠A,试说明DE∥AC的理由.解:因为DF∥AB(),所以∠1+=180°().因为∠1=∠A(已知),所以∠A+=180°().所以DE∥AC().9.如图,AC∥EF,∠1+∠3=180°.(1)AF与CD是否平行?请说明理由;(2)若AC平分∠FAB,AC⊥EB于点C,∠4=78°,求∠BCD的度数.10.已知BE平分∠ABD,DE平分∠BDC,且∠BED=∠ABE+∠EDC.(1)如图1,求证:AB∥CD;(2)如图2,若∠ABE=3∠ABF,且∠BFD=30°时,试求的值;(3)如图3,若H是直线CD上一动点(不与D重合),BI平分∠HBD,画出图形,并探究出∠EBI与∠BHD的数量关系.11.已知,如图①,点D,E,F,G是△ABC三边上的点,且FG∥AC,(1)若∠EDC=∠FGC,试判断DE与BC是否平行,并说明理由.(2)如图②,点M、N分别在边AC、BC上,且MN∥AB,连接GM,若∠A=60°,∠C=55°,∠FGM=4∠MGC,求∠GMN的度数.(3)点M、N分别在射线AC、BC上,且MN∥AB,连接GM.若∠A=α,∠ACB=β,∠FGM=n∠MGC,直接写出∠GMN的度数(用含α,β,n的代数式表示)12.如图,已知∠1+∠2=180°,∠3=∠B,(1)证明:EF∥AB.(2)试判断∠AED与∠C的大小关系,并说明你的理由.13.完成下列的推理说明.如图,已知直线EF分别交直线AB、CD与点M、N,AB∥CD,MG平分∠EMB,NH平分∠END.求证:MG∥NH.证明:∵AB∥CD(已知).∴∠EMB=∠END().∵MG平分∠EMB,NH平分∠END(已知).∴,().∴∠EMG=∠ENH().∴MG∥NH().14.已知:如图,∠1=∠2,∠B=∠C.(1)求证AB∥CD;(2)若∠A=30°,求∠D的度数.15.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.(1)如图1,求证:CF∥AB;(2)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;(3)如图3,在(2)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=7:13,BE平分∠ABG,求∠CBG的度数.参考答案1.(1)证明:∵AE平分∠BAC,∴∠BAE=∠CAE,∵∠CAE=∠CEA,∴∠CEA=∠BAE,∴AB∥CD;(2)证明:过F作FM∥AB,如图,∵AB∥CD,∴AB∥FM∥CD,∴∠BAF+∠AFM=180°,∠DEF+∠EFM=180°,∴∠BAF+∠AFM+∠DEF+∠EFM=360°,即∠BAF+∠AFE+∠DEF=360°;(3)解:设∠GEF=∠C=x°,∵∠GEF=∠C,∠GED=2∠GEF,∴∠GED=2x°,∵AB∥CD,∴∠C+∠BAC=180°,∴∠BAC=180°﹣x°,∵AE平分∠BAC,∴∠BAE=BAC=(180°﹣x°)=90°﹣x°,由(1)知:AB∥CD,∴∠BAE+∠AED=180°,∵∠AEF=35°,∴90﹣x+x﹣35+2x=180,解得:x=50,即∠C=50°.2.解:直线AD与BE平行,直线AB与DC平行.理由如下:∵∠DAE=∠E,(已知)∴AD∥BE,(内错角相等,两条直线平行)∴∠D=∠DCE.(两条直线平行,内错角相等)又∵∠B=∠D,(已知)∴∠B=∠DCE,(等量代换)∴AB∥DC.(同位角相等,两条直线平行)3.(1)证明:∵AC∥BD,∴∠DAE=∠BDA,∵∠BDA=∠C,∴∠DAE=∠C,∴AD∥BC;(2)证明:如图2,设CE与BD相交于点G,∠BGA=∠BDA+DAE,∵BD⊥BC,∴∠BGA+∠C=90°,∴∠BDA+∠DAE+∠C=90°,∵∠BDA=∠C,∴∠DAE+2∠C=90°;(3)如图3,设∠DAE=α,则∠DFE=8α,∵∠DFE+∠AFD=180°,∴∠AFD=180°﹣8α,∵DF∥BC,∴∠C=∠AFD=180°﹣8α,又∵2∠C+∠DAE=90°,∴2(180°﹣8α)+α=90°,∴α=18°,∴∠C=180°﹣8α=36°=∠ADB,又∵∠C=∠BDA,∠BAC=∠BAD,∴∠ABC=∠ABD=∠CBD=45°,△ABD中,∠BAD=180°﹣45°﹣36°=99°.答:∠BAD的度数是99°.4.解:(1)EF和AB的关系为平行关系.理由如下:∵CD∥AB,∠DCB=70°,∴∠DCB=∠ABC=70°,∵∠CBF=20°,∴∠ABF=∠ABC﹣∠CBF=50°,∵∠EFB=130°,∴∠ABF+∠EFB=50°+130°=180°,∴EF∥AB;(2)∵EF∥AB,CD∥AB,∴EF∥CD,∵∠CEF=70°,∴∠ECD=110°,∵∠DCB=70°,∴∠ACB=∠ECD﹣∠DCB,∴∠ACB=40°.5.解:∵∠BAE+∠AED=180°(已知),∴AB∥CD(同旁内角互补,两直线平行),∴∠BAE=∠AEC,又∵∠M=∠N(已知),∴AN∥EM(内错角相等,两直线平行),∴∠NAE=∠MEA(两直线平行,内错角相等),∴∠BAE﹣∠NAE=∠CEA﹣∠MEA(等量减等量,差相等),即∠1=∠2.故答案为:AB,CD,同旁内角互补,两直线平行;∠AEC;AN,EM,内错角相等,两直线平行;∠MEA,两直线平行,内错角相等;∠CEA,∠MEA,等量减等量,差相等.6.(1)证明:∵∠FPB=∠C,∴CD∥PF,∵AB∥PF,∴AB∥CD;(2)解:∵DC∥FP,∠FED=30°,∴∠FED=∠EFP=30°,∵AB∥FP,∠AGF=80°,∴∠AGF=∠GFP=80°,∴∠GFE=∠GFP+∠EFP=80°+30°=110°,∵FH平分∠EFG,∴∠GFH=∠GFE=55°,∴∠PFH=∠GFP﹣∠GFH=80°﹣55°=25°.7.(1)证明:∵EM∥FN,∴∠EFN=∠FEM.∵EM平分∠BEF,FN平分∠CFE,∴∠CFE=2∠EFN,∠BEF=2∠FEM.∴∠CFE=∠BEF.∴AB∥CD.(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:∵AB∥CD,∴∠AEF+∠CFE=180°,∵FN平分∠CFE,∴∠CFE=2∠CFN,∵∠AEF=2∠CFN,∴∠AEF=∠CFE=90°,∴∠CFN=∠EFN=45°,∴∠DFN=∠HFN=180°﹣45°=135°,同理:∠AEM=∠GEM=135°.∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.8.解:因为DF∥AB(已知),所以∠1+∠DEA=180°(两直线平行同旁内角互补).因为∠1=∠A(已知),所以∠A+∠DEA=180°(等量代换).所以DE∥AC(同旁内角互补两直线平行).故答案为:已知,∠DEA,两直线平行同旁内角互补,∠DEA,等量代换,同旁内角互补两直线平行.9.解:(1)AF∥CD,理由如下:∵AC∥EF,∴∠1+∠2=180°,又∵∠1+∠3=180°,∴∠2=∠3,∴FA∥CD;(2)∵AC平分∠FAB,∴∠2=∠CAD,∵∠2=∠3,∴∠CAD=∠3,∵∠4=∠3+∠CAD,∴∠3=∠4=×78°=39°,∵EF⊥BE,AC∥EF,∴AC⊥BE,∴∠ACB=90°,∴∠BCD=90°﹣∠3=51°.10.解:(1)如图1,延长BE交CD于点C,则∠BED=∠C+∠EDC.∵∠BED=∠ABE+∠EDC,∴∠ABE=∠C,∴AB∥CD;(2)由(1)可知,AB∥CD,∴∠ABD+∠BDC=180°,∵BE平分∠ABD,DE平分∠BDC,∴∠BED=(∠ABD+∠BDC)=90°,由∠ABE=3∠ABF,设∠ABF=α,则∠ABE=3α过F作FG平行于AB,如图2,则有∠ABF+∠CDF=∠F,∴∠CDF=30°﹣α过E作EH平行于AB,则有∠ABE+∠CDE=∠BED,∴∠CDE=90°﹣3α,∴∠FDE=60°﹣2α∴==;(3)当点H在点D的左侧时,如图3所示,∠BHD=2∠EBI.理由如下:∵AB∥CD∴∠ABH=∠BHD,∵BE平分∠ABD,BI平分∠HBD,∴∠ABE=∠EBD,∠HBI=∠IBD∵∠ABH=∠ABE+∠EBH=∠EBD+∠EBH=2(∠EBH+∠HBI),∴∠BHD=2∠EBI.当点H在点D的右侧时,如图4所示,∠EBI=90°﹣∠BHD.理由如下:∵AB∥CD∴∠GBH=∠BHD,∵BE平分∠ABD,BI平分∠HBD,∴∠ABE=∠EBD,∠HBI=∠IBD∵∠EBI=∠EBD+∠DBI=∠ABD+∠DBH=∠ABH=(180°﹣∠HBG)∴∠EBI=90°﹣∠BHD.11.解:(1)DE∥BC,理由如下:∵FG∥AC,∴∠FGB=∠C,∵∠EDC+∠ADE=180°,∠FGC+∠FGB=180°,∠EDC=∠FGC,∴∠ADE=∠FGB,∴∠ADE=∠C,∴DE∥BC;(2)∵∠A=60°,∠C=55°,∴∠B=180°﹣∠A﹣∠C=180°﹣60°﹣55°=65°,∵FG∥AC,∴∠FGB=∠C=55°,∵∠FGM=4∠MGC,∴∠FGM+∠MGC+∠FGB=5∠MGC+55°=180°,∴∠MGN=25°,∵MN∥AB,∴∠MNC=∠B=65°,∠MNC=∠MGN+∠GMN,∴∠GMN=∠MNC﹣∠MGN=65°﹣25°=40°;(3)①如图②所示:∵∠A=α,∠ACB=β,∴∠B=180°﹣∠A﹣∠ACB=180°﹣α﹣β,∵FG∥AC,∴∠FGB=∠C=β,∵∠FGM=n∠MGC,∴∠FGM+∠MGC+∠FGB=(n+1)∠MGC+β=180°,∴∠MGN=,∵MN∥AB,∴∠MNC=∠B=180°﹣α﹣β,∠MNC=∠MGN+∠GMN,∴∠GMN=∠MNC﹣∠MGN=180°﹣α﹣β﹣=(180°﹣β)﹣α.②如图③所示:设∠MGN=x,则∠GMN=∠GMA+∠NMC=α+180°﹣nx,∵(n﹣1)x+β=180°,∴x=,∴∠GMN=α+180°﹣nx=α+180°﹣n=α+.12.解:(1)∵∠1+∠DFE=180°(平角定义),∠1+∠2=180°(已知),∴∠2=∠DFE,∴EF∥AB(内错角相等,两直线平行);(2)∠AED与∠C相等.∵EF∥AB,∴∠3=∠ADE(两直线平行,内错角相等),∵∠3=∠B(已知),∴∠B=∠ADE(等量代换),∴DE∥BC(同位角相等,两直线平行),∴∠AED=∠C(两直线平行,同位角相等).13.证明:∵AB∥CD(已知)∴∠EMB=∠END(两直线平行,同位角相等)∵MG平分∠EMB,NH平分∠END(已知),∴∠EMG=∠EMB,∠ENH=∠END(角平分线的定义),∴∠EMG=∠ENH(等量代换)∴MG∥NH(同位角相等,两直线平行).故答案为:两直线平行,同位角相等;∠EMG=∠EMB,∠ENH=∠END;角平分线的定义;等量代换;同位角相等,两直线平行.14.解:(1)∵∠1=∠2,∠1=∠FMN,∴∠2=∠FMN,∴CF∥BE,∴∠C=∠BED.又∵∠B=∠C,∴∠B=∠BED,∴AB∥CD.(2)∵AB∥CD,∴∠A=∠D.又∵∠A=30°,∴∠D=30°.15.(1)证明:∵DE∥BC,∴∠ADE=∠B,∵∠BCF+∠ADE=180°.∴∠BCF+∠B=180°.∴CF∥AB;(2)解:如图2,过点E作EK∥AB,∴∠BEK=∠ABE=40°,∵CF∥AB,∴CF∥EK,∴∠CEK=∠ACF=60°,∴∠BEC=∠BEK+∠CEK=40°+60°=100°;(3)∵BE平分∠ABG,∴∠EBG=∠ABE=40°,∵∠EBC:∠ECB=7:13,∴设∠EBC=7x°,则∠ECB=13x°,∵DE∥BC,∴∠DEB=∠EBC=7x°,∠AED=∠ECB=13x°,∵∠AED+∠DEB+∠BEC=180°,∴13x+7x+100=180,解得x=4,∴∠EBC=7x°=28°,∵∠EBG=∠EBC+∠CBG,∴∠CBG=∠EBG﹣∠EBC=40°﹣28°=12°.。
专题 相交线与平行线章末重难点题型(举一反三)(北师大版)
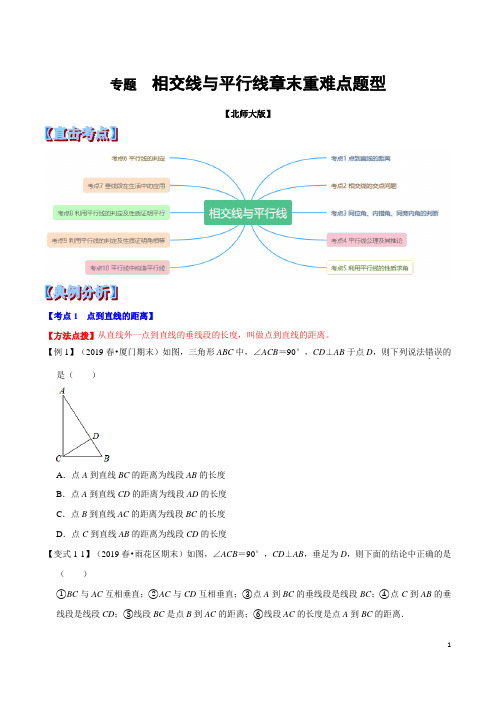
专题相交线与平行线章末重难点题型【北师大版】【考点1 点到直线的距离】【方法点拨】从直线外一点到直线的垂线段的长度,叫做点到直线的距离。
【例1】(2019春•厦门期末)如图,三角形ABC中,∠ACB=90°,CD⊥AB于点D,则下列说法错误..的是()A.点A到直线BC的距离为线段AB的长度B.点A到直线CD的距离为线段AD的长度C.点B到直线AC的距离为线段BC的长度D.点C到直线AB的距离为线段CD的长度【变式1-1】(2019春•雨花区期末)如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是()①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;④点C到AB的垂线段是线段CD;⑤线段BC是点B到AC的距离;⑥线段AC的长度是点A到BC的距离.A .①④③⑥B .①④⑥C .②③D .①④【变式1-2】(2019春•娄星区期末)如图所示,点A 到BC 所在的直线的距离是指图中线段( )的长度.A .ACB .AFC .BD D .CE【变式1-3】(2019春•天河区校级月考)如图,AC ⊥BC ,CD ⊥AB ,下列结论中,正确的结论有( ) ①线段CD 的长度是C 点到AB 的距离;②线段AC 是A 点到BC 的距离;③AB >AC >CD ;④线段BC 是B 到AC 的距离;⑤CD <BC <AB .A .2个B .3个C .4个D .5个【考点2 相交线的交点问题】【方法点拨】3条直线相交最多有3个交点,4条直线相交最多有6个交点,5条直线相交最多有10个交点,n 条直线相交,最多有1+2+3+…+(n ﹣1)=21n (n ﹣1)个交点. 【例2】(2019秋•旌阳区校级月考)在同一平面内的n 条直线两两相交,最多共有36个交点,则n =( )A .7B .8C .9D .10【变式2-1】(2019秋•鄄城县期末)两条直线最多有一个交点,三条直线最多有三个交点,四条直线最多有6个交点,……,那么7条直线最多( )A .28个交点B .24个交点C .21个交点D .15个交点【变式2-2】(2019春•沙坪坝区校级月考)同一平面内两两相交的四条直线,最多有m 个交点,最少有n 个交点,那么m n 是( )A.1B.6C.8D.4【变式2-3】(2019秋•江阴市校级月考)观察下列图形,并阅读图形下面的相关文字,如图所示:两条直线相交,最多有一个交点;三条直线相交,最多有三个交点;四条直线相交,最多有6个交点,像这样,11条直线相交,最多交点的个数是()A.40个B.50个C.55个D.66个【考点3 同位角、内错角、同旁内角的判断】【方法点拨】直线AB,CD被第三条直线EF所截。
相交与平行线经典例题

相交与平行线经典例题
1. 有一条直线L和一条平行于L的线段AB,AB的长度为
5cm。
现在在L上选取一点C,再选取一个点D,并且D是
AC的中点。
求CD的长度。
解法:由题意可知,CD平行于AB,且AC=2CD。
根据比例
关系,我们可以得到:AC/CD = AB/BD。
由于AC=2CD,
AB=5cm,所以2CD/CD = 5/BD,简化得到2=5/BD。
解方程
得到BD=5/2=2.5cm。
所以CD=AC/2=2.5/2=1.25cm。
2. 在平面上有两条直线L1和L2,L1与L2的交点为A。
由A
分别向两条直线做垂线,分别与两条直线交于B和C。
已知
AB=6cm,AC=8cm。
求BC的长度。
解法:由题意可知,AB垂直于L1,AC垂直于L2。
所以
ABC是直角三角形。
根据勾股定理,得到BC的长度:BC^2
= AB^2 + AC^2 = 6^2 + 8^2 = 36 + 64 = 100。
所以BC = 10cm。
3. 平面上有两条平行线L1和L2,L1上有一点P,分别向L1
和L2做两条垂线PA和PB,交于A和B。
已知AP=5cm,
PB=8cm。
求AB的长度。
解法:由题意可知,PA垂直于L1,PB垂直于L2。
所以PAB
是直角三角形。
根据勾股定理,得到AB的长度:AB^2 =
AP^2 + PB^2 = 5^2 + 8^2 = 25 + 64 = 89。
所以AB = √89 cm。
(专题精选)初中数学相交线与平行线难题汇编附答案解析

(专题精选)初中数学相交线与平行线难题汇编附答案解析一、选择题1.如图所示,某同学的家在P处,他想尽快赶到附近公路边搭公交车,他选择P→C路线,用几何知识解释其道理正确的是()A.两点确定一条直线B.垂直线段最短C.两点之间线段最短D.三角形两边之和大于第三边【答案】B【解析】【分析】根据垂线段的定义判断即可.【详解】解:直线外一点与直线上各点连接的所有线段中,垂线段最短,选:B.【点睛】直线外任意一点到这条直线的垂线段的长度,叫做点到这条直线的距离.直线外一点与直线上各点连接的所有线段中,垂线段最短.简称“垂线段最短”.2.如图,若AB∥CD,则∠α、∠β、∠γ之间关系是()A.∠α+∠β+∠γ=180°B.∠α+∠β﹣∠γ=360°C.∠α﹣∠β+∠γ=180°D.∠α+∠β﹣∠γ=180°【答案】D【解析】试题解析:如图,作EF∥AB,∵AB∥CD,∴EF∥CD,∴∠α+∠AEF=180°,∵EF ∥CD ,∴∠γ=∠DEF ,而∠AEF+∠DEF=∠β,∴∠α+∠β=180°+∠γ,即∠α+∠β-∠γ=180°.故选:D .3.如图,下列能判定AB ∥CD 的条件有几个( )(1)12∠=∠ (2)34∠=∠(3)5B ∠=∠ (4)180B BCD ∠+∠=︒.A .4B .3C .2D .1【答案】B【解析】【分析】 根据平行线的判定逐一判定即可.【详解】因为12∠=∠,所有AD ∥BC ,故(1)错误.因为34∠=∠,所以AB ∥CD ,故(2)正确.因为5B ∠=∠,所以AB ∥CD ,故(3)正确.因为180B BCD ∠+∠=︒,所以AB ∥CD ,故(4)正确.所以共有3个正确条件.故选B【点睛】本题考查的是平行线的判定,找准两个角是哪两条直线被哪条直线所截形成的同位角、同旁内角、内错角是关键.4.如图,已知AB ∥DC ,BF 平分∠ABE ,且BF ∥DE ,则∠ABE 与∠CDE 的关系是( )A .∠ABE =2∠CDEB .∠ABE =3∠CDEC .∠ABE =∠CDE +90°D .∠ABE +∠CDE =180°【解析】【分析】延长BF与CD相交于M,根据两直线平行,同位角相等可得∠M=∠CDE,再根据两直线平行,内错角相等可得∠M=∠ABF,从而求出∠CDE=∠ABF,再根据角平分线的定义解答.【详解】解:延长BF与CD相交于M,∵BF∥DE,∴∠M=∠CDE,∵AB∥CD,∴∠M=∠ABF,∴∠CDE=∠ABF,∵BF平分∠ABE,∴∠ABE=2∠ABF,∴∠ABE=2∠CDE.故选:A.【点睛】本题考查了平行线的性质和角平分线的定义,作辅助线,是利用平行线的性质的关键,也是本题的难点.5.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=()A.65°B.115°C.125°D.130°【答案】B【解析】试题分析:∵AB∥CD,∴∠C+∠CAB=180°,∵∠C=50°,∴∠CAB=180°﹣50°=130°,∵AE 平分∠CAB,∴∠EAB=65°,∵AB∥CD,∴∠EAB+∠AED=180°,∴∠AED=180°﹣65°=115°,故选B.考点:平行线的性质.6.如图,AB CD ∥,BF 平分ABE ∠,且BF DE ,则ABE ∠与D ∠的关系是( )A .2ABE D ∠=∠B .180ABE D ∠+∠=︒C .90ABED ∠=∠=︒D .3ABE D ∠=∠【答案】A【解析】【分析】 延长DE 交AB 的延长线于G ,根据两直线平行,内错角相等可得D G ∠=∠,再根据两直线平行,同位角相等可得G ABF ∠=∠,然后根据角平分线的定义解答.【详解】证明:如图,延长DE 交AB 的延长线于G ,//AB CD ,D G ∴∠=∠,//BF DE ,G ABF ∴∠=∠,D ABF ∴∠=∠, BF 平分ABE ∠,22ABE ABF D ∴∠=∠=∠,即2ABE D ∠=∠.故选:A .【点睛】本题考查了平行线的性质,角平分线的定义,熟记性质并作辅助线是解题的关键.7.如图所示,b ∥c ,a ⊥b ,∠1=130°,则∠2=( ).A .30°B .40°C .50°D .60°【答案】B【解析】【分析】 证明∠3=90°,利用三角形的外角的性质求出∠4即可解决问题.【详解】如图,反向延长射线a 交c 于点M ,∵b ∥c ,a ⊥b ,∴a ⊥c ,∴∠3=90°,∵∠1=90°+∠4,∴130°=90°+∠4,∴∠4=40°,∴∠2=∠4=40°,故选B .【点睛】本题考查平行线的性质,垂线的性质,三角形的外角的性质等知识,解题的关键是熟练掌握基本知识8.如图,□ABCD 的对角线AC ,BD 相交于点O(AD>AB).下列说法:①AB=CD;②AOB AOD S S ∆∆=;③∠ABD=∠CBD;④对边AB,CD 之间的距离相等且等于BC 的长。
相交线与平行线典型例题

解:∵ EF与AB相交,∠1+∠2=180°,
∠2+∠3= 180°, ∴∠2的补角有∠1和∠3; E
12
4
∵ CD与MN相交,∠5+∠8=180°,
3
∠5+∠6=180 °且∠2=∠5,
∴∠2的补角有∠6和∠8; ∴∠2的补角有∠1、∠3、∠6和∠8.
58 67
如图,直线AB,CD,EF相交于点O. (1)写出∠AOC, ∠BOE的邻补角; (2)写出∠DOA, ∠EOC的对 顶角; (3)如果∠AOC =50°,求∠BOD ,∠COB的度数.
=90°+55°=145°.
如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,
若∠EON=20°,求∠AOM和∠NOC的度数.
解:∵∠BOE=∠NOE,∴∠BON=2∠EON=40°, ∴∠NOC=180°-∠BON =180°-40°=140°,
∠MOC=∠BON=40°. ∵AO⊥BC,∴∠AOC=90°, ∴∠AOM=∠AOC-∠MOC=90°-40°=50°, ∴∠NOC=140°,∠AOM=50°.
E
C
F
56°
B O
∴ ∠AOE=∠BOF=34°(对顶角相等) . D
如图,直线AB、CD相交于点O,OE⊥AB, ∠1=55°,求
∠EOD的度数.
CE
解: ∵ AB⊥OE (已知),
A 1(
O
B
∴ ∠EOB=90° (垂直的定义).
∵ ∠BOD =∠1=55° (对顶角相等), D
∴ ∠EOD =∠EOB +∠BOD
C
解:如图所示: F
A
B
相交线平行线经典例题

相交线平行线经典例题英文回答:Parallel Lines and Intersecting Lines.Parallel lines are lines that never intersect, no matter how far they are extended. Intersecting lines are lines that cross each other at a single point.There are a few different ways to determine if two lines are parallel or intersecting. One way is to look at the slopes of the lines. If the slopes of the lines are equal, then the lines are parallel. If the slopes of the lines are not equal, then the lines are intersecting.Another way to determine if two lines are parallel or intersecting is to look at the intercepts of the lines. If the intercepts of the lines are equal, then the lines are parallel. If the intercepts of the lines are not equal, then the lines are intersecting.Example 1。
Determine if the lines y = 2x + 1 and y = 2x 3 are parallel or intersecting.Slopes: The slope of both lines is 2.Intercepts: The intercept of the first line is 1. The intercept of the second line is -3.Since the slopes of the lines are equal, the lines are parallel.Example 2。
平行线与相交线经典例题汇总3
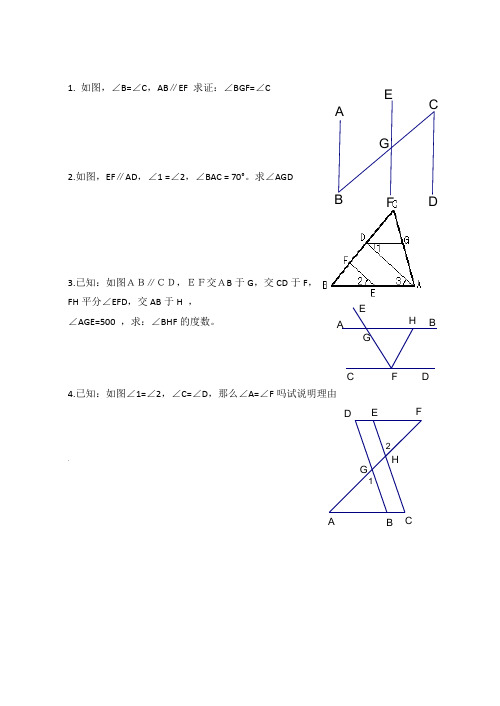
1. 如图,∠B=∠C ,AB ∥EF 求证:∠BGF=∠C2.如图,EF ∥AD ,∠1 =∠2,∠BAC = 70°。
求∠AGD-3.已知:如图AB∥CD,EF交AB 于G ,交CD 于F ,FH 平分∠EFD ,交AB 于H , ∠AGE=500 ,求:∠BHF 的度数。
4.已知:如图∠1=∠2,∠C=∠D ,那么∠A=∠F 吗试说明理由'HGF E D C BAHG21FEDCBAGFEDCBA5.已知:如图,AB E F AB CD 1D ∠=∠2∠C ∠EC AF ⊥O //AB CD //AC BD //AB CDE ∠=∠1F ∠=∠2AE CF O CF AE ⊥&8.如图13,AEB NFP ∠=∠,M C ∠=∠,判断A ∠与P ∠的大小关系,并说明理由.)9.如图14,AD 是CAB ∠的角平分线,//DE AB ,//DF AC ,EF 交AD 于点O . 请问:(1)DO 是EDF ∠的角平分线吗如果是,请给予证明;如果不是,请说明理由.F E M PCN 1图123O BCDE(2)若将结论与AD 是CAB 的角平分线、//DE AB 、//DF AC 中的任一条件 `交换,•所得命题正确吗《10.如图,AD 是∠EAC 的平分线,AD ∥BC ,∠B = 30°, 你能算出∠EAD 、∠DAC 、∠C 的度数吗11. 如图, ∠1=∠2 , ∠3=1050, 求 ∠4的度数。
|12.如图,EF ∥AD ,∠1 =∠2,∠BAC = 70°。
将求∠AGD 的过程填写完整。
因为EF ∥AD ,所以 ∠2 = 。
又因为 ∠1 = ∠2,所以 ∠1 = ∠3。
所以AB ∥ 。
所以∠BAC + = 180°。
又因为∠BAC = 70°,图14d c 31.ab24AD …BCEF1 23 4所以∠AGD = 。
平行线与相交线常见题型

相交线与平行线一.选择题(共12小题)1.如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=()A.56°B.66°C.24°D.34°2.如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为()A.80°B.90°C.100° D.102°3.如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为()A.35°B.45°C.50°D.55°4.如图,△ABC的面积为2,将△ABC沿AC方向平移至△DFE,且AC=CD,则四边形AEFB的面积为()A.6 B.8 C.10 D.125.如图,点D、E、F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件()A.∠1=∠2 B.∠1=∠DFE C.∠1=∠AFD D.∠2=∠AFD6.如图,与∠1是同旁内角的是()A.∠2 B.∠3 C.∠4 D.∠57.如图,在下列条件中,不能判定直线a与b平行的是()A.∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4=180°8.如图,直线a、b被直线c所截,下列条件能使a∥b的是()A.∠1=∠6 B.∠2=∠6 C.∠1=∠3 D.∠5=∠79.如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为()A.85°B.70°C.75°D.60°10.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=()A.65°B.115° C.125° D.130°11.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为()A.65°B.55°C.45°D.35°12.如图,直线a∥b,∠1=85°,∠2=35°,则∠3=()A.85°B.60°C.50°D.35°二.填空题(共12小题)13.如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是.14.如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BFA=34°,则∠DAE= 度.15.如图,m∥n,直角三角板ABC的直角顶点C在两直线之间,两直角边与两直线相交所形成的锐角分别为α、β,则α+β=.16.如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=,CD=,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为,则满足条件的点P有个.17.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是.18.如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2= .19.如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2= .20.如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是.21.如图,直线a∥b,直线c与直线a、b分别相交于A、B两点,若∠1=60°,则∠2= .22.如图,AB∥CD,直线EF分别交AB、CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于度.23.如图,△ABC中,BC=5cm,将△ABC沿BC方向平移至△A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则△ABC平移的距离为cm.24.如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°,∠D=120°,则∠C的度数为度.三.解答题(共16小题)25.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.26.如图,已知AC∥ED,AB∥FD,∠A=65°,求:∠EDF的度数.27.如图,已知AB∥CD,若∠C=40°,∠E=20°,求∠A的度数.28.如图,在△ABC中,∠B+∠C=110°,AD平分∠BAC,交BC于点D,DE∥AB,交AC于点E,求∠ADE的度数.29.如图,直线a∥b,BC平分∠ABD,DE⊥BC,若∠1=70°,求∠2的度数.30.如图,E为AC上一点,EF∥AB交AF于点F,且AE=EF.求证:∠BAC=2∠1.31.如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=76°,∠DOF=90°,求∠EOF的度数.32.如图,直线AB,CD相交于O点,OM⊥AB于O.(1)若∠1=∠2,求∠NOD;(2)若∠BOC=4∠1,求∠AOC与∠MOD.33.如图,两直线AB、CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11.(1)求∠COE的度数.(2)若射线OF⊥OE,请在图中画出OF,并求∠COF的度数.34.如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.35.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):(1)①若∠DCE=45°,则∠ACB的度数为;②若∠ACB=140°,求∠DCE的度数;(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE 角度所有可能的值(不必说明理由);若不存在,请说明理由.36.已知:如图,∠C=∠1,∠2和∠D互余,BE⊥FD于点G.求证:AB∥CD.37.已知:如图所示,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.(1)求证:AB∥CD;(2)试探究∠2与∠3的数量关系.38.如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.(1)AE与FC会平行吗?说明理由;(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么.39.如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A,G,H,D且∠1=∠2,∠B=∠C (1)找出图中相互平行的线,说说它们之间为什么是平行的;(2)证明:∠A=∠D.40.将△ABC纸片沿DE折叠,其中∠B=∠C.(1)如图1,点C落在BC边上的点F处,AB与DF是否平行?请说明理由;(2)如图2,点C落在四边形ABCD内部的点G处,探索∠B与∠1+∠2之间的数量关系,并说明理由.相交线与平行线提高题与常考题和培优题(含解析)参考答案与试题解析一.选择题(共12小题)1.(2017•新城区校级模拟)如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=()A.56°B.66°C.24°D.34°【分析】先根据平行线的性质,得出∠CEH=124°,再根据CD⊥EF,即可得出∠2的度数.【解答】解:∵AB∥CD,∠1=124°,∴∠CEH=124°,∴∠CEG=56°,又∵CD⊥EF,∴∠2=90°﹣∠CEG=34°.故选:D.【点评】本题主要考查了平行线的性质与垂线的定义,解题时注意:两直线平行,同位角相等.2.(2017•禹州市一模)如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为()A.80°B.90°C.100°D.102°【分析】根据平行线性质求出∠A,根据三角形外角性质得出∠2=∠1﹣∠A,代入求出即可.【解答】解:∵AB∥CD,∴∠A=∠3=40°,∵∠1=120°,∴∠2=∠1﹣∠A=80°,故选A.【点评】本题考查了平行线性质和三角形外角性质的应用,关键是求出∠A的度数和得出∠2=∠1﹣∠A.3.(2017•莒县模拟)如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为()A.35°B.45°C.50°D.55°【分析】根据两直线平行,同位角相等可得∠4=∠2,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【解答】解:如图,∵直线a∥b,∴∠4=∠2=55°,∴∠1=∠3﹣∠4=100°﹣55°=45°.故选B.【点评】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.4.(2017•莒县模拟)如图,△ABC的面积为2,将△ABC沿AC方向平移至△DFE,且AC=CD,则四边形AEFB的面积为()A.6 B.8 C.10 D.12【分析】直接利用平移的性质结合三角形面积求法得出答案.【解答】解:∵将△ABC沿AC方向平移至△DFE,且AC=CD,∴A点移动的距离是2AC,则BF=AD,连接FC,则S△BFC=2S△ABC,S△ABC=S△FDC=S△FDE=2,∴四边形AEFB的面积为:10.故选:C.【点评】此题主要考查了平移的性质以及三角形面积求法,正确得出三角形之间面积关系是解题关键.5.(2017春•杭州月考)如图,点D、E、F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件()A.∠1=∠2 B.∠1=∠DFE C.∠1=∠AFD D.∠2=∠AFD【分析】由平行线的性质得出∠1=∠2,再由∠1=∠DFE,得出∠2=∠DFE,由内错角相等,两直线平行即可得出DF∥BC.【解答】解:要使DF∥BC,只需再有条件∠1=∠DFE;理由如下:∵EF∥AB,∴∠1=∠2,∵∠1=∠DFE,∴∠2=∠DFE,∴DF∥BC;故选:B.【点评】本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质,并能进行推理论证是解决问题的关键.6.(2016•柳州)如图,与∠1是同旁内角的是()A.∠2 B.∠3 C.∠4 D.∠5【分析】根据同位角、内错角、同旁内角、对顶角的定义逐个判断即可.【解答】解:A、∠1和∠2是对顶角,不是同旁内角,故本选项错误;B、∠1和∠3是同位角,不是同旁内角,故本选项错误;C、∠1和∠4是内错角,不是同旁内角,故本选项错误;D、∠1和∠5是同旁内角,故本选项正确;故选D.【点评】本题考查了同位角、内错角、同旁内角、对顶角的定义的应用,能熟记同位角、内错角、同旁内角、对顶角的定义是解此题的关键,注意:数形结合思想的应用.7.(2016•来宾)如图,在下列条件中,不能判定直线a与b平行的是()A.∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4=180°【分析】直接用平行线的判定直接判断.【解答】解:A、∵∠1与∠2是直线a,b被c所截的一组同位角,∴∠1=∠2,可以得到a∥b,∴不符合题意,B、∵∠2与∠3是直线a,b被c所截的一组内错角,∴∠2=∠3,可以得到a∥b,∴不符合题意,C、∵∠3与∠5既不是直线a,b被任何一条直线所截的一组同位角,内错角,∴∠3=∠5,不能得到a∥b,∴符合题意,D、∵∠3与∠4是直线a,b被c所截的一组同旁内角,∴∠3+∠4=180°,可以得到a∥b,∴不符合题意,故选C【点评】此题是平行线的判定,解本题的关键是熟练掌握平行线的判定定理.8.(2016•百色)如图,直线a、b被直线c所截,下列条件能使a∥b的是()A.∠1=∠6 B.∠2=∠6 C.∠1=∠3 D.∠5=∠7【分析】利用平行线的判定方法判断即可.【解答】解:∵∠2=∠6(已知),∴a∥b(同位角相等,两直线平行),则能使a∥b的条件是∠2=∠6,故选B【点评】此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.9.(2016•营口)如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB 交于点E,则∠DEO的度数为()A.85°B.70°C.75°D.60°【分析】由平行线的性质求出∠AOC=120°,再求出∠BOC=30°,然后根据三角形的外角性质即可得出结论.【解答】解:∵AB∥OC,∠A=60°,∴∠A+∠AOC=180°,∴∠AOC=120°,∴∠BOC=120°﹣90°=30°,∴∠DEO=∠C+∠BOC=45°+30°=75°;故选:C.【点评】本题主要考查了平行线的性质、三角形的外角性质;熟练掌握平行线的性质和三角形的外角性质是解决问题的关键.10.(2016•陕西)如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=()A.65°B.115°C.125°D.130°【分析】根据平行线性质求出∠CAB的度数,根据角平分线求出∠EAB的度数,根据平行线性质求出∠AED的度数即可.【解答】解:∵AB∥CD,∴∠C+∠CAB=180°,∵∠C=50°,∴∠CAB=180°﹣50°=130°,∵AE平分∠CAB,∴∠EAB=65°,∵AB∥CD,∴∠EAB+∠AED=180°,∴∠AED=180°﹣65°=115°,故选B.【点评】本题考查了角平分线定义和平行线性质的应用,注意:平行线的性质有:①两条平行线被第三条直线所截,同位角相等,②两条平行线被第三条直线所截,内错角相等,③两条平行线被第三条直线所截,同旁内角互补.11.(2016•威海)如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为()A.65°B.55°C.45°D.35°【分析】利用已知条件易求∠ACD的度数,再根据两线平行同位角相等即可求出∠1的度数.【解答】解:∵DA⊥AC,垂足为A,∴∠CAD=90°,∵∠ADC=35°,∴∠ACD=55°,∵AB∥CD,∴∠1=∠ACD=55°,故选B.【点评】本题主要考查了平行线的性质,垂直的定义等知识点,熟记平行线的性质定理是解题关键.12.(2016•毕节市)如图,直线a∥b,∠1=85°,∠2=35°,则∠3=()A.85°B.60°C.50°D.35°【分析】先利用三角形的外角定理求出∠4的度数,再利用平行线的性质得∠3=∠4=50°.【解答】解:在△ABC中,∵∠1=85°,∠2=35°,∴∠4=85°﹣35°=50°,∵a∥b,∴∠3=∠4=50°,故选C.【点评】本题考查了平行线的性质和三角形的外角定理,比较简单;运用了三角形的一个外角等于与它不相邻的两个内角的和,及两直线平行,内错角相等;本题的解法有多种,也可以利用直线b下方的三角形和对顶角相等来求解.二.填空题(共12小题)13.(2017•辽宁模拟)如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是75°.【分析】由BD与AC平行,利用两直线平行同位角相等求出∠C的度数,再利用三角形内角和定理求出所求角度数即可.【解答】解:∵BD∥AC,∠1=65°,∴∠C=∠1=65°,在△ABC中,∠A=40°,∠C=65°,∴∠2=75°,故答案为:75°【点评】此题考查了平行线的性质,以及三角形内角和定理,熟练掌握平行线的性质是解本题的关键.14.(2017春•萧山区月考)如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BFA=34°,则∠DAE= 17 度.【分析】首先根据平行线的性质得到∠DAF的度数,再根据对折的知识即可求出∠DAE的度数.【解答】解:∵四边形ABCD是矩形,∴AD∥BC.∴∠BFA=∠DAF,∵∠BFA=34°,∴∠DAF=34°,∵△AFE是△ADE沿直线AE对折得到,∴∠DAE=∠FAE,∴∠DAE=∠DAF=17°,故答案为17.【点评】本题主要考查了平行线的性质,解题的关键是根据平行线的性质求出∠DAF的度数,此题难度不大.15.(2017•河北一模)如图,m∥n,直角三角板ABC的直角顶点C在两直线之间,两直角边与两直线相交所形成的锐角分别为α、β,则α+β=90°.【分析】根据平行线的性质即可得到结论.【解答】解:过C作CE∥m,∵m∥n,∴CE∥n,∴∠1=∠α,∠2=∠β,∵∠1+∠2=90°,∴∠α+∠β=90°,故答案为:90°.【点评】本题考查了平行线的性质,熟练掌握平行线的性质即可得到结论.16.(2016•凉山州)如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=,CD=,点P 是四边形ABCD四条边上的一个动点,若P到BD的距离为,则满足条件的点P有 2 个.【分析】首先作出AB、AD边上的点P(点A)到BD的垂线段AE,即点P到BD的最长距离,作出BC、CD的点P(点C)到BD的垂线段CF,即点P到BD的最长距离,由已知计算出AE、CF 的长为,比较得出答案.【解答】解:过点A作AE⊥BD于E,过点C作CF⊥BD于F,∵∠BAD=∠ADC=90°,AB=AD=,CD=2,∴∠ABD=∠ADB=45°,∴∠CDF=90°﹣∠ADB=45°,∵sin∠ABD=,∴AE=AB•sin∠ABD=3•sin45°=3>,CF=2<,所以在AB和AD边上有符合P到BD的距离为的点2个,故答案为:2.【点评】本题考查了解直角三角形和点到直线的距离,解题的关键是先求出各边上点到BD的最大距离比较得出答案.17.(2016•菏泽)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是15°.【分析】过A点作AB∥a,利用平行线的性质得AB∥b,所以∠1=∠2,∠3=∠4=30°,加上∠2+∠3=45°,易得∠1=15°.【解答】解:如图,过A点作AB∥a,∴∠1=∠2,∵a∥b,∴AB∥b,∴∠3=∠4=30°,而∠2+∠3=45°,∴∠2=15°,∴∠1=15°.故答案为15°.【点评】本题考查了平行线的性质:两直线平行,内错角相等.18.(2016•连云港)如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2= 72°.【分析】由AB∥CD,根据平行线的性质找出∠ABC=∠1,由BC平分∠ABD,根据角平分线的定义即可得出∠CBD=∠ABC,再结合三角形的内角和为180°以及对顶角相等即可得出结论.【解答】解:∵AB∥CD,∠1=54°,∴∠ABC=∠1=54°,又∵BC平分∠ABD,∴∠CBD=∠ABC=54°.∵∠CBD+∠BDC+∠DCB=180°,∠1=∠DCB,∠2=∠BDC,∴∠2=180°﹣∠1﹣∠CBD=180°﹣54°﹣54°=72°.故答案为:72°.【点评】本题考查了平行线的性质、角平分线的定义以及三角形内角和定理,解题的关键是找出各角的关系.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.19.(2016•青海)如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2= 65°.【分析】先根据平行线的性质得∠ABC+∠BCD=180°,根据对顶角相等得∠ABC=∠1=50°,则∠BCD=130°,再利用角平分线定义得到∠ACD=∠BCD=65°,然后根据平行线的性质得到∠2的度数.【解答】解:∵AB∥CD,∴∠ABC+∠BCD=180°,而∠ABC=∠1=50°,∴∠BCD=130°,∵CA平分∠BCD,∴∠ACD=∠BCD=65°,∵AB∥CD,∴∠2=∠ACD=65°.故答案为65°.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.20.(2016•金华)如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是80°.【分析】延长DE交AB于F,根据平行线的性质得到∠AFE=∠B,∠B+∠C=180°,根据三角形的外角的性质即可得到结论.【解答】解:延长DE交AB于F,∵AB∥CD,BC∥DE,∴∠AFE=∠B,∠B+∠C=180°,∴∠AFE=∠B=60°,∴∠AED=∠A+∠AFE=80°,故答案为:80°.【点评】本题考查了平行线的性质,三角形的外角的性质,熟练掌握平行线的性质是解题的关键.21.(2016•云南)如图,直线a∥b,直线c与直线a、b分别相交于A、B两点,若∠1=60°,则∠2= 60°.【分析】先根据平行线的性质求出∠3的度数,再由对顶角的定义即可得出结论.【解答】解:∵直线a∥b,∠1=60°,∴∠1=∠3=60°.∵∠2与∠3是对顶角,∴∠2=∠3=60°.故答案为:60°.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.22.(2016•吉林)如图,AB∥CD,直线EF分别交AB、CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于30 度.【分析】根据平行线的性质得到∠DNM=∠BME=75°,由等腰直角三角形的性质得到∠PND=45°,即可得到结论.【解答】解:∵AB∥CD,∴∠DNM=∠BME=75°,∵∠PND=45°,∴∠PNM=∠DNM﹣∠DNP=30°,故答案为:30.【点评】本题考查了平行线的性质,等腰直角三角形的性质,熟练掌握平行线的性质是解题的关键.23.(2016•泰州)如图,△ABC中,BC=5cm,将△ABC沿BC方向平移至△A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则△ABC平移的距离为 2.5 cm.【分析】根据平移的性质:对应线段平行,以及三角形中位线定理可得B′是BC的中点,求出BB′即为所求.【解答】解:∵将△ABC沿BC方向平移至△A′B′C′的对应位置,∴A′B′∥AB,∵O是AC的中点,∴B′是BC的中点,∴BB′=5÷2=2.5(cm).故△ABC平移的距离为2.5cm.故答案为:2.5.【点评】考查了平移的性质,平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.24.(2016•都匀市一模)如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°,∠D=120°,则∠C的度数为100 度.【分析】过点C作CF∥AB,由平行线性质可得∠B,∠D,∠BCF,∠DCF的关系,进而求得∠C.【解答】解:如图所示:过点C作CF∥AB.∵AB∥DE,∴DE∥CF;∴∠BCF=180°﹣∠B=40°,∠DCF=180°﹣∠D=60°;∴∠C=∠BCF+∠DCF=100°.故答案为:100.【点评】本题运用了两直线平行,同旁内角互补的性质,需要作辅助线求解,难度中等.三.解答题(共16小题)25.(2016•淄博)如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.【分析】根据同位角相等,两直线平行证明OB∥AC,根据同旁内角互补,两直线平行证明OA∥BC.【解答】解:OA∥BC,OB∥AC.∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC,∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC.【点评】本题考查的是平行线的判定,掌握平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解题的关键.26.(2016•槐荫区二模)如图,已知AC∥ED,AB∥FD,∠A=65°,求:∠EDF的度数.【分析】根据平行线的性质,即可解答.【解答】解:∵AC∥ED,∴∠BED=∠A=65°,∵AB∥FD,∴∠EDF=∠BED=65°.【点评】本题考查了平行线的性质,解决本题的关键是熟记平行线的性质.27.(2016•厦门校级一模)如图,已知AB∥CD,若∠C=40°,∠E=20°,求∠A的度数.【分析】根据两直线平行,同位角相等可得∠1=∠C,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【解答】解:如图,∵AB∥CD,∴∠1=∠C=40°,∴∠A=∠1﹣∠E=40°﹣20°=20°.【点评】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.28.(2016•江西模拟)如图,在△ABC中,∠B+∠C=110°,AD平分∠BAC,交BC于点D,DE∥AB,交AC于点E,求∠ADE的度数.【分析】根据三角形内角和定理求出∠BAC,根据角平分线定义求出∠BAD,根据平行线的性质得出∠ADE=∠BAD即可.【解答】解:∵在△ABC中,∠B+∠C=110°,∴∠BAC=180°﹣∠B﹣∠C=70°,∵AD是△ABC的角平分线,∴∠BAD=∠BAC=35°,∵DE∥AB,∴∠ADE=∠BAD=35°.【点评】本题考查了平行线的性质,三角形内角和定理,角平分线定义的应用,注意:两直线平行,内错角相等.29.(2016•江西模拟)如图,直线a∥b,BC平分∠ABD,DE⊥BC,若∠1=70°,求∠2的度数.【分析】根据平行线的性质得到∠1=∠ABD=70°,由角平分线的定义得到∠EBD=ABD=35°,根据三角形的内角和即可得到结论.【解答】解:∵直线a∥b,∴∠1=∠ABD=70°,∵BC平分∠ABD,∴∠EBD=ABD=35°,∵DE⊥BC,∴∠2=90°﹣∠EBD=55°.【点评】本题考查了平行线的性质,角平分线的定义,三角形的内角和,熟练掌握平行线的性质是解题的关键.30.(2016•朝阳区一模)如图,E为AC上一点,EF∥AB交AF于点F,且AE=EF.求证:∠BAC=2∠1.【分析】根据平行线的性质得到∠1=∠FAB,由等腰三角形的性质得到∠EAF=∠EFA,根据邻补角和对顶角的定义即可得到结论.【解答】证明:∵EF∥AB,∴∠1=∠FAB,∵AE=EF,∴∠EAF=∠EFA,∵∠1=∠EFA,∴∠EAF=∠1,∴∠BAC=2∠1.【点评】本题考查了平行线的性质,邻补角的定义,熟练掌握平行线的性质是解题的关键.31.(2016秋•宜兴市期末)如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=76°,∠DOF=90°,求∠EOF的度数.【分析】根据对顶角相等可得∠BOD=∠AOC,再根据角平分线的定义求出∠DOE,然后根据∠EOF=∠DOF﹣∠DOE代入数据计算即可得解.【解答】解:由对顶角相等得,∠BOD=∠AOC=76°,∵OE平分∠BOD,∴∠DOE=∠BOD=38°,∵∠DOF=90°,∴∠EOF=∠DOF﹣∠DOE=90°﹣38°=52°.【点评】本题考查了对顶角相等,角平分线的定义,熟记性质与概念并准确识图是解题的关键.32.(2016春•西华县期末)如图,直线AB,CD相交于O点,OM⊥AB于O.(1)若∠1=∠2,求∠NOD;(2)若∠BOC=4∠1,求∠AOC与∠MOD.【分析】(1)由已知条件和观察图形可知∠1与∠AOC互余,再根据平角的定义求解;(2)利用已知的∠BOC=4∠1,结合图形以及对顶角的性质求∠AOC与∠MOD.【解答】解:(1)因为OM⊥AB,所以∠1+∠AOC=90°.又∠1=∠2,所以∠2+∠AOC=90°,所以∠NOD=180°﹣(∠2+∠AOC)=180°﹣90°=90°.(2)由已知∠BOC=4∠1,即90°+∠1=4∠1,可得∠1=30°,所以∠AOC=90°﹣30°=60°,所以由对顶角相等得∠BOD=60°,故∠MOD=90°+∠BOD=150°.【点评】本题利用垂直的定义,对顶角的性质和平角的定义计算,要注意领会由垂直得直角这一要点.33.(2016春•双城市期末)如图,两直线AB、CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11.(1)求∠COE的度数.(2)若射线OF⊥OE,请在图中画出OF,并求∠COF的度数.【分析】(1)根据∠AOC+∠AOD=180°可得∠AOC和∠AOD的度数,根据对顶角相等可得∠BOD=70°,再利用角平分线定义可得∠DOE=35°,再根据邻补角定义可得∠COE的度数;(2)分两种情况画图,进而求出∠COF的度数.【解答】解:(1)∠AOC:∠AOD=7:11,∠AOC+∠AOD=180°,∴∠AOC=70°,∠AOD=110°,∵∠BOD=∠AOC,∴∠BOD=70°,∵OE平分∠BOD,∴∠DOE=35°,∴∠COE=180°﹣∠DOE=145°;(2)分两种情况,如图1,∵OF⊥OE,∴∠EOF=90°,∴∠COF=∠COE﹣∠EOF=145°﹣90°=55°,如图2,∠COF=∠360°﹣∠COE﹣∠EOF=125°.【点评】此题主要考查了垂线、邻补角、对顶角,关键是掌握对顶角相等,邻补角互补.34.(2016春•太仓市期末)如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.【分析】根据四边形的内角和定理和∠A=∠C=90°,得∠ABC+∠ADC=180°;根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等,从而证明两条直线平行.【解答】解:BE∥DF.理由如下:∵∠A=∠C=90°(已知),∴∠ABC+∠ADC=180°(四边形的内角和等于360°).∵BE平分∠ABC,DF平分∠ADC,∴∠1=∠2=∠ABC,∠3=∠4=∠ADC(角平分线的定义).∴∠1+∠3=(∠ABC+∠ADC)=×180°=90°(等式的性质).又∠1+∠AEB=90°(三角形的内角和等于180°),∴∠3=∠AEB(同角的余角相等).∴BE∥DF(同位角相等,两直线平行).【点评】此题运用了四边形的内角和定理、角平分线定义、等角的余角相等和平行线的判定,难度中等.35.(2016春•周口期末)将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):(1)①若∠DCE=45°,则∠ACB的度数为135°;②若∠ACB=140°,求∠DCE的度数;(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.【分析】(1)①首先计算出∠DCB的度数,再用∠ACD+∠DCB即可;②首先计算出∠DCB的度数,再计算出∠DCE即可;(2)根据(1)中的计算结果可得∠ACB+∠DCE=180°,再根据图中的角的和差关系进行推理即可;(3)根据平行线的判定方法可得.【解答】解:(1)①∵∠ECB=90°,∠DCE=45°,∴∠DCB=90°﹣45°=45°,∴∠ACB=∠ACD+∠DCB=90°+45°=135°,故答案为:135°;②∵∠ACB=140°,∠ACD=90°,∴∠DCB=140°﹣90°=50°,∴∠DCE=90°﹣50°=40°;(2)∠ACB+∠DCE=180°,∵∠ACB=∠ACD+∠DCB=90°+∠DCB,∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°;(3)存在,当∠ACE=30°时,AD∥BC,当∠ACE=∠E=45°时,AC∥BE,当∠ACE=120°时,AD∥CE,当∠ACE=135°时,BE∥CD,当∠ACE=165°时,BE∥AD.【点评】此题主要考查了角的计算,以及平行线的判定,关键是理清图中角的和差关系.36.(2016秋•郓城县期末)已知:如图,∠C=∠1,∠2和∠D互余,BE⊥FD于点G.求证:AB∥CD.【分析】首先由BE⊥FD,得∠1和∠D互余,再由已知,∠C=∠1,∠2和∠D互余,所以得∠C=∠2,从而证得AB∥CD.【解答】证明:∵BE⊥FD,∴∠EGD=90°,∴∠1+∠D=90°,又∠2和∠D互余,即∠2+∠D=90°,∴∠1=∠2,又已知∠C=∠1,∴∠C=∠2,∴AB∥CD.【点评】此题考查的知识点是平行线的判定,关键是由BE⊥FD及三角形内角和定理得出∠1和∠D 互余.37.(2016春•广州校级期末)已知:如图所示,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.(1)求证:AB∥CD;(2)试探究∠2与∠3的数量关系.【分析】(1)已知BE、DE平分∠ABD、∠BDC,且∠1+∠2=90°,可得∠ABD+∠BDC=180°,根据同旁内角互补,可得两直线平行.(2)已知∠1+∠2=90°,即∠BED=90°;那么∠3+∠FDE=90°,将等角代换,即可得出∠3与∠2的数量关系.【解答】证明:(1)∵BE、DE平分∠ABD、∠BDC,∴∠1=∠ABD,∠2=∠BDC;∵∠1+∠2=90°,∴∠ABD+∠BDC=180°;∴AB∥CD;(同旁内角互补,两直线平行)解:(2)∵DE平分∠BDC,∴∠2=∠FDE;∵∠1+∠2=90°,∴∠BED=∠DEF=90°;∴∠3+∠FDE=90°;∴∠2+∠3=90°.【点评】此题主要考查了角平分线的性质以及平行线的判定,难度不大.38.(2016秋•内江期末)如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.(1)AE与FC会平行吗?说明理由;(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么.【分析】(1)证明∠1=∠CDB,利用同位角相等,两直线平行即可证得;(2)平行,根据平行线的性质可以证得∠A=∠CBE,然后利用平行线的判定方法即可证得;(3)∠EBC=∠CBD,根据平行线的性质即可证得.【解答】解:(1)平行.理由如下:∵∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义),∴∠1=∠CDB,∴AE∥FC(同位角相等两直线平行);(2)平行.理由如下:∵AE∥CF,∴∠C=∠CBE(两直线平行,内错角相等),又∵∠A=∠C,∴∠A=∠CBE,∴AD∥BC(同位角相等,两直线平行);(3)平分.理由如下:∵DA平分∠BDF,∴∠FDA=∠ADB,∵AE∥CF,AD∥BC,∴∠FDA=∠A=∠CBE,∠ADB=∠CBD,∴∠EBC=∠CBD,∴BC平分∠DBE.【点评】本题考查了平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.39.(2016秋•双柏县期末)如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A,G,H,D且∠1=∠2,∠B=∠C(1)找出图中相互平行的线,说说它们之间为什么是平行的;(2)证明:∠A=∠D.【分析】(1)根据同位角相等,两直线平行可得CE∥FB,进而可得∠C=∠BFD,再由条件∠B=∠C 可得∠B=∠BFD,从而可根据内错角相等,两直线平行得AB∥CD;(2)根据(1)可得AB∥CD,再根据两直线平行,内错角相等可得∠A=∠D.【解答】(1)解:∵∠1=∠2,∴CE∥FB,∴∠C=∠BFD,∵∠B=∠C,∴∠B=∠BFD,∴AB∥CD;(2)证明:由(1)可得AB∥CD,∴∠A=∠D.【点评】此题主要考查了平行线的判定和性质,关键是掌握平行线的判定定理和性质定理.40.(2016春•邳州市期末)将△ABC纸片沿DE折叠,其中∠B=∠C.(1)如图1,点C落在BC边上的点F处,AB与DF是否平行?请说明理由;(2)如图2,点C落在四边形ABCD内部的点G处,探索∠B与∠1+∠2之间的数量关系,并说明理由.【分析】(1)AB与DF平行.根据翻折可得出∠DFC=∠C,结合∠B=∠C即可得出∠B=∠DFC,从而证出AB∥DF;(2)连接GC,由翻折可得出∠DGE=∠ACB,再根据三角形外角的性质得出∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,通过角的运算即可得出∠1+∠2=2∠B.【解答】解:(1)AB与DF平行.理由如下:由翻折,得∠DFC=∠C.又∵∠B=∠C,∴∠B=∠DFC,∴AB∥DF.(2)连接GC,如图所示.由翻折,得∠DGE=∠ACB.∵∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=(∠DGC+∠EGC)+(∠DCG+∠ECG)=∠DGE+∠DCE=2∠ACB.∵∠B=∠ACB,∴∠1+∠2=2∠B.【点评】本题考查了平行线的判定以及翻折得性质,解题的关键是:(1)找出∠B=∠DFC;(2)根据三角形外角的性质利用角的计算求出∠1+∠2=2∠B.本题属于基础题,难度不大,解决该题型题目时,找出相等(或互补)的角是关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 如图,∠B=∠C ,AB ∥EF 求证:∠BGF=∠C2.如图,EF ∥AD ,∠1 =∠2,∠BAC = 70°。
求∠AGD3.已知:如图AB∥CD,EF交AB 于G ,交CD 于F ,FH 平分∠EFD ,交AB 于H , ∠AGE=500 ,求:∠BHF 的度数。
4.已知:如图∠1=∠2,∠C=∠D ,那么∠A=∠F 吗?试说明理由5.已知:如图,AB//CD ,试解决下列问题: (1)∠1+∠2=___ ___; (2)∠1+∠2+∠3=___ __; (3)∠1+∠2+∠3+∠4=_ __ __;HG FEDC BAHG21FEDCBAGFEDCBA(4)试探究∠1+∠2+∠3+∠4+…+∠n = ;6.如图11,E 、F 分别在AB 、CD 上,1D ∠=∠,2∠与C ∠互余且EC AF ⊥, 垂足为O ,求证://AB CD .7.如图12,//AC BD ,//AB CD ,E ∠=∠1,F ∠=∠2,AE 交CF 于点O , 试说明:CF AE ⊥.图11图12O BCDE8.如图13,AEB NFP ∠=∠,M C ∠=∠,判断A ∠与P ∠的大小关系,并说明理由.9.如图14,AD 是CAB ∠的角平分线,//DE AB ,//DF AC ,EF 交AD 于点O . 请问:(1)DO 是EDF ∠的角平分线吗?如果是,请给予证明;如果不是,请说明理由.(2)若将结论与AD 是CAB ∠的角平分线、//DE AB 、//DF AC 中的任一条件 交换,•所得命题正确吗?10.如图,AD 是∠EAC 的平分线,AD ∥BC ,∠B = 30°, 你能算出∠EAD 、∠DAC 、∠C 的度数吗?图14F E M PACN B3AD BCEF 1 23 411. 如图, ∠1=∠2 , ∠3=1050, 求 ∠4的度数。
12.如图,EF ∥AD ,∠1 =∠2,∠BAC = 70°。
将求∠AGD 的过程填写完整。
因为EF ∥AD ,所以 ∠2 = 。
又因为 ∠1 = ∠2,所以 ∠1 = ∠3。
所以AB ∥ 。
所以∠BAC + = 180°。
又因为∠BAC = 70°, 所以∠AGD = 。
13.已知,如图,BCE 、AFE 是直线,AB ∥CD ,∠1=∠2,∠3=∠4。
AD 与BE 平行吗?为什么?。
14..如图∠1+∠2=180°,∠DAE=∠BCF,DA 平分∠BDF. (1)AE 与FC 会平行吗?说明理由. (2)AD 与BC 的位置关系如何?为什么? (3)BC 平分∠DBE 吗?为什么. ?15.如图10,已知:直线AB ,CD 被直线EF ,GH 所截,且∠1=∠2, 求证:∠3+∠4=180°.d c 31ab2 4FE21DC BA16.如图11,EF∥AD,∠1=∠2,∠BAC=70 o,求∠AGD。
17.已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH,求∠KOH的度数.18.如图13,AD是∠EAC的平分线,AD∥BC,∠B=30o,求∠EAD、∠DAC、∠C的度数。
20、如图,AB∥DF,DE∥BC,∠1=65°求∠2、∠3的度数(图12)(图13)ADFBEC 12321、已知:如图,∠=∠CDA CBA ,DE 平分∠CDA ,BF 平分∠CBA ,且∠=∠ADE AED 。
试说明DE FB //22、已知:如图,∠+∠=∠=∠BAP APD 18012,。
求证:∠=∠E F23、推理填空:如图,DF ∥AB ,DE ∥AC ,试说明∠FDE=∠A24、推理填空:如图17,AB ⊥BC 于B ,CD ⊥BC 于C ,∠1=∠2. 求证:BE ∥CF .25、如图,AB ⊥CD ,垂足为O ,EF 经过点O ,∠2=4∠1, 求∠2,∠3,∠BOE的度数A B1 EF 2 CPDD F CAE BFED CB AFEO DCBA32126、如图,AB∥CD,∠B=400,∠E=300,求∠D的度数27、如图,AD 是∠EAC 的平分线,AD ∥BC ,∠B=30°,求∠C 的度数28、如图,直线AB ∥CD,EF ⊥CD ,垂足为F ,射线FN 交AB 于M 。
∠NMB=136º,则∠EFN 为多少度?29、如图,∠ABD=•∠CBD ,•DF•∥AB ,•DE•∥BC ,•则∠1•与∠2•相等吗?为什么?B C FENA MDAED CBEDCBA30、如图,AB ∥DE ,∠1=∠ACB ,∠CAB =21∠BAD ,试说明AD ∥BC .31、如图,AB ∥CD ,∠1=∠2,∠3=∠4。
试说明:AD ∥BE 。
32、如图,EF ∥AD ,∠1 =∠2,∠BAC = 70°。
将求∠AGD 的过程填写完整。
∵EF ∥AD ,( ) ∴ ∠2 = 。
( ) 又∵ ∠1 = ∠2,( ) ∴ ∠1 = ∠3。
( ) ∴AB ∥ 。
( ) ∴∠BAC + = 180°。
( ) 又∵∠BAC = 70°,( )∴∠AGD = 。
( )33、如图所示,已知∠B=∠C ,AD ∥BC ,试说明:AD 平分∠CAEAD BC EF 12 3 4DEA BC2134、如图所示,已知直线EF 和AB,CD 分别相交于K,H,且EG ⊥AB,∠CHF=600,∠E=•30°,试说明AB ∥CD.35、如图,EF ∥AD ,∠1 =∠2,∠BAC = 70°。
将求∠AGD 的过程填写完整。
∵EF ∥AD ,( ) ∴ ∠2 = 。
( ) 又∵ ∠1 = ∠2,( ) ∴ ∠1 = ∠3。
( ) ∴AB ∥ 。
( ) ∴∠BAC + = 180°。
( ) 又∵∠BAC = 70°,( )∴∠AGD = 。
( )36、如图所示,已知∠B=∠C ,AD ∥BC ,试说明:AD 平分∠CAE37、如图所示,已知直线EF 和AB,CD 分别相交于K,H,且EG ⊥AB,∠CHF=600,∠E=•30°,试说明AB ∥CD.GHKF EDC B A GHKF EDC B A DEA BC2138.已知:如图,AB ⊥CD ,垂足为O ,EF 经过点O ,∠1=25°, 求∠2,∠3的度数。
(7分)39.如图:AE 平分∠DAC ,∠DAC=120°,∠C=60°,AE 与BC 平行吗?为什么?(6分)40.如图EF ∥AD ,∠1=∠2,∠BAC=70 o ,求∠AGD 的度数。
(7分)41.填空完成推理过程:(每空1分,共7分)如图,E 点为DF 上的点,B 为AC 上的点,∠1=∠2, ∠C =∠D 。
试说明:AC ∥DF 。
解:∵ ∠1=∠2(已知)FEO DCBA321ACBD E42.(10分)如图所示,直线AB∥CD,∠1=75°,求∠2的度数.43.(10分)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37º,求∠D的度数.44.(10分)如图,在△ABC中,CD是高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由。
45.(11分)如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线。
完成下列推理过程:证明:∵BD是∠ABC的平分线(已知)∴∠ABD=∠DBC ( ) ∵ED∥BC ( 已知)∴∠BDE=∠DBC ( )AEB CDF∴ ( 等 量 代 换 ) 又∵∠FED=∠BDE ( 已 知 )∴ ∥ ( ) ∴ ∠AEF=∠ABD ( ) ∴ ∠AEF=∠DEF ( 等 量 代 换 )∴EF 是∠AED 的平分线( )46、 如图,∵AB ∥EF ( 已知 ) ∴∠A + =180( ) ∵DE ∥BC ( 已知 )∴∠DEF= ( ) ∠ADE= ( )47 如图,已知AB BC ⊥,BC CD ⊥,12=∠∠.试判断BE 与CF 的关系,并说明你的理由.解:BE ∥CF.理由:∵AB BC ⊥,BC CD ⊥ (已知)∴__________ = ___________=o90 ( )∵12=∠∠ ( ) ∴∠ABC -∠1=∠BCD -∠2 ,即∠EBC=∠BCF∴________∥________ ( ) 48、本题11分)如图,已知DE ∥BC ,∠1=∠2,求证:∠B =∠C .ACD E FB49已知:如图∠1=∠2,∠C=∠D ,∠A=∠F 相等吗?试说明理由.50. 如图7,∠B=∠C ,AB ∥EF试说明:∠BGF=∠C答:因为∠B=∠C 所以AB ∥CD ( ) 又因为AB ∥EF 所以EF ∥CD ( ) 所以∠BGF=∠C ( )51. 如图8,AD ⊥BC 于D ,EG ⊥BC 于G ,∠E=∠3 试说明:AD 平分∠BAC答:因为AD ⊥BC ,EG ⊥BC 所以AD ∥EG ( )所以∠1=∠E ( )∠2=∠3( ) 又因为∠3=∠E 所以∠1=∠2所以AD 平分∠BAC ( )图7GAB CEF132图8BCE A1A BOF DEC (第18题)第17题A BC D MN 1252.(本题10分)如图,∠1=30°,AB ⊥CD ,垂足为O ,EF 经过点O .求∠2、∠3的度数.53.(本题24分,每空3分)如图16,点D 、E 、F 分别在AB 、BC 、AC 上,且DE∥AC ,EF ∥AB ,下面写出了说明“∠A+∠B+∠C =180°”的过程,请填空: 因为DE ∥AC ,所以∠1=∠ .( ) 因为AB ∥EF, 所以∠3=∠ .( ) 因为AB ∥EF ,所以∠2=∠___.( ) 因为DE ∥AC ,所以∠4=∠___.( ) 所以∠2=∠A (等量代换).因为∠1+∠2+∠3=180°,所以∠A+∠B+∠C =180°(等量代换). 54.(本题12分)已知,如图,CD ⊥AB ,GF ⊥AB ,∠B =∠ADE ,试说明∠1=∠2.55、如图所示,直线AB ∥CD ,∠1=75°,求∠2的度数。
56、如图,直线AB 、CD 相交于O ,OD 平分∠AOF ,OE ⊥CD 于点O ,∠1=50°,求∠COB 、∠BOF 的度数。
ABCED F1234 图16F21GE DCB AABCD O123EFAB CD E F1423第19题)E N M CD BA 57、如图AB∥CD,∠NCM =90°,∠NCB =30°,CM 平分∠BCE 求∠B 的大小。
