2019-2020学年人教版九年级数学上学期同步测试专题24-2:点和圆、直线和圆的位置关系
九年级数学上册第二十四章圆24.2点和圆、直线和圆的位置关系24.2.1点和圆的位置关系检测(含解

九年级数学上册第二十四章圆24.2 点和圆、直线和圆的位置关系24.2.1 点和圆的位置关系同步检测(含解析)(新版)新人教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(九年级数学上册第二十四章圆24.2 点和圆、直线和圆的位置关系24.2.1 点和圆的位置关系同步检测(含解析)(新版)新人教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为九年级数学上册第二十四章圆24.2 点和圆、直线和圆的位置关系24.2.1 点和圆的位置关系同步检测(含解析)(新版)新人教版的全部内容。
24.2。
1 点和圆的位置关系测试时间:30分钟一、选择题1.(2018广东广州花都期末)☉O的半径为5 cm,点A到圆心O的距离OA=4 cm,则点A与圆O的位置关系为( )A。
点A在圆上B。
点A在圆内 C.点A在圆外D。
无法确定2。
(2018北京门头沟期末)已知△ABC中,AC=3,CB=4,以点C为圆心,r为半径作圆,如果点A、点B只有一个点在圆内,那么半径r的取值范围是( ) A。
r〉3 B。
r≥4 C.3<r≤4D。
3≤r≤43.若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )A。
2B。
2—2 C。
2— D.-1二、填空题4。
(2017上海普陀一模)已知点P在半径为5的☉O外,如果设OP=x,那么x的取值范围是.5.(2018江苏徐州睢宁月考)正方形ABCD的边长为2 cm,以A为圆心,2 cm 为半径作☉A,则点B在☉A;点C在☉A;点D在☉A。
6。
我们把两个三角形的外心之间的距离叫做外心距。
如图,在Rt△ABC和Rt△ACD中,∠ACB=∠ACD=90°,点D在边BC的延长线上,BC=DC=3,∴BD=6,如果BC=DC=3,那么△ABC和△ACD的外心距是.三、解答题7.如图,☉O是△ABC的外接圆,AC是直径,过O作OD∥BC交AB于点D。
2019_2020学年九年级数学上册第二十四章圆测评(新版)新人教版

第二十四章测评(时间:45分钟,满分:100分)一、选择题(每小题4分,共32分)1.在矩形ABCD^ ,AB :8, BC=3 一,点P 在边AB 上,且BP=3AR 如果圆P 是以点P 为圆心,PD 为半径的 圆,那么下列判断正确的是( )BC 均在圆P 外B 在圆P 外、点C 在圆B 在圆P 内、点C 在圆 BC 均在圆P 内-海南中考)如图,点AB, C 在。
O 上,AC// OB Z BAO= ° ,则Z BO (的^度数为( B. 0 ° C.60° D.80°(第3题图)A. 点B. 点C. 点D. 点2. (2017 A.2 °3. (2017 D E是。
A.92° -江苏苏州中考)如图,在Rt △ ABC 中 , / ACB=0° , Z A=6 ° .以BC 为直径的。
O 上一点,且 ,连接OE 过点E 作EF 丄OE 交AC 的延长线于点F ,则Z F=( 0交AB 于点 B. 108°4. (2017 8,则圆O 的周长为(-内蒙古呼和浩特中考 )如图,CD 为圆0的直径,弦AB1 CD 垂足为 M 若AB=I2, OM MD=:A.26 nB.13 nC.96D. 9 10(第2题图)A.29°B. 27. 如图,点P是等边三角形ABC外接圆。
A. 当弦PB最长时,△ APC是等腰三角形B. 当厶APC是等腰三角形时,POL ACC. 当POL AC时,Z ACP=0 °D. 当Z ACP=0。
时,△ BPC是直角三角形8. 如图,以等边三角形ABC的BC边为直径画半圆,分别交ABAC于点E D DF是圆O的切线,过点F 作BC的垂线交O上的点,在下列判断中,不正确的是()A.4二、填空题(每小题4分,共20分)9. _______________________________ 。
2019-2020学年人教版九年级数学上学期同步测试专题24-1:圆的有关性质(含解析)
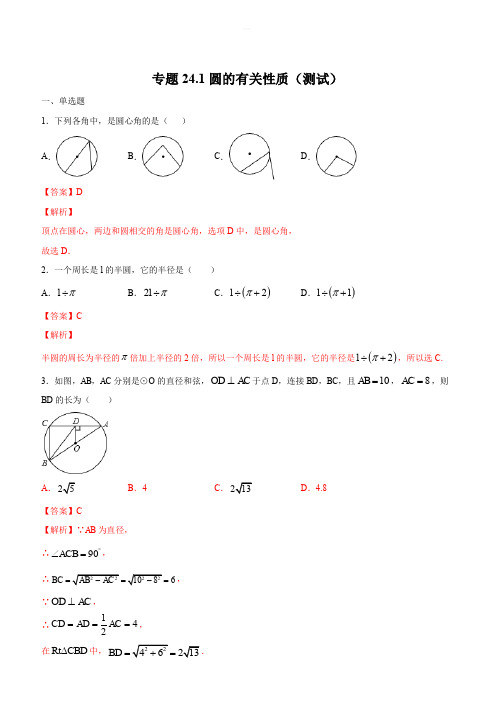
专题24.1圆的有关性质(测试)一、单选题1.下列各角中,是圆心角的是( )A .B .C .D .【答案】D 【解析】顶点在圆心,两边和圆相交的角是圆心角,选项D 中,是圆心角, 故选D .2.一个周长是l 的半圆,它的半径是( ) A .l π÷ B .2l π÷C .()2l π÷+D .()1l π÷+【答案】C 【解析】半圆的周长为半径的π倍加上半径的2倍,所以一个周长是l 的半圆,它的半径是()2l π÷+,所以选C. 3.如图,AB ,AC 分别是⊙O 的直径和弦,OD AC ⊥于点D ,连接BD ,BC ,且10AB =,8AC =,则BD 的长为( )A .B .4C .D .4.8【答案】C【解析】∵AB 为直径, ∴90ACB ︒∠=,∴6BC =, ∵OD AC ⊥, ∴142CD AD AC ===,故选C . 4.如图,AB 是O 的弦,OC AB ⊥交O 于点C ,点D 是O 上一点,30ADC ∠=︒,则BOC ∠的度数为( ).A .30°B .40°C .50°D .60°【答案】D【解析】解:如图,∵30ADC ∠=︒, ∴260AOC ADC ∠=∠=︒. ∵AB 是O 的弦,OC AB ⊥交O 于点C ,∴AC BC =.∴60AOC BOC ∠=∠=︒. 故选:D ..5.如图,有一圆形展厅,在其圆形边缘上的点A 处安装了一台监视器,它的监控角度是65°.为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器( )台.A .3B .4C .5D .6【答案】A【解析】设需要安装n (n 是正整数)台同样的监控器,由题意,得:65°×2×n ≥360°, 解得n ≥3613,∴至少要安装3台这样的监控器,才能监控整个展厅.故选:A .且10CD m =,则这段弯路所在圆的半径为( )A .25mB .24mC .30mD .60m【答案】A 【解析】解:OC AB ⊥,20AD DB m ∴==,在Rt AOD ∆中,222OA OD AD =+, 设半径为r 得:()2221020r r =-+, 解得:25r m =,∴这段弯路的半径为25m故选:A .7.若AB 和CD 的度数相等,则下列命题中正确的是( ) A .AB =CDB .AB 和CD 的长度相等C .AB 所对的弦和CD 所对的弦相等D .AB 所对的圆心角与CD 所对的圆心角相等 【答案】D【解析】如图,AB 与CD 的度数相等,A 、根据度数相等,不能推出弧相等,故本选项错误;B 、根据度数相等,不能推出两弧的长度相等,故本选项错误;C 、根据度数相等,不能推出所对应的弦相等,故本选项错误;D 、根据度数相等,能推出弧所对的两个圆心角相等,故本选项正确;8.如图,C、D为半圆上三等分点,则下列说法:①AD=CD=BC;②∠AOD=∠DOC=∠BOC;③AD =CD=OC;④△AOD沿OD翻折与△COD重合.正确的有()A.4个B.3个C.2个D.1个【答案】A【解析】∵C、D为半圆上三等分点,∴»»»AD CD BC==,故①正确,∵在同圆或等圆中,等弧对的圆心角相等,等弧对的弦相,∴AD=CD=OC,∠AOD=∠DOC=∠BOC=60°,故②③正确,∵OA=OD=OC=OB,∴△AOD≌△COD≌△COB,且都是等边三角形,∴△AOD沿OD翻折与△COD重合.故④正确,∴正确的说法有:①②③④共4个,故选A.9.下列说法:①优弧一定比劣弧长;②面积相等的两个圆是等圆;③长度相等的弧是等弧;④经过圆内的一个定点可以作无数条弦;⑤经过圆内一定点可以作无数条直径.其中不正确的个数是()A.1个B.2个C.3个D.4个【答案】C【解析】解:在同圆或等圆中,优弧一定比劣弧长,所以①错误;面积相等的两个圆半径相等,则它们是等圆,所以②正确;能完全重合的弧是等弧,所以③错误;经过圆内一个定点可以作无数条弦,所以④正确;经过圆内一定点可以作无数条直径或一条直径,所以⑤错误.10.如图所示,AB 是半圆O 的直径。
2019-2020学年度人教版九年级数学上册第24章:圆 单元测试 (含答案)

2019-2020学年度人教版九年级数学上册第24章:圆单元测试一.选择题(共10小题,每小题3分,共30分)1.如图,点A、B、C是O上的点,OA AB=,则C∠的度数为()A.30︒B.45︒C.60︒D.30︒或60︒2.如图,在O中,弦AB为8mm,圆心O到AB的距离为3mm,则O的半径等于()A.3mm B.4mm C.5mm D.8mm3.如图,在O中,半径OA垂直于弦BC,点D在O上,若70AOB∠=︒,则ADC∠的度数为() A.30︒B.35︒C.45︒D.70︒4.正六边形内接于圆,它的边所对的圆周角是()A.60︒B.120︒C.60︒或120︒D.30︒或150︒5.AB是O的弦,OQ AB⊥于Q,再以QO为半径作同心圆,称作小O,点P是AB上异于A,B,Q的任意一点,则P点位置是()A.在大O上B.在大O外部C.在小O内部D.在小O外而大O内6.如图,AB为O的直径,40BED∠=︒,则ACD∠的度数为()A.90︒B.50︒C.45︒D.80︒7.如图,在直角ABC∆中,90C∠=︒,3BC=,4AC=,D、E分别是AC、BC上的第1题图第2题图第3题图一点,且3DE =.若以DE 为直径的圆与斜边AB 相交于M 、N ,则MN 的最大值 为( ) A .85B .2C .125D .1458.下列说法错误的是( ) A .圆有无数条直径B .连接圆上任意两点之间的线段叫弦C .过圆心的线段是直径D .能够重合的圆叫做等圆9.如图,四边形ABCD 内接于O ,过B 点作BH AD ⊥于点H ,若135BCD ∠=︒,4AB =,则BH 的长度为( AB .22C .32D .不能确定10.已知抛物线225(3)(0)4y a x a =-+≠过点(0,4)C ,顶点为M ,与x 轴交于A ,B 两点.如图所示以AB 为直径作圆,记作D ,下列结论:①抛物线的对称轴是直线3x =;②点C 在D 外;③直线CM 与D 相切.其中正确的有( ) A .0个B .1个C .2个D .3个二.填空题(共8小题,每小题3分,共24分)11.有一张矩形的纸片,3AB cm =,4AD cm =,若以A 为圆心作圆,并且要使点D 在A 内,而点C 在A 外,A 的半径r 的取值范围是 .12.如图,AC 是O 的内接正六边形的一边,点B 在AC 上,且BC 是O 的内接正十边形的一边,若AB 是O 的内接正n 边形的一边,则n = .13.O 的半径10r =,圆心O 到直线l 的距离10d =,则O 与直线l 的位置关系是 .第7题图第9题图第10题第12题图第16题图 第17题图14.已知圆锥的底面半径为4cm ,母线长为6cm ,则它的侧面展开图的面积等于 . 15.一个扇形的弧长是20cm π,面积是2240cm π,则这个扇形的圆心角是 度. 16.如图,O 是ABC ∆的外接圆,已知50ACB ∠=︒,则ABO ∠的大小为 .17.如图,AB 为O 的直径,PAB ∆的边PA ,PB 与O 的交点分别为C 、D .若AC CD DB ==,则P ∠的大小为 度.18.如图,直线334y x =--交x 轴于点A ,交y 轴于点B ,点P 是x 轴上一动点,以点P 为圆心,以1个单位长度为半径作P ,当P 与直线AB 相切时,点P 的坐标是 .三.解答题(共7小题,满分66分,其中19、20题每小题8分,21、22题每小题9分,23、24题每小题10分,25题12分)19.如图所示,破残的圆形轮片上,弦AB 的垂直平分线交弧AB 于点C ,交弦AB 于点D .已知:24AB cm =,8CD cm =.(1)求作此残片所在的圆(不写作法,保留作图痕迹). (2)求残片所在圆的面积.20.如图,已知AB ,CG 是O 的两条直径,AB CD ⊥于点E ,CG AD ⊥于点F . (1)求AOG ∠的度数; (2)若2AB =,求CD 的长.21.如图,四边形ABCD 内接于O ,AD ,BC 的延长线交于点E ,F 是BD 延长线上一点,1602CDE CDF ∠=∠=︒(1)求证:ABC ∆是等边三角形;(2)判断DA ,DC ,DB 之间的数量关系,并证明你的结论.22.如图,PA 、PB 是O 的切线,CD 切O 于点E ,PCD ∆的周长为12,60APB ∠=︒.求:(1)PA 的长; (2)COD ∠的度数.23.如图AB 是O 的直径,点D 在AB 的延长线上,C 、E 是O 上的两点,CE CB =,BCD CAE ∠=∠,延长AE 交BC 的延长线于点F . (1)求证:CD 是O 的切线; (2)求证:CE CF =.24.如图,在Rt ABC ∆中,90C ∠=︒,6AC =,8BC =.(1)以直线BC 为轴,把ABC ∆旋转一周,求所得圆锥的底面圆周长. (2)以直线AC 为轴,把ABC ∆旋转一周,求所得圆锥的侧面积;25.已知二次函数2y x bx c =++的顶点M 在直线4y x =-上,并且图象经过点(1,0)A -. (1)求这个二次函数的解析式;(2)设此二次函数与x 轴的另一个交点为B ,与y 轴的交点为C ,求经过M 、B 、C 三点的圆O '的直径长; (3)设圆O '与y 轴的另一个交点为N ,经过(2,0)P -、N 两点的直线为l ,则圆心O '是否在直线上,请说明理由.2019—2020学年人教版九年级数学上册第24章《圆》单元测试参考简答一.选择题(共10小题)1.A . 2.C . 3.B . 4.D . 5.D . 6.B . 7.C . 8.C . 9.B . 10.C . 二.填空题(共8小题)11. 45cm r cm << . 12. 15 . 13 相切 . 14. 224cm π . 15. 150 . 16. 40︒ . 17. 60 . 18. 7(3-,0) .三.解答题(共7小题)19.如图所示,破残的圆形轮片上,弦AB 的垂直平分线交弧AB 于点C ,交弦AB 于点D .已知:24AB cm =,8CD cm =.(1)求作此残片所在的圆(不写作法,保留作图痕迹). (2)求残片所在圆的面积.【解】:(1)作弦AC 的垂直平分线与弦AB 的垂直平分线交于O 点,以O 为圆心OA 长为半径作圆O 就是此残片所在的圆,如图.(2)连接OA ,设OA x =,12AD cm =,(8)OD x cm =-, 则根据勾股定理列方程:22212(8)x x =+-, 解得:13x =. 即:圆的半径为13cm .所以圆的面积为:2213169()cm ππ⨯=.20.如图,已知AB ,CG 是O 的两条直径,AB CD ⊥于点E ,CG AD ⊥于点F . (1)求AOG ∠的度数; (2)若2AB =,求CD 的长.【解】:(1)连接OD ,AB CD ⊥,∴BC BD =,BOC BOD ∴∠=∠,由圆周角定理得,12A BOD ∠=∠,12A BOD ∴∠=∠,AOG BOD ∠=∠,12A AOG ∴∠=∠,90OFA ∠=︒, 60AOG ∴∠=︒;(2)60AOG ∠=︒, 60COE ∴∠=︒, 30C ∴∠=︒,1122OE OC ∴==,CE ∴= AB CD ⊥,2CD CE ∴==.21.如图,四边形ABCD 内接于O ,AD ,BC 的延长线交于点E ,F 是BD 延长线上一点,1602CDE CDF ∠=∠=︒(1)求证:ABC ∆是等边三角形;(2)判断DA ,DC ,DB 之间的数量关系,并证明你的结论.【解】:(1)证明:1602CDE CDF ∠=∠=︒,60CDE EDF ∴∠=∠=︒,四边形ABCD 内接于O , 60CDE ABC ∴∠=∠=︒,由圆周角定理得,60ACB ADB EDF ∠=∠=∠=︒, ABC ∴∆是等边三角形;(2)解:DA DC DB +=, 理由如下:在BD 上截取PD AD =,60ADP ∠=︒,APD ∴∆为等边三角形, AD AP ∴=,60APD ∠=︒,120APB ∴∠=︒,在APB ∆和ADC ∆中,APB ADC ABP ACD AP AD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()APB ADC AAS ∴∆≅∆, BP CD ∴=,BD BP PD CD AD ∴=+=+.22.如图,PA 、PB 是O 的切线,CD 切O 于点E ,PCD ∆的周长为12,60APB ∠=︒.求:(1)PA 的长; (2)COD ∠的度数.【解】:(1)CA ,CE 都是圆O 的切线,CA CE =∴,同理DE DB =,PA PB =,∴三角形PDE 的周长212PD CD PC PD PC CA BD PA PB PA ++=+++=+===,即PA 的长为6; (2)60P ∠=︒,120PCE PDE ∠+∠=︒∴,360120240ACD CDB ∠+∠=︒-︒=︒∴,CA ,CE 是圆O 的切线,12OCE OCA ACD ∠=∠=∠∴;同理:12ODE CDB ∠=∠, 1()1202OCE ODE ACD CDB ∠+∠=∠+∠=︒∴,18012060COD ∠=-︒=︒∴.23.如图AB 是O 的直径,点D 在AB 的延长线上,C 、E 是O 上的两点,CE CB =,BCD CAE ∠=∠,延长AE 交BC 的延长线于点F . (1)求证:CD 是O 的切线; (2)求证:CE CF =.【解】:(1)连接OC,AB是O的直径,∴∠=︒,ACB90∴∠+∠=︒,CAD ABC90=,CE CBCAE CAB∴∠=∠,∠=∠,BCD CAE∴∠=∠,CAB BCDOB OC=,∴∠=∠,OBC OCB90∴∠+∠=︒,OCB BCDOCD∴∠=︒,90∴是O的切线;CD(2)BAC CAE=,∠=∠=︒,AC AC ∠=∠,90ACB ACFABC AFC ASA∴∆≅∆,()∴=,CB CF又CB CE=,CE CF ∴=.24.如图,在Rt ABC ∆中,90C ∠=︒,6AC =,8BC =.(1)以直线BC 为轴,把ABC ∆旋转一周,求所得圆锥的底面圆周长.(2)以直线AC 为轴,把ABC ∆旋转一周,求所得圆锥的侧面积;【解】:(1)2612ππ⨯=.(2)90C ∠=︒,6AC =,8BC =,10AB ∴=,所以以直线AC 为轴,把ABC ∆旋转一周,得到的圆锥的侧面积11028802ππ=⨯⨯⨯=; 25.已知二次函数2y x bx c =++的顶点M 在直线4y x =-上,并且图象经过点(1,0)A -.(1)求这个二次函数的解析式;(2)设此二次函数与x 轴的另一个交点为B ,与y 轴的交点为C ,求经过M 、B 、C 三点的圆O '的直径长;(3)设圆O '与y 轴的另一个交点为N ,经过(2,0)P -、N 两点的直线为l ,则圆心O '是否在直线上,请说明理由.【解】:(1)二次函数2y x bx c =++的顶点M 的坐标为(2b -,24)4c b -在直线4y x =-上, ∴2442c b b -=-①,图象经过点(1,0)A -. 01b c ∴=-+②,联立①②得244201c b b b c ⎧-=-⎪⎨⎪=-+⎩①②,解得:23b c =-⎧⎨=-⎩,故223y x x =--;(2)2223(1)4y x x x =--=--; ∴与y 轴的交点C 的坐标是(0,3)-,顶点M 的坐标是(1,4)- 设0y =,则2230x x --=,解得1x =-或3, ∴二次函数与x 轴的另一个交点B 的坐标是(3,0), 过M 作ME OE ⊥,过B 作BF EM ⊥交EM 于F ,3OC ∴=,3OB =,1CE OE OC =-=,2MF =,4BF =,1EM = 在Rt BOC ∆,Rt CEM ∆,Rt BFM ∆中,利用勾股定理得:32BC =,2MC =25BM =,2220BC MC +=,2BM = 222BC MC BM ∴+=,MBC ∴∆为直角三角形,且90BCM ∠=︒,O ∴'的直径长为BM =;(3)圆心O '是在直线上,理由如下:过O '作x 轴的垂线,交x 轴于R ,过O '作y 轴的垂线,交y 轴于T ,交MQ 于S ,设O '与x 轴的另一个交点为Q ,连接MQ ,由BM 是O '的直径,知90BQM ∠=︒. (1,0)Q ∴,2BQ =,O R OB '⊥,1QR ∴=,2OR ∴=,在Rt △O RB '中,2O R '=,O ∴'的坐标为(2,2)-,2OT ∴=,3OC =, 1TC ∴=,1NC ∴=,1ON ∴=,N ∴的坐标为(0,1)-设过PN 的直线解析式为y kx b =+,把N 的坐标为(0,1)-和(2,0)P -分别代入求得12k =-,1b =-, ∴过PN 的直线解析式为112y x =--, O '的坐标为(2,2)-,122122∴-=-⨯-=-, ∴圆心O '是在直线上.。
2019年秋人教版九年级上册数学同步练习(PDF,无答案):24.2 点和圆、直线和圆的位置关系

是 ꎮ
4������ 已知☉O 的半径 r = 6ꎬ圆心 O 到直线 l 的距离 d 恰好是方程 x 2 - 6x + 5 = 0 的两根之和ꎬ试判断直线 l
与☉O 的位置关系是 ꎮ
5������ 直线 l 与半径为 r 的☉O 相交ꎬ且点 O 到直线 l 的距离为 6ꎬ则 r 的取值范围是( ) ꎮ
D������ 不能确定
7������ Rt△ABC 中ꎬ∠C = 90°ꎬAB = 10ꎬAC = 6ꎬ以 C 为圆心作☉C 和 AB 相切ꎬ则☉C 的半径长为( ) ꎮ
A������ 8
B������ 4
C������ 9������ 6
D������ 4������ 8
8������ 菱形对角线的交点为 Oꎬ以 O 为圆心ꎬ以 O 到菱形一边的距离为半径的圆与其他几边的关系为(
— 51 —
24������ 2������ 2 直线和圆的位置关系 第一课时 直线和圆的位置关系(1)
基础练习
1������ 已知☉O 的直径为 10 cmꎬ点 O 到直线 a 的距离为 dꎮ (1) 直线 a 与☉O 相切ꎬ则d = cmꎻ
(2) 若 d = 4 cmꎬ则直线 a 与☉O 有 个公共点ꎻ(3) 若 d = 6 cmꎬ则直线 a 与☉O ꎮ
4������ 已知:如图 24 ̄2 ̄35 所示ꎬAB 为☉O 直径ꎬBC 交☉O 于点 DꎬDE⊥AC 于 Eꎬ要使 DE 是☉O 的切线ꎬ那
么图中的角应满足的条件为 (只需填一个条件)ꎮ
图 24 ̄2 ̄33
图 24 ̄2 ̄34
图 24 ̄2 ̄35
— 53 —
5������ 如图 24 ̄2 ̄36 所示ꎬ已知☉O 中ꎬAB 是直径ꎬ过 B 点作☉O 的切线ꎬ连接 COꎬ若 AD∥OC 交☉O 于 Dꎬ 求证:CD 是☉O 的切线ꎮ
人教版 九年级上册数学 24.2 点和圆、直线和圆的位置关系 同步训练(含答案)

人教版九年级数学24.2 点和圆、直线和圆的位置关系同步训练一、选择题(本大题共10道小题)1. 下列直线中,一定是圆的切线的是()A.与圆有公共点的直线B.垂直于圆的半径的直线C.到圆心的距离等于半径的直线D.经过圆的直径一端的直线2. 下列说法中,正确的是()A.垂直于半径的直线是圆的切线B.经过半径的外端且垂直于这条半径的直线是圆的切线C.经过半径的端点且垂直于这条半径的直线是圆的切线D.到圆心的距离等于直径的直线是圆的切线3. 如图,P是⊙O外一点,OP交⊙O于点A,OA=AP.甲、乙两人想作一条经过点P且与⊙O相切的直线,其作法如下:甲:以点A为圆心,AP长为半径画弧,交⊙O于点B,则直线BP即为所求.乙:过点A作直线MN⊥OP,以点O为圆心,OP长为半径画弧,交射线AM于点B,连接OB,交⊙O于点C,直线CP即为所求.对于甲、乙两人的作法,下列判断正确的是()A.甲正确,乙错误B.乙正确,甲错误C.两人都正确D.两人都错误4. 已知⊙O的半径为5 cm,圆心O到直线l的距离为5 cm,则直线l与⊙O的位置关系为()A.相交B.相切C.相离D.无法确定5. 如图,AB为⊙O的切线,切点为A,连接AO,BO,BO与⊙O交于点C,延长BO与⊙O交于点D,连接AD.若∠ABO=36°,则∠ADC的度数为()A.54° B.36° C.32° D.27°6. 如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是()A.DE=DO B.AB=ACC.CD=DB D.AC∥OD7.⊙⊙⊙AB⊙⊙O⊙⊙⊙⊙AC⊙⊙O⊙A⊙BC⊙⊙O⊙⊙D⊙⊙⊙C⊙70°⊙⊙⊙AOD⊙⊙⊙⊙( )A. 70°B. 35°C⊙20°D. 40°8. 2020·黄石模拟如图,在平面直角坐标系中,A(-2,2),B(8,2),C(6,6),点P为⊙ABC的外接圆的圆心,将⊙ABC绕点O逆时针旋转90°,点P的对应点P′的坐标为()A.(-2,3) B.(-3,2)C.(2,-3) D.(3,-2)9. 如图,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在⊙O外、⊙O内、⊙O上,则原点O的位置应该在()图A.点A与点B之间靠近点AB.点A与点B之间靠近点BC.点B与点C之间靠近点BD.点B与点C之间靠近点C10. 如图,在⊙ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值为()A.5 B.4 2 C.4.75 D.4.8二、填空题(本大题共7道小题)11. 如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是__________.12. 如图,∠APB=30°,⊙O的半径为1 cm,圆心O在直线PB上,OP=3 cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为__________.13. 如图,半圆的圆心O 与坐标原点重合,半圆的半径为1,直线l 的解析式为y =x +t .若直线l 与半圆只有一个公共点,则t 的取值范围是________.14. 如图,⊙O 的半径为1,正方形ABCD 的对角线长为6,OA =4.若将⊙O 绕点A 按顺时针方向旋转360°,则在旋转的过程中,⊙O 与正方形ABCD 的边只有一个公共点的情况一共出现( )A .3次B .4次C .5次D .6次15. 如图所示,在半圆O 中,AB 是直径,D 是半圆O 上一点,C 是AD ︵的中点,CE ⊥AB 于点E ,过点D 的切线交EC 的延长线于点G ,连接AD ,分别交CE ,CB 于点P ,Q ,连接AC ,有下列结论:①∠BAD =∠ABC ;②GP =GD ;③点P 是⊙ACQ 的外心.其中正确的结论是________(只需填写序号).16.⊙⊙⊙⊙⊙⊙ABCD ⊙⊙⊙⊙8⊙M ⊙AB ⊙⊙⊙⊙P ⊙BC ⊙⊙⊙⊙⊙⊙⊙⊙PM ⊙⊙⊙P ⊙⊙⊙⊙PM ⊙⊙⊙⊙⊙⊙P .⊙⊙P ⊙⊙⊙⊙ABCD ⊙⊙⊙⊙⊙⊙BP ⊙⊙⊙________⊙17. 如图,⊙M的圆心为M(-2,2),半径为2,直线AB过点A(0,-2),B(2,0),则⊙M关于y轴对称的⊙M′与直线AB的位置关系是________.三、解答题(本大题共4道小题)18. 如图,点O在∠APB的平分线上,⊙O与P A相切于点C.求证:直线PB与⊙O相切.19.⊙⊙⊙⊙ABC⊙⊙⊙⊙O⊙⊙B⊙60°⊙CD⊙⊙O⊙⊙⊙⊙P⊙CD⊙⊙⊙⊙⊙⊙⊙⊙⊙AP⊙AC.(1)⊙⊙⊙P A⊙⊙O⊙⊙⊙⊙(2)⊙PD⊙5⊙⊙⊙O⊙⊙⊙⊙20. 在Rt⊙ABC中,∠C=90°,AB=13,AC=5.(1)以点A为圆心,4为半径的⊙A与直线BC的位置关系是________;(2)以点B为圆心的⊙B与直线AC相交,求⊙B的半径r的取值范围;(3)以点C为圆心,R为半径的⊙C与直线AB相切,求R的值.21. 如图,点E是⊙ABC的内心,AE的延长线交BC于点F,交⊙ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.求证:直线DM 是⊙O的切线.人教版九年级数学24.2 点和圆、直线和圆的位置关系同步训练-答案一、选择题(本大题共10道小题)1. 【答案】C2. 【答案】B3. 【答案】C[解析] 对于甲的作法:连接OB,如图①.∵OA=AP,∴OP为⊙A的直径,∴∠OBP=90°,即OB⊥PB,∴PB为⊙O的切线,∴甲的作法正确.对于乙的作法:如图②,∵MN ⊥OP ,∴∠OAB =90°.在⊙OAB 和⊙OCP 中,⎩⎨⎧OA =OC ,∠AOB =∠COP ,OB =OP ,∴△OAB ≌△OCP ,∴∠OAB =∠OCP =90°,即OC ⊥PC , ∴PC 为⊙O 的切线, ∴乙的作法正确.4. 【答案】B5. 【答案】D[解析] ∵AB 为⊙O 的切线,∴∠OAB =90°.∵∠ABO =36°,∴∠AOB =90°-∠ABO =54°. ∴∠ADC =12∠AOB =27°.故选D.6. 【答案】A7.【答案】D⊙⊙⊙⊙⊙AB ⊙⊙O ⊙⊙⊙⊙AC ⊙⊙O ⊙⊙A ⊙⊙⊙BAC ⊙90°⊙⊙⊙C ⊙70°⊙⊙⊙B ⊙20°⊙⊙⊙AOD ⊙⊙B ⊙⊙BDO ⊙2⊙B ⊙2×20°⊙40°.8. 【答案】A9. 【答案】C[解析] 如图.10. 【答案】D[解析] 如图,设PQ的中点为F,⊙F与AB 的切点为D,连接FD,FC,CD.∵AB=10,AC=8,BC=6,∴∠ACB=90°,∴PQ为⊙F的直径.∵⊙F与AB相切,∴FD⊥AB,FC+FD=PQ,而FC+FD≥CD,∴当CD为Rt△ABC的斜边AB上的高且点F在CD上时,PQ有最小值,为CD 的长,即CD为⊙F的直径.∵S△ABC =12BC·AC=12CD·AB,∴CD=4.8.故PQ的最小值为4.8.二、填空题(本大题共7道小题)11. 【答案】3<r<5[解析] 连接BD.在Rt⊙ABD中,AB=4,AD=3,则BD=32+42=5.由题图可知3<r<5.12. 【答案】1 cm或5 cm[解析] 当⊙O与直线PA相切时,点O到直线PA的距离为1 cm.∵∠APB=30°,∴PO=2 cm,∴圆心O移动的距离为3-2=1(cm)或3+2=5(cm).13. 【答案】t=2或-1≤t<1[解析] 若直线与半圆只有一个公共点,则有两种情况:直线和半圆相切于点C或从直线过点A开始到直线过点B结束(不包括直线过点A).直线y=x+t与x轴所形成的锐角是45°.当点O到直线l的距离OC=1时,直线l与半圆O相切,设直线l与y轴交于点D,则OD=2,即t= 2.当直线过点A时,把A(-1,0)代入直线l的解析式,得t=y-x=1.当直线过点B时,把B(1,0)代入直线l的解析式,得t=y-x=-1.即当t =2或-1≤t <1时,直线和半圆只有一个公共点. 故答案为t =2或-1≤t <1.14. 【答案】B[解析] ∵正方形ABCD 的对角线长为6,∴它的边长为3 2.如图,⊙O 与正方形ABCD 的边AB ,AD 只有一个公共点的情况各有1次,与边BC ,CD 只有一个公共点的情况各有1次,∴在旋转的过程中,⊙O 与正方形ABCD 的边只有一个公共点的情况一共出现4次.15. 【答案】②③[解析] ∵在半圆O 中,AB 是直径,D 是半圆O 上一点,C 是AD ︵的中点,∴AC ︵=DC ︵,但不一定等于DB ︵,∴∠BAD 与∠ABC 不一定相等,故①错误. 如图,连接OD ,则OD ⊥GD ,∠OAD =∠ODA .∵∠ODA +∠GDP =90°,∠OAD +∠GPD =∠OAD +∠APE =90°,∴∠GPD =∠GDP ,∴GP =GD ,故②正确. 补全⊙O ,延长CE 交⊙O 于点F . ∵CE ⊥AB ,∴A 为FC ︵的中点,即AF ︵=AC ︵. 又∵C 为AD ︵的中点,∴CD ︵=AC ︵,∴AF ︵=CD ︵, ∴∠CAP =∠ACP ,∴AP =CP . ∵AB 为⊙O 的直径,∴∠ACQ =90°,∴∠ACP +∠PCQ =90°,∠CAP +∠PQC =90°, ∴∠PCQ =∠PQC ,∴PC =PQ ,∴AP =PQ ,即P 为Rt △ACQ 的斜边AQ 的中点, ∴点P 为Rt △ACQ 的外心,故③正确.16. 【答案】3或4 3 [解析] 如图⊙,当⊙P 与CD 边相切时,设PC =PM =x .在Rt⊙PBM 中,⊙PM2=BM2+BP2,⊙x2=42+(8-x)2,⊙x=5,⊙PC=5,⊙BP=BC-PC=8-5=3.如图⊙,当⊙P与AD边相切时.设切点为K,连接PK,则PK⊙AD,四边形PKDC 是矩形,⊙PM=PK=CD=2BM,⊙BM=4,PM=8,在Rt⊙PBM中,BP=82-42=4 3.综上所述,BP的长为3或4 3.17. 【答案】相交[解析] ∵⊙M的圆心为M(-2,2),则⊙M关于y轴对称的⊙M′的圆心为M′(2,2).因为M′B=2>点M′到直线AB的距离,所以直线AB与⊙M′相交.三、解答题(本大题共4道小题)18. 【答案】证明:如图,连接OC,过点O作OD⊥PB于点D.∵⊙O与P A相切于点C,∴OC⊥P A.∵点O在∠APB的平分线上,OC⊥P A,OD⊥PB,∴OD=OC,∴直线PB与⊙O相切.19. 【答案】解:(1)证明:如图,连接OA.⊙⊙B=60°,⊙⊙AOC=2⊙B=120°.又⊙OA=OC,⊙⊙OAC=⊙OCA=30°.又⊙AP=AC,⊙⊙P=⊙OCA=30°,⊙⊙OAP=⊙AOC-⊙P=90°,⊙OA⊙P A.又⊙OA是⊙O的半径,⊙P A是⊙O的切线.(2)在Rt⊙OAP中,⊙⊙P=30°,⊙PO=2OA=OD+PD.又⊙OA=OD,⊙PD=OD=OA.⊙PD=5,⊙2OA=2PD=2 5,⊙⊙O的直径为2 5.20. 【答案】解:(1)∵AC⊥BC,而AC>4,∴以点A为圆心,4为半径的⊙A与直线BC相离.故答案为相离.(2)BC=AB2-AC2=12.∵BC⊥AC,∴当⊙B 的半径大于BC 的长时,以点B 为圆心的⊙B 与直线AC 相交,即r >12.(3)如图,过点C 作CD ⊥AB 于点D .∵12CD ·AB =12AC ·BC ,∴CD =5×1213=6013.即当R =6013时,以点C 为圆心,R 为半径的⊙C 与直线AB 相切.21. 【答案】证明:如图,作直径DG ,连接BG.∵点E 是⊙ABC 的内心,∴AD 平分∠BAC ,∴∠BAD =∠DAC.∵∠G =∠BAD ,∠BDM =∠DAC ,∴∠BDM =∠G.∵DG 为⊙O 的直径,∴∠GBD =90°,∴∠G +∠BDG =90°,∴∠BDM +∠BDG =90°,即∠MDG =90°.又∵OD 是⊙O 的半径,∴直线DM 是⊙O 的切线.。
新人教版九年级数学上24.2.1点和圆的位置关系同步测试含答案.doc
1《24.2.1 点和圆的位置关系》一、选择题1.下列说法正确的是( )A .过一点A 的圆的圆心可以是平面上任意点B .过两点A 、B 的圆的圆心在一条直线上C .过三点A 、B 、C 的圆的圆心有且只有一点D .过四点A 、B 、C 、D 的圆不存在2.若△ABC 的外接圆的圆心在△ABC 的内部,则△ABC 是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .无法确定3.在Rt △ABC 中,∠C=90°,AC=6cm ,BC=8cm ,则它的外心与顶点C 的距离为( ) A .5cm B .6cm C .7cm D .8cm4.如图所示,一圆弧过方格的格点A 、B 、C ,试在方格中建立平面直角坐标系,使点A 的坐标为(﹣2,4),则该圆弧所在圆的圆心坐标是( )A .(﹣1,2)B .(1,﹣1)C .(﹣1,1)D .(2,1)5.Rt △ABC 中,∠C=90°,AC=2,BC=4,如果以点A 为圆心,AC 为半径作⊙A ,那么斜边中点D 与⊙A 的位置关系是( )A .点D 在⊙A 外B .点D 在⊙A 上C .点D 在⊙A 内 D .无法确定6.若⊙A 的半径为5,圆心A 的坐标是(3,4),点P 的坐标是(5,8),你认为点P 的位置为( ) A .在⊙A 内 B .在⊙A 上 C .在⊙A 外 D .不能确定 7.如图,⊙O 是△ABC 的外接圆,若∠B=30°,AC=,则⊙O 的直径为( )2A .1B .C .2D .8.用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应该假设这个三角形中( )A .有一个内角小于60°B .每一个内角都小于60°C .有一个内角大于60°D .每一个内角都大于60° 二、填空题9.点A 在以O 为圆心,3cm 为半径的⊙O 内,则点A 到圆心O 的距离d 的范围是______. 10.如图,在△ABC 中,∠ACB=90°,AC=2cm ,BC=4cm ,CM 为中线,以C 为圆心,cm 为半径作圆,则A 、B 、C 、M 四点在圆外的有______,在圆上的有______,在圆内的有______.11.若AB=4cm ,则过点A 、B 且半径为3cm 的圆有______个.12.在△ABC 中,BC=24cm ,外心O 到BC 的距离为6cm ,则△ABC 外接圆的半径为______. 13.一点和⊙O 上的最近点距离为4cm ,最远距离为9cm ,则这个圆的半径是______.14.阅读下面材料:对于平面图形A ,如果存在一个圆,使图形A 上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A 被这个圆所覆盖.回答下列问题:(1)边长为1cm 的正方形被一个半径为r 的圆所覆盖,r 的最小值是______ cm ; (2)边长为1cm 的等边三角形被一个半径为r 的圆所覆盖,r 的最小值是______ cm .15.若Rt △ABC 的两条直角边a ,b 是方程x 2﹣3x+1=0的两根,则Rt △ABC 的外接圆面积是______. 三、解答题16.已知圆的半径等于5cm ,根据下列点P 到圆心的距离:(1)4cm ;(2)5cm ;(3)6cm ,判定点P 与圆的位置关系,并说明理由.17.在Rt△ABC中,∠C=90°,BC=3m,AC=4m,以B为圆心,以BC为半径作⊙B,D、E是AB、AC中点,A、C、D、E分别与⊙O有怎样的位置关系?(画出图形,写过程)18.(教材变式题)如图所示,△ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.19.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.(1)求证:BD=CD;(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.20.某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.3《24.2.1 点和圆的位置关系》参考答案与试题解析一、选择题1.下列说法正确的是()A.过一点A的圆的圆心可以是平面上任意点B.过两点A、B的圆的圆心在一条直线上C.过三点A、B、C的圆的圆心有且只有一点D.过四点A、B、C、D的圆不存在【解答】解:A、过一点A的圆的圆心可以是平面上任意点(A点外),故本选项错误,B、过两点A、B的圆的圆心在一条直线上,错误,C、正确,D、过四点A、B、C、D的圆可以存在,故本选项错误,故选:B.2.若△ABC的外接圆的圆心在△ABC的内部,则△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.无法确定【解答】解:△ABC的外接圆的圆心在△ABC的内部,则△ABC是锐角三角形.故选A.3.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为()A.5cm B.6cm C.7cm D.8cm【解答】解:∵∠C=90°,AC=6cm,BC=8cm,∴AB==10cm,∵Rt△ABC的外心为斜边AB的中点,∴Rt△ABC的外接圆半径为5cm,∴它的外心与顶点C的距离为5cm.故选A.454.如图所示,一圆弧过方格的格点A 、B 、C ,试在方格中建立平面直角坐标系,使点A 的坐标为(﹣2,4),则该圆弧所在圆的圆心坐标是( )A .(﹣1,2)B .(1,﹣1)C .(﹣1,1)D .(2,1) 【解答】解:如图所示, ∵AW=1,WH=3, ∴AH==;∵BQ=3,QH=1, ∴BH==;∴AH=BH , 同理,AD=BD ,所以GH 为线段AB 的垂直平分线, 易得EF 为线段AC 的垂直平分线, H 为圆的两条弦的垂直平分线的交点, 则BH=AH=HC , H 为圆心.于是则该圆弧所在圆的圆心坐标是(﹣1,1). 故选C .65.Rt △ABC 中,∠C=90°,AC=2,BC=4,如果以点A 为圆心,AC 为半径作⊙A ,那么斜边中点D 与⊙A 的位置关系是( )A .点D 在⊙A 外B .点D 在⊙A 上C .点D 在⊙A 内 D .无法确定 【解答】解:根据勾股定理求得斜边AB==2,则AD=,∵>2,∴点在圆外. 故选A .6.若⊙A 的半径为5,圆心A 的坐标是(3,4),点P 的坐标是(5,8),你认为点P 的位置为( ) A .在⊙A 内 B .在⊙A 上 C .在⊙A 外 D .不能确定 【解答】解:∵AP==2<5,∴点P 在⊙A 内, 故选A .7.如图,⊙O 是△ABC 的外接圆,若∠B=30°,AC=,则⊙O 的直径为( )A .1B .C .2D .【解答】解:作直径AD ,连结CD ,如图, ∵AD 为直径, ∴∠ACD=90°, ∵∠D=∠B=30°, ∴AD=2AC=2.故选D .78.用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应该假设这个三角形中( )A .有一个内角小于60°B .每一个内角都小于60°C .有一个内角大于60°D .每一个内角都大于60°【解答】解:用反证法证明“三角形中必有一个内角小于或等于60°”时, 应先假设三角形中每一个内角都不小于或等于60°,即每一个内角都大于60°. 故选:D . 二、填空题9.点A 在以O 为圆心,3cm 为半径的⊙O 内,则点A 到圆心O 的距离d 的范围是 0≤d <3cm . 【解答】解:∵点A 在以O 为圆心,3cm 为半径的⊙O 内, ∴点A 到圆心O 的距离d 的范围是:0≤d <3cm . 故答案为:0≤d <3cm .10.如图,在△ABC 中,∠ACB=90°,AC=2cm ,BC=4cm ,CM 为中线,以C 为圆心,cm 为半径作圆,则A 、B 、C 、M 四点在圆外的有 点B ; ,在圆上的有 点M ; ,在圆内的有 点A 、C . .【解答】解:∵△ABC 中,∠ACB=90°,AC=2cm ,BC=4cm , ∴AB==2,∵CM 为中线, ∴CM=AB=,8∴AC <cm ,BC >cm ,∴在圆外的有点B ,在圆上的有点M ,在圆内的有点C 和点A , 故答案为:点B ; 点M ; 点A 、C .11.若AB=4cm ,则过点A 、B 且半径为3cm 的圆有 两 个.【解答】解:这样的圆能画2个.如图,作AB 的垂直平分线l ,再以点A 为圆心,3cm 为半径作圆交l 于O 1和O 2,然后分别以O 1和O 2为圆心,以3cm 为半径作圆, 则⊙O 1和⊙O 2为所求圆.故答案为:两.12.在△ABC 中,BC=24cm ,外心O 到BC 的距离为6cm ,则△ABC 外接圆的半径为 .【解答】解:过O 作OD ⊥BC ,由垂径定理得, BD=BC=12cm ,在Rt △OBD 中,OD=6cm ,BD=12cm , ∴OB==cm ,即△ABC 外接圆的半径为cm .13.一点和⊙O 上的最近点距离为4cm ,最远距离为9cm ,则这个圆的半径是 6.5cm 或2.5cm .9【解答】解:点P 应分为位于圆的内部与外部两种情况讨论:①当点P 在圆内时,最近点的距离为4cm ,最远点的距离为9cm ,则直径是4+9=13cm ,因而半径是6.5cm ;②当点P 在圆外时,最近点的距离为4cm ,最远点的距离为9cm ,则直径是9﹣4=5cm ,因而半径是2.5cm .故答案为6.5cm 或2.5cm .14.阅读下面材料:对于平面图形A ,如果存在一个圆,使图形A 上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A 被这个圆所覆盖.回答下列问题: (1)边长为1cm 的正方形被一个半径为r 的圆所覆盖,r 的最小值是cm;(2)边长为1cm 的等边三角形被一个半径为r 的圆所覆盖,r 的最小值是cm .【解答】解:(1)正方形ABCD 的边长为1cm ,则正方形ABCD 被一个半径为r 的圆所覆盖,r 的最小值为其外接圆的半径,如图1,正方形ABCD 的外接圆为⊙0, ∵∠B=90°, ∴AC 为直径, ∴AC=AB=,∴OA=,∴r 的最小值是cm ; (2)边长为1cm 的等边三角形ABC 被一个半径为r 的圆所覆盖,r 的最小值为其外接圆的半径,如图2,等边三角形ABC 的外接圆为⊙0, 连结OB ,作OD ⊥BC 于D , ∵点O 为等边三角形ABC 的外心, ∴OB 平分∠ABC , ∴∠OBD=30°,10∵OD ⊥BC , ∴BD=BC=,在Rt △BOD 中,∵cos ∠OBD=,∴OB===,∴r 的最小值是cm . 故答案为;.15.若Rt △ABC 的两条直角边a ,b 是方程x 2﹣3x+1=0的两根,则Rt △ABC 的外接圆面积是π.【解答】解:∵圆的半径r=c ,根据两直角边a 、b 分别是一元二次方程x 2﹣3x+1=0的两根,可得 a+b=3,a •b=1,∴c 2=a 2+b 2=(a+b )2﹣2a •b=7, ∴Rt △的外接圆的面积为πr 2=π×()2=π.故答案为:π. 三、解答题11 16.已知圆的半径等于5cm ,根据下列点P 到圆心的距离:(1)4cm ;(2)5cm ;(3)6cm ,判定点P 与圆的位置关系,并说明理由.【解答】解:(1)当d=4 cm 时,∵d <r ,∴点P 在圆内;(2)当d=5 cm 时,∵d=r ,∴点P 在圆上;(3)当d=6 cm 时,∵d >r ,∴点P 在圆外.17.在Rt △ABC 中,∠C=90°,BC=3m ,AC=4m ,以B 为圆心,以BC 为半径作⊙B ,D 、E 是AB 、AC 中点,A 、C 、D 、E 分别与⊙O 有怎样的位置关系?(画出图形,写过程)【解答】解:∵BC=3=R ,∴点C 在⊙B 上,∵AB=5>3,∴点A 在⊙B 外,∵D 为BA 中点,∴, ∴点D 在⊙B 内,∵E 为AC 中点,∴, 连结BE ,∴BE===>3m , ∴E 在⊙B 外.1218.(教材变式题)如图所示,△ABC 中,AB=AC=10,BC=12,求△ABC 外接圆的半径.【解答】解:如图,作AD ⊥BC ,垂足为D ,则O 一定在AD 上,所以AD==8;设OA=r ,OB 2=OD 2+BD 2,即r 2=(8﹣r )2+62,解得r=.答:△ABC 外接圆的半径为.19.如图,AD 为△ABC 外接圆的直径,AD ⊥BC ,垂足为点F ,∠ABC 的平分线交AD 于点E ,连接BD ,CD .(1)求证:BD=CD ;(2)请判断B ,E ,C 三点是否在以D 为圆心,以DB 为半径的圆上?并说明理由.13 【解答】(1)证明:∵AD 为直径,AD ⊥BC ,∴由垂径定理得:∴根据圆心角、弧、弦之间的关系得:BD=CD .(2)解:B ,E ,C 三点在以D 为圆心,以DB 为半径的圆上.理由:由(1)知:,∴∠1=∠2,又∵∠2=∠3,∴∠1=∠3,∴∠DBE=∠3+∠4,∠DEB=∠1+∠5,∵BE 是∠ABC 的平分线,∴∠4=∠5,∴∠DBE=∠DEB ,∴DB=DE .由(1)知:BD=CD∴DB=DE=DC .∴B ,E ,C 三点在以D 为圆心,以DB 为半径的圆上.(7分)20.某公园有一个边长为4米的正三角形花坛,三角形的顶点A 、B 、C 上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.14【解答】解:(1)(2);(3)连接OB ,OA ,并延长AO 交BC 于D , ∵r=OB==, ∴S ⊙O =πr 2=≈16.75,又S 平行四边形=2S △ABC =2××42×sin60°=8≈13.86, ∵S ⊙O >S 平行四边形,∴选择建圆形花坛面积较大.15。
2019-2020学年人教版初三上《第24章圆》单元测试题(有答案)
单元测试(四) 圆(满分:120分 考试时间:120分钟)一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求)1.已知⊙O 的半径是5,直线l 是⊙O 的切线,则点O 到直线l 的距离是(C)A .2.5B .3C .5D .102.如图,在△ABC 中,AB =BC =2,以AB 为直径的⊙O 与BC 相切于点B ,则AC 等于(C)A. 2B. 3 C .2 2 D .2 33.如图,⊙O 是△ABC 的外接圆,连接OB ,OC.若OB =BC ,则∠BAC 等于(C)A .60°B .45°C .30°D .20°4.如图,AB ,CD 是⊙O 的直径,AE ︵=BD ︵.若∠AOE =32°,则∠COE 的度数是(D)A .32°B .60°C .68°D .64°5.如图,C ,D 是以线段AB 为直径的⊙O 上两点.若CA =CD ,且∠ACD =40°,则∠CAB =(B)A .10°B .20°C .30°D .40°6.如图,四边形ABCD 是⊙O 的内接四边形,⊙O 的半径为2,∠B =135°,则AC ︵的长(B)A .2πB .Π C.π2D.π37.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60 cm ,则这块扇形铁皮的半径是(A)A .40 cmB .50 cmC .60 cmD .80 cm8.如图,AB 是⊙O 的直径,CD 是弦,AB ⊥CD ,垂足为点E ,连接OD ,CB ,AC ,∠DOB =60°,EB =2,那么CD 的长为(D)A. 3 B .2 3 C .3 3 D .4 39.如图,△ABC 是一张三角形纸片,⊙O 是它的内切圆,点D 、E 是其中的两个切点,已知AD =6 cm ,小明准备用剪刀沿着与⊙O 相切的一条直线MN 剪下一块三角形(△AMN),则剪下的△AMN 的周长是(B)A .9 cmB .12 cmC .15 cmD .18 cm10.如图,在Rt △AOB 中,∠AOB =90°,OA =3,OB =2,将Rt △AOB 绕点O 顺时针旋转90°后得Rt △FOE ,将线段EF 绕点E 逆时针旋转90°后得线段ED ,分别以O ,E 为圆心,OA ,ED 长为半径画弧AF 和弧DF ,连接AD ,则图中阴影部分面积是(D)A .Π B.5π4C .3+π D .8-π二、填空题(每大题共5个小题,每小题3分,共15分)11.如图,在矩形ABCD中,AB=3,AD=4.若以点A为圆心,4为半径作⊙A,则点A,点B,点C,点D四点中在⊙A外的是点C.12.已知△ABC的三边长分别是6,8,10,则△ABC外接圆的直径是10.13.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为14.如图,AP为⊙O的切线,P为切点.若∠A=20°,C,D为圆周上的两点,且∠PDC=60°,则∠OBC等于65°.15.如图,四边形OABC是菱形,点B,C在以点O为圆心的弧EF上,且∠1=∠2.若扇形OEF的面积为3π,则菱形OABC的边长为3.三、解答题(本大题共8个小题,共75分.解答应写出文字说明,证明过程或演算步骤)16.(本大题共2小题,每小题5分,共10分)(1)如图,在△AOC中,∠AOC=90°,以点O为圆心,OA为半径的圆交AC于点B,且OB =BC,求∠A的度数.解:∵OA =OB ,OB =BC ,∴∠A =∠OBA ,∠BOC =∠C , 又∵∠OBA =∠BOC +∠C ,∴∠A =2∠C.∵△AOC 中,∠AOC =90°,∴∠A +∠C =90°,即3∠C =90°. ∴∠C =30°,∠A =60°.(2)如图,AB 是⊙O 的直径,∠ACD =25°,求∠BAD 的度数.解:∵AB 为⊙O 的直径, ∴∠ADB =90°.∵相同的弧所对应的圆周角相等,且∠ACD =25°, ∴∠B =25°.∴∠BAD =90°-∠B =65°.17.(本题6分)如图,在⊙O 中,AC ︵=CB ︵,CD ⊥OA 于D ,CE ⊥OB 于E ,求证:AD =BE. 证明:连接OC ,∵AC ︵=CB ︵, ∴∠AOC =∠BOC.∵CD ⊥OA 于D ,CE ⊥OB 于E , ∴∠CDO =∠CEO =90°. 在△COD 和△COE 中,⎩⎨⎧∠DOC =∠EOC ,∠CDO =∠CEO ,CO =CO ,∴△COD ≌△COE(AAS). ∴OD =OE.∵AO =BO , ∴AD =BE.18.(本题7分)“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”此问题的实质就是解决下面的问题:“如果CD 为⊙O 的直径,弦AB ⊥CD 于E ,CE =1寸,AB =10寸,那么直径CD 的长为多少寸?”请你求出CD 的长.解:设直径CD 的长为2x ,则半径OC =x ,OE =x -1. ∵CD 为⊙O 的直径,弦AB ⊥CD 于E ,AB =10, ∴AE =BE =12AB =12×10=5.连接OB ,则OB =x ,根据勾股定理,得x 2=52+(x -1)2, 解得x =13,CD =2x =2×13=26(寸).19.(本题9分)如图,在平面直角坐标系中,已知点A(1,3),B(3,3),C(4,2). (1)请在图中作出经过A ,B ,C 三点的⊙M ,并写出圆心M 的坐标; (2)若D(1,4),则直线BD 与⊙M 的位置关系是相切.解:如图所示,圆心M 的坐标为(2,1).20.(本题9分)如图,△ABC 是直角三角形,∠ACB =90°.(1)尺规作图:作⊙C ,使它与AB 相切于点D ,与AC 相交于点E ,保留作图痕迹,不写作法,请标明字母;(2)在你按(1)中要求所作的图中,若BC =3,∠A =30°,求DE ︵的长.解:(1)如图,⊙C 为所求.(2)∵⊙C 切AB 于D ,∴CD ⊥AB.∴∠ADC =90°.∴∠DCE =90°-∠A =90°-30°=60°.∴∠BCD =90°-∠ACD =30°. 在Rt △BCD 中,BC =3,∴BD =12BC =32,CD =BC 2-BD 2=332. ∴DE ︵的长为60·π·332180=32π.21.(本题9分)如图,⊙O 的直径AB =12 cm ,C 为AB 延长线上一点,CP 与⊙O 相切于点P ,过点B 作弦BD ∥CP ,连接PD. (1)求证:点P 为BD ︵的中点;(2)若∠C =∠D ,求四边形BCPD 的面积.解:(1)证明:连接OP ,交BD 于E.∵CP 与⊙O 相切于点P ,∴PC ⊥OP.∴∠OPC =90°. ∵BD ∥CP ,∴∠OEB =∠OPC =90°. ∴BD ⊥OP.∴点P 为BD ︵的中点.(2)∵∠C =∠D ,∠POB =2∠D ,∴∠POB =2∠C. ∵∠CPO =90°,∴∠C =30°.∵BD ∥CP ,∴∠C =∠DBA.∴∠D =∠DBA. ∴BC ∥PD.∴四边形BCPD 是平行四边形. ∵PO =12AB =6,∴PC =6 3.∵∠ABD =∠C =30°,∴OE =12OB =3.∴PE =3.∴四边形BCPD 的面积为PC·PE =63×3=183(cm 2).22.(本题12分)如图,△ABD 是⊙O 的内接三角形,E 是弦BD 的中点,点C 是⊙O 外一点且∠DBC =∠A ,连接OE 并延长与圆相交于点F ,与BC 相交于点C. (1)求证:BC 是⊙O 的切线;(2)若⊙O 的半径为6,BC =8,求弦BD 的长.解:(1)证明:连接OB ,∵E 是弦BD 的中点,∴BE =DE ,OE ⊥BD, BF ︵=DF ︵=12BD ︵. ∴∠BOE =∠A ,∠OBE +∠BOE =90°.∵∠DBC =∠A ,∴∠BOE =∠DBC.∴∠OBE +∠DBC =90°.∴∠OBC =90°,即BC ⊥OB. ∵OB 为⊙O 的半径, ∴BC 是⊙O 的切线.(2)∵OB =6,BC =8,BC ⊥OB ,∴OC =OB 2+BC 2=10. ∵△OBC 的面积为12OC·BE =12OB·BC ,∴BE =OB·BC OC =6×810=4.8. ∴BD =2BE =9.6,即弦BD 的长为9.6.23.(本题13分)先阅读材料,再解答问题:小明同学在学习与圆有关的角时了解到:在同圆或等圆中,同弧(或等弧)所对的圆周角相等.如图,点A ,B ,C ,D 均为⊙O 上的点,则有∠C =∠D.小明还发现,若点E 在⊙O 外,且与点D 在直线AB 同侧,则有∠D>∠E. 请你参考小明得出的结论,解答下列问题:(1)如图1,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).①在图1中作出△ABC的外接圆(保留必要的作图痕迹,不写作法);②若在x轴的正半轴上有一点D,且∠ACB=∠ADB,则点D的坐标为(7,0);(2)如图2,在平面直角坐标系xOy中,点A的坐标为(0,m),点B的坐标为(0,n),其中m>n>0,点P为x轴正半轴上的一个动点,当∠APB达到最大时,直接写出此时点P的坐标.解:(1)①如图.(2)当以AB为弦的圆与x轴正半轴相切时,作CD⊥y轴,连接CP,CB.∵点A的坐标为(0,m),点B的坐标为(0,n),∴点D的坐标是(0,m+n2),即BC=PC=m+n2.在Rt△BCD中,BC=m+n2,BD=m-n2,∴则CD=BC2-BD2=mn. ∴OP=CD=mn.∴点P的坐标是(mn,0).。
2019-2020年九年级数学上册24.2 点和圆、直线和圆的位置关系同步测试 新人教版
2019-2020年九年级数学上册24.2 点和圆、直线和圆的位置关系同步测试 新人教版 24.2.1 点和圆的位置关系 [见B 本P42]1.若⊙O 的半径为4 cm ,点A 到圆心O 的距离为3 cm ,那么点A 与⊙O 的位置关系是( A )A .点A 在圆内B .点A 在圆上C .点A 在圆外D .不能确定【解析】 d =3 cm <4 cm =r ,所以点A 在⊙O 内.2.已知⊙O 的半径为5 cm ,P 为⊙O 外一点,则OP 的长可能是( D )A .5 cmB .4 cmC .3 cmD .6 cm3.矩形ABCD 中,AB =8,BC =35,点P 在边AB 上,且BP =3AP ,如果圆P 是以点P 为圆心,PD 为半径的圆,那么下列判断正确的是( C )A .点B ,C 均在圆P 外B .点B 在圆P 外,点C 在圆P 内C .点B 在圆P 内,点C 在圆P 外D .点B ,C 均在圆P 内【解析】 如图所示.因为AP =14AB =14×8=2,AD =BC =35, 所以PD =AD 2+AP 2=(35)2+22=7, PB =8-2=6,所以PC =PB 2+BC 2=62+(35)2=9.因为PB <PD <PC ,所以点B 在圆P 内,点C 在圆P 外,故选C.4.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图24-2-1所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( B )A .第①块B .第②块C .第③块D .第④块【解析】 根据“不在同一直线上的三点确定一个圆”知所带的碎片必须含有圆弧的部分,只有②符合.图24-2-1图24-2-25.如图24-2-2,已知⊙O是△ABC的外接圆,∠AOB=110°,则∠C的度数为( A ) A.55° B.70° C.60° D.45°6.[xx·攀枝花]下列四个命题:①等边三角形是中心对称图形;②在同圆或等圆中,相等的弦所对的圆周角相等;③三角形有且只有一个外接圆;④垂直于弦的直径平分弦所对的两条弧.其中真命题的个数有( B )A.1个 B.2个 C.3个 D.4个【解析】∵等边三角形是轴对称图形,但不是中心对称图形,∴①是假命题;如图,AB=AE,但∠C和∠D不相等,∴②是假命题;三角形有且只有一个外接圆,外接圆的圆心是三角形三边的垂直平分线的交点,∴③是真命题;垂直于弦的直径平分弦,且平分弦所对的两条弧,∴④是真命题.7.在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△ABC 外接圆的圆心坐标是( D )A.(2,3) B.(3,2)C.(1,3) D.(3,1)【解析】作弦AB,AC的垂直平分线,交点即为圆心.8.一个三角形的外心在三角形的内部,则这个三角形是( C )A.任意三角形 B.直角三角形C.锐角三角形 D.钝角三角形9.已知⊙O的半径为10 cm,点P到圆心的距离为d cm,(1)当d=8 cm时,点P在⊙O__内__;(2)当d=10 cm时,点P在⊙O__上__;(3)当d=12 cm时,点P在⊙O__外__.10.图24-2-3中,△ABC的外接圆的圆心坐标是__(5,2)__.图24-2-3【解析】 分别作BC ,AB 的垂直平分线,交点坐标即为所求.11.已知线段AB =6 cm.(1)画半径为4 cm 的圆,使它经过A ,B 两点,这样的圆能画__2__个;(2)画半径为3 cm 的圆,使它经过A ,B 两点,这样的圆能画__1__个;(3)画半径为2 cm 的圆,使它经过A ,B 两点,这样的圆能画__0__个.图24-2-412.如图24-2-4,△ABC 中,∠ACB =90°,BC =5 cm ,AC =10 cm ,CD 为中线,以C 为圆心,以525 cm 为半径作圆,则点A ,B ,D 与⊙C 的位置关系如何? 【解析】 要确定点A ,B ,D 与⊙C 的位置关系,需计算出这些点与点C 的距离,再与⊙C的半径作比较即可.解:∵△ABC 为直角三角形,∠ACB =90°,∴BC 2+AC 2=AB 2,∴AB =BC 2+AC 2=52+102=55(cm).∵CD 为斜边上的中线,∴CD =12AB =52 5 cm.∵CA =10 cm >525 cm , ∴点A 在⊙C 外;而CB =5 cm <525 cm , ∴点B 在⊙C 内;又CD =525 cm ,∴点D 在⊙C 上.13.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是__10或8______.【解析】 ①当直角三角形的斜边长为16时,这个三角形的外接圆半径为8;②当两条直角边长分别为16和12,则直角三角形的斜边长=162+122=20,因此这个三角形的外接圆半径为10.综上所述:这个三角形的外接圆半径等于8或10.14.用反证法证明:圆内不是直径的两条弦不能互相平分.【解析】 根据反证法的一般步骤来证明.解:如图所示,已知AB ,CD 是⊙O 内的两条非直径弦,且AB 与CD 相交于点P .求证:AB 与CD 不能互相平分.证明:假设AB 与CD 能互相平分,则点P 既是AB 的中点,也是CD 的中点,连接OP .由垂径定理可知:OP ⊥AB ,OP ⊥CD .这表明过直线OP 上一点P ,有两条直线AB ,CD 与之垂直,这与“过一点有且只有一条直线与已知直线垂直”相矛盾,故假设不成立,即AB 与CD 不能互相平分.图24-2-515.如图24-2-5,AD 为△ABC 外接圆的直径,AD ⊥BC ,垂足为点F ,∠ABC 的平分线交AD于点E ,连接BD ,CD .(1)求证:BD =CD ;(2)请判断B ,E ,C 三点是否在以D 为圆心,以BD 为半径的圆上,并说明理由.解:(1)证明:∵AD 为直径,AD ⊥BC ,∴BD ︵=CD ︵.∴BD =CD .(2)B ,E ,C 三点在以D 为圆心,以DB 为半径的圆上.理由:由(1)知BD ︵=CD ︵,∴∠BAD =∠CBD .∵∠DBE =∠CBD +∠CBE ,∠DEB =∠BAD +∠ABE ,∠CBE =∠ABE ,∴∠DBE =∠DEB .∴DB =DE .又∵BD =CD ,∴DB =DE =DC .∴B ,E ,C 三点在以D 为圆心,以DB 为半径的圆上.16.用反证法证明:在一个三角形中,至少有一个内角小于或等于60°.已知:△ABC ,求证:△ABC 中至少有一个内角小于或等于60°.证明:假设△ABC 中没有一个内角小于或等于60°,即∠A >60°,∠B >60°,∠C >60°,于是∠A +∠B +∠C >60°+60°+60°=180°,这与三角形的内角和等于180°相矛盾,所以△ABC 中至少有一个内角小于或等于60°.17.如图24-2-6所示,⊙O 的半径为2,弦BD =23,A 为BD ︵的中点,E 为弦AC 的中点且在BD 上,求四边形ABCD 的面积.图24-2-6第17题答图解:如图所示,连接OA ,OB ,设OA 交BD 于F .∵A 为BD ︵的中点,∴FO ⊥BD ,∴BF =DF =12BD = 3. ∵OB =2,∴OF =1,∴AF =1,∴S △ABD =12BD ·AF =12×23×1= 3. ∵AE =CE ,∴S △ADE =S △CDE ,S △ABE =S △CBE ,∴S △ABD =S △BCD ,∴S 四边形ABCD =2S △ABD =2 3.-----如有帮助请下载使用,万分感谢。
2019-2020学年人教版九年级数学上学期同步测试专题24-3:正多边形和圆
专题24.3正多边形和圆(测试)一、单选题1.若正多边形的一个中心角是30°,则该正多边形的边数是( )A .6B .12C .16D .18【答案】B【解析】003603012÷=.故这个正多边形的边数为12.故选:B .2.正多边形的一边所对的中心角与它的一个外角的关系是( )A .相等B .互余C .互补D .互余或互补【答案】A【解析】设正多边形是正n 边形,则它的一边所对的中心角是360n ︒,正多边形的外角和是360°,则每个外角也是360n ︒,所以正多边形的一边所对的中心角与它的一个外角相等,故选A .3.在半径为R 的圆上依次截取等于R 的弦,顺次连接各分点得到的多边形是( )A .正三角形B .正四边形C .正五边形D .正六边形【答案】D【解析】解:由题意这个正n 边形的中心角=60°,∴n=36060︒︒=6∴这个多边形是正六边形,故选:D .4.如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为()A .1BCD .2【答案】C【解析】如图,作BG AC ⊥,依题可得:ABC ∆是边长为2的等边三角形,在Rt BGA ∆中,∵2AB =,1AG =,∴BG =故答案为:C.5 )A .πB .3πC .4πD .12π【答案】C【解析】解:如图,六边形ABCDEF 为正六边形,作OH ⊥AB 于H ,连接OA ,∴OA 为正六边形ABCDEF 的外接圆的半径,OH 为正六边形ABCDEF 的边心距,∴在Rt AOH 中,∠AOH=1806︒=30°,∴cos ∠AOH=OH OA == ∴OA=2, ∴它的外接圆的面积=2πOA ()=4π. 故选:C .6.如图,正八边形各边中点构成四边形,则正八边形边长与AB 的比是( )A.2B C D【答案】A【解析】过E作EF⊥AD于F,过G作GH⊥AD于H,则△AEF与△DGH是等腰直角三角形,四边形EFHG是矩形,∴AF=EF=DH=GH,EG=FH,设AF=EF=GH=DH=k,∴AE=DG k,∴EG=2AE=k,∴AB=AD=+2k,=∴正八边形边长与AB2故选A.7.如图,在半径为6的⊙O中,正方形AGDH与正六边形ABCDEF都内接于⊙O,则图中阴影部分的面积为()A .27﹣B .54﹣C .D .54【答案】B 【解析】解:设EF 交AH 于M 、交HD 于N ,连接OF 、OE 、MN ,如图所示:根据题意得:△EFO 是等边三角形,△HMN 是等腰直角三角形,∴EF =OF =6,∴△EFO 的高为:OF•sin60°=MN =2(6﹣12﹣ ∴FM =12(6﹣12+3, ∴阴影部分的面积=4S △AFM =4×12(3)×54﹣ 故选:B .8.一个圆形餐桌直径为2米,高1米,铺在上面的一个正方形桌布的四个角恰好刚刚接触地面,则这块桌布的每边长度为( )米A .12x xB .4 C.D .4π【答案】A【解析】解:正方形桌布对角线长度为圆形桌面的直径加上两个高,即2+1+1=4(米),设正方形边长是x 米,则x 2+x 2=42,解得:,所以正方形桌布的边长是米.故选:A .9.下面给出五个命题(1)正多边形都有内切圆和外接圆,且这两个圆是同心圆(2)各边相等的圆外切多边形是正多边形(3)各角相等的圆内接多边形是正多边形(4)正多边形既是轴对称图形又是中心对称图形(5)正n 边形的中心角360n a n ︒=,且与每一个外角相等 其中真命题有( )A .2 个B .3 个C .4 个D .5 个 【答案】A【解析】解:(1)正多边形都有一个内切圆和一个外接圆,是同心圆,圆心是正多边形的中心,故正确;(2)各边相等的圆外切多边形的角不一定相等,故不一定是正多边形,如菱形,故错误;(3)圆内接矩形,各角相等,但不是正多边形,故错误;(4)边数是偶数的正多边形既是轴对称图形又是中心对称图形,而边数是奇数的多边形是轴对称图形,不是中心对称图形;(5)正n 边形的中心角360n a n︒=,且与每一个外角相等. 故正确的是(1)(5).共有2个.故选:A .10.一个圆的内接正三角形的边长为( )AB .4C .D .【答案】D【解析】根据题意画图如下:过点O 作OD ⊥BC 于D ,连接OB ,∴BD=CD=12, ∵△ABC 是等边三角形,∴∠ABC=60°,∴∠OBD=30°,∴OD=12OB , ∴OB 2-(12OB)2=BD 2, 解得:OB=2,即圆的半径为2,∴该圆的内接正方形的对角线长为4,设正方形的边长为x ,∴x 2+x 2=42,解得x=∴该圆的内接正方形的边长为故选D.11.如图,⊙O是正六边形ABCDEF的外接圆,P是弧EF上一点,则∠BPD的度数是()A.30°B.60°C.55°D.75°【答案】B【解析】连接OB,OD,∵六边形ABCDEF是正六边形,∴∠BOD==120°,∴∠BPD=∠BOD=60°,故选:B.12.距资料,我国古代数学家祖冲之和他的儿子发展了刘徽的“割圆术”(即圆的内接正多边形边数不断增加,它的周长就越接近圆周长),他们从圆内接正六边形算起,一直算到内接正24576边形,将圆周率精确到小数点后七位,使中国对圆周率的计算在世界上领先了一千多年,依据“割圆术”,由圆内接正六边形算得的圆周率的近似值是( )A.B.3 C.D.【答案】B【解析】解:由题意n=6时,π≈ =3,故选:B .13.如图,用四根长为5cm 的铁丝,首尾相接围成一个正方形(接点不固定),要将它的四边按图中的方式向外等距离移动a cm ,同时添加另外四根长为5cm 的铁丝(虚线部分)得到一个新的正八边形,则a 的值为( )A .4cmB .5cmC . D【答案】D【解析】如图,由题意可知:△ABC 是等腰直角三角形,AB=5,AC=BC=a .则有:a 2+a 2=52,∴a=2或-2(舍弃)故选:D .14.如图,将边长为5的正六边形ABCDEF 沿直线MN 折叠,则图中阴影部分周长为()A .20B .24C .30D .35【答案】C【解析】由翻折不变性可知,阴影部分的周长等于正六边形ABCDEF 的周长=5×6=30,故选:C .15.如图,已知O 的周长等于6cm ,则它的内接正六边形ABCDEF 的面积是( )A .4B .4C .2D .【答案】C【解析】过点O 作OH ⊥AB 于点H ,连接OA ,OB ,设⊙O 的半径为r ,∵⊙O 的周长等于6πcm ,∴2πr=6π,解得:r=3,∴⊙O 的半径为3cm ,即OA=3cm ,∵六边形ABCDEF 是正六边形,∴∠AOB=16×360°=60°,OA=OB ,∴△OAB 是等边三角形,∴AB=OA=3cm ,∵OH ⊥AB ,∴AH=12AB ,∴AB=OA=3cm ,∴AH=32cm ,=2cm ,∴S 正六边形ABCDEF =6S △OAB =6×12×3×2=2(cm2).故选C.16.⊙O 是一个正n 边形的外接圆,若⊙O 的半径与这个正n 边形的边长相等,则n 的值为() A .3 B .4 C .6 D .8【答案】C【解析】⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n边形的边长相等,则这个正n边形的中心角是60°,÷︒=360606n的值为6,故选:C二、填空题17.若正多边形的一个外角为60°,则这个正多边形的中心角的度数是___________.【答案】60°【解析】∵正多边形的一个外角为60°,∴正多边形的边数为=6,即正多边形为六边形,∴这个正多边形的中心角的度数==60°.故答案为60°18.如图,六边形ABCDEF是正六边形,若l1∥l2,则∠1﹣∠2=_____.【答案】60°【解析】解:如图,过A作l∥l1,则∠4=∠2,∵六边形ABCDEF是正六边形,∴∠FAB=120°,即∠4+∠3=120°,∴∠2+∠3=120°,即∠3=120°﹣∠2,∵l1∥l2,∴l∥l2,∴∠1+∠3=180°,∴∠1+120°﹣∠2=180°,∴∠1﹣∠2=180°﹣120°=60°,故答案为:60°.19.如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=_____.【答案】75°【解析】解:设该正十二边形的中心为O,如图,连接A10O和A3O,由题意知,37105 12A A A=⊙O的周长,∴∠A3OA10=536012︒⨯=150°,∴∠A3A7A10=75°,故答案为:75°.20.已知正方形MNKO和正六边形ABCDEF边长均为1,把正方形放在正六边形外边,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形外绕点B顺时针旋转,使KN边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使NM边与CD边重合,完成第二次旋转;………在这样连续6次旋转的过程中,点M在图中直角坐标系中的纵坐标可能是()A .2B .﹣2.2C .2.3D .﹣2.3【答案】A【解析】如图,∵正方形MNKO 和正六边形ABCDEF 边长均为1∴第一次旋转后点M 1 纵坐标坐标为12 ,第二次、第三次旋转后点M 2(M 3,四次旋转后点M 4的纵坐标为﹣12﹣2,第五次旋转后点M 5的纵坐标为 12+2,第六次旋转后的点M 6的纵坐标为2. 故选:A .三、解答题21.如图,已知O .(1)用尺规作正六边形,使得O 是这个正六边形的外接圆,并保留作图痕迹; (2)用两种不同的方法把所做的正六边形分割成六个全等的三角形.【答案】(1)答案见解析;(2)答案见解析【解析】解:(1)如图所示:,(2)如图所示:22.如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,求△ABC的面积.【答案】【解析】延长AB,再作出过点C与格点所在的直线,交于格点E.∵正六边形的边长为1,∴正六边形的半径是1,则CE=4,则△BCE 的边EC ,△ACE 边EC ,则S △ABC =S △AEC -S △BEC =12×4×)=23.回顾旧知:在探究有关正多边形的有关性质时,我们是从那几个方面展开的?探究的方法与过程又是怎样的?(不要求回答)温馨提示,如图1,是一个边长为a 的正六边形.我们知道它具有如下的性质:①正六边形的每条边长度相等;②正六边形的六个内角相等,都是120°;③正六边形的内角和为720°;④正六边形的外角和为360°.等.解答问题:(1)观察图2,请你在下面的横线上,再写出边长为a 的正六边形所具有不同于上述的性质(不少于5条): .(2)尺规作图:在图2中作出圆内接正六边形的内切圆(不要求写作法,只保留作图痕迹);(3)求出这个正六边形外接圆半径与内切圆半径的比值.【答案】(1)见解析;(2)作图见解析;(3). 【解析】(1)①正六边形既是轴对称图形,又是中心对称图形;②正六边形的面积为: a 2,周长为6a ;③正六边形有一个内切圆、外接圆,它们是同心圆;④圆内接正六边形的每条边在圆内所对的优弧长度相等;⑤圆内接正六边形的每条边在圆内所对的优弧的弧度相等;⑥圆内接正六边形的每条边(或说弦)在圆内所对的劣弧的长度相等;⑦圆内接正六边形的每条边(或说弦)在圆内所对的劣弧的弧度相等;⑧圆内接正六边形的每条边(或说弦)在圆内所对的圆心角(中心角)相等,都是60°;⑨圆内接正六边形的边长等于圆的半径;⑩圆内接正六边形的边心距为: a 等.(2)如图2所示:(3)如图2,连结EO,在Rt△ONE中,∵OE=DE=a,∠EON=DOE=30°,∴OE=a,∴边长为a正六边形外接圆半径与内切圆半径的比值为:.24.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC.下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.证明:在AP上截取AE=CP,连接BE∵△ABC是正三角形∴AB=CB∵∠1和∠2的同弧圆周角∴∠1=∠2∴△ABE≌△CBP(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:PA=PC+ PB.(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.【答案】(1)见解析;(2)见解析;(3)【解析】证明:(1)延长BP至E,使PE=PC,连接CE.∵∠1=∠2=60°,∠3=∠4=60°,∴∠CPE=60°,∴△PCE是等边三角形,∴CE=PC,∠E=∠3=60°;又∵∠EBC=∠P AC,∴△BEC≌△APC,∴P A=BE=PB+P C.(2)过点B作BE⊥PB交P A于E.∵∠1+∠2=∠2+∠3=90°∴∠1=∠3,又∵∠APB=45°,∴BP=BE,∴;PE=又∵AB=BC,∴△ABE≌△CBP,∴PC=AE.∴PA AE PE PC=+=.=+;(3)答:PA PC证明:在AP上截取AQ=PC,连接BQ,∵∠BAP=∠BCP,AB=BC,∴△ABQ≌△CBP,∴BQ=BP.又∵∠APB=30°,∴PQ==+=∴PA PQ AQ25.如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.(1)求图①中∠MON的度数;(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).【答案】90°72°【解析】(1)方法一:如图①,连接OB,OC.图①∵正三角形ABC内接于⊙O,∴∠OBM=∠OCN=30°,∠BOC=120°.又∵BM=CN,OB=OC,∴△OBM≌△OCN,∴∠BOM=∠CON,∴∠MON=∠BOC=120°.方法二:如图②,连接OA,OB.图②∵正三角形ABC内接于⊙O,∴AB=BC,∠OAM=∠OBN=30°,∠AOB=120°.∵BM=CN,∴AM=BN.又∵OA=OB,∴△AOM≌△BON,∴∠AOM=∠BON,∴∠MON=∠AOB=120°.(2)90°72°(3)∠MON=.26.如图,一个圆形街心花园,有三个出口A,B,C,每两个出口之间有一条60米长的道路,组成正三角形ABC,在中心点O处有一亭子,为使亭子与原有的道路相通,需再修三条小路OD,OE,OF,使另一出口D、E、F分别落在ΔABC分成三个全等的多边形,以备种植不同品种的花草.(1)请你按以上要求设计两种不同的方案,将你的设计方案分别画在图1,图2中,并附简单说明.(2)要使三条小路把ΔABC分成三个全等的等腰梯形,应怎样设计?请把方案画在图3中,并求此时三条小路的总长.(3)请你探究出一种一般方法,使得出口D不论在什么位置,都能准确地找到另外两个出口E、F的位置,请写明这个方法.(4)你在(3)中探究出的一般方法适用于正五边形吗?请结合图5予以说明,这种方法能推广到正n边形吗?【答案】(1)方案1:D,E,F与A,B,C重合,方案2:OD,OE,OF分别垂直于AB,BC,AC;(2)60;(3)如图(4)见解析;(4)可推广到正n边形.【解析】(1)方案1:D,E,F与A,B,C重合,连OD,OE,OF.方案2:OD,OE,OF分别垂直于AB,BC,AC.(2)OD//AC,OE//AB,OF//BC,如图(3),作OM⊥BC于M,连OB,∵ΔABC是等边Δ,∴BM=BC=30,且∠OBM=30°,∴OM=10,∵OE//AB,∴∠OEM=60°,OE==20,又OE=OF=OD,∴OE+OF+OD=3OE=60,答:略.(3)如图(4),方法1:在BC,CA,AB上分别截取BE=CF=AD,连结OD,OE,OF,方法2:在AB上任取一点D,连OD,逆时针旋转OD120°两次,得E,F.(4)设M1为A1A2上任一点,在各边上分别取A2M2=A3M3=A4M4=A5M5=A1M1,连OM1……OM5即可,∴可推广到正n边形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题24.2点和圆、直线和圆的位置关系(测试)一、单选题1.已知⊙O 的半径为 5,直线 EF 经过⊙O 上一点 P (点 E ,F 在点 P 的两旁),下列条件能判定直线 EF 与⊙O 相切的是( )A .OP =5B .OE =OFC .O 到直线 EF 的距离是 4D .OP ⊥EF【答案】D【解析】 ∵点 P 在⊙O 上,∴只需要 OP ⊥EF 即可, 故选:D .2.如图,O 内切于ABC ∆,切点分别为,,D E F 。
已知0055,60EDF C ∠=∠=,连接,,DE,DF OE OF ,那么B Ð等于( )A .55°B .50°C .60°D .65°【答案】B 【解析】解:∵E ,F 是圆的切点,∴OE ⊥AB ,OF ⊥AC ,∴∠AEO=∠AFO=90°,∵∠EOF=2∠EDF=255110⨯︒=︒,∴A 18011070∠=︒-︒=︒,∴B 180706050∠=︒-︒-︒=︒故选择:B.3.如图,等腰ABC ∆的内切圆⊙O 与AB ,BC ,CA 分别相切于点D ,E ,F ,且5A B A C ==,6BC =,则DE 的长是( )A B .5 C D .5【答案】D【解析】连接OA 、OE 、OB ,OB 交DE 于H ,如图,等腰ABC ∆的内切圆⊙O 与AB ,BC ,CA 分别相切于点D ,E ,FOA ∴平分BAC ∠, OE BC ⊥, ⊥OD AB ,BE BD =,AB AC =,AO BC ∴⊥,∴点A 、O 、E 共线,即AE BC ⊥,3BE CE ∴==,在Rt ABE ∆中, 4AE ==,3BD BE ==,2AD ∴=,设⊙O 的半径为r ,则OD OE r ==, 4AO r =-,在Rt AOD ∆中,2222(4)r r +=-,解得32r =,在Rt BOE ∆中,OB = BE BD =,OE OD =,OB ∴垂直平分DE ,DH EH ∴=,OB DE ⊥, 1122HE OB OE BE ⋅=⋅,33OE BEHEOB⨯⋅∴===2DE EH∴==,故选D.4.如图,在Rt ABC∆中,90︒∠=C,4AC=,3BC=,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是()A.5 B.6 C.7 D.8【答案】B【解析】如图,设⊙O与AC相切于点D,连接OD,作OP BC⊥垂足为P交⊙O于F,此时垂线段OP最短,PF最小值为OP OF-,∵4AC=,3BC=,∴5AB=∵90OPB︒∠=,∴OP AC∵点O是AB的三等分点,∴210533OB=⨯=,23OP OBAC AB==,∴83OP=,∵⊙O与AC相切于点D,∴OD AC⊥,∴OD BC∥,∴13 OD OABC AB==,∴1 OD=,∴MN最小值为85133 OP OF-=-=,如图,当N在AB边上时,M与B重合时,MN经过圆心,经过圆心的弦最长,MN最大值1013133=+=,513+=633,∴MN长的最大值与最小值的和是6.故选:B.5.三角形的外心是()A.三角形三条边上中线的交点B.三角形三条边上高线的交点C.三角形三条边垂直平分线的交点D.三角形三条内角平分线的交点【答案】C【解析】解:三角形的外心是三角形中三边垂直平分线的交点,故选:C.6.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心作圆,如果圆A与线段BC没有公共点,那么圆A的半径r的取值范围是()A.5≥r≥3B.3<r<5 C.r=3或r=5 D.0<r<3或r>5【答案】D【解析】∵在Rt△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心作圆,当圆A 的半径0<r <3或r >5时,圆A 与线段BC 没有公共点;故选D .7.如图,两个圆都以点O 为圆心,大圆的弦AB 与小圆相切,已知AB=10cm ,则两圆形成的圆环的面积等于( )A .25πcmB .225πcmC .250πcmD .2100πcm【答案】B【解析】 连接OC 、OA ,则OC ⊥AB ,在Rt △AOC 中,22221()2OA OC AC AB -===25 ∴环形的面积为2225OA OC πππ-=8.如图,等边三角形ABC 的边长为8,以BC 上一点O 为圆心的圆分别与边AB ,AC 相切,则O 的半径为( )A .B .3C .4D .4 【答案】A【解析】设O 与AC 的切点为E ,连接AO ,OE ,∵等边三角形ABC 的边长为8,∴8AC =,60C BAC ∠=∠=︒,∵圆分别与边AB ,AC 相切, ∴1302BAO CAO BAC ∠=∠=∠=︒, ∴90AOC ∠=︒, ∴142OC AC ==, ∵OE AC ⊥,∴2OE OC ==∴O 的半径为故选:A .9.如图,△ABC 的内切圆⊙O 与AB ,BC ,CA 分别相切于点D ,E ,F ,且AD =2,△ABC 的周长为14,则BC 的长为( )A.3 B.4 C.5 D.6【答案】C【解析】∵⊙O与AB,BC,CA分别相切于点D,E,F∴AF=AD=2,BD=BE,CE=CF,∵△ABC的周长为14,∴AD+AF+BE+BD+CE+CF=14∴2(BE+CE)=10∴BC=5故选:C.10.如图,AB为O的切线,切点为A,连接AO BO、,BO与O交于点C,延长BO与O交于点D,∠的度数为( )连接AD,若36∠=o,则ADCABOA.54o B.36o C.32o D.27o【答案】D【解析】切线性质得到90∠=oBAOo o oAOB903654∴∠=-=QOD OA=∠=∠∴OAD ODAQ∠=∠+∠AOB OAD ODA∴∠=∠=o27ADC ADO故选D11.平面上O与直线1l,2l,3l,4l的位置关系如图.如果O的半径为20 cm,且点O到其中一直线的距离为14 cm,那么此直线为()A .1lB .2lC .3lD .4l【答案】B 【解析】因为所求直线到圆心O 点的距离为14cm<半径20 cm ,所以此直线为圆O 的割线,即为直线2l .故选B.12.如图,在矩形ABCD 中,4AB =,5AD =,AD 、AB 、BC 分别与O 相切于E 、F 、G 三点,过点D 作O 的切线交BC 于点M ,切点为N ,则DM 的长为( ).A .133B .92CD .【答案】A【解析】连接OE ,OF ,ON ,OG ,在矩形ABCD 中,∵∠A=∠B=90°,CD=AB=4,∵AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,∴∠AEO=∠AFO=∠OFB=∠BGO=90°,∴四边形AFOE ,FBGO 是正方形,∴AF=BF=AE=BG=2,∴DE=3,∵DM是⊙O的切线,∴DN=DE=3,MN=MG,∴CM=5-2-MN=3-MN,在Rt△DMC中,DM2=CD2+CM2,∴(3+NM)2=(3-NM)2+42,∴43x=,∴413333 DM=+=.故选A.13.如图,在扇形OAB中,点C是弧AB上任意一点(不与点A,B重合),CD∥OA交OB于点D,点I 是△OCD的内心,连结OI,BI.若∠AOB=β,则∠OIB等于()A.180°1 2-βB.180°-βC.90°+ 12βD.90°+β【答案】A【解析】连接IC,∵CD∥OA ,∴∠AOC=∠OCD,∵∠AOC+∠COB=∠AOB= β ,∴∠OCD+∠COB= β ,∵点I是△OCD的内心,∴∠COI+∠OCI=11 ()22OCD COBβ∠+∠=,∴∠OIC=180°-(∠COI+∠OCI)= 180°- 12β ;在△COI与△BOI中,∵OC=OB,∠COI=∠BOI,OI=OI, ∴△COI≌△BOI,∴∠OIB =∠OIC= 180°- 1 2β.故答案为:A.14.如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,AB=4,BC=6,点O是边BC上一点,以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是()A.4<OC≤133B.4≤OC≤133C.4<OC143≤D.4≤OC143≤【答案】B【解析】作DE⊥BC于E,如图所示:则DE=AB=4,BE=AD=2,∴CE=4=DE,当⊙O与边AD相切时,切点为D,圆心O与E重合,即OC=4;当OA=OC时,⊙O与AD交于点A,设OA=OC=x,则OB=6﹣x,在Rt△ABO中,由勾股定理得:42+(6﹣x)2=x2,解得:x=133;∴以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是4≤x≤133;故选:B.15.以O为中心点的量角器与直角三角板ABC如图所示摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角板只有一个公共点P,若点P的读数为35°,则∠CBD的度数是()A.55°B.45°C.35°D.25【答案】C【解析】∵AB是⊙O的切线,∴∠OPB=90°,∵∠ABC=90°,∴OP∥BC,∴∠CBD=∠POB=35°,故选:C.16.如图,点I是Rt△ABC的内心,∠C=90°,AC=3,BC=4,将∠ACB平移使其顶点C与I重合,两边分别交AB于D、E,则△IDE的周长为()A.3 B.4 C.5 D.7【答案】C【解析】连接AI、BI,∵∠C=90°,AC=3,BC=4,∴AB 5∵点I为△ABC的内心,∴AI平分∠CAB,∴∠CAI=∠BAI,由平移得:AC∥DI,∴∠CAI=∠AID,∴∠BAI=∠AID,∴AD=DI,同理可得:BE=EI,∴△DIE的周长=DE+DI+EI=DE+AD+BE=AB=5故选:C.17.如图,已知直线y=34x﹣6与x轴、y轴分别交于B、C两点,A是以D(0,2)为圆心,2为半径的圆上一动点,连结AC、AB,则△ABC面积的最小值是()A.26 B.24 C.22 D.20 【答案】C【解析】解:过D作DM⊥AB于M,连接BD,如图,由题意:B(8,0),C(0,﹣6),∴OB=8,OC=6,BC=10,则由三角形面积公式得,12×BC×DM=12×OB×DC,∴10×DM=64,∴DM=6.4,∴圆D上点到直线y=x﹣6的最小距离是6.4﹣2=4.4,∴△ABC面积的最小值是12×10×4.4=22,故选:C.二、填空题18.如图,I为△ABC的内切圆,AB=9,BC=8,AC=10,点D.E分别为AB、AC上的点,且DE为I的切线,则△ADE的周长为___.【答案】11【解析】如图设DE 、BD 、BC 、CE 与I 的切点分别为F. G 、H 、M ,由切线长定理知:BH=BG 、CH=CM 、EM=EF 、FD=DG 、AM=AG ;则AG+AM=AB+AC −BC=11;所以△ADE 的周长=AD+DE+AE=AD+DG+EM+AE=AG+AM=11.19.直角三角形的两条直角边分别是5和12,则它的内切圆半径为_____.【答案】2【解析】直角三角形的斜边13==, 所以它的内切圆半径5121322+-==. 20.如图,Rt ABC ∆中,90C ∠=︒,12AC =,点D 在边BC 上,5CD =,13BD =.点P 是线段AD 上一动点,当半径为6的圆P 与ABC ∆的一边相切时,AP 的长为________.【答案】132或【解析】∵在Rt △ABC 中,∠C=90°,AC=12,BD+CD=18,∴AB =在Rt △ADC 中,∠C=90°,AC=12,CD=5,∴13AD =,当⊙P 于BC 相切时,点P 到BC 的距离=6,过P作PH⊥BC于H,则PH=6,∵∠C=90°,∴AC⊥BC,∴PH∥AC,∴△DPH∽△DAC,∴PD PH DA AC=,∴6 1312 PD=,∴PD=6.5,∴AP=6.5;当⊙P于AB相切时,点P到AB的距离=6,过P作PG⊥AB于G,则PG=6,∵AD=BD=13,∴∠PAG=∠B,∵∠AGP=∠C=90°,∴△AGP∽△BCA,∴AP PG AB AC=,612=,∴∵CD=5<6,∴半径为6的⊙P不与△ABC的AC边相切,综上所述,AP的长为6.5或故答案为:6.5或21.如图所示,在平面直角坐标系xOy 中,一组同心圆的圆心为坐标原点O ,它们的半径分别为1,2,3,…,按照“加1”依次递增;一组平行线,0l ,1l ,2l ,3l ,…都与x 轴垂直,相邻两直线的间距为l ,其中0l 与y 轴重合若半径为2的圆与1l 在第一象限内交于点1P ,半径为3的圆与2l 在第一象限内交于点2P ,…,半径为1n +的圆与n l 在第一象限内交于点n P ,则点n P 的坐标为_____.(n 为正整数)【答案】(n 【解析】连接1OP ,2OP ,3OP ,1l 、2l 、3l 与x 轴分别交于1A 、2A 、3A ,如图所示:在11Rt OA P ∆中11OA =,12OP =,∴11A P ===同理:22A P ==33A P ==……,∴1P 的坐标为(,2P 的坐标为(,3P 的坐标为(,……,…按照此规律可得点n P 的坐标是(n ,即(n ,故答案为:(n .三、解答题22.如图所示,已知矩形 的边 , .(1)以点为圆心,为半径作,则点,,与的位置关系如何?(2)若以点为圆心作,使,,三点中至少有一个点在圆内,且至少有一点在圆外,则的半径的取值范围是什么?【答案】(1)点在内,点在上,点在外;(2)的半径的取值范围是:.【解析】(1)连接,∵,,∴,∴点在内,点在上,点在外;(2)∵以点为圆心作,使,,三点中至少有一个点在圆内,且至少有一点在圆外,∴的半径的取值范围是:.23.如图,⊙O为∆ABC的外接圆,D为OC与AB的交点,E为线段OC延长线上一点,且∠EAC=∠ABC.(1)求证:直线AE是⊙O的切线;(2)若D为AB的中点,CD=3,AB=8.①求⊙O的半径;②求∆ABC的内心I到点O的距离.【答案】(1)见解析;(2)①⊙O的半径256r=;②∆ABC的内心I到点O的距离为52.【解析】(1)如图,连接AO则∠EAC =∠ABC=1AOC 2∠.又∵AO=BO,∴∠ACO=∠CAO=18019022AOC AOC -∠=-∠ ∴∠EAO=∠EAC+∠CAO=12∠AOC +1902AOC -∠=90 ∴EA ⊥AO ∴直线AE 是⊙O 的切线;(2)①设⊙O 的半径为r,则OD=r-3,∵D 为AB 的中点,∴OC ⊥AB ,∠ADO=90,AD=4∴222AD OD AO +=,即22243)r r +-=( 解得256r = ②如下图,∵D 为AB 的中点,∴5AC BC ==且CO 是ACB ∠的平分线,则内心I 在CO 上,连接AI,BI,过I 作AC,BC 的垂线,垂足分别为F,G.易知DI=FI=GI,设其长为a.由面积可知:11112222ABC S AB CD AB DI AC FI BC DI ∆==++ 即1111838552222a a a ⨯⨯=⨯+⨯+⨯ 解得43a = ∴42553362OI DI DO =+=+-= ∴∆ABC 的内心I 到点O 的距离为5224.如图,点P 在⊙O 外,PC 是⊙O 的切线,C 为切点,直线PO 与⊙O 相交于点A 、B .(1)若∠A =30°,求证:P A =3PB ;(2)小明发现,∠A 在一定范围内变化时,始终有∠BCP =12(90°﹣∠P )成立.请你写出推理过程.【答案】(1)见解析;(2)推理过程见解析.【解析】(1)连接OC ,∵AB 是直径,∴∠ACB =90°,又∵∠A=30°,∴∠ABC=90°-30°=60°,∵OB=OC ,∴△OBC 是等边三角形,∴OB=BC=OC ,∠COB=60°,∵PC 是⊙O 的切线,OC 是半径,∴∠OCP=90°,∴∠P =90°-∠BOC =30°,∴PO=2OC ,∴PB=OB ,∵AB=2OB ,∴AP=AB+PB=3PB ;(2)如图,连接OC ,∵AB 是直径,∴∠ACB =90°,即∠ACO+∠BCO=90°,∵PC 是⊙O 的切线,OC 是半径,∴∠OCP=90°,即∠BCP+∠BCO=90°,∴∠BCP=∠ACO ,∵OA=OC ,∴∠A=∠ACO ,∴∠BCP =∠A ,∵∠A+∠P+∠ACB+∠BCP =180°,且∠ACB =90°,∴2∠BCP =180°﹣∠P ,∴∠BCP =12(90°﹣∠P). 25.如图,Rt ACB ∆中,ACB=90∠︒,O 为AB 上一点,O 经过点,与AC 相交于点E ,与AB 交于点,连接EF .(I).如图,若B=30∠︒,AE=2,求AF 的长.(II)如图,DA 平分CAB ∠,交CB 于点D ,O 经过点D . ①求证:BC 为O 的切线;②若AE=3,CD=2,求AF 的长.【答案】(Ⅰ)AF=4;(Ⅱ)①证明见解析;②AF=5.【解析】(Ⅰ)∵AF 为⊙O 的直径, ∴ AEF=90∠︒.∵ACB=90∠︒,B=30∠︒,∴ BAC=60∠︒,∴ AFE=30∠︒,∴AF=2AE=4.(Ⅱ)①连接OD.∵DA 平分CAB ∠,CAD=DAB ∠∠∴,∵OA=OD ,∴ DAB=ODA ∠∠,∴ CAD=ODA ∠∠,∴ OD//AC ,∵∠C=90°,∴ ODB=C=90∠∠︒,即CB OD ⊥,∴BC 为⊙O 的切线.②设OD 与EF 交于点H ,∵AEF=C=ODC=90∠∠∠︒,∴四边形CDHE 为矩形.∴EH=CD=2,OHE=90∠︒.∴ OD EF ⊥.∴EF=2EH=4.∴.26.木匠黄师傅用长3AB =,宽2BC =的矩形木板做一个尽可能大的圆形桌面,他设计了如图1三种方案:方案一:直接锯一个半径最大的圆;方案二:沿对角线AC 将矩形ABCD 锯成两个三角形,适当平移三角形并锯一个最大的圆;方案三:锯一块小矩形BCEF 拼到矩形AFED 下面,且所拼成的图形为轴对称图形,利用拼成的木板锯一个尽可能大的圆.(1)求出方案一、方案二中圆的半径.(2)在方案三中,设()01CE x x =<<,圆的半径为y .①求y 关于x 的函数解析式;②当x 取何值时圆的半径最大,最大半径为多少?(3)说明三种方案中哪一个圆形桌面的面积最大.【答案】(1)1,65;(2)①见解析;②54;(3)见解析. 【解析】(1)方案一:因为长方形的长宽分别为3、2,那么直接取圆直径最大为2,则半径最大为1; 方案二:如图2,作ON BF ⊥于N ,OMAB ⊥于M .设半径为r ,在AOM ∆和OFN ∆中, A FON ∠=∠,OMA FNO ∠=∠,∴AOMOFN ∆∆, ∴OM FN AM ON =,∴23r r r r -=-,解得65r =.(2)①∵()01CE x x =<<,∴新拼图形水平方向最大跨度为3x -,竖直方向最大跨度为2x +.类似(1),所截出圆的直径最大为3x -或2x +中较小的.当32x x -<+时,即当112x <<时,()132y x =-; 当32x x -=+时,即当12x =时,1153224y ⎛⎫=-= ⎪⎝⎭; 当32x x ->+时,即当102x <<时,()122y x =+. ②当112x <<时,()1115332224y x ⎛⎫=-<-= ⎪⎝⎭;当12x =时,1153224y ⎛⎫=-= ⎪⎝⎭; 当102x <<时,()1115222224y x ⎛⎫=+<+= ⎪⎝⎭; ∴当12x =时,方案三中y 最大为54. (3)∵65154<<,∴方案三可取得圆桌的面积最大.。
