广东省惠州市2007届高三第一次调研考试数学试题(理科卷)(200610)
2006—2007学年度高三第一次摸底考试数学试题(理科)

2006—2007学年度高三第一次摸底考试数学试题(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷(选择题 共60分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型(A 或B )用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上。
3.考试结束后,考生将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
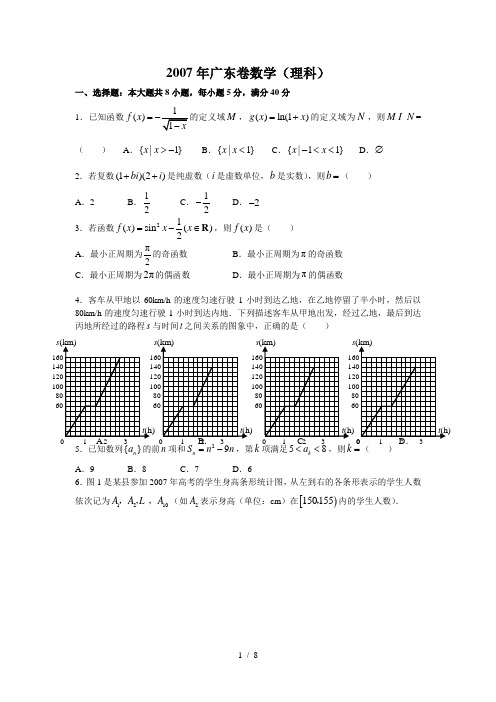
在每小题给出的四个选项中,只有一项是符合题目要求的. 1.i 是虚数单位,复数ii -12等于( )A .1 + iB .1-iC .-1 + iD .-1-i 2.一个空间几何体的正视图、侧视图为两个边长是1的正方形,俯视图是直角边长为1的等腰直角三角形,则这个几何体的 表面积等于 ( ) A .22+ B .23+ C .24+ D .63.给出30个数:1,2,4,7,11,……其规律是 第一个数是1,第二数比第一个数大1, 第三个数比第二个数大2, 第四个数比第三个数大3,……以此类推,要计算这30个数的和,现已给出了该问题的程序框图如右图所示,那么框图中判断框①处和执行 框②处应分别填入 ( ) A .i ≤30?;p = p + i -1 B .i ≤29?;p = p + i + 1 C .i ≤31?;p = p + i D .i ≤30?;p = p + i 4.由曲线y 2 = x 与y = x 2所围图形的面积为 ( )A .31 B .32 C .1D .25.某考察团对全国10个城市进行职工人均工资水平x (千元)与居民人均消费水平y (千元)统计调查,y 与x 具有相关关系,回归方程y = 0.66x + 1.562,若某城市居民人均消费水平为7.675(千元),估计该城市人均消费额占人均工资收入的百分比约为 ( )A .83%B .72%C .67%D .66% 6.函数f (x ) =-x 3 + x 2 +x -2的零点分布情况为( )A .一个零点,在)31,(--∞内B .二个零点,分别在)31,(--∞、),0(+∞内C .三个零点,分别在)31,(--∞、)0,31(-、),1(+∞内D .三个零点,分别在)31,(--∞、)1,0(、),1(+∞内7.在等差数列{a n }中,a 10 < 0,a 11 > 0,且a 11 >| a 10 |,若{a n }的前n 项和S n < 0,则n 的最大值是( )A .17B .18C .19D .208.将函数)2||,0()sin(πϕωϕω<>+=x y 的图象,向左平移3π个单位,所得曲线的一部分如图所示, 则ω、ϕ的值分别为 ( ) A .1,3π B .1,-3πC .2,3πD .2,-3π9.已知双曲线的两个焦点)0,5(1-F 、)0,5(2F ,P 为双曲线上一点,且PF 1⊥PF 2,|PF 1|·|PF 2|= 2,则双曲线的标准方程为( )A .13222=-y xB .12322=-y xC .1422=-y xD .1422=-y x 10.三棱锥P —ABC 中,底面△ABC 是边长为2的正三角形, PA ⊥底面ABC ,且PA = 2,则此三棱 锥外接球的半径为 ( )A .2B .5C .2D .321 11.如果对于函数f (x )定义域内任意的x ,都有f (x )≥M (M 为常数),称M 为f (x )的下界,下界M 中的最大值叫做f (x )的下确界,下列函数中,有下确界的所有函数是 ( )①x x f sin )(=②x x f lg )(=③xe xf =)(④⎪⎩⎪⎨⎧-<-=>=)1(1)0(0)0(1)(x x x x fA .①B .④C .②③④D .①③④12.甲、乙两人约定上午7:00至8:00之间到某站乘公共汽车,在这段时间内有3班公共汽车,它们开车时刻分别为7:20,7:40,8:00,如果他们约定,见车就乘,则甲、乙同乘一车的概率为(假定甲、乙两人到达车站的时刻是互相不牵连的,且每人在7时到8时的任何时刻到达车站是等可能的)( )A .21 B .41 C .31 D .61第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在题中横线上.13.防疫站对学生进行身体健康调查,采用分层抽样法抽取.红星中学共有学生1600名,抽取一个容量为200的样本.已知女生比男生少抽了10人,则该校的女生人数应是 人. 14.已知n xx )21(3-展开式的第4项为常数项,则展开式中各项系数的和为 .15.如图,在直角坐标系xoy 中,O 是正△ABC 的中心, A 点的坐标为(0,2),动点P (x ,y )是△ABC 内的点(包括 边界).若目标函数z = ax + by 的最大值为2,且此时的最 优解(x ,y )确定的点P (x ,y )是线段AC 上的所有点,则目 标函数z = ax + by 的最小值为 . 16.给定下列结论:①已知命题p :1tan ,=∈∃x R x ;命题q :.01,2>+-∈∀x x R x则命题“q p ⌝∧”是假命题;②已知直线l 1:01:,0132=++=-+by x l y ax ,则l 1⊥l 2的充要条件是3-=ba; ③若31)sin(,21)sin(=-=+βαβα,则βαtan 5tan =; ④圆012422=+-++y x y x 与直线x y 21=相交,所得弦长为2.其中正确命题的序号为 (把你认为正确的命题序号都填上).三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)设函数n m x f ⋅=)(,其中向量R x x x n x m ∈==),2sin 3,(cos ),1,cos 2(.(Ⅰ)求f (x )的最小正周期与单调递减区间;(Ⅱ)在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,已知f (A ) =2,b = 1,△ABC 的面积为23,求C B c b sin sin ++的值.18.(本小题满分12分)某旅游公司为3个旅游团提供a ,b ,c ,d 四条线路,每个旅游团任选其中一条. (Ⅰ)求3个旅游团选择3条不同线路的概率; (Ⅱ)求恰有2条线路没有被选择的概率;(Ⅲ)求选择a 线路旅游团数的分布列及数学期望.19.(本小题满分12分)设函数xx f )21()(=,数列{a n }满足)()2(1)1(),0(*1N n a f a f f a n n ∈--=+=(Ⅰ)求数列{a n }的通项公式;(Ⅱ)令1322121111,,)21(++++=+++==n n n n n an a a a a a a T b b b S b n , 试比较n S 与n T 34的大小,并加以证明.20.(本小题满分12分)已知四棱锥P —ABCD 的底面是直角梯形,AB ∥CD ,∠DAB = 90°,PA ⊥底面ABCD ,AB =2,2=AD ,DC = 1,PA = 4,与M 、N 分别为PB 、PD 的中点,平面CMN 交AP 于点Q .(Ⅰ)求平面CMN 与平面ABCD 所成二面角的大小; (Ⅱ)确定点Q 的位置.21.(本小题满分12分) 已知函数x x f ln )(= (Ⅰ)若)()()(R a xax f x F ∈+=,求)(x F 的极大值; (Ⅱ)若kx x f x G -=2)]([)(在定义域内单调递减,求满足此条件的实数k 的取值范围.22.(本小题满分14分)已知直线1+-=x y 与椭圆)0(12222>>=+b a by a x 相交于A 、B 两点.(Ⅰ)若椭圆的离心率为33,焦距为2,求线段AB 的长; (Ⅱ)若向量与向量互相垂直(其中O 为坐标原点),当椭圆的离心率 ]22,21[∈e 时,求椭圆的长轴长的最大值.山东省济宁市2006—2007学年度高三年级第一次摸底考试数学试题(理科)参考答案一、选择题:每小题5分,共60分.1.C 2.B 3.D 4.A 5.A 6.A 7.C 8.D 9.C 10.D 11.D 12.C 二、填空题:每小题4分,共16分. 13.760 14.32115.-4 16.①③三、解答题:17.解:(Ⅰ)x x x f 2sin 3cos 2)(2+=⋅= 1)62s i n (212c o s 2s i n 3++=++=πx x x ……………………………………3分∴函数f (x )的最小正周期ππ==22T ………………………………………… 4分 令)(,2236222Z k k x k ∈+≤+≤+πππππ,解得.326ππππk x k +≤≤+ ∴函数f (x )的单调递减区间是Z k k k ∈++],32,6[ππππ ……………………… 6分 (Ⅱ)由f (A ) = 2,得21)62sin(,21)62sin(2=+=++ππA A ,在△ABC 中,π<<A 0 ππππ26626+<+<∴A6562ππ=+∴A ,解得.3π=A …………………………………………………8分 又2323121sin 21=⨯⨯⨯==∆c A bc S ABC ,解得c = 2. △ABC 中,由余弦定理得:32121241cos 2222=⨯⨯⨯-+=-+=A bc c b a , ∴a = 3. …………………………………………………………………………10分由233sin sin sin ===A aC c B b ,得2sin sin ,sin 2,sin 2=++∴==CB cb Cc B b18.解:(Ⅰ)3 个旅游团选择3条不同线路的概率为.834333341==A C P ………………3分(Ⅱ)恰有2条线路没有被选择的概率为.169432223242=⋅=A C C P …………………6分 (Ⅲ)设选择a 线路的旅游团数为ξ,则3,2,1,0=ξ其中642743)1(642743)0(321333=⋅=====C P P ξξ .6414)3(64943)2(333323====⋅==C P C P ξξ ………………………… 10分 ∴ξ的分布列为:从而.4643642641640=⨯+⨯+⨯+⨯=ξE ……………………………… 12分 19.解:(Ⅰ)1)21()0()21()(01===∴=f a x f x又)2(1)(1n n a f a f --=+.)21()21(1)21(221+--==∴+n n n a a a ……………………………………………………2分21+=∴+n n a a 即 21=-+n n a a ∴数列{a n }是首项为1,公差为2的等差数列 .122)1(1-=⨯-+=∴n n a n …………………………………………………… 4分(Ⅱ)12)21()21(-==n a n nb 41)21()21(12121==∴-++n n nn b b 即数列{b n }是首项为21,公比为41的等比数列 ])41(1[32411])41(1[2121n n n n b b b S -=--=+++=∴ ……………………………6分)12)(12(153131*********+-++⨯+⨯=+++=-n n a a a a a a T n n n)1211(21)]121121()5131()311[(21+-=+--++-+-=n n n )1211(3234+-=∴n T n ………………………………………………………………8分 故比较S n 与n T 34的大小,只需比较n )41(与121+n 的大小即可即只需比较2n + 1与4n 的大小 ………………………………………………………10分121331)31(41+>+≥+⋅+=+=∴n n C n n n故n n T S 34>(或用数学归纳法证明) …………………………………………… 12分 20.解:解法一:(Ⅰ)如图以A 为原点,AD ,AB ,AP所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则A (0,0,0),)0,0,2(D ,B (0,2,0),)0,1,2(C ,P (0,0,4),M (0,1,2),N (2,0,22)…………2分 ∵PA ⊥面ABCD ,AP ∴为平面ABCD 的法向量,且)4,0,0(=设平面CMN 的法向量),,(z y x =)2,1,22()2,0,2(--=-= 由⎪⎩⎪⎨⎧=+--=+-⇒⎪⎩⎪⎨⎧=⋅=⋅02222200z y x z x n CN CM 令z = 1得 1,2==y x )1,1,2(=∴n …………………………………………………………………………4分21244),cos(=⋅==n AP 60),(],180,0[),(=∴∈n AP n AP即二面角的大小为60° ………………………………………………………………6分 (Ⅱ)设Q (0,0,a ) 则),1,2(a CQ --=由平面向量基本原理存在唯一实数对),(μλ使CN CM CQ μλ+= 即)2,1,22()2,0,2(),1,2(--+-=-μλa …………………………………… 9分⎪⎪⎩⎪⎪⎨⎧===⎪⎪⎪⎩⎪⎪⎪⎨⎧+=-=---=-∴3121:2212222a u a μλλμμλ解得 即Q (0,0,3) ∴Q 点在AP 上且分AP 的比为3:1 ………………………………………………12分 解法二:(Ⅰ)过N 作NG ⊥AD ,∵N 是PD 中点,∴G 为AD 中点连结BD ,则MN ∥BD ,∴MN ∥平面ABCD ,过C 用BD 的平行线l ,则MN ∥l , 即平面CMN ∩平面ABCD = l过G 作CH ⊥l 交l 于H ,连结NH ,则∠NHG 为平面CMN 与平面ABCD所成二面角的平面角 …………………………………………………………………3分 设A C ∩BD = O ,容易证明AC ⊥BD333323332622=-=-==⋅=⋅=AO AC OC BD AB AD AO 332333321=+=+=∴OC AO CH 又221==PA NG 6033322tan =∠∴===∠∴NHG GH NG NHG 即平面CMN 与平面ABCD 所成二面角的大小为60°………………………………6分(Ⅱ)取PA 中点R ,连结MR ,DR ,∵MRAB 21∴MR CD ∴CM ∥DR ,…………………………………………………………………………9分 过N 作NQ ∥DR ,则Q 所求,且PA PQ 41=即Q 分AP 的比为3:1 ……………………………………………………………12分 (注:Ⅰ也可用面积射影定理求) 21.解:(Ⅰ)xax x a x f x F +=+=ln )()( 定义域为),0(+∞∈x 2ln )1()(x xa x F --=∴ ……………………………………………………………2分令ae x x F -=='10)(得 由aex x F -<<>'100)(得由ae x x F -><'10)(得 …………………………………………………………4分即),0()(1aex F -在上单调递增,在),(1+∞-a e 上单调递减a e x -=∴1时,F (x )取得极大值11)1(---=+-=a aa e eaa e F ……………………6分 (Ⅱ)kx x x G -=2)(ln )( 的定义域为(0+∞) k xxx G -='∴ln 2)( 由G (x )在定义域内单调递减知:0ln 2)(<-='k xxx G 在(0+∞)内恒成立 ………8分 令k x x x H -=ln 2)(,则2)ln 1(2)(x x x H -=' 由e x x H =='得0)(∵当),0(e x ∈时)(,0)(x H x H >'为增函数当),(+∞∈e x 时0)(<'x H )(x H 为减函数 ……………………………………10分 ∴当x = e 时,H (x )取最大值k ee H -=2)( 故只需02<-k e 恒成立,e k 2>∴ 又当e k 2=时,只有一点x = e 使得0)()(=='x H x G 不影响其单调性.2ek ≥∴ ………………………………………………………………………………12分22.解:(Ⅰ)33,22,33===a c c e 即 2,322=-==∴c ab a 则 ∴椭圆的方程为12322=+y x …………………………………………………………2分 联立⎪⎩⎪⎨⎧+-==+112322x y y x 消去y 得:03652=--x x 设),(),,(2211y x B y x A 则53,562121-==+x x x x 2122122212214)(])1(1[)()(||x x x x y y x x AB -+-+=-+-=∴538512)56(22=+= ……………………………………………………………6分 (Ⅱ)设),(),,(2211y x B y x A⊥ 0=⋅∴,即02121=+y y x x由⎪⎩⎪⎨⎧+-==+112222x y b y a x 消去y 得0)1(2)(223222=-+-+b a x a x b a由0)1)((4)2(222222>-+=-=∆b b a a a 整理得122>+b a ……………8分 又22222122221)1(2ba b a x x b a a x x +-=+=+ 1)()1)(1(21212121++-=+-+-=∴x x x x x x y y由02121=+y y x x 得:01)(22121=++-x x x x012)1(22222222=++-+-∴ba ab a b a 整理得:022222=-+b a b a ……………………………………………………10分 222222e a a c a b -=-=∴代入上式得221112e a -+= )111(2122e a -+=∴ …………………………………………12分 2221≤≤e21412≤≤∴e 431212≤-≤∴e 211342≤-≤∴e 3111372≤-+≤∴e 23672≤≤∴a 适合条件122>+b a 由此得26642≤≤a 62342≤≤∴a 故长轴长的最大值为6 …………………………………………………………… 14分。
2007年高考全国1卷数学理科试卷含答案

2007年普通高等学校招生全国统一考试理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至4页.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效.3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 参考公式:如果事件A B ,互斥,那么球的表面积公式 ()()()P A B P A P B +=+24πS R =如果事件A B ,相互独立,那么其中R 表示球的半径 ()()()P A B P A P B =球的体积公式如果事件A 在一次试验中发生的概率是p ,那么34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径()(1)(012)k kn k n n P k C p p k n -=-=,,,…,一、选择题(1)α是第四象限角,5tan 12α=-,则sin α=( ) A .15B .15-C .513D .513-(2)设a 是实数,且1i1i 2a +++是实数,则a =( ) A .12B .1C .32D .2(3)已知向量(56)=-,a ,(65)=,b ,则a 与b ( ) A .垂直B .不垂直也不平行C .平行且同向D .平行且反向(4)已知双曲线的离心率为2,焦点是(40)-,,(40),,则双曲线方程为( )A .221412x y -= B .221124x y -= C .221106x y -= D .221610x y -= (5)设a b ∈R ,,集合{}10b a b a b a⎧⎫+=⎨⎬⎩⎭,,,,,则b a -=( ) A .1B .1-C .2D .2-(6)下面给出的四个点中,到直线10x y -+=的距离为2,且位于1010x y x y +-<⎧⎨-+>⎩,表示的平面区域内的点是( ) A .(11),B .(11)-,C .(11)--,D .(11)-,(7)如图,正四棱柱1111ABCD A B C D -中,12AA AB =,则异面直线1A B 与1AD 所成角的余弦值为( )A .15B .25C .35 D .45(8)设1a >,函数()log a f x x =在区间[]2a a ,上的最大值与最小值之差为12,则a =( ) AB .2C.D .4(9)()f x ,()g x 是定义在R 上的函数,()()()h x f x g x =+,则“()f x ,()g x 均为偶函数”是“()h x 为偶函数”的( ) A .充要条件B .充分而不必要的条件C .必要而不充分的条件D .既不充分也不必要的条件AB 1B1A1D1C CD(10)21nx x ⎛⎫- ⎪⎝⎭的展开式中,常数项为15,则n =( )A .3B .4C .5D .6(11)抛物线24y x =的焦点为F ,准线为l ,经过F 的直线与抛物线在x 轴上方的部分相交于点A ,AK l ⊥,垂足为K ,则AKF △的面积是( )A .4B .C .D .8(12)函数22()cos 2cos 2xf x x =-的一个单调增区间是( ) A .233ππ⎛⎫ ⎪⎝⎭,B .62ππ⎛⎫ ⎪⎝⎭,C .03π⎛⎫ ⎪⎝⎭,D .66ππ⎛⎫- ⎪⎝⎭,第Ⅱ卷注意事项:1.答题前,考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,然后贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.第Ⅱ卷共2页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,在试题卷上作答无效.3.本卷共10题,共90分.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在横线上. (13)从班委会5名成员中选出3名,分别担任班级学习委员、文娱委员与体育委员,其中甲、乙二人不能担任文娱委员,则不同的选法共有 种.(用数字作答)(14)函数()y f x =的图像与函数3log (0)y x x =>的图像关于直线y x =对称,则()f x = .(15)等比数列{}n a 的前n 项和为n S ,已知1S ,22S ,33S 成等差数列,则{}n a 的公比为 .(16)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为 .三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分10分)设锐角三角形ABC 的内角A B C ,,的对边分别为a b c ,,,2sin a b A =. (Ⅰ)求B 的大小;(Ⅱ)求cos sin A C +的取值范围. (18)(本小题满分12分)某商场经销某商品,根据以往资料统计,顾客采用的付款期数ξ的分布列为商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.η表示经销一件该商品的利润.(Ⅰ)求事件A :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率()P A ; (Ⅱ)求η的分布列及期望E η. (19)(本小题满分12分)四棱锥S ABCD -中,底面ABCD 为平行四边形,侧面SBC ⊥底面ABCD .已知45ABC =∠,2AB =,BC =SA SB =(Ⅰ)证明SA BC ⊥;(Ⅱ)求直线SD 与平面SAB 所成角的大小.(20)(本小题满分12分) 设函数()e e x xf x -=-.(Ⅰ)证明:()f x 的导数()2f x '≥;(Ⅱ)若对所有0x ≥都有()f x ax ≥,求a 的取值范围.(21)(本小题满分12分)已知椭圆22132x y +=的左、右焦点分别为1F ,2F .过1F 的直线交椭圆于B D ,两点,过2F 的直线交椭圆于A C ,两点,且AC BD ⊥,垂足为P .(Ⅰ)设P 点的坐标为00()x y ,,证明:2200132x y +<; (Ⅱ)求四边形ABCD 的面积的最小值. (22)(本小题满分12分)已知数列{}n a 中12a =,11)(2)n n a a +=+,123n =,,,…. (Ⅰ)求{}n a 的通项公式; (Ⅱ)若数列{}n b 中12b =,13423n n n b b b ++=+,123n =,,,…,43n n b a -<≤,123n =,,,….2007年普通高等学校招生全国统一考试 理科数学试题(必修+选修Ⅱ)参考答案一、选择题: (1)D(2)B(3)A(4)A(5)C(6)C(7)D(8)D(9)B(10)D(11)C(12)A二、填空题:(13)36 (14)3()xx ∈R(15)13(16)三、解答题: (17)解:(Ⅰ)由2sin a b A =,根据正弦定理得sin 2sin sin A B A =,所以1sin 2B =, 由ABC △为锐角三角形得π6B =. (Ⅱ)cos sin cos sin A C A A π⎛⎫+=+π-- ⎪6⎝⎭cos sin 6A A π⎛⎫=++ ⎪⎝⎭1cos cos 2A A A =++3A π⎛⎫=+ ⎪⎝⎭.由ABC △为锐角三角形知,22A B ππ->-,2263B ππππ-=-=. 2336A πππ<+<,所以1sin 23A π⎛⎫+<⎪⎝⎭.3A π⎛⎫<+< ⎪⎝⎭所以,cos sin A C +的取值范围为322⎛⎫⎪ ⎪⎝⎭,. (18)解:(Ⅰ)由A 表示事件“购买该商品的3位顾客中至少有1位采用1期付款”. 知A 表示事件“购买该商品的3位顾客中无人采用1期付款”2()(10.4)0.216P A =-=,()1()10.2160.784P A P A =-=-=.(Ⅱ)η的可能取值为200元,250元,300元.(200)(1)0.4P P ηξ====,(250)(2)(3)0.20.20.4P P P ηξξ===+==+=,(300)1(200)(250)10.40.40.2P P P ηηη==-=-==--=.η的分布列为2000.42500.43000.2E η=⨯+⨯+⨯240=(元).(19)解法一:(Ⅰ)作SO BC ⊥,垂足为O ,连结AO ,由侧面SBC ⊥底面ABCD ,得SO ⊥底面ABCD .因为SA SB =,所以AO BO =,又45ABC =∠,故AOB △为等腰直角三角形,AO BO ⊥,由三垂线定理,得SA BC ⊥.(Ⅱ)由(Ⅰ)知SA BC ⊥,依题设ADBC ∥, 故SA AD ⊥,由AD BC ==SA =AO =1SO =,SD =.SAB △的面积211122S ABSA ⎛=-= ⎝连结DB ,得DAB △的面积21sin13522S AB AD == 设D 到平面SAB 的距离为h ,由于D SAB S ABD V V --=,得121133h S SO S =,解得h =设SD与平面SAB 所成角为α,则sin 11h SD α===. 所以,直线SD 与平面SBC 所成的我为arcsin 11. 解法二:(Ⅰ)作SO BC ⊥,垂足为O ,连结AO ,由侧面SBC ⊥底面ABCD ,得SO ⊥平面ABCD .因为SA SB =,所以AO BO =.又45ABC =∠,AOB △为等腰直角三角形,AOOB ⊥. 如图,以O 为坐标原点,OA 为x0)A ,,(0B ,(0C -,,(001)S ,,,(2,(0CB =,0SA CB =,所以SA BC ⊥.(Ⅱ)取AB 中点E ,022E ⎛⎫⎪ ⎪⎝⎭,,连结SE ,取SE 中点G ,连结OG ,1442G ⎛⎫⎪ ⎪⎝⎭,,. 1442OG ⎛⎫= ⎪ ⎪⎝⎭,,,122SE ⎛⎫= ⎪ ⎪⎝⎭,,(AB =. 0SE OG =,0AB OG =,OG 与平面SAB 内两条相交直线SE ,AB 垂直.所以OG ⊥平面SAB ,OG 与DS 的夹角记为α,SD 与平面SAB 所成的角记为β,则α与β互余.D,(DS =.22cos 11OG DS OG DSα==,sin 11β=,所以,直线SD 与平面SAB 所成的角为arcsin . (20)解:(Ⅰ)()f x 的导数()e e xxf x -'=+.由于e e 2x -x +=≥,故()2f x '≥. (当且仅当0x =时,等号成立). (Ⅱ)令()()g x f x ax =-,则()()e e x xg x f x a a -''=-=+-,(ⅰ)若2a ≤,当0x >时,()e e 20x xg x a a -'=+->-≥,故()g x 在(0)+,∞上为增函数,所以,0x ≥时,()(0)g x g ≥,即()f x ax ≥.(ⅱ)若2a >,方程()0g x '=的正根为1ln 2a x +=,此时,若1(0)x x ∈,,则()0g x '<,故()g x 在该区间为减函数.所以,1(0)x x ∈,时,()(0)0g x g <=,即()f x ax <,与题设()f x ax ≥相矛盾. 综上,满足条件的a 的取值范围是(]2-∞,. (21)证明: (Ⅰ)椭圆的半焦距1c ==,由AC BD ⊥知点P 在以线段12F F 为直径的圆上,故22001x y +=,所以,222200021132222y x y x ++=<≤.(Ⅱ)(ⅰ)当BD 的斜率k 存在且0k ≠时,BD 的方程为(1)y k x =+,代入椭圆方程22132x y +=,并化简得2222(32)6360k x k x k +++-=. 设11()B x y ,,22()D x y ,,则2122632k x x k +=-+,21223632k x x k -=+22212221221)(1)()432k BD x x kx x x x k +⎡=-=++-=⎣+;因为AC 与BC 相交于点P ,且AC 的斜率为1k-, 所以,2211132k AC k⎫+⎪⎝⎭==⨯+ 四边形ABCD 的面积222222222124(1)(1)962(32)(23)25(32)(23)2k k S BD AC k k k k +24+===++⎡⎤+++⎢⎥⎣⎦≥. 当21k =时,上式取等号.(ⅱ)当BD 的斜率0k =或斜率不存在时,四边形ABCD 的面积4S =.综上,四边形ABCD 的面积的最小值为9625. (22)解: (Ⅰ)由题设:11)(2)n n aa +=+1)(1)(2n a =+1)(n a =11)(n n a a +=.所以,数列{n a 是首项为21的等比数列,1)n n a ,即n a的通项公式为1)1n n a ⎤=+⎦,123n =,,,…. (Ⅱ)用数学归纳法证明.(ⅰ)当1n =2<,112b a ==,所以11b a <≤,结论成立.(ⅱ)假设当n k =43k k b a -<≤,也即430k k b a -<.当1n k =+时,13423k k k b b b ++-=-+(3(423k k b b -+-=+(3023k k b b -=>+,又1323k b <=-+ 所以1(323k k k b b b +-=+2(3(k b <-4431)(k a -≤41k a +=也就是说,当1n k =+时,结论成立.43n n b a -<≤,123n =,,,….。
惠州市2007届高考调研(一)数学试卷分析(精)

惠州市2007届高考调研(一)数学试卷分析(文科)11.导数知识欠缺,不知利用导数求曲线在某点处斜率,或者即使求出导数,也不知代坐标求斜率.平均分1.49,难度系数0.298.12.求解中不注意审题,忽略条件中”正实数”的要求.平均分2.04,难度系数0.408. 13.关于空间几何命题判断,空间想象能力不够.平均分3.255,难度系数0.651.14.关于选做题,不注意填写所选题号,有时题目虽然解题正确,但无序号表题,故不能得分.平均分1.98,难度系数0.396.总之,对于填空题不够规范,例如,直线方程不化简,填写时不注意要求.填空题平均分8.765,难度系数0.43825.15.数列:平均分2.5,难度系数0.2083.⑴.大部分同学只做了第⑴小题,第⑵小题不会做或没有做对.平均分估计为6分. ⑵.知道公式1(1)2n n n s na d -=+,但运算错了的同学有一部分. ⑶.已知公式2(1)n b n n =+时,不会裂项求和,而是用数学归纳法证明122n b b b +++<(证明是错误的).16.平均分3.4,难度系数0.2833.本题考查概率(古典概率)属于常规容易题,相当大部分学生对基础知识,基本概率掌握不牢误解题意,抛掷两枚骰子得到的情形作答成为21种,出现了倍数的情形.作答为7种,另一部分学生混乱,表达混乱,再有一部分无解答步骤,所以整体得分率较低.17.(三角函数) 平均分5.7,难度系数0.4071.该题考查了三角函数的二倍角公式,正(余)弦函数的和(差)角公式的应用,特殊角的三角函数值,三角函数的周期性,以及简单的三角方程等知道,属中等偏易的基础题,特别是与向量的解决是本题的另一亮点.从学生答题抽样情况看,主要存在以下问题:⑴.对二倍角公式不熟悉,特别是二倍角公式的常用.⑵.对特殊角的三角函数值记忆不准确,如sin63ππ==.⑶.该题解题方法较多,特别是第(1)问:可化为cos cos )0x x x +=,同学们直接两边除以cos x 而无解,说明思维的严密性不够.⑷.个别学生对向量的垂直与平行的关系容易混淆,导致起步失分.⑸.对单调区间的求法,大多数同学是用整体代换的思想去求解,问题出现在不会解不等式,因此,同学们对于综合科知识还较欠缺.㈠.值得商榷的地方:文科学生,对形如sin(2)3x π+= ㈡.备考建议:①.加强基础知识的教学.②.关注学生的学习,找到适合学生的学习方法及教法,真正为学生服务,自己的教法尽量适合学生.③.注意学科知识内部的整合,特别是学科知识的交汇点处例题,将是高考命题的方向. 18题(立几) 平均分4.9,难度系数0.35.① 从试题本身而言,前两问相对而言比较基础简单,而第三问就感觉有点超出学生的能力范围,不常规.② 从得分情况来看,估计平均分大概在4—6分左右,大多数同学得分0分,只有少部分同学得满分.③ 从学生答题情况来看,主要存在以下几个问题:⑴很多学生都认为FM AD 或FM AB⑵不会做辅助线⑶知识点,概念,定理含糊不清, 在做第2问时,很多学生都是认为1FM BD ⊥,就可以推出11FM DD B ⊥面B ,有的同学干脆就是东拉西扯一点边都没沾上.在做第3问时,很多学生的答案是45°,但并不是题目所要求的二面角,学生几乎都把1BD 与平面ABCD 所成的线面角当成了二面角.⑷书写不规范,推理论证的依据不充分.⑸也有相当一部分学生采用向量法,但是建立不正确. ④ 答题方法而言有以下几种:(二面角) ⑴定义法 ⑵射影法 ⑶向量法⑤ 启示:要加强学生基础知识,要培养学生的空间感书写,论证更要加强,明确方法,尤其常用方法.19题分析:平均分3.3,难度系数0.275.本题考查三次函数,利用求导解决极值,单调性,方程根的问题,难度适当,学生解答情况,中等水平学生都能解决第1问的解,尖子生第二问基本能解决,得分率平均3分左右. 20题分析:平均分0.1,难度系数0.00715.该题为解析几何题,经批改后,总结如下:该题得分较低,分数得0—2分,小部分得7—9分,很少得满分. ①常见错误: 第一问:1.第一问没有使用A,B 为抛物线上的点推出12,,x x m σ与的关系,只用“AB PB λ=”推导证明.2.第1问中,由“AB PB λ=”推出“APPBλ=”对向量运算概念不清. 3. 第1问中,欲证“()QP QA QB λ⊥-”即证“()1QP QA OB λ⋅-=-”将“向量垂直的积为0”与“两直线垂直,斜率相乘为-1”混淆.4. 第一问中,对γ取特殊值,来证明.5. 第一问运算量较大,大部分学生运算过程混乱,或是为得出所需结论,跳过关键运算步骤.第一部错误暴露原因小结:运算能力的薄弱,对向量相关的基础知识点理解不清晰. 第二问:1. 受第一问运算的影响,第二问动笔的不多.2. 第二问分数只算出交点的坐标,但会有因y 将(4,4)-舍掉. 3. 第二问最多的错误是将AB 作为所求圆的直径来计算. 4. 第二问同样暴露了运算能力的问题. ② 其它解法问题:第一问: 211(,)4x A x 222(,)4x B x ,由1212()44x x AP PB x x m m λλλ-=⎧⎪=⇒⎨-=-⎪⎩ ② 2212(,()44x xQA QB x x m m λλλ-=-+-+ ③ 将②③结合得,12(,0)QA QB x x λλ-=-()0()QP QA QB QP QA QB λλ∴-=⇒⊥-第二问:① 求出切线斜率,结合A 点点坐标,求得过A 点与切线垂直的直线方程. ② 求出AB 的中垂线方程.结合①②求得交点即为所求圆的圆心, 即得圆的方程.总之:文科试题题型合理,知识覆盖率90%以上,试题很有梯度,区分度高,基础题占试卷的110左右,难度题为选择题第10题,5分,解答题第18题第3问,4分,第19题第2问,8分,第20题,14分.试题适合新课标要求.平均分59.2,难度系数0.395,试题偏难,调研二要吸取教训. 今后解题注意:① 计算量降低, ② 有关内容考查难度过大,如二面角计算,解析几何等. 学生解答情况见阅卷组的分析.惠州市2007届高考调研(一)数学试卷分析(理科)9.读程序,新增内容,对于条件的满足很多同学理解错误,导致答错.平均分3.4425,难度系数0.6885.10.关于几何概型问题,很多同学对于基本有利事件有误,或者计算出错,分数化小数取余出错.平均分3.985,难度系数0.797.11.关于定积分问题,部分学校未讲究选修,这部分内容未学,以致此题得分不高.平均分3.55,难度系数0.71.12.题目的理解不正确,很多读不懂题,得分率偏低.平均分0.565,难度系数0.113. 13.关于命题正确选择,答题不全面.平均分2.073,难度系数0.4145.14.此题为“三选一”,很多同学三题全做,结果后两题虽正确,但因为第一题错误不能得分,因此.此题丢分较亏.平均分2.455,难度系数0.491.总之,理科选择题得分大多的是10~~15分之间,失分较多. 理科15题:平均分9.2675,难度系数0.7723.本题考察三角函数的化简和求值,从试卷反映情况来看,,绝对部分学生对常用公式(两倍角的正切,余弦及和角公式)掌握得较好,大部分学生都注意了角的范围对函数的影响,知道应该取舍,出现的主要问题是学生运算能力差,有不少同学解错简单的方程及简单的乘除运算错,还有些化简的手法不太简明,总体来说,学生对这部分内容掌握得还好. 理科16题分析:平均分5.79,难度系数0.4825.本题考查概率知识,较好地体现了新课程的阅读理解能力的要求,但文字传述及图表冗长,学生对本类型题目缺乏心理素质来应对,大约13以上的学生全部空白,少数学生做得较好,但也存在表达不规范的问题,希望在以后的教学中加强学生对文字题的理解(应用题)的解题教学和应对心理训练及表达训练!理科17题:平均分5.145,难度系数0.3675.与文科15题基本类似.但理科前面比文科多了一些运算要求:求1,a d ,所以有少数同学算不出1,a d .建议:在提倡简便方法解数列问题的同时,要加强计算1,a d 的基本方法(解方程组)的训练. 18题 (立几)评价:平均分9.1175,难度系数0.65125.一. 试题情况:试题不错,是一道比较常规的题目,能够考察学生空间概念及数量关系,立体几何的几个重要方法都可在题目中体现,题目难度也适中. 二. 学生答题情况:① 第一问答对的可能是3成左右,大部分同学推理不严密,不知道用勾股定理,还有约2成的同学默认,AO BCD ⊥平面而建立空间直角坐标系.② 第二问做到cos cos 44OBM OBM ∠=∠=的约有65﹪,但能得出正确结果的约45﹪.③ 第3问做对的约3成,很多同学建立坐标用法向量,但是或是坐标写错或算错数,方法很多同学都会,但得到正确结果的没有一半. 三. 启示:① 明确方法:立几是难度不太的题,只要明确几类常用方法,一般的学生都能做. ② 加强运算的准确性,要是算错数了,得分会很低. 19题答题分析:平均分1.365,难度系数0.0975.该题为解析几何题,经批改后,总结如下:① 该题得分较低,分数得0—2分,小部分得7—9分,很少得满分.② 常见错误:第一问: 1. 第一问没有使用A,B 为抛物线上的点推出12,,x x m σ与的关系,只用“AB PB λ=” 推导证明.2. 第1问中,由“AB PB λ=”推出“APPBλ=”对向量运算概念不清. 3. 第1问中,欲证“()QP QA QB λ⊥-”即证“()1QP QA OB λ⋅-=-”将“向量垂直的积为0”与“两直线垂直,斜率相乘为-1”混淆.4. 第一问中,对γ取特殊值,来证明.5. 第一问运算量较大,大部分学生运算过程混乱,或是为得出所需结论,跳过关键运算步骤.第一部错误暴露原因小结:运算能力的薄弱,对向量相关的基础知识点理解不清晰.第二问: 1. 受第一问运算的影响,第二问动笔的不多.2. 第二问分数只算出交点的坐标,但会有因y 将(4,4)-舍掉. 3. 第二问最多的错误是将AB 作为所求圆的直径来计算. 4. 第二问同样暴露了运算能力的问题. ③ 其它解法问题:第一问: 211(,)4x A x 222(,)4x B x ,由1212()44x x x x m m AP PB λλλ-=-=-⎧=⇒⎨⎩ ②2212(,()44x xQA QB x x m m λλλ-=-+-+ ③ 将②③结合得,12(,0)QA QB x x λλ-=-()0()QP QA QB QP QA QB λλ∴-=⇒⊥-第二问:③ 求出切线斜率,结合A 点点坐标,求得过A 点与切线垂直的直线方程. ④ 求出AB 的中垂线方程.结合①②求得交点即为所求圆的圆心, 即得圆的方程. 理科20题试题分析:平均分0.185,难度系数0.0132. 本题得分率较低,主要原因有以下几点:① 前19题的计算量较大,大部分学生没有时间做20题.② 20题第一问需用反证法,虽然一部分学生知道用反证法,但相当一部分学生不知道反证法的步骤,证明过程不够严谨,传述不规范.③20题第二问需要对所证不等式变形,考察相应函数的单调性,同时需用到导数的性质,但学生在这方面的能力较弱.④20题第二问主要考察导数,函数与不等式的综合应用,能力要求较高.总之:数学理科试卷,有不少题具有新意,个别题目是原创题.有一定的梯度和区分度.由于第一轮复习没有结束,各学校复习进度也不一样,很自然较难考出好成绩.平均分65.7,难度系数0.438,试题偏难,调研二要吸取教训.各分数段分析:可以看出:要提高理科数学平均成绩必须抓好41~66分这一群体学生的成绩,要提高文科数学平均成绩必须抓好30~84分这一群体学生的成绩,怎么抓?首先,我们要分析文、理科学生数学能力的差异;其次,我们要研究对策.文、理科学生数学能力的差异是显著的.在数学上,理科学生更善于反思,能主动寻找新旧知识的联系,通过新知识的学习深化对旧知识的理解,从而有意识地整合知识,提高解题的能力,增强学好数学的自信心,激发内心对数学美的欣赏,进一步提高数学成绩来证实自己的能力,形成良好的循环.而文科学生缺乏反思的意识,不能行之有效地自我控制学习的内容,不会主动寻找已学的有关知识来理解新内容、解决新问题,更缺乏对数学美的欣赏.思维方式的差异:文理学生在对待同一问题时,由于他们所持的态度和采取的行为方式有较大的差异,文科学生更倾向于借助形象思维分析问题,理科学生更倾向于进行抽象思维的逻辑思考,理科学生观察数学问题常常是全方位和多角度的,文科学生往往是局部、孤立的.理科学生往往能够通过多个不同角度对题中的数、形、结构等方面的特征进行审查和对比联想,并尝试移植方法,使问题熟悉化、简单化,而文科学生往往只停留在“认知”阶段,或虽有深入,但也不善于分解转化问题.理科中的优秀学生观察事物经常具有“动中窥静,静中思动”的良好观察品质,他们能利用运动和静止的辨证关系来观察、分析和处理数学问题,使解题左右逢源,得心应手,游刃有余.数学思维能力的差异:在数学抽象概括能力方面,文理科学生有较大的差异,理科学生在收集数学材料所提供的信息时,能迅速地完成抽象概括的任务,同时具有概括的欲望,乐意地、积极主动地进行概括工作,文科学生的概括能力较差,积极性也不高,在数学推理能力方面,理科学生在逻辑推理方面有较大的优势,而文科学生更乐于直觉推理.在选择判断能力方面,理科学生在判断选择中较少受表面非本质因素的干扰,判断的准确率较高,判断迅速,对做出的判断具有清晰的认识,能区分逻辑判断和直觉猜测,他们具有明显的追求最合理的解法,探究最清晰、最简单同时也是最“优美”的解法的心理倾向;而文科学生则更注重的题型的记忆.在数学探索能力方面,理科学生表现出来的灵活性,对数学问题的监控能力及思维过程中的自我意识,提出问题,大胆猜测等能力,都明显地好于文科学生.造成这些差异的原因是多方面的,这里不一一分析.有什么对策呢?1.序渐进,加强学法指导:①.帮助学生提高听课效率:做到精力高度集中②.做好复习和总结:③.科学训练:2.正视差异,因材施教:3.要重视“读(阅读、理解)、写(书写表达)、算(心算、口算、数字计算、字母运算)、记(记忆)、练(规范练习)”能力的提高.我们在课堂教学的过程中,要时刻关注培养学生什么能力?通过什么途径来培养这些能力?教学语言要注意些什么?怎样通过语言的表现力、感染力来凝聚学生的思维能力?谢谢大家!。
2007年普通高等学校招生全国统一考试理科数学试卷及答案-广东卷

绝密★启用前2007年普通高等学校招生全国统一考试(广东卷)数学(理科)本试卷共4页,21小题,满分150分,考试时间120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的铅笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上、将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题的题号(或题组号)对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式sh V 31=,其中S 是锥体的底面积,h 是锥体的高。
如果事件A 、B 互斥,那么)()()(B P A P B A P +=+. 如果事件A 、B 相互独立,那么()()()P A B P A P B ⋅=⋅.用最小二乘法求线性回归方程系数公式 1221,ni i i ni i x y n x ybay b x x n x==-==--∑∑. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项符合要求的. 1.已知函数xx f -=11)(的定义域为M ,)1ln()(x x g +=的定义域为N ,则=⋂N MA.{}1x x >-B.{}1x x <C.{}11x x -<<D.φ2.若复数)2)(1(i bi ++是纯虚数(i 是虚数单位,b 是实数)则b =A.2B.21 C.21-D.2-3.若函数21()s in (),()2f x x x R f x =-∈则是A.最小正周期为2π的奇函数 B.最小正周期为π的奇函数C.最小正周期为π2的偶函数D.最小正周期为π的偶函数4.客车从甲地以60 km/h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80 km/h 的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图象中,正确的是A B C D5.已知数|a n |的前n 项和29n S n n =-,第k 项满足58k a <<,则k =A. 9B. 8C. 7D. 66.图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A 1、A 2、…、A 10(如A 2表示身高(单位:cm )(150,155)内的学生人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是A. i<6B. i<7C. i<8D. i<97.图3是某汽车维修公司的维修点环形分布图,公司在年初分配给A 、B 、C 、D 四个维修点的这批配件分别调整为40、45、61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(n 件配件从一个维修点调整到相邻维修点的调动件次为n )为A. 15B. 16C. 17D. 188.设S 是至少含有两个元素的集合,在S 上定义了一个二元运算“*”(即对任意的,a b S ∈,对于有序元素对(,)a b ,在S 中有唯一确定的元素a ﹡b 与之对应).若对任意的,a b S ∈,有a﹡(b ﹡)a b =,则对任意的,a b S ∈,下列等式中不.恒成立的是 A. (a ﹡b )﹡a a = B. [a ﹡(b ﹡)a ]﹡(a ﹡b )a =C. b ﹡(b ﹡b )b =D. (a ﹡b )﹡[b ﹡(a ﹡b )b =二、填空题:本大题共7小题,每小题5分,满分30分,其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.9.甲、乙两个袋中均装有红、白两种颜色的小球,这些小球除颜色外完全相同.其中甲袋装有4个红球,2个白球,乙袋装有1个红球,5个白球. 现分别从甲、乙两袋中各随机取出一个球,则取出的两球都是红球的概率为 .(答案用分数表示)10.若向量,a b满足1,a b a == 与b 的夹角为120°,则a a a b ⋅+⋅= .11.在平面直角坐标系xOy 中,有一定点A (2,1),若线段OA 的垂直平分线过抛物线22 (0)y p x p =>的焦点,则该抛物线的准线方程是 .12.如果一个凸多面体n 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条.这些直线中共有)(n f 对异面直线,则)4(f = 图4 ; )(n f = .(答案用数字或n 的解析式表示)13.(坐标系与参数方程选做题)在平面直角坐标系xOy 中,直线l 的参数方程为33x t y t=+⎧⎨=-⎩,(参数t R ∈),圆C 的参数方程为2c o s 2sin 2x y θθ=⎧⎨=+⎩(参数[]02θπ∈,),则圆C 的圆心坐标为 ,圆心到直线l 的距离为 .14.(不等式选讲选做题)设函数)2(,312)(-++-=f x x x f 则= ;若2)(≤x f ,则x 的取值范围是 .15.(几何证明选讲选做题)如图5所示,圆O 的直径6=AB ,C为圆周上一点,3=BC ,过C 作圆的切线l ,过A 作l 的垂线AD ,AD 分别与直线l 、圆交于点D 、E ,则∠DAC = ,线段AE 的长为 .图5三、解答题:本大题共有6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知△ABC 顶点的直角坐标分别为)0,()0,0()4,3(c C B A 、、.(1)若5=c ,求sin ∠A 的值;(2)若∠A 是钝角,求c 的取值范围. 17.(本题满分12分)下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y ((1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程y =ax b +;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:3×2.5+4×3+5×4+6×4.5=66.5) 18.(本小题满分14分)在平面直角坐标系x O y 中,已知圆心在第二象限,半径为22的圆C 与直线y x =相切于坐标原点O .椭圆9222yax +=1与圆C 的一个交点到椭圆两点的距离之和为10.(1)求圆C 的方程.(2)试探究圆C 上是否存在异于原点的点Q ,使Q 到椭圆右焦点F 的距离等于线段OF 的长.若存在,请求出点Q 的坐标;若不存在,请说明理由. 19.(本小题满分14分)如图6所示,等腰△ABC 的底边AB =66,高CD =3,点E 是线段BD 上异于点B 、D 的动点.点F 在BC 边上,且EF ⊥AB .现沿EF 将△BEF 折起到△PEF 的位置,使PE ⊥AE .记B E x = V (x )表示四棱锥P-ACFE 的体积. (1)求V (x )的表达式;(2)当x 为何值时,V (x )取得最大值?(3)当V (x )取得最大值时,求异面直线AC 与PF 所成角的余弦值 20.(本小题满分14分)已知a 是实数,函数2()223.f x a x x a =+--如果函数()y f x =在区间[1,1]-上有零点,求a 的取值范围. 21.(本小题满分14分)已知函数2()1, f x x x αβ=+-、是方程()0f x =的两个根()αβ>,()f x '是()f x 的导数.设11()1,(1,2,)()n n n n f a a a a n f a +==-=' ,(1)求αβ、的值;(2)证明:对任意的正整数n ,都有n a α>;(3)记ln (1,2,)n n n a b n a βα-==- ,求数列{}n b 的前n 项和n S .参考答案一. CADBB CBA 二. 9.1910.1211. 54x =-12.22n n + ,12 ,(1)(2)2n n n --13. (0,2), 14. 6, [1, 1]- 15. 30, 3三.解答题16.(1)解:A C =设AC 中点为M,则c o s s in 55A M A A A B===(2)解:(3,4),(3,4)A C c A B =--=--,若A ∠是钝角,则253(3)1603A C AB c c ⋅=--+<∴> . 17. 解: (1) 散点图略(2) 4166.5i i i X Y ==∑ 4222221345686i i X ==+++=∑ 4.5X = 3.5Y =266.54 4.5 3.566.563ˆ0.7864 4.58681b -⨯⨯-===-⨯- ; ˆˆ 3.50.7 4.50.35a Y b X =-=-⨯= 所求的回归方程为 0.70.35y x =+(3) 100x =, 1000.70.3570.35y =⨯+=吨,预测生产100吨甲产品的生产能耗比技改前降低9070.3519.65-=(吨) 18. 解:(1) 设圆C 的圆心为 (,)m n则,0,0m n m n =-⎧⎪<>⎪= 解得22m n =-⎧⎨=⎩所求的圆的方程为 22(2)(2)8x y ++-=(2) 由已知可得 210a = 5a = 椭圆的方程为221259xy+= , 右焦点为 (4,0)F .设存在点(,)Q x y C ∈满足条件,则2222(2)(2)8(4)16x y x y ⎧++-=⎪⎨-+=⎪⎩解得412(,)55Q故存在符合要求的点412(,)55Q .19.解: (1)11) (032V x x x =-⋅<<即336V x =-(0x <<;(2)226)1212V xx '=-=-,(0,6)x ∴∈时,0;V '>(6,x ∴∈时,0;V '<6x ∴=时()V x 取得最大值.(3)以E 为空间坐标原点,直线EF 为x 轴,直线EB 为y 轴,直线EP 为z 轴建立空间直角坐标系,则(0,60),(3,60),(3,0)A C A C --=;(0,0,6)6,0,0)(6,0,6)P F P F ∴=- ,设异面直线AC 与PF 夹角是θ1c o s 7θ∴==20.解:若0a =,则()23f x x =-有唯一零点为3[1,1]2∉-,故0a =不符合要求;由2()2230f x a x x a =+--=2232(21)32(21)x a x x a x -∴-=-∴=-, [1,1]x ∈-且2x ≠±.由2222(261)(21)xx x a x -+'=-当22610x x -+=时,13[1,1],2x -=∈-2312x +=>,当1[1,(,)22x x ∈---时,0a '>,a 在两个区间上分别递增;当1(,),(22x x ∈时, 0a '<,a 在两个区间上分别递减;A由1x =-时,5,a =1x =时,1a =,12x =时,2a =-3(,[1,)2a +∴∈-∞-+∞分析如图:解法二: 若0a = , ()23f x x =- ,显然在上没有 零点, 所以 0a ≠令 ()248382440a a a a ∆=++=++=得2a =当32a --=时, ()y f x =恰有一个零点在[]1,1-上;当 ()()()()11150f f a a -⋅=--≤即 15a << 时, ()y f x =也恰有一个零点在[]1,1-上;当 ()y f x =在[]1,1-上有两个零点时, 则()()208244011121010a a a a f f >⎧⎪∆=++>⎪⎪-<-<⎨⎪≥⎪⎪-≥⎩或()()208244011121010a a a a f f <⎧⎪∆=++>⎪⎪-<-<⎨⎪≤⎪⎪-≤⎩ 解得5a ≥或32a --<因此a 的取值范围是2a ≤或 ; 1a ≥21解:(1) 由 210x x +-=得12x -±=12α-+∴=12β--=(2)(数学归纳法)①当1n =时,112a =>命题成立;②假设当*(1,)n k k k N =≥∈时命题成立,即2k a >21511118221212222k k k k k a a a a a α+++∴==+-≥⋅=++,又等号成立时2k a =2k a ∴>时,1k a β+>1n k ∴=+时命题成立;由①②知对任意*n N ∈均有n a α>.(3) ()21f x x '=+ 221112121n n n n n n n a a a a a a a ++-+∴=-=++1n a β+∴-=22221()(1)()212121n n n n n n a a a a a a βββββ+--+---==+++同理 1n a α+∴-=2()21n n a a α-+21111()ln2lnn n n n n n n n a a a a a a a a ββββαααα++++----∴=∴=----∴ 12n n b b += 又111lnln4ln2a b a βα-===- ∴数列{}n b 是一个首项为4ln2公比为2的等比数列;∴()()14ln122421ln122nnn S +-==--。
2007广东高考数学(理科)考试及详解
2007年广东卷数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分 1.已知函数()f x =M ,()ln(1)g x x =+的定义域为N ,则M N =( ) A .{|1}x x >-B .{|1}x x <C .{|11}x x -<<D .∅2.若复数(1)(2)bi i ++是纯虚数(i 是虚数单位,b 是实数),则b =( ) A .2B .12C .12-D .2-3.若函数21()sin ()2f x x x =-∈R ,则()f x 是( ) A .最小正周期为π2的奇函数 B .最小正周期为π的奇函数 C .最小正周期为2π的偶函数D .最小正周期为π的偶函数4.客车从甲地以60km/h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h 的速度匀速行驶1小时到达内地.下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图象中,正确的是( )5.已知数列{}n a 的前n 项和29n S n n =-,第k 项满足58k a <<,则k =( )A .9B .8C .7D .6 6.图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为1210A A A ,,,(如2A 表示身高(单位:cm )在[)150155,内的学生人数).s s ss图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm (含160cm ,不含180cm )的学生人数,那么在流程图中的判断框内应填写的条件是( ) A.6i < B.7i < C.8i <7.图3是某汽车维修公司的维修点环形分布图.公司在年初分配给A B C D ,,,四个维修点某种配件各50件.在使用前发现需将A B C D ,,,四个维修点的这批配件分别调整为40,45,54,61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(n 件配件从一个维修点调整到相邻维修点的调动件次为n )为( ) A.15B.16C.17D.188.设S 是至少含有两个元素的集合,在S 上定义了一个二元运算“*”(即对任意的a b S ∈,,对于有序元素对(a b ,),在S 中有唯一确定的元素*a b 与之对应).若对任意的a b S ∈,,有()**a b a b =,则对任意的a b S ∈,,下列等式中不恒成立的是( ) A .()**a b a a = B .[()]()****a b a a b a = C .()**b b b b =D .()[()]****a b b a b b =二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.9.甲、乙两个袋中装有红、白两种颜色的小球,这些小球除颜色外完全相同,其中甲袋装图3 图1 图2身高/cm有4个红球,2个白球,乙袋装有1个红球,5个白球.现分别从甲、乙两袋中各随机取出一个球,则取出的两球是红球的概率为 .(答案用分数表示) 10.若向量,a b 满足1==a b ,a 与b 的夹角为120,则a a +a b = . 11.在平面直角坐标系xOy 中,有一定点(21)A ,,若线段OA 的垂直平分线过抛物线22(0)y px p =>的焦点,则该抛物线的准线方程是 .12.如果一个凸多面体是n 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条,这些直线中共有()f n 对异面直线,则(4)f = ;()f n = .(答案用数字或n 的解析式表示) 13.(坐标系与参数方程选做题)在平面直角坐标系xOy 中,直线l 的参数方程为33x t y t=+⎧⎨=-⎩(参数t ∈R ),圆C 的参数方程为2cos 2sin 2x y θθ=⎧⎨=+⎩(参数[)02θ∈π,),则圆C 的圆心坐标为 ,圆心到直线l 的距离为 .14.(不等式选讲选做题)设函数()213f x x x =-++,则(2)f -= ;若()5f x ≤,则x 的取值范围是 .15.(几何证明选讲选做题)如图5所示,圆O 的直径6AB =,C 为圆周上一点,3BC =.过C 作圆的切线l ,过A 作l 的垂线AD ,AD 分别与直线l 、圆交于点D E ,,则DAC =∠ ,线段AE 的长为 .三、解答题:本大题共6小题,满分80分.16.(12分)已知ABC △顶点的直角坐标分别为(34)A ,,(00)B ,,(0)C c ,.(1)若5c =,求sin A ∠的值;(2)若A ∠是钝角,求c 的取值范围. 17.(12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆy bxa=+; (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3 2.543546 4.566.5⨯+⨯+⨯+⨯=)图5图418.(14分)在平面直角坐标系xOy ,已知圆心在第二象限、半径为C 与直线y x=相切于坐标原点O .椭圆22219x y a +=与圆C 的一个交点到椭圆两焦点的距离之和为10. (1)求圆C 的方程;(2)试探究圆C 上是否存在异于原点的点Q ,使Q 到椭圆右焦点F 的距离等于线段OF 的长,若存在,请求出点Q 的坐标;若不存在,请说明理由.19.(14分)如图6所示,等腰ABC △的底边AB =高3CD =,点E 是线段BD 上异于点B D ,的动点,点F 在BC 边上,且EF AB ⊥,现沿EF 将BEF △折起到PEF△的位置,使PE AE ⊥,记BE x =,()V x 表示四棱锥P-(1)求()V x 的表达式;(2)当x 为何值时,()V x 取得最大值?(3)当()V x 取得最大值时,求异面直线AC 与PF20.(14分)已知a 是实数,函数2()223f x ax x a =+--,如果函数()y f x =在区间[]11-,上有零点,求a 取值范围.21.(14分)已知函数2()1f x x x =+-,αβ,是方程()0f x =的两个根(αβ>),()f x '是()f x 的导数,设11a =,1()(12)()n n n n f a a a n f a +=-=',,. (1)求αβ,的值;(2)证明:对任意的正整数n ,都有n a α>; (3)记ln (12)n n n a b n a βα-==-,,,求数列{}n b 的前n 项和n S .图6AB2007年(广东卷)数学(理科B )参考答案一.选择题 CDDC BBCA 1.101110x x x ->⎧⇒-<<⎨+>⎩故选(C )2.(1)(2)(2)(21)bi i b b i ++=-++为纯虚数2b ⇒=,故选(D )3.22111()sin (12sin )cos 2222f x x x x =-=--=- 故选(D ) 4.60(01)60(1 1.5)80( 1.5)60(1.5 2.5)t t s t t t ≤≤⎧⎪=<≤⎨⎪-+<≤⎩,故选(C )5.182(5)6n n n a s s n a -=-=-⇒=,k=8,(或5<2k -10<8)故选(B ) 6.计算4567A A A A +++,由算法框图知,8i < 故选(B ) 7.A D →11件,B C →4件,B A →1件,共16件,故选(C ) 8.()a b a b **=∴当a b =时()b b b b **=,又[()]()()a b a a b b a b a ****=**=;()[()]()a b b a b a b a b ****=**=,故选(A ) 二.填空题9.411()()()669P AB P A P B ==⋅= 10.2cos12012⋅+⋅+=a ab a a a b = 11.线段OA 的垂直平分线方程为152(1)(,0)24y x F -=--⇒⇒准线方程54x =-12.21(1)2n n n C ++=;12;21(1)(2)2n n n n n C ---⋅=13.参数方程化普通方程得直线方程为60x y +-=,圆的方程为22(2)4x y +-= 因此圆心为(0,2),圆心到直线的距离为d ==14.41(2)236f ---=-+=;21()5211x f x x x -≤⇒≤-⇒-≤≤三.解答题16.(1)当5c =时,5,5,cos sin AB BC AC A A ===∠=⇒∠=(2)AC BC c ==,A 为钝角222AB AC AB +<⇒2225(3)16c c +-+<253c ∴>17.(1)(略)(2)97,22x y ==,4166.5i i i x y ==∑,42186i i x ==∑,414221466.5630.786814i ii i i x y x yb x x==--===--∑∑0.35a y bx =-=,故现线性回归方程为0.70.35y x =+(3)当100x =时,70.35y =,9070.3519.65-=,故预测生产100吨甲产品的生产能耗比技改前降低19.65吨标准煤。
广东省惠州市2007届高三第一次调研考试数学

广东省惠州市2007届高三第一次调研考试数学试题(理科卷)(2006.10)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.第Ⅰ卷(选择题,共40分)一、选择题(每小题5分,共40分)1、化简=+-ii13 A .i 21- B. i 21+ C. i +2 D. i -22、命题:“设b a bc ac R c b a >>∈则若22,,,”以及它的逆命题、否命题、逆否命题中,真命题的个数为 A .0 B. 1 C. 2 D. 33、幂函数①1-=x y 及直线②x y =③1=y ④1=x将直角坐标系第一象限分成八个“卦限”Ⅲ,Ⅳ,Ⅴ,Ⅵ,Ⅶ,Ⅷ(如图所示),那么幂函 数23-=xy 的图象在第一象限中经过的“卦限”是A Ⅳ ⅦB Ⅳ ⅧC Ⅲ ⅧD Ⅲ Ⅶ4、某次考试,班长算出了全班40人数学成绩的 平均分为M ,如果把M N ,那么M :N 为A 4140B 4041 C 2 D 15、函数),52sin(2)(ππ+=x x f 若对任意R x ∈,都有)()()(21x f x f x f ≤≤成立,则||21x x -的最小值为A 4B 2C 1D 216、等比数列{}n a 前n 项的积为T n ,若1863a a a 是一个确定的常数,那么数列25171310,,,T T T T ,中也是常数项的是 A 10T B 13T C 17T D 25T7、从6人中选出4人分别到巴黎、伦敦、香港、莫斯科四个城市游览,要求每个城市有一人游览,每人只能游览一个城市,且这6人中甲、乙两人不去巴黎游览,则不同的选择方案共有 A 240种 B 300种 C 144种 D 96种8、设奇函数]1,1[)(-在x f 上是增函数,且,1)1(-=-f 若函数12)(2+-≤at t x f 对所有的[]1,1-∈x 都成立,则当[]1,1-∈a 时,t 的取值范围是A 22≤≤-tB 202≥=-≤t t t 或或C 2121≤≤-tD 21021≥=-≤t t t 或或第Ⅱ卷(填空题、解答题共110分)二、填空题(每小题5分,共910、如图在边长为25cm 为23cm 是11.=-⎰dx x x )32(2212、我们知道:“过圆心为O 的圆外一点P 作它的两条切线 P A 、PB ,其中A 、B 为切点, 则POB POA ∠=∠.”这个性 质可以推广到所有圆锥曲线,请你写出其中一个: (注意:不要求证明结论的正确性)13.关于二项式2006)1(-x ,有下列三个命题:①该二项式展开式中非常数项的系数和是1-;②该二项式展开式中第10项是1996102006xC ;③当2006=x 时,2006)1(-x 除以2006的余数是1,其中正确的命题序号是(把你认为正确的序号都填上) 14、(本小题有三个小题供选作,考生只能在①、②、③题中选做一题!多做不给分!) ①圆C :{θθcos 1sin +==x y (θ为参数)的普通方程为 ,设O 为坐标原点,点M ),(00y x 在C 上运动,点P ),(y x 是线段OM 的中点,则点P 的轨迹方程为②、若BE 、CF 是△ABC 的高,且BCEF S S 四边形=ABC △,则A ∠= ③、已知,143,,=+∈b a R b a 则22b a +的最小值为 三、解答题(6个小题,共80分)15.(本题满分12分)已知πθπθ22,222tan <<-=.⑴求θtan 的值; ⑵求)4sin(21sin 2cos 22πθθθ+--的值.16.(本题满分12分)月饼是一种时间性很强的商品,若在中秋节前出售,每盒月饼将获利5元,若到中秋节还没能及时售完,中秋节之后只能降价出售,每盒将亏损3元,根据市场调查,销量(百盒)的概率分布如下:.(1)设订购量为x 百盒时,获利额为y 元,下表表示与x 对应的y 的分布列,请在空格处填入适当的y 的值,并计算相应的获利期望值Ey ;第10题图17.(本题满分14分)已知等差数列{}n a 的前n 项和为n S ,21),(,133*=∈=b a N n S b n n 且,2153=+S S (1) 求数列{}n b 的通项公式; (2) 求证:221<+++n b b b18.(本题满分14分)如图,四面体ABCD 中,O 、E 分别是BD 、中点,2====BD CD CB CA ,2==AD AB .⑴求证:BCD AO 平面⊥⑵求异面直线CD AB 与所成角的余弦值; ⑶求点E 到平面ACD 的距离.19.(本题满分14分)如图过抛物线y x 42=的对称轴上任一点)(,0(m m p 作直线与抛物线交于A 、B 两点,点Q 是点P 关于原点的对称点.⑴设点P 满足),1,(-≠=λλλ为实数 证明:);(λ-⊥⑵设直线的方程是AB 0122=+-y x , 过A 、B 两点的圆C 与抛物线在点A 处有共同的切线,求圆C 的方程.20.(本题满分14分)已知函数)(x f 的导数)(x f '满足1)(0<'<x f ,常数α为方程x x f =)(的实数根.⑴若函数)(x f 的定义域为I ,对任意[][],,,,0b a x I b a ∈⊆存在使等式)()()()(0x f a b a f b f '-=-成立, 求证: 方程x x f =)(不存在异于a 的实数根⑵求证:当;)(,成立总有时x x f a x <>⑶对任意1x ,2x ,若满足2)()(,1,12121<-<-<-x f x f a x a x 求证EB惠州市2007届高三第一次调研考试 数学试题(理科卷)(2006.10) 参考答案9、729 10、62596 11、3412、过抛物线)0(22>=p py x 外一点P 作抛物线的两条切线PA 、PB (A 、B 为切点),若F 为抛物线的焦点,则PFB PFA ∠=∠(如果学生写出的是椭圆或双曲线,只要正确就给满分)13、①③14、①14)12(,1)1(2222=+-=+-y x y x ② 90° ③ 251三、解答题:(本大题共6小题,共80分) 15、(1)由22tan -=θ解得22tan -=θ或2tan =θ 3分 22tan ,2,22-=∴<<∴<<θπθππθπ 7分 (2)原式=223)22(1)22(1tan 1tan 1cos sin 1sin cos 1+=-+--=+-=+--+θθθθθθ 12分 16、((2)由上表可见:预订400盒月饼时获利的数学期望Ey 最大,因此最合理 17、(1)设等差数列{}n a 的公差为d ,由33332,21S a b a ==得 2分 即d a d a 334211+=+,得d a =1 4分1:,21138,,211153===+=+d a d a S S 解得得又 6分所以)1(2,11+==-+=n n b n n a n n 8分(2))111(2)1(2+-=+=n n n n b n 10分得2)111(221<+-=+++n b b b n 14分 18 (1)证明略 5分 (2) 异面直线CD AB 与所成角的余弦值为4211分 (3) 求点E 到平面ACD 的距离为72114分19解:(1)直线AB 的斜率存在可设直线AB 的方程为m kx y +=代入抛物线并化简得0442=--m kx x 2分设A 、B 两点的坐标分别是A (),11y x ),(22y x B 则21,x x 是方程0442=--m kx x 的两根,所以m x x 421-= 3分由点P 满足),1,(-≠=λλλ为实数得2121,01x xx x -==++λλλ即点Q 是点P 关于原点的对称点,故点)2,0(),,0(m m Q =-从而的坐标是))1(,(),(),(21212211m y y x x m y x m y x λλλλλ-+--=+-+=-)(λ-⊥])1([221m y y m λλ-+-=])1(44[221222121m x x x x x x m ++⋅+=2212144)(2x mx x x x m +⋅+=0444)(2221=+-⋅+=x mm x x m 6分所以)(λ-⊥ 7分 (2)由⎩⎨⎧==+-yx y x 401222得点A,B 的坐标分别是(6,9)、)4,4(- 由y x 42=得x y x y 21,412='=所以,抛物线在点A 处切线的斜率为3|6='=x y 9分设圆C 的方程是222)()(r b y a x =-+-则⎪⎩⎪⎨⎧-++=-+--=--2222)4()4()9()6(3169b a b a a b 11分解得:223,23=-=b a 2125)4()4(222=-++=b a r 13分所以,圆C 的方程是2125)223()23(22=-++y x 14分 20、(1)用反证法,设方程x x f =)(有异于α的实根β,即αβββ>=不妨设,)(f ,则)()(αβαβf f -=-,在α与β之间必存在一点c ,αβ>>c由题意等式)()()()(c f f f '-=-=-αβαβαβ成立, 3分因为βα≠所以必有1)(='c f ,但这与1)(0<'<c f 矛盾因此,若β也是方程x x f =)(的根,则必有αβ=,即方程x x f =)(不存在异于α的实数根. 6分(2)令)()(x f x x h -= 7分0)(1)(>'-='x f x h )(x h ∴为增函数 8分又)(,0)(,,0)()(x f x x h x f a h >>>∴=-=即时当ααα 9分 (3)不妨设)()(,)(,1)(0,2121x f x f x f x f x x ≤∴<'<≤即为增函数 10分x x f x f -∴<-')(,01)(函数又 为减函数 11分12122211)()(0,)()(x x x f x f x x f x x f -≤-≤∴-≥-即 12分即2||||||.|||)()(|12121212<-+-≤--≤-ααx x x x x x x f x f ,2|)()(|21<-∴x f x f 14分。
2007年高考.广东卷.理科数学试题及解答

绝密★启用前2007年普通高等艺术招生全国统一考试(广东卷)数学(理科)本试卷共4页,21小题,满分150分,考试时间120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的铅笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上、将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题的题号(或题组号)对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式sh V 31=,其中S 是锥体的底面积,h 是锥体的高。
如果事件A 、B 互斥,那么)()()(B P A P B A P +=+. 如果事件A 、B 相互独立,那么)()()(B P A P B A P ∙=∙.用最小工乘法求线性回归方程系数公式x b y a x n i x yx n xiyi ni ni -=--=∑∑==,2121ξ.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项符合要求的. 1.已知函数xx f -=11)(的定义域为M ,)1ln()(x x g +=的定义域为N ,则=⋂N MA.{}1 x xB.{}1 x xC.{}11 x x -D.φ2.若复数)2)(1(i bi ++是纯虚数(i 是虚数单位,b 是实数)则b = A.2 B.21C.21-D.-23.若函数是则)(R),(21sin )(2x f x x x f ∈-=A.最小正周期为2π的奇函数 B.最小正周期为π的奇函数C.最小正周期为π2的偶函数D.最小正周期为π的偶函数4.客车从甲地以60km/h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h 的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图象中,正确的是A. B C. D.5.已知数|a n |的前n 项和S n =n 2-9n ,第k 项满足5<a n <8,则k=A.9B.8C.7D.66.图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A 1、A 2、…、A 10(如A 2表示身高(单位:cm )(150,155)内的学生人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是A.i<6B. i<7C. i<8D. i<97.图3是某汽车维修公司的维修点环形分布图,公司在年初分配给A 、B 、C 、D 四个维修点的这批配件分别调整为40、45、61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(n 件配件从一个维修点调整到相邻维修点的调动件次为n )为A.15B.16C.17D.188.设S 是至少含有两个元素的集合,在S 上定义了一个二元运算“*”(即对任意的a,b ∈S ,对于有序元素对(a,b ),在S 中有唯一确定的元素a*b 与之对应),若对任意的a,b ∈S,有a*(b*a)=b,则对任意的a,b ∈S,下列等式中不恒成立的是A.(a*b )*a=aB.[a*(b*a)]*(a*b)=aC.b*(b*b)=bD.(a*b)* [b*(a*b)]=b二、填空题:本大题共7小题,每小题5分,满分30分,其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.9.甲、乙两个袋中均装有红、白两种颜色的小球,这些小球除颜色外完全相同.其中甲袋装有4个红球,2个白球,乙袋装有1个红球,5个白球. 现分别从甲、乙两袋中各随机取出一个球,则取出的两球都是红球的概率为 .(答案用分数表示)10. 若向量,与,1==的夹角为120°,则∙+∙=11.在平面直角坐标系xOy 中,有一定点A (2,1),若线段OA 的垂直平分线过抛物线)0(22 p px y =的焦点,则该抛物线的准线方程是 . 12.如果一个凸多面体n 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条.这些直线中共有)(n f 对异面直线,则)4(f = ; )(n f = .(答案用数字或n 的解析式表示)13.(坐标系与参数方程选做题)在平面直角坐标系xOy 中,直线l 的参数方程为)(33R t t y t x ∈⎩⎨⎧-=+=参数,圆C 的参数方程为[])20(2sin 2cos 2πθθθ,参数∈⎩⎨⎧+==y x ,则题C 的圆心坐标为 ,圆心到直线l 的距离为 .14.(不等式选讲选做题)设函数)2(,312)(-++-=f x x x f 则= ;若2)(≤x f ,则x 的取值范围是 .15.(几何证明选讲选做题)如图5所法,圆O 的直径6=AB ,C为圆周上一点,3=BC ,过C 作圆的切线l ,过A 作l 的垂线AD ,AD 分别与直线l 、圆交于点D 、E ,则∠DAC = ,线段AE 的长为 .图5三、解答题:本大题共有6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分) 已知△ABC 顶点的直角坐标分别为)0,()0,0()4,3(c C B A 、、.(1)若5=c ,求sin ∠A 的值;(2)若∠A 是钝角,求c 的取值范围.17.(本题满分12分)下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y ((1(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程y =a x b+;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5)18.(本小题满分14分)在平面直角坐标系xOy 中,已知圆心在第二象限,半径为22的圆C 与直线y=x 相切于坐标原点O .椭圆9222y ax +=1与圆C 的一个交点到椭圆两点的距离之和为10.(1)求圆C 的方程.(2)试探安C 上是否存在异于原点的点Q ,使Q 到椭圆右焦点P 的距离等于线段OF 的长.若存在,请求出点Q 的坐标;若不存在,请说明理由.19.(本小题满分14分)如图6所示,等腰△ABC 的底边AB =66,高CD =3,点B 是线段BD 上异于点B 、D 的动点.点F 在BC 边上,且EF ⊥AB .现沿EF 将△BEF 折起到△PEF 的位置,使PE ⊥AE .记BE =x ,V (x )表示四棱锥P-ACFE 的体积.(1)求V (x )的表达式;(2)当x 为何值时,V (x )取得最大值?(3)当V (x )取得最大值时,求异面直线AC 与PF 所成角的余弦值20.(本小题满分14分)已知a 是实数,函数f (x )=2ax 2+2x -3-a ,如果函数y =f (x )在区间[-1,1]上有零点,求a 的取值范围.21.(本小题满分14分)已知函数f (x )=x 2+x -1,α、β是方程f (x )=0的两个根(α>β).f ′(x )是f (x )的导数.设a 1=1,a n +1=a n -)()(n n a f a f '(n =1,2,…). (1)求α、β的值;(2)证明:任意的正整数n ,都有a n >a ;(3)记b n -αβ--n n a a ln (n =1,2,…),求数列{b n }的前n 项和S n .2007年普通高等学校全国招生统一考试(广东卷)数学(理科)参考答案9.91 10.21 11.x= -25 12.2)1(+n n ,12,2)1)(2(--n n n13.(0,2),22 14. 6,[ -1,1] 15.30°,3三、解答题16. 解:(1) (3,4)AB =--, (3,4)AC c =--当c=5时,(2,4)AC =- cos cos ,A AC AB ∠=<>=进而sin 5A ∠=(2)若A 为钝角,则AB ﹒AC= -3(c -3)+( -4)2<0解得c>325显然此时有AB 和AC 不共线,故当A 为钝角时,c 的取值范围为[325,+∞)17. 解: (1)如下图(2)y x ini i ∑=1=3⨯2.5+4⨯3+5⨯4+6⨯4.5=66.5x =46543+++=4.5y =45.4435.2+++=3.5∑=ni x i12=32+42+52+62=86266.54 4.5 3.566.563ˆ0.7864 4.58681b-⨯⨯-===-⨯- ˆˆ 3.50.7 4.50.35a Y bX =-=-⨯=故线性回归方程为y=0.7x+0.35(3)根据回归方程的预测,现在生产100吨产品消耗的标准煤的数量为0.7⨯100+0.35=70.35 故耗能减少了90-70.35=19.65(吨)18. 解: (1)设圆心坐标为(m ,n)(m<0,n>0),则该圆的方程为(x -m )2+(y -n )2=8已知该圆与直线y=x 相切,那么圆心到该直线的距离等于圆的半径,则2n m -=22 即nm -=4 ①又圆与直线切于原点,将点(0,0)代入得 m 2+n 2=8 ②联立方程①和②组成方程组解得⎩⎨⎧=-=22n m92y252x故圆的方程为(x +2)2+y 2=8 (2)a=5,∴a 2=25,则椭圆的方程为+ =1其焦距c=925-=4,右焦点为(4,0),那么OF=4。
惠州一中2007届数列单元检测

南充市高2006届第一次高考适应性考试数 学 试 卷(满分150分,时间120分钟)第Ⅰ卷选择题(满分60分)一、选择题(共12小题,每小题5分,满分60分;每小题只有一个选项符合要求)。
⑴(理)=+-ii i 1)1( A 、 iB 、i -C 、1D 、-1 (文)若函数)10(≠<=a a y x 在[0,1]上的最大值与最小值之和等于3,则a=A 、41B 、21 C 、2 D 、4 ⑵在等比数列}{n a 中,若2365π=a a ,则=)sin(74a a A 、21 B 、0 C 、1 D 、-1 ⑶(理)=+-→xx x x x 230lim A 、0B 、21C 、1D 、-1 (文)若函数221+=-x y 的反函数)(1x f y -=图象经过一个定点,则这个定点的坐标是 A 、(1,2)B 、(2,1)C 、(1,3)D 、(3,1) ⑷已知P 、q 为简单命题,则“p 且q ”为假是“p 或q ”为假的( )条件A 、充分不必要B 、必要不充分C 、充要D 、既不充分也不必要A 、⎩⎨⎧≥+--≥0221y x yB 、⎩⎨⎧≤+--≥0221y x y C 、⎪⎩⎪⎨⎧≥+--≥≤02210y x y xD 、⎪⎩⎪⎨⎧≤+--≥≤02210y x y x ⑹在等差数列}{n a 中,前n 项和为Sn ,若==8442,31s s s s 则A 、81B 、31C 、91D 、103 ⑺设函数⎪⎩⎪⎨⎧>≤-=-)0()0(12)(21x x x x f x 若f(x 0)>1,则x 0的取值范围是A 、(-1,1)B 、(-1,+∞)C 、(-∞,-2)∪(0,+∞)D 、(-∞,-1)∪(1,+∞)⑻(理)若函数x b x a x f cos sin )(-=对任意的实数x 都有)4()4(x f x f -=+ππ成立,则直线02=+-c by ax 的倾斜角为A 、arctan2B 、arctan(-2)C 、2arctan -πD 、2arctan +π (文)已知53sin =α,α是第二象限的角,且tan(α+β)=1,则tan β= A 、-7 B 、7 C 、43- D 、43 ⑼b、b b 、b a b a a 1log 1log log ,10则已知<<<的大小顺序是 A 、b b b a a b log 1log 1log << B 、bb b a a b 1log log 1log << C 、b b b a b a 1log 1log log << D 、b b b b a a 1log log 1log << ⑽已知双曲线12222=-bx a x 和椭圆)0,0(12222>>>=+b m a b x m x 离心率互为倒数,那么以a 、b 、m 为边的三角形一定是A 、直角三角形B 、等腰三角形C 、锐角三角形D 、钝角三角形⑾(理)在函数x x y ln =(0,5)上是A 、单调增函数B 、单调减函数C 、在上递增在上递减)51()1,0(,e ,e D 、上递减在上递增在)51()1,0(,e ,e (文)曲线处的切线方程是在点),(12e e x e y =A 、2-=ex yB 、2+=ex yC 、e x y +=2D 、e x y -=2 ⑿将一个四棱锥的每个顶点都染上一种颜色,并使同一条棱上的两个端点异色,若只有5种颜色可供使用,则不同的染色方法总数为A 、240种B 、300种C 、360种D 、420种第Ⅱ卷 非选择题(满分90分)二、填空题(本大题共4个小题,每小题4分,共16分)⒀已知n x )21(-的展式中,二项式系数的和是64,则它的二项式的中间项是__________; ⒁奇函数.________3123的值为则处有极值在c b a ,x cx bx ax y ++=++= ⒂(理)已知随机变量ξ和η,其中η=12ξ+ 7,若E η=34,ξ的分布列如右表,则m 的值为_____________.(文)某校有教职工x 人,高一学生1200人,高二学生1000人,高三学生800人,现用分层抽样的方法抽取一个容量为16样本,已知从高二抽取的人数为5人,则教职工的人数是____________;⒃将正整数排列成下表:12 3 45 6 7 8 910 11 12 13 14 15 16………………其中第i 行第j 列的那个数记为i j M ,则数表中的2008应记为___________.三、解答题(本大题共6个小题,共74分,解答应写出文字说明、证明过程或演算步骤)⒄(本小题满分12分) 已知向量)()(cos),3,cos 2(),sin 2,(cos 为常数m m b a x f x b x x a +∙=== ① 求函数)(x f 的最小正周期;② 当的值求为的最大值与最小值之和函数时m ,x f ,x 3)(]6,6[ππ-∈⒅(本小题满分12分)(理)已知a>0,设命题P:函数x a y )1(-=在R 上是单调递减; 命题q :R ;a x x 的解集为>-++|)7||3lg(|如果p 和q 有且仅有一个正确,求a 的范围 (文)设关于x 的不等式.|)7||3lg(|a x x >-++①当a=1时,解这个不等式;②当a 为何值时,这个不等式的解集为R 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省惠州市2007届高三第一次调研考试数学试题(理科卷)(2006.10)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.第Ⅰ卷(选择题,共40分)一、选择题(每小题5分,共40分)1、化简=+-ii13 A .i 21- B. i 21+ C. i +2 D. i -22、命题:“设b a bc ac R c b a >>∈则若22,,,”以及它的逆命题、否命题、逆否命题中,真命题的个数为 A .0 B. 1 C. 2 D. 33、幂函数①1-=x y 及直线②x y =③1=y ④1=x将直角坐标系第一象限分成八个“卦限”Ⅲ,Ⅳ,Ⅴ,Ⅵ,Ⅶ,Ⅷ(如图所示),那么幂函 数23-=xy 的图象在第一象限中经过的“卦限”是A Ⅳ ⅦB Ⅳ ⅧC Ⅲ ⅧD Ⅲ Ⅶ4、某次考试,班长算出了全班40人数学成绩的 平均分为M ,如果把M N ,那么M :N 为A 4140B 4041 C 2 D 15、函数),52sin(2)(ππ+=x x f 若对任意R x ∈,都有)()()(21x f x f x f ≤≤成立,则||21x x -的最小值为A 4B 2C 1D 216、等比数列{}n a 前n 项的积为T n ,若1863a a a 是一个确定的常数,那么数列25171310,,,T T T T ,中也是常数项的是A 10TB 13TC 17TD 25T7、从6人中选出4人分别到巴黎、伦敦、香港、莫斯科四个城市游览,要求每个城市有一人游览,每人只能游览一个城市,且这6人中甲、乙两人不去巴黎游览,则不同的选择方案共有 A 240种 B 300种 C 144种 D 96种8、设奇函数]1,1[)(-在x f 上是增函数,且,1)1(-=-f 若函数12)(2+-≤at t x f 对所有的[]1,1-∈x 都成立,则当[]1,1-∈a 时,t 的取值范围是A 22≤≤-tB 202≥=-≤t t t 或或C 2121≤≤-t D 21021≥=-≤t t t 或或第Ⅱ卷(填空题、解答题共110分)二、填空题(每小题5分,共30910、如图在边长为25cm 为23cm 是11.=-⎰dx x x )32(20212、我们知道:“过圆心为O 的圆外一点P 作它的两条切线 P A 、PB ,其中A 、B 为切点, 则POB POA ∠=∠.”这个性 质可以推广到所有圆锥曲线,请你写出其中一个: (注意:不要求证明结论的正确性)13.关于二项式2006)1(-x ,有下列三个命题:①该二项式展开式中非常数项的系数和是1-;②该二项式展开式中第10项是1996102006xC ;③当2006=x 时,2006)1(-x 除以2006的余数是1,其中正确的命题序号是(把你认为正确的序号都填上) 14、(本小题有三个小题供选作,考生只能在①、②、③题中选做一题!多做不给分!) ①圆C :{θθcos 1sin +==x y (θ为参数)的普通方程为 ,设O 为坐标原点,点M ),(00y x 在C 上运动,点P ),(y x 是线段OM 的中点,则点P 的轨迹方程为②、若BE 、CF 是△ABC 的高,且BCEF S S 四边形=ABC △,则A ∠= ③、已知,143,,=+∈b a R b a 则22b a +的最小值为 三、解答题(6个小题,共80分)15.(本题满分12分)已知πθπθ22,222tan <<-=.⑴求θtan 的值; ⑵求)4sin(21sin 2cos22πθθθ+--的值.16.(本题满分12分)月饼是一种时间性很强的商品,若在中秋节前出售,每盒月饼将获利5元,若到中秋节还没能及时售完,中秋节之后只能降价出售,每盒将亏损3元,根据市场调查,销量(百盒)的概率分布如下:. (1)设订购量为x 百盒时,获利额为y 元,下表表示与x 对应的y 的分布列,请在空格处填入适当的y 的值,并计算相应的获利期望值Ey ;第10题图17.(本题满分14分)已知等差数列{}n a 的前n 项和为n S ,21),(,133*=∈=b a N n S b n n 且,2153=+S S (1) 求数列{}n b 的通项公式; (2) 求证:221<+++n b b b18.(本题满分14分)如图,四面体ABCD 中,O 、E 分别是BD 、中点,2====BD CD CB CA ,2==AD AB .⑴求证:BCD AO 平面⊥⑵求异面直线CD AB 与所成角的余弦值; ⑶求点E 到平面ACD 的距离.19.(本题满分14分)如图过抛物线y x 42=的对称轴上任一点)(,0(m m p 作直线与抛物线交于A 、B 两点,点Q 是点P 关于原点的对称点.⑴设点P 满足),1,(-≠=λλλ为实数 证明:);(λ-⊥⑵设直线的方程是AB 0122=+-y x , 过A 、B 两点的圆C 与抛物线在点A 处有共同的切线,求圆C 的方程.20.(本题满分14分)已知函数)(x f 的导数)(x f '满足1)(0<'<x f ,常数α为方程x x f =)(的实数根.⑴若函数)(x f 的定义域为I ,对任意[][],,,,0b a x I b a ∈⊆存在使等式)()()()(0x f a b a f b f '-=-成立, 求证: 方程x x f =)(不存在异于a 的实数根⑵求证:当;)(,成立总有时x x f a x <>EB⑶对任意1x ,2x ,若满足2)()(,1,12121<-<-<-x f x f a x a x 求证惠州市2007届高三第一次调研考试 数学试题(理科卷)(2006.10) 参考答案9、729 10、62596 11、3412、过抛物线)0(22>=p py x 外一点P 作抛物线的两条切线PA 、PB (A 、B 为切点),若F 为抛物线的焦点,则PFB PFA ∠=∠(如果学生写出的是椭圆或双曲线,只要正确就给满分)13、①③14、①14)12(,1)1(2222=+-=+-y x y x ② 90° ③ 251三、解答题:(本大题共6小题,共80分)15、(1)由22tan -=θ解得22tan -=θ或2tan =θ 3分22tan ,2,22-=∴<<∴<<θπθππθπ 7分 (2)原式=223)22(1)22(1tan 1tan 1cos sin 1sin cos 1+=-+--=+-=+--+θθθθθθ 12分 16、((2)由上表可见:预订400盒月饼时获利的数学期望Ey 最大,因此最合理 17、(1)设等差数列{}n a 的公差为d ,由33332,21S a b a ==得 2分 即d a d a 334211+=+,得d a =1 4分1:,21138,,211153===+=+d a d a S S 解得得又 6分所以)1(2,11+==-+=n n b n n a n n 8分(2))111(2)1(2+-=+=n n n n b n 10分得2)111(221<+-=+++n b b b n 14分18 (1)证明略 5分 (2) 异面直线CD AB 与所成角的余弦值为4211分 (3) 求点E 到平面ACD 的距离为72114分 19解:(1)直线AB 的斜率存在可设直线AB 的方程为m kx y +=代入抛物线并化简得0442=--m kx x 2分设A 、B 两点的坐标分别是A (),11y x ),(22y x B 则21,x x 是方程0442=--m kx x 的两根,所以m x x 421-= 3分由点P 满足),1,(-≠=λλλ为实数得2121,01x xx x -==++λλλ即点Q 是点P 关于原点的对称点,故点)2,0(),,0(m m Q =-从而的坐标是))1(,(),(),(21212211m y y x x m y x m y x λλλλλ-+--=+-+=-)(λ-⊥])1([221m y y m λλ-+-=])1(44[221222121m x x x x x x m ++⋅+=2212144)(2x mx x x x m +⋅+=0444)(2221=+-⋅+=x mm x x m 6分所以)(λ-⊥ 7分(2)由⎩⎨⎧==+-y x y x 401222得点A,B 的坐标分别是(6,9)、)4,4(- 由y x 42=得x y x y 21,412='=所以,抛物线在点A 处切线的斜率为3|6='=x y 9分设圆C 的方程是222)()(r b y a x =-+-则⎪⎩⎪⎨⎧-++=-+--=--2222)4()4()9()6(3169b a b a a b 11分 解得:223,23=-=b a 2125)4()4(222=-++=b a r 13分所以,圆C 的方程是2125)223()23(22=-++y x 14分 20、(1)用反证法,设方程x x f =)(有异于α的实根β,即αβββ>=不妨设,)(f ,则)()(αβαβf f -=-,在α与β之间必存在一点c ,αβ>>c由题意等式)()()()(c f f f '-=-=-αβαβαβ成立, 3分因为βα≠所以必有1)(='c f ,但这与1)(0<'<c f 矛盾因此,若β也是方程x x f =)(的根,则必有αβ=,即方程x x f =)(不存在异于α的实数根. 6分(2)令)()(x f x x h -= 7分0)(1)(>'-='x f x h )(x h ∴为增函数 8分又)(,0)(,,0)()(x f x x h x f a h >>>∴=-=即时当ααα 9分 (3)不妨设)()(,)(,1)(0,2121x f x f x f x f x x ≤∴<'<≤即为增函数 10分x x f x f -∴<-')(,01)(函数又 为减函数 11分12122211)()(0,)()(x x x f x f x x f x x f -≤-≤∴-≥-即 12分即2||||||.|||)()(|12121212<-+-≤--≤-ααx x x x x x x f x f ,2|)()(|21<-∴x f x f 14分。
