材料力学第二章-11 温度应力和装配应力
刘鸿文版材料力学第二章

A 1
45°
图示结构,试求杆件AB、CB的 应力。已知 F=20kN;斜杆AB为直 径20mm的圆截面杆,水平杆CB为 15×15的方截面杆。
B
C
2
FN 1
FN 2 45°
y
B F
F
解:1、计算各杆件的轴力。 (设斜杆为1杆,水平杆为2杆) 用截面法取节点B为研究对象
x
∑F ∑F
x y
=0
目录
§2.4 材料拉伸时的力学性能
力学性能:在外力作用下材料在变形和破坏方 面所表现出的力学特性。 一 试 件 和 实 验 条 件
常 温 、 静 载
目录
§2.4 材料拉伸时的力学性能
目录
§2.4 材料拉伸时的力学性能
二 低 碳 钢 的 拉 伸
目录
§2.4 材料拉伸时的力学性能
σ
e
b
σb
f
2、屈服阶段bc(失去抵 抗变形的能力)
目录
FRCy
W
§2.2 轴向拉伸或压缩时横截面上的内力和应力
B d
由三角形ABC求出
0.8m
C 1.9m
α
sin α =
A
Fmax
BC 0.8 = = 0.388 AB 0.82 + 1.92 W 15 = = = 38.7kN sin α 0.388
Fmax
斜杆AB的轴力为
FN = Fmax = 38.7kN
F
a
a′ b′
c
c′ d′
F
b
d
平面假设—变形前原为平面的横截面, 变形后仍保持为平面且仍垂直于轴线。
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
2-11、2-12、2-13
理论应力集中因数: 理论应力集中因数 按线弹性理论或相应的数值方法得出的最大局部应力
σmax与该截面上名义应力σnom之比,即 σ max K tσ = σ nom
其中Ktσ的下标tσ表示是对应于正应力的理论应力集中 K t 因数。名义应力σnom为截面突变的横截面上σmax作用点处 按不考虑应力集中时得出的应力(对于轴向拉压的情况即 为横截面上的平均应力)。 具有小孔的均匀受拉平板, Ktσ≈3。
A
∑X = N sinβ + N sinβ = 0
1 2
∆L2
∆L3
A1 N3
∆L1
∑Y = N cosβ + N cosβ + N
1 2
3
=0
几何方程:
∆ L1 = ∆ L3 cos β
N1
α α
A P
Ni Li 物理方程: ∆Li = + ∆Tαi Li Ei Ai N2
3
、补充方程
N1L1 N 3 L3 + ∆Tα1L1 = ( + ∆Tα 3 L3 ) cos β E1 A1 E3 A3
1 2
1
2
3
A1 A
பைடு நூலகம்
δ
、几何方程
(δ − ∆ L3 ) cos α = ∆ L1
11
N3 N1 α
、物理方程及补充方程:
α N2
A1
N1L1 N 3 L3 = (δ − ) cos α E1 A1 E3 A3
、解平衡方程和补充方程,得:
∆L3 A 1
δ
∆L1
A
E1 A1 cos2 α N1 = N 2 = ⋅ L3 1 + 2 cos3 α E1 A1 / E3 A3
温度(T)应力、装配应力

目的和意义
目的
研究温度应力和装配应力的产生机理 、影响因素和应对措施,以提高产品 的可靠性和使用寿命。
意义
随着工业技术的不断发展,对产品性 能和可靠性的要求越来越高,因此对 温度应力和装配应力的研究具有重要 的实际意义和应用价值。
02 温度应力
温度应力的定义
01
02
03
温度应力
由于温度变化引起的材料 内部应力。
何共同影响材料的各种性能。这有助于更全面地理解材料在不同环境下
的行为,为材料科学和工程领域的发展提供支持。
02
发展新型材料和工艺
随着科技的不断进步,新型材料和工艺不断涌现。未来的研究可以关注
这些新材料和工艺在温度和应力作用下的性能表现,为实际工程应用提
预测和模拟的准确性
温度(t)应力、装配应力
目录
• 引言 • 温度应力 • 装配应力 • 温度(t)应力与装配应力的关系 • 应对措施 • 结论
01 引言
主题介绍
温度应力
由于温度变化引起的应力,通常 是由于材料热膨胀系数不同或温 度分布不均匀而产生的。
装配应力
由于装配过程中施加的外力或约 束产生的应力,如紧固件装配、 焊接等工艺过程中产生的应力。
04 温度(t)应力与装配应力的 关系
相互影响
温度应力对装配应力的影响
温度变化会导致材料膨胀或收缩,从而产生温度应力。这种应力可能会影响装 配部件的紧固程度,导致装配应力发生变化。
装配应力对温度应力的影响
装配过程中,由于装配部件之间的相互作用力,会产生装配应力。装配应力的 存在可能会影响材料在温度变化时的膨胀或收缩,进而影响温度应力的分布和 大小。
影响其使用寿命和可靠性。
材料力学应力应变部分

材料力学应力应变部分材料力学(应力应变部分)→规定载荷作用下,强度要求,就是指构件应有足够的抵抗破坏的能力。
刚度要求,就是指构件应有足够的抵抗变形的能力。
→变形的基本假设:连续性假设,均匀性假设,各向同性假设。
→沿不同方向力学性能不同的材料,称为各向异性材料,如木材、胶合板和某些人工合成材料。
→ 分布力表面力集中力(火车轮对钢轨压力,滚珠轴承对轴的反作用力)体积力是连续分布于物体内各点的力,例如物体的自重和惯性力等。
→动载荷,静载荷→应力p应分解为正应力? ,切应力τ。
26→应力单位pa,1pa=1N/m;常用Mpa,1Mpa=10pa。
第二章拉伸、压缩与剪切2.2 轴向拉伸或压缩时横截面上的内力和应力→习惯上,把拉伸的轴力规定为正,压缩时的轴力规定为负。
→用横截面上的应力来度量杆件的受力程度。
→FN=?A ;?(x)=FN(x)/A(x)2.3 直杆轴向拉伸或压缩时斜截面上的内力和应力α轴向拉伸(压缩)时,在杆件的横截面上,正应力为最大值;在与杆件轴线成45°的斜截面上,切应力为最大值。
最大切应力在数值上等于最大正应力的二分之一。
此外,α=90°时,?α=τα=0 ,这表示在平行于杆件轴线的纵向截面上无任何应力。
(应力,p=F/A,45°斜截面上,力→ ,面积→ 。
) 2.7 安全因数许用应力和安全因数的数值,可以在有关部门的一些规范中查到。
目前一般机械制造中,在静载的情况下,对塑性材料可取ns=1.2~2.5。
脆性材料均匀性较差,且断裂突然发生,有更大的危险性,所以取nb=2~3.5,甚至取到3~9。
2.8 轴向拉伸或压缩时的变形→胡克定律,当应力不超过材料的比例极限时,应力与应变成正比。
?=Eε,弹性模量E的值随材料而不同。
2222=ε=E=AE ;?l=AE ?FFL即,对长度相同,受力相等的杆件,有EA越大则变形Δl越小,所以称EA为杆件的抗拉/压刚度。
→泊松比,当应力不超过比例极限时横向应变ε’与轴向应变ε之比的绝对值是一个常数,即�O�O=μ。
温度应力、装配应力
图示齿轮用平键与轴连接, 已知轴的直径d=70mm,键的尺寸 为 b h l 2012100mm,
传递的扭转力偶矩Me=2kN·m,键的 许用应力[τ]=60MPa,[ bs]=
100MPa。试校核键的强度。
平键连接
b h n n }F
dO
Me
(a)
n FS n
b
l
O Me
(b)
即当 max 达到 b 时,该处首先产生破坏。
b
(b)动载荷作用下: 无论是塑性材料制成的构件还是脆
性材料所制成的构件都必须要考虑应力 集中的影响。
F
§2-13 剪切和挤压的实用计算
一.剪切的实用计算 剪床剪钢板
铆钉连接
n n
n-n,剪切面
F F
目录
销轴连接
F
F
剪切受力特点:作用在构件两侧面上的外力合 力大小相等、方向相反且作用线很近。 变形特点:位于两力之间的截面发生相对错动。
Ⅱ
Ⅰ
2
2
FS
A
FS A
4F
2d 2
4 15 103
2 20103
2
23.9 MPa
bs
Fbs Abs
bs
bs
Fbs Abs
F 1.5dt
15 103
12 103 20 103
62.5 MPa bs
挤压强度条件:
bs
Fbs Abs
bs
bs 许用挤压应力,常由实验方法确定
塑性材料: bs 1.5 2.5 脆性材料: bs 0.9 1.5
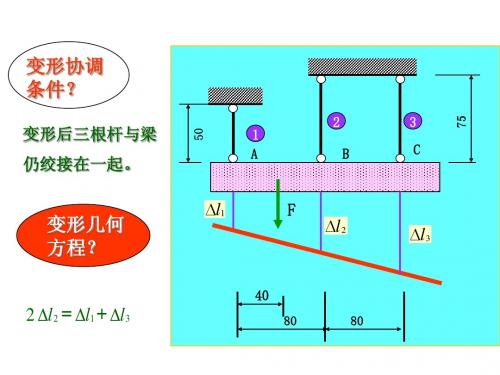
温度应力和装配应力

DC
3
B
DC
3
1
2
1
2
A
A
l1 A
l3
y
FN1
FN2
x
A FN3
补充方程
FN1l FN3l E1A1 cos2 E3 A3
平衡方程
Fx 0,FN2 sin FN1 sin 0 Fy 0,FN2 cos FN1 cos FN3 0
联立解得
FN1
FN2
E1A1E3 A3 cos2 l(2E1A1 cos3 E3 A3 )
,
FN3
2 E1A1E3 A3 cos3 l(2E1A1 cos3 E3 A3 )
例 链条的一节由三根长为 l 的钢杆组成,如图(a) 所示。若三杆的横截面面积相等,材料相同,中 间钢杆短于名义长度,加工误差为 1 ,试求
2000
各杆的装配应力。
左端螺栓受力如图所示,本题为 一次超静定问题。平衡方程为
2FN1 FN2
变形几何方程为
l1
l2
l 2000
物理方程为
l1
FN1l EA
,
l2
FN2l EA
补充方程为
FN1
FN2
EA 2000
补充方程和平衡方程联立解得
FN1
EA 6000
,
FN2
EA 3000
装配应力为
1
FN1 A
E 6000
33.3MPa,拉应力
2
FN 2 A
E 3000
66.7MPa,压应力
温度应力
一.温度内力/温度应力
A
图示静定杆件,当温度升高时, 会自由伸长,由线膨胀定律:
lt l t l
温度应力、装配应力

两端用刚性块连接在一起的两根 相同的钢杆1、 2(图a),其长度 l =200 mm,直径d =10 mm。求将 长度为200.11 mm,亦即e=0.11 mm的铜杆3(图b)装配在与杆1和 杆2对称的位置后(图c)各杆横截 面上的应力。已知:铜杆3的横截 面为20 mm×30 mm的矩形,钢的弹 性模量E=210 GPa,铜的弹性模量 E3=100 GPa。
解:
F
x
0, FN3 2FN1 0
(d)
变形协调方程(图c)为
F l F l N1 N3 利用物理关系得补充方程: e EA E3 A3
将补充方程与平衡方程联立求解得: eE3 A3 eEA 1 , FN 3 FN1 FN 2 l 1 2 EA l E3 A3 各杆横截面上的装配应力如下:
1 2
FN1 74.53 MPa(拉) A
l1 l3 e
1 EA 1 3 3 2 EA
3
FN3 19.51 MPa(压) A3
§2.12 应力集中的概念
应力集中:由于杆件外形突 然变化而引起局部应力急剧
增大的现象。
Ⅱ Ⅰ
2
2
FS A FS 4F A 2d 2 4 15 103 3 2 2 20 10 23.9 MPa
Fbs bs bs Abs Fbs F bs Abs 1.5dt
15 103 12 10 3 20 10 3 62.5 MPa bs
目录
F F F
n
F F
F 2
n
F
m m m FS m
F F
材料力学刘鸿文第六版最新课件 第二章 拉伸 压缩 剪切(2.10-2.11)

3、物理关系
FN 1l FN 3l l1 l3 E1 A1 cos E3 A3
5、求解方程组,得
FN 1 FN 2 F cos 2 , EA 2 cos3 3 3 E1 A1
4、补充方程
FN 1l F l N 3 cos E1 A1 cos E3 A3
a
R1
a
B1
2、变形协调方程
F
l2 2l1 cos
3、物理方程
FN 2l FN 1l解方程组得
FN 2l FN 1l l1 , l2 EA cos EA
3F FN 1 , FN 2 3 4 cos 1
6F cos2 4cos3 1
F FN 3 EA 1 2 1 1 cos3 E3 A3
F
选A
F
§2.11 温度应力和装配应力
温度应力
定义:在超静定结构中,由于温度变化引起的变形受到
约束的限制,因此在杆内将产生内力和应力,称为温度
应力和热应力。
超静定问题: 高压蒸汽锅炉和
原动机用管道连接,相对于锅炉 和原动机,管道刚度较小,故可 把管道两端简化为固定端。
B
D
未知力数:5 平衡方程数:3 静不定次数 = 2
A
C
超静定问题
FP
4 一般超静定问题的解法与步骤
(1)画受力图,列静力平衡方程; (2)画变形几何关系图,列变形几何(协调)方程; (3)列物理方程;
(4)在(2)和(3)的基础上建立补充方程;
(5)将静力平衡方程与补充方程联立解出约束反力
或内力;
a
FN 1
A
C
a
FN 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-11 温度应力和装配应力
一、温度应力
超静定问题用三关系法求解
1、静力学关系
①取AB为研究对象
②变形受压
③列平衡方程
2、物理关系
①轴力引起的变形量
②温度引起的变形量
【分析】温度变化要涨开,轴力变化不允许涨
3、协调方程
6、求应力
代入应力=F/A
6、如何避免温度应力
(一)、温度不变AC拉伸取正BC压缩取负δ=AC-BC=0.1(二)、温度升高30℃
3.δ=△l
衡量受到3个力,3个点构成平面平行力系、两个方程、3
个未知数、1次超静定问题
1、静力学关系
①确定研究对象(安装后的AB横梁)
N1+N3-N3=0
N1=N3
2、物理关系
△l1=△l3=?
△l2=?
3、协调关系
4、N1l/EA=△-N2l/EA
【练习】
1、静力学问题外载的一半使外面两杆变形量没有超过中间短柱长度1.5mm
2、超静定问题
变形量中的δ不用考虑
1、静力学关系
①-2aN1+3aN2-4aN3=0
2、物理关系
△l1 △l2 △l3
3、协调关系。
