第八讲相位匹配原理
相位匹配理论

又称折射率曲面,k 方向上 k 或 n 的大小。
ne
2
•
•
no与conso22无 关 ,sinn球e22面 ;1
课后思考?
与 无关,旋转椭球
no
ne
y
• 无论 no或 ne , n 正常色散
折射率椭球: 偏振方向上折射率大小
I类匹配,基波取同偏振 o 光
(3)什么是激光倍频技术?什么是相位匹配角、转换效率? (4)激光倍频晶体是各向同性还是各向异性的?为什么?
不足:波长无法进行连续调谐
气 类型原子
体
激
分子
光
器
离子
名称 He-Ne CO2
N2 Ar+ He-Cd
工作物质 He-Ne CO2 N2 Ar+ He-Cd
波长(μm ) 0.6328 10.6 0.3371 0.4880 0.4416
激励方式 气体放电 气体放电 气体放电 气体放电 气体放电
固体 激光
器
红宝石 Nd3+-YAG
Cr3+- Nd3A+-l2OY3AG
0.6943 1.06
光泵浦 光泵浦
钕玻璃
Nd3+
1.06
光泵浦
液体激光器
染料
染料
0.32
激光泵浦
半导体 激光器
GaAs/ GaAlAs
InP/InGaAsP
GaAs InP
0.85
电流注入
1.30
电流注入
特征 广泛 高功率输出 无谐振腔 常用作 泵浦源
(4)海洋水色和海洋资源探测 400~450nm之间的蓝色激光光源是感知系海洋水色的有 力武器,可用于探测海洋渔业资源。
shg的相位匹配条件

shg的相位匹配条件1.引言1.1 概述相位匹配是在光学中非常重要的概念。
在激光技术、光通信、光谱分析等领域中,相位匹配条件的实现对于光的传播和调控具有关键性的影响。
相位匹配条件是指在非线性光学效应中,通过调整光的波矢或折射率,使得不同频率的光在介质中传播时,相位速度保持一致的条件。
在这种匹配条件下,不同频率的光能够进行相互作用,从而实现一系列重要的光学过程。
对于二阶非线性光学过程,如二次谐波产生(SHG),相位匹配条件是其有效实现的关键。
在SHG过程中,通过将两个频率相互关联的入射光束输入到非线性晶体中,可以实现光频率的加倍。
然而,由于不同频率的光在晶体中的传播速度不同,如果不满足相位匹配条件,那么SHG的效率将会大大降低。
在实际应用中,为了满足相位匹配条件,可以通过选择合适的晶体材料、调整入射光束的入射角度或改变晶体的温度等方法来实现。
这些调控手段可以有效地使得不同频率的光在晶体中传播时,其相位速度保持一致,从而最大限度地提高二次谐波产生的效率。
相位匹配条件的实现对于光学器件的性能和效率有着重要的影响。
因此,在光学领域中,对相位匹配条件的研究是一个非常热门和重要的课题。
通过深入理解相位匹配条件的原理和调控方法,可以为光学器件的设计和应用提供有力的理论指导和技术支持。
本文将重点探讨SHG的相位匹配条件及其在光学领域中的应用。
接下来的章节将分别介绍相位匹配条件的基本原理、相位匹配条件的调控方法,以及未来相位匹配技术的发展趋势。
通过对这些内容的深入研究,我们可以更加全面地认识和理解相位匹配条件在光学中的重要作用,为光学器件的设计和优化提供有益的启示。
1.2文章结构文章结构部分的内容可以这样编写:1.2 文章结构本文分为引言、正文和结论三个部分。
在引言部分,将概述相关背景信息,介绍shg的相位匹配条件的重要性,并明确文章的目的。
接下来,在正文部分,将分别讨论第一个要点和第二个要点。
在第一个要点中,将详细介绍shg的相位匹配条件的基本原理、公式和模型,并给出实际应用中的示例。
相位匹配及实现方法
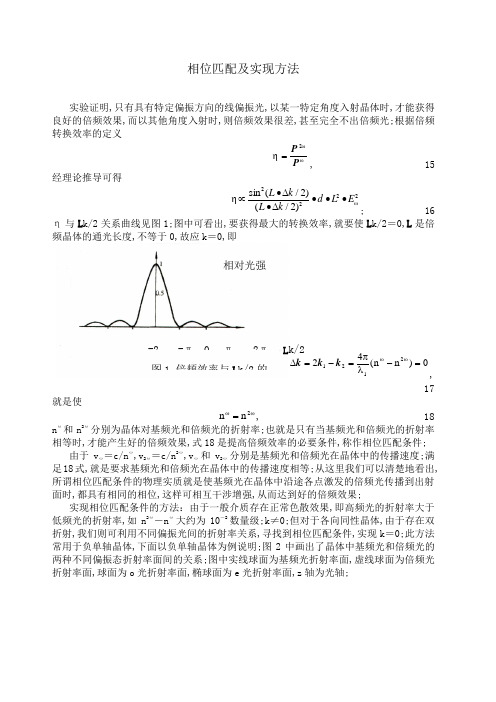
相位匹配及实现方法实验证明,只有具有特定偏振方向的线偏振光,以某一特定角度入射晶体时,才能获得良好的倍频效果,而以其他角度入射时,则倍频效果很差,甚至完全不出倍频光;根据倍频转换效率的定义ωω2ηP P =, 15经理论推导可得2ω222)2/()2/(sin ηE L d k L k L •••∆•∆•∝; 16 η与L k/2关系曲线见图1;图中可看出,要获得最大的转换效率,就要使L k/2=0,L 是倍频晶体的通光长度,不等于0,故应k =0,即0)n n (422121=-λπ=-=∆ωωk k k ,17就是使ωω=2n n , 18n ω和n 2ω分别为晶体对基频光和倍频光的折射率;也就是只有当基频光和倍频光的折射率相等时,才能产生好的倍频效果,式18是提高倍频效率的必要条件,称作相位匹配条件;由于v ω=c/n ω,v 2ω=c/n 2ω,v ω和v 2ω分别是基频光和倍频光在晶体中的传播速度;满足18式,就是要求基频光和倍频光在晶体中的传播速度相等;从这里我们可以清楚地看出,所谓相位匹配条件的物理实质就是使基频光在晶体中沿途各点激发的倍频光传播到出射面时,都具有相同的相位,这样可相互干涉增强,从而达到好的倍频效果;实现相位匹配条件的方法:由于一般介质存在正常色散效果,即高频光的折射率大于低频光的折射率,如n 2ω―n ω大约为10-2数量级;k ≠0;但对于各向同性晶体,由于存在双折射,我们则可利用不同偏振光间的折射率关系,寻找到相位匹配条件,实现k =0;此方法常用于负单轴晶体,下面以负单轴晶体为例说明;图2中画出了晶体中基频光和倍频光的两种不同偏振态折射率面间的关系;图中实线球面为基频光折射率面,虚线球面为倍频光折射率面,球面为o 光折射率面,椭球面为e 光折射率面,z 轴为光轴;图1 倍频效率与L k/2的相对光强-22π π -π L k/2折射率面的定义:从球心引出的每一条矢径到达面上某点的长度,表示晶体以此矢径为波法线方向的光波的折射率大小;实现相位匹配条件的方法之一是寻找实面和虚面交点位置,从而得到通过此交点的矢径与光轴的夹角;图中看到,基频光中o 光的折射率可以和倍频光中e 光的折射率相等,所以当光波沿着与光轴成θm 角方向传播时,即可实现相位匹配,θm 叫做相位匹配角,θm 可从下式中计算得出22o 22e 22o 2o m 2)n ()n ()n ()n (sin -ω-ω-ω-ω--=θ,19式中ωωω2e 2o o n ,n ,n 都可以查表得到,表1列出几种常用的数值;法线的夹角;为了减少反射损失和便于调节,实验中一般总希望让基频光正入射晶体表面;所以加工倍频晶体时,须按一定方向切割晶体,以使晶体法线方向和光轴方向成θm ,见图3;以上所述,是入射光以一定角度入射晶体,通过晶体的双折射,由折射率的变化来补偿正常色散而实现相位匹配的,这称为角度相位匹配;角度相位匹配又可分为两类;第一类是入射同一种线偏振光,负单轴晶体将两个e 光光子转变为一个倍频的o 光光子;第二类是入射光中同时含有o 光和e 光两种线偏振光,负单轴晶体将两个不同的光子变为倍频的e 光光子,正单轴晶体变为一个倍频的o 光光子;见表2图 2 负单轴晶体折射图3 非线性晶体的切晶体图5 基频光与倍频光的脉宽及相对线I ω I 2ω t 1t 2t 1t t 1′′ t 2′ t 2t ν1 ν1′ ν2′ ν2 νν 偏振性质 相位匹配条件 偏振性质相位匹配条件正单轴 负单轴本实验用的是负单轴铌酸锂晶体第一类相位匹配;相位匹配的方法除了前述的角度匹配外,还有温度匹配,这里不作细述;在影响倍频效率的诸因素中,除前述的比较重要的三方面外,还需考虑到晶体的有效长度L s 和模式状况;图4为晶体中基频光和倍频光振幅随距离的变化;如果晶体过长,例L>L s 时,会造成倍频效率饱和;晶体过短;例L<L s ,则转换效率比较低;L s 的大小基本给出了倍频技术中应该使用的晶体长度;模式的不同也影响转换效率,如高阶横模,方向性差,偏离光传播方向的光会偏离相位匹配角;所以在不降低入射光功率的情况下,以选用基横模或低阶横模为宜;1.5. 倍频光的脉冲宽度和线宽通过对倍频光脉冲宽度t 和相对线宽v 的观测,还可看到两种线宽都比基频光变窄的现象;这是由于倍频光强与入射基频光强的平方成比例的缘故;图5中,假设在t =t 0时;基频和倍频光具有相同的极大值;基频光在t 1和t 1'时,功率为峰值的1/2,脉冲宽度t 1=t 1'―t 1,而在相同的时间间隔内,倍频光的功率却为峰值的1/4,倍频光的半值宽度t 2 '―t 2< t 1'―t 1,即t 2<t 1,脉冲宽度变窄;同样道理可得到倍频后的谱线宽度也会变窄; 1064→532:I 类匹配为theta=90 phi=25C II 类为theta= phi=9025 CLBO 匹配分两种,一种为非临界相位匹配,一种为临界相位匹配即角度匹配.后一种都是在常温下使用的,也可以根据不同的工作温度进行角度的调整;L s L2L s图 4 晶体中基频光和倍频光。
第八讲相位匹配原理

4 o
2ne2
2
m 2
L
若 o 1.06m L 5cm n 0.08
7.9mr
m 90 , 90 匹配,非临界匹配(失配角可以很大) m 90 , 非 90 匹配,临界匹配(失配角要求苛刻)
第八讲 相位匹配原理和有效非线性系数
no2
2
第八讲 相位匹配原理和有效非线性系数
3
考虑色散曲线
一、角相位匹配
n
• no 随频率(波长)变化,
no2 曲线A: o 光折射率
no
ne2
mI
曲线B:
e
光主折射率
ne2
ne
以曲线 A为代表;
• ne也随频率(波长)变
化,同时随 变化; 0 时,与曲线
n
a
由波矢面决定 s 的方向
tg
dn
nd
1
ne2
ne2
m
o
4Lne2
I m
(k)
4 o
ne2
m
L
第八讲 相位匹配原理和有效非线性系数
8
对于负晶体 II 类匹配
o e e2
当 T Tm 当 T Tm
kT
2 2o
no T ne2 T 0
kT
2 o2
no T
T
ne2 T
T
T Tm T
相位匹配及实现方法

相位匹配及实现方法相位匹配(Phase Matching)是光学领域中一个重要的概念,指的是将不同波长或频率的光束进行匹配,使其在特定的光学介质中具有相同的相位速度,并能够有效地进行光学交互或干涉。
在光学器件或系统中,相位匹配是实现各种光学效应和应用的关键步骤,如广义的非线性光学过程(如和二次谐波,差频,和和频,以及光学参量放大等),光学波导中的耦合效应,以及光学分子束松弛和谐变等。
相位匹配是基于光波的相位速度相等原理,即在特定的介质中,不同波长的光束的相位速度差等于零。
光波的相位速度是指波前通过其中一点的速度,一般用vg表示。
相位速度等于光速c除以折射率n,即vg = c/ n。
在普通的介质中,折射率随波长而变化,从而导致不同波长的光束具有不同的相位速度。
为了实现相位匹配,需要通过选择合适的光学材料、设计合理的结构或施加特殊的相位调制手段,来调节不同波长光束的相位速度,使其相等。
相位匹配的实现方法有多种,下面列举几种常用的方法:1.正常相位匹配:正常相位匹配是最简单的相位匹配方式,即通过选择合适的光学材料,使得光束在该材料中的折射率随波长的变化足够小,从而实现相位匹配。
这种方法适用于波长较长(红外或中红外)的光束。
2.利用非线性光学晶体:非线性光学晶体具有特殊的频率响应特性,可以实现泵浦光和信号光在特定波长下的相位匹配。
这种方法常用于二次谐波,和差频等非线性光学过程。
3.使用光学波导:光学波导是一种能够限制光的传播方向和有效控制光传输的器件。
通过选择合适的波导材料和结构,可以实现不同波长光束在波导中的相位匹配,从而实现光的耦合和传输。
4.利用光栅或光子晶体:通过在特定的光学材料中制作周期性的光栅结构或光子晶体结构,可以实现不同波长光束的衍射,使其相位速度相等化。
这种方法常用于光学滤波器和光学分光仪等光学设备。
5.使用光学段通用接口(OBCI)技术:OBCI技术是一种基于宏观时间相位匹配思想的光传输接口。
信号相位匹配原理及其应用

信号相位匹配原理及其应用
信号相位匹配是指将由一个信号源产生的不同相位的信号两两匹配,使得两个不同信号的电磁特性趋于相等,当把调节后的信号转换成相应的功率时,这两个功率会有很大的不同。
信号相位匹配的原理可以分为三个步骤:首先,测量信号源处发出的两个信号相位之间的差;其次,通过调整电平器来调节这两个信号,使信号的相位和方向接近;最后,将这两个信号拼接起来,以形成一个单一的信号。
信号相位匹配的应用包括:首先,可以确保在较高的频率下发送信号,从而提高传输的速度;其次,可以消除邻近信号之间的干扰,从而改善信号质量;最后,可以将多个信号组合之后,特殊地将电路连接起来,使它们成为一个单一的信号。
一般来说,相位匹配可以大大提高信号传输的稳定性,使得信号更容易传播,在此基础上,可以有效地改善信号质量。
同时,它还可以将多个信号拼接起来,有助于满足更多的应用需求。
也因此,近年来信号相位匹配越来越受到重视,有效地应用了信号相位匹配技术,可以大大提高信号传输效率,为实现信号传输做出巨大贡献。
相位调制原理

相位调制原理相位调制是一种常见的调制方式,它是通过改变载波信号的相位来传输信息的一种技术。
在通信系统中,相位调制被广泛应用于数字调制和模拟调制中,它具有传输效率高、抗干扰能力强等优点,因此在现代通信系统中占据着重要地位。
首先,我们来了解一下相位调制的基本原理。
相位调制是通过改变载波信号的相位来传输信息的一种调制方式,它可以将数字信号或模拟信号转换为相位变化,从而实现信息的传输。
在相位调制中,载波信号的频率和幅度保持不变,只是通过改变相位来传输信息。
相位调制的核心就是在信号中引入相位变化,通过这种相位变化来表示信息。
在相位调制中,我们常用的调制方式有两种,分别是BPSK(二进制相移键控)和QPSK(四进制相移键控)。
BPSK是通过改变载波信号的相位来表示数字信号的一种调制方式,它将数字信号分别映射为0和π两种相位,通过这种方式来传输信息。
而QPSK是将数字信号分别映射为0、π/2、π和3π/2四种相位,通过这种方式来实现信息的传输。
这两种调制方式在数字通信中得到了广泛的应用,它们能够有效地提高信号的传输效率和抗干扰能力。
相位调制在通信系统中有着广泛的应用,它不仅可以用于数字通信,还可以用于模拟通信。
在数字通信中,相位调制可以将数字信号转换为相位变化的载波信号,从而实现高效的传输。
而在模拟通信中,相位调制可以通过改变载波信号的相位来传输模拟信号,从而实现信息的传输。
因此,相位调制在通信系统中具有非常重要的作用。
除了在通信系统中的应用,相位调制还被广泛应用于其他领域。
在雷达系统中,相位调制可以用于测距和测速,通过改变载波信号的相位来实现目标的探测和跟踪。
在光纤通信中,相位调制可以用于提高光纤传输的容量和速率,从而实现高速的数据传输。
在无线通信中,相位调制可以用于提高信号的传输效率和抗干扰能力,从而实现更可靠的通信。
总之,相位调制作为一种重要的调制方式,在通信系统中发挥着重要的作用。
它通过改变载波信号的相位来传输信息,具有传输效率高、抗干扰能力强等优点,在数字通信、模拟通信、雷达系统、光纤通信和无线通信等领域都得到了广泛的应用。
相位匹配及实现方法

相位匹配及实现方法 Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】相位匹配及实现方法实验证明,只有具有特定偏振方向的线偏振光,以某一特定角度入射晶体时,才能获得良好的倍频效果,而以其他角度入射时,则倍频效果很差,甚至完全不出倍频光。
根据倍频转换效率的定义ωω2ηP P =, (15)经理论推导可得2ω222)2/()2/(sin ηE L d k L k L •••∆•∆•∝。
(16) η与L k/2关系曲线见图1。
图中可看出,要获得最大的转换效率,就要使L k/2=0,L 是倍频晶体的通光长度,不等于0,故应k =0,即0)n n (422121=-λπ=-=∆ωωk k k , (17)就是使ωω=2n n , (18)n ω和n 2ω分别为晶体对基频光和倍频光的折射率。
也就是只有当基频光和倍频光的折射率相等时,才能产生好的倍频效果,式(18)是提高倍频效率的必要条件,称作相位匹配条件。
由于v ω=c/n ω,v 2ω=c/n 2ω,v ω和v 2ω分别是基频光和倍频光在晶体中的传播速度。
满足(18)式,就是要求基频光和倍频光在晶体中的传播速度相等。
从这里我们可以清楚地看出,所谓相位匹配条件的物理实质就是使基频光在晶体中沿途各点激发的倍频光传播到出射面时,都具有相同的相位,这样可相互干涉增强,从而达到好的倍频效果。
实现相位匹配条件的方法:由于一般介质存在正常色散效果,即高频光的折射率大于低频光的折射率,如n 2ω―n ω大约为10-2数量级。
k ≠0。
但对于各向同性晶体,由于存在双折射,我们则可利用不同偏振光间的折射率关系,寻找到相位匹配条件,实现k =0。
此方法常用于负单轴晶体,下面以负单轴晶体为例说明。
图2中画出了晶体中基频光和倍频光的两种不同偏振态折射率面间的关系。
图中实线球面为基频光折射率面,虚线球面为倍频光折射率面,球面为o 光折射率面,椭球面为e 光折射率面,z 轴为光轴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若
I I θ m = 90o , sin 2θ m ~ 0
k 的展开式:
(k ) (k ) = k θ =θm + θ
若
θ m = 90o
2 4π 2 ne ω (θ ) θ =θm θ + ω λo θ 2
θ =θm
(θ )
2
=
π
L
λoω = 1.06 m L = 5cm n = 0.08
第八讲 相位匹配原理和有效非线性系数
一,角相位匹配; θ m 二,温度相位匹配; θ = 90o 三,有效非线性系数; m
相位失配: k 由于 ω
= k2
2ω
k1 k1
ω
ω
↑ n↑ ,通常 n(2ω ) > n(ω ) ,利用双折射,选择 θ m
2ω [n(2ω ) n(ω )] C
d eff = e2 d ( ω 2 ; ω1 , ω1 ) : e1e1
θ = 7.9mr
θ m = 90o , 90o 匹配,非临界匹配(失配角可以很大) θ m ≠ 90o ,
非
90o 匹配,临界匹配(失配角要求苛刻)
11
第八讲 相位匹配原理和有效非线性系数
取 θ = 90 ,通过改变温度实现相位匹配
o
二,温度相位匹配
有些晶体折射率随温度变化很 大,且 ne 比 no 变化大 例如,LiNbO3 ,对YAG激光
ω
ω
2ω
z
I θm
k(I)
ω no
y
2 ne ω (θ )
[
]
I 满足 θ m 的所有 方向都满足相位匹配,是一个圆.
由
2 ne
cos θ sin θ (θ ) = 2 + 2 ne no
2 2
1
解出:sin
2
I θm
(n ) ( ) = (n ω ) ( )
ω 2
o 2 e 2
k
s (法线)
dn tgρ = a 2 1 ne ω (θ ) dn ρ ≈ tgρ = = 2ω ndθ ne (θ ) θ
a dθ ≈ n
由波矢面决定 s 的方向
θ =θ m
λω o θ = 2 I 4 Ln e ω θ m ρ
( )
2 4π ne ω (θ ) ( k ) = ω λo θ
第八讲 相位匹配原理和有效非线性系数 2
I类匹配,基波取同偏振 o 光
一,角相位匹配
o +o →e k = k 2 k1 k1 = 0 2 ω ne ω (θ ) no
2ω 2ω ω ne (θ ) no = 0 C
ω I 2 ne ω (θ )与 no 的交点决定 k(I) 和 θ m ;
[ ]
y
x
cosθ cos 同理 e e = cosθ sin = b j sin θ
[ ]
给定晶体后,从附录中查出
d ( ) 的具体形式
14
第八讲 相位匹配原理和有效非线性系数
对 4 2 m 晶体
o+ d eff o→e = e e d ( ) : e o e o
三,有效非线性系数
z
k (II)
[
]
II θm
y
( ) [
ω
( )]
对于正晶体( I 类: II类:
ne > no )
ω
2ω
e +e =o oω + eω = o 2ω
思考:对于负单轴晶体,倍频 光能不能是 o 光? 同样,对于正晶体,倍 频光能不能是 e 光?
5
第八讲 相位匹配原理和有效非线性系数
2,相位匹配角宽度
↓θ
ω ne
θ = 0o 时,与曲线 θ = 90o 时,下移到
λ
曲线 B. 对于负单轴晶体 I 类匹配,要求 2ω I ; 平线,找到
ne θ m
( )
2 ω ω ne ω (θ ) = no ,从 no ( A) 作水 2 ω ne ω < no ,总可以找到匹配点.
曲线 A,B之间为匹配区,只要
> ne)
KDP (KH2PO4) 磷酸二氢钾 LN (LiNbO3) 铌酸锂
2 no ω
z
cos θ sin θ + ne (θ ) = 2 2 ne no
2 2 2
no与 θ
无关,球面;
1
ω no
与
无关,旋转椭球
ne
正常色散
ω
y
无论 no 或
ne , ↑ n ↑ ω
折射率椭球: 偏振方向上折射率大小
k (T ) =
2π
[n
(T ) ne2ω (T )] = 0 o
ω
对 LiNbO3
T = 0.33o / L(cm)
角度宽松的代价是 温度的苛刻
12
第八讲 相位匹配原理和有效非线性系数
一,角相位匹配; 二,温度相位匹配; 三,有效非线性系数;
第八讲 相位匹配原理和有效非线性系数
13
以负单轴晶体 I 类匹配为例
Lρ = w 近似
9
=
λoω
高斯光束发散角
第八讲 相位匹配原理和有效非线性系数
一,角相位匹配; 二,温度相位匹配; 三,有效非线性系数;
第八讲 相位匹配原理和有效非线性系数
10
问题提出:
θ = ±
二,温度相位匹配
2 2 I 4 L no ω ne ω sin 2θ m
(
λω o
)
θ = ±0.06mr
判据
(k ) π (k ) = k θ =θ m + θ =θ m θ = θ L 求出允许的 θ 的范围
第八讲 相位匹配原理和有效非线性系数 6
= θ m附近展开:
一,角相位匹配
考虑偏离最佳匹配角(仍以负单轴晶体 I 类匹配为例) 2ω 2ω ω 展开式 k = ne (θ ) no (k ) π C (k ) = k θ =θ m + θ = θ =θ m 1 θ L cos 2 θ sin 2 θ 2
o θ = θ m 或 θ = 90 +温度匹配
π
,故
2
=
π
4
1 2
习题:2.7, 2.9
提示: (1 + x )
1 ≈ 1 x 2
15
第八讲 相位匹配原理和有效非线性系数
本讲小结
2ω [n(2ω ) n(ω )] 选择 θ m k = C
d eff = e2 d ( ω 2 ; ω1 , ω1 ) : e1e1
θ =θ m θ
=
π
L
第八讲 相位匹配原理和有效非线性系数
8
一,角相位匹配
对于负晶体 II 类匹配
o +e →e
孔径长度满足:
ω
ω
2ω
光轴 z
θm
ω ko ω so
ω ke
2 ke ω
La ρ = w (光束宽度)
考虑高斯光束
ρ
La
ω se 2 se ω
θ =
πne
2ω
λω o
(θ )w πLne 2ω (θ )ρ
第八讲 相位匹配原理和有效非线性系数
4
II类匹配,基波取正交偏振的两个波(仍以负晶体为例)
一,角相位匹配
oω + eω → e 2ω
k = k 2 k1 k1 = 0 ω 2ω ω ω 2ne (θ ) no ne (θ ) = 0 C 相同的 θ 1 ω 2ω II ω II ne θ m = no + ne θ m 2 等效于基频双折射减少
2 a1 2 a2 0 0 0 0 d 36 0 2a1a2
o+ d eff o→e = [b1 b2
0 0 0 d14 b3 ]0 0 0 0 0 0 0 0
0 d14 0
= d 36 sin θ sin 2
由角相位匹配,决定 为使d eff 最大, 2 =
三,有效非线性系数
o + o →e d eff
= e d ( ): e e
e
o o
如何确定
角,使 deff 最大?
主平面 Ee
写出 E e,E o各分量
o E x = E o sin o E y = E o cos o Ez = 0
z
k
E o θm
sin eo = cos = a j 0
θ
一,角相位匹配
以上讨论仅限于理想平面波,实际中由于 光路调整偏离 θ m ;(即使是理想平面波) 坡印廷矢量偏离;( k 和
s 偏离)
高斯光束发散; 偏离波矢匹配条件使倍频效率降低,问题:偏离角
θ 允许多大?
kL 2
判据: kL ≤ π 2 2
将 k 在 θ
η SHG ~ sin c 2
θ = ±0.06mr(毫弧度) 很小!! 若 θ I = 90 o , 2θ I ~ 0 , θ 可以很大 sin m m
I sin 2θ m ~ 1
计算得到
第八讲 相位匹配原理和有效非线性系数
7
考虑坡印廷矢量的离散
光轴 z 切线
光轴 z
一,角相位匹配
dθ
θm
dn
切线
a ρ s (法线)
n
k
θm
θ =
2 πLne ω (θ )ρ
λω o
取 θ = 90o ,通过改变温度实现相位匹配
第八讲 相位匹配原理和有效非线性系数 16
�
与基波及倍频波的偏振方向有关,选择
m
1
