应用题9方案选择问题
应用题9方案选择问题【范本模板】

方案选择问题1、根据下面的两种移动电话计费方式表,考虑下列问题.一个月内在本地通话200分和350分,按方式一需交费多少元?按方式二呢?对于某个本地通话时间,会出现按两种计费方式收费一样多吗?2、一家游泳馆每年6~8月出售夏季会员证,每张会员证80元,只限本人使用,凭证购入场券每张1元,不凭证购入场券每张3元,讨论并回答:(1)什么情况下,购会员证与不购证付一样多的钱?(2)什么情况下,购会员证比不购划算?(3)什么情况下,不购会员证比购证划算?3、公园门票价格规定如下表:某校初一(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:(1)两班各有多少学生?(2)如果两班联合起来,作为一个团体购票,可省多少钱?(3)如果初一(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?4、甲、已两个团体共120人去某风景区旅游。
风景区规定超过80人的团体可购买团体票,已知每张团体比个人票优惠20%,而甲、乙两团体人数均不足80人,两团体决定合起来买团体票,共优惠了 480元,则团体票每张多少元?5、张老师带领该校七年级“三好学生"去开展夏令营活动,甲旅行社说:“如果老师买全票一张,则学生可享受半价优惠。
”乙旅行社说:“包括老师在内按全票价的6折优惠。
”若全票价为240元,当学生从数为多少人时,两家旅行社的收费一样多?6、某厂生产一种计算器,其成本价为每只36元,现有两种销售方式:第一种是直接由厂门市部销售,每只售价为48元,但需要每月支出固定费用6480元(固定费用指门市部房租、水电费用、销售人员工资等);第二种是批发给文化用品商店销售,批发价为每只42元,又知两种销售方式均需缴纳税款为销售金额的10%。
(1)求该厂每月销售多少只计算器时两种方式所获利润相等?(2)若该厂今年6月份计划销售这种计算器1500只,问:哪种方式最合适?7、某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元。
初一方案选择问题
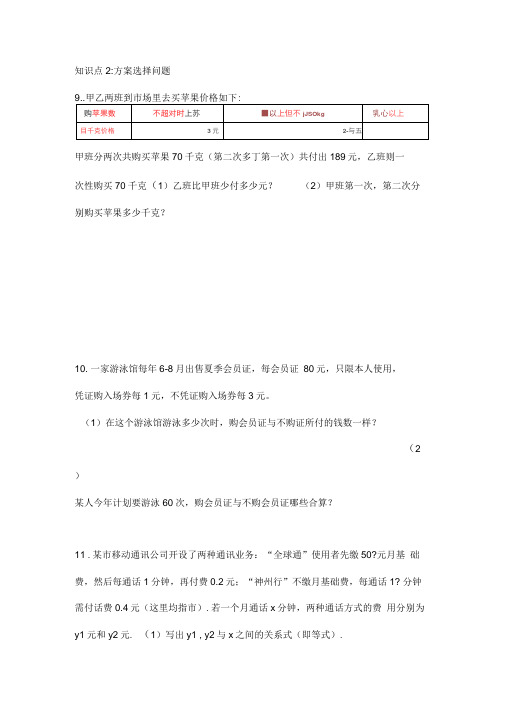
知识点2:方案选择问题甲班分两次共购买苹果70千克(第二次多丁第一次)共付出189元,乙班则一次性购买70千克(1)乙班比甲班少付多少元?(2)甲班第一次,第二次分别购买苹果多少千克?10. 一家游泳馆每年6-8月出售夏季会员证,每会员证80元,只限本人使用,凭证购入场券每1元,不凭证购入场券每3元。
(1)在这个游泳馆游泳多少次时,购会员证与不购证所付的钱数一样?(2)某人今年计划要游泳60次,购会员证与不购会员证哪些合算?11 .某市移动通讯公司开设了两种通讯业务:“全球通”使用者先缴50?元月基础费,然后每通话1分钟,再付费0.2元;“神州行”不缴月基础费,每通话1? 分钟需付话费0.4元(这里均指市).若一个月通话x分钟,两种通话方式的费用分别为y1元和y2元. (1)写出y1 , y2与x之间的关系式(即等式).(2)一个月通话多少分钟,两种通话方式的费用相同?(3)若某人预计一个月使用话费120元,则应选择哪一种通话方式较合算?解:(1) y1=0.2x+50 , y2=0.4x .(2)由y1=y2 得0.2x+50=0.4x,解得x=250 .即当一个月通话250分钟时,两种通话方式的费用相同.(3)由0.2x+50=120 ,解得x=350由0.4x+50=120 ,得x=300因为350>300故第一种通话方式比较合算.12.小明用的练习本可以到甲商店购买,也可以到乙商店购买,已知两商店的标价都是每本1元,甲商店的优惠条件是,购买10本以上,从第11本开始按标价的70%卖,乙商店的优惠条件是,从第一本开始按标价的80%卖。
(1)小明要买20本时,到哪家商店省钱?(2)买多少本时到两个商店买都一样?(3)小明现在乂31元钱,最多可以买多少本?1、15 本,甲商店:10*1+5*1*70%=13.5 (元);乙商店:15*1*85%=12.75 (元)。
在乙商店买便宜些。
2、设买X 本(大于10), 10+70% (X-10 )=85%X , X=20,即买20 本时,在两家商店负的钱相等。
初一的方案选择问题应用题

初一的方案选择问题应用题初一的方案选择问题应用题一、背景介绍初一学生在选择方案时常常面临一定的困惑。
这个问题不仅涉及到学科选择,还包括社团活动、兴趣班等方面的选择。
初一学生正处在青春期的重要阶段,他们对未来的选择产生了浓厚的兴趣和好奇心。
因此,为了帮助初一学生解决方案选择问题,我们需要制定一套科学、实用的方案。
二、方案一:学科选择1. 初一学生在学科选择上应充分发挥自己的兴趣和优势,尽量选择自己喜欢和擅长的学科。
2. 学科选择要考虑到未来的发展方向和职业规划。
可以通过职业规划测试、就业前景调研等方式了解各个学科的就业前景和发展趋势,从而做出科学的选择。
3. 学科选择还要考虑到个人的兴趣爱好和性格特点。
可以根据自己的兴趣和特长来选择相应的学科,这样可以更加激发学习的动力。
三、方案二:社团活动选择1. 初一学生可以参加学校提供的各种社团活动,如音乐社团、美术社团、科技社团等。
通过参加社团活动,学生可以培养自己的兴趣爱好,锻炼自己的团队合作能力和领导能力。
2. 在选择社团活动时,初一学生可以结合自己的兴趣和特长来选择适合自己的社团。
可以参加一两个自己感兴趣的社团,这样可以更加全面地发展自己的各个方面。
四、方案三:兴趣班选择1. 初一学生可以参加各种兴趣班,如舞蹈班、音乐班、体育班等。
通过参加兴趣班,学生可以培养自己的兴趣爱好,提高自己的技能水平。
2. 在选择兴趣班时,初一学生可以根据自己的兴趣和特长来选择适合自己的兴趣班。
可以选择一两个自己感兴趣的兴趣班,这样可以更加全面地发展自己的各个方面。
五、方案四:家长的指导和参与1. 家长在初一学生方案选择中起着重要的作用。
家长可以通过与孩子的沟通了解孩子的兴趣和特长,帮助孩子做出科学的选择。
2. 家长可以提供一些参考意见和建议,但不应当强制孩子做出选择。
应该尊重孩子的意愿和选择,给予他们充分的自主权。
六、方案五:专业辅导和咨询1. 初一学生可以通过咨询老师和专业辅导师的帮助来解决方案选择问题。
初一方案设计选择问题

知识点2:方案选择问题9..甲乙两班到市场里去买苹果价格如下:甲班分两次共购买苹果70千克(第二次多于第一次)共付出189元,乙班则一次性购买70千克(1)乙班比甲班少付多少元?(2)甲班第一次,第二次分别购买苹果多少千克?10.一家游泳馆每年6-8月出售夏季会员证,每张会员证80元,只限本人使用,凭证购入场券每张1元,不凭证购入场券每张3元。
(1)在这个游泳馆游泳多少次时,购会员证与不购证所付的钱数一样?(2)某人今年计划要游泳60次,购会员证与不购会员证哪些合算?11.某市移动通讯公司开设了两种通讯业务:“全球通”使用者先缴50•元月基础费,然后每通话1分钟,再付电话费0.2元;“神州行”不缴月基础费,每通话1•分钟需付话费0.4元(这里均指市内电话).若一个月内通话x分钟,两种通话方式的费用分别为y1元和y2元.(1)写出y1,y2与x之间的关系式(即等式).(2)一个月内通话多少分钟,两种通话方式的费用相同?(3)若某人预计一个月内使用话费120元,则应选择哪一种通话方式较合算?解:(1)y1=0.2x+50,y2=0.4x.(2)由y1=y2得0.2x+50=0.4x,解得x=250.即当一个月内通话250分钟时,两种通话方式的费用相同.(3)由0.2x+50=120,解得x=350由0.4x+50=120,得x=300因为350>300故第一种通话方式比较合算.12.小明用的练习本可以到甲商店购买,也可以到乙商店购买,已知两商店的标价都是每本1元,甲商店的优惠条件是,购买10本以上,从第11本开始按标价的70%卖,乙商店的优惠条件是,从第一本开始按标价的80%卖。
(1)小明要买20本时,到哪家商店省钱?(2)买多少本时到两个商店买都一样?(3)小明现在又31元钱,最多可以买多少本?1、15本,甲商店:10*1+5*1*70%=13.5(元);乙商店:15*1*85%=12.75(元)。
方案问题应用题及答案

方案问题应用题及答案一、背景介绍在现代社会,方案的制定和解决问题是非常重要的。
无论是在工作中还是日常生活中,我们都需要通过制定方案来解决问题,提高工作效率,创造更好的生活。
本文将通过一个具体的应用题来探讨方案问题的解决方法,并给出详细的答案。
二、问题描述假设你是一家糕点店的店长,你接到了一个任务:为一位客户的生日聚会准备一些糕点。
要求如下:1. 客户的生日聚会将有50个宾客参加;2. 糕点的种类可自由选择,但必须包括巧克力蛋糕、水果塔和奶油泡芙;3. 糕点的数量需要保证每个宾客都能够品尝到每种糕点,但又不能过多浪费;4. 假设每个宾客都会品尝每种糕点,并且每个人对每种糕点的需求量都一样。
三、问题分析根据问题描述,我们可以知道需要准备的糕点种类有三种,参与人数为50人。
为了保证每个宾客都能够品尝到每种糕点,我们需要计算出每种糕点的合理数量。
四、解决方案1. 计算糕点的总数量根据问题描述,我们需要计算出每种糕点的合理数量,首先我们需要计算出糕点的总数量。
我们知道参与人数为50人,假设每个人对每种糕点的需求量都是n个,那么糕点的总数量就是3n。
因为每个宾客都要品尝每种糕点,所以每种糕点的数量应该是n个。
2. 计算每种糕点的合理数量根据上面的计算结果,我们知道每种糕点的数量应该是n个。
为了保证每个宾客都能够品尝到每种糕点,我们需要计算出每种糕点的合理数量。
由于参与人数为50人,糕点的总数量为3n个,所以每种糕点的合理数量应该是3n/3 = n个。
3. 结果分析根据上面的计算结果,我们可以得出每种糕点的合理数量应该是n 个。
因此,巧克力蛋糕、水果塔和奶油泡芙的合理数量都应该是n个。
这样每个宾客就能够品尝到每种糕点,并且不会有太多的浪费。
五、答案展示根据上述分析,我们得出的答案是:1. 巧克力蛋糕的合理数量为n个;2. 水果塔的合理数量为n个;3. 奶油泡芙的合理数量为n个。
六、总结通过对该方案问题的分析和解答,我们可以看出合理的方案是非常重要的。
一元一次方程应用题方案选择问题训练题(含解析)

一元一次方程应用题方案选择问题(含解析)一、单选题(共5题;共10分)1.(2020·丰南模拟)下图为歌神KTV的两种计费方案说明.若晓莉和朋友们打算在此KTV的一间包厢里连续欢唱6小时,经服务生计算后,告知他们选择包厢计费方案会比人数计费方案便宜,则他们在同一间包厢里欢唱的至少()A. 6人B. 7人C. 8人D. 9人2.(2020·黑龙江)母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支2元,百合每支3元.小明将30元钱全部用于购买这两种花(两种花都买),小明的购买方案共有()A. 3种B. 4种C. 5种D. 6种3.(2019七上·合肥月考)“欢乐购”元旦促销活动即将到来,小芳的妈妈计划花费1000元,全部用来购买价格分别为80元和120元的两种商品若干件,则可供小芳妈妈选择的购买方案有()A. 4种B. 5种C. 6种D. 7种4.(2019七上·崇川月考)小明和爸爸妈妈三人暑假准备参加旅游团去北京旅游,甲旅行社说:“如果父母买全票,小孩可半价优惠”:乙旅行社说:“全部按全票价的8 折优惠”,若全票价为1200元,则小明应选择哪家旅行社()A. 选择甲B. 选择乙C. 选择甲、乙都一样D. 无法确定5.(2016·赤峰)8月份是新学期开学准备季,东风和百惠两书店对学习用品和工具实施优惠销售.优惠方案分别是:在东风书店购买学习用品或工具书累计花费60元后,超出部分按50%收费;在百惠书店购买学习用品或工具书累计花费50元后,超出部分按60%收费,郝爱同学准备买价值300元的学习用品和工具书,她在哪家书店消费更优惠()A. 东风B. 百惠C. 两家一样D. 不能确定二、综合题(共16题;共173分)6.(2020七上·武威月考)某市移动通讯公司开设了两种通讯业务:“全球通”使用者先缴50元月基础费,然后每通话1分钟,再付电话费0.2元;“神州行”不缴月基础费,每通话1分钟需付话费0.4元(这里均指市内电话),若一个月内通话分钟,两种通话方式的费用分别为元和元.(1)写出,与之间的函数关系式(即等式).(2)一个月内通话多少分钟,两种通话方式的费用相同?(3)若某人预计一个月内使用话费120元,则应选择哪一种通话方式较合算?7.(2020八上·宁波月考)某体育用品商店对甲、乙两种品牌的足球开展促销活动,已知甲、乙两种品牌的足球的标价分别是160元/个,60元/个,现有如下两种优惠方案;方案一:未购买会员卡时,甲品牌足球享受八五折优惠,乙品牌足球买5个(含5个)以上时所有足球享受八五折,5个以下必须按标价购买方案二:办理一张会员卡100元,会员卡只限本人使用,全部商品享受七五折优惠(1)若购买甲品牌足球3个,乙品牌足球4个,哪一种方案更优惠?优惠了多少元?(2)如果购买甲品牌足球若干个,乙品牌足球6个,方案一与方案二所付钱数一样多,求购买甲品牌的足球的个数8.(2020七上·合肥期中)合肥庐阳区实验学校七(6)班为迎接学校秋季运动会计划购买30支签字笔,若干本笔记本(笔记本数量超过签字笔数量),用来奖励运动会中表现出色的运动员和志愿者,甲、乙两家文具店的标价都是签字笔8元/支、笔记本2元/本,甲店的优惠方式是签字笔打九折,笔记本打八折;乙店的优惠方式是每买5支签字笔送1本笔记本,签字笔不打折,购买的笔记本打七五折.(1)如果购买笔记本数量为60本,并且只在一家店购买的话,请通过计算说明,到哪家店购买更合算?(2)若都在同一家店购买签字笔和笔记本,试问购买笔记本数量是多少时,两家店的费用一样?9.(2020七上·庐阳期中)某校组织学生外出研学,旅行社报价每人收费300元,当研学人数超过50人时,旅行社给出两种优惠方案:方案一:研学团队先交1500元后,每人收费240元;方案二:5人免费,其余每人收费打九折(九折即原价的90%)(1)用代数式表示,当参加研学的总人数是x()人时,用方案一共收费________元;用方案二共收费________元;(2)当参加旅游的总人数是80人时,采用哪种方案省钱?说说你的理由10.(2020七上·沂南期中)甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同,甲商场规定:凡超过元的电器,超出的金额按收取;乙商场规定:凡超过元的电器,超出的金额按收取,某顾客购买的电器价格是元.(1)当时,分别用代数式表示在两家商场购买电器所需付的费用(2)当时,该顾客应选择哪一家商场购买比较合算?说明理由.11.(2020七上·吉安期中)初一年级学生在5名教师的带领下去公园秋游,公园的门票为每人30元,现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都7.5折收费.(1)若有m名学生,用代数式表示两种优惠方案各需多少元?(2)当m=70时,采用哪种方案优惠?12.(2020七上·新津期中)某市电话拨号入网有两种收费方式,用户可以任选其一:(A)计时制:3元/时;(B)包月制:60元/月(限一部个人住宅电话上网);此外,每一种上网方式都得加收通信费1.2元/时.(1)某用户某月上网的时间为x小时,请分别写出两种收费方式下该用户应该支付的费用;(2)当某用户某月上网的时间为90小时,你认为采用哪种方式较为合算?(3)根据上网时间的不同,你认为采用哪种方式较为合算?13.(2020七上·舒城月考)某学校班主任暑假带领该班三好学生去旅游,甲旅行社说:“如果教师买全票一张,其余学生享受半价优惠;”乙旅行社说:“教师在内全部按票价的6折优惠;”若全部票价是240元. (1)如果有10名学生,应参加哪个旅行社,并说出理由;(2)当学生人数是多少时,两家旅行社收费一样多?14.(2020七上·慈溪期中)甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元。
一元一次方程应用题9大类型解析

一元一次方程应用题类型目录:一、列一元一次方程解应用题的一般步骤二、一元一次方程解决应用题的分类1、市场经济、打折销售问题2、方案选择问题3、储蓄、储蓄利息问题4、工程问题5、行程问题6、环行跑道与时钟问题7、若干应用问题等量关系的规律8、数字问题9、日历问题一、列一元一次方程解应用题的一般步骤(1)审题:弄清题意.(2)找出等量关系:找出能够表示本题含义的相等关系.(3)设出未知数,列出方程:设出未知数后,表示出有关的含字母的式子,•然后利用已找出的等量关系列出方程.(4)解方程:解所列的方程,求出未知数的值.(5)检验,写答案:检验所求出的未知数的值是否是方程的解,•是否符合实际,检验后写出答案.二、一元一次方程解决应用题的分类1、市场经济、打折销售问题(一)知识点:(1)商品利润=商品售价-商品成本价×100%(2)商品利润率=商品利润商品成本价(3)商品销售额=商品销售价×商品销售量(4)商品的销售利润=(销售价-成本价)×销售量(5)商品打几折出售,就是按原价的百分之几十出售,如商品打8折出售,即按原价的80%出售.(二)例题解析1、某高校共有5个大餐厅和2个小餐厅.经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2280名学生就餐.(1)求1个大餐厅、1个小餐厅分别可供多少名学生就餐;(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.解:(1)设1个小餐厅可供y名学生就餐,则1个大餐厅可供(1680-2y)名学生就餐,根据题意得:2(1680-2y )+y=2280解得:y=360(名)所以1680-2y=960(名)(2)因为9605360255205300⨯+⨯=>,所以如果同时开放7个餐厅,能够供全校的5300名学生就餐.2、工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.该工艺品每件的进价、标价分别是多少元?解:设该工艺品每件的进价是x 元,标价是(45+x )元.依题意,得:8(45+x )×=(45+x-35)×12-12x解得:x=155(元)所以45+x=200(元)3、某地区居民生活用电基本价格为每千瓦时元,若每月用电量超过a 千瓦则超过部分按基本电价的70%收费.(1)某户八月份用电84千瓦时,共交电费元,求a .(2)若该用户九月份的平均电费为元,则九月份共用电多少千瓦?•应交电费是多少元?解:(1)由题意,得 0.4a+(84-a )××70%=解得a=60(2)设九月份共用电x 千瓦时, ×60+(x-60)××70%=解得x=90所以×90=(元)答: 90千瓦时,交元.4、某商店开张为吸引顾客,所有商品一律按八折优惠出售,已知某种旅游鞋每双进价为60元,八折出售后,商家所获利润率为40%。
七年级数学人教版下册第九章一元一次不等式组的实际应用分配问题与方案选择问题

讲解答案
解题方法
雄鹰必须比鸟飞得高,因为它的猎物就是鸟。 治天下者必先立其志。 雄鹰必须比鸟飞得高,因为它的猎物就是鸟。 志,气之帅也。 强行者有志。 沧海可填山可移,男儿志气当如斯。
贫困能造就男子1气、概。根据题目中的关键词找出不等关系,列不等式(组).
志不立,如无舵这舟,无衔之马,漂荡奔逸,终亦何所底乎。 人无志向,和迷途的盲人一样。
例题讲解-答案
解题方法
1、根据两种商品之间的等量关系,建立方程求解.
2、根据题目中的关键词找出不等关系,列不等式(组).
3、 有几种方案
回答数字几种
有哪几种方案
回答数字,并写出具体方案.
应用练习1
某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两 种奖品共20件.其中甲种奖品每件40元,乙种奖品每件30元 (1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买 了多少件?
应用练习3
某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B 型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元. (1)求每辆A型车和B型车的售价各为多少万元.
应用练习3
某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B 型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元. (2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130 万元,且不超过140万元.则有哪几种购车方案?
应用练习2
某校组织夏令营活动,现有36座和42座两种客车供选择租用,若 只租用36座客车若干辆,则刚好坐满;若只租用42座客车,则能少租 一辆,而且还有一辆没有坐满,但超过30人,问: (1)该校有多少人参加夏令营活动?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方案选择问题
1、根据下面的两种移动电话计费方式表,考虑下列问题.
一个月内在本地通话200分和350分,按方式一需交费多少元?按方式二呢?
对于某个本地通话时间,会出现按两种计费方式收费一样多吗?
2、一家游泳馆每年6~8月出售夏季会员证,每张会员证80元,只限本人使用,凭证购入场券每张1元,
不凭证购入场券每张3元,讨论并回答:
(1)什么情况下,购会员证与不购证付一样多的钱?
(2)什么情况下,购会员证比不购划算?
(3)什么情况下,不购会员证比购证划算?
3、公园门票价格规定如下表:
某校初一(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.
经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果初一(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
4、甲、已两个团体共120人去某风景区旅游。
风景区规定超过80人的团体可购买团体票,已知每张团体
比个人票优惠20%,而甲、乙两团体人数均不足80人,两团体决定合起来买
团体票,共优惠了 480元,则团体票每张多少元?
5、张老师带领该校七年级“三好学生”去开展夏令营活动,甲旅行社说:“如果老师买全票一张,则学生
可享受半价优惠。
”乙旅行社说:“包括老师在内按全票价的6折优惠。
”若全票价为240元,当学生从数为多少人时,两家旅行社的收费一样多?
6、某厂生产一种计算器,其成本价为每只36元,现有两种销售方式:第一种是直接由厂门市部销售,每
只售价为48元,但需要每月支出固定费用6480元(固定费用指门市部房租、水电费用、销售人员工资等);第二种是批发给文化用品商店销售,批发价为每只42元,又知两种销售方式均需缴纳税款为销售金额的10%。
(1)求该厂每月销售多少只计算器时两种方式所获利润相等?
(2)若该厂今年6月份计划销售这种计算器1500只,问:哪种方式最合适?
7、某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价相同,随身听和书包单价之和是452
元,且随身听的单价比书包单价的4倍少8元.
(1)求该同学看中的随身听和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打8折销售,超市B全场购物满100元返
购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说服他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?(12分)
8、有一些相同的房间需要粉刷,一天3名师傅去粉刷8个房间,结果其中有40 m2墙面未来得及刷;同
样的时间内5名徒弟粉刷了9个房间的墙面.每名师傅比徒弟一天多刷30m2的墙面.
(1)求每个房间需要粉刷的墙面面积;
(2)张老板现有36个这样的房间需要粉刷,若请1名师傅带2名徒弟去,需要几天完成?
*9、(2009年益阳市)开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本;小亮用31元买了同样的钢笔2支和笔记本5本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作
为奖品,奖给校运会中表现突出的同学,要求笔记本数不少于钢笔数,共有多少种购买方案?
请你一一写出.。
