数学必修1专题1:抽象函数的单调性
【课件】函数的单调性(第1课时)课件高一上学期数学人教A版(2019)必修第一册

抽象概括:由特殊函数f (x)=x²到一般函数的单调性f(x)=x² 类比 一般函数f(x)定义域为R 定义域为Dy 轴右边:(0 ,+0)) 区间IC D
总结新知用定义证明函数单调性的步骤:1.取值 即设x₁,x₂是该区间内的任意两个值,且x₁ <x₂2.作差变形 即作差f(x₁)-f(x₂) (或f(x₂)-f(x₁)), 并 通过因式分解、配方、有理化等方法,向有利于判断差 的符号的方向变形;(变形至利用x₁,x₂ 可以判断)3.定号 确定差f(x₁)-f(x₂) ( 或f(x₂)-f(x₁) 的符号,当符号不确定时,可以进行分类讨论;4.判断根据定义作出结论
=—x —6—
y65433 -2 0-1
2+1十-1-1+-2+-3-4
-3 -22 4 6 x
v=2x
s手
4
2
单调区间为定义域单调递增单调区间为定义域单调递减
增函数减函数
函数的单调性
学习新知【 例1】根据定义,研究函数 f(x)=kx+b(k≠0)的单调性.解:函数f(x)=kx+ b(k≠0) 的定义域是R,Vx ₁,x₂∈R, 且x₁<x₂, 则f(x₁)-f(x₂)=(kx₁+b)-(kx₂+b)=k(x₁-x₂)由x₁<x₂ , 得x₁-x₂<0. 所以①当k>0 时,k(x₁—x₂)<0. 于是,f(x₁)-f(x₂)<0, 即f(x₁)<f(x₂ ).这时f(x)=kx +b 是增函数 .② 当k<0 时 ,k(x₁-x₂)>0. 于是,f(x₁)-f(x₂)>0, 即f(x₁)>f(x₂). 这时f(x)=kx +b 是减函数 .
高一数学必修1-函数的单调性-精品PPT课件

y2
1
x -2 -1 O 1 2
练习2 证明函数f(x)=1/x在(-∞,0)上是减函数。
想一想:函数f(x)=1/x在(0,
+∞)上的单调性呢?
在整个定义域内 f(x)=1/x是不是减函数呢?
反例:取x1= - 1 , x2=1,则f(-1)=-1,f(1)=1
可见 x1 < x2 时; f(x1) > f(x2)不一定成立。
对于二次函数f(x)=x2 ,我们可以这样来描述“在区 间(0,+∞) 上随着x的增大,相应的f(x)也随着增大.”:
试一试:你能仿照这样的描述,说明函数 f(x)=x2在区间(-∞,0]上是减函数吗?
定义:
如果对于定义域I内的某个区间D上的 任意两个自变量的值x1,x2,当x1<x2时,都有 f(x1)<f(x2),那么就说函数f(x)在区间D上是 增函数.
解:函数y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5]. 其中y=f(x)在区间[-5,-2) ,[1,3)上是减函数,在区间[-2,1), [3,5]上是增函数.
例2 物理学中的波意耳定律p=k/V(k为正常数)告诉我 们,对于一定量的气体,当其体积V减小时,压强p将增大.试 用函数的单调性证明之.
练习:证明函数 f (x) -2x 1 在 R上是
减函数.
小结:
• 1.函数的单调性概念; • 2.增(减)函数的定义; • 3.增(减)函数的图象特征; • 4.增(减)函数的判定; • 5.增(减)函数的证明.
练习1 画出下列函数图象,并写出单调区间:
(1) y x2 2
单调增区间为, 0 单调减区间为0,
1.3.1 函数的单调性
抽象函数的单调性

抽象函数的单调性抽象函数的含义:没有解析式的函数,在考试中抽象函数始终作为一大难点出现在考生面前。
思路:添项法。
类型:一次函数型,幂函数型,指数函数型,对数函数型。
函数满足:或例1、 ()f x 对任意,x y R ∈都有:()()()f x y f x f y +=+,当0,()0x f x ><时,判断()f x 在R 上的单调性。
例2、f(x)对任意实数x 与y 都有()()()2f x f y f x y -=--,当x>0时,f(x)>2(1)求证:f(x)在R 上是增函数; (2)若f(1)=5/2,解不等式f(2a-3) < 3【专练】:1、已知函数f x ()对任意x y R ,∈有f x f y f x y ()()()+=++2,当x >0时,f x ()>2,f ()35=,求不等式f a a ()2223--<的解集。
2、定义在R 上的函数f(x)满足:对任意x ,y ∈R 都有()()()f x y f x f y -=-,且当0,()0x f x <<时(1)求证f(x)为奇函数; (2)若f(k ·3x )+f(3x -9x -2)<0对任意x ∈R 恒成立,求实数k 的取值范围.或例1、f(x)是定义在x>0的函数,且f(xy) = f(x) + f(y);当x>1时有f(x)<0;f(3) = -1.(1)求f(1)和f(1/9)的值;(2)证明f(x)在x>0上是减函数;(3)解不等式f(x) + f(2-x)< 2。
例2、定义在(0,)+∞上函数()y f x =对任意的正数,a b 均有:()()()a f f a f b b=-,且当1x <时,()0f x >,(I )求(1)f 的值;(II )判断()f x 的单调性,【专练】:1、定义在(0,)+∞上的函数f(x)对任意的正实数,x y 有)()()(y f x f yx f -=且当01x <<时,()0f x <. 求:(1))1(f 的值. (2)若1)6(=f ,解不等式2)1()3(<-+xf x f ; 2、 函数()f x 的定义域是0x ≠的一切实数,对定义域内的任意12,x x 都有1212()()()f x x f x f x ⋅=+,且当1x >时()0,(2)1f x f >=又, (1)求证:()f x 是偶函数;(2)()f x 在(0,)+∞上是增函数(3)解不等式2(21)2f x -<3、设()f x 是定义在(0,)+∞上的函数,对任意,(0,)x y ∈+∞,满足()()()f xy f x f y =+且当1x >时,()0f x >。
抽象函数的奇偶性与单调性-完整版课件
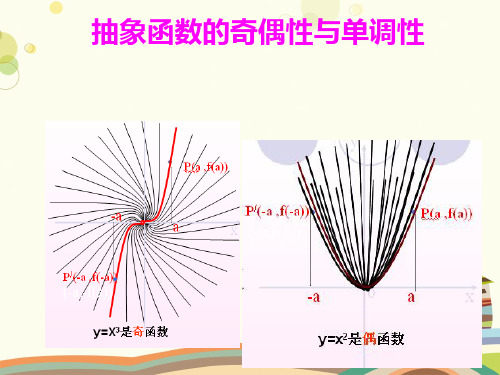
二、抽象函数的奇偶性与单调性的证明 4、已知函数f(x),当x,y∈R时,恒有f(x+y) =f(x)+f(y), (1)求证:f(x)是奇函数; (2)如果x为正实数,f(x)<0,并且 试求f(x)在区间 [-2,6]上的最值.
5、函数f (x)对任意的 x, y R ,都有 f (x y) f (x) f ( y) 1
,并且当x 0 时 f (x) 1
.
(1)证明:f (x) 在R上是增函数;
(2)若 f (4) 5 ,解不等式 f (3m2偶性解不等式 1、已知奇函数f(x)是定义在[-1,1]上的增函数,
且f(x-1)+f(1-2x)<0,求实数x的取值范围.
变式1、若偶函数f(x)的定义域为[-1,1],且在[0,1]上单 调递减,若f(1-m)<f(m)成立,求m的取值范围.
变式2、已知偶函数 f (x) 是定义在 [0, 上) 单调递增,
解不等式 f (2x 1) f (1)的x的取值范围.
3
2、已知偶函数 f (x) 是定义在 [2, 1上] 单调递减函数,
则 f (3), f (1), f (2)的大小关系为 ____
3、定义在R上的奇函数 f (x)满足 f (x 4) f (x) ,
且在区间[0,2]单调递增,试比较 f (1), f (3), f (4) 的大小
3.2.1函数的单调性5—赋值法与配凑法课件-2024-2025学年高一上学期数学人教A版必修1

①解:令x=y=0,则f(0)f(0)=f(0) ∴f(0)[f(0)-1]=0 ∴f(0)=0或f(0)=1
∵f(x)是定义域在R恒不等于零的函数 ∴f(0)=1
例2:设f(x)是定义域在R恒不等于零的函数,且对
x,y∈R满足f(x)f(y)=f(x+y),且f(x)>0
①求f(o)的值,
②设当x<0时,都有f(x)>f(0),证明f(x)在R上是减函数
练1:已知f(x)对x,y∈R恒有f(x+y)=f(x)+f(y) 且x>0时,f(x)<0,证明f(x)在R上是减函数
解:设x1,x2∈R,且x1<x2 ∴x2-x1>0
∵x>0时,f(x)<0
凑已知
∴f(x2-x1)<0
∵f(x1)-f(x2)=f(x1)-f[(x2-x1)+x1)]
=f(x1)-f(x2-x1)+f(x1)
f
(x2 )
f (x1)
f (x1 •
x2 ) x1
f (x1)
f
( x2 ) x1
f (x1)
f (x1)
f ( x2 ) x1
∵0
x1
x2 ,
x2 x1
1
f
(x2 )
f
( x1 )
0
必修一数学抽象函数习题精选含答案

1.抽象函数的图像判断单调性
例1.如果奇函数 在区间 上是增函数且有最小值为5,那么 在区间 上是( )
A.增函数且最小值为 B.增函数且最大值为
C.减函数且最小值为 D.减函数且最大值为
分析:画出满足题意的示意图,易知选B。
2、抽象函数的图像求不等式的解集
例2、已知定义在 上的偶函数 满足 ,并且 在 上为增函数。若 ,则实数 的取值范围.
(2)证明解:(1)令 得 , 或 。
若 ,当 时,有 ,这与当 时, 矛盾, 。
(2)设 ,则 ,由已知得 ,因为 , ,若 时, ,由
,
(3)由 得
得 (2)
从(1)、(2)中消去 得 ,因为
即 。
例9. 已知 是定义在 上的奇函数,且 ,若 时,有 .(1)判断函数 在 上是增函数,还是减函数,并证明你的结论;(2)解不等式:f(x+ )<f( ).
例7.已知函数 对任意 有 ,当 时, , ,求不等式 的解集。
解:设 且 ,则 , ,则
,
,故 为增函数,
又
因此不等式 的解集为 。
五、综合问题求解
解题时需把握好如下三点:一是注意函数定义域的应用,二是利用函数的奇偶性去掉函数符号“ ”前的“负号”,三是利用函数单调性去掉函数符号“ ”。
例8.设函数 定义在R上,当 时, ,且对任意 ,有 ,当 时 。(1)证明 ;
解:(1)设任意x1,x2∈[-1,1],且x1<x2.由于f(x)是定义在 上的奇函数,
∴f(x2)-f(x1)=f(x2)+f(-x1).因为x1<x2,所以x2+(-x1)≠0,
由已知有 >0,∵x2+(-x1)=x2-x1>0
高考数学复习----《抽象函数的单调性、奇偶性、周期性、对称性》典型例题讲解

高考数学复习----《抽象函数的单调性、奇偶性、周期性、对称性》典型例题讲解【典型例题】例1、(2023·广东·高三统考学业考试)已知函数()f x 对任意,R x y ∈,都有()()()f x y f x f y +=+成立.有以下结论:①()00f =;②()f x 是R 上的偶函数;③若()22f =,则()11f =;④当0x >时,恒有()0f x <,则函数()f x 在R 上单调递增.则上述所有正确结论的编号是________【答案】①③【解析】对于①令0x y ==,则()()()0000f f f +=+,解得()00f =,①正确;对于②令y x =−,则()()()00f f x f x =+−=,∴()()f x f x −=−,∴()f x 是R 上的奇函数,②错误;对于③令1x y ==,则()()()()211212f f f f =+==,∴()11f =,③正确;对于④设12x x >,则120x x −>,∴()()()12120f x x f x f x −=+−<,则()()()122f x f x f x <−−=,∴()f x 在R 上单调递减,④错误.故答案为:①③.例2、(2022·山东聊城·二模)已知()f x 为R 上的奇函数,()22f =,若对1x ∀,()20,x ∈+∞,当12x x >时,都有()()()1212210f x f x x x x x ⎡⎤−−<⎢⎥⎣⎦,则不等式()()114x f x ++>的解集为( ) A .()3,1−B .()()3,11,1−−−C .()(),11,1−∞−− D .()(),31,−∞−⋃+∞ 【答案】B【解析】由()()121221()[]0f x f x x x x x −−<,得()()11221212()[]0x f x x f x x x x x −−<, 因为121200x x x x −>>,,所以()()11220x f x x f x −<,即()()1122x f x x f x <,设()()g x xf x =,则()g x 在()0,∞+上单调递减,而()()()()()1114222g x x f x f g +=++>==,则012x <+<,解得:11x −<<;因为()f x 为R 上的奇函数,所以()()()()g x xf x xf x g x −=−−==,则()g x 为R 上的偶函数,故()g x 在(,0)−∞上单调递增,()()()()11142g x x f x g +=++>=−,则210x −<+<,解得:31x −<<−;综上,原不等式的解集为(),111)3(,−−−.故选:B .例4、(2022·全国·模拟预测(理))已知定义在R 上的奇函数()f x 的图像关于直线1x =对称,且()y f x =在[]0,1上单调递增,若()3a f =−,12b f ⎛⎫=− ⎪⎝⎭,()2c f =,则a ,b ,c 的大小关系为( )A .c b a <<B .b a c <<C .b c a <<D .c a b <<【答案】C【解析】 由函数()f x 的图像关于直线1x =对称可得()()31f f =−,结合奇函数的性质可知 ()3a f =−()()()311f f f =−=−−=,()()200c f f ===.由奇函数的性质结合()y f x =在[]0,1上单调递增可得()y f x =在[]1,1−上单调递增, 所以()()1012f f f ⎛⎫−<< ⎪⎝⎭, 所以b c a <<.故选:C例5、(2022·黑龙江大庆·三模(理))已知定义域为R 的偶函数满足()()2f x f x −=,当01x ≤≤时,()1e 1x f x −=−,则方程()11f x x =−在区间[]3,5−上所有解的和为( ) A .8B .7C .6D .5【答案】A【解析】 解:因为函数()f x 满足()()2f x f x −=,所以函数()f x 的图像关于直线1x =对称, 又函数()f x 为偶函数,所以()()()2−==−f x f x f x ,所以函数()f x 是周期为2的函数, 又1()1g x x =−的图像也关于直线1x =对称, 作出函数()f x 与()g x 在区间[]3,5−上的图像,如图所示:由图可知,函数()f x 与()g x 的图像在区间[]3,5−上有8个交点,且关于直线1x =对称, 所以方程。
复合函数及抽象函数的单调性ppt课件

例2:设f(x)是定义在实数集R上的偶函数, 且在区间(-∞,0]上是增函数,又 f(2a2+a+1)<f(3a2-2a+1),试求a的取值范围。
(0<a<3)
.
例2: 定 R 义 上 在的 f函 (x)满 数足 : (1)f(2)1 (2)f(xy)f(x)f(y) (3)xy时 f, (x)f(y) (4)f(x)f(x3)2 求x的 取 值 . 范 围 解(3 : )知 f(x )在 由 R 上减 f(4 ) f( , 2 ) f(2 ) 又 2
•复合函数的单调性
引理2:已知函数y=f[g(x)],若u=g(x)在区间(a,b) 上是减函数,其值域为(c,d),又函数y=f(u)在区间 (c,d)上是减函数,那么,原复合函数y=f[g(x)]在 区间(a,b)上是增函数。
证明:在区间(a,b)内任取两个数x1,x2,使a<x1<x2<b,
【讲解】很明显这是一个复合函数的单调性问题,所以 应“分层剥离”为两个函数
t=-x2+2 ① y = f ( t ) =-t 2 + 2t + 8 ②
【解题思路】 x∈某区间A
t∈性
g ( x )在A上的 单调性
关键是A的端点如何确定?
.
【解】设t =-x2 + 2
.
•复合函数的单调性
若u=g(x) 增函数 减函数 增函数 减函数
y=f(u) 增函数 减函数 减函数 增函数
则y=f[g(x)] 增函数 增函数 减函数 减函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学必修1专题1:抽象函数的单调性
1. 三类抽象函数的类型及其单调性分析
(1) 已知定义在R 上的函数)(x f 对任意实数y x 、都满足)()()(y f x f y x f +=+,且当0>x 时,0)(>x f .判断)(x f 的单调性并证明.
证明:令0==y x ,则)0()0()00(f f f +=+ ∴0)0(=f
令x y -=,则0)()()0()(=-+==-x f x f f x x f ∴)()(x f x f =-
在R 上任取21x x ,,且使21x x <
0)()()()()(121212<-=-+=-x x f x f x f x f x f 即)()(12x f x f <
由定义可知)(x f 在R 上为单调递减函数
(2) 已知函数)(x f 的定义域是()∞+,0,
满足)()()(y f x f xy f +=,且当1>x 时,0)(>x f .判断)(x f 的单调性并证明.
证明:令1==y x ,则)1()1()1(f f f += ∴0)1(=f 令x y 1=,则0)1()()1()1·(=+==x f x f f x x f ∴)()1(x f x
f -= 任取()∞+∈,,021x x ,且使21x x <
0)()1()()()(1
21212>=+=-x x f x f x f x f x f 即)()(12x f x f > 由定义可知)(x f 在()∞+,0上为单调递增函数
(3) 已知函数)(x f 的定义域是()∞+,0,且对一切00>>y x ,都有)()()(y f x f y
x
f -=,当1>x 时,有0)(>x f .判断)(x f 的单调性并证明.
证明:令1==y x ,则)1()1()1(f f f += ∴0)1(=f
任取()∞+∈,,021x x ,且使21x x < 则0)(
)()(1212>=-x x f x f x f 即)()(12x f x f > 由定义可知)(x f 在()∞+,0上为单调递增函数
2. 简短评价
(1) 注意三类函数的定义域不同的区别;
(2) 其实我们可以看出解题的思路大致一样:求出)0(f 或)1(f ;令x y -=或x
y 1=
针对练习:
1. 已知函数)(x f 的定义域是()∞+,0,满足1)2(=f ,且对于定义域内任意x 、y 都有)()()(y f x f xy f +=成立,那么=+)4()1(f f _______
2. 定义在R 上的函数)(x f 满足xy y f x f y x f 2)()()(++=+ )(R y x ∈,,2)1(=f ,则=-)3(f _______
3. 已知函数)(x f 在定义域()∞+,0上为增函数,且满足)()()3(y f x f xy f +=,1)3(=f
(1) 求)27()9(f f ,的值;
(2) 解不等式2)8()(<-+x f x f
4. 设函数)(x f 对任意的R b a ∈,,都有1)()()(-+=+b f a f b a f ,且当0>x 时,1)(>x f
(1) 求证:)(x f 是R 上的增函数
(2) 若5)4(=f ,解不等式3)23(2<--m m f
5. 设函数)(x f 是定义域为R ,并满足)()()(y f x f y x f +=+,1)3
1
(=f ,且当0>x 时,0)(>x f
(1) 求)0(f 的值;
(2) 判断函数的奇偶性;
(3) 如果2)2()(<++x f x f ,求x 的取值范围
6. 已知函数)(x f 对一切R y x ∈,,都有)()()(y f x f y x f +=+,若a f =-)3(,则是否可以用a 表示)12(f
7. 已知函数)(x f 的定义域是()∞+,0,当1>x 时,0)(>x f ,且)()()(y f x f xy f +=
(1) 求)1(f
(2) 证明:)(x f 在定义域上是增函数
(3) 如果1)3
1(-=f ,求满足不等式2)21()(≥--x f x f 的x 的取值范围 8.(河南省许昌市四校高一(上)期中联考)已知定义域为(0,+∞)的函数)(x f 满足:①x >1时,
0)(<x f ;②1)2
1(=f ③对任意的正实数x ,y ,都有)()()(y f x f xy f += (1) 求证:0)1(=f ,)()1(x f x
f -=; (2) 求证:)(x f 在定义域内为减函数;
(3) 求不等式2)5()2(-≥-+x f f 的解集.
9.(湖南永州市祁阳四中高一(上)期中数学试卷)已知定义在R 上的函数)(x f 满足)()()(y x f y f x f +=+,当x <0时2)1(0)(=<f x f ,;
(1) 求证:)(x f 为奇函数;
(2) 求)(x f 在[﹣3,3]的最值;
(3) 当t >2时,0)2log (log )log (2222<--+t f t k f 恒成立,求实数k 的取值范围.
10. 已知函数)(x f 定义域为[﹣1,1],若对任意的]11[,,
-∈y x ,都有)()()(y f x f y x f +=+,且0>x 时,有0)(>x f
(1) 证明:)(x f 为奇函数;
(2) 证明:)(x f 在[﹣1,1]上为单调递增函数;
(3) 设1)(=x f ,若12)(2+-<am m x f ,对所有]11[,,-∈y x ,]11[,-∈a 恒成立,求实数m 的取值范围。
11. 已知)(x f 的定义域为()∞+,0,且满足)()()(1)2(y f x f xy f f +==,
,又当y x >时,)()(y f x f >
(1) 求)4()1(f f 、的值;
(2) 如果2)3()(≤-+x f x f ,求x 的范围
12. 设)(x f 是定义在()∞+,0上的增函数,且对任意()∞+∈,、
0y x 都有)()()(y f x f y x f -= (1) 求)1(f
(2) 若1)4(=f ,解不等式2)1
()6(>-+x f x f。
