蒲丰投针问题
蒲丰投针问题

此外,随便说出3个正数,以这3个正数为边长可以围成一个钝角三角形的概率P也与π有关,这个概率为 (π-2)/4,证明如下:
设这三个正数为x,y,z,不妨设x≤y≤z,对于每一个确定的z,则必须满足x+y>z,x^2+y^2﹤z^2,容易 证明这两个式子即为以这3个正数为边长可以围成一个钝角三角形的充要条件,用线性规划可知满足题设的可行域 为直线x+y=z与圆x^2+y^2=z^2;围成的弓形,总的可行域为一个边长为z的正方形,则可以围成一个钝角三角形 的概率P=S弓形/S正方形=(πz^2/4-z^2/2)/z^2=(π-2)/4.因为对于每一个z,这个概率都为(π-2)/4, 因此对于任意的正数x,y,z,有P=(π-2)/4,命题得证。
投针步骤
实验数据
证明
下面是利用这个公式,用概率的方法得到圆周率的近似值的一些资料。
公元1901年,意大利数学家拉兹瑞尼宣称进行了多次的投针试验,每次投针数为3408次,平均相交数为1808 次,给出π的值为3.——准确到小数后6位。不过,不管拉兹瑞尼是否实际上投过针,他的实验还是受到了美国 犹他州奥格登的国立韦伯大学的L·巴杰的质疑.通过几何、微积分、概率等广泛的范围和渠道发现π,这是着实 令人惊讶的!
布丰投针实验是第一个用几何形式表达概率问题的例子,他首次使用随机实验处理确定性数学问题,为概率 论的发展起到一定的推动作用。
证明一:找一根铁丝弯成一个圆圈,使其直径恰恰等于平行线间的距离d。可以想象得到,对于这样的圆圈来 说,不管怎么扔下,都将和平行线有两个交点。因此,如果圆圈扔下的次数为n次,那么相交的交点总数必为2n。 设想把圆圈拉直,变成一条长为πd的铁丝。显然,这样的铁丝扔下时与平行线相交的情形要比圆圈复杂些,可能 有4个交点,3个交点,2个交点,1个交点,甚至于都不相交。由于圆圈和直线的长度同为πd,根据机会均等的 原理,当它们投掷次数较多,且相等时,两者与平行线组交点的总数期望也是一样的。这就是说,当长为πd的铁 丝扔下n次时,与平行线相交的交点总数应大致为2n。
比丰投针概率求法

比丰投针概率求法
丰投针是一种概率问题,目的是求解在一定条件下,丰投针的概率。
丰投针问题的条件为:有一片木板,上面有若干平行的线条,线条之间的间距为d,投针的长度为l (l<=d)。
当投针的任意一端落在线条上方时,称为丰投,要求求解丰投概率P。
丰投针概率的求解方法可以通过数学计算来进行,其中最著名的是皮埃尔·索恩世纪问题。
索恩世纪问题提出了丰投概率的公式:
P = (2l)/(πd)
其中,π是圆周率。
这个公式可以通过数学推导得到,但是需要一定的数学知识和技巧。
在实际运用中,如果不涉及到很复杂的条件和特殊情况,我们也可以通过模拟实验的方法来估计丰投针的概率。
具体方法如下:
1.准备一片木板,上面绘制出若干平行的线条,线条之间的间距为d。
2.制作一根投针,长度为l,注意确保l小于等于d。
3.反复进行丰投实验,将投针随机抛掷到木板上,并观察投针的任意一端是否落在线条上方,记录丰投的次数以及总的实验次数。
4.通过丰投次数与总实验次数的比值,即可估计丰投概率P。
在实际模拟实验中,需要进行足够多的实验次数,以保证估计结果的准确性。
一般来说,实验次数越多越好,可以通过增加实验次数来提高结果的可靠性。
需要注意的是,以上的方法是估计丰投概率的一种方式,得到的结果是近似值,并不是准确值。
如果需要精确的计算结果,还是需要通过数学方法来进行求解。
蒲丰投针问题

蒲丰投针问题1.蒲丰简介蒲丰有的时候翻译成布丰,是18世纪法国著名的博物学家。
他喜欢研究数学和生物学。
主要的贡献有:(1)翻译了牛顿的《流数法》,流数法按现在的说法就叫微积分。
(2)写了一本巨著,这部巨著的名字叫《自然史》,因为他特别喜欢研究生物。
这个自然史一共有44卷,其中他生前写了36卷,后来他学生又完成了。
这本书对后来的世界有很大的影响,尤其影响到一个人叫达尔文,所以蒲丰这个人其实是很厉害的。
2.蒲丰投针1777年,在蒲丰晚年的时候,他有一次举行了一个家庭宴会。
邀请了一大堆他的朋友来帮他做实验。
做什么实验呢,就“投针”。
那朋友来了之后发现,就是桌子上有很多根间距相等的平行线。
然后蒲丰就说了,给你们同样大的针,你把这些针随机扔到这个桌子上。
然后宾客就随便扔吗,有可能这样,有可能这样……,随便扔是吧,这都有可能,什么情况都有可能。
有的针就没有跟平行线相交,比如这个,这个,这个,就没有相交,也有相交的,比如这个,这个,这个,这是相交的,对吧,然后他就数,他说这个针一共投了多少个呢?一共投了n =2212个。
其中与这个平行线相交的针有多少个,数了一下有m =704个。
然后他说,我现在可以计算圆周率了,别人都不信,他说你看我圆周率怎么算,我只要把这两个数相除就行了。
我用n 除以m ,这个数除完了大概是3.142,这个就是圆周率了。
别人说好神奇,这怎么回事儿,蒲丰说我给你解释解释这个原理是什么?其实这个原理并不复杂,我们来看一下它的原理是什么。
3. 蒲丰投针原理(1)首先,它这个平行线是严格平行的,那平行线之间的距离是固定的,是a 。
然后我随意地把一根针投上去,也许相交,也许不相交,这不一定。
比如说这个针投上去了,投上去了之后,针的总长是b ,针有一个中点叫M ,对吧,这个M 到它比较近的平行线之间的距离我们设为x ,大家注意,这个是针的中点到比较近的平行线的距离是x ,所以我们应该知道x 的范围。
x 的最小值就是这个终点正好落在平行线上,那最小值是0,对吧。
蒲丰(Buffon)投针试验

一、利用Matlab计算机语言验证蒲丰(Buffon)投针试验问题给定a=10,b=5时,模拟100万次投针实验的Matlab程序如下:a=10;b=5;n=1000000;p=10; % a为平行线间距,b为针的长度,n为投掷次数,p为有效数字位数x=unifrnd(0,a/2,[n,1]);phi=unifrnd(0,pi,[n,1]); % 产生均匀分布的随机数,分别模拟针的中点与最近平行线的距离和针的倾斜角y=x<0.5*b*sin(phi); m=sum(y); % 计数针与平行线相交的次数PI=vpa(2*b*n/(a*m),p)运行结果PI =3.138919145二、利用C++计算机语言编程通过大量重复实验验证以下结论:三个阄,其中一个阄内写着“有”字,两个阄内不写字,三人依次抓取,各人抓到“有”字阄的概率均为1/3。
程序如下:#include<stdio.h>#include<stdlib.h>#include<time.h>void main(){int n=500000;int i,a[3]={0};srand(time(NULL));for(i=0;i<n;i++)a[rand()%3]++;printf("共测试%d次,其中有字事件有%d次, 占%.2f%%\n""抓到无字事件1有%d次,占%.2f%%\n""抓到无字事件2有%d次,占%.2f%%\n""抓到无字事件共%d次,占%.2f%%",n,a[0],a[0]*100.0/n,a[1],a[1]*100.0/n,a[2],a[2]*100.0/n,a[1]+a[2],(a[1]+a[2])*100.0/n);return 0;}。
蒲丰投针实验模拟

一、蒲丰投针问题在平面上画有等距离的一些平行线,平行线间的距离为a(a>0) ,向平面上随机投一长为l(l<a)的针,针与平行线相交的概率p,结果发现π =2*l/(a*p).二、试验方法能够采纳MATLAB软件进行模拟实验,即用MATLAB编写程序来进行“蒲丰投针实验”。
1、基来源理因为针投到纸上的时候,有各样不一样方向和地点,但是,每一次投针时,其地点和方向都能够由两个量独一确立,那就是针的中点和偏离水平的角度。
以 x 表示针的中点到近来的一条平行线的距离,β表示针与平行线的交角。
明显有0<=x<=a/2 ,0<=β <=Pi 。
用边长为 a/2 及 Pi 的长方形表示样本空间。
为使针与平行线相交,一定x<=l*sinβ * ,知足这个关系的地区面积是从0 到Pi的l*sinβ对β的积分,可计算出这个概率值是(2l)/(Pi*a)。
只需随机生成n 对这样的x 和β,就能够模拟 n 次的投针实验,而后统计知足 x<=l*sin β * 的 x 的个数,就能够以为这是订交的次数。
而后利用公式求得π值。
2、MATLAB编程clear ('n')clear('a')clear('x')clear('f')clear ('y')clear ('m')disp(' 本程序用来进行投针实验的演示, a 代表两线间的宽度,针的长度 l=a/2 ,n 代表实验次数 '); a=input(' 请输入 a:');n=input(' 请输入 n:');x=unifrnd(0,a/2,[n,1]);f=unifrnd(0,pi,[n,1]);y=x<*a*sin(f);m=sum(y);PI=vpa(a*n/(a*m))三、实验数据 ( 部分程序截屏见后 )a n PI第一次310000第二次310000第三次3100000第四次3100000第五次31000000第六次31000000第七次3第八次3第九次3第十次3四、实验结论从上述数据剖析可知,跟着模拟次数的愈来愈多, PI 的值渐渐稳固在π值邻近,即愈来愈趋近于π,故蒲丰投针实验的确能够模拟出π的值。
浦丰投针问题

怎么办呢?
如果我们将针的每一个位置看作是一个基 本事件,此时,假定每一个位置都“同等可能” 是合理的。这样就可以用几何概率去解决。
模型建立与求解
x 以M 表示针落下后的中点, 表示中点 M 到最近一条平行线的距离, 表示针于平行线
x
a 2
的交角
则基本事件区域为 a 0 x : 2 0
这种方法由于来源于浦丰投针问题,常常被 称为随机投针法。更进一步的,这种方法成为了 现代计算机模拟的基础——蒙特卡洛方法。
结束
L ( A)
a
x
x
a 2
投针简图
0
1 l sin d l 2
o
从而所求概率为 L( A) l 2l p L ( ) 1 a a 2
模型分析
2l 2)由于 p a
l 1)当比值 不变时, 值始终不变 p a
2l a 所以可以利用它来计算 的近似值
o
基本事件简图
它为 ox 平面上的一个矩形,其面积为:
a L() 2M 为使针与平线(这线必定是它与 最近的一条平行线)相交,其充要条件是 l 0 x sin , A 2 (为什么?) 0 显然A 是Ω 中的一个区域(如图) , 而 A 的面积为
对于一些不确定的自然现象和科学实验 结果,我们通常用概率统计学去研究,建立 概率统计模型(随机现象)
问题:平面上画有等距离为a ( a 0) l 的一些平行线,向此平面投一长为 (l a ) 的针,试求此针与任一平行线 相交的概率?
分析: 针投到平面上与平行线的关系有两种可能:
针与这些平行线中的某一根相交,或不相交。 这两种可能性一般来说不一样大,即不具有等 可能性。因此无法用古典概率来求解。
浦丰投针

l
l sin 2
l 针与一平行线相交 0 x sin , 2
设 A=“针与一平行线相交”,则
l A : 0 x sin , 2 m ( A) P ( A) m (Ω)
l x sin 2
x a/2 A
0
0
l sin d 2l 2 . a a 2
1777年,法国科学家蒲丰( Buffon )提出了投针 试验问题.平面上画有等距离a (a>0)的一些平行线, 向平面任意投一长为l (l<a)的针,试求针与平行线 相交的概率. 解 设M表示针落下后,针 的中心,x 表示M与最近 一平行线的距离, 表示 针与这平行线的夹角,则 样本空间: a 0 x , 0 , 2
试验者
Wolf Smith De Morgan
时间
1850 1855 1860
针长 投掷次数
0.8 0.6 1.0 5000 3204 600
相交次 π的近似值 数
2532 1218 382 3.1596 3.1554 3.137
Fox Lazzerini Reina
1884 1901 1925
0.75 0.83 0.5419
1030 3408 2520
489 1808 859
3.1595 3.1415929 3.1795
蒲丰投针试验的应用及意义
2l P ( A) = aπ
根据频率的稳定性,当投针试验次数n很大时, m 算出针与平行直线相交的次数m,则频率值 即可 n 作为P(A)的近似值代入上式,那么
m 2l 2ln π n aπ am
蒲丰投针原理
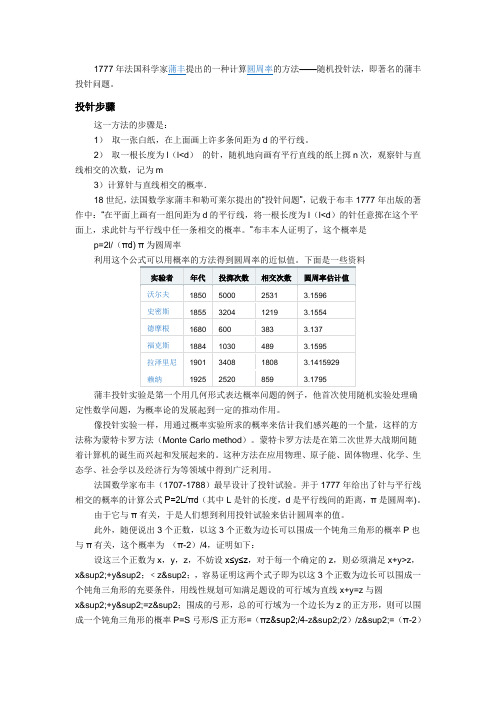
/4.因为对于每一个z,这个概率都为(π-2)/4,因此对于任意的正数x,y,z,有P=(π-2)/4,命题得证。
为了估算π的值,我们需要通过实验来估计它的概率,这一过程可交由计算机编程来实现,事实上x+y>z,x²+y²;﹤z²;等价于(x+y-z)(x²+y²-z²;)﹤0,因此只需检验这一个式子是否成立即可。
若进行了m 次随机试验,有n次满足该式,当m足够大时,n/m趋近于(π-2)/4,令n/m=(π-2)/4,解得π=4n/m+2,即可估计出π值。
值得注意的是这里采用的方法:设计一个适当的试验,它的概率与我们感兴趣的一个量(如π)有关,然后利用试验结果来估计这个量,随着计算机等现代技术的发展,这一方法已经发展为具有广泛应用性的蒙特卡罗方法。
计算π最稀奇方法之一计算π的最为稀奇的方法之一,要数18世纪法国的博物学家C·布丰和他的投针实验:在一个平面上,用尺画一组相距为d的平行线;一根长度小于d的针,扔到画了线的平面上;如果针与线相交,则该次扔出被认为是有利的,否则则是不利的.布丰惊奇地发现:有利的扔出与不利的扔出两者次数的比,是一个包含π的表示式.如果针的长度等于d,那么有利扔出的概率为2/π.扔的次数越多,由此能求出越为精确的π的值.公元1901年,意大利数学家拉兹瑞尼作了3408次投针,给出π的值为3.1415929——准确到小数后6位.不过,不管拉兹瑞尼是否实际上投过针,他的实验还是受到了美国犹他州奥格登的国立韦伯大学的L·巴杰的质疑.通过几何、微积分、概率等广泛的范围和渠道发现π,这是着实令人惊讶的!证明下面就是一个简单而巧妙的证明。
找一根铁丝弯成一个圆圈,使其直径恰恰等于平行线间的距离d。
可以想象得到,对于这样的圆圈来说,不管怎么扔下,都将和平行线有两个交点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蒙特卡罗方法概述
§ 8.2 引例:蒲丰投针问题
在用传统方法难以解决的问题中,有很大一部分可以用概率模型进行描述.由于这类模型含有不确定的随机因素,分析起来通常比确定性的模型困难.有的模型难以作定量分析,得不到解析的结果,或者是虽有解析结果,但计算代价太大以至不能使用.在这种情况下,可以考虑采用Monte Carlo 方法。
下面通过例子简单介绍Monte Carlo 方法的基本思想.
Monte Carlo 方法是计算机模拟的基础,它的名字来源于世界著名的赌城——摩纳哥的蒙特卡洛,其历史起源于1777年法国科学家蒲丰提出的一种计算圆周π的方法——随机投针法,即著名的蒲丰投针问题。
这一方法的步骤是:
1) 1) 取一张白纸,在上面画上许多条间距为d 的平行线,见图8.1(1)
2) 2) 取一根长度为)(d l l <的针,随机地向画有平行直线的纸上掷n 次,观察针与直线相交的次数,记为m
3)计算针与直线相交的概率.
由分析知针与平行线相交的充要条件是
ϕsin 21≤
x 其中
πϕ≤≤≤≤0,2
0d x 建立直角坐标系),(x ϕ,上述条件在坐标系下将是曲线所围成的曲边梯形区域,见图
8.l (2).
由几何概率知
(*)22
sin 210d l d d G g p ππϕϕπ===⎰的面积的面积 4)经统计实验估计出概率,n m P ≈由(*)式即?2=⇒=ππd
l n m Monte Carlo 方法的基本思想是首先建立一个概率模型,使所求问题的解正好是该模型的参数或其他有关的特征量.然后通过模拟一统计试验,即多次随机抽样试验(确定m 和n ),统计出某事件发生的百分比.只要试验次数很大,该百分比便近似于事件发生的概率.这实际上就是概率的统计定义.利用建立的概率模型,求出要估计的参数.蒙特卡洛方法属于试验数学的一个分支.
************************************************************************* 提示:设x 是一个随机变量,它服从区间[0,d/2]是的均匀分布,同理,ϕ是一个随机变量,它服从区间],0[π上的均匀分布。
按照某种抽样法,产生随机变量的可能取值,例如
进行n 次抽样,得到样本值n i x i i ,,2,1),,( =ϕ,统计出满足不等式
i i d x ϕsin 2
≤
的次数m(m<n),从而可以计算出p 的估计值n m p /ˆ=. **************************************************************************** 使用MATLAB 语言编程实现(4.m)
l=1
d=2;
m=0;
for k =l :n
x =unifmd (0,d /2);
p =unifmd (0,pi );
if )sin(15.0y x ⨯⨯<
m=m +1
elsc
end
end
p=m/n
pi_m=1/p
运行,取n=1000,simu4回车,即得结果
*************************************************************************** 想:1)在上述的程序中任意调整n 的取值,会发现什么规律?
2)参数 l ,d 的不同选择,会导致什么结果?
*************************************************************************** 蒙特卡洛方法适用范围很广泛,它既能求解确定性的问题,也能求解随机性的问题以及科学研究中的理论问题.例如利用蒙特卡洛方法可以近似地计算定积分,即产生数值积分问题.
任意曲边梯形面积的近似计算
一个古老的问题:用一堆石头测量一个水塘的面积.应该怎样做呢?测量方法如下:假定水塘位于一块面积已知的矩形农田之中.如图8.2所示.随机地向这块农田扔石头使得它们都落在农田内.被扔到农田中的石头可能溅上了水,也可能没有溅上水,估计被“溅上水的”石头量占总的石头量的百分比.试想如何利用这估计的百分比去近似计算该水塘面积?
结合图8.2中的图形(1)分析,只要已知各种参数及函数(a ,b ,H ,f(x)),有以下两种方法可近似计算水塘面积.
1.随机投点法
1)赋初值:试验次数n=0,成功次数m=0;规定投点试验的总次数N ;
2)随机选择m 个数对,1,,m i y x i i <<,其中H y b x a i i <<<<0,,置 n =n +l ;
3)判断N n ≤,若是,转4,否则停止计算;
4)判断条件)(i i x f y <(表示一块溅水的石头)是否成立,若成立则置m=m+1,转2,否则转2;
5)计算水塘面积的近似值N m a b H S /)(⨯-⨯=.
2.平均值估计法
1)产生[a,b]区间的均匀随机数;,,2,1,N i x i =
2) 计算;,,2,1),(N i x f i =
3)计算∑=-=N
i i x f N a b S 1
)()(。
该方法的特点是估计函数f(x)在[a,b]上的平均值,面积近似等于该平均值乘以(b-a). *************************************************************************** 做:用MA TLAB 软件编制程序实现,并对以上两种方法进行比较.。
