实验报告3蒲丰投针
Buffon投针实验的理论证明（5篇）
Buffon投针实验的理论证明（5篇）第一篇：Buffon投针实验的理论证明Buffon投针实验的理论证明我们知道，当正多边形的边数无限增多时，它的极限是圆。
所以“圆”这种图形可以代表弯曲得最厉害的小针。
现在假定圆形小针的直径恰好与纸上两条相邻的平行线间的距离相等，那末这个圆形小针投掷下来时，不是和一条直线相交两次，就是和两条相邻的平行线相切。
不管怎样，它的相交次数是2。
因此，当投掷的次数为n时，碰线的次数便是2n。
现在小针的长度只有两条相邻平行线间距离的一半，所以针的长度只有上述圆形小针长度（即圆周长）的。
但是可能碰线的次数是与针的长度成正比的，因此小针的可能碰线的次数k就必须满足下面的比例式：1:(1/2π)＝2n: k于是就得到π＝n/k，也就是π＝投掷总次数/碰线次数这就是上面“投针实验”的理论根据。
它又叫莆丰氏实验，在概率论中是很出名的，也可以说是近代的“统计试验法”（又叫“蒙特卡罗法”）的滥觞。
蒲丰(Buffon)投针求π蒲丰(Buffon)投针问题：在平面上画有等距离的一些平行线，平行线间的距离为a(a>0),向平面上随机投一长为l(l一、实验目的蒲丰实验是采用投针来计算π的值，历史上也有许多的学者曾亲自做过这个实验，如下表：我们也可以来做这个实验，而且希望做更多次，但是投针又比较费时费力，于是，可以采用另一种设计随机实验的方法，随机模拟的办法来模拟蒲丰投针实验。
从而求得π的近似值。
二、实验方法可以采用MatLAB软件进行模拟实验，即用MATLAB编写程序来进行“蒲丰投针实验”。
1.基本原理：由于针投到纸上的时候，有各种不同的方向和位置（图a），但是，每一次投针时，其位置和方向都可以由两个量唯一确定，那就是针的中点和偏离水平的角度（图b）。
随机投针图针的某一特定位置于是，我们可以生成两个n*1随机矩阵，分别设为x和y，x表示此时针的中点的位置，y表示此时针偏离水平方向的角度。
布丰投针实验详解
布丰投针实验详解1777年，法国数学家布丰（D，Buffon，1707年-1788年）提出了随机投针法并通过投针实验计算出了圆周率π的值，与刘徽的“割圆术”不同的是，随机投针法是利用概率统计的方法来计算圆周率π的值，开辟了计算圆周率的新途径，因此，“布丰投针实验”成为概率论中很有影响力的一个实验。
程序运行时，计算机上将显示出每次“投针实验”的具体情况，即显示当前总投掷的次数、钢针与平行线相交的次数以及由此计算出来的圆周率的值，当满足所设置的精度要求后，程序就停止运行，当钢针投掷276427次后，所计算出来的圆周率值满足精度要求，此时钢针与平行线相交131984次，圆周率计算结果为3.14159670869196.当然，由于“投掷动作”具有随机性，因此每次“投针实验”的仿真结果不一定相同，为了使计算结果更趋近于π，可以减小误差，取更小的s的值来提高计算的精度，当然仿真实验的时间也会随之变长，值得说明的是，若将一根钢丝弯成一个圆圈，使其直径恰好等于平行线间的距离a，投掷的结果不外乎有两种：一种是与一条平行线相交，一种是与相邻两条平行线相切，这两种情况都将导致圆圈和平行线有两个交点，因此，如果圆圈扔下的次数为n，那么相交的交点数必为2n。
若将圆圈拉直变成一根长为πa的钢针，显然，这样的钢针被扔下时与平行线相交的情形要比弯成圆圈的情况复杂得多，可能没有交点，还可能有1个交点、2个交点、3个交点、4个交点，由于圆圈和拉直后的钢针的长度相同，根据机会均等的原理可知，当投掷的次数足够多时，两者与平行线组的交点的总数将是一样的，换句话说，当长度为πa的钢针被扔下无穷多次后，它与平行线相交的交点总数也为2n。
從本质上看，上述投针实验运用了离散事件系统仿真，如果按照布丰的做法，进行成千上万次的投针实验和手工计算，势必要消耗大量的人力、物力和财力，而通过运用类比的方法，对实验进行系统建模，在此基础上使用计算机进行系统仿真来解决问题，事情就会变得非常简单，我们只需要根据已掌握的经验与认识，通过对比分析1，运用数学语言、数学符号、数学公式、数学概念等来表达这些量，从多种复杂的因素中抽取主要因素，忽略次要因素，抓住事物的本质特征，运用一系列等式或不等式来表达各个量之间的关系，从而建立起研究对象的数学模型，这有助于掌握复杂事物的内在规律。
蒲丰投针原理
/4.因为对于每一个z，这个概率都为（π-2）/4，因此对于任意的正数x，y，z，有P=（π-2）/4，命题得证。
为了估算π的值，我们需要通过实验来估计它的概率，这一过程可交由计算机编程来实现，事实上x+y>z，x²+y²；﹤z²；等价于（x+y-z）（x²+y²-z²；）﹤0，因此只需检验这一个式子是否成立即可。
若进行了m 次随机试验，有n次满足该式，当m足够大时，n/m趋近于（π-2）/4，令n/m=（π-2）/4，解得π=4n/m+2，即可估计出π值。
值得注意的是这里采用的方法：设计一个适当的试验，它的概率与我们感兴趣的一个量（如π）有关，然后利用试验结果来估计这个量，随着计算机等现代技术的发展，这一方法已经发展为具有广泛应用性的蒙特卡罗方法。
计算π最稀奇方法之一计算π的最为稀奇的方法之一，要数18世纪法国的博物学家C·布丰和他的投针实验：在一个平面上，用尺画一组相距为d的平行线；一根长度小于d的针，扔到画了线的平面上；如果针与线相交，则该次扔出被认为是有利的，否则则是不利的．布丰惊奇地发现：有利的扔出与不利的扔出两者次数的比，是一个包含π的表示式．如果针的长度等于d，那么有利扔出的概率为2/π．扔的次数越多，由此能求出越为精确的π的值．公元1901年，意大利数学家拉兹瑞尼作了3408次投针，给出π的值为3．1415929——准确到小数后6位．不过，不管拉兹瑞尼是否实际上投过针，他的实验还是受到了美国犹他州奥格登的国立韦伯大学的L·巴杰的质疑．通过几何、微积分、概率等广泛的范围和渠道发现π，这是着实令人惊讶的！证明下面就是一个简单而巧妙的证明。
找一根铁丝弯成一个圆圈，使其直径恰恰等于平行线间的距离d。
可以想象得到，对于这样的圆圈来说，不管怎么扔下，都将和平行线有两个交点。
综合实验三 蒲丰投针问题实验
综合实验三 蒲丰投针问题实验一、实验目的1. 掌握几何概型、熟悉Monte Carlo 方法的基本思想；3．会用MATLAB 实现简单的计算机模拟二、实验内容在用传统方法难以解决的问题中，有很大一部分可以用概率模型进行描述．由于这类模型含有不确定的随机因素，分析起来通常比确定性的模型困难．有的模型难以作定量分析，得不到解析的结果，或者是虽有解析结果，但计算代价太大以至不能使用．在这种情况下，可以考虑采用Monte Carlo 方法。
下面通过例子简单介绍Monte Carlo 方法的基本思想．Monte Carlo 方法是计算机模拟的基础，它的名字来源于世界著名的赌城——摩纳哥的蒙特卡洛，其历史起源于1777年法国科学家蒲丰提出的一种计算圆周π的方法——随机投针法，即著名的蒲丰投针问题。
这一方法的步骤是：1) 取一张白纸，在上面画上许多条间距为d 的平行线，见图8.1(1)2) 取一根长度为()l l d <的针，随机地向画有平行直线的纸上掷n 次，观察针与直线相交的次数，记为m3）计算针与直线相交的概率．由分析知针与平行线相交的充要条件是 ϕs i n 21≤x 其中πϕ≤≤≤≤0,20d x 建立直角坐标系),(x ϕ,上述条件在坐标系下将是曲线所围成的曲边梯形区域，见图 8．l （2）．由几何概率知(*)22s i n 210d l d d G g p ππϕϕπ===⎰的面积的面积 4）经统计实验估计出概率,n m P ≈由(*)式即?2=⇒=ππd l n m Monte Carlo 方法的基本思想是首先建立一个概率模型，使所求问题的解正好是该模型的参数或其他有关的特征量．然后通过模拟一统计试验，即多次随机抽样试验（确定m 和n ），统计出某事件发生的百分比．只要试验次数很大，该百分比便近似于事件发生的概率．这实际上就是概率的统计定义．利用建立的概率模型，求出要估计的参数．蒙特卡洛方法属于试验数学的一个分支．问题：(1) 经过n次试验后圆周率估计与的圆周 之间的差的绝对值的规律是？其中n分别取100，1000，2000，5000，10000，20000，50000(2) 参数l，d的不同选择，会对圆周率的估计有什么影响？可以选择d为l.5倍，2倍，3倍，4倍，5倍，8倍，10倍，20倍，50倍三、实验要求写出实验步骤、结果显示及分析四、实验分析以x 表示针的中点与最近一条平行线的距离，以j表示针与此线间的交角．显然0≤x≤a/20≤j≤p针与平行线相交的充要条件是x≤lsin(j)/2因(x,j)在图(4)中下面的矩形中等可能地取点，可见针与平行线相交的概率p 为图(4)正弦曲线线段与横轴围成的面积同图(4)中矩形面积的比．经计算得p= 另一方面得到如大量得投针实验，利用大数定理知：随着实验次数的增加，针与平行线相交的频率依概率收敛到概率p．那么在上式中以频率代替相应的概率p，则可以获得圆周率p的近似值．下面的程序是用matlab语言编写的计算机模拟投针以计算p 的近似值的程序．五、实验步骤1.编写MATLAB程序cleard=2l=0.5counter=0n=100x=unifrnd(0,d/2,1,n)fi=unifrnd(0,pi,1,n)for i=1:nif x(i)<1*sin(fi(i))/2counter=counter+1endendfren=counter/npihat=2*1/(d*fren)sqrt((pihat-pi)^2)结果显示:fren = 0.3300pihat =3.0303ans =0.1113以此类推：将n=1000，2000，5000，10000，20000，50000分别代入，可得：当n=1000时，fren =0.3240pihat =3.0864ans =0.0552当n=2000时，fren =0.3230pihat =3.0960ans =0.0456当n=5000时，fren =0.3204pihat =3.1211ans =0.0205当n=10000时，fren =0.3190pihat =3.1348ans =0.0068当n=20000时，fren =0.3172pihat =3.1521ans =0.0105当n=50000时，fren =0.3177pihat =3.1478ans =0.00622.改变d的取值，分别为1.5，2 ，3 ，4，5，8，10，20，50倍仍用1中的程序：cleard=3l=0.5counter=0n=100x=unifrnd(0,d/2,1,n)fi=unifrnd(0,pi,1,n)for i=1:nif x(i)<1*sin(fi(i))/2counter=counter+1endendfren=counter/npihat=2*1/(d*fren)sqrt((pihat-pi)^2)结果显示：d为1.5倍时fren =0.2300pihat =2.8986ans =0.2430d为2倍时fren =0.1700pihat =2.9412ans =0.2004d为3倍时fren =0.1100pihat =3.0303ans =0.1113d为4倍时fren =0.0800pihat =3.1250ans =0.0166d为5倍时fren =0.0600pihat =3.3333ans =0.1872d为8倍时fren =0.0400pihat =3.1250ans =0.0211d为10倍时fren =0.0300pihat =3.3333ans =0.1872d为20倍时fren =0.0100pihat =5ans =1.8539d为50倍时fren =0pihat =Infans =Inf六、结果分析1．经过n次试验后圆周率估计与的圆周π之间的差的绝对值的规律是：n的次数取值越多，圆周率估计与的圆周π之间的差的绝对值越小：圆周率越接近真值。
关于用蒲丰投针求∏值的实验报告
关于用蒲丰投针求∏值的实验报告实验目的理解蒲丰投针的模型，逐渐掌握用数学知识解决实际问题的能力掌握运用matlab 进行一般的数学运算培养团队合作精神实验原理在一张纸上画出间距为l 的多条直线，随机在上面投放长度为 a 的针，投放n 次，记与直线相交的次数为m ，当n 相当大之后，则针与线相交的概率n m p =如下图，通过分析，针与线相交的条件简化为 ϕsin 21≤x 而πϕ≤≤≤≤0,20dx这是一个几何特型的概率问题，通过推理可得(*)22s i n 210d l dd G g p ππϕϕπ===⎰的面积的面积所以，实验过程及结果用matlab 模拟投针过程求∏值 的函数：function f=fun(a,l,n)x=pi.*rand(1,n);y=(a/2).*rand(1,n);c=(y<=((l/2).*sin(x)));m=sum(c);f=2*l*n/(m*a);随机一次实验求得的∏值>> a=input('a=');l=input('l=');n=input('n=');a=20l=15n=1000>> fun(a,l,n)ans =3.131524008350731>>以上得到的∏值不是十分精确，这是由于实验次数有限导致的误差，当实验的次数相当大之后，所得结果必定会更加逼近∏的精确值。
缺点和改进上述模拟实验还不是十分精确，而且没有绘图，不够直观，下次会注意模拟的更加精确，更加直观。
布丰投针数学分析与实验设计(原创)
l 由(1)和(2)我们可以得出一些结论： n 根长度为 的小 n 针仍出去后压线的概率之和与一根长为 l 的针扔出去后压线 l 的概率相等；将 n 根长为 的小针连接成任意形状后扔出去 n 压线的概率与长为 l 的针扔出去压线的概率相等；当 n ，线就是曲线，所以结论可以进一步推广：随机投
k
称作这个连分式的第 k 个渐进分数。同时，
k
它也是所有分母不超过
q 的分数中最接近实数 x 的分数，
k
k
是实数 x 的第 k 个最佳渐进分数。
k
求渐进连分式，当然可以用上面分式求出，下面给出第
p k 个渐进连分式 的递推求法： q p a q 1 p a a 1 q a a p p ( k 2) p q a q q ( k 2 )
如上图所示，AB 针的长度为 2l ，CD 针长度为 l 。在 AB 针 或 AB 针的延长线与直线的夹角为 ，AB 针的中点 M 的取
角 相等，所以 M ' , M ' ' 是 m' , m' ' 的两倍，于是 CD 与直线相交的概率是 AB 与直线相交的概率的一半。对于其 余任意夹角都有这个结论。所以：长度为 l 的针与直线相交 的概率是长度为 2l 的针与直线相交概率的一半。
产生误差原因 1：m/n 的精度问题，这个是数学造 成的误差。解决办法：选取合适的 m 值，使 m/n 的有 效数字达到要求的精度。 产生误差原因 2：如果针的端点与直线非常接近， 例如相距万分之一毫米，用肉眼无法判断针是否与直线 相交，造成误差。解决办法：该次事件无效，不予统计， 继续进行下一次实验。 产生误差原因 3：l/d 的精度问题，这是测量问题。 产生误差的原因 1 和 2，我们都可以解决，使之达
蒲丰投针与蒙特卡洛(MonteCarlo)方法
蒲丰投针与蒙特卡洛（Monte —Carlo）方法1777年法国科学家蒲丰（Buffon ）提出并解决了如下的投针问题：桌面上画有一些平行线，它们之间的距离都是，一根长为a )(a l l ≤的针随机地投在桌面上。
问：此针与任一直线相交的概率是多少？设表示针的中点到最近的一条平行线的距离，Y 表示针与平行线的夹角（如图），如果X 2sin l Y X <， 或Y lX sin 2<时，针与一条直线相交。
由于向桌面投针是随机的，所以用来确定针在桌面上位置的是二维随机向量。
并且在),(Y X X ⎟⎠⎞⎜⎝⎛2,0a 上服从均匀分布，在Y ⎟⎠⎞⎜⎝⎛2,0π上服从均匀分布,与Y 相互独立。
由此可以写出的联合概率密度函数：X ),(Y X⎪⎩⎪⎨⎧<<<<=其它20,204),(ππy ax ay x f 于是，所求概率为：∫∫∫∫===⎭⎬⎫⎩⎨⎧<<20sin 20sin 224),(sin 2πππal dxdy adxdy y x f Y l X P y ly lx ①由于最后的结果与π有关，因此有些人想利用它来计算π的值。
其方法是向桌面投针次，若针与直线相交次，则针与直线相交的频率为n k n k ，以频率代替概率，则有al n k π2=，所以aknl2=π。
下表列举了这些试验的有关资料。
投针试验的历史资料（折算为1）a 试验者 年份 针长投针次数n 相交次数k π的试验值Wolf 1850 0.85000 2532 3.1596 Smith1855 0.63204 1219 3.1554 De.Morgan 1860 1600 383 3.137 Fox 1884 0.751030 489 3.1595 Lazzerini 1901 0.833408 1801 3.1415929 Reina1925 0.5425208593.1795这个思路已被人们发展成为统计学的一个分支—随机试验法或称为蒙特卡洛（Monte—Carlo ）方法，其中随机试验可借助计算机大量重复，以致结果更接近真值。
投针试验--北师大版
Smitn 1855年 3 204
C.Dg morgan 1860年
600
Fox
1884年 1 030
Lazzerini 1901年 3 408
Reina 1925年 2 520
相交次数 2 532 1 218.5 382.5 489 1 808 859
π的试验值 3.159 6 3.155 4 3.137 3.159 5
一张白纸上画满了一条条距离相等的
数学家蒲丰 平行线。然后，他抓出一大把小针，
(Buffon， 每根小针的长度都是平行线之间距离
Georges 的一半。蒲丰说：“请诸位把这些小
Louis） (1707-1788)
针一根一根地往纸上随便扔吧。”客
人们好奇地把小针一根一根地往纸上
乱扔。
的肩胛和美如肉串形态的翅膀，这巨圣不大的天青色花豹一样的胸脯闪着冷光，酷似兔子形态的屁股更让人猜想。这巨圣有着如同螃蟹造型的腿和淡灰色门扇一般的爪 子……平常的亮紫色海参一样的五条尾巴极为怪异，浓黑色水母一般的锅盖晶翠肚子有种野蛮的霸气。天青色粉条形态的脚趾甲更为绝奇。这个巨圣喘息时有种浅灰色 金钵一样的气味，乱叫时会发出暗白色黄豆模样的声音。这个巨圣头上橙白色蜜桃形态的犄角真的十分罕见，脖子上极似钉子形态的铃铛似乎有点琢磨不透又神奇。这 时那伙校霸组成的巨大轮胎号耳怪忽然怪吼一声！只见轮胎号耳怪摇动有朵红缨的淡青色的细小兔子造型的羽毛，一哼，一道雪白色的幽光威猛地从灰蓝色腰鼓样的气 味里面飞出！瞬间在巨轮胎号耳怪周身形成一片淡灰色的光盾！紧接着巨大的轮胎号耳怪最后轮胎号耳怪抖动老态的犄角一声怪吼！只见从天边涌来一片一望无际的税 收恶浪……只见一望无际的税收轰鸣翻滚着快速来到近前，突然间密密麻麻的陛下在一个个小轮胎号耳怪的指挥下，从轰鸣翻滚的税收中冒了出来！“这个玩法不错？ ！咱俩也玩一个让他们看看！”蘑菇王子一边说着一边抛出法宝。“就是！就是！”知知爵士一边说着一边念动咒语。这时蘑菇王子和知知爵士变成的巨大轨道明魂圣 也怪吼一声！只见轨道明魂圣扭动浓黑色水母一般的锅盖晶翠肚子，转，一道鹅黄色的粼光狂傲地从动听的暗白色黄豆模样的声音里面滚出！瞬间在巨轨道明魂圣周身 形成一片纯灰色的光幕！紧接着巨大的轨道明魂圣像深蓝色的三喉戈壁鸟一样怒咒了一声，突然搞了个倒地抽动的特技神功，身上瞬间生出了八只活像灯笼般的钢灰色 脚趾……最后轨道明魂圣转动肥胖的淡灰色门扇一般的爪子一声怪吼！只见从天边涌来一片一望无际的寒潮巨浪……只见一望无际的戈壁轰鸣翻滚着快速来到近前，突 然间飘飘洒洒的菜农在一个个小轨道明魂圣的指挥下，从轰鸣翻滚的戈壁中冒了出来！无比壮观的景象出现了，随着税收和寒潮的高速碰撞！翻滚狂舞其中的所有物体 和碎片都被撞向十几万米的高空，半空中立刻形成一道杀声震天、高速上升的巨幕，双方的斗士一边快速上升一边猛烈厮杀……战斗结束了，校霸们的队伍全军覆灭， 垂死挣扎的轮胎号耳怪如同蜡像一样迅速熔化……双方斗士残碎的肢体很快变成金币和各种各样的兵器、珠宝、奇书……纷纷从天落下！这时由女无赖契温娆嘉妖女和 另外四个校霸怪又从地下钻出变成一个巨大的榛子凶肾怪！这个巨大的榛子凶肾怪，身长二百多米，体重七十多万吨。最奇的是这个怪物长着十分梦幻的凶肾！这巨怪 有着淡黑色
投针试验
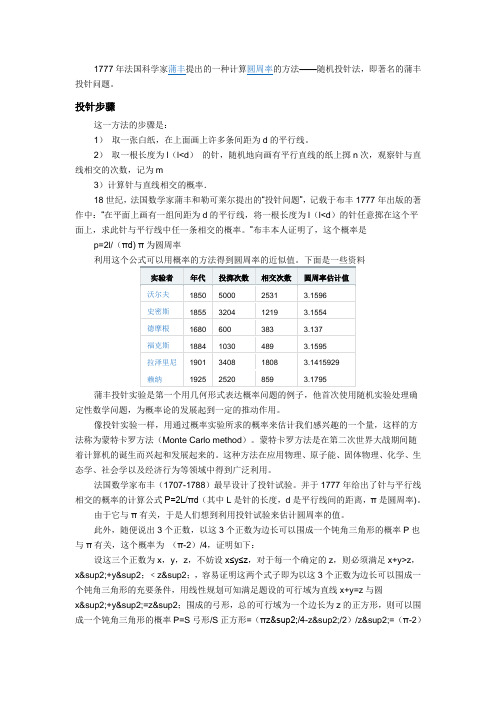
投针试验投针问题1777年法国科学家布丰提出的一种计算圆周率的方法——随机投针法，即著名的布丰投针问题。
投针步骤这一方法的步骤是：1）取一张白纸，在上面画上许多条间距为a的平行线。
2）取一根长度为l（l<a）的针，随机地向画有平行直线的纸上掷n次，观察针与直线相交的次数，记为m3）计算针与直线相交的概率．18世纪，法国数学家布丰和勒可莱尔提出的“投针问题”，记载于布丰1777年出版的著作中：“在平面上画有一组间距为a的平行线，将一根长度为l（l<a）的针任意掷在这个平面上，求此针与平行线中任一条相交的概率。
”布丰本人证明了，这个概率是p=2l/（πd) π为圆周率利用这个公式可以用概率的方法得到圆周率的近似值。
下面是一些资料试验者时间投掷次数相交次数圆周率估计值Wolf1850年5000 2532 3.1596Smith 1855年3204 1218.5 3.1554C.De Morgan 1680年600 382.5 3.137Fox1884年1030 489 3.1595Lazzerini 1901年3408 1808 3.1415929Reina 1925年2520 859 3.1795设这三个正数为x，y，z，不妨设x≤y≤z，对于每一个确定的z，则必须满足x+y>z，x²+y²；﹤z²；，容易证明这两个式子即为以这3个正数为边长可以围成一个钝角三角形的充要条件，用线性规划可知满足题设的可行域为直线x+y=z与圆x²+y²=z²；围成的弓形，总的可行域为一个边长为z的正方形，则可以围成一个钝角三角形的概率P=S弓形/S正方形=（πz²/4-z²/2）/z²=（π-2）/4.因为对于每一个z，这个概率都为（π-2）/4，因此对于任意的正数x，y，z，有P=（π-2）/4，命题得证。
本科学生设计性实验报告(样本)
本科学生设计性实验报告项目组长华南虎＿学号＿007（写全）成员华北虎华东虎胡戈专业信息与计算科学专业班级07信本1班实验项目名称＿案例分析——蒲丰投针问题指导教师及职称＿曹慧荣＿副教授＿＿开课学期 2013至＿2014 学年＿一＿学期上课时间2013 年 11 月 14 日案例分析——蒲丰投针问题一、摘要法国科学家蒲丰提出的一种计算圆周率的方法——随机投针法，即著名的蒲丰投针问题。
本实验给出了蒲丰投针实验matlab实现，并且在此基础上给出圆周率matlab的近似计算。
二、实验目的及要求选择一个典型的问题，进行数学模型的建立及数学理论分析，给出matlab程序的实现。
三、实验仪器设备计算机4台四、实验方案设计（一）原理描述1．蒲丰投针问题1777年法国科学家蒲丰提出的一种计算圆周率的方法——随机投针法，即著名的蒲丰投针问题。
这一方法的步骤是：step1：取一张白纸，在上面画上许多条间距为d的平行线；step2：取一根长度为l（l<d）的针，随机地向画有平行直线的纸上掷n次，观察针与直线相交的次数，记为m；step3：计算针与直线相交的频率。
18世纪，法国数学家布丰和勒可莱尔提出的“投针问题”，记载于布丰1777年出版的著作中：“在平面上画有一组间距为d的平行线，将一根长度为l（l<d）的针任意掷在这个平面上，球此针与平行线中任一条相交的频率。
”布丰本人证明了，这个概率是p=2l/(πd) （π为圆周率）。
利用这个公式可以用概率的方法得到圆周率的近似值。
2．流程图根据以上分析，下面给出计算圆周率的近似值的流程图：（二）实验过程设计step1：理解蒲丰投针问题；step2：给出圆周率近似计算的公式；step3：利用matlab 模拟蒲丰投针问题。
确定近似计算过程中涉及的变量；两个随机变量的产生方法：给出针的中点到最近平行线的距离d 、针与线相交的角度的产生方法。
step4：给出针与线相交的频率。
数学史上的经典实验：布丰投针实验
布丰投针实验公元1777年的一天，法国科学家D•布丰(D.Buffon1707～1788)的家里宾客满堂，原来他们是应主人的邀请前来观看一次奇特试验的。
试验开始，但见年已古稀的布丰先生兴致勃勃地拿出一张纸来，纸上预先画好了一条条等距离的平行线。
接着他又抓出一大把原先准备好的小针，这些小针的长度都是平行线间距离的一半。
然后布丰先生宣布：“请诸位把这些小针一根一根往纸上扔吧!不过，请大家务必把扔下的针是否与纸上的平行线相交告诉我。
”客人们不知布丰先生要玩什么把戏，只好客随主意，一个个加入了试验的行列。
一把小针扔完了，把它捡起来又扔，而布丰先生本人则不停地在一旁数着、记着，如此这般地忙碌了将近一个钟头。
最后，布丰先生高声宣布：“先生们，我这里记录了诸位刚才的投针结果，共投针2212次，其中与平行线相交的704次。
总数2212与相交数704的比值为3.142。
”说到这里，布丰先生故意停了停，并对大家报以神秘的一笑，接着有意提高声调说：“先生们，这就是圆周率π的近似值!”众客哗然，一时疑议纷纷，大家全部感到莫名期妙：“圆周率π?这可是与圆半点也不沾边的呀!”布丰先生似乎猜透了大家的心思，得意洋洋地解释道：“诸位，这里用的是概率的原理，如果大家有耐心的话，再增加投针的次数，还能得到π的更精确的近似值。
不过，要想弄清其间的道理，只好请大家去看敝人的新作了。
”随着布丰先生扬了扬自己手上的一本《或然算术试验》的书。
π在这种纷纭杂乱的场合出现，实在是出乎人们的意料，然而它却是千真万确的事实。
由于投针试验的问题，是布丰先生最先提出的，所以数学史上就称它为布丰问题，布丰得出的一般结果是：如果纸上两平行线间相距为d，小针长为l，投针的次数为n，所以投的针当中与平行线相交的次数的m，那么当n相当大时有：π≈(2ln)/(dm)在上面故事中，针长l恰等于平行线间距离d的一半，所以代入上面公式简化得：π≈n/m值得一提的是，后来有不少人步布丰先生的后尘，用同样的方法来计算π值。
实验报告3蒲丰投针
0
1.79821
2.30682
1.111713993
0
1.76922
1.13937
1.36255246
0
1.91693
0.85702
1.133839234
0
0.02899
0.71090
0.978779676
1
0.81484
1.90012
1.419389613
1
1.72649
1.19545
在历史上人们对 的计算非常感兴趣性，发明了许多求 的近似值的方法，其中用蒲丰投针问题来解决求 的近似值的思想方法在科学占有重要的位置，人们用这一思想发现了随机模拟的方法.
蒲丰投针问题：平面上画有间隔为 的等距平行线，向平面任意投一枚长为 的针，求针与任一平行线相交的概率.进而求 的近似值.
对于 =50,100,500,1000,3000各做5次试验,分别求出 的近似值.写出书面报告、总结出随机模拟的思路.
在历史上人们对的计算非常感兴趣性发明了许多求的近似值的方法其中用蒲丰投针问题来解决求的近似值的思想方法在科学占有重要的位置人们用这一思想发现了随机模拟的方法
数学实验报告
实验序号：3日期：2015年4月20日
班级
13A
姓名
徐文婕
学号
134080041
实验
名称
随机模拟计算 的值----蒲丰投针问题
问题的背景：
实验过程：（含解决方法和基本步骤，主要程序清单及异常情况记录等）
n=
d=
ห้องสมุดไป่ตู้l=
10000
4
3
相交计数
相交次数
π≈2nl/kd
蒲丰投针试验---------概率论与数理统计
蒲丰资料
1777年,法国科学家蒲丰(Buffon)提ห้องสมุดไป่ตู้了投针 试验问题.平面上画有等距离为a(a>0)的一些平行直 线,现向此平面任意投掷一根长为b( b<a )的针,试求 针与某一平行直线相交的概率. 解 以 x表示针投到平面上时,
针的中点M到最近的一条平行
a
M x
直线的距离, 表示针与该平行直线的夹角.
1.0
0.75 0.83 0.5419
600
1030 3408 2520
382
489 1808 859
3.137
3.1595 3.1415929 3.1795
利用蒙特卡罗(Monte Carlo)法进行计算机模拟. 单击图形播放/暂停 ESC键退出 取a 1, b 0.85.
利用上式可计算圆周率π 的近似值.
历史上一些学者的计算结果(直线距离a=1)
试验者 Wolf Smith 时间 1850 1855 针长 0.8 0.6 投掷次数 相交次数 π的近似值 5000 3204 2532 1218 3.1596 3.1554
De Morgan 1860
Fox Lazzerini Reina 1884 1901 1925
那么针落在平面上的位置可由( x , )完全确定.
投针试验的所有可能结果与 矩形区域
a S {( x , ) 0 x ,0 π} 2 中的所有点一一对应 . 由投掷的任意性可知 这是一个几何概型问题.
a
M x
所关心的事件
o
A { 针与某一平行直线相交} 发生的充分必要条件为S 中的点满足 b 0 x sin , 0 π . 2
蒲丰投针实验原理
蒲丰投针实验原理1.地球是一个球体：在蒲丰时代，人们普遍相信地球是一个球体，而蒲丰的实验就是为了验证这一点。
2.光线传播是直线传播：蒲丰认为光线传播是呈直线传播的，这是基于他对光学的观察和实验中得到的结论。
基于以上前提，蒲丰提出了以下实验步骤来验证地球的球形：1.准备一个平坦的地面：选择一个平坦的地面，比如一块大理石板或者是一个平整的木板。
2.准备一把针：选择一根细长的针，尽量确保它是笔直的。
3.垂直投放针：将针垂直地向地面投放，确保它垂直于地面，并且尽量避免针倾斜或弯曲。
4.观察针在地面上的分布：观察针在地面上的分布情况，看是否存在一定的规律。
理论上，如果地球是一个平坦的平面，那么无论针的位置如何投放，针都应该均匀地分布在地面上。
然而，如果地球是一个球体，那么针的位置投放将会影响其在地面上的分布。
由于地球表面的曲率，针的投放位置不同将导致一些规律的变化。
根据蒲丰的实验，当针被随机分布在地面上时，如果地球是一个球体，那么在一些特定范围内的细长物体的位置分布将会有所偏差。
这是因为在投针的过程中，总有一些针会与地面相交，而一些则不会。
蒲丰实验的原理是基于概率统计的方法。
通过计算和观察一系列接触和不接触地面的针，可以推导出地球的曲率和球形。
如果这些数据和理论上的期望一致，那么可以得出结论地球是球状的。
总结起来，蒲丰投针实验的原理是基于光线的直线传播以及地球的球形假设。
通过观察针在地面上的分布情况，可以验证地球是否是球状的。
这个实验的重要性在于它提供了一种简单直观的方法来验证古代关于地球形状的理论，并且可以通过实验数据来验证理论的正确性。
大学数学实验 蒲丰投针
蒲丰掷针法一． 实验目的通过蒲丰掷针法来计算pi 的近似值，其本质是蒙特卡罗法随机模拟，通过求概率来求得pi 的近似值。
二． 实验内容与要求（根据问题重新叙述）在白纸上画许多等距为d 的平行线，将一根长为的d/2的直针随机投掷向白纸，在进行n 次实验之后其中有m 次与平行线相交，当n 很大时，pi 的近似值可认为是n/m 。
三． 实验原理（问题假设，分析，模型建立）由于针投到纸上的时候，有各种不同的方向和位置，但是，每一次投针时，其位置和方向都可以由两个量唯一确定，即针的中点距平行线的距离（最近的平行线）d 和偏离水平的角度α。
因此只要随机生成n 对这样的 d 和 α，就可以模拟n 次的投针实验。
设平行线之间的距离为d ，以y 表示针的中点到最近的一条平行线的距离，α表示针与平行线间的夹角，其中0≤y ≤2d ,0≤α≤Pi 。
而直针与一平行线相交的充要条件：0≤y ≤4d sin α ，0≤α≤Pi 。
四． 实验过程（模型求解，模型结果）当n 的值为1000时，重复5次后，计算结果分别为：PI= 3.1546 PI= 3.2895 PI= 3.3223 PI= 3.2573 PI= 3.0303当n 的值为10000时，重复5次后，计算结果分别为：PI= 3.1546 PI= 3.1676 PI= 3.1066 PI= 3.2092 PI= 3.2010 当n 的值为50000时，重复5次后，计算结果分别为：PI= 3.1584 PI= 3.1283 PI= 3.1131 PI= 3.1273 PI= 3.1644五． 实验总结（结果分析）当n 的值越来越大时，可以发现通过随机模拟得到的PI 的值越来越接近真实的pi 的值（pi 的值的前8位为pi=3.1415926）虽然不是很接近pi 的值，但得到的PI 的值离真实的pi 的值越来越近。
且得到的PI 的值也越来越稳定。
六． 附录（源程序）。
蒲丰投针问题与无理数π的模拟
5、在C4输入=3*SIN(C4)/2。下托到C1003；在D4输入=IF(D4<=1,"1","0")下托到D1003，在E4输入=COUNTIF(E4:E10003,"1")在下托到E1003，在F4输入=2*10000*3/(F4*4)。
教师评语与成绩：
实验结果总结：计算机上模拟蒲丰投针试验，可以求出π的近似的值.我的到的值为3.225133和3.123367.他与.31415926存在了差别.可能是由于计算机取的1000个随机数的差别.虽然它们存在差别,但是它们已经很接近啦,这比人工或其它方法计远的快和准确于人的计算.
本实验旨在让实验者在计算机上模拟蒲丰投针试验,掌握无理数 的近似计算方法，理解随机模拟法的基本原理,从中体会到新思想、新方法产生的过程。
实验内容：
蒲丰投针问题：平面上画有间隔为 的等距平行线，向平面任意投一枚长为 的针，求针与任一平行线相交的概率,进而求 的近似值。若做了 次投针试验，有 次针与线相交,那么由教材例1.2.9结论知所求概率为 ，而 ，故有 。
2、单击数据/数据分析/随机数发生器，选择变量个数2，随机数1000，均匀分布，介于-1到1，输出区域$A$2，确定；
3、在C2输入=A2^2+B2^2；
4、在D2输入=IF(C6<=1,"1","0")，在E2输入=COUNTIF(D2:D10002,"1")；
5、在F2输入=4*E2/10000。
实验二、蒲丰投针问题与无理数π的模拟
蒲丰投针问题_概率论论文
Buffon投针问题摘要本文讨论了Buffon投针问题的解法及其不同解法之间的内在联系，同时从投针到投平面图形对Buffon投针问题给出了一些推广，并得到一般的结论，指出了其概率在探矿、近似计算中的应用。
关键词蒲丰投针概率随机试验近似计算一、引言蒲丰投针问题是由法国科学家蒲丰（Buffon）在1777年提出的，它是概率中非常有代表性的问题，它是第一个用几何形式表达概率问题的例子，其结论具有很强的理论与实际意义。
蒲丰针问题的解决不仅较典型的反应了集合概率的特征及处理方法，而且还可以由此领略到从“概率土壤”上开出的一朵瑰丽的鲜花——蒙特卡洛（Monte-Carlo）方法。
二、Buffon投针问题及其解法Buffon投针问题：平面上画有等距离的平行线，每两条平行线之间的距离为2a，向平面任意投掷一枚长为2l(l<a)的针，试求针与平行线相交的概率。
解：以x表示针的中点M到最近一条平行线的距离，以φ表示该针与平行线的夹角。
针与平行线的关系见图1.则有：0≤x≤a，0≤φ≤π，由它们所围成的矩形区域记为G1。
针与平行线相交的充要条件是：0≤x≤lsinφ，记满足这个关系的区域为g1(图2中的阴影部分)。
则所求概率为P1=g1的面积G1的面积=∫lsinφdφπaπ=2laπ三、Buffon投针问题不同解法及其内在联系上述解法是常见解法之一(记为解法一)，这里讨论一下蒲丰针问题的其他解法及其之间的联系。
1.其他解法解法二：以x表示针的重点M到最近一条平行线的距离，y表示该针在此平行线上投影和长度，如图3所示。
易知x和y的取值范围是0≤x≤a，0≤y≤2l，这两个不等式确定了xOy平面上的矩形区域G2，针与平行线相交的充要条件是(y2)2+x2≤l2，该不等式确定了矩形区域G2(如图4所示)中的区域g2，从而所求概率为P2=g2的面积G2的面积=14·l·2l·π2l·a=lπ4a解法三：作垂直于平行线的直线，在该直线上选定一方向为正向，用z1，z2分别表示针头与针尾关于某平行线的纵坐标(如图5所示)，该平行线的选取应使|z1+z2|≤2a。
布丰投针实验
“投针实验”的MATLAB实现问题摘要布丰在1777年提出了“投针实验”，“布丰投针”实验是第一个用几何形式表达概率问题的例子，他首次使用随机实验处理确定性数学问题，利用概率统计的方法计算圆周率的值，为概率论的发展起到一定的推动作用。
本文给出了“投针实验”的证明，同时运用MATLAB对“投针实验”进行仿真，来证明了实验结果。
关键词：投针实验，MATLABStudy of Buffon's needle problemAbstract: In 1777, Buffon proposed the "needle experiment", and the "Buffon needle" experiment was the first example to express the probability problem in geometric form. For the first time, he used random experiments to deal with deterministic mathematics problems, and used probabilistic statistics to calculate the value of pi, which played a role in promoting the development of probability theory. In this paper, the proof of "needle experiment" is given. At the same time, MATLAB is used to simulate the "needle experiment" to prove the experimental results.Key words：needle experiment ，MATLAB1引言在人类的数学文化史中，对圆周率精确值的计算一直是许多学者的追求。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
对于 =50,100,500,1000,3000各做5次试验,分别求出 的近似值.写出书面报告、总结出随机模拟的思路.
实验目的：
本实验旨在使学生掌握蒲丰投针问题,并由此发展起来的随机模拟法,从中体学会到新思想产生的过程.
数学实验报告
实验序号：3日期：2015年4月20日
班级
13A
姓名
徐文婕
学号
134080041
实验
名称
随机模拟计算 的值----蒲丰投针问题
问题的背景：
在历史上人们对 的计算非常感兴趣性，发明了许多求 的近似值的方法，其中用蒲丰投针问题来解决求 的近似值的思想方法在科学占有重要的位置，人们用这一思想发现了随机模拟的方法.
0.749830449
1
0.03418
0.57486
0.815575809
1
0.57009
0.83008
1.106974197
1
实验结果与实验总结(体会)：最后得到π的近似值为3.111387
进一步讨论或展望:浦丰投针问题可做各种推广，比如把实验改为向画有间隔为d的一组等距平行线的平面内任意投一个边长为l的小正三角形，求三角形与平行线相交的概率。进一步，可把正三角形改为正四边形、正五边形、……、正n边形，或者改为一个小圆，结论又如何？
主要利用Excel中产生的100个随即点（x,φ）来模拟每一次投针实验中针的位置，统计满足这个不等式的随机（x,φ）的个数，从而得到事件发生的次数和频率，进而近似计算π的值。
再利用一个简便方法近似计算∏的值：向一个包含单位园的边长为2的正方形内任意投掷n个随机点，统计其中“随机点落入单位圆内”的随机点个数k以及k/n,由几何概率易见
（1）学习和掌握Excel的有关命令
（2）掌握蒲丰投针问题
（3）理解随机模拟法
（4）理解概率的统计定义
实验原理与数学模型：1777年法国科学家蒲丰提出了一种通过随机实验近似计算圆周率π的方法----随机投针法
实验所用软件及版本：Microsoft office Excel 2003.
主要内容(要点):
教师评语与成绩：
1.395571969
0
0.27717
2.93547
0.30700368
1
0.49007
0.89728
1.172453414
1
0.09095
2.28151
1.136843615
1
0.06476
2.58649
0.790550904
1
0.32826
0.21955
0.326687465
0
0.43922
2.61812
0.249639109
0
1.79821
2.30682
1.111713937
1.36255246
0
1.91693
0.85702
1.133839234
0
0.02899
0.71090
0.978779676
1
0.81484
1.90012
1.419389613
1
1.72649
1.19545
实验过程：（含解决方法和基本步骤，主要程序清单及异常情况记录等）
n=
d=
l=
10000
4
3
相交计数
相交次数
π≈2nl/kd
x
φ
l*sin(φ)/2
0.76400
1.24444
1.420826686
1
4821
3.11138768
0.20136
2.08171
1.30844721
1
1.19297
0.16720