高频电子线路第4章习题参考答案
高频电子线路第4章作业答案

(4)L1C1 < L2C2 = L3C3,可知ω01 > ω0 2 = ω0 3。此电 路不能振荡,原因是L2C2、L3C3两回路性质相同, 不能满足X be、X ce同性质,X cb与X be、X ce反性质。
( 4-9:1)串联谐振频率 f q为 : 1 1 = fq = 2π Lq C q 2π 19.5 × 0.00021 × 10 −12 = 2.4870996 ( MHz )
注:也可采用下列公式计算: Cq 0.00021 6 f p − fq = fq = 2.4870996×10 × = 52.229( Hz) 2C0 2×5 ωq Lq 2π × 2.4871×106 ×19.5 5
(3)Qq = rq
2
=
110
= 4.4 ×10
R p = Qq rq = (4.4 ×105 ) 2 ×110 = 21.296 ×1012 (Ω)
作业 •4-4 •4-5 •4-9
4-4 (a)能振荡 属于电感三点式振荡电路 能振荡,属于电感三点式振荡电路 能振荡 (b) 、(c) 、
设LC并联谐振回路的谐振频率为ω0,ω > ω0时回 路呈容抗特性,ω < ω0时回路呈感抗特性,
1 解:设L1C1回路谐振频率为ω01= ,L2C2回路谐振 L1C1 1 1 频率为ω02= ,L3C3回路谐振频率为ω03= , L2C2 L3C3 能满足振荡的相位条件是X be、X ce同电抗性质,X cb与 X be、X ce反性质。
( )L1C1 > L2C2 > L3C3,可知ω01 < ω0 2 < ω0 3。若振 1 荡频率满足ω01 < ω0 2 < ω0 < ω0 3条件,则L1C1回路 等效为容抗、L2C2回路等效为容抗、L3C3回路等效 为感抗, 满足X be、X ce同性质,X cb与X be、X ce反性质, 可能振荡。为电容三点式振荡器 (2)L1C1 < L2C2 < L3C3,可知ω01 > ω0 2 > ω0 3。若振 荡频率满足ω01 > ω0 2 > ω0 > ω0 3条件,则L1C1回路 等效为感抗、L2C2回路等效为感抗、L3C3回路等效 为容抗, 满足X be、X ce同性质,X cb与X be、X ce反性质, 可能振荡。为电感三点式振荡器
高频电子线路第4章 正弦波振荡电路习题解答

C
C3串(C4
// C5), C
(C4 C5 )C3 (C4 C5 ) C3
,
f0
2
1 L13C
2
1
L13
(C4 C5 )C3 (C4 C5 ) C3
4.8 (1)旁路、耦合
(2) f
1
, L C2
(3)耦合,阻抗变换
参考答案 4.1 答:(a) 同名端标于二次侧线圈的上端 (b) 同名端标于二次侧线的圈下端(c) 同名端标于二次侧线圈的上端
4.2
4.3
答:(a)构成正反馈(b)构成三点式
VCC
VCC
(a)
(b)
4.4 (a)不能 (b)不能 (c)可能 4.5 同名端标于二次侧线圈的下端,
f0
2
1 LC
4.15 (1)4MHz; (2)
f s 2
1 Lq C q
;
fp
2
1
;
Lq
CqC0 Cq C0
(3)并联型晶体振荡器,JT 在电路中起电感作用。调 C4 可以微调振荡频率,使其
达到晶振的标称频率。
2
1
8kHz
0.1u 4m
4.6
(2)CB 耦合,隔直,CE 旁路
(3)不能,不满足三点式条件
(4) f0 2
1 L C1C2
C1 C2
4.7 (1)1、5 为同名端 (2)
51 43
(3) 影响反馈系数 F;影响 Q;L23 增大:F 增大 Q 减小
(4)C1:旁路,基极交流接地;C2:耦合,隔直;C2:对振荡没有直接影响; C1:去掉后,信号经电阻衰减可能无法满足幅度平衡条件,C1 不应去掉。 (5)
高频电路课后答案

C2 510PF
Cj
Rb2
Rb1 C1
51PF
Re
L
5µF
C
C
6800 PF
RP1 R2
47K
-VEE
R1
Z
C
6800 PF
C2
题图图P44.-1155
(a)
-VZ
vΩ
R2
C1
RP1
RP2
Cj
Cj
(b)
(c)
解:(1)高频等效电路如右(a)图所示。晶体作为电感用,属于晶体的并联谐振。
(2)变容管的直流偏置电路如右(b)所示,电位器 RP1 的作用为调节二极管的直流偏置电压。 (3)变容管的低频控制通路如右(c)所示,电位器 RP2 是调节低频信号的大小。
+Vcc
5. 6K
20K
T1
200 P
3/10P
C
300 P 20 PF
C
L
4 .7µH
2.7K
C
0.1µF
T2
V0
1. 5K
题图图P44-.1414
3~10PF
20PF T1
200PF
CL
解:(1)其交流等效电路如右图所示。晶体在电路中谐振时作电感用,属于晶体的并联谐振。
(2)LC 回路的作用是等效为电容,并且选择晶体的泛音频率,晶体管 T2 的作用是跟随输出,
种类型?
(2) 若石英晶振器频率为 f0 ,L1C1、L2C2 回路的谐振频率分别为 f01、f02 ,试分析三个
频率之间具备什么关系时,电路才能产生振荡?
C1 R1
+Vcc L1
R2 Ce
L2 C2 Re
高频第四章答案-陈

4-3 为了满足电路起振的相位条件,给图题4.3中互感耦合线圈标注正确的同名端。
(a)(b)(d)图题4.3解:(a)(b)(d)图题4.3中互感的同名端标注4-5 图题4.5为有L1与C1、L2与C2、L3与C3三回路的振荡器的等效电路,设有以下六种情况:(1)112233L C L C L C>>;(2)112233L C L C L C<<;(3)113322L C L C L C>>;(4)113322L C L C L C<<;(5)221133L C L C L C>>;(6)221133L C L C L C<<。
试分析上述六种情况是否可能振荡,振荡频率f0与三个回路谐振频率有何关系?1图题4.5解:设123ωωω==(1)123ωωω<<,有可能,回路1和回路2呈容性,回路3 呈感性,1203f f f f<<<。
(2)123ωωω>>,有可能,回路1和回路2呈感性,回路3 呈容性,1203f f f f>>>。
(3)132ωωω<<,不可能。
(4)132ωωω>>,不可能。
(5)213ωωω<<,有可能,回路1和回路2呈容性,回路3 呈感性,2103f f f f<<<。
(6)213ωωω>>,有可能,回路1和回路2呈感性,回路3 呈容性,2103f f f f>>>。
4-8 如图题4.8所示的LC振荡器中,若电感L = 2μH,要使振荡频率为48 MHz,试求C4的值。
图题4.8EE解:等效电路如下图所示。
L图题4.8等效电路444123112.53 (pF)1111116.2305C C C C C C C ∑=+=+≈+++++,12222126c 115.5010(F)4 3.144810210C L ω-∑-==≈⨯⨯⨯⨯⨯⨯,4 2.53 2.97 (pF)C C ∑≈-≈。
《高频电子线路》习题解答完整答案

RS
,R
' L
1 P22
RL 。此时有谐振阻抗: RT
R0 // RS'
//
R
' L
,回路总电容:C
C,
有载品质因素: Qe
RT
RT 0C ,其中0
1。 LC
《高频电子线路》习题解答(周选昌)
8
(g)令接入系数 P1
N3
N3 N2
N1
,接入系数 P2
N2 N3 N3 N2 N1
解: S
1
Q f0
1 2Q
f f0
2
2f
1
640 1
1
1 16
S2
2 20 0.72
BW0.7
f0 Q
640 16
40 KHz 。
当信号频率为 680KHZ 时,则频率偏移为 f 680 640 40KHz ,则信号的抑制比 S 为
又 RT RS // RP // RL ,即 GT GS GP GL ,所以有:
GL
GT
GS
GP
0.377
0.167 0.05 0.16mS
RL
1 GL
6.25K
1-7 设计一并联谐振回路,要求其谐振频率 f0 10MHz ;当失谐频率 f 10.6MHz 时,
11.76H
Q0
RT
RT
Q0
0 LQ0
12.49 K
若希望回路的通频带宽展宽一倍,则要求品质因素 Q 降低一倍,即谐振电阻减少一倍,则
高频电子线路v第四章习题解答

4-1 如图是用频率为1 000 kHz 的载波信号同时传输两路信号的频谱图。
试写出它的电压表达式,并画出相应的实现方框图。
计算在单位负载上的平均功率P av 和频谱宽度BW AM 。
解:(1)为二次调制的普通调幅波。
为二次调制的普通调幅波。
第一次调制:调制信号:F = 3 kHz 载频:f 1 = 10 kHz ,f 2 = 30 kHz第二次调制:两路已调信号叠加调制到主载频f c = 1000 kHz 上。
上。
令 W = 2p ´ 3 ´ 103 rad/sw 1 = 2p ´ 104rad/sw 2= 2p ´ 3 ´ 104rad/s w c = 2p ´ 106rad/s第一次调制:v 1(t ) = 4(1 + 0.5cos W t )cos w 1tv 2(t ) = 2(1 + 0.4cos W t )cos w 2t第二次调制:v O (t ) = 5 cos w c t + [4(1 + 0.5cos W t )cos w 1t + 2(1 + 0.4cos W t )cos w 2t ] cos w c t= 5[1+0.8(1 + 0.5cos W t )cos w 1t + 0.4(1 + 0.4cos W t )cos w 2t ] cos w c t (2) 实现方框图如图所示实现方框图如图所示(3) 根据频谱图,求功率。
根据频谱图,求功率。
○1 载频为10 kHz 的振幅调制波平均功率的振幅调制波平均功率 V m01 = 2V ,M a1 = 0.5W 5.4)211(2W 22121a 01av1201m 01=+===M P P V P ;○2 f 2 = 30 kHz V m02 = 1V ,M a2 = 0.4W 08.1)211(2W 5.02122a 02av2202m 02=+===M P P V P ; ○3 主载频f c = 1000 kHz V m0 = 5VW 5.122120m 0==V P总平均功率P av = P 0 + P av1 + P av2 = 18.08 W ○4 BW AM 由频谱图可知F max = 33 kHz得BW AM = 2F = 2(1033 -1000) = 66 kHz4-3 试画出下列三种已调信号的波形和频谱图。
高频第四章作业答案
4.2解:a、b、e图不能够产生振荡:a和b不满足三点式振荡器电路组成法则,e中的L 和C1串联谐振电路在环路中起阻抗作用(输入是电流,输出是电压),不满足负斜率的相频稳定条件。
c、d图可以产生振荡:c满足三点式振荡器电路组成法则,d满足正反馈和负斜率的相频稳定条件。
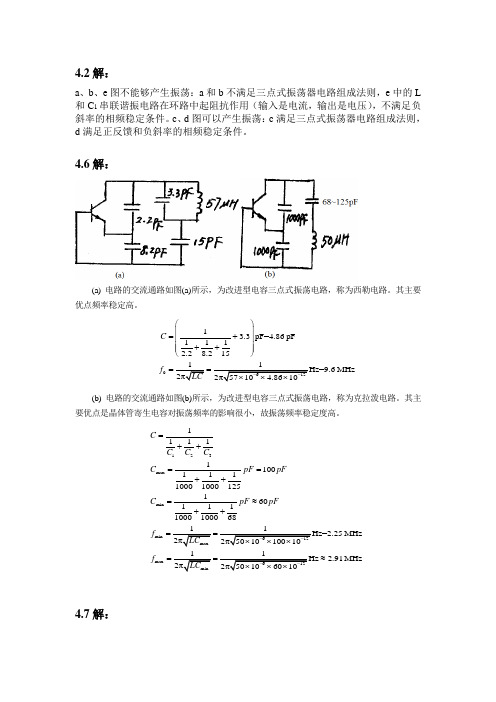
4.6解:(a) 电路的交流通路如图(a)所示,为改进型电容三点式振荡电路,称为西勒电路。
其主要优点频率稳定高。
13.3pF=4.86pF1112.28.215MHzCf⎛⎫⎪=+⎪⎪++⎪⎝⎭==(b) 电路的交流通路如图(b)所示,为改进型电容三点式振荡电路,称为克拉泼电路。
其主要优点是晶体管寄生电容对振荡频率的影响很小,故振荡频率稳定度高。
123maxminminmax11111100100010001251601111000100068MHz2.91MHzCC C CC pF pFC pF pFff=++==++=≈++====≈4.7解:(a)、由三点式振荡电路的组成法则,11C L 和22C L 并联电路必须呈感性,为电感三点式电路,所以振荡频率f 0必须满足:f 1,f 2>f 0(b)、根据三点式振荡电路的组成法则,11C L 呈必须感性,22C L 必须呈容性,为电容三点式电路,所以振荡频率f 0必须满足:f 1 >f 0 >f 2 4.9解:交流等效电路分别如图(a)和图(b)。
图(a)中晶体呈感性。
晶体作为高Q 元件与其它元件构成并联谐振回路。
反馈系数12012120013001050.4551111()150********f oIU F U I ωωω---⨯⨯===≈+⨯⨯⨯⨯ 图(b)中晶体工作在串联谐振状态,在振荡器中用作高选择性短路元件。
反馈系数12012120012701010.137117.28()431027010f oIU F U I ωωω---⨯⨯===≈+⨯⨯⨯⨯4.11解:振荡电路简化交流通路如图所示。
(完整版)高频电子线路(胡宴如耿苏燕主编)习题答案

高频电子线路(胡宴如 耿苏燕 主编)习题解答目 录第2章 小信号选频放大器 1 第3章 谐振功率放大器 4 第4章 正弦波振荡器10 第5章 振幅调制、振幅解调与混频电路 22 第6章 角度调制与解调电路 38 第7章 反馈控制电路49第2章 小信号选频放大器2.1 已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解] 90-6120.035610Hz 35.6MHz 2π2π102010f LCH F-===⨯=⨯⨯6312640.71010022.4k 22.361022.36k 201035.610Hz35.610Hz 356kH z100p HR Q Ff BW Q ρρ--===Ω=⨯Ω=Ω⨯⨯===⨯=2.2 并联谐振回路如图P2.2所示,已知:300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解] 0465kHz 2π2π390μH 300PFf LC≈==⨯0.70390μH100114k Ω300PF////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω371.14k Ω390μH/300 PF/465kHz/37=12.6kHzp e s p Lee e R Q R R R R R Q BWf Q ρρ===========2.3 已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ,应在回路两端并接一个多大的电阻?[解] 6262120115105μH (2π)(2π1010)5010L H f C --===⨯=⨯⨯⨯⨯ 6030.7101066.715010f Q BW ⨯===⨯2236022*********.78.11010p oU f Q f U ••⎛⎫⎛⎫∆⨯⨯=+=+= ⎪ ⎪⨯⎝⎭⎝⎭ 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯g而471266.7 2.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯g由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω2.4 并联回路如图P2.4所示,已知:360pF,C =1280μH,L ==100,Q 250μH,L =12=/10,n N N =L 1k R =Ω。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)因为
Beb
2f
1011
2f
1 105
题4-6图
(2f )2 1016 2f 105
1
39.4384 102 2f 105
1
0, 呈感性,所以
Bec
2fC1
2f
1 3 105
=(2f )2 3 105 C1 2f 3 105
43.8mS
IeQ gmVT 43.8 26 1.14mA
14
4-8 在图示的电容三端式电路中,试求电路振荡频率和维持 振荡所必须的最小电压增益。
解4-8
回路总电容 C = C2C1 = 30000 = 75pF C2 + C1 400
振荡频率 f1
f0
=
2
1 LC
1
2.6MHz
1 应该呈容性,及
(2f )2 2 105 C2 1 0, 2f C2
1
1
C2 (2f )2 2 105 42 1014 2 105 12.7 pF
11
(2)实际电路如下
LC CC
C1
30 H
20 H
Cb
10pF
10 H
C2
1,也应呈感性,即
10
(2f )2 3 105 C1 2f 3 105
1
0
,
C1
1 (2f )2 3 105
42
1 1014 3 105
109 122
8.5 pF
X bc
2f
2 105
1 2f C2
(2f
)2 2 105 C2 2f C2
(3)fo1=f02<f03, 因此,当满足fo1=f02<f<f03,就可能振荡, 此时L1C1回路和L2C2回路呈容性,而L3C3回路呈感性,构 成一个电容反馈振荡器。
(4)fo1>f02=f03不能振荡,因为在任何频率下,L3C3回路和 L2C2回路都呈相同性质,不可能满足相位条件。
6
4-4 试检查图示的振荡器线路,有哪些错误?并加以改正。
51 2051
0.02487
总电容为C C1C2 102000 50pF C1 C2 2051
固有谐振电导g0
1 Q0
C 1 L 100
50 106 62S, 1.3
13
负载电导gL
1 RL
1 1000
1mS
放大器增益K
gm g
gm
gL
g0
KF2
根据给定条件,可知
(1)fo1<f02<f03,因此,当满足fo1<f02<f<f03,就可能振荡,此 时L1C1回路和L2C2回路呈容性,而L3C3回路呈感性,构成 一个电容反馈振荡器。
(2)fo1>f02>f03,因此,当满足fo1>f02>f>f03,就可能振荡,此 时L1C1回路和L2C2回路呈感性,而L3C3回路呈容性,构成 一个电感反馈振荡器。
题4-4图
7
解4-4 改正过的电路图如下
Ec
•
g
Cb
EC C1 C2
8
4-5 将图示的几个互感耦合振荡器交流通路改画为实际线路 ,并注明互感的同名端。
题4-5图
解4-5, 画出的实际电路如下
• •
•
•
••
9
4-6 振荡器交流等效电路如图所示,工作频室为10 MHZ, (1)计算C1、C2取值范围。(2)画出实际电路。
4
4-3 图示是一三回路振荡器的等效电路,设有下列四种情况
:
(1) L1C1>L2C2>L3C3; (2)L1C1<L2C2<L3C3; (3)L1C1=L2C2>L3C3; (4)L1C1<L2C2=L3C3。
试分析上述四种情况是否都能振荡,振荡频率f1与回路谐振 频率有何关系?
题4—3图
5
解4-3
无载Q。=100,负载电阻R=1kΩ,晶体管输入电阻
T
(
j) 1 (T )
2n,
振幅条件 n 0,1, 2..... 相位条件.
平衡条件:T
(
j)
1,即
T
(
j) (T )
1
2n,
振幅条件 n 0,1, 2......相位条件
T
稳定条件:
U
i
0
Ui UiA
L
0
1
第4章习题参考答案
4-1
4-2
4-3
4-4
4-5
4-6
4-7
4-8
4-9
4-
10
4-11 4-12 4-13 4-14 415
4-16 4-17 4-18ቤተ መጻሕፍቲ ባይዱ
1
4-1 什么是振荡器的起振条件、平衡条件和稳定条件?振荡 器输出信号的振幅和频率分别是由什么条件决定?
答4-1
起振条件:T
(
j)
1,即
Re re Re re
gL
gm g0
KF2gm
环路增益T(1 )
KFK
gL
gmKF g0 KF2gm
1时满足起振条件,即
gmKF gL g0 KF2gm ,
gm
1 KF (1
KF)
(gL
g0)
(1 0.062) 103 0.02487(1 0.02487)
振幅稳定条件 相位稳定条件
2
4-2 试从相位条件出发,判断图示交流等效电路中,哪些可能 振荡,哪些不可能振荡。能振荡的属于哪种类型振荡器?
题4—2图
3
(b) 不能, (c) 不能, (d) 不能, (e) 可能振荡,振荡的条件是L1C1回路呈
容性,L2C2回路呈感性,即要求 f01<f<f02,这时是一个电感反馈振荡器, (f) 可能振荡,振荡的条件是LC3支路呈感 性,即要求f03<f,这时是一个电容反馈 振荡器
2 50 106 75 1012
当以uce作为放大器的输出时,
题4 8图
反馈系数 KF
=
C1 C2
要维持振荡,应满足K KF
1,即K= 1 KF
C2 C1
300 100
3
15
4-9 图示是一电容反馈振荡器的实际电路,已知C1=50 pF, C2=100 pF,C3= 10~260pF,要求工作在波段范围, 即f=10~1OMHz,试计算回路电感L和电容C。设回路
12
4-7 在图示的三端式振荡电路中,已知 L=1.3μH,C1=51pF, C2=2000pF,Q0=100,RL=1kΩ,Re=500Ω试问IEQ应满足 什么要求时振荡器才能振荡?
解4-7
以回路两端为放大器的输出,则当忽略晶体管的影响后
反馈系数K F
C1 C1 C2
51 51 2000
