流体力学第9章
第九讲流体力学优秀课件

v
层流特点:只有切向速度,没有径向速度。
二、牛顿粘性定律
速度梯度 vx
y
y
v
f
v2
lim vx dvx
v1
x0 y dy
作用在面元S上的粘滞力f
z
x
f dυx S
dy
f S
f dvx dy
: 粘滞系数或内摩擦系数
f 6πrv
重力场中,流体中小球的沉降问题
小球在静止液体中自由下落
G 4 πr3g
f f
3
f 6πrv
G
f 4 πr3g
3
f f
小球做匀速运动时
浮力的方向竖直向上,且通过排开流体的重心。 F浮m液g
讨论:浸没在流体中的物体的稳定性以及悬浮在流体 中的物体的稳定性问题
五、表面张力
液体表面或两种不相容液体的交界面或液体与
气体的交界面上,存在表现为张力的相互作用,称
为表面张力。
l f
f
实验表明
f l
称为表面张力系数
Nm1
六、毛细现象
接触角
ds
vdt
S
ds
质量流量
单位时间内流过面元的流体体积
dQV
dV dt
ds
vdt dt
cos
v ds
对一封闭曲面S
体积流量
QV
dQV
v ds
S
流体中单位时间内流过某一横截面的流体质量
dQm v ds
Qm
dQm
v ds
S
二、流体的连续性原理
V dt 时间内流过闭合曲面的 流体 质量
新版流体力学知识点大全课件.doc

流体力学-笔记参考书籍:《全美经典-流体动力学》《流体力学》张兆顺、崔桂香《流体力学》吴望一《一维不定常流》《流体力学》课件清华大学王亮主讲目录:第一章绪论第二章流体静力学第三章流体运动的数学模型第四章量纲分析和相似性第五章粘性流体和边界层流动第六章不可压缩势流第七章一维可压缩流动第八章二维可压缩流动气体动力学第九章不可压缩湍流流动第十章高超声速边界层流动第十一章磁流体动力学第十二章非牛顿流体第十三章波动和稳定性第一章绪论1、牛顿流体:剪应力和速度梯度之间的关系式称为牛顿关系式,遵守牛顿关系式的流体是牛顿流体。
2、理想流体:无粘流体,流体切应力为零,并且没有湍流?。
此时,流体内部没有内摩擦,也就没有内耗散和损失。
层流:纯粘性流体,流体分层,流速比较小;湍流:随着流速增加,流线摆动,称过渡流,流速再增加,出现漩涡,混合。
因为流速增加导致层流出现不稳定性。
定常流:在空间的任何点,流动中的速度分量和热力学参量都不随时间改变,3、欧拉描述:空间点的坐标;拉格朗日:质点的坐标;4、流体的粘性引起剪切力,进而导致耗散。
5、无黏流体—无摩擦—流动不分离—无尾迹。
流体力学- 16、流体的特性:连续性、易流动性、压缩性D不可压缩流体:0Dtconst是针对流体中的同一质点在不同时刻保持不变,即不可压缩流体的密度在任何时刻都保持不变。
是一个过程方程。
7、流体的几种线流线:是速度场的向量线,是指在欧拉速度场的描述;同一时刻、不同质点连接起来的速度场向量线;dr U x,t dr U 0迹线:流体质点的运动轨迹,是流体质点运动的几何描述;同一质点在不同时刻的位移曲线;涡线:涡量场的向量线,U , dr x,t dr 0涡线的切线和当地的涡量或准刚体角速度重合,所以,涡线是流体微团准刚体转动方向的连线,形象的说:涡线像一根柔性轴把微团穿在一起。
第二章流体静力学1、压强:p limA 0 F dF A dA静止流场中一点的应力状态只有压力。
流体力学PDF
第七章 功與能 4. 表面張力的計算:
表面張力存在於液體之表面,如下之問題,有兩面(前後、裡外、上下、…等 等),必須算兩次。
把針放在水面上的小技巧:針放在衛生紙上,讓衛生紙慢慢下沉。
P ∝ e−ah
第七章 功與能
第七章 功與能
流體力學→界面現象→表面張力→毛細管
090509
毛細管與毛細現象
1.成因: 以水為例: 玻璃與水之間的作用力 > 水與水之間的作用力 即,附著力大於內聚力,故玻璃會將液柱往上拉
3.進階應用:
靜力平衡(分析液柱):
向上的力=向下的力
mg = T cosα ⋅ 2πr
(ρπr2 y)g = T cosα ⋅ 2πr 故
y
=
2T cosα ρgr
靜力平衡(分析整段水):
向上的力=向下的力
mg = T cosα ⋅ 2l
(ρdhl)g = T cosα ⋅ 2l
故
h
=
2T cosα ρgd
h
相等
h
【口訣】:同一種液體,同一高度,壓力相同
4.進階思考: 三容器在桌面造成的壓力何者最大?
三容器內的液體在容器底部造成的壓力何者最大?
容器甲及丙對水的力為何?
第七章 功與能
命題焦點 9.2→大氣壓力
090201 大氣壓力:
1、壓力的來源:
種類
氣體壓力
氣體壓力
來源
氣體的重量
氣體的碰撞
章別
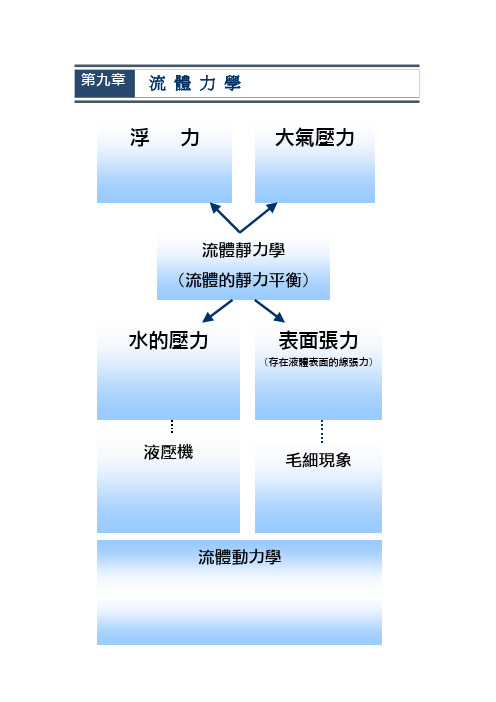
第九章
When a body is fully or partially submerged in a fluid, a buoyant force from the
surrounding fluid acts on the body. The force is directed upward and has a magnitude
[工程流体力学(水力学)]第二版--禹华谦1-10章习题解答
![[工程流体力学(水力学)]第二版--禹华谦1-10章习题解答](https://img.taocdn.com/s3/m/e3696bd46294dd88d0d26bff.png)
第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少?[解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆ 1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)?[解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]第二章 流体静力学2-1.一密闭盛水容器如图所示,U 形测压计液面高于容器内液面h=1.5m ,求容器液面的相对压强。
水力学第九章讲义

第九章 孔口、管嘴出流和有压管道 本章在定量分析沿程水头损失和局部水头损失的基础上,对工程实际中最常见的有压管道恒定流动和孔口、管嘴出流进行水力计算。
§9—1 孔口与管嘴的恒定出流液体从孔口以射流状态流出,流线不能在孔口处急剧改变方向,而会在流出孔口后在孔口附近形成收缩断面,此断面可视为处在渐变流段中,其上压强均匀。
● 孔口出流的分类:小孔口出流、大孔口出流(按H /D 是否大于10来判定);恒定出流、非恒定出流;淹没出流、非淹没出流;薄壁出流、厚壁出流。
薄壁出流确切地讲就是锐缘孔口出流,流体与孔壁只有周线上接触,孔壁厚度不影响射流形态,否则就是厚壁出流,如孔边修圆的情况,此时孔壁参与了出流的收缩,但收缩断面还是在流出孔口后形成。
如果壁厚达到3~4D ,孔口就可以称为管嘴,收缩断面将会在管嘴内形成,而后再扩展成满流流出管嘴。
管嘴出流的能量损失只考虑局部损失,如果管嘴再长,以致必须考虑沿程损失时就是短管了。
一. 薄壁孔口出流● 非淹没出流的收缩断面上相对压强均为零。
对上游断面O 和收缩断面C 运用能量方程即可得到小孔口非淹没出流公式:00221gH gH v C C ϕζα≡+=,0022gH A gH A A v Q C C μϕε≡==. 其中H 0是作用总水头;ϕ称为孔口的流速系数,主要取决于水头损失系数;μ是孔口的流量系数,它是流速系数ϕ与小孔口断面收缩系数A A C /=ε的乘积。
● 由于边壁的整流作用,它的存在会影响收缩系数,故有完全收缩与非完全收缩之分,视孔口边缘与容器边壁距离与孔口尺寸之比的大小而定,大于3则可认为完全收缩。
● 小孔口淹没出流的相应公式只需将作用总水头改成孔口上下游水位差即可。
● 大孔口出流的流量公式形式不变,只是相应的水头应为孔口形心处的值,具体的流量系数也与小孔口出流不同。
二. 厚壁孔口出流厚壁孔口出流与薄壁孔口出流的差别在于收缩系数和边壁性质有关,注意到收缩系数定义中的A 为孔口外侧面积,容易看出孔边修圆后,收缩减小,收缩系数和流量系数都增大。
南京理工大学工程流体力学基础 第9章__膨胀波和激波

§9-3 正激波前后的参数关系
p2 2 1 2 Ma1 p1 1 1
2
1v1 2v2
p2 p1 1v1 2v2
2 2
v1 p1 v2 p2 2 1 1 2 1 2
2
波后与波前压强比取决于波前的马 赫数以及气体的性质。
v1 c v c 1 ccr 1 2 2 2 1 2 1 1 2
Ma1 1 Ma2
2
1
Ma2
Ma1 1
2
1
§9-2 激 波
激波的产生
以超声速飞行的飞行器。
附体激波
Ma1>1 ε
流线
脱体激波
Ma1>1 Ma<1
Ma=1 Ma>1
近似正激波
附体激波
近似斜激波
脱体激波
§9-2 激 波
激波的产生
半无限长直管道中活塞逐渐加速。
静止活塞从t=0加速 到 t=t1 , 形 成 一 系 列压缩波。 气体压缩后温度上 升,音速提高,后 面的波传播速度较 快。 后波赶前波,最后 形成压力间断面, 即激波。
工程流体力学基础
第九章 膨胀波和激波
主要内容
膨胀波 激波 正激波前后的参数关系 斜激波 激波的反射与相交 拉瓦尔喷管与激波
膨胀波和激波
超声速流与亚声速流有很大不同。超声速流中 通常会出现膨胀波和激波,这是其基本特征。 膨胀波:流体发生膨胀,通过膨胀波后,流 体的压强、温度和密度降低,流速增大。 激波:气体流动状态的突然改变。
总压比 由压强比关系式和总压关系式
1Ma 2 1 2 p02 2 1Ma1 2 1 2 p01 Ma1 1 1
水力学 第九章课后题答案

az
2u x
2u z
fx
fz g cos
ℎ3
sin
3
于是,N-S方程化简为
1 p
2u x
0 g sin
x
z 2
0 g cos
1 p
z
这组方程有两个未知数,即ux和p。
由此求得p:
p gz cos c
u
x z 0
2 z
x
x
y
z
1
2
1
2
u y
u
x
y
x
0
流函数存在的充分必要条件为不可压缩液体的连续性方程式。
即
u y
u x
0
x
y
9.10什么叫边界层?边界层液流有哪些特点?
答:边界层:从平板表面到未扰动的的液流之间存在着一个流速分布不均匀的区域,这个区域就是
水流受平板影响的范围,叫做边界层。
边界层液流的特点:
(1)边界层内的液流形态可能是层流,也可能是湍流。
(2)在板端附近边界层极薄,流速自零迅速增至U0,因此流速梯度极大,以致产生很大的内摩擦
阻力,所以板端附近边界层内的液流往往是层流。
(3)距板端距离愈远,边界层厚度愈厚,流速梯度随边界层厚度增大而变小,内摩擦阻力也相应
ux
uy
uz
z
t
x
y
z
压力
粘滞力
单位质量力
适用条件:适用于不可压缩粘滞性液体。
惯性力
其中:
2 为拉普拉斯算子,
流体力学—渗流讲解

集水廊道 和井的产 水量计算
二、达西渗流定律
19世纪50年代法国工程师达西在沙质土壤中进行了 大量的试验研究,得出了著名的渗流基本定律——达西渗 流定律。
由实验得
Q A hw s
Q kA hw s
§9-1 渗流基本定律
或
v Q k hw kJ
As
上式即为达西渗流定律,式中k称为渗流系数,一般
k=f(土壤性质、流体性质、作用力等),由实验确定。
§9-3 集水廊道和井
二、潜水井(无压井)产水量计算
仅研究完全潜水井 潜水井的产水量计算公式推导
Q Av 2 rzkJ
A 2 rz
v kJ
2k rz dz 2krz dz Nhomakorabeads
dr
J dz dr ds ds
§9-3 集水廊道和井
分离变量 Q dr 2 kzdz
大口井的渗流形式有两种假定: 过流断面为半球面,适用于含水层厚度很大的情况; 过流断面为椭球面。适用于含水层厚度较小的情况。
§9-3 集水廊道和井
对于渗流过流断面为半球面的大口井,其产水量公式为 Q=2πkr0S
对于渗流过流断面为椭球面的大口井,其产水量公式为 Q=4kr0S
§9-4 井群
一、井群的定义
本章主要研究了重力水在均质各向同性土壤中的 恒定流动规律。渗流理论广泛应用于诸多学科领域, 其中土木工程中的路基排水、隧道防水、桥梁及建筑 工程的基础施工降水、城市防洪工程设计等,也将用 到有关渗流知识。因此本章要求重点掌握的内容如 下:
本章小结(END)
渗流的基 本概念
重点 掌握
达西渗流 定律
均匀渗流 和渐变渗 流的特性
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 绕流与射流重点阐述不可压缩粘性流体绕流二维和回转物体绕流现象及其绕流阻力的计算,分析工业生产中常遇到的紊流射流问题。
§9-1 绕流阻力与阻力系数当粘性流体绕流物体时,物体总是受到压力和摩擦力的作用。
作用在整个物体一表面上的压力和摩擦力的合力F 可分解为两个分力,即绕流物体的未受干扰时来流速度∞V 方向上的分力F D ,及垂直来流速度∞V 方向上的分力F L 。
对于在静止流体中运动的物体来讲,由于F D 与物体运动方向相反,是阻碍物体运动的力,故称之为绕流阻力;F L 称为绕流升力。
于是D L F F F +=绕流阻力和升力二者都包含摩擦力和压力两个分量,因此,物体所受摩擦力和压力的大小及二者的变化是分析绕流阻力的基础。
一、绕流阻力一般分析物体壁面所受摩擦阻力是粘性直接作用的结果,所受压力又称压差阻力,是粘性间接作用的结果,当粘生流体绕流物体时,边界层分离是引起压差阻力的主要原因。
下面以圆柱绕流为例来说明绕流阻力的变化规律。
在绕流未分离的情况下,由理想流体所确定的物面上的压强分布如图6-12所示,在第六章的第四节详细地讨论过这个解,物体所受压力阻力为零。
在绕流圆柱体发生严重分离的情况下,由于柱体后部背流面存在分离区,此时主流区的边界处在分离区的外缘,柱面上的压强分布不同于未分离时的压强分布,从分离点开始,柱体后部受到的流体压强大约等于分离处的压强,而不能恢复到理想流体绕圆柱体流动时应有的压强数值,从而产生对圆柱体的压差阻力。
图9-1(b)所示是有边界层分离的圆柱面上的无因次压强分布,实验曲线见图6-12中的II 、III 曲线。
对于摩擦阻力,其形成过程比较清楚。
实验表时,象机翼、船只和其它一些流线型物DF体都有较大的摩擦阻力。
钝体如圆柱、球、桥墩和汽车等都有较大的甚至压倒优势的压差阻力。
由于压差阻力的大小与物体的形状有很大关系,因此,压差阻力又称为形状阻力。
二、阻力系数虽然绕流物体阻力的形成过程从物理观点看完全清楚,但要想从理论上通过面积分求解一个任意形状物体的阻力是十分困难的,目前都是由实验测得,工程上习惯借助无因次阻力系数来确定总阻力的大小,即A V C F 2DD 21∞=ρ (1) A V F C 2D D 21∞=ρ (2)式中A 为物体的投影面积,当物体主要受压差阻力时,采用物体垂直于来流速度方向的投影面积,即迎流面积。
物体的阻力系数的大小,主要取决于雷诺数Re 的大小和物体的形状,也与物体在流场中的方位密切相关。
由相似定律知道,对于不同的不可压缩流体中的几何相似体,如果Re相等且在流场中的方位相同,则它们的阻力系数相等。
因此,在不可压缩流体中,对于与来流方向具有相同方位的几何相似体,如果Re 相等且在流场中的方位相同,则它们的阻力系数相等。
因此,在不可压缩流体中,对于与来流方向具有相同方位的几何相似体,其阻力系数C D 只是Re(vlV ∞=Re ,式中l 为特征尺寸)的函数,即 ()Re D f C = (3)图9-2和图9-3给出了无限长圆柱体和球体阻力系数与Re 的实验关系曲线。
由图可知,在不同的Re 下,流动现象的差异和阻力系数的大小是明显的。
下面仍以圆柱为例,具体分析随着Re 的变化绕流现象的变化过程及阻力系数的大小。
(1) 在Re ≤1的范围内,流动如图9-4(a),边界层没有分离,其特点为圆柱表面上下、前后流动对称且呈层流流态。
流动阻力来源于柱面摩擦阻力的合力,C D 与Re 成反比,如图中直线部分。
(2) 在3~5<Re<30~40范围内,流动如图9-4(b),其特点为在圆柱背流面发生边界层分离且形成对称驻涡区。
绕流阻力由摩擦阻力和压差阻力两部分组成,它们具有同等的重要性。
(3) 30~40<Re<60~90范围内,随着Re 的增大,圆柱背流面分离区逐渐变宽,对称涡(a)Re ≤1;(b)3~5<Re<30~40;(c)30~40<Re<60~90;(d)60~90<Re<1.5×105;(e)Re>1.5×105区出现摆动,如图9-4(c)所示。
此范围内,压差阻力在总阻力中占的比例逐渐增大,虽然摩擦阻力和压差阻力有同等重要地位,但压差阻力已逐渐占主要部分。
(4) 在60~90<Re<1.5×105范围内,圆柱背流面旋涡交替脱落,形成两排向下游运动的涡列,称之为卡门涡街,如图9-4(d)所示。
随着Re的增大,边界层分离点最终移向迎流面,该流动情况称为绕流物体的亚临界状态,如图9-4(e)所示。
绕流阻力仍由摩擦阻力和压差阻力组成,但压差阻力已明显地占绝大部分。
(5) 在Re>1.5×105条件下,随着的Re的增大,分离点前的边界层由层流转变为紊流,紊流边界层的强烈混合效应使得分离点向后移,尾涡区变窄,绕流得以改善,如图9-4(f)所示。
该流动情况称为绕流的超临界状态,阻力系数亦随之下降,即从Re=1.5×105~5×105,C D从1.2急剧下降到0.3,如图9-2所示,由于物体阻力以压差阻力为主,故绕流总阻力是下降的。
应指出,层流边界层可以人为地转变为紊流边界层,即亚临界状态可人为地提前转变为超临界状态。
转变的办法是扰动来流,增加上游的紊流度,普朗特曾用下面的实验证实了这一现象,他在紧靠圆球上层流边界层分离点的稍前面套上一圈细金属丝,人工地把层流边界层转变为紊流边界层,则Re在小于3×105的亚临界时,阻力就显著下降,此时分离点从原来的圆球前驻点后约80°处向后移到约110°~120°。
通过上述分析,可归纳如下:为了减小绕流阻力,应设法避免边界层分离。
在不发生边界层分离的情况下,边界层应尽可能保持层流。
如果已发生分离,则应在发生分离处稍前设法使边界层流转变为紊流,以使分离点后移。
由于发生边界层分离的条件是沿流向压强增大和动能不足,因此,如果在压强增大处采取减压措施或使流体增加流速,均能消除边界层分离而降低阻力,这种措施称为边界层控制,这里不再介绍,可能参阅有关文献。
§9-1 卡门涡街不可压缩粘性流体绕流圆柱体,在60~90<Re<15×105的绕流条件下,圆柱背流面将产生卡门涡街(Karman vortex street),本节的主要内容是分析卡门涡街的脱落频率以及由卡门涡街引起的声学共振现象。
一、卡门涡街的脱落频率1911年,匈牙利科学家卡门在德国专门研究了这种圆柱背后涡流的运动规律。
研究表明,圆柱背后生成的旋涡是交替脱落、在尾流中交叉排列,旋转方向相反的有规则的两行涡,故称为卡门涡街或卡门涡列。
卡门涡街的稳定条件为:两行旋涡间距与同行相邻两旋涡间距之比h /l =0.281。
如图9-5所示,此时的Re ≈150。
近年来,许多学者对卡门涡街进行了研究,认为当流体绕流单根圆柱体时,在250<Re<1.5×105范围内,柱后交替脱落的旋涡频率为⎟⎠⎞⎜⎝⎛−=∞Re 7.191198.0dV f (1)式中f ——涡街脱落频率;d ——圆柱直径;∞V ——来流速度;上式中的f 、∞V 、d 可组成一无因次系数,用St 表示,即∞=V fdSt (2) 式中的St 称作斯特罗哈数,是用该方面的早期研究者斯特罗哈(V ·Strouhal)名字命名的,根据罗斯柯(A ·Roshko)1954年的实验结果,在Re=800~1.5×105范围内,St 数近似等于常数,即St ≈0.21。
如图9-6所示。
绕流圆柱体形成的卡门涡街尾流,当Re 约大于300时为紊流尾流,卡门涡街不断消失在紊流尾流中,但当Re ≈3.3×105达到超临界时,有规则的旋涡脱落不再存在,这种情况一直要持续到Re=3.5×106,大于这个数值时,又会形成卡门涡街,这时的St 数为0.27。
根据卡门涡街的上述性质,可制成卡门涡街流量计,即垂直插入管道一根圆柱验测杆,管内流体流经验测杆时,在其下游产生卡门涡街,测得了涡街的脱落频率,便可求出管内流速,进而确定管内流量,测定卡门涡街脱落频率的方法有热敏电阻丝法,超声波束法等。
二、卡门涡街作用力对卡门涡街的研究尚发现,由于柱面上的涡以一定的频率交替脱落,因而柱面压力和切向力也以相同的频率发生规则的变化,产生交变的横向力,横向力的方向总是指向刚脱落旋涡的那一侧面。
这是由于刚脱落完旋涡绕流得以改善的柱面与准备脱落涡的柱面压力分布不同(见图6-12),前者无因次压强系数明显小于后者,尤其在小于亚临界雷诺数时,垂直于来流方向的横向变力比来流方向的横向交变力要大得多,后者可不考虑。
因此这个垂直来流方向的横向交变力可按下式计算t A V C F k k ωρsin 22∞= (3)式中F k ——卡门涡街作用力;C k ——卡门作用力系数,当Re=102~107时,C k =1; A ——圆柱投影面积;ω——圆频率,由卡门涡街脱落频率决定,ω=2πf ; t ——时间。
如果这个施加在圆柱(管)上的横向交变力与圆柱(管)的固有频率相等,就会引起柱(管)的共振,使其振幅越来越大直至破坏。
1940年华盛顿州的塔可马吊桥被风吹毁就是这个原因。
三、卡门涡街声振在日常生活中,常听到风吹输电线嘘嘘发响的呜叫声,这种呜响也是由于卡门涡街的交替脱落引起空气中压强脉动所造成的声波。
在工程设备中(例如管式空气预热器),空气横向绕流管束,卡门涡街的交替脱落会引起管箱中气柱的振动。
特别是当旋涡脱落频率与管箱中的声学驻波振动频率相等时,便会发生声学共振现象,产生严重的噪声,并使器壁在脉动压力作用下弯曲变形,甚至振裂。
最严重的情况是气室的声学驻波振动频率、管束的固有频率、卡门涡街的脱落频率三者相合时,将造成设备的严重破坏。
通常,消除声学共振破坏的措施是提高设备气室的声学驻波频率,也就是顺着流体流动的方向加若干块隔板,将设备气室的横向尺寸分隔成若干段,提高其声学共振频率,使之与卡门涡街的声振频率错开。
这种简单的方法实践证明是行之有效的,但具体做时要通过试验及必要的计算来解决。
上述讨论的着眼点是流体绕流单根圆柱(管)的情况,实际工程设备中都是排列有序的管排,这种情况下的卡门涡街脱落过程将更复杂,与管子排列方式密切相关。
参见曲线图9-7,可根据管束的排列方式查取St数,然后计算卡门涡街的脱落频率。
§9-3 球形物体的自由悬浮速度下面研究圆球在静止流体中的运动情况。
圆球在静止流体中由静止开始自由下落,由于重力作用而逐渐加速,同时阻力也随之加大,当圆球的重量等于作用在圆球上流体的浮力与阻力之和时,即满足:W =F B +F D圆球在流体中以等速V f 自由降落(类似跳降落伞,主要是压差阻力),临界速度V f 又称为圆球的自由降落速度。
