七年级数学上册第一章《基本的几何图形》知识点
七年级上册数学几何图形初步知识点梳理+例题详解
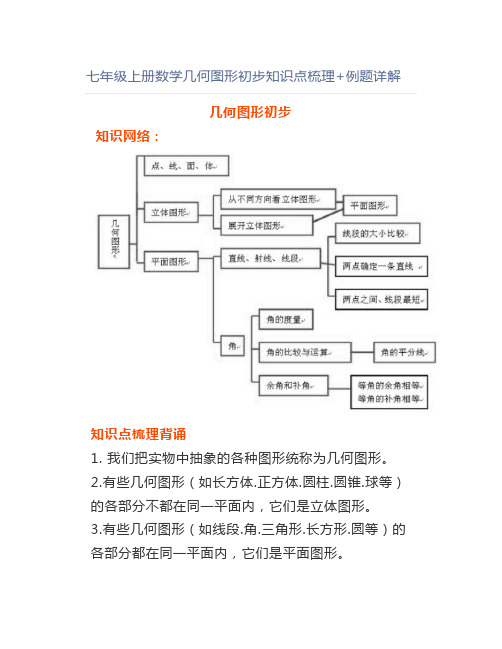
七年级上册数学几何图形初步知识点梳理+例题详解几何图形初步知识网络：知识点梳理背诵1. 我们把实物中抽象的各种图形统称为几何图形。
2.有些几何图形（如长方体.正方体.圆柱.圆锥.球等）的各部分不都在同一平面内，它们是立体图形。
3.有些几何图形（如线段.角.三角形.长方形.圆等）的各部分都在同一平面内，它们是平面图形。
4.将由平面图形围成的立体图形表面适当剪开，可以展开成平面图形，这样的平面图形称为相应立体图形的展开图。
5.几何体简称为体。
6.包围着体的是面，面有平的面和曲的面两种。
7.面与面相交的地方形成线，线和线相交的地方是点。
8.点动成面，面动成线，线动成体。
9.经过探究可以得到一个基本事实：经过两点有一条直线，并且只有一条直线。
简述为：两点确定一条直线（公理）。
10.当两条不同的直线有一个公共点时，我们就称这两条直线相交，这个公共点叫做它们的交点。
11.点M把线段AB分成相等的两条线段AM和MB，点M叫做线段AB的中点。
12.经过比较，我们可以得到一个关于线段的基本事实：两点的所有连线中，线段最短。
简单说成：两点之间，线段最短。
（公理）13.连接两点间的线段的长度，叫做这两点的距离。
14.角∠也是一种基本的几何图形。
15.把一个周角360等分，每一份就是1度的角，记作1°；把一度的角60等分，每一份叫做1分的角，记作1′；把1分的角60等分，每一份叫做1秒的角，记作1″。
16.从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线。
17.如果两个角的和等于90°（直角），就是说这两个叫互为余角，即其中的每一个角是另一个角的余角。
18.如果两个角的和等于180°（平角），就说这两个角互为补角，即其中一个角是另一个角的补角。
19.等角的补角相等，等角的余角相等。
例题精讲。
七年级一单元图形知识点
七年级一单元图形知识点一、点、线、面概念在几何学中，点是没有大小的点，线是由点组成的，它没有厚度和宽度，线段是有两个端点的线，它有一定的长度；面是有长度和宽度的，它由无数的点和线构成。
二、平面和立体图形平面是只有长度和宽度的图形，如正方形、三角形等；立体图形是有长度、宽度和高度的图形，如立方体、正方体等。
三、基本图形的特征及名称1.正方形正方形是四个边长相等、四个角都是直角的四边形。
2.长方形长方形是两个相对的边长度相等的四边形，对角线相等。
3.三角形三角形是有三条边和三个角的图形，分为等边三角形、等腰三角形、直角三角形、普通三角形等。
4.梯形梯形是有两个平行边的四边形。
5.圆形圆形是由半径相等的所有点组成的图形。
四、图形的面积和周长如果我们想了解图形的大小，我们可以计算它的面积和周长。
1.计算面积计算平面图形面积时，我们要用到不同的公式：正方形：面积=边长×边长长方形：面积=长×宽三角形：面积=(底边×高)/2梯形：面积=(上底+下底)×高/2圆形：面积=π×半径×半径2.计算周长周长表示图形全部边的长度之和，因此对于不同的图形，周长的计算公式也不同。
正方形：周长=4×边长长方形：周长=2×(长+宽)三角形：周长=三条边的长度之和梯形：周长=四边长度之和圆形：周长=2×π×半径五、图形的相似和全等1.相似两个图形被称为相似，当且仅当它们形状相同但大小不同，且对应边的比例相同。
2.全等两个图形被称为全等，当且仅当它们形状相同且对应边长相等。
六、常见图形的应用1.使用长方形计算面积和周长长方形被广泛应用于生活中的各种场合，特别是建筑和制造业。
我们可以通过计算长方形的面积和周长来确定物体的大小和形状。
2.使用圆形计算面积和周长圆形也是广泛应用于生活中的图形，比如轮胎、饼干和钟表等。
我们可以通过计算圆形的面积和周长来确定物体的大小和形状。
七年级数学知识点几何图形
七年级数学知识点几何图形七年级数学知识点：几何图形几何图形是数学中非常重要的一部分，它是数学中的一种实物描述形式。
七年级学生首先学习的是基本的几何图形，如圆形、正方形、矩形、三角形和梯形等。
本文将介绍七年级数学知识点中的几何图形，以帮助学生更好地掌握这些知识点。
圆形圆形是一个非常简单的几何图形，它的特点是所有点到圆心的距离都相等。
圆形的面积公式为πr²，其中π≈3.14，r是圆的半径。
圆形的周长公式为2πr。
正方形正方形是四边相等、四个角都为直角的四边形。
正方形的面积公式为a²，其中a表示正方形的边长。
正方形的周长公式为4a。
矩形矩形是四边都有两条相对边相等的四边形。
矩形的面积公式为lw，其中l表示矩形的长度，w表示矩形的宽度。
矩形的周长公式为2(l+w)。
三角形三角形是一个有三个内角的几何图形。
三角形的面积公式为½bh，其中b表示三角形底边的长度，h表示三角形高的长度。
三角形的周长需要根据三角形类型来计算。
梯形梯形是一个有四边的几何图形，且有两条相对边是平行的。
梯形的面积公式为½(a+b)h，其中a、b分别是梯形的两边长度，h表示梯形的高。
梯形的周长需要根据梯形类型来计算。
除了上述基本图形，七年级还会学习到一些其他的几何图形，比如平行四边形、菱形、正六边形等。
这些图形的面积和周长公式都有一些特别之处，在学习的时候需要注意。
总结：几何图形是数学中的一个重要部分，学生需要掌握基本几何图形的面积和周长计算方法。
在学习的过程中，需要多做几何练习，加深对这些几何图形的理解。
只有掌握了几何图形的基本知识点，才能在数学学习中更加得心应手。
人教版七年级数学上册 几何图形初步 知识点归纳
4.1几何图形知识点归纳从实物中抽象出来的各种图形叫做几何图形。
几何图形包括立体几何图形和平面几何图形。
各部分不都在同一平面内的几何图形叫做立体几何图形。
认识立体几何图形：长方体正方体球圆柱圆锥三棱柱三棱锥上下底面的形状大小相同且互相平行，侧棱平行且相等的封闭几何体叫做棱柱。
在棱柱中：①互相平行的两个面叫做棱柱的底面，其它面都是棱柱的侧面。
②两个面的公共边叫做棱柱的棱，两个相邻侧面的公共边叫做棱柱的侧棱。
③侧面与两个底面的公共顶点叫做棱柱的顶点。
④两个底面之间的距离叫做棱柱的高。
如果一个棱柱的底面是n边形，那么这个棱柱叫做n棱柱。
有一个面是多边形，其它面都是三角形且有一个公共顶点，这样的封闭几何体叫做棱锥。
在棱锥中：①形状是多边形的那个面叫做棱锥的底面，其它面都是棱锥的侧面。
②两个面的公共边叫做棱锥的棱，两个相邻侧面的公共边叫做棱锥的侧棱。
③相邻两个面的公共顶点叫做棱锥的顶点。
*在口头表述中，有时候说棱锥的顶点，可能指的是各个侧面的公共点。
下面④所说的顶点就是这个点。
④顶点到底面的距离叫做棱锥的高。
如果一个棱锥的底面是n边形，那么这个棱柱叫做n棱锥。
各部分都在同一平面内的几何图形叫做平面几何图形。
认识平面几何图形：线段角三角形长方形正方形平行四边形圆平面几何图形和立体几何图形是互相联系的，立体几何图形中的一部分可能是平面几何图形。
例子：圆柱的上底和下底都是圆，长方体的侧面可能是长方形，正方体的每个面都是正方形。
要观察立体几何图形，我们一般可以从三个方向来看：从正面看、从左面看、从上面看。
有一些立体几何图形是由一些平面几何图形围成的，如果将它们的表面用适当的方法剪开，就可以展开成平面几何图形。
这样的平面几何图形就是它们对应的立体几何图形的展开图。
几何体可以简称为体，包围着体的是面，面面相交的地方是线，线线相交的地方是点。
点动成线，线动成面，面动成体。
几何图形都是由点、线、面、体组合而构成的。
其中点是构成几何图形的基本元素。
初一(七年级)上册数学几何图形初步知识点总结
初一(七年级)上册数学几何图形初步知识点总结除了课堂上的学习外,数学知识点也是学生提高数学成绩的重要途径，本文为大家提供了初一(七年级)上册数学几何图形初步知识点总结，希望对大家的学习有一定帮助。
五、知识点、概念总结1.几何图形：点、线、面、体这些可帮助人们有效的刻画错综复杂的世界，它们都称为几何图形。
从实物中抽象出的各种图形统称为几何图形。
有些几何图形的各部分不在同一平面内，叫做立体图形。
有些几何图形的各部分都在同一平面内，叫做平面图形。
虽然立体图形与平面图形是两类不同的几何图形，但它们是互相联系的。
2.几何图形的分类：几何图形一般分为立体图形和平面图形。
13.角的种类：角的大小与边的长短没有关系;角的大小决定于角的两条边张开的程度，张开的越大，角就越大，相反，张开的越小，角则越小。
在动态定义中，取决于旋转的方向与角度。
角可以分为锐角、直角、钝角、平角、周角、负角、正角、优角、劣角、0角这10种。
以度、分、秒为单位的角的度量制称为角度制。
此外，还有密位制、弧度制等。
锐角：大于0，小于90的角叫做锐角。
直角：等于90的角叫做直角。
钝角：大于90而小于180的角叫做钝角。
平角：等于180的角叫做平角。
优角：大于180小于360叫优角。
劣角：大于0小于180叫做劣角，锐角、直角、钝角都是劣角。
周角：等于360的角叫做周角。
负角：按照顺时针方向旋转而成的角叫做负角。
正角：逆时针旋转的角为正角。
0角：等于零度的角。
余角和补角：两角之和为90则两角互为余角，两角之和为180则两角互为补角。
等角的余角相等，等角的补角相等。
对顶角：两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线，这样的两个角叫做互为对顶角。
两条直线相交，构成两对对顶角。
互为对顶角的两个角相等。
还有许多种角的关系，如内错角，同位角，同旁内角(三线八角中，主要用来判断平行)!14.几何图形分类(1)立体几何图形可以分为以下几类：第一类：柱体;包括：圆柱和棱柱，棱柱又可分为直棱柱和斜棱柱，棱柱体按底面边数的多少又可分为三棱柱、四棱柱、N棱柱;棱柱体积统一等于底面面积乘以高，即V=SH，第二类：锥体;包括：圆锥体和棱锥体，棱锥分为三棱锥、四棱锥以及N棱锥;棱锥体积统一为V=SH/3，第三类：球体;此分类只包含球一种几何体，体积公式V=4R3/3，其他不常用分类：圆台、棱台、球冠等很少接触到。
七年级数学上册几何知识总结
七年级上册几何知识总结一、知识清单 1、【立体图形与平面图形】(1)、把 的各种图形统称为几何图形。
几何图形包括立体图形和平面图形。
各部分不都在同一平面内的图形是 图形；如 各部分都在同一平面内的图形是 图形。
如 ▲会画出同一个物体从不同方向（正面、上面、侧面）看得的平面图形（视图）[1]. ▲知道并会画出常见几何体的表面展开图.(2)、点、线、面、体组成几何图形，点是构成图形的 基本元素。
点、线、面、体之间有如图所示的联系：▲ 知道由常见平面图形经过旋转所得的几何体的形状。
2、【直线、射线、线段】、(1)直线公理：经过两点有一条直线， 一条直线。
简述)为： .·两条不同的直线有一个 时，就称两条直线相交， 这个公共点叫它们的 。
·射线和线段都是直线的一部分。
(2)、直线、射线、线段的记法【如下表示】 (3)、线段的中点——把一条线段分成相等的两条线段的点，叫做线段的中点。
·如图，点M 是线段AB 的中点，则有AM=MB=21AB 或 2AM=2MB=AB用符号语言表示就是： ∵点M 是线段AB 的中点∴AM=MB=21( 或 AM=2 =AB)类似的，把线段分成相等的三条线段的点，叫线段的三等分点。
把线段分成相等的n 条线段的点，叫线段的n 等分点。
(4)、线段公理：两点的所有连线中，线段最短。
简述为： 之间， 最短。
·两点之间的距离的定义：连接两点之间的 ，叫做这两点的距离。
▲会结合图形比较线段的大小；会画线段的“和”“差”图[2]。
▲会根据几何作图语句画出符合条件的图形[3]，会用几何语句描述一个图形。
名称 表示法作法叙述 端点 直线 直线AB （BA ） （字母无序） 过A 点或B 点作直线AB 无端点 射线 射线AB （字母有序） 以A 为端点作 射线AB 一个 线段线段AB （BA ）（字母无序）连接AB两个点 线 面点 体点 动 交 交 交 动 动 图形语言3、【角】的定义(从构成上看)Ⅰ: 有 的两条 组成的图形叫做角。
七年级数学上册知识点归纳
初一数学上册总复习第一章基本的几何图形一、几何图形几何图形: 点、线、面、体以及他们的组合都是几何图形。
几何图形包括平面图形和立体图形平面图形:所有点都在同一平面内。
立体图形:所有点不都在同一平面内.⑴点动成线，线动成面，面动成体。
（体是由面围成的；面有平面和曲面）⑵线与线相交（点）面与面相交（线）棱顶点它们的面都是平的，像这样的几何体，也称多面体N棱柱面数棱数顶点数N棱锥面数棱数顶点数点是组成几何图形的基本元素，数学上所说的点是没有大小的.正方体展开图知识点（1）立方体的展开过程需要剪七刀,同一正方体有多种平面展开图.（2）相对面规律：隔面有面是对面，隔面无面就拐弯（3）不能围成正方体的情况：整体没有“田”字、“凹”字和“7”字正方体的平面展开图类型共有四大类（11种）：“一四一型”“二三一型”“二二二型”“三三型”二、线段、射线、直线1、直线的基本性质：两点确定一条直线线段、射线和直线用两个大写英文字母表示线段、射线和直线用一个小写字母表示。
直线的性质：经过两点有且只有一条直线。
两点之间，线段最短。
平面上的n条直线，最多有n(n-1)/2 个交点；直线a上有n个点最多表示出条n(n-1)/2线段2n-2条射线.类型端点数延伸度量直线无端点向两个方向无限延伸不可度量射线1个向一个方向无限延伸不可度量线段2个不向任何方向延伸可度量两点之间连线的长度，叫做这两点的距离。
中点:若点M把线段AB分成相等的两条线段AM与BM，那么点M叫做线段AB的中点。
AM=BM=1/2AB 类似还有三等分点、四等分点等线段的大小比较方法有：①测量法②叠合法③截取法（圆规）线段及线段和差的画法：（尺规作图）递推①五个人若其中每两个人都握一次手，他们总共握多少次手？②往返于甲、乙两地的火车中途要停靠三个站，则有（）种不同的票价（来回票价一样），需准备（）种车票．线段中点的概念非常重要，应学会用符号语言表述，并会应用线段中点的性质进行有关线段的计算. 运用了数形结合和整体代换的思想方法，解题中注意线段中点性质的应用。
青岛版七年级数学上册第一章 基本的几何图形课件(62张PPT)
D
直线相交；这时两条直线有唯一的公共点， A
这个公共点叫做它们的交点。
O B
C
如图，直线AB与直线CD相交，点O是 想一想，平面上的两条直线除相交外， 它们的交点。 还有其他位置关系吗？
平面上的两条直线，有相交与不相交两种位置关系
思考
（1)两条直线相交，能不能有两个交点？为什么？
（2）平面上的2条直线，最多有1个交点；3条直线，最 多有3个交点；平面上有4条直线，最多有几个交点？
• 如果一个几何图形上的所有点都在同一平面内，那么这样的几 何图形叫做平面图形。
（1）这个正方体是由几个面围成的？各个面的形状是 怎样的平面图形？这些图形的大小和形状都相同吗？ （2）正方体有几条棱？几个顶点？这些棱的长短都一 样吗？ （3）正方体的每个顶点处各有几条棱？它们都在同一 平面上吗？ （4）从一个顶点出发，沿它的一些棱剪开，使其平铺 在同一平面上，你能找出多少种可能？请分别画出来。
DCB
FE
• 小林同学在一个正方体盒子的每个面上都写了一个字，分别是：我、喜、欢、数、学、课，其表面展开图 如图所示，那么在该正方体盒子中，和“课”相对的面上所写的字是“（ ）”．
下边的4个图形中，哪一个是由左边的盒子展开而成的。
（A〕
（B） （C）
（D）
A
A
思考题
挑战自我
（1）用剪刀将一张正方形的纸片剪去一个角，还剩几个 角？剪一刀后，能使纸上剩六个角吗？试一试。
B
D C
1.4 线段的比较与做法
你
这两条线段那条比较长？
如何比较线段的长短？
如何比较线段AB与线段CD的长短？
A
B
C
D
叠合
借助圆规
青岛版七年级上册数学学科素养解读课件：第1章 基本的几何图形
知识点 几何图形
1.图形的分割问题; 2.图形的组合问题; 3.图形的绘制问题.
知识点 几何图形的形成
下雨了,开始落下的雨滴给我们一个点的形象,接着连续 落下的雨滴就成了一条线,然后无数的雨滴连续落下,直 接形成雨幕(面),阻挡了我们的视线.
知识点 平面图形与立体图形
立体图形的侧面可以是平面,也可以是曲面,由此可区分 圆锥和棱锥.
知识点 直线
1.建筑工人砌墙;
知识点 直线
2.木工取直;
知识点 直线
3.植树问题.
知识点 点与直线
汽车在笔直的公路上行驶,远远望去,就是一个点在一条 直线上移动.
知识点 点与直线
1.公路的建设问题; 2.车辆的行驶问题.
第1章基本的几何图形
1.4 线段的比较与作法
知识点 线段长度的比较
知识点 线段的中点
1.线段的度量与计算问题; 2.绘图问题.
水杯
楼房
香蕉路障
魔方
知识点 数学上所说的平面
从太空中拍摄的地球图片中,可以看出地球是由 一个曲面围成的美丽的球体
知识点 数学上所说的平面
数学中所说的平面具有无限的延展性,实际生活 中遇到的面均是数学中所说的面的一个部分.
第1章基本的几何图形
1.2 几何图形
知识点 几何图形
我们使用的数学教材就是一个长方体的实例,它 的一个封面和一个侧面就相交于一条线(棱),同一 个面上相邻的两条棱就相交于一个点.
第1章基本的几何图形
1.3 线段、射线和直线
知识点 线段
一支铅笔,一条绷直的皮筋都是线段的一种实例.
斑马线两端不可延伸都有端点,可以看成线段
知识点 线段
线段一定是“直”的.
七年级数学上册 第一章《基本的几何图形》 知识点
第一章 基本的几何图形复习范围：基本的几何图形知识点回顾：知识点一：几何体的认识1.我们常见的几何体有：正方体 、长方体、圆锥、圆柱、棱柱、棱台、棱锥、球，其中____________属于柱体， _________属于锥体。
2. 像棱台、棱锥的都是______的，这样的几何体也称多面体．同步测试：1．下列判断正确的有（ ）①长方体是棱柱，正方体不是长方体②正方体是棱柱，长方体也是棱柱③正方体是柱体，圆柱也是柱体④正方体不是柱体，圆柱是柱体Ａ．个 Ｂ．个 Ｃ．个 Ｄ．个2．下列几何体不属于柱体的有（ ）A．正方体 B．长方体 C．圆锥 D．圆柱知识点二： 几何体的展开与平面图形的折叠：1．数学上所说的平面没有边界，可以向四面八方无限_________. 2．三角形、正方形、长方形、平行四边形、梯形、圆等都是__________.同步测试：1．下列图形折叠后的几何体是五棱柱的是（ ）A． B． C． D．2．下列图形是四棱柱的展开图的是（ ）A． B． C． D．知识点三：几何体的基本要素：点、线、面、体1. 天上一颗颗闪烁的星星给我们以“______”的形象；划过夜空的流星给我们以“_________”的形象；打开的折扇给我们以“__________”的形象；宾馆里旋转的大门给我们以“___________”的形象.几何图形是由_____、______、______、______组成的.2．一个立方体共有______个面，______条棱，______个顶点．同步测试：1.将三角形绕直线l旋转一周，可以得到图1所示的立体图形的是（ ）.A． B． C． D．图12．五棱柱的棱数和侧面数分别是（ ）A．5，5 B．15，5 C．10，7 D．5，7知识点四：线段、直线、射线1. “拔河时，拉直的绳子给我们以________的形象.”把线段向两方无限延伸，就得到________；将线段向一个方向无限延伸就形成了__________；射线有____个端点，线段有____个端点，而直线________端点．2. 线段、直线、射线都可以用两个大写的字母或一个小写的字母表示，而表示射线时表示端点的大写字母必须写在________．同步测试：1.下列说法中，错误的是（ ）．A．经过一点的直线可以有无数条 B．经过两点的直线只有一条C．一条直线只能用一个字母表示 D．线段CD和线段DC是同一条线段2. 下列图形中，能够相交的是( )．知识点四：线段的基本性质，线段的度量与比较1. 经过一点可以画______条直线，经过两点能且只能画_______条直线，也就是说_______确定一条直线.如果两条直线经过同一个点，那么这两条直线________，这个点叫做这两条直线的________.2.两点之间的所有连线中，_______最短；两点之间的线段的长度叫做这两点之间的________.3.如图2，如果点M把线段AB分成相等的两条线段AM与BM，那么点M叫做这条线段AB的________，记作AM = BM = AB.ABM图2同步测试：1. 如图3,小华的家在A处，书店在B处，星期日小明到书店去买书，他想尽快的赶到书店，请你帮助他选择一条最近的路线（ ）．A．A→C→D→B B．A→C→F→BC．A→C→E→F→B D． A→C→M→B图3图42. 如图4所示，线段AB的长为8cm，点C为线段AB上任意一点，若M为线段AC的中点，N为线段CB的中点，则线段MN的长是_______________．3．已知点A、B、C都是直线l上的点，且AB=5cm，BC=3cm，那么点A与点C之间的距离是（ ）.A．8cm B．2cm C．8cm或2cm D．4cm例题讲解：例1. 下列几何体中是圆柱的为（ ）. 析解：解决本题的关键是根据图形特征，区分三棱锥与圆锥、四棱锥、五棱锥，可从底面的形状入手进行判断。
七年级上册几何初步知识点
七年级上册几何初步知识点几何是数学的一个分支，是研究空间形状、大小、位置、变形等问题的数学学科。
在初中阶段，几何学习是数学教育中的重要部分，也是学生数学素养的基础。
本文旨在介绍七年级上册几何初步知识点，供学生参考。
一、平面图形的认识1.1 点、线、面的基本概念点是几何中最简单的基本概念，用“A”、“B”、“C”等字母表示。
线是由无数个点组成的，在几何中用一条直线表示，如“AB”表示以点A、B为端点的直线。
面是由无数个线组成的，通常表示为一个不闭合的图形，如三角形、矩形等。
1.2 三角形、四边形、多边形三角形是由三个顶点和三条边组成的平面图形，可以分为等腰三角形、等边三角形、直角三角形等。
四边形是由四个顶点和四条边组成的平面图形，可以分为矩形、正方形、菱形等。
多边形是由多个顶点和边组成的平面图形，根据边数可以分为五边形、六边形等。
多边形可以分为凸多边形和凹多边形，凸多边形的内角和总和为180度以下，而凹多边形的内角和总和为180度以上。
二、平面图形的性质2.1 角的概念角是由两条射线共同起点按一定方向转动形成的图形。
一个角包含两个部分，即顶点和两条边。
角可以分为锐角、直角、钝角等。
2.2 直线、线段和射线的定义及其性质直线是不断延伸而不断接近的线，没有两个端点。
线段是由两个端点和这两个端点之间的线段组成的线。
射线是由一个端点和一个方向组成的线段。
直线图形具有平移不变性、旋转不变性、翻转不变性等特点。
线段与射线也具有相似的性质。
2.3 物体的转动物体的转动分为旋转和翻折。
旋转是指物体绕一个固定点旋转，可以分为顺时针旋转和逆时针旋转。
翻折是指物体沿一个平面反转，可以分为对称轴翻折和不对称轴翻折。
三、坐标系和图形的位置关系3.1 直角坐标系直角坐标系是由x轴和y轴两条互相垂直的直线组成的平面，用来表示平面内的点的位置关系。
坐标系原点是两条直线的交点。
3.2 图形的位置关系在直角坐标系中，通过比较两个平面图形各点的坐标，可以判断它们的位置关系。
青岛版七年级上册数学第一章基本的几何图形知识点梳理
第一章基本的几何图形1.1我们身边的图形世界1．体的概念如果对于我们看到的物体，只研究它们的形状、大小和位置关系，而不考虑颜色、质量、原料等其他性质时，就得到各种几何体，几何体简称体。
平面与曲面平面：平的面，（1）没有厚薄，（2）没有边界，（3）向四周无限延展。
曲面：曲的面2.几何体的分类常见的几何体通常分为三类：柱体，锥体和球体。
柱体包括圆柱和棱柱，结构特征是上下底面是两个平行且形状相同，大小相等的面，圆柱的底面是圆，棱柱的底面是多边形。
锥体包括圆锥和棱锥，圆锥的底面是圆，底面是多边形。
3.体与面的关系体是由面围成的。
包括只含有平面的几何体（如长方体，正方体等棱柱，棱锥）与只含有曲面的几何体（如球），既含有平面又含有曲面的几何体，（如圆柱，圆锥）习题：1.说出下列几何体的名称：（1）2.下列实物形状类似于哪种几何体？茶叶桶——（），蛋糕帽——（），足球——（），漏斗——（）3.圆柱由几个面组成？有几个曲面？有几个平面？4.圆锥由几个面组成？有几个曲面？有几个平面？1.2几何图形1.几何图形：点、线、面、体以及它们的组合都是几何图形。
2.点：线与线的交接处是点，点是组成几何图形的基本元素。
在长方体或正方体中，棱与棱的公共点叫做长方体或正方体的顶点。
3.线：一般地，两个面的交接处是一条线，线可以是直的，也可以是曲的。
（1）长方体和正方体中，相邻两个面的交接处是一段直的线，叫做棱。
（2）圆柱和圆锥中，侧面与底面的交接处都是圆，圆是一条封闭的曲线。
4.在数学上，点无大小，线无粗细，面无厚薄。
5.点、线、面、体之间的关系:点动成线，线动成面，面动成体。
6.几何图形的分类：平面图形与立体图形（1）立体图形：如果一个几何图形上的点不都在同一平面内，那么这样的几何图形叫做立体图形（2）平面图形：如果一个几何图形上所有的点都在同一个正方体的表面展开图：11种（1）一四一型：中间四连方，两侧各一个共6种（2）二三一型：中间三连方，二一两侧放共3种（3）二二二型：中间二连方，台阶逐级上共1种（4）三三型：两排三连方，一日放光芒共1种8.正方体表面展开图折成正方体时，相对的面有以下规律：“隔一相对法”（1）若正方体中相对的两个面在展开图的同行或同列中，则它们中间一定隔着一个正方形；（2）若展开图中正方形A在同行或同列中隔正方形C 的位置是空白的，则与该空白位置相邻的正方形B与正方形A是相对面习题：1.正方体有几个面？几个顶点？几条棱？2.五棱柱有几个面？几个顶点？几条棱？3.流星划过夜空留下的痕迹可用什么定理解释？风扇旋转的过程运用什么定理解释？硬币在桌面快速旋转，形成一个球的印象，运用了什么定理？4.正方体的平面展开图都分几种类型？5.找出下列正方体平面展开图的对立面？1.3线段、射线和直线1.线段（1）特征：①有两个端点；②有长短（即可度量）；③无方向(2)表示方法：①用表示线段端点的两个大写字母表示，如线段AB或线段BA（字母无序）②用一个小写字母表示，如线段a2.射线：将线段向一个方向无限延伸就得到射线（1）特征：①有一个端点；②无长短（即可度量）；③有方向（只向一个方向无限延伸）(2)表示方法：①用两个大写字母表示，第一个字母表示射线的端点，第二个字母是射线上任意一点，与字母排序有关②用一个小写字母表示，如射线a3.直线：将线段向两个方向无限延伸就得到直线（1）特征：①无端点；②无长短（即可度量）；③无方向(2)表示方法：①用直线上任意两个点的大写字母表示，与字母排序无关②用一个小写字母表示，如直线a4.直线、射线、与线段的关系：射线、线段都是直线的一部分，线段向一个方向无限延伸就得到射线，向两个方向无限延伸就得到直线5.点与直线的位置关系：（1）点在直线上（或直线经过点）；（2）点在直线外（或直线不经过点）6.直线的确定：两点确定一条直线7.两条直线的关系：平面上的两条直线有相交（有一个交点）与不相交（无交点）两种位置关系如果两条直线经过同一个点，就称这两条直线相交。
青岛版七年级数学上册知识点总汇
第一章基本的几何图形1.2 几何图形一、几何图形现实生活中的物体我们只管它的形态、大小、位置而得到的图形，叫做几何图形。
1.基本元素：点、线、面、体。
⑪点动成线，线动成面，面动成体。
（体是由面围成的，很多立体图形是由一些平面图形围成的，将它们适当地剪开，就可以绽开成平面图形。
面有平面和曲面）（举例）笔写字、汽车在雨中行驶,雨刷器来回摇摆成面、硬币旋转会产生一个圆球。
⑫线与线相交（点）面与面相交（线）棱顶点（长方体，正方体）2. 分类长方体、正方体、球、圆柱、圆锥等都是立体图形。
此外棱柱、棱锥也是常见的立体图形。
长方形、正方形、三角形、圆等都是平面图形。
几何图形有平面图形和立体图形（两者之间的转化）几何体：①柱体（圆柱和棱柱）②锥体（圆锥和棱锥）③球④台体3.正方体的平面绽开图有“11种”（至少剪7条棱正方体展成平面图形）考点：1.识别常见的几何体1.在六角螺母、乒乓球、圆形烟囱、书本、热水瓶胆等物体中，形态类似于棱州钦丽美 爱我柱的有___1__个，球体有____1_个。
2.圆锥由__2__个面围成，其中__1____个平面，__1___个曲面．3．写出你所熟识的、由三个面围成的几何体的名称是 圆柱4.六棱柱由几个面围成（ C ）A.6个B.7个C.8个D.9个5.下列平面绽开图是由5个大小相同的正方形组成，其中沿正方形的边不能折成无盖小方盒的是（B ）6.一个正方体的每个面都有一个汉字，其平面绽开图如图所示，则该正方体中与“美”字相对的面上的字是7.如图，各图中的阴影图形围着直线旋转360度，各能形成怎样的立体图形。
8.图甲能围成 圆锥 ；图乙能围成 三棱锥 ；图丙能围成 长方体 。
A B C D 丙甲乙1.3 线段、射线、直线线段有两个端点。
将线段向一个方向无限延长就得到射线，射线有一个端点。
将线段向两个方向无限延长就得到线段，线段有两个端点。
1.线段、射线、直线的区分和联系.留意：线段、射线、直线的表示方法，要会画图形。
七年级上第一章数学知识点
七年级上第一章数学知识点作为初中数学的第一章，七年级上数学课程涉及到了不少基础知识。
在这个章节中，将会涵盖几何、代数以及统计学的内容。
本文将带领大家一一了解这些知识点。
一、几何1. 平面几何平面几何是数学中的一个分支，主要研究2D图形和其性质。
在初中数学中，我们学习了常见的几何图形：点、线段、射线、直线、角、三角形、四边形、圆等。
同时，我们也需要掌握这些图形的性质，如：线段的长度、角的度数、各种图形的周长和面积计算等。
2. 空间几何空间几何是平面几何的延伸，主要研究3D图形和其性质。
在初中数学中，我们需要学习常见的3D图形：球、立方体、正方体、棱柱、棱锥、圆锥等。
同时，我们也需要掌握这些图形的性质，如：体积、表面积计算等。
二、代数代数是数学中的另一个分支，主要研究数字和字母的关系，以及各种数学符号的运用。
在初中数学中，我们主要学习到了以下内容：1. 代数式的表示和运算代数式是指由数字、字母以及数学符号（如加减乘除、指数、括号等）组成的表达式。
我们需要学习如何表示代数式、如何进行代数式的加减乘除、如何进行代数式的化简、如何进行代数式的因式分解等。
2. 一元一次方程式一元一次方程式是代数中比较基础的概念，主要指由一个未知数和一个一次项组成的方程式。
我们需要学习如何解一元一次方程式，如何通过方程式求解未知数的值等。
三、统计学统计学是数学中的另一个重要分支，主要研究数据的收集、整理、分析以及处理。
在初中数学中，我们主要学习以下内容：1. 数据收集和整理数据收集和整理是进行统计分析的第一步，我们需要学习如何收集数据、如何整理数据。
2. 数据分析和展示在收集和整理数据之后，我们需要对数据进行分析和展示。
我们需要学习如何绘制各种图表，并进行相应的分析和解读。
以上就是初中数学七年级上第一章的主要内容，如有不足之处，还请多多指教。
初一(七年级)上册数学几何图形初步知识点总结
1.几何图形：点、线、面、体这些可帮助人们有效的刻画错综复杂的世界，它们都称为几何图形。
从实物中抽象出的各种图形统称为几何图形。
有些几何图形的各局部不在同一平面内，叫做立体图形。
有些几何图形的各局部都在同一平面内，叫做平面图形。
虽然立体图形与平面图形是两类不同的几何图形，但它们是互相联络的。
2.几何图形的分类：几何图形一般分为立体图形和平面图形。
3.直线：几何学根本概念，是点在空间内沿一样或相反方向运动的轨迹。
从平面解析几何的角度来看，平面上的直线就是由平面直角坐标系中的一个二元一次方程所表示的图形。
求两条直线的交点，只需把这两个二元一次方程联立求解，当这个联立方程组无解时，二直线平行;有无穷多解时，二直线重合;只有一解时，二直线相交于一点。
常用直线与X轴正向的夹角(叫直线的倾斜角)或该角的正切(称直线的斜率)来表示平面上直线(对于X轴)的倾斜程度。
4.射线：在欧几里德几何学中，直线上的一点和它一旁的局部所组成的图形称为射线或半直线。
5.线段：指一个或一个以上不同线素组成一段连续的或不连续的图线，如实线的线段或由“长划、短间隔、点、短间隔、点、短间隔〞组成的双点长划线的线段。
线段有如下性质：两点之间线段最短。
6. 两点间的间隔：连接两点间线段的长度叫做这两点间的间隔。
7. 端点：直线上两个点和它们之间的局部叫做线段，这两个点叫做线段的端点。
线段用表示它两个端点的字母或一个小写字母表示，有时这些字母也表示线段长度，记作线段AB或线段BA，线段a。
其中AB表示直线上的任意两点。
8.直线、射线、线段区别：直线没有间隔。
射线也没有间隔。
因为直线没有端点，射线只有一个端点，可以无限延长。
9.角：具有公共端点的两条不重合的射线组成的图形叫做角。
这个公共端点叫做角的顶点，这两条射线叫做角的两条边。
一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形叫做角。
所旋转射线的端点叫做角的顶点，开场位置的射线叫做角的始边，终止位置的射线叫做角的终边。
七年级第一章数学几何知识点整理
几何图形初步一、本节学习指导本节知识点比较简单，都是基础，当看书应该就能理解。
二、知识要点1、几何图形从实物中抽象出来的各种图形，包括立体图形和平面图形。
立体图形：有些几何图形的各个部分不都在同一平面内，它们是立体图形。
比如：正方体、长方体、圆柱等平面图形：有些几何图形的各个部分都在同一平面内，它们是平面图形。
比如：三角形、长方形、圆等2、点、线、面、体（1）几何图形的组成点：线和线相交的地方是点，它是几何图形中最基本的图形。
线：面和面相交的地方是线，分为直线和曲线。
面：包围着体的是面，分为平面和曲面。
体：几何体也简称体。
（2）点动成线，线动成面，面动成体。
3、生活中的立体图形4、棱柱及其有关概念：棱：在棱柱中，任何相邻两个面的交线，都叫做棱。
侧棱：相邻两个侧面的交线叫做侧棱。
n棱柱有两个底面，n个侧面，共（n+2）个面；3n条棱，n条侧棱；2n个顶点。
棱柱的所有侧棱长都相等，棱柱的上下两个底面是相同的多边形，直棱柱的侧面是长方形。
棱柱的侧面有可能是长方形，也有可能是平行四边形。
5、正方体的平面展开图：11种6、其他常见图形的平面展开图：侧面可以展开成长方形的是：圆柱和棱柱侧面可以展开为扇形的是：圆锥7 截一个正方体：用一个平面去截一个正方体，截出的面可能是三角形，四边形，五边形，六边形。
可能出现的：锐角三角型、等边、等腰三角形，正方形、矩形、非矩形的平行四边形、非等腰梯形、等腰梯形、五边形、六边形、正六边形不可能出现：钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形8.多边形：由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形，叫做多边形。
1.从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，可以把这个n边形分割成（n-2）个三角形。
2.若用f表示正多面体的面数，e表示棱数，v表示顶点数，则有：f+v-e=2 弧：圆上A、B两点之间的部分叫做弧。
扇形：由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形。
七年级数学上册几何初步知识点
七年级数学上册几何初步知识点本文将为七年级数学上册的同学们详细介绍几何初步知识点，帮助大家更好地理解和掌握几何知识。
一、点、线、面的基本概念1. 点：不占据空间，只有位置，用一个大写字母表示，如A、B、C等。
2. 线段：由两个端点和它们之间的所有点组成的有限线段，用两个字母表示，中间加一线，如AB、CD等。
3. 直线：有无限多个点，无限延伸的线段，用两个字母表示，不加线，如AB、CD等。
4. 射线：只有一个端点，另一侧无限延伸的线段，用一个字母表示，补上一个箭头表示方向，如AB→、CD→等。
5. 面：由三条或三条以上的线段围成的区域，用大写字母表示，如△ABC、△DEF等。
二、角的概念角是由两条射线共同确定一个平面角的部分，用A表示。
其中一个射线叫做这个角的始边，固定不动，另一个射线叫作这个角的终边，可以围绕始边旋转。
终边旋转的方向称为角的方向，以度数表示。
可以用直角、钝角、锐角来划分角的大小。
三、三角形和四边形的性质1. 三角形：是由三条线段围成的面，分为等边三角形、等腰三角形和普通三角形三种。
三角形的内角和为180度，可以用正弦、余弦和正切等来计算。
2. 四边形：是有四条线段围成的图形，分为平行四边形、矩形、正方形和菱形等。
四边形的内角和为360度，可以用直角边、对角线等来计算。
四、圆的概念圆是由一个固定点（圆心）和一个动点（圆周上任意一点）组成的动点轨迹，圆周上的任何一点到圆心的距离都相等。
圆周的长度称为周长，圆内部所占据的空间称为圆面积，可以用π来计算。
以上就是七年级数学上册几何初步知识点的详细介绍，同学们在学习几何的过程中，务必要掌握好这些基础知识，以便更好地应用于实际问题中。
希望本文能够对同学们的学习有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章基本的几何图形
知识点回顾：
知识点一：几何体的认识
1.我们常见的几何体有：正方体、长方体、圆锥、圆柱、棱柱、棱台、棱锥、球，其中____________属于柱体， _________属于锥体。
2. 像棱台、棱锥的都是______的，这样的几何体也称多面体．
同步测试：
1．下列判断正确的有（）
①长方体是棱柱，正方体不是长方体②正方体是棱柱，长方体也是棱柱
③正方体是柱体，圆柱也是柱体④正方体不是柱体，圆柱是柱体
Ａ．1个Ｂ．2个Ｃ．3个Ｄ．4个
2．下列几何体不属于柱体的有（）
A．正方体B．长方体C．圆锥D．圆柱
知识点二：几何体的展开与平面图形的折叠：
1．数学上所说的平面没有边界，可以向四面八方无限_________.
2．三角形、正方形、长方形、平行四边形、梯形、圆等都是__________.
同步测试：
1．下列图形折叠后的几何体是五棱柱的是（）
A．B．C．D．
2．下列图形是四棱柱的展开图的是（）
知识点三：几何体的基本要素：点、线、面、体
1. 天上一颗颗闪烁的星星给我们以“______”的形象；划过夜空的流星给我们以“_________”的形象；打开的折扇给我们以“__________”的形象；宾馆里旋转的大门给我们以“___________”的形象.几何图形是由_____、______、______、______组成的.
2．一个正方体共有______个面，______条棱，______个顶点．
同步测试：
1.将三角形绕直线l 旋转一周，可以得到图1所示的立体图形的是（ ）.
2．五棱柱的棱数和侧面数分别是（ ）
A ．5，5
B ．15，5
C ．10，7
D ．5，7
知识点四：线段、直线、射线
1. “拔河时，拉直的绳子给我们以________的形象.”把线段向两方无限延伸，就得到________；将线段向一个方向无限延伸就形成了__________；射线有____个端点，线段有____个端点，而直线________端点．
2. 线段、直线、射线都可以用两个大写的字母或一个小写的字母表示，而表示射线时表示端点的大写字母必须写在________．
同步测试：
1.下列说法中，错误的是（ ）．
A ．
B ．
C ．
D ．
图1 A ． B ． C ． D ．
A ．经过一点的直线可以有无数条
B ．经过两点的直线只有一条
C ．一条直线只能用一个字母表示
D ．线段CD 和线段DC 是同一条线段
2. 下列图形中，能够相交的是( )．
知识点四：线段的基本性质，线段的度量与比较
1. 经过一点可以画______条直线，经过两点能且只能画_______条直线，也就是说_______确定一条直线.如果两条直线经过同一个点，那么这两条直线________，这个点叫做这两条直线的________.
2. 两点之间的所有连线中，_______最短；两点之间的线段的长度叫做这两点之间的________.
3.如图2，如果点M 把线段AB 分成相等的两条线段AM 与BM ，那么点M 叫做这条线段AB 的________，记作AM = BM
= 21AB . 同步测试：
1. 如图3,小华的家在A 处，书店在B 处，星期日小明到书店去买书，
他想尽快的赶到书店，请你帮助他选择一条最近的路线（ ）．
A ．A →C →D →
B B ．A →
C →F →B
C ．A →C →E →F →B
D ． A →C →M →B
2. 如图4所示，线段AB 的长为8cm ，点C 为线段AB 上任意一点，若M 为线段AC 的中点，N 为线段CB 的中点，则线段MN 的长是_______________．
图4 图3 A B
M 图2
3．已知点A、B、C都是直线l上的点，且AB=5cm，BC=3cm，那么点A与点C之间的距离是（）. A．8cm B．2cm C．8cm或2cm D．4cm
例题讲解：
例1.下列几何体中是圆柱的为（）.
例2.下面4个图均由6个小正方形组成，若以每个小正方形为面，则可以折叠成正方体的是（）.
Ａ．Ｂ．Ｃ．Ｄ．例3．如图，直线a和射线OA能相交的是______？为什么？
例4.下列说法正确的是（）
A．线段AB和线段BA表示的是同一条线段；
B．射线AB和射线BA表示的是同一条射线；
C．直线AB和直线BA表示的是两条直线；
D．如右图5，点M在直线AB上，则点M在射线AB上．
随堂检测:
1.圆柱是由下列哪一种图形绕虚线旋转一周得到的（）
2.下面四个图形中，经过折叠能围成如图只有三个面上印有图案的正方体纸盒的是（）
3.下列四个生活、生产现象：①用两个钉子就可以把木条固定在墙上；②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；③从A地到B地架设电线，总是尽可能沿着线段AB架设；④把弯曲的公路改直，就能缩短路程，其中可用公理“两点之间，线段最短”
来解释的现象有( )
Ａ．①②Ｂ．①③Ｃ．②④Ｄ．③④
4.已知A、B、C是同一直线上的三个点，且AB=5cm，BC=4cm，，则AC的长为( ）
A.1cm
B.9cm
C.1cm或9cm
D.不能确定
5.观察下列图形，并阅读图形下面的相关文字：
两条直线相交，三条直线相交，四条直线相交，
最多有1个交点；最多有3个交点；最多有6个交点；……
像这样，十条直线相交，最多交点的个数是（）.
(A) 40 (B) 45 (C) 50 (D) 55
同步练习
1．正方形纸片绕它的一边旋转一周所得到的几何体是（）
A ．正方体
B ．圆锥
C ．圆柱
D ．球
2．如图7的几何体中，属于棱柱的有（ ）
A ．6个
B ．5个
C ．4人
D ．3个
3．圆柱是由下列哪一种图形绕虚线旋转一周得到的（ ）
4．下列平面图形中，不能折叠成几何体的是（ ）
5．下面的两个图形都是由两个圆、两个三角形、两条线段组合而成的.请你用两个圆、两个三角形、两条线段再设计出几幅新奇、有趣的图形，并给出文字说明.
6.
如下左图中共有_____条直线，_____条射线，______条线段．
B C A D
图7 A ． B ． C ． D ． 两盏电灯 两杯冰淇凌 A ． B ．
C ．
D ．
7.要在墙上固定一根直木条，至少要钉______个钉子
8. 如图，点C是线段AB内任意一点，M、N分别是线段AC、BC的中点，如果AB=8厘米，那么，
MN=_______厘米
.
那么有________种不同的票价．
10.如图8所示是一个几何体的展开图，每个面上都标有相应的字母．（1）如果A面有几何体的底部，上面的是哪一面？（2）若F面在前面，B面在左面，上面是哪一面？
（3）C面在右面，D面在后面，上面是哪一面？
图8
11. 已知线段AB=7cm，在直线AB上画线段BC=3cm，则线段AC=_______.
12.在同一条公路旁，住着五个人，他们在同一家公司上班，如图9,不妨设这五个人的家分别
住在点ABDEF位置，公司在C点，若AB=4km，BC=2km，CD=3km，DE=3km，EF=1km，他们全部乘出租车上班，车费单位报销．出租车收费标准是：起步价3元（3km以内，包括3km），以后每千米1.5元（不足1km，以1km计算），每辆车能容纳3人．
（1）若他们分别乘出租车去上班，公司在支付车费多少元？
（2）如果你是公司经理，你对他们有
没有什么建议？
图9。