哈工大电路理论基础课后习题答案9
哈工大电路理论基础课后习题答案1

i2 3A 0.5A 2.5A
节点②:
i1 i2 i3 2.5A 2A 4.5A
对回路 l 列 KVL 方程:
10 i2 5 3A u 8V
得
u 32V 电压源发出的功率
P US 8V i1 8V 4.5A 36W
得
u2 280V
网络 N 吸收的功率
PN uN 3A 30W
电流源发出的功率
P iS u2 5A 1400W
注释:根据电流源的特性, 图中与电流源串联的电阻只影响电流源端电压或者说 只影响电流源提供的功率。 答案 1.11 解:设各元件电压电流方向如图所示。
i2 3A 0.5A 2.5A
i2 8A 3A 1A 2A 4A
① 1A
A
⑤
i2
3A
8A
i1
i3 ④ ② i4
2A
B
③ (b)
答案 1.5 解:如下图所示
5V i1
②
l3 1A
①
2A
l1 l2
7V
1A
i4
⑤ 1A ③
6V
l4 8V
i2
④
i3
(1)由 KCL 方程得 节点①:
i1 2A 1A 3A
①
i1 10 + 5A 5 u2 l2 10V l1 -
3A
50
N
25V
对节点①列 KCL 方程
i1 5A 3A 2A
对回路列 KVL 方程 回路 l1 :
i1 10 3A 5 uN 25V 10V
哈工大数电课本课后习题答案

[00100011-00010010]补=[00100011]补+[-00010010]补=00010001=[00010001]补
00100011-00010010=00010001
(b) [00001100]补=00001100
[-00100000]补=11100000
[00001100-00100000]补=[00001100]补+[-00100000]补=11101100=[10010100]补
= AC + BC + AB
【3-12】解:
CD AB 00
CD AB 00 01 11 10
00
11 1
01 1 1 1 1
11 1 1
1
11 1 1
1
10 1 1 1 1
10 1 1 1 1
四种: F1 = AB + CD + AC + BD F2 = AB + CD + AD + BC
先画出 Y1 和 Y2 的卡诺图,根据与、或和异或运算规则直接画出 Y1 ⋅ Y2 ,Y1 + Y2 ,Y1 ⊕ Y2
的卡诺图,再化简得到它们的逻辑表达式:
CD AB 00 01 11 10
00
111
01
11
11 1 1 1 1
10
11
CD AB 00 01 11 10
00
11
01
1
11
1
10
111
00001100-00100000=10010100
(c) [01111100]补=01111100
[-01000011]补=10111101
[01111100-01000011]补=[01111100]补+[-01000011]补=00111001=[00111001]补
电路理论基础课后答案(哈工大陈希有)第9章
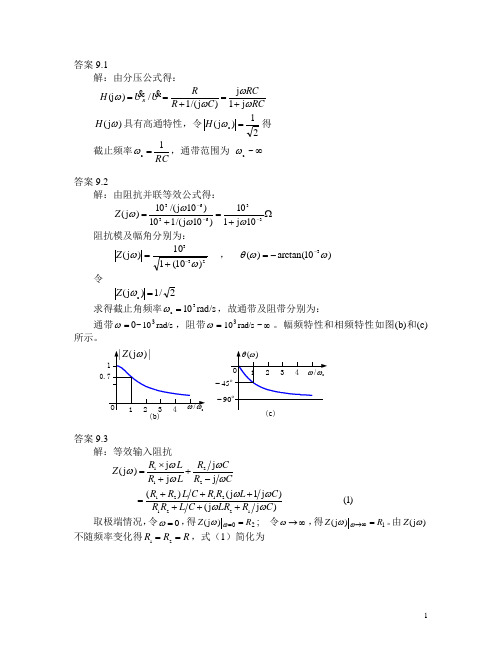
答案9.1解:由分压公式得:U U H R/)(j =ωRCRC C R R ωωωj 1j )j /(1+=+= )j (ωH 具有高通特性,令21)j (c =ωH 得截止频率RC1c =ω,通带范围为∞~c ω答案9.2解:由阻抗并联等效公式得:Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为:233)10(110)j (ωω-+=Z , )10arctan()(3ωωθ--= 令2/1)j (c =ωZ求得截止角频率rad/s 103c =ω,故通带及阻带分别为:通带=ω0~rad/s 103,阻带=ωrad/s 103~∞。
幅频特性和相频特性如图(b)和(c)所示。
(b)--答案9.3解:等效输入阻抗)1()j j ()j 1j ()(j j j j )j (122121212211C R LR C L R R C L R R C L R R CR CR L R L R Z ωωωωωωωωω++++++=-++⨯=取极端情况,令0=ω,得20)j (R Z ==ωω; 令∞→ω,得1)j (R Z =∞→ωω。
由)j (ωZ 不随频率变化得R R R ==21,式(1)简化为)j 1j ()j 1j (2)j 1j ()j 1j (2)j (22C L RC L R C L R CL RC L R C L R C L R C L R Z ωωωωωωωωω+++++=+++++= 由)j (ωZ 为实数得:CL R R C L R R C L =+=2,2 故当C L R R ==21时端口电流与端口电压的波形相似,此时C L Z =)j (ω。
答案9.4解: RC 并联的等效阻抗RCRC R C R Z RC ωωωj 1j /1j /+=+=RC RCZ L Z U U H +==ωωj /)j (12 RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时,1)j (=ωH ;当∞→ω时,0)j (=ωH所以它具有低通特性。
第9章习题解答哈工大习题册

第9章 线性动态电路暂态过程的复频域分析9.1根据定义求()()f t t t ε=和()e ()at f t t t ε-=的象函数。
解:(1)2020001e 1d e 1e d e )()(-s s t s stt t t s F stst stst =-=+-==∞-∞-∞-∞----⎰⎰ε (2)20)(20)(00)(1e)(1d e 1e d e )(e )(-ααααεααα+=+-=+++-==∞+-∞+-∞-∞-----⎰⎰s s ts s t t t t s F ts t s st st t9.2 求下列函数的原函数。
(a)6512)(2+++=s s s s F , (b) )2)(1(795)(23+++++=s s s s s s F , (c) 623)(2++=s s s F 。
解:(a) 6512)(2+++=s s s s F 3221+++=s A s A 3|31221-=++=-=s s s A , 3|31221-=++=-=s s s A所以 t t s s t f 321e 5e 3}3523{)(---+-=+++-=L(b))2)(1(795)(23+++++=s s s s s s F 212)2)(1(3221+++++=+++++=s A s A s s s s s 2|2311=++=-=s s s A 1|1321-=++=-=s s s A 所以 t t t t s s s L t f 21e e 2)(2)(}21122{)(----++'=+-++++=δδ(c)623)(2++=s s s F 22)5()1(5)5/3(++⨯=s , 查表得)5sin(e 53)(t t f t -= 9.3求图示电路的等效运算阻抗。
图题9.3解:由运算电路(略)求得端口等效运算阻抗为:11262241)3/(142)]3/(14[21)(22i ++++=++++=s s ss s s s s s Z , 112611430)(22++++=s s s s s Z i 9.4 图示电路,已知2S e ()t u t ε-=V ,求零状态响应u 。
电路理论基础(哈尔滨工业大学陈希有第3版) 第1章-第5章

a 电位: 任选一点p作为电位参考点,电路中某点与参考点之间的电压称为该点的电 位,用 表示。有了电位的概念,两点之间的电压便等于这两点的电位之差。
uab Ec dl
a A
(a)
a A
(b)
u ab
u ba
A
(c)
a uA
b
b
b
电压参考方向的表示法
一个元件上的电压和电流的参考方向取成相同的,并称为关联参考方向。
2 基尔霍夫电流定律
基尔霍夫电流定律(Kirchhoff's Current Law,简称KCL)表述为:在集中 参数电路中,任一时刻流出(或流入)任一节点的支路电流代数和等于零, 即
i
k
0
( ik 表示第 k 条支路电流)
规定: ik 参考方向为流出节点时, ik 前面 取“+”号; 流入节点时, ik 前面取“-”号。
i1
A
i2
1、在集中参数电路中,任一时刻流出(或流入) 任一闭合边界 S 的支路电流代数和等于零。
KCL的其它表述
2、任一时刻,流出任一节点(或闭合边界)电 流的代数和等于流入该节点电流的代数和。
根据右图,列写KCL方程 1)基本表述方 式——对节点
3 i3
④
S
4 i4 i6 7 i7 ③
节点① :
① u1 1
u
电压降
= u电压升
6 ③ u6 l1 5 u5 l2 7 u7 ⑤ 基尔霍夫电压定律示例
u2
l3 ②
2
说明:平面电路网孔上的KVL方程是一组独立方程。设电路有b个支路n个节 点,可以证明:平面电路的网孔数即独立KVL方程的个数等于b-(n-1)。当然 取网孔列方程只是获得独立KVL方程的充分条件,而不是必要条件。
数电课后题答案(哈工大版)课后习题答案
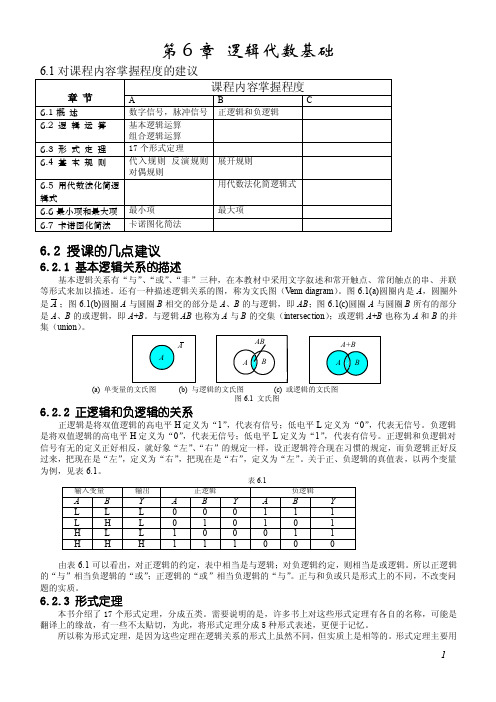
第6章 逻辑代数基础6.2 授课的几点建议6.2.1 基本逻辑关系的描述基本逻辑关系有“与”、“或”、“非”三种,在本教材中采用文字叙述和常开触点、常闭触点的串、并联等形式来加以描述。
还有一种描述逻辑关系的图,称为文氏图(V enn diagram )。
图6.1(a)圆圈内是A ,圆圈外是A ;图6.1(b)圆圈A 与圆圈B 相交的部分是A 、B 的与逻辑,即AB ;图6.1(c)圆圈A 与圆圈B 所有的部分是A 、B 的或逻辑,即A +B 。
与逻辑AB 也称为A 与B 的交集(intersection );或逻辑A +B 也称为A 和B 的并集(union )。
(a) 单变量的文氏图 (b) 与逻辑的文氏图 (c) 图6.1 文氏图6.2.2 正逻辑和负逻辑的关系正逻辑是将双值逻辑的高电平H 定义为“1”,代表有信号;低电平L 定义为“0”,代表无信号。
负逻辑是将双值逻辑的高电平H 定义为“0”,代表无信号;低电平L 定义为“1”,代表有信号。
正逻辑和负逻辑对信号有无的定义正好相反,就好象“左”、“右”的规定一样,设正逻辑符合现在习惯的规定,而负逻辑正好反过来,把现在是“左”,定义为“右”,把现在是“右”,定义为“左”。
关于正、负逻辑的真值表,以两个变量为例,见表6.1。
表6.1由表6.1可以看出,对正逻辑的约定,表中相当是与逻辑;对负逻辑约定,则相当是或逻辑。
所以正逻辑的“与”相当负逻辑的“或”;正逻辑的“或”相当负逻辑的“与”。
正与和负或只是形式上的不同,不改变问题的实质。
6.2.3 形式定理本书介绍了17个形式定理,分成五类。
需要说明的是,许多书上对这些形式定理有各自的名称,可能是翻译上的缘故,有一些不太贴切,为此,将形式定理分成5种形式表述,更便于记忆。
所以称为形式定理,是因为这些定理在逻辑关系的形式上虽然不同,但实质上是相等的。
形式定理主要用于逻辑式的化简,或者在形式上对逻辑式进行变换,它有以下五种类型:1.变量与常量之间的关系;2.变量自身之间的关系;3.与或型的逻辑关系;4.或与型的逻辑关系;5.求反的逻辑关系——摩根(Morgan )定理。
哈工大电路理论基础课后习题答案(PDF精品)

答案2.1解:本题练习分流、分压公式。
设电压、电流参考方向如图所示。
(a) 由分流公式得:23A 2A 23I R Ω⨯==Ω+解得75R =Ω(b) 由分压公式得:3V 2V 23R U R ⨯==Ω+解得47R =Ω答案2.2解:电路等效如图(b)所示。
20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得:220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯= 再对图(a)使用分压公式得:13==30V 1+3U U ⨯答案2.3解:设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1) 由已知条件得如下联立方程:32113130.05(2) 40k (3)eqR U UR R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω 再将3R 代入(1)式得210k 3R =Ω答案2.4解:由并联电路分流公式,得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=-答案2.5解:首先将电路化简成图(b)。
图 题2.5120Ω(a)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-= 再由图(a)得321201A 360120I I =⨯=+由KVL 得,3131200100400V U U U I I =-=-=-答案2.6xRx(a-1)图2.6解:(a )设R 和r 为1级,则图题2.6(a)为2级再加x R 。
哈尔滨理工大学电路1-9章习题集答案解析
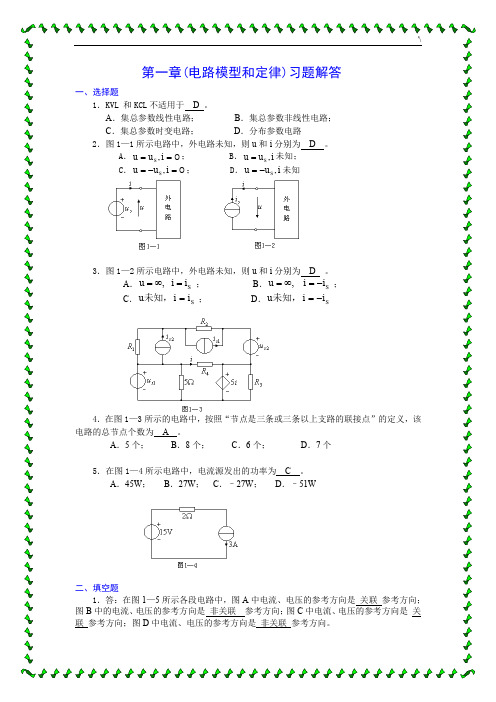
第一章(电路模型和定律)习题解答一、选择题1.KVL 和KCL 不适用于 D 。
A .集总参数线性电路;B .集总参数非线性电路;C .集总参数时变电路;D .分布参数电路2.图1—1所示电路中,外电路未知,则u 和i 分别为 D 。
A .0==i u uS ,; B .i u u S ,=未知;C .0=-=i u uS ,; D .i u u S ,-=未知3.图1—2所示电路中,外电路未知,则u 和i 分别为 D 。
A .S i i u =∞=, ;B .S i i u -=∞=, ;C .S i i u =未知, ; D .S i i u -=未知,4.在图1—3所示的电路中,按照“节点是三条或三条以上支路的联接点”的定义,该电路的总节点个数为 A 。
A .5个;B .8个;C .6个;D .7个5.在图1—4所示电路中,电流源发出的功率为 C 。
A .45W ;B .27W ;C .–27W ;D .–51W二、填空题1.答:在图1—5所示各段电路中,图A 中电流、电压的参考方向是 关联 参考方向;图B 中的电流、电压的参考方向是 非关联 参考方向;图C 中电流、电压的参考方向是 关联 参考方向;图D 中电流、电压的参考方向是 非关联 参考方向。
2.答:图1—6所示电路中的u 和i 对元件A 而言是 非关联 参考方向;对元件B 而言是 关联 参考方向。
3.答:在图1—7所示的四段电路中,A 、B 中的电压和电流为关联参考方向,C 、D中的电压和电流为非关联参考方向。
4.答:电路如图1—8所示。
如果10=R Ω,则10=U V ,9-=I A ;如果1=R Ω,则 10=U V ,0=I A 。
5.答:在图1—9 (a)所示的电路中,当10=R Ω时,=2u 50V ,=2i 5A ;当5=R Ω时,=2u 50V , =2i 10A 。
在图1—9 (b)所示的电路中,当R =10Ω时,2002=u V ,202=i A ;当5=R Ω时,1002=u V, 202=i A 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由于电容 C 变化时,Yab 的实部不变,所以,当并联部分发生谐振时, Yab 最小, 电压 U ab I S / Yab 为最大,因此电流 I 也为最大。令
( L2 M ) 1 2 0 1/ C M R 2 ( L2 M ) 2
得
L2 M 2 10 6 F 0.2μF 2 R L2 ( L2 M ) 4 3 2 由分流公式求得: j(M 1 / C ) j4 I 2I 45 I I S S S j(M 1 / C ) R j ( L2 M ) 2 j2 故当 C 0.2μF 时, I max 2 I S 14.14mA C
答案 9.1 解:由分压公式得:
R jRC R 1/( jC ) 1 jRC 1 得 H ( j ) 具有高通特性,令 H ( j c ) 2 1 截止频率 c ,通带范围为 c ~ RC
/U H (j ) U R
答案 9.2 解:由阻抗并联等效公式得: 103 /( j10 6 ) 103 Z ( j ) 3 10 1/( j10 6 ) 1 j10 3 阻抗模及幅角分别为: 103 Z ( j ) , ( ) arctan(10 3 ) 3 2 1 (10 ) 令
不随频率变化得 R1 R2 R ,式(1)简化为
LC ( jL 1 jC ) 2 R L C R ( jL 1 jC ) R Z ( j ) 2 R LC R L C R( jL 1 jC ) R ( jL 1 jC ) R 由 Z ( j ) 为实数得: LC LC L 2 R , R2 R R C 故当 R1 R2 L C 时端口电流与端口电压的波形相似, 此时 Z ( j ) L C 。 答案 9.4 解: RC 并联的等效阻抗 R / jC R Z RC R 1/ jC 1 jRC Z RC /U H ( j ) U 2 1 jL Z RC R 1 2 R jL(1 jRC ) 1 LC jL / R 幅频特性 1 H ( j ) (1 2 LC ) 2 (L / R) 2
2 2 1 2 1
两线圈电压的有效值分别为
U1 2 2 82 8.24V , U 2 4 2 12 2 12.65V
当两线圈反接时,等效电感
L' L1 L2 2M 0.01H
谐振角频率
0.01 20 10 j MI 5 0.4A 2V U 1 ( R1 j 2 L1 ) I 2 ( R j L ) I j MI (10 j22.36) 0.4A (4 j8.95)V U 2 2 2 2 2 此时两线圈电压的有效值分别为
/ c
45
1 2 3 (b) 4
O
/ c
90
(c)
答案 9.3 解:等效输入阻抗 R j L R jC Z ( j ) 1 2 R1 j L R2 j C
( R1 R2 ) L C R1 R2 ( jL 1 jC ) (1) R1 R2 L C ( jLR2 R1 jC ) 取极端情况, 令 0 , 得 Z ( j ) 0 R2 ; 令 , 得 Z ( j ) R1 。 由 Z ( j )
Z ( j c ) 1/ 2
求得截止角频率 c 103 rad/s ,故通带及阻带分别为: 通带 0~ 103 rad/s ,阻带 103 rad/s ~ 。幅频特性和相频特性如图 (b) 和 (c) 所示。
| Z ( j ) |
1 0.7
( )
O 1 2 3 4
2f C 2 C1
所以
2L 1 0 2 LRC RC Q
6
2
1
2.236 103 rad/s
U1 2V , U 2 42 8.952 9.8V
答案 9.13 解:(1)消去互感后,得图(b)所示等效电路。 a L2 M I L1 M S I M R C b
(b)
当等效电感 M 和电容 C 发生串联谐振时,即 C 1/ 2 M 1/ 106 1 1μF , ab 端相当于短路,端电压为零,则电流 I 也为零。所以电流 I 的最小值为 I min 0 (2)先分析 ab 端的等效导纳,由图(b)得 1 1 Yab R j ( L2 M ) jM j / C ( L2 M ) R 1 2 j[ 2 ] 2 2 1/ C M R 2 ( L2 M ) 2 R ( L2 M )
0
其中
1 R , Q 0 CR , 0 L LC 画出幅频特性如图(b) 所示。由幅频特性可以看出 H R ( j ) 是带通函数 在截止频率处
0
1 (CR R L) 2 2
由此解得
C1
L L2 4 R 2 LC 2 RLC
, C 2
答案 9.8 解:(1)根据题意,电路发生谐振时,存在下列关系:
1 / LC 10 4 rad/s I U / R 1A U LI 10V L
解得
R 0.1 L 1 mH C 10 F
品质因数 U 10 Q L 100 U 0.1 (2) I (j C ) 10 10 90 V 10 90 V U C 即有 uC 10 2 cos( t 90)V
H ( j ) 0
H ( j )
12 ( RC ) 2 12 ( RC ) 2
1
相频特性 ( ) 2arctg( RC ) 当 从 0 变到 时, ( ) 从 0 变化到 。 注释:图中电路幅频特性为常量,与频率无关,具有全通特性,常用作移相。 答案 9.6 解:设
2
2
当 0 时, H ( j ) 1 ;当 时, 所以它具有低通特性。 答案 9.5 解:由 KVL 及分压公式得 R U U ( 1 j C U )U 2 cb db 1 R 1 j C R 1 j C 整理得 U 1 j RC H ( j ) 2 1 j RC U 1 其幅频特性
R1 R2 1 1 , Z 2 R2 // jC2 R2 jR2C2 jC1 R1 jR1C1 由分压公式得: Z2 U U 2 1 Z1 Z 2 U R2 (1 j R1C1 ) H ( j ) 2 R (1 j R C ) R (1 j R C ) U Z1 R1 //
2 U L I R2 X L 544.94V
答案 9.15 解:端口等效阻抗 1 jL R ( L) 2 R LR 2 1 Z ( j ) 2 j[ ] 2 2 2 j C R j L R ( L) R ( L) C 令 ImZ 0 ;解得谐振角频率
2
答案 9.14 解:电路达到谐振时,有 1 1 C 2 F 63.39 F 2 L (100 ) 160 10 3 X L L X C 1 C 50.24 谐振时电流
I U 179 2 10.55A R 12
故电容器的端电压 U C X C I 530.03V , 线圈的端电压0 7 F (2 875) 2 0.32
谐振频率为
f c1 (
1 1 1) f 0 759Hz 2Q 4Q 2
f c2 (
1 1 1) f 0 1009Hz 2Q 4Q 2
(2) 谐振时电路的平均功率为: P0 I 02 R (23.2 / 502.65) 2 502.65 1.071W 在截止频率处,电流下降至谐振电流 I 0 的 1/ 2 ,故功率减小到 P0 的一半,所以 当 f 759Hz 和 f 1009Hz 时,电路平均功率均为 P P0 / 2 0.535W (3) U L U C QU 3.5 23.2 81.2V
L L1 L2 2M 0.05H
谐振角频率
1
1 1 103 rad s 6 LC 0.05 20 10
60V ,则谐振时的电流 取U
U 60 A 0.40A R1 R2 5 10 由互感的元件方程得: ( R j L ) I j MI [(5 j10) 0.4 j10 0.4]V (2 j8)V U 1 1 1 1 1 ( R j L ) I j MI [(10 j20) 0.4 j10 0.4]V (4 j12)V U I
答案 9.11
解: 谐振时 L 1/ C ,即 C 1 /( 2 L) 1/( 4 2 f 2 L) 由上式求得,当 f 550kHz 时 C 262pF ,当 f 1.6 MHz 时 C 31pF 所以可变电容 C 的变化范围应为 31 ~ 262pF 答案 9.12 解:当两线圈顺接时,等效电感
(1)
0
R R 2 LC L2
将 0 代回式(1) ,得 Z ( j 0 ) L RC 答案 9.16
解:
H R ( j )
R I U 1 R I S (1 R jC j L)U 1 j(CR R L) 1 1 H R ( j ) 1 (CR R L) 2 1 Q2 ( 0 )2
1 1 2 2 2 1 1
R2 当 R1C1 =R2 C2 时,得 H ( j ) ,此网络函数模及辐角均不与频率无关。 R1 R2
答案 9.7 解:因为电路处于谐振状态,故电感与电容串联电路相当于短路,因此有
