【高考数学】2018最新考前两个月数学高考理科(江苏专用)总复习训练题:压轴大题突破练2 Word版含答案
2018年江苏省高考冲刺压轴数学试卷(附答案)
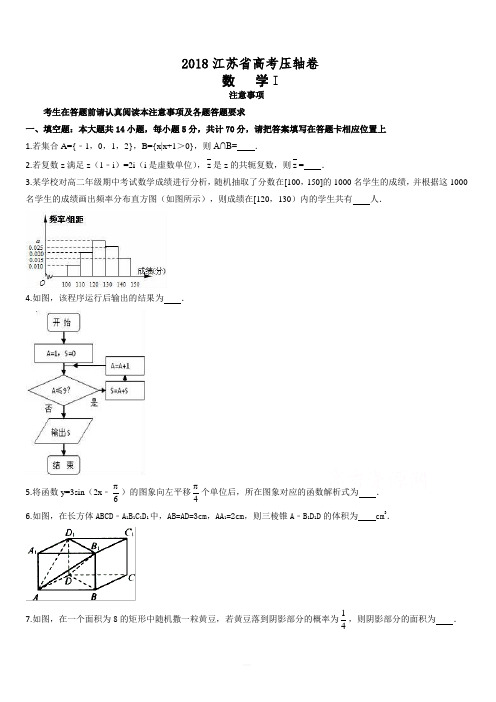
2018江苏省高考压轴卷数 学I注意事项考生在答题前请认真阅读本注意事项及各题答题要求一、填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡相应位置上 1.若集合A={﹣1,0,1,2},B={x|x+1>0},则A∩B= .2.若复数z 满足z (1﹣i )=2i (i 是虚数单位),z 是z 的共轭复数,则z = .3.某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有 人.4.如图,该程序运行后输出的结果为 .5.将函数y=3sin (2x ﹣6π)的图象向左平移4π个单位后,所在图象对应的函数解析式为 . 6.如图,在长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=3cm ,AA 1=2cm ,则三棱锥A ﹣B 1D 1D 的体积为 cm 3.7.如图,在一个面积为8的矩形中随机撒一粒黄豆,若黄豆落到阴影部分的概率为41,则阴影部分的面积为 .8.已知双曲线﹣=1(a>0,b>0)的左、右端点分别为A、B两点,点C(0, b),若线段AC的垂直平分线过点B,则双曲线的离心率为.9.设公比不为1的等比数列{a n}满足a1a2a3=﹣81,且a2,a4,a 3成等差数列,则数列{a n}的前4项和为.10.设定义在R上的偶函数f(x)在区间(﹣∞,0]上单调递减,若f(1﹣m)<f(m),则实数m的取值范围是.11.已知函数f(x)=,若a、b、c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是.12.如图,在△ABC中,已知AN=21AC,P是BN上一点,若AP=m AB+41AC,则实数m的值是.13.已知非零向量a,b满足|a|=|b|=|a+b|,则a与2a-b夹角的余弦值为.14.已知函数f(x)=⎩⎨⎧≥++-<1x,ax25x9x1x,xsin23,若函数f(x)的图象与直线y=x有三个不同的公共点,则实数a的取值集合为.15.如图,在三棱柱ABC A1B1C1中,AB AC,点E,F分别在棱BB1 ,CC1上(均异于端点),且∠ABE∠ACF,AE⊥BB1,AF⊥CC1.求证:(1)平面AEF⊥平面BB1C1C;(2)BC // 平面AEF.16.在△ABC中,角,,A B C的对边分别为,,a b c,且()2cos cosa b C c B-⋅=⋅.AA1B1C1BCFE(第16题)(1)求角C 的大小;(2)若2c =,△ABC 的面积为3,求该三角形的周长.17.已知中心在坐标原点的椭圆C ,F 1,F 2 分别为椭圆的左、右焦点,长轴长为6,离心率为(1)求椭圆C 的标准方程;(2)已知点P 在椭圆C 上,且PF 1=4,求点P 到右准线的距离.18.如图,四棱锥P ﹣ABCD 中,PA ⊥平面ABCD ,四边形ABCD 为直角梯形,AD ∥BC ,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E ,F ,G 分别为BC ,PD ,PC 的中点. (1)求EF 与DG 所成角的余弦值;(2)若M 为EF 上一点,N 为DG 上一点,是否存在MN ,使得MN ⊥平面PBC ?若存在,求出点M ,N 的坐标;若不存在,请说明理由.19.设等比数列a 1,a 2,a 3,a 4的公比为q ,等差数列b 1,b 2,b 3,b 4的公差为d ,且10q d ≠≠,. 记i i i c a b =+(i1,2,3,4).(1)求证:数列123c c c ,,不是等差数列; (2)设11a =,2q =.若数列123c c c ,,是等比数列,求b 2关于d 的函数关系式及其定义域; (3)数列1234c c c c ,,,能否为等比数列?并说明理由. 20.(16分)已知f (x )=x 2+mx+1(m ∈R ),g (x )=e x .(1)当x ∈[0,2]时,F (x )=f (x )﹣g (x )为增函数,求实数m 的取值范围; (2)若m ∈(﹣1,0),设函数 G(x)=)x (g )x (f ,H(x)=﹣41x+45,求证:对任意x 1,x 2∈[1,1﹣m],G (x 1)<H (x 2)恒成立.数学II (附加题)注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共2页,均为非选择题(第21题 ~第23题)。
2018考前两个月数学高考理科(江苏专用)总复习训练题:考前回扣3 Word版含答案

回扣3 三角函数与平面向量1.准确记忆六组诱导公式 对于“k π2±α,k ∈Z ”的三角函数值与α角的三角函数值的关系口诀:奇变偶不变,符号看象限.2.三角函数恒等变换“四大策略”(1)常值代换:特别是“1”的代换,1=sin 2θ+cos 2θ=tan45°等. (2)降次与升次:正用二倍角公式升次,逆用二倍角公式降次. (3)弦、切互化:一般是切化弦.(4)灵活运用辅助角公式a sin α+b cos α=a 2+b 2sin(α+φ)⎝⎛⎭⎪⎫其中tan φ=b a . 3.三种三角函数的性质4.函数y =A sin(ωx +φ)(ω>0,A >0)的图象 (1)“五点法”作图设z =ωx +φ,令z =0,π2,π,3π2,2π,求出相应的x 的值与y 的值,描点、连线可得.(2)由三角函数的图象确定解析式时,一般利用五点中的零点或最值点作为解题突破口. (3)图象变换y =sin x ―――――――――→向左(φ>0)或向右(φ<0)平移|φ|个单位长度y =sin(x +φ) ――――――――――――→横坐标变为原来的1ω(ω>0)倍纵坐标不变y =sin(ωx +φ) ―――――――――――→纵坐标变为原来的A (A >0)倍横坐标不变y =A sin(ωx +φ). 5.正弦定理及其变形asin A=b sin B =csin C=2R (2R 为△ABC 外接圆的直径).变形:a =2R sin A ,b =2R sin B ,c =2R sin C . sin A =a 2R ,sin B =b 2R ,sin C =c2R.a ∶b ∶c =sin A ∶sin B ∶sin C .6.余弦定理及其推论、变形a 2=b 2+c 2-2bc cos A ,b 2=a 2+c 2-2ac cos B , c 2=a 2+b 2-2ab cos C .推论:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab.变形:b 2+c 2-a 2=2bc cos A ,a 2+c 2-b 2=2ac cos B ,a 2+b 2-c 2=2ab cos C .7.面积公式S △ABC =12bc sin A =12ac sin B =12ab sin C .8.平面向量的数量积(1)若a ,b 为非零向量,夹角为θ,则a·b =|a||b |cos θ. (2)设a =(x 1,y 1),b =(x 2,y 2),则a·b =x 1x 2+y 1y 2. 9.两个非零向量平行、垂直的充要条件 若a =(x 1,y 1),b =(x 2,y 2),则 (1)a ∥b ⇔a =λb (b ≠0)⇔x 1y 2-x 2y 1=0. (2)a ⊥b ⇔a·b =0⇔x 1x 2+y 1y 2=0. 10.利用数量积求长度。
2018考前三个月高考数学理科(江苏专用)总复习训练题(冲刺集合195页)

2018考前三个月高考数学理科(江苏专用)总复习训练题(冲刺集合195页)附加题高分练+解答题滚动练+小题满分练 +中档大题规范练+压轴大题突破练+考前回扣中档大题规范练 1.解三角形1.(2017·苏锡常镇调研)在△ABC 中,a ,b ,c 分别为角A ,B ,C 的对边.已知a cos B =3,b cos A =1,且A -B =π6.(1)求c 的长; (2)求B 的大小.解 (1)方法一 在△ABC 中,a cos B =3,由余弦定理,得a ·a 2+c 2-b 22ac=3,得a 2+c 2-b 2=6c ,①b cos A =1,则b ·b 2+c 2-a 22bc=1,得b 2+c 2-a 2=2c ,②①+②得2c 2=8c ,所以c =4.方法二 因为在△ABC 中,A +B +C =π, 则sin A cos B +sin B cos A =sin(A +B ) =sin(π-C )=sin C , 由asin A =b sin B =c sin C ,得sin A =a sin C c ,sin B =b sin C c,代入上式得 c =a cos B +b cos A =3+1=4.(2)由正弦定理得a cos Bb cos A =sin A cos B sin B cos A =tan Atan B=3. 又tan(A -B )=tan A -tan B 1+tan A tan B =2tan B 1+3tan 2B =33, 解得tan B =33.又B ∈(0,π),所以B =π6. 2.(2017·苏州暑假测试)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知b cos C +c cos B =2a cos A .(1)求角A 的大小;(2)若AB →·AC →=3,求△ABC 的面积.解 (1)方法一 在△ABC 中,由正弦定理及b cos C +c cos B =2a cos A , 得sin B cos C +sin C cos B =2sin A cos A , 即sin A =2sin A cos A .因为A ∈(0,π),则sin A ≠0,所以cos A =12,所以A =π3.方法二 在△ABC 中,由余弦定理及b cos C +c cos B =2a cos A ,得b ·a 2+b 2-c 22ab +c ·a 2+c 2-b 22ac =2a ·b 2+c 2-a 22bc ,所以a 2=b 2+c 2-bc ,所以cos A =b 2+c 2-a 22bc =12.因为A ∈(0,π),所以A =π3. (2)由AB →·AC →=bc cos A =3,得bc =23, 所以△ABC 的面积S =12bc sin A =12×23sin π3=32.3.(2017·南京、盐城一模)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且b sin2C =c sin B .(1)求角C 的大小;(2)若sin ⎝⎛⎭⎪⎫B -π3=35,求sin A 的值.解 (1)由b sin2C =c sin B ,根据正弦定理得 2sin B sin C cos C =sin C sin B .因为sin B >0,sin C >0,所以cos C =12.又C ∈(0,π),所以C =π3.(2)因为C =π3,所以B ∈⎝ ⎛⎭⎪⎫0,2π3,所以B -π3∈⎝ ⎛⎭⎪⎫-π3,π3,又sin ⎝⎛⎭⎪⎫B -π3=35,又A +B =2π3,即A =2π3-B ,所以sin A =sin ⎝⎛⎭⎪⎫2π3-B =sin ⎣⎢⎡⎦⎥⎤π3-⎝ ⎛⎭⎪⎫B -π3 =sin π3cos ⎝ ⎛⎭⎪⎫B -π3-cos π3sin ⎝ ⎛⎭⎪⎫B -π3=32×45-12×35=43-310. 4.(2017·徐州、连云港、宿迁三检)如图,在△ABC 中,已知点D 在边AB 上,AD =3DB ,cos A =45,cos ∠ACB =513,BC =13.(1)求cos B 的值; (2)求CD 的长.解 (1)在△ABC 中,cos A =45,A ∈(0,π),所以sin A =1-cos 2A =1-⎝ ⎛⎭⎪⎫452=35. 同理可得,sin ∠ACB =1213.所以cos B =cos[π-(A +∠ACB )]=-cos(A +∠ACB ) =sin A sin ∠ACB -cos A cos ∠ACB =35×1213-45×513=1665.(2)在△ABC 中,由正弦定理,得AB =BCsin A sin ∠ACB =1335×1213=20.又AD =3DB ,所以BD =14AB =5.在△BCD 中,由余弦定理,得CD =BD 2+BC 2-2BD ·BC cos B=52+132-2×5×13×1665=9 2.3.空间平行与垂直1.(2017·南京学情调研)如图,在直三棱柱ABC-A1B1C1中,M,N分别为线段A1B,AC1的中点.(1)求证:MN∥平面BB1C1C;(2)若D在边BC上,AD⊥DC1,求证:MN⊥AD.证明(1)如图,连结A1C,在直三棱柱ABC-A1B1C1中,侧面AA1C1C为平行四边形,又因为N为线段AC1的中点,所以A1C与AC1相交于点N,即A1C经过点N,且N为线段A1C的中点.因为M为线段A1B的中点,所以MN∥BC.又MN⊄平面BB1C1C,BC⊂平面BB1C1C,所以MN∥平面BB1C1C.(2)在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,又AD⊂平面ABC,所以CC1⊥AD.因为AD⊥DC1,DC1⊂平面BB1C1C,CC1⊂平面BB1C1C,CC1∩DC1=C1,所以AD⊥平面BB1C1C. 又BC⊂平面BB1C1C,所以AD⊥BC.由(1)知MN∥BC,所以MN⊥AD.2.如图,在四棱锥P-ABCD中,底面ABCD是正方形,AC与BD交于点O,PC⊥底面ABCD,E为PB上一点,G为PO的中点.(1)若PD∥平面ACE,求证:E为PB的中点;(2)若AB=2PC,求证:CG⊥平面PBD.证明 (1)连结OE ,由四边形ABCD 是正方形知,O 为BD 的中点, 因为PD ∥平面ACE ,PD ⊂平面PBD ,平面PBD ∩平面ACE =OE , 所以PD ∥OE .因为O 为BD 的中点,所以E 为PB 的中点. (2)在四棱锥P -ABCD 中,AB =2PC , 因为四边形ABCD 是正方形,所以OC =22AB , 所以PC =OC .因为G 为PO 的中点,所以CG ⊥PO . 又因为PC ⊥底面ABCD ,BD ⊂底面ABCD , 所以PC ⊥BD .而四边形ABCD 是正方形,所以AC ⊥BD , 因为AC ,PC ⊂平面PAC ,AC ∩PC =C , 所以BD ⊥平面PAC ,因为CG ⊂平面PAC ,所以BD ⊥CG . 因为PO ,BD ⊂平面PBD ,PO ∩BD =O , 所以CG ⊥平面PBD .3.如图,已知平面PAC ⊥平面ABC ,AC ⊥BC ,PE ∥CB ,M 是AE 的中点. (1)若N 是PA 的中点,求证:平面CMN ⊥平面PAC ; (2)若MN ∥平面ABC ,求证:N 是PA 的中点.证明 (1)因为平面PAC ⊥平面ABC ,平面PAC ∩平面ABC =AC ,AC ⊥BC ,BC ⊂平面ABC , 所以BC ⊥平面PAC ,因为M ,N 分别为AE ,AP 的中点,所以MN ∥PE , 又因为PE ∥BC ,所以MN ∥BC , 即MN ⊥平面PAC ,又MN ⊂平面CMN , 所以平面CMN ⊥平面PAC .(2)因为PE ∥CB ,BC ⊂平面ABC ,PE ⊄平面ABC , 所以PE ∥平面ABC ,设平面PAE 与平面ABC 的交线为l ,则PE ∥l . 又MN ∥平面ABC ,MN ⊂平面PAE ,所以MN ∥l . 所以MN ∥PE ,因为M 是AE 的中点,所以N 为PA 的中点.4.如图,在直三棱柱ABC -A 1B 1C 1中,D 为棱BC 上一点. (1)若AB =AC ,D 为棱BC 的中点,求证:平面ADC 1⊥平面BCC 1B 1; (2)若A 1B ∥平面ADC 1,求BD DC的值.(1)证明 因为AB =AC ,点D 为BC 的中点, 所以AD ⊥BC .因为ABC -A 1B 1C 1是直三棱柱,所以BB 1⊥平面ABC . 因为AD ⊂平面ABC ,所以BB 1⊥AD .因为BC ∩BB 1=B ,BC ⊂平面BCC 1B 1,BB 1⊂平面BCC 1B 1, 所以AD ⊥平面BCC 1B 1.因为AD ⊂平面ADC 1,所以平面ADC 1⊥平面BCC 1B 1.(2)解 连结A 1C ,交AC 1于O ,连结OD ,所以O 为A 1C 的中点.因为A 1B ∥平面ADC 1,A 1B ⊂平面A 1BC ,平面ADC 1∩平面A 1BC =OD ,所以A 1B ∥OD . 因为O 为A 1C 的中点,所以D 为BC 的中点, 所以BD DC=1.4.应用题1.(2017·苏锡常镇调研)某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图).设计要求彩门的面积为S (单位:m 2),高为h (单位:m)(S ,h 为常数).彩门的下底BC 固定在广场底面上,上底和两腰由不锈钢支架组成,设腰和下底的夹底为α,不锈钢支架的长度之和记为l .(1)请将l 表示成关于α的函数l =f (α); (2)问:当α为何值时l 最小,并求最小值.解 (1)过D 作DH ⊥BC 于点H ,则∠DCB =α⎝ ⎛⎭⎪⎫0<α<π2,DH =h ,设AD =x .则DC =h sin α,CH =h tan α,BC =x +2htan α.因为S =12⎝ ⎛⎭⎪⎫x +x +2h tan α·h ,则x =S h -htan α, 则l =f (α)=2DC +AD =S h+h ⎝⎛⎭⎪⎫2sin α-1tan α⎝⎛⎭⎪⎫0<α<π2.(2)f ′(α)=h ·⎝⎛⎭⎪⎫-2cos αsin 2α--1sin 2α=h ·1-2cos αsin 2α, 令f ′(α)=h ·1-2cos αsin 2α=0,得α=π3. 当α变化时,f ′(α),f (α)的变化情况如下表:所以l min =f ⎝ ⎛⎭⎪⎫π3=3h +h .答 当α=π3时,l 有最小值,为3h +Sh(m).2.(2017·南京学情调研)如图,某城市有一块半径为40m 的半圆形绿化区域(以O 为圆心,AB 为直径),现计划对其进行改建,在AB 的延长线上取点D ,OD =80m ,在半圆上选定一点C ,改建后的绿化区域由扇形区域AOC 和三角形区域COD 组成,其面积为S m 2.设∠AOC =x rad.(1)写出S 关于x 的函数关系式S (x ),并指出x 的取值范围; (2)试问∠AOC 多大时,改建后的绿化区域面积S 取得最大值?解 (1)因为扇形AOC 的半径为40m ,∠AOC =x rad ,所以扇形AOC 的面积S 扇形AOC =x ·OA 22=800x,0<x <π.在△COD 中,OD =80,OC =40,∠COD =π-x , 所以△COD 的面积S △COD =12OC ·OD ·sin∠COD=1600sin(π-x )=1600sin x ,从而S =S △COD +S 扇形AOC =1600sin x +800x,0<x <π. (2)由(1)知,S (x )=1600sin x +800x,0<x <π, 则S ′(x )=1600cos x +800=1600⎝ ⎛⎭⎪⎫cos x +12, 由S ′(x )=0,解得x =2π3,从而当0<x <2π3时,S ′(x )>0;当2π3<x <π时,S ′(x )<0,因此S (x )在区间⎝ ⎛⎭⎪⎫0,2π3上单调递增,在区间⎝⎛⎭⎪⎫2π3,π上单调递减.所以当x =2π3时,S (x )取得最大值.答 当∠AOC =2π3时,改建后的绿化区域面积S 最大.3.某宾馆在装修时,为了美观,欲将客户的窗户设计成半径为1m 的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形ABCD 为中心在圆心的矩形,现计划将矩形ABCD 区域设计为可推拉的窗口.(1)若窗口ABCD 为正方形,且面积大于14m 2(木条宽度忽略不计),求四根木条总长的取值范围;(2)若四根木条总长为6m ,求窗口ABCD 面积的最大值.解 (1)设一根木条长为x m ,因为S 四边形ABCD >14,所以4-x 2>14,即x <152.又因为四根木条将圆分成9个区域,所以x >2, 所以42<4x <215.答 四根木条总长的取值范围为(42,215).(2)方法一 设AB 所在的木条长为a m ,则BC 所在的木条长为(3-a )m. 因为a ∈(0,2),3-a ∈(0,2),所以a ∈(1,2).S 矩形ABCD =41-a 24·1-(3-a )24=4-a 2·4-(3-a )2=a 4-6a 3+a 2+24a -20, 设f (a )=a 4-6a 3+a 2+24a -20,则f ′(a )=4a 3-18a 2+2a +24=2(a +1)(2a -3)(a -4), 令f ′(a )=0,得a =32或a =-1(舍去)或a =4(舍去).当a 变化时,f ′(a ),f (a )的变化情况如下表:所以当a =32时,f (a )max =f ⎝ ⎛⎭⎪⎫32=4916,即S max =74.答 窗口ABCD 面积的最大值为74m 2.方法二 设AB 所在的木条长为a m ,BC 所在的木条长为b m .由条件知,2a +2b =6,即a +b =3.因为a ,b ∈(0,2),所以b =3-a ∈(0,2),从而a ,b ∈(1,2). 由于AB =21-b 24,BC =21-a 24,S 矩形ABCD =41-b 241-a 24=4-b24-a 2,因为4-b24-a 2≤8-(a 2+b 2)2≤8-(a +b )222=74,当且仅当a =b =32∈(1,2)时,S 矩形ABCD =74为最大值.答 窗口ABCD 面积的最大值为74m 2.4.某隧道设计为双向四车道,车道总宽20m ,要求通行车辆限高4.5m ,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xOy . (1)若最大拱高h 为6m ,则隧道设计的拱宽l 是多少?(2)为了使施工的土方工程量最小,需隧道口截面面积最小.现隧道口的最大拱高h 不小于6m ,则应如何设计拱高h 和拱宽l ,使得隧道口截面面积最小?隧道口截面面积公式为S =23lh.解 (1)设抛物线的方程为y =-ax 2(a >0),则抛物线过点⎝⎛⎭⎪⎫10,-32,代入抛物线方程解得a =3200, 令y =-6,解得x =±20,则隧道设计的拱宽l 是40m.(2)抛物线最大拱高为h m ,h ≥6,抛物线过点⎝⎛⎭⎪⎫10,-h +92,代入抛物线方程得a =h -92100.令y =-h ,则-h -92100x 2=-h ,解得x 2=100hh -92,则⎝ ⎛⎭⎪⎫l 22=100h h -92,h =92l 2l 2-400.因为h ≥6,所以92l 2l 2-400≥6,即20<l ≤40.所以S =23lh =23l ·92l 2l 2-400=3l3l 2-400(20<l ≤40).所以S ′=9l 2(l 2-400)-3l 3·2l (l 2-400)2=3l 2(l 2-1200)(l 2-400)2=3l 2(l +203)(l -203)(l 2-400)2, 当20<l <203时,S ′<0;当203<l ≤40时,S ′>0,即S 在(20,203)上单调递减,在(203,40]上单调递增,所以S 在l =203时取得最小值,此时l =203,h =274.答 当拱高为274m ,拱宽为203m 时,使得隧道口截面面积最小.5.直线与圆1.已知圆心为C 的圆,满足下列条件:圆心C 位于x 轴正半轴上,与直线3x -4y +7=0相切,且被y 轴截得的弦长为23,圆C 的面积小于13. (1)求圆C 的标准方程;(2)设过点M (0,3)的直线与圆C 交于不同的两点A ,B ,以OA ,OB 为邻边作平行四边形OADB .是否存在这样的直线l ,使得直线OD 与MC 恰好平行?如果存在,求出l 的方程;若不存在,请说明理由.解 (1)设圆C :(x -a )2+y 2=r 2(a >0),由题意知⎩⎪⎨⎪⎧|3a +7|32+(-4)2=r ,a 2+3=r ,解得a =1或a =138,又S =πr 2<13,∴a =1,∴圆C 的标准方程为(x -1)2+y 2=4.(2)当斜率不存在时,直线l 为x =0,不满足题意.当斜率存在时,设直线l :y =kx +3,A (x 1,y 1),B (x 2,y 2),又l 与圆C 相交于不同的两点,联立得⎩⎪⎨⎪⎧y =kx +3,(x -1)2+y 2=4,消去y 得(1+k 2)x 2+(6k -2)x +6=0.∴Δ=(6k -2)2-24(1+k 2)=12k 2-24k -20>0, 解得k <1-263或k >1+263.x 1+x 2=-6k -21+k 2,y 1+y 2=k (x 1+x 2)+6=2k +61+k2, OD →=OA →+OB →=(x 1+x 2,y 1+y 2),MC →=(1,-3), 假设OD →∥MC →,则-3(x 1+x 2)=y 1+y 2,解得k =34∉⎝ ⎛⎭⎪⎫-∞,1-263∪⎝ ⎛⎭⎪⎫1+263,+∞,假设不成立,∴不存在这样的直线l .2.如图,在平面直角坐标系xOy 中,已知圆C :x 2+y 2-4x =0及点A (-1,0),B (1,2).(1)若直线l ∥AB ,与圆C 相交于M ,N 两点,MN =AB ,求直线l 的方程; (2)在圆C 上是否存在点P ,使得PA 2+PB 2=12?若存在,求点P 的个数;若不存在,请说明理由.解 (1)圆C 的标准方程为(x -2)2+y 2=4, 所以圆心C (2,0),半径为2.因为l ∥AB ,A (-1,0),B (1,2),所以直线l 的斜率为2-01-(-1)=1,设直线l 的方程为x -y +m =0,则圆心C 到直线l 的距离为d =|2-0+m |2=|2+m |2.因为MN =AB =22+22=22,而CM 2=d 2+⎝ ⎛⎭⎪⎫MN 22,所以4=(2+m )22+2,解得m =0或m =-4,故直线l 的方程为x -y =0或x -y -4=0.(2)假设圆C 上存在点P ,设P (x ,y ),则(x -2)2+y 2=4,PA 2+PB 2=(x +1)2+(y -0)2+(x -1)2+(y -2)2=12即x 2+y 2-2y -3=0,即x 2+(y -1)2=4.因为|2-2|<(2-0)2+(0-1)2<2+2,所以圆(x -2)2+y 2=4与圆x 2+(y -1)2=4相交, 所以点P 的个数为2.3.在平面直角坐标系xOy 中,已知椭圆C :x 24+y 23=1的左顶点为A ,右焦点为F ,P ,Q 为椭圆C 上两点,圆O :x 2+y 2=r 2(r >0).(1)若PF ⊥x 轴,且满足直线AP 与圆O 相切,求圆O 的方程;(2)若圆O 的半径为3,点P ,Q 满足k OP ·k OQ =-34,求直线PQ 被圆O 截得的弦长的最大值.解 (1)因为椭圆C 的方程为x 24+y 23=1,所以A (-2,0),F (1,0).如图,因为PF ⊥x 轴,所以P ⎝⎛⎭⎪⎫1,±32, 根据对称性,可取P ⎝ ⎛⎭⎪⎫1,32,则直线AP 的方程为y =12(x +2),即x -2y +2=0.由圆O 与直线AP 相切,得r =25,所以圆O 的方程为x 2+y 2=45.(2)易知,圆O 的方程为x 2+y 2=3. ①当PQ ⊥x 轴时,k OP ·k OQ =-k 2OP =-34,所以k OP=±32,不妨设OP :y =32x ,联立⎩⎪⎨⎪⎧y =32x ,x 24+y23=1,解得x =2,y =62,即P ⎝⎛⎭⎪⎫2,62, 此时得直线PQ 被圆O 截得的弦长为2. ②当PQ 与x 轴不垂直时,设直线PQ 的方程为y =kx +b ,P (x 1,y 1),Q (x 2,y 2)(x 1x 2≠0), 由k OP ·k OQ =-34,得3x 1x 2+4y 1y 2=0,即3x 1x 2+4(kx 1+b )(kx 2+b )=0,所以(3+4k 2)x 1x 2+4kb (x 1+x 2)+4b 2=0.(*)联立⎩⎪⎨⎪⎧y =kx +b ,x 24+y23=1消去y ,得(3+4k 2)x 2+8kbx +4b 2-12=0,将x 1+x 2=-8kb 3+4k 2,x 1x 2=4b 2-123+4k 2代入(*)式,得2b 2=4k 2+3.由于圆心O 到直线PQ 的距离为d =|b |k 2+1,所以直线PQ 被圆O 截得的弦长为l =23-d 2=4+2k 2+1,故当k =0时,l 有最大值 6. 综上,因为6>2,所以直线PQ 被圆O 截得的弦长的最大值为 6.4.如图,某市有一条东西走向的公路l ,现欲经过公路l 上的O 处铺设一条南北走向的公路m .在施工过程中发现在O 处的正北1百米的A 处有一汉代古迹.为了保护古迹,该市决定以A 为圆心,1百米为半径设立一个圆形保护区.为了连通公路l ,m ,欲再建一条公路PQ ,点P ,Q 分别在公路l ,m 上,且要求PQ 与圆A 相切.(1)当P 距O 处2百米时,求OQ 的长; (2)当公路PQ 长最短时,求OQ 的长.解 以O 为原点,直线l ,m 分别为x 轴,y 轴建立平面直角坐标系.设PQ 与圆A 相切于点B ,连结AB ,以1百米为单位长度,则圆A 的方程为x 2+(y -1)2=1.(1)由题意可设直线PQ 的方程为x 2+yq =1,即qx +2y -2q =0(q >2), ∵PQ 与圆A 相切, ∴|2-2q |q 2+22=1,解得q =83,故当P 距O 处2百米时,OQ 的长为83百米.(2)设直线PQ 的方程为x p +y q=1, 即qx +py -pq =0(p >1,q >2), ∵PQ 与圆A 相切,∴|p -pq |q 2+p 2=1,化简得p 2=q q -2, 则PQ 2=p 2+q 2=qq -2+q 2, 令f (q )=qq -2+q 2(q >2), ∴f ′(q )=2q -2(q -2)2=2(q -1)(q 2-3q +1)(q -2)2(q >2),当q >3+52时,f ′(q )>0,即f (q )在⎝ ⎛⎭⎪⎫3+52,+∞上单调递增,∴f (q )在q =3+52时取得最小值,故当公路PQ 长最短时,OQ 的长为3+52百米.6.圆锥曲线1.(2017·苏州期末)如图,已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,且过点P (2,-1).(1)求椭圆C 的方程;(2)设点Q 在椭圆C 上,且PQ 与x 轴平行,过点P 作两条直线分别交椭圆C 于A (x 1,y 1),B (x 2,y 2)两点,若直线PQ 平分∠APB ,求证:直线AB 的斜率是定值,并求出这个定值.解 (1)由e =ca =32,得a ∶b ∶c =2∶1∶3, 椭圆C 的方程为x 24b 2+y 2b2=1.把P (2,-1)代入,得b 2=2, 所以椭圆C 的方程是x 28+y 22=1.(2)由已知得PA ,PB 的斜率存在,且互为相反数. 设直线PA 的方程为y +1=k (x -2),其中k ≠0.由⎩⎪⎨⎪⎧y +1=k (x -2),x 2+4y 2=8消去y ,得x 2+4[kx -(2k +1)]2=8,即(1+4k 2)x 2-8k (2k +1)x +4(2k +1)2-8=0, 因为该方程的两根为2,x A ,所以2x A =4(2k +1)2-81+4k 2,即x A =8k 2+8k -21+4k 2, 从而y A =4k 2-4k -14k 2+1. 把k 换成-k ,得x B =8k 2-8k -21+4k 2,y B =4k 2+4k -14k 2+1. 故k AB =y B -y A x B -x A =8k -16k =-12,是定值. 2.(2017·常州期末)已知圆C :(x -t )2+y 2=20(t <0)与椭圆E :x 2a 2+y 2b2=1(a >b >0)的一个公共点为B (0,-2),F (c,0)为椭圆E 的右焦点,直线BF 与圆C 相切于点B . (1)求t 的值以及椭圆E 的方程;(2)过点F 任作与两坐标轴都不垂直的直线l 与椭圆交于M ,N 两点,在x 轴上是否存在一定点P ,使PF 恰为∠MPN 的平分线? 解 (1)由题意得b =2. 因为C (t,0),B (0,-2), 所以BC =t 2+4=20, 所以t =±4.因为t <0,所以t =-4.因为BC ⊥BF ,所以20+c 2+4=(c +4)2, 所以c =1,所以a 2=b 2+c 2=5. 所以椭圆E 的方程为x 25+y 24=1.(2)设M (x 1,y 1),N (x 2,y 2),设l :y =k (x -1)(k ≠0),代入x 25+y 24=1,化简得(4+5k 2)x 2-10k 2x +5k 2-20=0,所以⎩⎪⎨⎪⎧x 1+x 2=10k 24+5k2,x 1x 2=5k 2-204+5k2.若点P 存在,设P (m,0),由题意k PM +k PN =0, 所以y 1x 1-m +y 2x 2-m =k (x 1-1)x 1-m +k (x 2-1)x 2-m=0,所以(x 1-1)(x 2-m )+(x 2-1)(x 1-m )=0, 即2x 1x 2-(1+m )(x 1+x 2)+2m=2·5k 2-204+5k 2-(1+m )10k 24+5k 2+2m =0,所以8m -40=0,所以m =5.所以存在定点P (5,0),使PF 恰为∠MPN 的平分线.3.(2017·无锡期末)已知椭圆x 24+y 23=1,动直线l 与椭圆交于B ,C 两点(点B 在第一象限).(1)若点B 的坐标为⎝ ⎛⎭⎪⎫1,32,求△OBC 面积的最大值; (2)设B (x 1,y 1),C (x 2,y 2),且3y 1+y 2=0,求当△OBC 的面积最大时直线l 的方程. 解 (1)直线OB 方程为y =32x ,即3x -2y =0,设过点C 且平行于OB 的直线l ′方程为y =32x +b .则当l ′与椭圆只有一个公共点时,△OBC 的面积最大.由⎩⎪⎨⎪⎧x 24+y 23=1,y =32x +b消去y 整理得3x 2+3bx +b 2-3=0,此时Δ=9b 2-12(b 2-3),令Δ=0,解得b =±23, 当b =23时,C ⎝ ⎛⎭⎪⎫-3,32; 当b =-23时,C ⎝⎛⎭⎪⎫3,-32, 所以△OBC 面积的最大值为12×1+94×|33+3|13= 3. (2)显然,直线l 与y 轴不垂直,设直线l 的方程为x =my +n .由⎩⎪⎨⎪⎧x 24+y 23=1,x =my +n消去x 并整理得(3m 2+4)y 2+6mny +3n 2-12=0,所以⎩⎪⎨⎪⎧y 1+y 2=-6mn3m 2+4,y 1y 2=3n 2-123m 2+4.因为3y 1+y 2=0,所以⎩⎪⎨⎪⎧y 1=3mn3m 2+4,y 21=4-n23m 2+4,从而9n 2m 2(3m 2+4)2=4-n 23m 2+4, 即n 2=3m 2+43m 2+1,所以S △OBC =12|n |·|y 1-y 2|=2|n |·|y 1|=6|m |n 23m +4=6|m |3m +1.因为B 在第一象限,所以x 1=my 1+n =3m 2n3m 2+4+n >0,所以n >0.因为y 1>0,所以m >0, 所以S △OBC =6m 3m 2+1=63m +1m≤623=3,当且仅当3m =1m ,即m =33时取等号,此时n =102,4.(2017·南京、盐城二模)如图,在平面直角坐标系xOy 中,焦点在x 轴上的椭圆C :x 28+y 2b 2=1经过点(b,2e ),其中e 为椭圆C 的离心率.过点T (1,0)作斜率为k (k >0)的直线l 交椭圆C 于A ,B 两点(A 在x 轴下方). (1)求椭圆C 的标准方程;(2)过点O 且平行于l 的直线交椭圆C 于M ,N 两点,求AT ·BTMN 2的值; (3)记直线l 与y 轴的交点为P ,若AP →=25TB →,求直线l 的斜率k .解 (1)由点(b,2e )在椭圆C 上,得b 28+4e 2b =1.因为e 2=c 2a 2=8-b 28=1-b 28,所以b 28+4b 2=32.又b 2<a 2=8,解得b 2=4, 所以椭圆C 的标准方程是x 28+y 24=1.(2)设A (x 1,y 1),B (x 2,y 2),M (x 0,y 0), 由对称性知N (-x 0,-y 0),其中y 1<0. 因为MN ∥AB ,所以AT ·BT MN 2=-y 1y 24y 20. 直线AB 的方程为y =k (x -1),直线MN 的方程为y =kx ,其中k >0.由⎩⎪⎨⎪⎧ y =k (x -1),x 2+2y 2=8消去x ,得(1+2k 2)y 2+2ky -7k 2=0,所以y 1y 2=-7k21+2k2.由⎩⎪⎨⎪⎧y =kx ,x 2+2y 2=8消去x ,得(1+2k 2)y 2=8k 2,所以y 2=8k 21+2k ,从而得AT ·BT MN =732. (3)由AP →=25TB →,得-x 1=25(x 2-1).由⎩⎪⎨⎪⎧y =k (x -1),x 2+2y 2=8消去y ,得(1+2k 2)x 2-4k 2x +2k 2-8=0, 所以x 1+x 2=4k 21+2k 2,x 1x 2=2k 2-81+2k 2.又因为-x 1=25(x 2-1),所以x 1=-4k 2+23(1+2k 2),x 2=16k 2-23(1+2k 2),从而-4k 2+23(1+2k 2)·16k 2-23(1+2k 2)=2k 2-81+2k 2.整理得50k 4-83k 2-34=0, 解得k 2=2或k 2=-1750(舍).因为k >0,所以k = 2.压轴大题突破练 1.函数与导数1.设函数f (x )=x ln x +ax ,a ∈R .(1)当a =1时,求曲线y =f (x )在点(1,f (1))处的切线方程;(2)求函数y =f (x )在⎣⎢⎡⎦⎥⎤1e ,e 上的最小值; (3)若g (x )=f (x )+12ax 2-(2a +1)x ,求证:a ≥0是函数y =g (x )在x ∈(1,2)时单调递增的充分不必要条件.(1)解 由f (x )=x ln x +ax ,得f ′(x )=ln x +a +1. 当a =1时,f ′(x )=ln x +2,f (1)=1,f ′(1)=2, 求得切线方程为y =2x -1. (2)解 令f ′(x )=0,得x =e -(a +1).∴当e-(a +1)≤1e ,即a ≥0时,x ∈⎣⎢⎡⎦⎥⎤1e ,e 时f ′(x )≥0恒成立,f (x )单调递增, 此时f (x )min =f ⎝ ⎛⎭⎪⎫1e =a -1e .当e-(a +1)≥e ,即a ≤-2时,x ∈⎣⎢⎡⎦⎥⎤1e ,e 时f ′(x )≤0恒成立,f (x )单调递减,此时f (x )min=f (e)=a e +e.当1e <e -(a +1)<e ,即-2<a <0时,x ∈⎣⎢⎡⎭⎪⎫1e ,e -(a +1)时f ′(x )<0,f (x )单调递减;当x ∈(e -(a +1),e)时,f ′(x )>0,f (x )单调递增,此时f (x )min =f (e -(a +1))=-e-(a +1).(3)证明 g ′(x )=f ′(x )+ax -(2a +1) =ln x +ax -a =ln x +a (x -1),∴当a ≥0时,x ∈(1,2)时,ln x >0,a (x -1)≥0,g ′(x )>0恒成立,函数y =g (x )在x ∈(1,2)时单调递增,充分条件成立; 又当a =-12时,代入g ′(x )=ln x +a (x -1)=ln x -12x +12.设h (x )=g ′(x )=ln x -12x +12,x ∈(1,2),则h ′(x )=1x -12=2-x2x >0恒成立,∴当x ∈(1,2)时,h (x )单调递增.又h (1)=0,∴当x ∈(1,2)时,h (x )>0恒成立. 而h (x )=g ′(x ),∴当x ∈(1,2)时,g ′(x )>0恒成立, 函数y =g (x )单调递增, ∴必要条件不成立.综上,a ≥0是函数y =g (x )在x ∈(1,2)时单调递增的充分不必要条件. 2.设函数f (x )=e x-|x -a |,其中a 是实数. (1)若f (x )在R 上单调递增,求实数a 的取值范围;(2)若函数有极大值点x 2和极小值点x 1,且f (x 2)-f (x 1)≥k (x 2-x 1)恒成立,求实数k 的取值范围.解 (1)因为f (x )=e x-|x -a |=⎩⎪⎨⎪⎧e x-x +a ,x ≥a ,e x+x -a ,x <a ,则f ′(x )=⎩⎪⎨⎪⎧e x-1,x ≥a ,e x+1,x <a ,因为f (x )在R 上单调递增,所以f ′(x )≥0恒成立,当x <a 时,f ′(x )=e x+1≥1>0恒成立,当x ≥a 时,f ′(x )=e x-1≥0恒成立, 故应f ′(a )≥0,即a ≥0.(2)由(1)知当a ≥0时,f (x )在R 上单调递增,不符合题意,所以有a <0. 此时,当x <a 时,f ′(x )=e x+1≥1>0,f (x )单调递增, 当x ≥a 时,f ′(x )=e x-1,令f ′(x )=0,得x =0,所以f ′(x )<0在(a,0)上恒成立,f (x )在(a,0)上单调递减,f ′(x )>0在(0,+∞)上恒成立,f (x )在(0,+∞)上单调递增,所以f (x )极大=f (a )=e a,f (x )极小=f (0)=1+a ,即a <0符合题意.由f (x 2)-f (x 1)≥k (x 2-x 1)恒成立,可得e a-a -1≥ka 对任意a <0恒成立, 设g (a )=e a-(k +1)a -1,求导,得g ′(a )=e a-(k +1),①当k ≤-1时,g ′(a )>0恒成立,g (a )在(-∞,0)上单调递增,又因为g (-1)=1e +k <0,与g (a )>0矛盾;②当k ≥0时,g ′(a )<0在(-∞,0)上恒成立,g (a )在(-∞,0)上单调递减, 又因为g (0)=0,所以此时g (a )≥0恒成立,符合题意;③当-1<k <0时,g ′(a )>0在(-∞,0)上的解集为(ln(k +1),0),即g (a )在(ln(k +1),0)上单调递增,又因为g (0)=0,所以g (ln (k +1))<0不符合题意.综上,实数k 的取值范围为[0,+∞).3.(2017·江苏泰兴中学质检)已知函数f (x )=13x 3-mx 2-x +13m ,其中m ∈R .(1)求函数y =f (x )的单调区间;(2)若对任意的x 1,x 2∈[-1,1],都有|f ′(x 1)-f ′(x 2)|≤4,求实数m 的取值范围; (3)求函数f (x )的零点个数. 解 (1)f ′(x )=x 2-2mx -1,由f ′(x )≥0,得x ≤m -m 2+1或x ≥m +m 2+1;故函数f (x )的单调增区间为(-∞,m -m 2+1),(m +m 2+1,+∞), 由f ′(x )<0,得m -m 2-1<x <m +m 2+1,故函数f (x )的单调减区间为(m -m 2+1,m +m 2+1).(2)“对任意的x 1,x 2∈[-1,1],都有|f ′(x 1)-f ′(x 2)|≤4”等价于“函数y =f ′(x ),x ∈[-1,1]的最大值与最小值的差小于等于4”. 对于f ′(x )=x 2-2mx -1,对称轴x =m .①当m <-1时,f ′(x )的最大值为f ′(1),最小值为f ′(-1), 由f ′(1)-f ′(-1)≤4,即-4m ≤4,解得m ≥-1,舍去;②当-1≤m ≤1时,f ′(x )的最大值为f ′(1)或f ′(-1),最小值为f ′(m ),由⎩⎪⎨⎪⎧f ′(1)-f ′(m )≤4,f ′(-1)-f ′(m )≤4,即⎩⎪⎨⎪⎧m 2-2m -3≤0,m 2+2m -3≤0,解得-1≤m ≤1;③当m >1时,f ′(x )的最大值为f ′(-1),最小值为f ′(1), 由f ′(-1)-f ′(1)≤4,即4m ≤4,解得m ≤1,舍去. 综上,实数m 的取值范围是[-1,1]. (3)由f ′(x )=0,得x 2-2mx -1=0,因为Δ=4m 2+4>0,所以y =f (x )既有极大值也有极小值. 设f ′(x 0)=0,即x 20-2mx 0-1=0,x 20=2mx 0+1,则f (x 0)=13x 30-mx 20-x 0+13m =-13mx 20-23x 0+13m =-23x 0(m 2+1),所以极大值f (m -m 2+1)=-23(m -m 2+1)(m 2+1)>0,极小值f (m +m 2+1)=-23(m +m 2+1)(m 2+1)<0,故函数f (x )有三个零点.4.已知函数f (x )=x 3+ax 2-a 2x +2,a ∈R . (1)若a <0,试求函数y =f (x )的单调递减区间;(2)若a =0,且曲线y =f (x )在点A ,B (A ,B 不重合)处切线的交点位于直线x =2上,证明:A ,B 两点的横坐标之和小于4;(3)如果对于一切x 1,x 2,x 3∈[0,1],总存在以f (x 1),f (x 2),f (x 3)为三边长的三角形,试求正实数a 的取值范围.(1)解 函数f (x )的导函数f ′(x )=3x 2+2ax -a 2=3(x +a )⎝ ⎛⎭⎪⎫x -a 3.因为a <0,由f ′(x )<0,解得a3<x <-a .所以函数y =f (x )的单调递减区间为⎝ ⎛⎭⎪⎫a3,-a . (2)证明 当a =0时,f (x )=x 3+2.设在点A (x 1,x 31+2),B (x 2,x 32+2)处的切线交于直线x =2上一点P (2,t ). 因为y ′=3x 2,所以曲线y =f (x )在点A 处的切线斜率为k =3x 21, 所以在点A 处的切线方程为y -(x 31+2)=3x 21(x -x 1). 因为切线过点P ,所以t -(x 31+2)=3x 21(2-x 1), 即2x 31-6x 21+(t -2)=0. 同理可得2x 32-6x 22+(t -2)=0, 两式相减得2(x 31-x 32)-6(x 21-x 22)=0,即(x 1-x 2)(x 21+x 1x 2+x 22)-3(x 1-x 2)(x 1+x 2)=0, 因为x 1-x 2≠0,所以x 21+x 1x 2+x 22-3(x 1+x 2)=0, 即(x 1+x 2)2-x 1x 2-3(x 1+x 2)=0. 因为x 1x 2≤⎝ ⎛⎭⎪⎫x 1+x 222,且x 1≠x 2,所以x 1x 2<⎝⎛⎭⎪⎫x 1+x 222.从而上式可以化为(x 1+x 2)2-⎝⎛⎭⎪⎫x 1+x 222-3(x 1+x 2)<0,即(x 1+x 2)(x 1+x 2-4)<0.解得0<x 1+x 2<4,即A ,B 两点的横坐标之和小于4. (3)解 由题设知,f (0)<f (1)+f (1), 即2<2(-a 2+a +3),解得-1<a <2. 又因为a >0,所以0<a <2. 因为f ′(x )=3(x +a )⎝ ⎛⎭⎪⎫x -a 3,所以当x ∈⎝ ⎛⎭⎪⎫0,a 3时,f ′(x )<0,f (x )单调递减,当x ∈⎝ ⎛⎭⎪⎫a3,1时,f ′(x )>0,f (x )单调递增.所以当x =a 3时,f (x )有最小值f ⎝ ⎛⎭⎪⎫a 3=-527a 3+2. 从而条件转化为⎩⎪⎨⎪⎧f ⎝ ⎛⎭⎪⎫a 3=-527a 3+2>0, ①f (0)<2⎝ ⎛⎭⎪⎫-527a 3+2, ②f (1)<2⎝ ⎛⎭⎪⎫-527a 3+2. ③由①得a <33235;由②得a <335,再根据0<a <2,得0<a <335.不等式③化为1027a 3-a 2+a -1<0.令g (a )=1027a 3-a 2+a -1,则g ′(a )=109a 2-2a +1>0,所以g (a )为增函数.又g (2)=-127<0,所以当a ∈⎝ ⎛⎭⎪⎪⎫0,335时,g (a )<0恒成立,即③成立. 所以a 的取值范围为⎝⎛⎭⎪⎪⎫0,335.2.数 列1.已知数列{a n }中a 1=1,a n +1=⎩⎪⎨⎪⎧13a n +n ,n 为奇数,a n -3n ,n 为偶数.(1)是否存在实数λ,使得数列{a 2n -λ}是等比数列?若存在,求出λ的值;若不存在,请说明理由;(2)若S n 是数列{a n }的前n 项和,求满足S n >0的所有正整数n . 解 (1)由已知,得a 2(n +1)=13a 2n +1+(2n +1)=13[a 2n -3(2n )]+2n +1=13a 2n +1. 令a 2(n +1)-λ=13(a 2n -λ),得a 2(n +1)=13a 2n +23λ,所以λ=32.此时,a 2-λ=13+1-32=-16.所以存在λ=32,使得数列{a 2n -λ}是等比数列.(2)由(1)知,数列⎩⎨⎧⎭⎬⎫a 2n -32是首项为-16,公比为13的等比数列,所以a 2n -32=-16⎝ ⎛⎭⎪⎫13n -1=-12·13n ,即a 2n =12⎝ ⎛⎭⎪⎫3-13n .由a 2n =13a 2n -1+(2n -1),得a 2n -1=3a 2n -3(2n -1)=32⎝ ⎛⎭⎪⎫3-13n -6n +3,所以a 2n -1+a 2n =32⎝ ⎛⎭⎪⎫3-13n -6n +3+12⎝ ⎛⎭⎪⎫3-13n=-2⎝ ⎛⎭⎪⎫13n-6n +9,所以S 2n =(a 1+a 2)+(a 3+a 4)+…+(a 2n -1+a 2n )=-2⎣⎢⎡⎦⎥⎤13+⎝ ⎛⎭⎪⎫132+…+⎝ ⎛⎭⎪⎫13n -6(1+2+…+n )+9n =13n -3n 2+6n -1,从而S 2n -1=S 2n -a 2n =32×13n -3n 2+6n -52.因为13n 和-3n 2+6n =-3(n -1)2+3在n ∈N *时均单调递减,所以S 2n 和S 2n -1均各自单调递减.计算得S 1=1,S 2=73,S 3=-73,S 4=-89,所以满足S n >0的所有正整数n 的值为1和2.2.已知数列{a n }的前n 项和为S n ,设数列{b n }满足b n =2(S n +1-S n )S n -n (S n +1+S n )(n ∈N *). (1)若数列{a n }为等差数列,且b n =0,求数列{a n }的通项公式;(2)若a 1=1,a 2=3,且数列{a 2n -1},{a 2n }都是以2为公比的等比数列,求满足不等式b 2n <b 2n -1的所有正整数n 的集合.解 (1)设等差数列{a n }的公差为d , 所以a n +1=a 1+nd ,S n =na 1+n (n -1)2d .由b n =2(S n +1-S n )S n -n (S n +1+S n )(n ∈N *), 得b n =2a n +1S n -n (2S n +a n +1). 又由b n =0,得2(a 1+nd )⎣⎢⎡⎦⎥⎤na 1+n (n -1)2d -n [2na 1+n (n -1)d +a 1+nd ]=0对一切n ∈N *都成立,即(d 2-d )n 2+(3a 1d -d 2-2a 1)n +2a 21-a 1d -a 1=0对一切n ∈N *都成立. 令n =1,n =2,解得⎩⎪⎨⎪⎧d =0,a 1=0或⎩⎪⎨⎪⎧d =1,a 1=1,经检验,符合题意.所以数列{a n }的通项公式为a n =0或a n =n . (2)由题意得a 2n -1=2n -1,a 2n =3×2n -1,S 2n =2n -1+3(2n -1)=4×2n -4,S 2n -1=S 2n -a 2n =4×2n -4-3×2n -1=5×2n -1-4. b 2n =2a 2n +1S 2n -2n (2S 2n +a 2n +1)=2×2n×(4×2n-4)-2n (8×2n-8+2n) =2n +1(2n +2-9n -4)+16n .b 2n -1=2a 2n S 2n -1-(2n -1)(2S 2n -1+a 2n )=6×2n -1×(5×2n -1-4)-(2n -1)(10×2n -1-8+3×2n -1)=2n -1(30×2n -1-26n -11)+16n-8.所以b 2n -b 2n -1=2n +1(2n +2-9n -4)+16n -[2n -1(30×2n -1-26n -11)+16n -8]=2n⎝⎛⎭⎪⎫2n -1-5n -52+8=22n -1+8-2n ⎝⎛⎭⎪⎫5n +52. 记f (n )=22n -1+8-2n ⎝⎛⎭⎪⎫5n +52,即f (n )=2n ⎣⎢⎡⎦⎥⎤12×2n-⎝⎛⎭⎪⎫5n +52+8.记g (n )=12×2n-⎝⎛⎭⎪⎫5n +52,则g (n +1)-g (n )=12×2n +1-⎝⎛⎭⎪⎫5n +152-12×2n +5n +52=12×2n-5,当n =1,2,3时,g (n +1)-g (n )<0;当n ∈N *时,n ≥4,g (n +1)-g (n )=12×2n -5>0,因为当n =1时,g (1)=-132<0,所以g (4)<0,且g (6)=-12<0,g (7)=532>0.所以f (n )=2n ⎣⎢⎡⎦⎥⎤12×2n -⎝ ⎛⎭⎪⎫5n +52+8在n ≥7(n ∈N *)时也单调递增,当n =1时,f (1)=-5<0; 当n =2时,f (2)=-34<0; 当n =3时,f (3)=-100<0; 当n =4时,f (4)=-224<0; 当n =5时,f (5)=-360<0; 当n =6时,f (6)=-24<0; 当n =7时,f (7)=3400>0,所以满足条件的正整数n 的集合为{1,2,3,4,5,6}.3.已知等差数列{a n }的前n 项和为S n ,且2a 5-a 3=13,S 4=16. (1)求数列{a n }的前n 项和S n ;(2)设T n =∑ni =1(-1)i a i ,若对一切正整数n ,不等式λT n <[a n +1+(-1)n +1a n ]2n -1恒成立,求实数λ的取值范围;(3)是否存在正整数m ,n (n >m >2),使得S 2,S m -S 2,S n -S m 成等比数列?若存在,求出所有的m ,n ;若不存在,请说明理由. 解 (1)设数列{a n }的公差为d . 因为2a 5-a 3=13,S 4=16,所以⎩⎪⎨⎪⎧2(a 1+4d )-(a 1+2d )=13,4a 1+6d =16,解得⎩⎪⎨⎪⎧a 1=1,d =2,所以a n =2n -1,S n =n 2.(2)①当n 为偶数时,设n =2k ,k ∈N *,则T 2k =(a 2-a 1)+(a 4-a 3)+…+(a 2k -a 2k -1)=2k . 代入不等式λT n <[a n +1+(-1)n +1a n ]·2n -1,得λ·2k <4k,从而λ<4k2k.设f (k )=4k2k ,则f (k +1)-f (k )=4k +12(k +1)-4k2k =4k(3k -1)2k (k +1).因为k ∈N *,所以f (k +1)-f (k )>0,所以f (k )是递增的,所以f (k )min =2,所以λ<2. ②当n 为奇数时,设n =2k -1,k ∈N *, 则T 2k -1=T 2k -(-1)2ka 2k =2k -(4k -1)=1-2k . 代入不等式λT n <[a n +1+(-1)n +1a n ]2n -1,得λ(1-2k )<(2k -1)4k ,从而λ>-4k .因为k ∈N *,所以-4k的最大值为-4,所以λ>-4. 综上,λ的取值范围为(-4,2).(3)假设存在正整数m ,n (n >m >2),使得S 2,S m -S 2,S n -S m 成等比数列, 则(S m -S 2)2=S 2(S n -S m ),即(m 2-4)2=4(n 2-m 2), 所以4n 2=(m 2-2)2+12,即4n 2-(m 2-2)2=12, 即(2n -m 2+2)(2n +m 2-2)=12.因为n >m >2,所以n ≥4,m ≥3,所以2n +m 2-2≥15.因为2n -m 2+2是整数,所以等式(2n -m 2+2)(2n +m 2-2)=12不成立, 故不存在正整数m ,n (n >m >2),使得S 2,S m -S 2,S n -S m 成等比数列.4.若一个数列从第2项起,每一项与它前一项的差都大于2,则称这个数列为“A 型数列”. (1)若首项为1,公差为整数的等差数列{a n }为“A 型数列”,且其前n 项和为S n ,若对于任意n ∈N *,都有S n <32n 2+n ,求{a n }的通项公式;(2)已知等比数列{a n }的每一项均为正整数,且{a n }为“A 型数列”,b n =23a n ,c n =a n(n +1)·2n -5,当数列{b n }不是“A 型数列”时,试判断数列{c n }是否为“A 型数列”,并说明理由. 解 (1)设等差数列{a n }的公差为d ,则d >2, 由a 1=1,得S n =n +n (n -1)2d ,且S 1<52.由题意,得n +n (n -1)2d <32n 2+n 对n ∈N *均成立,即d <3nn -1对n ≥2均成立, ∵3n n -1=3+3n -1>3, ∴d ≤3,又d >2, ∴d =3,∴a n =3n -2.(2)设数列{a n }的公比为q ,则a n =a 1q n -1,∵{a n }的每一项均为正整数, 且a n +1-a n =a n q -a n =a n (q -1)>2>0, ∴a 1>0,且q >1,∵a n +1-a n =q (a n -a n -1)>a n -a n -1, 即在{a n -a n -1}中,a 2-a 1为最小项, 同理,在{b n -b n -1}中,b 2-b 1为最小项,由{a n }为“A 型数列”,可知只需a 2-a 1>2,即a 1(q -1)>2, 又∵{b n }不是“A 型数列”,且b 2-b 1为最小项, ∴b 2-b 1≤2,即a 1(q -1)≤3,由数列{a n }的每一项均为正整数,可得a 1(q -1)=3, ∴a 1=1,q =4或a 1=3,q =2. ①当a 1=1,q =4时,a n =4n -1,则c n =4n -1(n +1)·2n -5=2n +3n +1, 令d n =c n +1-c n (n ∈N *),则d n =2n +4n +2-2n +3n +1=2n +3·n (n +1)(n +2),令e n =d n +1-d n (n ∈N *),则e n =2n +4·n +1(n +2)(n +3)-2n +3·n (n +1)(n +2)=2n +3n +2·n 2+n +2(n +1)(n +3)>0,∴{d n }为递增数列, 即d n >d n -1>d n -2>…>d 1,即c n +1-c n >c n -c n -1>c n -1-c n -2>…>c 2-c 1, ∵c 2-c 1=323-8=83>2,∴对任意的n ∈N *都有c n +1-c n >2, 即数列{c n }为“A 型数列”. ②当a 1=3,q =2时,a n =3·2n -1,则c n =3·2n +1(n +1)·2n -5=48n +1, 显然,{c n }为递减数列,c 2-c 1<0≤2, 故数列{c n }不是“A 型数列”; 综上所述,当a n =4n -1时,数列{c n }为“A 型数列”,当a n =3·2n -1时,数列{c n }不是“A 型数列”.小题满分练小题满分练11.设全集U=R,A={x|x2-2x≤0},B={y|y=cos x,x∈R},则图中阴影部分表示的区间是________.答案(-∞,-1)∪(2,+∞)解析因为A={x|0≤x≤2}=[0,2],B={y|-1≤y≤1}=[-1,1],所以A∪B=[-1,2],所以∁R(A∪B)=(-∞,-1)∪(2,+∞).2.(2017·苏州暑假测试)命题“∃x>1,x2≥2”的否定是________.答案∀x>1,x2<2解析根据存在性命题的否定规则得“∃x>1,x2≥2”的否定是“∀x>1,x2<2”.3.若复数z满足z i=1+2i,则z的共轭复数是________.答案2+i解析∵z i=1+2i,∴z=1+2ii=2-i,∴z=2+i.4.(2017·徐州、连云港、宿迁三检)已知一组数据3,6,9,8,4,则该组数据的方差是________.答案265(或5.2)解析这组数据的平均数x=15(3+6+9+8+4)=6,方差s2=15(9+0+9+4+4)=265.5.若流程图如图所示,则该程序运行后输出的值是________.答案10000。
2018年江苏省高考冲刺压轴数学试卷(有答案)

绝密★启封前2018江苏省高考压轴卷数 学I注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共4页,包含非选择题(第1题 ~第20题,共20题).本卷满分为160分,考试时间为120分钟。
考试结束后,请将本试卷和答题卡一并交回。
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题上所粘贴的条形码上的姓名、准考证号与本人是否相符。
4.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。
5.如需改动,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗一、填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡相应位置上 1.若集合A={﹣1,0,1,2},B={x|x+1>0},则A∩B= .2.若复数z 满足z (1﹣i )=2i (i 是虚数单位),z 是z 的共轭复数,则z = .3.某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有 人.4.如图,该程序运行后输出的结果为 .5.将函数y=3sin (2x ﹣6π)的图象向左平移4π个单位后,所在图象对应的函数解析式为 . 6.如图,在长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=3cm ,AA 1=2cm ,则三棱锥A ﹣B 1D 1D 的体积为 cm 3.7.如图,在一个面积为8的矩形中随机撒一粒黄豆,若黄豆落到阴影部分的概率为41,则阴影部分的面积为 .8.已知双曲线﹣=1(a >0,b >0)的左、右端点分别为A 、B 两点,点C (0, b ),若线段AC的垂直平分线过点B ,则双曲线的离心率为 . 9.设公比不为1的等比数列{a n }满足a 1a 2a 3=﹣81,且a 2,a 4,a 3成等差数列,则数列{a n }的前4项和为 . 10.设定义在R 上的偶函数f (x )在区间(﹣∞,0]上单调递减,若f (1﹣m )<f (m ),则实数m 的取值范围是 .11.已知函数f (x )=,若a 、b 、c 互不相等,且f (a )=f (b )=f (c ),则a+b+c 的取值范围是 .12.如图,在△ABC 中,已知=21,P 是BN 上一点,若AP =m AB +41,则实数m 的值是 .13.已知非零向量a ,b 满足|a |=|b |=|a +b |,则a 与2a -b 夹角的余弦值为 .14.已知函数f(x)=⎩⎨⎧≥++-<1x ,a x 25x 9x 1x ,x sin 23,若函数f (x )的图象与直线y=x 有三个不同的公共点,则实数a 的取值集合为 . 15.如图,在三棱柱1B 1C 1中,,点E ,F 分别在棱BB 1 ,CC 1上(均异于端点),且∠∠ACF ,AE ⊥BB 1,AF ⊥CC 1.求证:(1)平面AEF ⊥平面BB 1C 1C ; (2)BC // 平面AEF .16.在△ABC 中,角,,A B C 的对边分别为,,a b c ,且()2cos cos a b C c B -⋅=⋅. (1)求角C 的大小;(2)若2c =,△ABC 3.17.已知中心在坐标原点的椭圆C ,F 1,F 2 分别为椭圆的左、右焦点,长轴长为6,离心率为(1)求椭圆C 的标准方程;(2)已知点P 在椭圆C 上,且PF 1=4,求点P 到右准线的距离.18.如图,四棱锥P ﹣ABCD 中,PA ⊥平面ABCD ,四边形ABCD 为直角梯形,AD ∥BC ,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E ,F ,G 分别为BC ,PD ,PC 的中点. (1)求EF 与DG 所成角的余弦值;(2)若M 为EF 上一点,N 为DG 上一点,是否存在MN ,使得MN ⊥平面PBC ?若存在,求出点M ,N 的坐标;若不存在,请说明理由.19.设等比数列a 1,a 2,a 3,a 4的公比为q ,等差数列b 1,b 2,b 3,b 4的公差为d ,且10q d ≠≠,. 记i i i c a b =+(,2,3,4).(1)求证:数列123c c c ,,不是等差数列; (2)设11a =,2q =.若数列123c c c ,,是等比数列,求b 2关于d 的函数关系式及其定义域; (3)数列1234c c c c ,,,能否为等比数列?并说明理由. 20.(16分)已知f (x )=x 2+mx+1(m ∈R ),g (x )=e x .(1)当x ∈[0,2]时,F (x )=f (x )﹣g (x )为增函数,求实数m 的取值范围; (2)若m ∈(﹣1,0),设函数 G(x)=)x (g )x (f ,H(x)=﹣41x+45,求证:对任意x 1,x 2∈[1,1﹣m],G (x 1)<H (x 2)恒成立.AA 11C 1B C FE(第16题)数学II (附加题)注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共2页,均为非选择题(第21题 ~第23题)。
2018考前两个月数学[高考总复习资料]理科(江苏专用)总复习训练题:考前回扣2 Word版含答案
![2018考前两个月数学[高考总复习资料]理科(江苏专用)总复习训练题:考前回扣2 Word版含答案](https://img.taocdn.com/s3/m/1da4282cf78a6529647d5383.png)
回扣2 导数1.导数的几何意义(1)f′(x0)的几何意义:曲线y=f(x)在点(x0,f(x0))处的切线的斜率,该切线的方程为y -f(x0)=f′(x0)·(x-x0).(2)切点的两大特征:①在曲线y=f(x)上;②在切线上.2.利用导数研究函数的单调性(1)求可导函数单调区间的一般步骤①求函数f(x)的定义域;②求导函数f′(x);③由f′(x)>0的解集确定函数f(x)的单调增区间,由f′(x)<0的解集确定函数f(x)的单调减区间.(2)由函数的单调性求参数的取值范围①若可导函数f(x)在区间M上单调递增,则f′(x)≥0(x∈M)恒成立;若可导函数f(x)在区间M上单调递减,则f′(x)≤0(x∈M)恒成立;②若可导函数在某区间上存在单调递增(减)区间,f′(x)>0(或f′(x)<0)在该区间上存在解集;③若已知f(x)在区间I上的单调性,区间I中含有参数时,可先求出f(x)的单调区间,则I是其单调区间的子集.3.利用导数研究函数的极值与最值(1)求函数的极值的一般步骤①确定函数的定义域;②解方程f′(x)=0;③判断f′(x)在方程f′(x)=0的根x0两侧的符号变化:若左正右负,则x0为极大值点;若左负右正,则x0为极小值点;若不变号,则x0不是极值点.(2)求函数f(x)在区间[a,b]上的最值的一般步骤①求函数y=f(x)在[a,b]内的极值;②比较函数y=f(x)的各极值与端点处的函数值f(a),f(b)的大小,最大的一个是最大值,最小的一个是最小值.1.已知可导函数f (x )在(a ,b )上单调递增(减),则f ′(x )≥0(≤0)对∀x ∈(a ,b )恒成立,不能漏掉“=”,且需验证“=”不能恒成立;已知可导函数f (x )的单调递增(减)区间为(a ,b ),则f ′(x )>0(<0)的解集为(a ,b ).2.f ′(x )=0的解不一定是函数f (x )的极值点.一定要检验在x =x 0的两侧f ′(x )的符号是否发生变化,若变化,则为极值点;若不变化,则不是极值点.1.曲线y =f (x )=x x 2+1在点(1,f (1))处的切线方程是____________. 答案 y =12解析 ∵f (x )=x x 2+1的导数f ′(x )=1-x 2(1+x 2)2, ∴曲线在点(1,f (1))处的切线斜率k =0, ∵切点为⎝ ⎛⎭⎪⎫1,12, ∴曲线在点(1,f (1))处的切线方程为y =12. 2.(2016·四川)已知a 为函数f (x )=x 3-12x 的极小值点,则a =__________. 答案 2解析 ∵f (x )=x 3-12x ,∴f ′(x )=3x 2-12,令f ′(x )=0,则x 1=-2,x 2=2.当x ∈(-∞,-2),(2,+∞)时,f ′(x )>0,f (x )单调递增;当x ∈(-2,2)时,f ′(x )<0,f (x )单调递减,∴f (x )的极小值点为a =2.3.f (x )=x 2+3xf ′(2),则1+f ′(1)=________.答案 -3解析 由f (x )=x 2+3xf ′(2),求导可得f ′(x )=2x +3f ′(2),f ′(2)=4+3f ′(2), f ′(2)=-2,则f ′(x )=2x -6,f ′(1)=2-6=-4,所以1+f ′(1)=-3.4.设曲线f (x )=-e x -x (e 为自然对数的底数)上任意一点处的切线为l 1,总存在曲线g (x )=3ax +2cos x 上某点处的切线l 2,使得l 1⊥l 2,则实数a 的取值范围为____________.答案 ⎣⎢⎡⎦⎥⎤-13,23 解析 由f (x )=-e x -x ,得f ′(x )=-e x -1,因为e x +1>1,所以1e x +1∈(0,1), 由g (x )=3ax +2cos x ,得g ′(x )=3a -2sin x ,又-2sin x ∈[-2,2],所以3a -2sin x ∈[-2+3a,2+3a ],要使过曲线f (x )=-e x -x 上任意一点的切线l 1,总存在过曲线g (x )=3ax +2cos x 上一点处的切线l 2,使得l 1⊥l 2,则⎩⎪⎨⎪⎧-2+3a ≤0,2+3a ≥1, 解得-13≤a ≤23. 5.函数f (x )=x 3+ax 2+bx +a 2在x =1处有极小值10,则a +b 的值为________.答案 -7解析 ∵f ′(x )=3x 2+2ax +b ,由已知可得⎩⎪⎨⎪⎧ f ′(1)=3+2a +b =0,f (1)=1+a +b +a 2=10,解得a =4,b =-11或a =-3,b =3,经验证,a =4,b =-11符合题意,故a +b =-7.6.若函数f (x )=x 2-12ln x +1在其定义域内的一个子区间(k -1,k +1)内不是单调函数,则实数k 的取值范围是______________.答案 ⎣⎢⎡⎭⎪⎫1,32 解析 因为f (x )的定义域为(0,+∞),f ′(x )=2x -12x, 由f ′(x )=0,得x =12. 利用图象可得⎩⎪⎨⎪⎧ k -1<12<k +1,k -1≥0,解得1≤k <32. 7.已知奇函数f (x )是定义在R 上的可导函数,其导函数为f ′(x ),当x >0时,有2f (x )+xf ′(x )>x 2,则不等式(x +2018)2f (x +2018)+4f (-2)<0的解集为____________. 答案 (-∞,-2016)解析 由题观察联想可设g (x )=x 2f (x ),g ′(x )=2xf (x )+x 2f ′(x ),结合条件x >0,2f (x )+xf ′(x )>x 2,得 g ′(x )=2xf (x )+x 2f ′(x )>0,g (x )=x 2f (x )在(0,+∞)上为增函数.又f (x )为R 上的奇函数,所以g (x )为奇函数,所以g (x )在(-∞,0)上为增函数. 由(x +2018)2f (x +2018)+4f (-2)<0,可得(x +2018)2f (x +2018)<4f (2),即g (x +2018)<g (2),所以x +2018<2,故x <-2016.8.若函数f (x )=⎩⎪⎨⎪⎧ 12x -1,x <1,ln x x 2,x ≥1,则函数y =|f (x )|-18的零点个数为________. 答案 4解析 当x <1时,f (x )=12x -1单调递减,且f (x )>-12;当x ≥1时,f (x )=ln x x 2,则f ′(x )=1-2ln x x 3,令f ′(x )=0,得x =e ,当∈[1,e)时,f ′(x )>0,f (x )单调递增,当x ∈(e ,+∞)时,f ′(x )<0,f (x )单调递减,所以f (x )max =f (e)=12e >18,且f (x )≥0,当x 趋近于+∞时,f (x )趋近于0.作出函数y =|f (x )|的大致图象如图所示,由图可知,函数y =|f (x )|-18的零点个数为4.9.已知函数f (x )=x +1e x (e 为自然对数的底数).(1)求函数f (x )的单调区间;(2)设函数φ(x )=xf (x )+tf ′(x )+1e x ,存在实数x 1,x 2∈[0,1],使得2φ(x 1)<φ(x 2)成立,求实数t 的取值范围.解 (1)∵函数的定义域为R ,f ′(x )=-xe x ,∴当x <0时,f ′(x )>0,当x >0时,f ′(x )<0,∴f (x )在(-∞,0)上单调递增,在(0,+∞)上单调递减.∴f (x )的单调增区间为(-∞,0),单调减区间为(0,+∞).(2)存在x 1,x 2∈[0,1],使得2φ(x 1)<φ(x 2)成立,则2[φ(x )]min <[φ(x )]max .∵φ(x )=xf (x )+tf ′(x )+e -x =x 2+(1-t )x +1e x , ∴φ′(x )=-x 2+(1+t )x -t e x =-(x -t )(x -1)e x . ①当t ≥1时,φ′(x )≤0,φ(x )在[0,1]上单调递减,∴2φ(1)<φ(0),即t >3-e 2>1; ②当t ≤0时,φ′(x )≥0,φ(x )在[0,1]上单调递增,∴2φ(0)<φ(1),即t <3-2e <0;③当0<t <1时,若x ∈[0,t ),φ′(x )<0,φ(x )在[0,t )上单调递减,若x ∈(t,1],φ′(x )≥0,φ(x )在(t,1]上单调递增,∴2φ(t )<max{φ(0),φ(1)},即2t +1e t <max ⎩⎨⎧⎭⎬⎫1,3-t e .(*) 由(1)知,g (t )=2·t +1e t 在[0,1]上单调递减,故4e ≤2t +1e t ≤2,而2e ≤3-t e ≤3e, ∴不等式(*)无解.综上所述,存在t ∈(-∞,3-2e)∪⎝ ⎛⎭⎪⎫3-e 2,+∞,使得命题成立. 10.(2017·山东)已知函数f (x )=13x 3-12ax 2,a ∈R. (1)当a =2时,求曲线y =f (x )在点(3,f (3))处的切线方程;(2)设函数g (x )=f (x )+(x -a )cos x -sin x ,讨论g (x )的单调性并判断有无极值,有极值时求出极值.解 (1)由题意f ′(x )=x 2-ax ,所以当a =2时,f (3)=0,f ′(x )=x 2-2x ,所以f ′(3)=3,因此曲线y =f (x )在点(3,f (3))处的切线方程是y =3(x -3),即3x -y -9=0.(2)因为g (x )=f (x )+(x -a )cos x -sin x ,所以g ′(x )=f ′(x )+cos x -(x -a )sin x -cos x=x (x -a )-(x -a )sin x =(x -a )(x -sin x ).令h (x )=x -sin x ,则h ′(x )=1-cos x ≥0,所以h (x )在R 上单调递增.因为h (0)=0,所以当x >0时,h (x )>0;当x <0时,h (x )<0.①当a <0时,g ′(x )=(x -a )(x -sin x ),当x ∈(-∞,a )时,x -a <0,g ′(x )>0,g (x )单调递增;当x ∈(a,0)时,x -a >0,g ′(x )<0,g (x )单调递减;当x ∈(0,+∞)时,x -a >0,g ′(x )>0,g (x )单调递增.所以当x =a 时,g (x )取到极大值,极大值是g (a )=-16a 3-sin a ; 当x =0时,g (x )取到极小值,极小值是g (0)=-a .②当a =0时,g ′(x )=x (x -sin x ),当x ∈(-∞,+∞)时,g ′(x )≥0,g (x )单调递增;所以g (x )在(-∞,+∞)上单调递增,g (x )无极大值也无极小值;③当a >0时,g ′(x )=(x -a )(x -sin x ),当x ∈(-∞,0)时,x -a <0,g ′(x )>0,g (x )单调递增;当x ∈(0,a )时,x -a <0,g ′(x )<0,g (x )单调递减;当x ∈(a ,+∞)时,x -a >0,g ′(x )>0,g (x )单调递增.所以当x =0时,g (x )取到极大值,极大值是g (0)=-a ;当x =a 时,g (x )取到极小值,极小值是g (a )=-16a 3-sin a . 综上所述,当a <0时,函数g (x )在(-∞,a )和(0,+∞)上单调递增,在(a,0)上单调递减,函数既有极大值,又有极小值,极大值是g (a )=-16a 3-sin a ,极小值是g (0)=-a ; 当a =0时,函数g (x )在(-∞,+∞)上单调递增,无极值;当a>0时,函数g(x)在(-∞,0)和(a,+∞)上单调递增,在(0,a)上单调递减,函数既有极大值,又有极小值,极大值是g(0)=-a,极小值是g(a)=-16a3-sin a.。
2018最新考前两个月数学高考理科(江苏专用)总复习训练题:解答题滚动练7 Word版含答案

解答题滚动练71.如图,在三棱柱ABC -A 1B 1C 1中,所有棱长都相等,且∠ABB 1=60°,D 为AC 的中点,求证:(1)B 1C ∥平面A 1BD ;(2)AB ⊥B 1C .证明 (1)连结AB 1交A 1B 于点E ,连结DE .因为D ,E 分别为AC ,AB 1的中点,所以DE ∥B 1C .因为DE ⊂平面A 1BD ,B 1C ⊄平面A 1BD ,所以B 1C ∥平面A 1BD .(2)取AB 的中点O ,连结OC ,OB 1.因为BA =BB 1,且∠ABB 1=60°,所以△ABB 1为正三角形,而O 为AB 的中点,所以OB 1⊥AB . 在正三角形ABC 中,O 为AB 中点,所以OC ⊥AB .因为OB 1∩OC =O ,且OB 1⊂平面OB 1C ,OC ⊂平面OB 1C ,所以AB ⊥平面OB 1C .又因为B 1C ⊂平面OB 1C ,所以AB ⊥B 1C .2.已知数列{a n }的前n 项和S n 满足:S n =t (S n -a n +1)(t 为常数,且t ≠0,t ≠1).(1)证明:{a n }成等比数列;(2)设b n =a 2n +S n ·a n ,若数列{b n }为等比数列,求t 的值.(1)证明 当n =1时,S 1=t (S 1-a 1+1),得a 1=t ,当n ≥2时,S n =t (S n -a n +1),即(1-t )S n =-ta n +t ,(1-t )S n -1=-ta n -1+t , 所以a n =ta n -1,故{a n }成等比数列.(2)解 由(1)知{a n }成等比数列且公比是t ,∴a n =t n , 故b n =(t n )2+t (1-t n )1-t ·t n ,即b n =t 2n +t n +1-2t 2n +11-t . 若数列{b n }是等比数列,则有b 22=b 1·b 3,而b 1=2t 2,b 2=t 3(2t +1),b 3=t 4(2t 2+t +1),故[t 3(2t +1)]2=(2t 2)·t 4(2t 2+t +1),解得t =12,再将t =12代入b n 得b n =⎝ ⎛⎭⎪⎫12n , 由b n +1b n =12知{b n }为等比数列,所以t =12. 3.图1是一段半圆柱形水渠的直观图,其横断面如图2所示,其中C 为半圆弧ACB 的中。
【配套K12】2018考前两个月数学高考理科(江苏专用)总复习训练题:压轴大题突破练2 Word版含
2.数 列1.已知数列{a n }中a 1=1,a n +1=⎩⎪⎨⎪⎧ 13a n +n ,n 为奇数,a n -3n ,n 为偶数.(1)是否存在实数λ,使得数列{a 2n -λ}是等比数列?若存在,求出λ的值;若不存在,请说明理由;(2)若S n 是数列{a n }的前n 项和,求满足S n >0的所有正整数n .解 (1)由已知,得a 2(n +1)=13a 2n +1+(2n +1) =13[a 2n -3(2n )]+2n +1=13a 2n +1. 令a 2(n +1)-λ=13(a 2n -λ),得a 2(n +1)=13a 2n +23λ,所以λ=32. 此时,a 2-λ=13+1-32=-16. 所以存在λ=32,使得数列{a 2n -λ}是等比数列. (2)由(1)知,数列⎩⎨⎧⎭⎬⎫a 2n -32是首项为-16,公比为13的等比数列, 所以a 2n -32=-16⎝ ⎛⎭⎪⎫13n -1=-12·13n , 即a 2n =12⎝ ⎛⎭⎪⎫3-13n . 由a 2n =13a 2n -1+(2n -1),得a 2n -1=3a 2n -3(2n -1)=32⎝ ⎛⎭⎪⎫3-13n -6n +3, 所以a 2n -1+a 2n =32⎝ ⎛⎭⎪⎫3-13-6n +3+12⎝ ⎛⎭⎪⎫3-13 =-2⎝ ⎛⎭⎪⎫13n -6n +9, 所以S 2n =(a 1+a 2)+(a 3+a 4)+…+(a 2n -1+a 2n )=-2⎣⎢⎡⎦⎥⎤13+⎝ ⎛⎭⎪⎫132+…+⎝ ⎛⎭⎪⎫13n -6(1+2+…+n )+9n =13n -3n 2+6n -1, 从而S 2n -1=S 2n -a 2n =32×13n -3n 2+6n -52. 因为13n 和-3n 2+6n =-3(n -1)2+3在n ∈N *时均单调递减,所以S 2n 和S 2n -1均各自单调递减.计算得S 1=1,S 2=73,S 3=-73,S 4=-89, 所以满足S n >0的所有正整数n 的值为1和2.2.已知数列{a n }的前n 项和为S n ,设数列{b n }满足b n =2(S n +1-S n )S n -n (S n +1+S n )(n ∈N *).(1)若数列{a n }为等差数列,且b n =0,求数列{a n }的通项公式;(2)若a 1=1,a 2=3,且数列{a 2n -1},{a 2n }都是以2为公比的等比数列,求满足不等式b 2n < b 2n -1的所有正整数n 的集合.解 (1)设等差数列{a n }的公差为d ,所以a n +1=a 1+nd ,S n =na 1+n (n -1)2d . 由b n =2(S n +1-S n )S n -n (S n +1+S n )(n ∈N *),得b n =2a n +1S n -n (2S n +a n +1).又由b n =0,得2(a 1+nd )⎣⎢⎡⎦⎥⎤na 1+n (n -1)2d -n [2na 1+n (n -1)d +a 1+nd ]=0对一切n ∈N *都成立,即(d 2-d )n 2+(3a 1d -d 2-2a 1)n +2a 21-a 1d -a 1=0对一切n ∈N *都成立.令n =1,n =2,解得⎩⎪⎨⎪⎧ d =0,a 1=0或⎩⎪⎨⎪⎧ d =1,a 1=1,经检验,符合题意.所以数列{a n }的通项公式为a n =0或a n =n .(2)由题意得a 2n -1=2n -1,a 2n =3×2n -1,S 2n =2n -1+3(2n -1)=4×2n -4,S 2n -1=S 2n -a 2n =4×2n -4-3×2n -1=5×2n -1-4.b 2n =2a 2n +1S 2n -2n (2S 2n +a 2n +1)=2×2n ×(4×2n -4)-2n (8×2n -8+2n )=2n +1(2n +2-9n -4)+16n .b 2n -1=2a 2n S 2n -1-(2n -1)(2S 2n -1+a 2n )=6×2n -1×(5×2n -1-4)-(2n -1)(10×2n -1-8+3×2n -1)=2n -1(30×2n -1-26n -11)+16n -8.所以b 2n -b 2n -1=2n +1(2n +2-9n -4)+16n -[2n -1(30×2n -1-26n -11)+16n -8] =2n ⎝ ⎛⎭⎪⎫2n -1-5n -52+8=22n -1+8-2n ⎝⎛⎭⎪⎫5n +52. 记f (n )=22n -1+8-2n ⎝⎛⎭⎪⎫5n +52,即 f (n )=2n ⎣⎢⎡⎦⎥⎤12×2n -⎝ ⎛⎭⎪⎫5n +52+8.记g (n )=12×2n -⎝⎛⎭⎪⎫5n +52, 则g (n +1)-g (n )=12×2n +1-⎝⎛⎭⎪⎫5n +152-12×2n +5n +52=12×2n -5, 当n =1,2,3时,g (n +1)-g (n )<0;当n ∈N *时,n ≥4,g (n +1)-g (n )=12×2n -5>0, 因为当n =1时,g (1)=-132<0, 所以g (4)<0,且g (6)=-12<0,g (7)=532>0. 所以f (n )=2n ⎣⎢⎡⎦⎥⎤12×2n -⎝ ⎛⎭⎪⎫5n +52+8在n ≥7(n ∈N *)时也单调递增, 当n =1时,f (1)=-5<0;当n =2时,f (2)=-34<0;当n =3时,f (3)=-100<0;当n =4时,f (4)=-224<0;当n =5时,f (5)=-360<0;当n =6时,f (6)=-24<0;当n =7时,f (7)=3400>0,所以满足条件的正整数n 的集合为{1,2,3,4,5,6}.3.已知等差数列{a n }的前n 项和为S n ,且2a 5-a 3=13,S 4=16.(1)求数列{a n }的前n 项和S n ;(2)设T n =∑ni =1(-1)i a i ,若对一切正整数n ,不等式λT n <[a n +1+(-1)n +1a n ]2n -1恒成立,求实数λ的取值范围; (3)是否存在正整数m ,n (n >m >2),使得S 2,S m -S 2,S n -S m 成等比数列?若存在,求出所有的m ,n ;若不存在,请说明理由.解 (1)设数列{a n }的公差为d .因为2a 5-a 3=13,S 4=16,所以⎩⎪⎨⎪⎧ 2(a 1+4d )-(a 1+2d )=13,4a 1+6d =16,解得⎩⎪⎨⎪⎧ a 1=1,d =2,所以a n =2n -1,S n =n 2.(2)①当n 为偶数时,设n =2k ,k ∈N *,则T 2k =(a 2-a 1)+(a 4-a 3)+…+(a 2k -a 2k -1)=2k .代入不等式λT n <[a n +1+(-1)n +1a n ]·2n -1,得λ·2k <4k ,从而λ<4k 2k . 设f (k )=4k 2k ,则f (k +1)-f (k )=4k +12(k +1)-4k 2k =4k (3k -1)2k (k +1).因为k ∈N *,所以f (k +1)-f (k )>0,所以f (k )是递增的,所以f (k )min =2,所以λ<2.②当n 为奇数时,设n =2k -1,k ∈N *,则T 2k -1=T 2k -(-1)2k a 2k =2k -(4k -1)=1-2k .代入不等式λT n <[a n +1+(-1)n +1a n ]2n -1,得λ(1-2k )<(2k -1)4k ,从而λ>-4k . 因为k ∈N *,所以-4k 的最大值为-4,所以λ>-4.综上,λ的取值范围为(-4,2).(3)假设存在正整数m ,n (n >m >2),使得S 2,S m -S 2,S n -S m 成等比数列,则(S m -S 2)2=S 2(S n -S m ),即(m 2-4)2=4(n 2-m 2),所以4n 2=(m 2-2)2+12,即4n 2-(m 2-2)2=12,即(2n -m 2+2)(2n +m 2-2)=12.因为n >m >2,所以n ≥4,m ≥3,所以2n +m 2-2≥15.因为2n -m 2+2是整数,所以等式(2n -m 2+2)(2n +m 2-2)=12不成立,故不存在正整数m ,n (n >m >2),使得S 2,S m -S 2,S n -S m 成等比数列.4.若一个数列从第2项起,每一项与它前一项的差都大于2,则称这个数列为“A 型数列”.(1)若首项为1,公差为整数的等差数列{a n }为“A 型数列”,且其前n 项和为S n ,若对于任意n ∈N *,都有S n <32n 2+n ,求{a n }的通项公式; (2)已知等比数列{a n }的每一项均为正整数,且{a n }为“A 型数列”,b n =23a n ,c n =a n (n +1)·2n -5,当数列{b n }不是“A 型数列”时,试判断数列{c n }是否为“A 型数列”,并说明理由. 解 (1)设等差数列{a n }的公差为d ,则d >2,由a 1=1,得S n =n +n (n -1)2d ,且S 1<52. 由题意,得n +n (n -1)2d <32n 2+n 对n ∈N *均成立, 即d <3n n -1对n ≥2均成立, ∵3n n -1=3+3n -1>3, ∴d ≤3,又d >2,∴d=3,∴a n=3n-2.(2)设数列{a n}的公比为q,则a n=a1q n-1,∵{a n}的每一项均为正整数,且a n+1-a n=a n q-a n=a n(q-1)>2>0,∴a1>0,且q>1,∵a n+1-a n=q(a n-a n-1)>a n-a n-1,即在{a n-a n-1}中,a2-a1为最小项,同理,在{b n-b n-1}中,b2-b1为最小项,由{a n}为“A型数列”,可知只需a2-a1>2,即a1(q-1)>2,又∵{b n}不是“A型数列”,且b2-b1为最小项,∴b2-b1≤2,即a1(q-1)≤3,由数列{a n}的每一项均为正整数,可得a1(q-1)=3,∴a1=1,q=4或a1=3,q=2.①当a1=1,q=4时,a n=4n-1,则c n=4n-1(n+1)·2n-5=2n+3n+1,令d n=c n+1-c n(n∈N*),则d n=2n+4n+2-2n+3n+1=2n+3·n(n+1)(n+2),令e n=d n+1-d n(n∈N*),则e n=2n+4·n+1(n+2)(n+3)-2n+3·n(n+1)(n+2)=2n+3n+2·n2+n+2(n+1)(n+3)>0,∴{d n}为递增数列,即d n>d n-1>d n-2>…>d1,即c n+1-c n>c n-c n-1>c n-1-c n-2>…>c2-c1,∵c2-c1=323-8=83>2,∴对任意的n∈N*都有c n+1-c n>2,即数列{c n}为“A型数列”.②当a1=3,q=2时,a n=3·2n-1,则c n=3·2n+1(n+1)·2n-5=48n+1,显然,{c n}为递减数列,c2-c1<0≤2,故数列{c n}不是“A型数列”;综上所述,当a n=4n-1时,数列{c n}为“A型数列”,当a n=3·2n-1时,数列{c n}不是“A型数列”.。
2018最新考前两个月数学高考理科(江苏专用)总复习训练题:解答题滚动练5 Word版含答案
f(x)的单调增区间为(0,1),f(x)的单调减区间为(1,+∞).
(2)g(x)=f(x)-b+ =-x2+ +lnx-b,x∈(0,2018).
则g′(x)=-2x+ + ,
令g′(x)=0,得x=2,负值舍去.
当0<x<2时,g′(x)>0,g(x)的单调增区间为(0,2),
1.已知α∈(0,π),且sin = .
(1)求sin 的值;
(2)求cos 的值.
解 方法一 联立 ⇒4sin2α-( - )sinα-(1+ )=0,
解得sinα= 或sinα=- ,
因为α∈(0,π),所以sinα= ,
所以cosα= .
(1)sin =sinαcos -cosαsin = × - × = × = .
解得t∈[- , ].
方法二 设过E的切线与圆C切于切点F,EF2=EM·EN,
又M是线段NE的中点,所以EN=2MN,EM=MN,所以EF2=2MN2,
又EF2=EC2-CF2=22+t2-1=t2+3,MN≤2,
所以t2+3≤8,
所以t∈[- , ].
4.已知函数f(x)=-x2-(2a+1)x+lnx,且该函数在x=1处取得极值.
在Rt△CBT中,BC=1,∠CBT=60°,
得CT= .
由(1)知,AD= ,所以CT=T是平行四边形,
所以CN∥TS.
因为TS⊂平面PAB,CN⊄平面PAB,
所以CN∥平面PAB.
3.已知圆O:x2+y2=4,两个定点A(a,2),B(m,1),其中a∈R,m>0.P为圆O上任意一点,且 =k(k为常数).
所以AD⊥平面PAB.
2018江苏省高考压轴卷 数学 含答案解析
绝密★启封前2018江苏省高考压轴卷数学I注意事项考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷共4页,包含非选择题(第1题~ 第20题,共20题).本卷满分为160分,考试时间为120分钟。
考试结束后,请将本试卷和答题卡一并交回。
2. 答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题上所粘贴的条形码上的姓名、准考证号与本人是否相符。
4.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。
5.如需改动,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗一、填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡相应位置上1.若集合A={﹣1,0,1,2},B={x|x+1>0},则A∩B=.2.若复数z满足z(1﹣i)=2i(i是虚数单位),z是z的共轭复数,则z=.3.某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有人.4.如图,该程序运行后输出的结果为.5.将函数y=3sin (2x ﹣6π)的图象向左平移4π个单位后,所在图象对应的函数解析式为 . 6.如图,在长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=3cm ,AA 1=2cm ,则三棱锥A ﹣B 1D 1D 的体积为 cm 3.7.如图,在一个面积为8的矩形中随机撒一粒黄豆,若黄豆落到阴影部分的概率为41,则阴影部分的面积为 .8.已知双曲线﹣=1(a >0,b >0)的左、右端点分别为A 、B 两点,点C (0, b ),若线段AC 的垂直平分线过点B ,则双曲线的离心率为 .9.设公比不为1的等比数列{a n }满足a 1a 2a 3=﹣81,且a 2,a 4,a 3成等差数列,则数列{a n }的前4项和为 . 10.设定义在R 上的偶函数f (x )在区间(﹣∞,0]上单调递减,若f (1﹣m )<f (m ),则实数m 的取值范围是 .11.已知函数f (x )=,若a 、b 、c 互不相等,且f (a )=f (b )=f (c ),则a+b+c 的取值范围是 .12.如图,在△ABC 中,已知AN =21AC ,P 是BN 上一点,若AP =m AB +41AC ,则实数m 的值是 .13.已知非零向量a ,b 满足|a |=|b |=|a +b |,则a 与2a -b 夹角的余弦值为 .14.已知函数f(x)=⎩⎨⎧≥++-<1x ,a x 25x 9x 1x ,x sin 23,若函数f (x )的图象与直线y=x 有三个不同的公共点,则实数a 的取值集合为 .15.如图,在三棱柱1B 1C 1中,,点E ,F 分别在棱BB 1 ,CC 1上(均异 于端点),且∠∠ACF ,AE ⊥BB 1,AF ⊥CC 1.求证:(1)平面AEF ⊥平面BB 1C 1C ;(2)BC // 平面AEF .16.在△ABC 中,角,,A B C 的对边分别为,,a b c ,且()2cos cos a b C c B -⋅=⋅.(1)求角C 的大小;(2)若2c =, △ABC 3,求该三角形的周长.17.已知中心在坐标原点的椭圆C ,F 1,F 2 分别为椭圆的左、右焦点,长轴长为6,离心率为(1)求椭圆C 的标准方程;(2)已知点P 在椭圆C 上,且PF 1=4,求点P 到右准线的距离. 18.如图,四棱锥P ﹣ABCD 中,PA ⊥平面ABCD ,四边形ABCD 为直角梯形,AD ∥BC ,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E ,F ,G 分别为BC ,PD ,PC 的中点.(1)求EF 与DG 所成角的余弦值;(2)若M 为EF 上一点,N 为DG 上一点,是否存在MN ,使得MN ⊥平面PBC ?若存在,求出点M ,N 的坐标;若不存在,请说明理由.19.设等比数列a 1,a 2,a 3,a 4的公比为q ,等差数列b 1,b 2,b 3,b 4的公差为d ,且10q d ≠≠,. 记i i i c a b =+(,2,3,4).(1)求证:数列123c c c ,,不是等差数列; (2)设11a =,2q =.若数列123c c c ,,是等比数列,求b 2关于d 的函数关系式及其定义域; (3)数列1234c c c c ,,,能否为等比数列?并说明理由. AA 1B 1C 1BC F E(第16题)20.(16分)已知f(x)=x2+mx+1(m∈R),g(x)=e x.(1)当x∈[0,2]时,F(x)=f(x)﹣g(x)为增函数,求实数m的取值范围;(2)若m∈(﹣1,0),设函数G(x)=)x(g )x(f,H(x)= ﹣41x+45,求证:对任意x1,x2∈[1,1﹣m],G(x1)<H(x2)恒成立.数学II(附加题)注意事项考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷共2页,均为非选择题(第21题~ 第23题)。
[推荐学习]2018考前两个月数学高考理科(江苏专用)总复习训练题:考前回扣1 Word版含答案
考前回扣回扣1 函数的图象与性质1.函数的定义域和值域(1)求函数定义域的类型和相应方法①若已知函数的解析式,则函数的定义域是使解析式有意义的自变量的取值范围; ②若已知f (x )的定义域为[a ,b ],则f (g (x ))的定义域为不等式a ≤g (x )≤b 的解集;反之,已知f (g (x ))的定义域为[a ,b ],则f (x )的定义域为函数y =g (x )(x ∈[a ,b ])的值域. (2)常见函数的值域①一次函数y =kx +b (k ≠0)的值域为R ;②二次函数y =ax 2+bx +c (a ≠0):当a >0时,值域为⎣⎢⎡⎭⎪⎫4ac -b 24a ,+∞,当a <0时,值域为⎝ ⎛⎦⎥⎤-∞,4ac -b 24a ;③反比例函数y =kx(k ≠0)的值域为{y ∈R|y ≠0}. 2.函数的奇偶性、周期性(1)奇偶性是函数在其定义域上的整体性质,对于定义域内的任意x (定义域关于原点对称),都有f (-x )=-f (x )成立,则f (x )为奇函数(都有f (-x )=f (x )成立,则f (x )为偶函数). (2)周期性是函数在其定义域上的整体性质,一般地,对于函数f (x ),如果对于定义域内的任意一个x 的值,若f (x +T )=f (x )(T ≠0),则f (x )是周期函数,T 是它的一个周期. 3.关于函数周期性、对称性的结论 (1)函数的周期性①若函数f (x )满足f (x +a )=f (x -a ),则f (x )是周期函数,2a 是它的一个周期; ②设f (x )是R 上的偶函数,且图象关于直线x =a (a ≠0)对称,则f (x )是周期函数,2a 是它的一个周期;③设f (x )是R 上的奇函数,且图象关于直线x =a (a ≠0)对称,则f (x )是周期函数,4a 是它的一个周期. (2)函数图象的对称性①若函数y =f (x )满足f (a +x )=f (a -x ), 即f (x )=f (2a -x ),则f (x )的图象关于直线x =a 对称;②若函数y =f (x )满足f (a +x )=-f (a -x ), 即f (x )=-f (2a -x ),则f (x )的图象关于点(a,0)对称;③若函数y =f (x )满足f (a +x )=f (b -x ), 则函数f (x )的图象关于直线x =a +b2对称.4.函数的单调性函数的单调性是函数在其定义域上的局部性质. ①单调性的定义的等价形式:设x 1,x 2∈[a ,b ], 那么(x 1-x 2)[f (x 1)-f (x 2)]>0⇔f (x 1)-f (x 2)x 1-x 2>0⇔f (x )在[a ,b ]上是增函数;(x 1-x 2)[f (x 1)-f (x 2)]<0⇔f (x 1)-f (x 2)x 1-x 2<0⇔f (x )在[a ,b ]上是减函数.②若函数f (x )和g (x )都是减函数,则在公共定义域内,f (x )+g (x )是减函数;若函数f (x )和g (x )都是增函数,则在公共定义域内,f (x )+g (x )是增函数;根据同增异减判断复合函数y =f (g (x ))的单调性. 5.函数图象的基本变换 (1)平移变换y =f (x )――――→h >0,右移h <0,左移y =f (x -h ), y =f (x )――――→k >0,上移k <0,下移y =f (x )+k . (2)伸缩变换y =f (x )――――→0<ω<1,伸ω>1,缩y =f (ωx ), y =f (x )――――→0<A <1,缩A >1,伸y =Af (x ). (3)对称变换y =f (x )――→x 轴y =-f (x ), y =f (x )――→y 轴y =f (-x ), y =f (x )――→原点y =-f (-x ).6.准确记忆指数函数与对数函数的基本性质 (1)定点:y =a x(a >0,且a ≠1)恒过(0,1)点;y =log a x (a >0,且a ≠1)恒过(1,0)点.(2)单调性:当a >1时,y =a x在R 上单调递增;y =log a x 在(0,+∞)上单调递增;当0<a <1时,y =a x在R 上单调递减;y =log a x 在(0,+∞)上单调递减. 7.函数与方程(1)零点定义:x 0为函数f (x )的零点⇔f (x 0)=0⇔(x 0,0)为f (x )的图象与x 轴的交点. (2)确定函数零点的三种常用方法 ①解方程判定法:解方程f (x )=0;②零点定理法:根据连续函数y =f (x )满足f (a )f (b )<0,判断函数在区间(a ,b )内存在零点;③数形结合法:尤其是方程两端对应的函数类型不同时多用此法求解.1.解决函数问题时要注意函数的定义域,要树立定义域优先原则. 2.解决分段函数问题时,要注意与解析式对应的自变量的取值范围.3.求函数单调区间时,多个单调区间之间不能用符号“∪”和“或”连接,可用“及”连接或用“,”隔开.单调区间必须是“区间”,而不能用集合或不等式代替.4.判断函数的奇偶性,要注意定义域必须关于原点对称,有时还要对函数式化简整理,但必须注意使定义域不受影响.5.准确理解基本初等函数的定义和性质.如函数y =a x(a >0,且a ≠1)的单调性容易忽视字母a 的取值讨论,忽视a x>0;对数函数y =log a x (a >0,且a ≠1)容易忽视真数与底数的限制条件.6.易混淆函数的零点和函数图象与x 轴的交点,不能把函数零点、方程的解、不等式解集的端点值进行准确互化.1.若函数f (x )=⎩⎪⎨⎪⎧2x +2,x ≤0,2x-4,x >0,则f (f (1))=________.答案 -2解析 f (f (1))=f (21-4)=f (-2)=2×(-2)+2=-2.2.函数f (x )=x 2-2ax +2在区间(-∞,1]上递减,则a 的取值范围是________. 答案 [1,+∞)解析 函数f (x )=x 2-2ax +2=x 2-2ax +a 2-a 2+2=(x -a )2-a 2+2, ∵二次函数图象开口向上,对称轴为直线x =a ,且在区间(-∞,1]上递减, ∴a 的取值范围是[1,+∞).3.(2017·江苏南通天星湖中学质检)若函数f (x )=⎩⎪⎨⎪⎧x (x -b ),x ≥0,ax (x +2),x <0(a ,b ∈R)为奇函数,则f (a +b )的值为________.答案 -1解析 因为函数f (x )为奇函数,所以f (-1)=-f (1),f (-2)=-f (2),即⎩⎪⎨⎪⎧a (-1+2)=1(1-b ),2a (-2+2)=2(2-b ),解得a =-1,b =2.经验证a =-1,b =2满足题设条件, 所以f (a +b )=f (1)=-1.4.(2017·江苏如东中学质检)设函数f (x )=ax 2-2x +2,对于满足1<x <4的一切x 值都有f (x )>0,则实数a 的取值范围为________.答案 ⎝ ⎛⎭⎪⎫12,+∞解析 由题意得a >2x -2x2对1<x <4恒成立,又2x -2x 2=-2⎝ ⎛⎭⎪⎫1x -122+12,14<1x <1, ∴⎝ ⎛⎭⎪⎫2x -2x 2max =12,∴a >12.5.已知函数f (x )=||x +2||x ,且满足f (a -1)<f (2),则实数a 的取值范围是________. 答案 (-1,3)解析 因为f (-x )=f (x ),所以函数f (x )是偶函数,当x ≥0时,f (x )=x +2x是单调增函数,故由偶函数的性质及f (a -1)<f (2)可得|a -1|<2,即-2<a -1<2, 即-1<a <3.6.已知定义在R 上的奇函数f (x )满足f (x +2)=-f (x ),且f (-1)=2,则f (2017)=________. 答案 -2解析 由题意得f (x +4)=-f (x +2)=f (x ),所以函数是以4为周期的周期函数,所以f (2017)=f (1)=-f (-1)=-2.7.已知函数f (x )为奇函数,且在[0,2]上单调递增,若f (log 2m )<f (log 4(m +2))成立,则实数m 的取值范围是________________.答案 ⎣⎢⎡⎭⎪⎫14,2 解析 因为函数f (x )是奇函数,且在[0,2]上单调递增,所以函数f (x )在[-2,2]上单调递增.故由f (log 2m )<f (log 4(m +2)),可得⎩⎪⎨⎪⎧-2≤log 2m ≤2,-2≤log 4(m +2)≤2,log 2m <log 4(m +2),m >0,m +2>0,故有⎩⎪⎨⎪⎧14≤m ≤4,116≤m +2≤16,m 2<m +2,m >0,m +2>0,解得14≤m <2.综上可知,m 的取值范围是⎣⎢⎡⎭⎪⎫14,2. 8.定义在R 上的函数f (x )满足f (-x )=-f (x ),f (x -2)=f (x +2),且当x ∈(-1,0)时,f (x )=2x +15,则f (log 220)=__________.答案 -1解析 由f (x -2)=f (x +2)⇒f (x )=f (x +4), 因为4<log 220<5,所以0<log 220-4<1, -1<4-log 220<0.又因为f (-x )=-f (x ),所以f (log 220)=f (log 220-4)=-f (4-log 220)=-f ⎝ ⎛⎭⎪⎫log 245=-1.9.若函数f (x )=⎩⎪⎨⎪⎧(3-a )x -3,x ≤7,a x -6,x >7单调递增,则实数a 的取值范围是________.答案 ⎝ ⎛⎭⎪⎫94,3解析 因为函数f (x )=⎩⎪⎨⎪⎧(3-a )x -3,x ≤7,a x -6,x >7单调递增,所以1<a <3.又由题意得7(3-a )-3<a ,解得a >94,所以实数a 的取值范围是⎝ ⎛⎭⎪⎫94,3.10.已知函数f (x )=⎩⎪⎨⎪⎧2-|x |,x ≤2,(x -2)2,x >2,函数g (x )=3-f (2-x ),则函数y =f (x )-g (x )的零点个数为__________.答案 2解析 当x >2时,g (x )=x -1,f (x )=(x -2)2; 当0≤x ≤2时,g (x )=3-x ,f (x )=2-x ; 当x <0时,g (x )=3-x 2,f (x )=2+x .由于函数y =f (x )-g (x )的零点个数就是方程f (x )-g (x )=0的根的个数.当x >2时,方程f (x )-g (x )=0可化为x 2-5x +5=0,其根为x =5+52或x =5-52(舍去);当0≤x ≤2时,方程f (x )-g (x )=0可化为2-x =3-x ,无解;当x <0时,方程f (x )-g (x )=0可化为x 2+x -1=0,其根为x =-1-52或x =-1+52(舍去).所以函数y =f (x )-g (x )的零点个数为2.11.设函数f (x )=⎩⎪⎨⎪⎧x 2-6x +6,x ≥0,3x +4,x <0,若互不相等的实数x 1,x 2,x 3满足f (x 1)=f (x 2)=f (x 3),则x 1+x 2+x 3的取值范围是____________.答案 ⎝ ⎛⎭⎪⎫113,6解析 由题意可得函数f (x )的图象如图所示,若存在互不相等的实数x 1,x 2,x 3满足f (x 1)=f (x 2)=f (x 3)=k ,则k ∈(-3,4),不妨令x 1<x 2<x 3,则x 1∈⎝ ⎛⎭⎪⎫-73,0,x 2+x 3=6,故x 1+x 2+x 3∈⎝⎛⎭⎪⎫113,6.12.定义在R 上的函数f (x )满足f (x +2)=2f (x )-2,当x ∈(0,2]时,f (x )=⎩⎪⎨⎪⎧x 2-x ,x ∈(0,1),1x,x ∈[1,2],若当x ∈(0,4]时,t 2-7t2≤f (x )≤3-t 恒成立,则实数t 的取值范围是______________. 答案 [1,2]解析 当x ∈(0,1)时,f (x )=x 2-x ,函数无最大值,最小值为-14;当x ∈[1,2]时,f (x )=1x ,函数最大值为1,最小值为12;当x ∈(2,3)时,f (x )=2f (x -2)-2=2x 2-10x +10,函数值满足-52≤f (x )<-2;当x ∈[3,4]时,f (x )=2f (x -2)-2=2x -2-2,函数值满足-1≤f (x )≤0.综上,当x ∈(0,4]时,函数f (x )的最小值为-52,最大值为1.由t 2-7t 2≤f (x )≤3-t 恒成立,得⎩⎪⎨⎪⎧t 2-7t 2≤-52,3-t ≥1,∴⎩⎪⎨⎪⎧1≤t ≤52,t ≤2,∴1≤t ≤2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
令n=1,n=2,解得 或 经检验,符合题意.
所以数列{an}的通项公式为an=0或an=n.
(2)由题意得a2n-1=2n-1,a2n=3×2n-1,
S2n=2n-1+3(2n-1)=4×2n-4,
S2n-1=S2n-a2n=4×2n-4-3×2n-1=5×2n-1-4.
令a2(n+1)-λ= (a2n-λ),得a2(n+1)= a2n+ λ,所以λ= .
此时,a2-λ= +1- =- .
所以存在λ= ,使得数列{a2n-λ}是等比数列.
(2)由(1)知,数列 是首项为- ,公比为 的等比数列,
所以a2n- =- n-1=- · ,
即a2n= .
由a2n= a2n-1+(2n-1),得a2n-1=3a2n-3(2n-1)= -6n+3,
b2n=2a2n+1S2n-2n(2S2n+a2n+1)
=2×2n×(4×2n-4)-2n(8×2n-8+2n)
=2n+1(2n+2-9n-4)+16n.
b2n-1=2a2nS2n-1-(2n-1)(2S2n-1+a2n)
=6×2n-1×(5×2n-1-4)-(2n-1)(10×2n-1-8+3×2n-1)=2n-1(30×2n-1-26n-11)+16n-8.
解(1)设数列{an}的公差为d.
因为2a5-a3=13,S4=16,
所以
解得
所以an=2n-1,Sn=n2.
(2)①当n为偶数时,设n=2k,k∈N*,
则T2k=(a2-a1)+(a4-a3)+…+(a2k-a2k-1)=2k.
代入不等式λTn<[an+1+(-1)n+1an]·2n-1,得λ·2k<4k,从而λ< .
计算得S1=1,S2= ,S3=- ,S4=- ,
所以满足Sn>0的所有正整数n的值为1和2.
2.已知数列{an}的前n项和为Sn,设数列{bn}满足bn=2(Sn+1-Sn)Sn-n(Sn+1+Sn)(n∈N*).
(1)若数列{an}为等差数列,且bn=0,求数列{an}的通项公式;
(2)若a1=1,a2=3,且数列{a2n-1},{a2n}都是以2为公比的等比数列,求满足不等式b2n<
即(2n-m2+2)(2n+m2-2)=12.
因为n>m>2,所以n≥4,m≥3,所以2n+m2-2≥15.
因为2n-m2+2是整数,所以等式(2n-m2+2)(2n+m2-2)=12不成立,
故不存在正整数m,n(n>m>2),使得S2,Sm-S2,Sn-Sm成等比数列.
因为k∈N*,所以-4k的最大值为-4,所以λ>-4.
综上,λ的取值范围为(-4,2).
(3)假设存在正整数m,n(n>m>2),使得S2,Sm-S2,Sn-Sm成等比数列,
则(Sm-S2)2=S2(Sn-Sm),即(m2-4)2=4(n2-m2),
所以4n2=(m2-2)2+12,即4n2-(m2-2)2=12,
b2n-1的所有正整数n的集合.
解(1)设等差数列{an}的公差为d,
所以an+1=a1+nd,Sn=na1+ d.
由bn=2(Sn+1-Sn)Sn-n(Sn+1+Sn)(n∈N*),
得bn=2an+1Sn-n(2Sn+an+1).
又由bn=0,得2(a1+nd) -n[2na1+n(n-1)d+a1+nd]=0对一切n∈N*都成立,
当n=1,2,3时,g(n+1)-g(n)<0;
当n∈N*时,n≥4,g(n+1)-g(n)= ×2n-5>0,
因为当n=1时,g(1)=- <0,
所以g(4)<0,且g(6)=- <0,g(7)= >0.
所以f(n)=2n +8在n≥7(n∈N*)时也单调递增,
当n=1时,f(1)=-5<0;
当n=2时,f(2)=-34<0;
设f(k)= ,则f(k+1)-f(k)= - = .因为k∈N*,所以f(k+1)-f(k)>0,
所以f(k)是递增的,所以f(k)min=2,所以λ<2.
②当n为奇数时,设n=2k-1,k∈N*,
则T2k-1=T2k-(-1)2ka2k=2k-(4k-1)=1-2k.
代入不等式λTn<[an+1+(-1)n+1an]2n-1,得λ(1-2k)<(2k-1)4k,从而λ>-4k.
1.已知数列{an}中a1=1,an+1=
(1)是否存在实数λ,使得数列{a2n-λ}是等比数列?若存在,求出λ的值;若不存在,请说明理由;
(2)若Sn是数列{an}的前n项和,求满足Sn>0的所有正整数n.
解(1)由已知,得a2(n+1)= a2n+1+(2n+1)
= [a2n-3(2n)]+2n+1= a2n+1.
所以a2n-1+a2n= -6n+3+
=-2 n-6n+9,
所以S2n=(a1+a2)+(a3+a4)+…+(a2n-1+a2n)
=-2 -6(1+2+…+n)+9n= -3n2+6n-1,
从而S2n-1=S2n-a2n= × -3n2+6n- .
因为 和-3n2+6n=-3(n-1)2+3在n∈N*时均单调递减,所以S2n和S2n-1均各自单调递减.
所以b2n-b2n-1=2n+1(2n+2-9n-4)+16n-[2n-1(30×2n-1-26n-11)+16n-8]
=2n +8=22n-1+8-2n .
记f(n)=22n-1+8-2n ,即
f(n)=2n +8.
记g(n)= ×2n- ,
则g(n+1)-g(n)= ×2n+1- - ×2n+5n+ = ×2n-5,
当n=3时,f(3)=-100<0;
当n=4时,f(4)=-224<0;
当n=,f(6)=-24<0;
当n=7时,f(7)=3400>0,
所以满足条件的正整数n的集合为{1,2,3,4,5,6}.
3.已知等差数列{an}的前n项和为Sn,且2a5-a3=13,S4=16.
(1)求数列{an}的前n项和Sn;
(2)设Tn= (-1)iai,若对一切正整数n,不等式λTn<[an+1+(-1)n+1an]2n-1恒成立,求实数λ的取值范围;
(3)是否存在正整数m,n(n>m>2),使得S2,Sm-S2,Sn-Sm成等比数列?若存在,求出所有的m,n;若不存在,请说明理由.
