【2013-7到2015-7】浙江省学考真题专题汇总-----必修4---【第2章】向量
浙江省学业水平考试语文试题集共4份(14年,15年)教案

【第1练】浙江省普通高中学业水平考试(2015年7月)一、选择题(本大题共18小题,每小题3分,共54分。
1.下列加点字读音全正确的一项是()A.胚.胎(pēi)筛.选(shāi)坍圮.(jǐ)相形见绌.(chù)B.簇.拥(zú)栖.息(qī)积淀.(diàn)百舸.争流(gě)C.寒暄.(xuān)顷.刻(qǐng)恪.守(kè)纨绔.子弟(kuà)D.僻.静(pì)憨.厚(hān)惊愕.(è)销声匿.迹(nì)2.下列句子没有错别字的一项是()A.我极报歉的是,由于篇幅的限制,我不能对于那些慷慨帮助我的自然学者一一表示谢意。
B.要不然,则当佳节大典之际,他们拿不出东西来,只好瞌头贺喜,讨一点残羹冷炙做奖赏。
C.北美电影界正处于令人沮丧的境地:观众去电影院的频律降到了20年来的最低水平。
D.书法是中华文明史上的一朵艺术奇葩,它的魅力源于历代书法巨匠不懈的艺术追求。
3.一次填入下列句子横线处的词语,恰当的一项是()①中纪委监察会议强调,一定要加强对领导干部的反腐教育,并且要采取有效措施保证他们廉洁奉公,避免变质。
②近日,落户我市的全国首座家庭体验型商城正式,这是我市文化创意产业建设取得的又一重大成果。
③不管它们内容的深浅,作用的大小,时间的久暂,空间的广狭,它们存在过,它们便是传统文化。
A.蜕变起用只有B.蜕化启用只要C.退化启用只有D.退化起用只要4.下列句子加点的成语运用不恰当的一项是()A.为了养家糊口,他什么生意都做,从卖菜,卖玩具到卖服装,无所不为....,真是让人钦佩。
B.“五水共治”虽然已取得了初步成效,但这是一场艰苦的持久战,不可能一劳永逸....。
C.有人认为传统节庆已与今天的时代格格不入....,觉得它离人们的文化需求已很遥远。
D.十多年来,我校持续开展“书香伴我行”主题读书系列活动,经典阅读已蔚然成风....。
2019版数学浙江省学业水平考试专题复习必修4 §3

知识点一 两角和与差的余弦、正弦、正切公式cos(α-β)=cos αcos β+sin αsin β;(C (α-β))cos(α+β)=cos_αcos_β-sin_αsin_β;(C (α+β))sin(α-β)=sin_αcos_β-cos_αsin_β;(S (α-β))sin(α+β)=sin_αcos_β+cos_αsin_β;(S (α+β))tan(α-β)=tan α-tan β1+tan αtan β;(T (α-β)) tan(α+β)=tan α+tan β1-tan αtan β.(T (α+β)) 知识点二 二倍角公式sin 2α=2sin_αcos_α;(S 2α)cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α;(C 2α)tan 2α=2tan α1-tan 2α.(T 2α) 知识点三 辅助角公式及常用变形公式1.辅助角公式(1)a sin α+b cos α=a 2+b 2sin(α+φ)⎝⎛⎭⎫其中a >0,tan φ=b a ,-π2<φ<π2; (2)a cos α-b sin α=a 2+b 2cos(α+φ)⎝⎛⎭⎫其中a ,b >0,tan φ=b a ,0<φ<π2. 特别提醒:常用的6个式子:①sin α±cos α=2sin ⎝⎛⎭⎫α±π4; ②3sin α±cos α=2sin ⎝⎛⎭⎫α±π6; ③sin α±3cos α=2sin ⎝⎛⎭⎫α±π3;④cos α-sin α=2cos ⎝⎛⎭⎫α+π4; ⑤3cos α-sin α=2cos ⎝⎛⎭⎫α+π6; ⑥cos α-3sin α=2cos ⎝⎛⎭⎫α+π3. 2.常用变形公式(1)tan α±tan β=tan(α±β)(1∓tan_αtan_β);(2)cos 2α=1+cos 2α2,sin 2α=1-cos 2α2; (3)①1+sin 2α=(sin α+cos α)2,②1-sin 2α=(sin α-cos α)2,③1+cos 2α=2cos 2α,④1-cos 2α=2sin 2α.知识点四 简单的三角恒等变换1.变换对象:角、名称和形式,三角变换只变其形式,不变其性质.2.变换目标:利用公式简化三角函数式,达到化简、计算或证明的目的.3.变换依据:两角和与差的正弦、余弦、正切公式和二倍角的正弦、余弦、正切公式.4.变换思路:明确变换目标,选择变换公式,设计变换途径.题型一 两角和与差的公式的应用例1 (1)已知0<β<π2<α<π,且cos ⎝⎛⎭⎫α-β2=-19,sin ⎝⎛⎭⎫α2-β=23,则cos(α+β)的值为________.(2)已知α,β∈(0,π),且tan(α-β)=12,tan β=-17,则2α-β的值为________. 答案 (1)-239729 (2)-3π4解析 (1)∵0<β<π2<α<π, ∴-π4<α2-β<π2,π4<α-β2<π, ∴cos ⎝⎛⎭⎫α2-β= 1-sin 2⎝⎛⎭⎫α2-β=53, sin ⎝⎛⎭⎫α-β2= 1-cos 2⎝⎛⎭⎫α-β2=459,∴cos α+β2=cos ⎣⎡⎦⎤⎝⎛⎭⎫α-β2-⎝⎛⎭⎫α2-β =cos ⎝⎛⎭⎫α-β2cos ⎝⎛⎭⎫α2-β+sin ⎝⎛⎭⎫α-β2sin ⎝⎛⎭⎫α2-β =⎝⎛⎭⎫-19×53+459×23=7527, ∴cos(α+β)=2cos 2α+β2-1 =2×⎝⎛⎭⎫75272-1=-239729. (2)∵tan α=tan [(α-β)+β]=tan (α-β)+tan β1-tan (α-β)tan β =12-171-12×⎝⎛⎭⎫-17=13>0, ∴0<α<π2, 又∵tan 2α=2tan α1-tan 2α=2×131-⎝⎛⎭⎫132=34>0, ∴0<2α<π2, ∴tan(2α-β)=tan 2α-tan β1+tan 2αtan β=34+171+34×⎝⎛⎭⎫-17=1. ∵tan β=-17<0, ∴π2<β<π,∴-π<2α-β<0, ∴2α-β=-3π4. 感悟与点拨 (1)解题中注意变角,如本题中α+β2=⎝⎛⎭⎫α-β2-⎝⎛⎭⎫α2-β. (2)通过求角的某种三角函数值来求角,在选取函数时,遵照以下原则:①已知正切函数值,选正切函数;②已知正弦、余弦函数值,选正弦或余弦函数;若角的范围是⎝⎛⎭⎫0,π2,选正弦、余弦皆可;若角的范围是(0,π),选余弦较好;若角的范围为⎝⎛⎭⎫-π2,π2,选正弦较好. 跟踪训练1 (1)(2017年4月学考)已知θ为锐角,且sin θ=35,则sin(θ+45°)等于( ) A.7210 B .-7210 C.210 D .-210(2)已知α∈⎝⎛⎭⎫0,π2,β∈⎝⎛⎭⎫π2,π,cos 2β=-79,sin(α+β)=79.则sin α=________. 答案 (1)A (2)13解析 (1)∵θ为锐角且sin θ=35, ∴cos θ=45. ∴sin(θ+45°)=sin θcos 45°+cos θsin 45°=35×22+45×22=7210. (2)∵β∈⎝⎛⎭⎫π2,π,∴cos β<0,sin β>0.又cos 2β=2cos 2β-1=-79,∴cos β=-13. sin β=1-cos 2β=223. 而α+β∈⎝⎛⎭⎫π2,3π2,且sin(α+β)=79, ∴α+β∈⎝⎛⎭⎫π2,π∴cos(α+β)=-1-sin 2(α+β)=-429. 故sin α=sin[(α+β)-β]=sin(α+β)cos β-cos(α+β)sin β=79×⎝⎛⎭⎫-13-⎝⎛⎭⎫-429×223=13. 题型二 二倍角公式的应用例2 (1)方程3sin x =1+cos 2x 在区间[0,2π]上的解为____________. (2)⎝⎛⎭⎫cos π12-sin π12⎝⎛⎭⎫cos π12+sin π12=________.答案 (1)π6或5π6 (2)32解析 (1)∵3sin x =1+cos 2x =2-2sin 2x ,∴2sin 2x +3sin x -2=0,∴sin x =12,sin x =-2(舍去). 又x ∈[0,2π],∴x =π6或5π6. (2)⎝⎛⎭⎫cos π12-sin π12⎝⎛⎭⎫cos π12+sin π12 =cos 2π12-sin 2π12=cos π6=32. 感悟与点拨 (1)三角函数式的化简要遵循“三看”原则,一看角,二看名,三看式子的结构与特征.(2)对于给角求值问题,往往所给角都是非特殊角,解决这类问题的基本思路有①化为特殊角的三角函数值;②化为已知角的三角函数值.跟踪训练2 (1)(2016年10月学考)函数f (x )=1-2sin 22x 是( )A .偶函数且最小正周期为π2B .奇函数且最小正周期为π2C .偶函数且最小正周期为πD .奇函数且最小正周期为π(2)若tan α=34,则cos 2α+2sin 2α等于( ) A.6425B.4825 C .1 D.1625答案 (1)A (2)A解析 (1)由题意知f (x )=1-2sin 22x =cos 4x ,则f (-x )=cos(-4x )=cos 4x =f (x ).T =2π4=π2,所以f (x )为偶函数,最小正周期为π2. (2)cos 2α+2sin 2α=cos 2α+4sin αcos α=cos 2α+4sin αcos αsin 2α+cos 2α=1+4tan α1+tan 2α=6425. 题型三 三角变换的应用例3 (2017年4月学考)已知函数f (x )=2cos 2x -1,x ∈R .(1)求f ⎝⎛⎭⎫π6的值;(2)求函数f (x )的最小正周期;(3)设g (x )=f ⎝⎛⎭⎫π4-x +3cos 2x ,求g (x )的值域.解 (1)由已知可得f (x )=cos 2x ,∴f ⎝⎛⎭⎫π6=cos π3=12. (2)T =2π2=π. (3)∵g (x )=f ⎝⎛⎭⎫π4-x +3cos 2x ,∴g (x )=cos ⎝⎛⎭⎫π2-2x +3cos 2x =sin 2x +3cos 2x=2⎝⎛⎭⎫12sin 2x +32cos 2x =2sin ⎝⎛⎭⎫2x +π3, ∴g (x )∈[-2,2].感悟与点拨 三角变换和三角函数的性质相结合是考试的一个热点,解题时要注意观察角、式子间的联系,利用整体思想解题.跟踪训练3 (1)已知函数f (x )=sin 2x +2sin x cos x +3cos 2x ,求:①函数f (x )的最大值及取得最大值时自变量x 的集合;②函数f (x )的单调递增区间.(2)已知函数f (x )=4tan x sin ⎝⎛⎭⎫π2-x cos ⎝⎛⎭⎫x -π3- 3.①求f (x )的定义域与最小正周期;②讨论f (x )在区间⎣⎡⎦⎤-π4,π4上的单调性. 解 (1)①∵f (x )=(sin 2x +cos 2x )+2sin x cos x +2cos 2x=2sin x cos x +1+2cos 2x=sin 2x +cos 2x +2 =2⎝⎛⎭⎫22sin 2x +22cos 2x +2 =2+2sin ⎝⎛⎭⎫2x +π4, ∴当2x +π4=2k π+π2(k ∈Z ), 即x =k π+π8(k ∈Z )时,f (x )取得最大值2+ 2. 此时函数f (x )取得最大值的自变量x 的集合为⎩⎨⎧⎭⎬⎫x ⎪⎪x =k π+π8,k ∈Z . ②由①得f (x )=2+2sin ⎝⎛⎭⎫2x +π4, 令2k π-π2≤2x +π4≤2k π+π2(k ∈Z ), 得k π-3π8≤x ≤k π+π8(k ∈Z ), 因此函数f (x )的单调递增区间为⎣⎡⎦⎤k π-3π8,k π+π8(k ∈Z ). (2)①f (x )的定义域是⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π+π2,k ∈Z . f (x )=4tan x cos x cos ⎝⎛⎭⎫x -π3- 3 =4sin x cos ⎝⎛⎭⎫x -π3- 3 =2sin x cos x +23sin 2x - 3=sin 2x -3cos 2x=2sin ⎝⎛⎭⎫2x -π3. ∴f (x )的最小正周期T =2π2=π. ②令-π2+2k π≤2x -π3≤π2+2k π,k ∈Z , 则-π12+k π≤x ≤5π12+k π,k ∈Z . 令π2+2k π≤2x -π3≤3π2+2k π,k ∈Z ,则5π12+k π≤x ≤11π12+k π,k ∈Z . ∵⎣⎡⎦⎤-π12+k π,5π12+k π(k ∈Z )∩⎣⎡⎦⎤-π4,π4 =⎣⎡⎦⎤-π12,π4, ⎣⎡⎦⎤5π12+k π,11π12+k π(k ∈Z )∩⎣⎡⎦⎤-π4,π4 =⎣⎡⎦⎤-π4,-π12, ∴f (x )在⎣⎡⎦⎤-π12,π4上单调递增,在⎣⎡⎦⎤-π4,-π12上单调递减.一、选择题1.已知角α的终边经过点P (-3,4),则tan 2α等于( )A.247B.83 C .-83D .-247答案 A解析 ∵tan α=4-3=-43, ∴tan 2α=2tan α1-tan 2α=2×⎝⎛⎭⎫-431-⎝⎛⎭⎫-432=247. 2.cos 160°sin 10°-sin 20°cos 10°等于( )A .-32 B.32 C .-12 D.12 答案 C解析 cos 160°sin 10°-sin 20°cos 10°=-cos 20°sin 10°-sin 20°cos 10°=-(cos 20°sin 10°+sin 20°cos 10°)=-sin 30° =-12,故选C.3.已知α,β为锐角,且cos(α+β)=35,sin α=513,则cos β的值为( ) A.5665 B.3365 C.1665 D.6365答案 A解析 根据题意知,α,β为锐角,若sin α=513,则cos α=1213, 若cos(α+β)=35,则α+β也为锐角, 则sin(α+β)=45, 所以cos β=cos [(α+β)-α]=cos(α+β)cos α+sin(α+β)sin α=35×1213+45×513=5665. 4.已知sin 2α=13,则cos 2⎝⎛⎭⎫α-π4等于( ) A .-13B .-23 C.13D.23答案 D解析 cos 2⎝⎛⎭⎫α-π4=1+cos ⎝⎛⎭⎫2α-π22=1+sin 2α2=1+132=23. 5.当-π2≤x ≤π2时,函数f (x )=sin x +3cos x 的( ) A .最大值是1,最小值是-1B .最大值是1,最小值是-12C .最大值是2,最小值是-2D .最大值是2,最小值是-1答案 D解析 ∵f (x )=sin x +3cos x=2⎝⎛⎭⎫12sin x +32cos x=2sin ⎝⎛⎭⎫x +π3,∵x ∈⎣⎡⎦⎤-π2,π2,∴x +π3∈⎣⎡⎦⎤-π6,56π,∴sin ⎝⎛⎭⎫x +π3∈⎣⎡⎦⎤-12,1,∴f (x )∈[-1,2],故选D.6.在△ABC 中,tan B =-2,tan C =13,则A 等于() A.π4 B.3π4 C.π3 D.π6答案 A解析 ∵在△ABC 中,tan B =-2,tan C =13,∴tan A =tan [π-(B +C )]=-tan(B +C )=-tan B +tan C1-tan B tan C=--2+131-(-2)×13=1,又A ∈(0,π),∴A =π4.7.已知sin ⎝⎛⎭⎫π4-x =35,则sin 2x 等于( ) A.725 B.1625 C.1425 D.1925答案 A解析 ∵sin ⎝⎛⎭⎫π4-x =22(cos x -sin x )=35,∴cos x -sin x =325,两边平方得1-2sin x cos x =1825, ∴sin 2x =725.8.设函数f (x )=2sin x cos x -23cos 2x +3的图象为C ,有下面三个说法:①图象C 关于x =11π12对称;②函数f (x )在区间⎝⎛⎭⎫-π12,5π12内是增函数;③由f (x )=2sin 2x 的图象向右平移π3个单位长度可以得到图象C .以上说法中,正确的个数是( )A .0B .1C .2D .3答案 C解析 f (x )=2sin x cos x -23cos 2x + 3=sin 2x -23×1+cos 2x 2+ 3=sin 2x -3cos 2x=2sin ⎝⎛⎭⎫2x -π3.①T =2π2=π,且f (x )=2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π6,令2⎝⎛⎭⎫x -π6=k π+π2,k ∈Z ,解得x =5π12+k π2,k ∈Z ,∴图象C 关于直线x =5π12+k π2,k ∈Z 对称,当k =1时,x =11π12,即①正确;②令-π2+2k π≤2x -π3≤π2+2k π,k ∈Z ,解得-π12+k π≤x ≤5π12+k π,k ∈Z .当k =0时,x ∈⎣⎡⎦⎤-π12,5π12,②正确;③∵f (x )=2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π6可以由f (x )=2sin 2x 向右平移π6个单位长度得到,∴③错误.9.已知函数f (x )=2sin x (3cos x -sin x )+1,若f (x -φ)为偶函数,则φ的一个值为() A.π2 B.π3C.π4D.π6解析 f (x )=2sin x (3cos x -sin x )+1=23sin x cos x -2sin 2x +1 =3sin 2x +cos 2x=2sin ⎝⎛⎭⎫2x +π6, 又函数g (x )=f (x -φ)=2sin ⎣⎡⎦⎤2(x -φ)+π6 =2sin ⎝⎛⎭⎫2x -2φ+π6为偶函数, 所以π6-2φ=π2+k π,k ∈Z , 即φ=-π6-k π2,k ∈Z . 当k =-1时,φ=π3. 10.已知函数f (x )=32sin 2x +12cos 2x ,若其图象是由y =sin 2x 图象向左平移φ(φ>0)个单位长度得到,则φ的最小值为( ) A.π6B.5π6C.π12D.5π12答案 C解析 f (x )=32sin 2x +12cos 2x =sin ⎝⎛⎭⎫2x +π6, 函数y =sin 2x 的图象向左平移φ(φ>0)个单位长度后的解析式为y =sin [2(x +φ)],∴φ=π12+k π(k ∈Z ). ∴φ的最小值为π12.11.若cos 2αsin ⎝⎛⎭⎫α-π4=-22,则sin α+cos α=________. 答案 12解析 ∵cos 2αsin ⎝⎛⎭⎫α-π4=-cos 2α-sin 2α22(cos α-sin α) =-2(cos α+sin α)=-22, ∴cos α+sin α=12. 12.已知sin ⎝⎛⎭⎫x +π4=35,sin ⎝⎛⎭⎫x -π4=45,则tan x =________. 答案 -7解析 由sin ⎝⎛⎭⎫x +π4=35,sin ⎝⎛⎭⎫x -π4=45, 得sin x +cos x =325,sin x -cos x =425, 解得sin x =7210,cos x =-210, 所以tan x =sin x cos x=-7. 13.在锐角△ABC 中,sin(A +B )=35,sin(A -B )=513,则tan 2B =________. 答案 -5633解析 因为在锐角△ABC 中,sin(A +B )=sin C =35, sin(A -B )=513,所以A +B >90°,0°<A -B <90°. 所以cos(A +B )=-45,cos(A -B )=1213. 所以tan(A +B )=-34,tan(A -B )=512. 所以tan 2B =tan [(A +B )-(A -B )]=tan (A +B )-tan (A -B )1+tan (A +B )tan (A -B )=-34-5121+⎝⎛⎭⎫-34×512=-5633. 14.若函数f (x )=(sin x +cos x )2-2cos 2x -m 在⎣⎡⎦⎤0,π2上有零点,则实数m 的取值范围是________.答案 [-1,2]解析 函数f (x )=(sin x +cos x )2-2cos 2x -m =sin 2x -cos 2x -m =2sin ⎝⎛⎭⎫2x -π4-m 在⎣⎡⎦⎤0,π2上有零点,故函数y =2sin ⎝⎛⎭⎫2x -π4的图象和直线y =m 在⎣⎡⎦⎤0,π2上有交点,函数y =2sin ⎝⎛⎭⎫2x -π4在⎣⎡⎦⎤0,π2上的值域为[-1,2],故m ∈[-1,2]. 三、解答题15.(2018年6月学考)已知函数f (x )=12sin x +32cos x ,x ∈R . (1)求f ⎝⎛⎭⎫π6的值;(2)求函数f (x )的最大值,并求出取到最大值时x 的集合.解 (1)f ⎝⎛⎭⎫π6=12sin π6+32cos π6=14+34=1.(2)因为f (x )=cos π3sin x +sin π3cos x =sin ⎝⎛⎭⎫x +π3, 所以,函数f (x )的最大值为1,当x +π3=2k π+π2,k ∈Z , 即x =2k π+π6,k ∈Z 时,f (x )取到最大值, 所以,取到最大值时x 的集合为⎩⎨⎧⎭⎬⎫x ⎪⎪x =2k π+π6,k ∈Z . 16.已知函数f (x )=2cos 2x +23sin x cos x (x ∈R ).(1)当x ∈[0,π]时,求函数f (x )的单调递增区间;(2)若关于x 的方程f (x )-t =1在⎣⎡⎦⎤0,π2内有两个不相等的实数解,求实数t 的取值范围. 解 (1)f (x )=2cos 2x +23sin x cos x=cos 2x +3sin 2x +1=2⎝⎛⎭⎫32sin 2x +12cos 2x +1=2sin ⎝⎛⎭⎫2x +π6+1. 令2k π-π2≤2x +π6≤2k π+π2(k ∈Z ), 解得k π-π3≤x ≤k π+π6(k ∈Z ). 因为x ∈[0,π],所以f (x )的单调递增区间为⎣⎡⎦⎤0,π6,⎣⎡⎦⎤2π3,π. (2)依题意,得2sin ⎝⎛⎭⎫2x +π6+1-t =1, 所以t =2sin ⎝⎛⎭⎫2x +π6,即函数y =t 与y =2sin ⎝⎛⎭⎫2x +π6的图象在⎣⎡⎦⎤0,π2内有两个交点. 因为x ∈⎣⎡⎦⎤0,π2,所以2x +π6∈⎣⎡⎦⎤π6,7π6. 当2x +π6∈⎣⎡⎦⎤π6,π2时,sin ⎝⎛⎭⎫2x +π6∈⎣⎡⎦⎤12,1, y =2sin ⎝⎛⎭⎫2x +π6∈[1,2];当2x +π6∈⎣⎡⎦⎤π2,7π6时, sin ⎝⎛⎭⎫2x +π6∈⎣⎡⎦⎤-12,1,y =2sin ⎝⎛⎭⎫2x +π6∈[-1,2].由函数y =t 与y =2sin ⎝⎛⎭⎫2x +π6的图象(图略), 得1≤t <2,所以实数t 的取值范围是[1,2).。
2019版数学浙江省学业水平考试专题复习必修4 §2
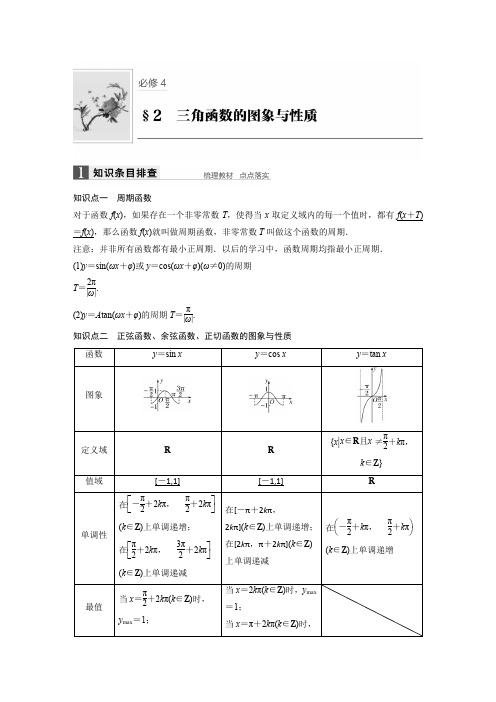
知识点一周期函数对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期.注意:并非所有函数都有最小正周期.以后的学习中,函数周期均指最小正周期.(1)y=sin(ωx+φ)或y=cos(ωx+φ)(ω≠0)的周期T=2π|ω|.(2)y=A tan(ωx+φ)的周期T=π|ω|.知识点二正弦函数、余弦函数、正切函数的图象与性质知识点三 y =A sin(ωx +φ)的图象1.用五点法画y =A sin(ωx +φ)一个周期内的简图时,要找五个特征点.如下表所示:2.y =A sin(ωx +φ)的有关概念知识点四 函数y =sin x 的图象经变换得到y =A sin(ωx +φ)(A >0,ω>0)的图象的步骤题型一 三角函数的周期性、对称性及单调性例1 (1)(2017年11月学考)下列函数中,最小正周期为π的是( ) A .y =sin xB .y =cos xC .y =tan xD .y =sin x2(2)函数f (x )=sin ⎝⎛⎭⎫x -π4的图象的一条对称轴是( ) A .x =π4 B .x =π2 C .x =-π4 D .x =-π2答案 (1)C (2)C解析 (1)y =sin x ,y =cos x 的周期是2π, y =sin x2的周期为4π,y =tan x 的周期为π,故选C.(2)∵正弦函数图象的对称轴过图象的最高点或最低点, ∴令x -π4=k π+π2,k ∈Z ,得x =k π+3π4,k ∈Z .取k =-1,则x =-π4.感悟与点拨 (1)掌握y =sin x ,y =cos x ,y =tan x 的周期.(2)对于复杂的三角函数可先化为y =A sin(ωx +φ)(或y =A cos(ωx +φ))的形式,然后再求周期:T =2π|ω|.(3)在求对称轴或单调区间时,通常把“ωx +φ”看作一个整体.跟踪训练1 (1)(2016年4月学考)已知函数f (x )=2sin ⎝⎛⎭⎫x +π2+3,x ∈R ,则f (x )的最小正周期是______,最小值是________.(2)若函数f (x )=sin ωx (ω>0)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω=________.答案 (1)2π 1 (2)32解析 (1)T =2π|ω|=2π1=2π,∵sin ⎝⎛⎭⎫x +π2∈[-1,1], ∴当sin ⎝⎛⎭⎫x +π2=-1时, f (x )min =2×(-1)+3=1.(2)f (x )=sin ωx 的图象过原点, 由已知条件画图象(图略)可知, π3为该函数的四分之一周期, 所以2πω=4π3,得ω=32.题型二 函数y =Asin(ωx +φ)的图象及变换例2 (1)(2018年6月学考)要得到函数f (x )=sin ⎝⎛⎭⎫2x -π4的图象,只需将函数g (x )=sin 2x 的图象( )A .向右平移π8个单位长度B .向左平移π8个单位长度C .向右平移π4个单位长度D .向左平移π4个单位长度(2)将函数y =sin ⎝⎛⎭⎫2x -π3图象上的点P ⎝⎛⎭⎫π4,t 向左平移s (s >0)个单位长度得到点P ′.若P ′位于函数y =sin 2x 的图象上,则( ) A .t =12,s 的最小值为π6B .t =32,s 的最小值为π6C .t =12,s 的最小值为π3D .t =32,s 的最小值为π3答案 (1)A (2)A解析 (2)由题意得t =sin ⎝⎛⎭⎫2·π4-π3=12, 故此时P ′所对应的点为P ′⎝⎛⎭⎫π4-s ,12, 若P ′位于函数y =sin 2x 的图象上, 则sin ⎝⎛⎭⎫π2-2s =cos 2s =12, 所以2s =±π3+2k π,k ∈Z ,得s =±π6+k π,k ∈Z .由s >0,得当k =0时,s min =π6.感悟与点拨 三角函数的图象变换,有两种选择:一是先伸缩再平移,二是先平移再伸缩.特别注意平移变换时,当自变量x 的系数不为1时,要将系数先提出,翻折变换要注意翻折的方向;三角函数名不同的图象变换问题,应先将三角函数名称统一,再进行变换. 跟踪训练2 (1)要得到余弦曲线y =cos x ,只需将正弦曲线y =sin x 向左平移( ) A.π2个单位长度 B.π3个单位长度 C.π4个单位长度 D.π6个单位长度 (2)若把函数y =sin ⎝⎛⎭⎫ωx -π6的图象向左平移π3个单位长度,所得到的图象与函数y =cos ωx 的图象重合,则ω的一个可能取值是( ) A .2 B.32 C.23 D.12答案 (1)A (2)A解析 (1)∵cos x =sin ⎝⎛⎭⎫x +π2, ∴余弦函数y =cos x 的图象可看作正弦函数y =sin x 的图象向左平移π2个单位长度得到,故选A.(2)把函数y =sin ⎝⎛⎭⎫ωx -π6的图象向左平移π3个单位长度, 得到函数y =sin ⎝⎛⎭⎫ωx +ω3π-π6的图象. ∵函数y =sin ⎝⎛⎭⎫ωx +ω3π-π6的图象与函数y =cos ωx 的图象重合, ∴由诱导公式可得ω3π-π6=π2+2k π(k ∈Z ),解得ω=2+6k (k ∈Z ), 当k =0时,ω=2.题型三 求函数y =Asin(ωx +φ)的解析式例3 (1)已知函数f (x )=2sin(ωx +φ)⎝⎛⎭⎫其中ω>0,|φ|<π2的最小正周期是π,且f (0)=3,则( )A .ω=12,φ=π6B .ω=12,φ=π3C .ω=2,φ=π6D .ω=2,φ=π3(2)已知函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,|φ|<π2,ω>0的图象的一部分如图所示,则该函数的解析式为________________.答案 (1)D (2)f (x )=2sin ⎝⎛⎭⎫2x +π6 解析 (1)∵f (x )=2sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2的最小正周期为π,∴T =2πω=π,∴ω=2. ∵f (0)=2sin φ=3,即sin φ=32⎝⎛⎭⎫|φ|<π2,∴φ=π3.(2)观察图象可知,A =2且点(0,1)在图象上, ∴1=2sin(ω·0+φ),即sin φ=12.∵|φ|<π2,∴φ=π6.又∵1112π是函数的一个零点,且是图象递增穿过x 轴形成的零点, ∴11π12ω+π6=2π,∴ω=2. ∴f (x )=2sin ⎝⎛⎭⎫2x +π6. 感悟与点拨 根据y =A sin(ωx +φ)+k (A >0,ω>0)的图象求其解析式的问题,主要从以下四个方面来考虑:(1)A 的确定:根据图象的最高点和最低点,确定函数的最大值和最小值,则A =最大值-最小值2;(2)k 的确定:k =最大值+最小值2;(3)ω的确定:结合图象,先求出周期T ,然后由T =2πω(ω>0)来确定ω;(4)φ的确定:常用的方法有:①五点法:由函数y =A sin(ωx +φ)+k 最开始与x 轴的交点(最靠近原点图象上升)的横坐标为-φω⎝⎛⎭⎫即令ωx +φ=0,x =-φω来确定φ;②代入法:把图象上的一个已知点代入解析式(此时A ,ω,k 已知)求解,要注意已知点是在上升区间上还是下降区间上.跟踪训练3 已知函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,0<φ<π2的部分图象如图所示,则f (x )的解析式是( )A .f (x )=2sin ⎝⎛⎭⎫2x +π3 B .f (x )=2sin ⎝⎛⎭⎫x +π3 C .f (x )=2sin ⎝⎛⎭⎫2x +π6 D .f (x )=2sin ⎝⎛⎭⎫x +π6 答案 B解析 由图象知函数的最大值为2,即A =2, 函数的周期T =4⎝⎛⎭⎫7π6-2π3=2π=2πω,解得ω=1, 即f (x )=2sin(x +φ),由题图知2π3+φ=π+2k π,k ∈Z ,又0<φ<π2,所以φ=π3,故f (x )=2sin ⎝⎛⎭⎫x +π3. 题型四 函数y =A sin(ωx +φ)的应用例4 已知函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,|φ|<π2,x ∈R 的图象的一部分如图所示.(1)求函数f (x )的解析式;(2)当x ∈⎣⎡⎦⎤-6,-23时,求函数y =f (x )+f (x +2)的最大值与最小值及相应的x 值. 解 (1)由图象知A =2,T =8, ∵T =2πω=8,∴ω=π4.又图象经过点(-1,0),∴2sin ⎝⎛⎭⎫-π4+φ=0. ∵|φ|<π2,∴φ=π4,∴f (x )=2sin ⎝⎛⎭⎫π4x +π4. (2)y =f (x )+f (x +2)=2sin ⎝⎛⎭⎫π4x +π4+2sin ⎝⎛⎭⎫π4x +π2+π4 =2sin ⎝⎛⎭⎫π4x +π4+2cos ⎝⎛⎭⎫π4x +π4 =22sin ⎝⎛⎭⎫π4x +π2 =22cos π4x .∵x ∈⎣⎡⎦⎤-6,-23,∴-3π2≤π4x ≤-π6, ∴当π4x =-π6,即x =-23时,y =f (x )+f (x +2)取得最大值6; 当π4x =-π,即x =-4时, y =f (x )+f (x +2)取得最小值-2 2.感悟与点拨 利用函数的图象确定解析式后,求出y =f (x )+f (x +2),然后化成一个角的三角函数形式,利用整体思想(将ωx +φ视为一个整体)求函数的最值.跟踪训练4 (1)已知函数y =2sin(ωx +θ)为偶函数(ω>0,0<θ<π),其图象与直线y =2的某两个交点的横坐标为x 1,x 2,若|x 2-x 1|的最小值为π,则( ) A .ω=2,θ=π2B .ω=12,θ=π2C .ω=12,θ=π4D .ω=2,θ=π4(2)已知f (x )=sin ⎝⎛⎭⎫ωx +π3(ω>0),f ⎝⎛⎭⎫π6=f ⎝⎛⎭⎫π3,且f (x )在区间⎝⎛⎭⎫π6,π3上有最小值,无最大值,则ω=________.答案 (1)A (2)143解析 (1)∵y =2sin(ωx +θ)为偶函数,0<θ<π, ∴θ=π2.∵图象与直线y =2的两个交点的横坐标为x 1,x 2, 且|x 2-x 1|min =π,∴2πω=π,ω=2. (2)∵f (x )在⎝⎛⎭⎫π6,π3上只有最小值,无最大值, 且f ⎝⎛⎭⎫π6=f ⎝⎛⎭⎫π3,∴f (x )在x =π6+π32=π4处取得最小值,∴π4ω+π3=-π2+2k π(k ∈Z ), ∴ω=8k -103(k ∈Z ),由ω>0得,①当k =1时,ω=143,②当k =2时,ω=383,此时f (x )在区间⎝⎛⎫π6,π3内存在最大值,不合题意.故ω=143.一、选择题1.f (x )=tan 2x 是( ) A .奇函数B .偶函数C .既是奇函数又是偶函数D .非奇非偶函数答案 A2.函数y =cos ⎝⎛⎭⎫2x +π3的图象的一条对称轴方程是( ) A .x =-π2B .x =-π4C .x =πD .x =-π6答案 D解析 由2x +π3=k π,k ∈Z ,得x =-π6+k2π,k ∈Z ,当k =0时,x =-π6.3.函数y =sin x 2的图象是( )答案 D解析 因为y =sin x 2为偶函数,所以它的图象关于y 轴对称,排除A ,C 选项;当x =π2时,y =sin π24≠1,排除B 选项,故选D.4.函数f (x )=tan ⎝⎛⎭⎫2x -π3的单调递增区间是( ) A.⎝⎛⎭⎫k π2+π6,k π2+2π3(k ∈Z )B.⎝⎛⎭⎫k π2-π12,k π2+5π12(k ∈Z )C.⎝⎛⎭⎫k π+π6,k π+2π3(k ∈Z ) D.⎝⎛⎭⎫k π-π12,k π+5π12(k ∈Z ) 答案 B解析 由k π-π2<2x -π3<k π+π2,k ∈Z , 解得k π2-π12<x <k π2+5π12,k ∈Z , ∴f (x )的单调递增区间为⎝⎛⎭⎫k π2-π12,k π2+5π12(k ∈Z ).5.把函数y =sin ⎝⎛⎭⎫2x +π3的图象向右平移π12个单位长度,再把所得图象上各点的横坐标伸长到原来的2倍,则所得图象的一条对称轴方程可以是( )A .x =π4B .x =π3C .x =5π6D .x =-π4答案 B解析 由y =sin ⎝⎛⎭⎫2x +π3向右平移π12个单位长度后, 得f (x )=sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π12+π3, 即f (x )=sin ⎝⎛⎭⎫2x +π6,将f (x )的图象中所有点的横坐标伸长为原来的2倍,得g (x )=sin ⎝⎛⎭⎫x +π6,由x +π6=π2+k π(k ∈Z ),得x =π3+k π(k ∈Z ), 当k =0时,x =π3. 6.设f (x )=sin ⎝⎛⎭⎫2x -π2,x ∈R ,则f (x )是( ) A .周期为π的奇函数B .周期为π的偶函数C .周期为π2的奇函数 D .周期为π2的偶函数 答案 B解析 ∵f (x )=sin ⎝⎛⎭⎫2x -π2=-cos 2x ,∴T =π. 7.函数①y =cos|2x |;②y =|cos x |;③y =cos ⎝⎛⎭⎫2x +π6;④y =tan ⎝⎛⎭⎫2x -π4中,最小正周期为π的所有函数为( )A .②④B .①③④C .①②③D .①③答案 C解析 分别求出各个函数的最小正周期T .①y =cos|2x |=cos 2x ,T =π;②由图象(图略)知,函数的周期T =π;③T =π;④T =π2. 综上可知,最小正周期为π的所有函数为①②③.8.已知函数f (x )=sin ⎝⎛⎭⎫2x +π3,下列判断错误的是( ) A .函数f (x )的最小正周期为πB .直线x =π12是函数f (x )图象的对称轴 C .函数f (x )的图象关于点⎝⎛⎭⎫-π6,0对称 D .函数f (x )在区间⎝⎛⎭⎫-π12,5π12上单调递增 答案 D解析 对于函数f (x )=sin ⎝⎛⎭⎫2x +π3, 它的最小正周期为2π2=π,故A 正确; 令x =π12,求得f (x )=1,为函数的最大值, 可得直线x =π12是函数f (x )图象的对称轴,故B 正确; 令x =-π6,求得f (x )=0,可得函数f (x )的图象关于点⎝⎛⎭⎫-π6,0对称,故C 正确; 在区间⎝⎛⎭⎫-π12,5π12上,2x +π3∈⎝⎛⎭⎫π6,7π6,即函数f (x )=sin ⎝⎛⎭⎫2x +π3在区间⎝⎛⎭⎫-π12,5π12上没有单调性,故D 错误,故选D. 9.已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x )=A sin(ωx +φ)+B 图象的两条相邻的对称轴,则φ为( )A.π2B.π3C.π4D.π6答案 C解析 ∵直线x =π4和x =5π4是函数 f (x )=A sin(ωx +φ)+B 图象的两条相邻的对称轴,∴T =2⎝⎛⎭⎫5π4-π4=2π,∵ω>0,∴ω=2πT=1, 即f (x )=A sin(x +φ)+B ,∴A sin ⎝⎛⎭⎫π4+φ+B 与A sin ⎝⎛⎭⎫5π4+φ+B 分别为最大值和最小值,∵0<φ<π,∴φ=π4. 10.已知函数f (x )=sin(2x +φ),其中φ为实数,若f (x )≤⎪⎪⎪⎪f ⎝⎛⎭⎫π6对x ∈R 恒成立,且f ⎝⎛⎭⎫π2>f (π),则f (x )的单调递增区间是( )A.⎣⎡⎦⎤k π-π3,k π+π6(k ∈Z ) B.⎣⎡⎦⎤k π,k π+π2(k ∈Z ) C.⎣⎡⎦⎤k π+π6,k π+2π3(k ∈Z ) D.⎣⎡⎦⎤k π-π2,k π(k ∈Z ) 答案 C解析 若f (x )≤⎪⎪⎪⎪f ⎝⎛⎭⎫π6对x ∈R 恒成立, 则f ⎝⎛⎭⎫π6为函数的最大值或最小值,即2×π6+φ=k π+π2,k ∈Z , 则φ=k π+π6,k ∈Z . 又f ⎝⎛⎭⎫π2>f (π),所以sin(π+φ)>sin φ,即sin φ<0,令k =-1,φ=-5π6,满足条件, 此时f (x )=sin ⎝⎛⎭⎫2x -5π6. 令2k π-π2≤2x -5π6≤2k π+π2,k ∈Z , 解得k π+π6≤x ≤k π+2π3,k ∈Z , 即函数的单调递增区间是⎣⎡⎦⎤k π+π6,k π+2π3(k ∈Z ). 二、填空题11.函数f (x )=sin ⎝⎛⎭⎫2x -π4,x ∈⎣⎡⎦⎤0,π2的值域为________. 答案 ⎣⎡⎦⎤-22,1 解析 ∵0≤x ≤π2, ∴0≤2x ≤π,-π4≤2x -π4≤3π4, ∴-22≤sin ⎝⎛⎭⎫2x -π4≤1, ∴函数的值域为⎣⎡⎦⎤-22,1. 12.函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,|φ|<π2的部分图象如图所示,则f (x )的解析式为_________________________.答案 f (x )=2sin ⎝⎛⎭⎫π3x +π6解析 根据题图判断,周期T =2(4-1)=6,A =2, 所以2πω=6,解得ω=π3. 因为2sin ⎝⎛⎭⎫π3+φ=2, 所以π3+φ=2k π+π2,k ∈Z ,所以φ=2k π+π6,k ∈Z . 因为|φ|<π2,所以φ=π6. 所以f (x )的解析式为f (x )=2sin ⎝⎛⎭⎫π3x +π6.13.已知函数f (x )=cos ⎝⎛⎭⎫2πx +π3,若对任意x ∈R 都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值是________.答案 12解析 ∵对任意x ∈R 都有f (x 1)≤f (x )≤f (x 2),∴f (x 1)是函数f (x )的最小值,f (x 2)是函数f (x )的最大值.∴|x 1-x 2|的最小值为函数的半个周期,∵T =2π2π=1,∴|x 1-x 2|的最小值为12. 14.将函数f (x )=sin ωx (ω>0)的图象向右平移π4个单位长度,所得图象关于点⎝⎛⎭⎫3π4,0对称,则ω的最小值是________.答案 2解析 将函数f (x )=sin ωx (ω>0)的图象向右平移π4个单位长度, 可得y =sin ω⎝⎛⎭⎫x -π4=sin ⎝⎛⎭⎫ωx -ωπ4的图象, 再根据所得图象关于点⎝⎛⎭⎫3π4,0对称,可得ω·3π4-ωπ4=k π,k ∈Z , 求得ω=2k ,k ∈Z ,又ω>0,故ω的最小值为2.15.关于y =f (x )=3sin ⎝⎛⎭⎫2x -π4有以下命题: ①若f (x 1)=f (x 2)=0,则x 1-x 2=k π(k ∈Z );②函数的解析式可化为y =3cos ⎝⎛⎭⎫2x -π4; ③f (x )的图象关于x =-π8对称;④f (x )的图象关于点⎝⎛⎭⎫-π8,0对称. 其中正确的是________.(填序号)答案 ③解析 关于y =3sin ⎝⎛⎭⎫2x -π4, 若f (x 1)=f (x 2)=0,则2x 1-π4=k 1π, 2x 2-π4=k 2π(k 1,k 2∈Z ), 即x 1-x 2=12k π(k =k 1-k 2,k ∈Z ),故①不正确; 函数的解析式y =3sin ⎝⎛⎭⎫2x -π4=3cos ⎣⎡⎦⎤π2-⎝⎛⎭⎫2x -π4 =3cos ⎝⎛⎭⎫2x -3π4≠3cos ⎝⎛⎭⎫2x -π4,故②不正确; 令x =-π8,求得y =-3,为函数f (x )的最小值, 故函数的图象关于x =-π8对称,故③正确,④不正确. 三、解答题16.如图所示为y =A sin(ωx +φ)的图象的一段(|φ|<π).(1)求其解析式;(2)若将y =A sin(ωx +φ)的图象向左平移π6个单位长度后得y =f (x ),求f (x )的对称轴方程. 解 (1)由图象知A =3,以M ⎝⎛⎭⎫π3,0为第一个零点,N ⎝⎛⎭⎫5π6,0为第二个零点,列方程组⎩⎨⎧ ω·π3+φ=0,ω·5π6+φ=π,解得⎩⎪⎨⎪⎧ω=2,φ=-2π3.∴所求解析式为y =3sin ⎝⎛⎭⎫2x -2π3. (2)由题意知f (x )=3sin ⎣⎡⎦⎤2⎝⎛⎭⎫x +π6-2π3 =3sin ⎝⎛⎭⎫2x -π3, 令2x -π3=π2+k π(k ∈Z ),则x =512π+k π2(k ∈Z ), ∴f (x )的对称轴方程为x =512π+k π2(k ∈Z ).。
【2013-7到2015-7】浙江省学考真题专题汇总-----必修4---【第2章】向量

【2013-7到2015-7】浙江省学考真题专题汇总-----必修4---【第2章】向量浙江省学考真题专题汇总-----必修4---第二章向量【2013-7】17.若平面向量,a b 的夹角为60 ,且|2|=|a b |,则()(A)()⊥+a b a (B)()⊥-a b a(C)()⊥+b b a (D)()⊥-b b a27.已知平面向量(2,3)=a ,(1,)m =b ,且//a b ,则实数m 的值为.【2014-1】10、设a ,b 是两个平面向量,则“a =b ”是“|a |=|b |”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件29、设P 是半径为1的圆上一动点,若该圆的弦AB=3,则AP AB ? 的取值范围是4.已知ABC Rt ?的斜边AB 的长为4,设P 是以C 为圆心1为半径的圆上的任意一点,则PB PA ?的取值范围是()A. ]25,23[-B. ]25,25[- C. ]5,3[- D. ]321,321[+-【2015-1】3、向量a =(2,1),b =(1,3),则a +b =() A.(3,4) B.(2,4) C.(3,-2)D.(1,-2)30、如图,已知AB ⊥AC ,AB=3,AC=3,圆A 是以A 为圆心半径为1的圆,圆B 是以B 为圆心的圆。
设点P ,Q 分别为圆A ,圆B 上的动点,且12AP BQ = ,则CP CQ ?的取值范围是 Q C B A P (第30题图)10.若b a ,是两个单位向量,则()A.b a =B.b a =C.0=?b aD.1=?b a30.如图所示,在直角三角形AOB 中,OA=1,OB=2,M 是斜边AB 的中点,过M 的直线分别交射线OA,OB 于P,Q 两点,N 是线段PQ 的中点,则ON OM ?的最小值是O AB M。
(完整版)浙江省学考真题专题汇总-----必修4---第一章三角函数定义

浙江省学考真题专题汇总-----必修4---第一章三角函数定义【2013-7】4.函数R))(3π2sin()(∈+=x x x f 的最小正周期为 ( ) (A)2π(B) π (C) π2 (D) 4π31.(本题7分) 已知,54sin ),π,2π(=∈θθ求θcos 及)3πsin(+θ的值.【2014-1】5、与角-6π终边相同的角是( )A.56πB.3πC.116πD.23π31、(本题7分)已知3sin ,052παα=<<,求cos α和sin()4πα+的值.【2014-7】7.)cos(απ+=( )A. αcosB. αcos -C. αsinD. αsin -11.将函数)4sin()(π-=x x f 图象上的所有点向左平移4π个单位长度,则所得图象的函数解析式是( )A. x y sin =B. x y cos =C. x y sin -=D. x y cos -=15.设函数),23,23(,tan )(ππ-∈=x x x x f 且2π±≠x ,则该函数的图像大致是( )28.已知函数)0)(3sin(2)(>+=ωπωx x f 的最小正周期为π,则=ω .【2015-1】 31、(本题7分)已知1cos ,032x x π=<<,求sinx 与sin2x 的值.【2015-10】5.要得到余弦曲线y=cosx ,只需将正弦曲线y=sinx 向左平移 ( ) A.个单位2πB.个单位3πC.个单位4πD.个单位6π【2016-1】5. =-∈)sin(απα,则设RA.αcosB.αcos -C.αsinD.αsin - 13. 将函数cos ,y x x R =∈图像上的每个点向右平移3π个单位,再向上平移2个单位,得到的图像对应的函数解析式为 A. cos()23y x π=+- B. cos()23y x π=++ C. cos()23y x π=-- D. cos()23y x π=-+ 31.(本题7分)).4sin(sin ),2,0(,53cos πααπαα+∈=及求已知【2016-4】2. 已知角α的终边经过点P (3,4),则=αsin ( ) A.53B. 43C. 54D.34【2016-10】4.若点P (-3,4)在角α的终边上,则cos α= ( ) A.53-B.53C.54-D.54【2017-4】8. 已知θ为锐角,且sinθ=53,则sin (θ+4π)= ( )A.1027 B.1027- C.102 D.102-【2017-11】3.设θ为锐角,sin θ=31,则cos θ= A.32 B.32 C.36 D.3225.下面函数中,最小正周期为π的是A.y=sin xB.y=cos xC.y=tan xD.y=sin 2x【2018-1】7.下列角中,终边在y 轴正半轴上的是 ( )A. 4πB. 2πC. πD.23π 31.(本题7分)的值。
最新版数学浙江省学业水平考试专题复习必修4-§5

n 知识条目排查梳理教材点点落实知识点一平面向量的数量积定义设两个非零向量a, b 的夹角为0,则数量|a ||b |cos 0叫做a 与b 的数量积(或内积),记作a b ,即a b = |a ||b |cos 0 投影 |a |cos 0叫做向量a 在b 方向上的投影,|b |cos 0叫做向量b 在a 方向上的投影几何意义数量积a b 等于a 的长度|a |与b 在a 的方向上的投影|b |cos 0的乘积特别提醒: ⑴两非零向量a = OA , b = OB ,则a 与b 夹角为/ AOB ,其范围是[0, n ; (2) 数量积是一个实数;(3) 零向量与任一向量的数量积为零. 知识点二平面向量数量积的性质及运算律 1 .数量积的重要性质 对于非零向量a , b ,(1) e a = a e = |a |cos 0,其中 B 为a 与e 的夹角,e 为单位向量; (2) a 丄 b ? a b = 0;⑶当a 与b 同向时,ab = |a || b |;当a 与b 反向时,a b =- |a ||b |, a a = |a f, |a |= • a a ; (4) cos 9=-07,其中0为a 与b 的夹角;|a || b | (5) 1 a b |__< __|a ||b |. 2 •数量积满足的运算律 (1) a b = b a ;(2) ( :a) b = \a b )= a ( b )(入为实数); (3) ( a + b ) c = a c + b c . 知识点三平面向量数量积、模、夹角的坐标表示设 a = (x i , y i ), b =(X 2, y 2). 必修4§5平面向量的数量积(1) a b= X1X2 + Y i y g.(2) |a|= x1+ y或 |a|2= x1±_y?a b x i X2 + y i y2⑶cos 0=丽厂—x1+y厂x2+ y知识点四向量垂直的充要条件设向量a= (x i, y i), b=(X2, y2),贝U a丄b? a b= 0 ? x i x2+ y i y2= 0(a, b 为非零向量).题型分类剖析典例演练诔层突破题型一向量的夹角与模的问题例i (i)(20i6 年i0 月学考)设向量a= (x- 2,2), b= (4, y), c= (x, y), x, y€ R,若a丄b, 则|c|的最小值是()A号B.4/ C•于D. 5(2)(20i6年4月学考)已知平面向量a, b满足|a匸;3, b= 心(氐R),其中e i, e?为不共线的单位向量,若对符合上述条件的任意向量a, b恒有|a —b|> 3,则e i, e夹角的最小值4为()n n 2 n 5 nA.6B.3 c.§ D.6答案(i)B (2)B解析(i)由题意得a b= (x—2,2) (4, y) = 0,即2x+ y= 4.方法一••• |c|=寸2+ y2=p2+ (4 —2x 2=5x2_i6x+ i6= .5 x— 5 2+ 警誓方法二V |c|= x2+ y2,即直线2x+ y- 4= 0上的点(x, y)到原点(0,0)的距离,|2 X 0 + 0—4| 4^5• |c|min = -2_ = 5 .\22+ 12 52 V |a—b|> —,二 a 2- 2a b + b 2= |b |2—fblcos 〈 a , b 〉+ 簷》箱, [3|b |2— ^blcos 〈a , b > >0, 即 |b |^2"cos 〈 a , b >. 即|b |》^, 2 3•••心+ ?e| >4, 设e i 与e 2的夹角为B,贝U222 3e i + 2 入e i ||e 2|cos 0+ 入e 2》4,2 1 -|ei |= |e 2|= 1,贝U 入 + (2cos2 1--△= 4cos 0— 4 X — w 0,411n• -cos 0< 2 又 0€ [0 , n] • 0的最小值为 3. x 2+ y 2 ⑵利用 |a |2= a 2,即 |a |= a a .(3) 利用方程与函数的思想构建关于角或模的函数或方程求解.跟踪训练1 (1)已知向量a 与b 的夹角为120° |a |= 3, |a + b |= .13,则|b |等于( )A . 1B . 3C . 4D . 5⑵(2018年4月学考)若平面向量 a , b 满足2a + b = (1,6), a + 2b = (— 4,9),则a b = _____________⑶已知△ ABC 外接圆的圆心为 O ,且O A W S OB + 2OC = 0,则/ AOC = _____________ . 答案(1)C(2) — 2 ⑶ 2f解析 ⑴根据条件,(a + b )2= a 2+ 2a b + b 22=9 — 3|b |+ |b |2= 13, 解得|b |= 4或|b |=— 1(舍去).感悟与点拨(1)求夹角或模可以直接利用公式:cos0=卫=|a ||b |X 1X 2+ y i y 2a(2) •/ 2a + b = (1,6), a + 2b = (-4,9), ••• a = (2,1), b = (- 3,4), ••• a b = (2,1) (-3,4) = - 6+ 4=- 2. ⑶设 |0A|= |OB|=|OC|= 1,OA + 20C = - 3(0B ,两边平方,• 12+ 4 OA OC + 4X 12 = 3X 12,• OA O C 一 22 n•/ 0 <Z AOC < n •/ AOC =」 3 -题型二 向量的平行与垂直例2 已知平面向量 a = (2, x), b = (2, y), c = (3, - 4),且a // c , b ±c ,贝U a 与b 的夹角为答案扌解析•/ a // c , • - 8- 3x = 0, 解得x =- |.33T b 丄 c, •- 6— 4y = 0,解得 y =• a = 2,― 3 , b = 2, 2 .设a 与b 的夹角为B,且氏[0 , n] •- 0=n 即向量a 与b 的夹角为n ⑵在△ ABC 中,点 A(2, - 1), B(3,2), C(-3, - 1), AD 为边BC 上的高,求 AD 与点D 的 坐标.解 设点D 的坐标为(x , y),二 cos 〈OA , OC 〉 1 2,则 cos 0=a b |a ||b |2X 2-£X 3则AD = (x - 2, y + 1), BC = (- 6,- 3), BD =(X - 3, y — 2),•••点D 在直线BC 上,即卩BD , BC 共线, •••存在实数人使BD = ?BC , 即(X - 3, y - 2) = X - 6,- 3).[x — 3 =- 6 X …得x — 2y + 1 = 0.①l y -2 = - 3 X又••• AD 丄 BC , ••• AD BC = 0, 即(x — 2, y + 1) (•- 6,- 3) = 0, 即 2x + y - 3 = 0•② 由①②,得x = 1, y = 1,• AD =(-1,2),点D 的坐标为(1,1). 感悟与点拨a= (x 1, y”,b = (x 2, y 2), b 为非零向量.(1)a // b ? a = ?b? X 1y 2 — x 2y 1 = 0. (2)a 丄 b ? a b = 0? X 1X 2 + y 〔y 2= 0. 跟踪训练2(1)设a = (1,2), b = (1,1), c = a + k b .若b ±c ,则实数k 的值为(5 C.3 答案 A解析 T c = (1 + k,2+ k),又 b c = 0,3•1+k + 2+ k =0, • k =- 3.(2)在平面四边形 ABCD 中,向量 a = AB = (4,1), b = BC = (3, - 1), c = CD ① 若向量a + 2b 与向量b- k c 垂直,求实数k 的值; ② 若DB = mI D A + nDC ,求实数 m , n.3 D.?(-1 , - 2).解①T向量a+ 2b与向量b—k c垂直,•••(a + 2b ) (b — k c ) = 0.•••(10, — 1) (3 + k , — 1 + 2k)= 0.••• 30 + 10k + 1 — 2k = 0, • k = ②••• BD = BC + CD = (2, — 3), • DB = (— 2,3).••• AD = AB + BC + CD = (6,DB = mDA + nDC ,•••( — 2,3) = m(— 6,2)+ n (1,2),[—2 = — 6m + n ,• • I3= 2m + 2n ,题型三 平面向量的综合应用例3 (1)已知平面向量 a , b 满足a i =|b |= 2,存在单位向量 e ,使得(a — e ) (b -e )= 0,则|a —b |的取值范围是 __________________ .⑵已知平面向量 a , b , |a |= 1, |b |= 2, a b = 1,若c 为平面单位向量,则|ac |+ |b c |的最大值是 _______ . 答案(1)[ 7 — 1,7 +1](2).7解析 (1)由(a — e ) (-b — e )= 0,得 a b + 1 = e (a + b ),所以 |a b + 1|= |e (a + b )|< |a + b |,即(a b + 1)2w |a + b |2,所以(a b )2 < 7,所以 a b € [ — 7, 7],所以 |a — b |=- 8— 2a b € [ 7— 1, 7 +1].其几何意义为a 在c 方向上的投影的绝对值与 b 在c 方向上投影的绝对值的和,当 c 与a + b 共线时,取得最大值. • • (|a c |+ |b c |)max = |a + b | 「'|a |2+ |b |2+ 2a b = 7.31y. —2),•- DA = (— 6,2), DC = (1,2).(1m = 2 解得 2n = 1.感悟与点拨(1)熟练进行数量积、模、夹角的计算与转化.(2) 充分利用向量加减运算,数量积运算的几何意义.(3) 充分利用“数形结合”.(4) 将向量坐标化,通过坐标运算来解决问题.跟踪训练3 (1)已知点G ABC的重心,/ A= 120° AB AC =—2,则|AG|的最小值是()3 .2 2 3A.T B2 C・3 D・4⑵已知向量a, b, |a|= 1, |b|= 2,若对任意单位向量e,均有|a e|+ |b e|< . 6,则a b的最大值是 ________ .1答案(1)C (2)1解析(1)设BC的中点为M,则AG = |A M.又M为BC的中点,所以A M = |(A B+A C),-> 2 ~1 -> ->所以AG = 3AM = 'AB + AC),所以|AG|的最小值为2,故选C.(2)因为 |(a + b ) e |= |a e + b e |w |a e |+ |b e |w • 6, 所以 |(a + b ) e |w |a + b |w . 6,22平方得 |a | + |b | + 2a b < 6,22即 1 + 2 + 2a b w 6, 1 1则a b < ^,故a b 的最大值是一、选择题1 .设向量a , b 均为单位向量,且|a + b |= 1,则a 与b 的夹角B 为()n n 2 n 3 n代3 B .2 C .§ D .4答案 C2 .已知向量 a = (1,2), a b = 5, |a — b |= 2 ,5,则 |b |等于( )A. 5 B . 2.5 C . 5 D . 25答案 C3 .已知向量 a , b 满足 a + b = (1, — 3), a — b = (3,7),贝U a b 等于( )A . — 12B . — 20C . 12D . 20 答案 A解析 方法一 ••• (a + b ) + (a — b )= 2a = (4,4),—之2 ~之 ~之+ AC + 2AB A C所以|AG| =又因为 AB AC = — 2, / A = 120° 所以 |AB|AC|= 4. 当且仅当AB|=|AC|时取“=”,23,对点专项课后检考尷化.••• a = (2,2) ,••• b= (a+ b) —a= (- 1,—5),••• a b= 2X (—1) —2X 5=—12.方法二•/ (a + b)2—(a—b)2=—48, • 4a b=—48,•- a b=—12.4 .已知菱形 ABCD 的边长为a ,/ ABC = 60 °则BD CD 等于()3 B. — 4a ^3 2 f 3 2 C.&a D.^a 答案 D解析 如图所示,••• BD = BA + BC , CD = BA ,BD CD = (BA + BC) BA = BA + BC BA = a + a acos 60 = ~a .故选 D.5. 已知向量a , b 满足|a |= 2, a (b — a )=— 3,贝U b 在a 方向上的投影为(答案 C解析■/ |a |= 2, a (b — a ) = — 3,a b — a 2 = a b — 22=— 3,a b = 1,•••向量b 在a 方向上的投影为 誓=£故选C. |a | 26. 如图所示,半圆的直径 AB = 4, O 为圆心,C 是半圆上不同于 A , B 的任意一点,若 P 为半 径OC 上的动点,贝U (PA + PB ) PC 的最小值是( )A . 2B . 0C .— 1D . — 2答案 D解析 由平行四边形法则得 PA + PB = 2PO , 故(FA + PB) PC = 2PO PC ,又 |PC|= 2 — |PO|,且PO , PC 反向,设|PO|= t(0W t w 2),3A . — ga2 A.3 B . 2 1—3 C.2 D .进而可得C(1,1), M 1, 2 , 设 E(x,0)(0 w x w 1),所以 EC = (1 — x,1), EM = 1— x , 1 ,~~1 2 3 2 1所以 EC EM = (1 — x)(1 — x) + 1 X 2= x — 2x + 2= (x — 1) + -.因为O w x w 1,— — 1所以当 x = 1 时,(EC EM)min = 2 ;f f 3当 x = 0 时,(EC EM )max = 2.—f —f 1 —f —f —f8.如图,在厶ABC 中,D 是BC 的中点,|AD|= 3,点P 在AD 上,且满足AP = §PD ,则PA (PBPC )等于(则(FA+ PB) PC = 2PO PC 2=-2t(2 — t)= 2(t — 2t)=2[(t — 1)2— 1].因为O w t w 2,所以当t = 1时,(PA + PB ) PC 取得最小值—2,故选D.7.在边长为1的正方形 ABCD 中,点M 为BC 的中点,点E 在线段AB 上运动,则EC EM 的取值范围是(A.J ,"C._1 2答案 C解析 如图,以AB , AD 所在的直线分别为 x 轴、y 轴建立平面直角坐标系,A . 4C . - 2答案 D解析由|AD|= 3,点P 在AD 上,且满足 A p = 2PD ,-> 1 -> ->可得 |PA|= 3AD|= 1 , |PD| = 2,由D 是BC 的中点,可得2PD = PB + PC ,即有 PA (PB + PC) = 2PA PD9.如图,在平行四边形 ABCD 中,AB = 8, AD = 5, CP = 3PD , AP BP = 2,贝UAB AD 等于(D. 25答案 A=A D 2-3AD AB + 4A B AD - ^A B 2 4 4 16=25- ^A D A B - 3 X 64= 2.a b = 0,若向量c 满足|c - a - b |= 1,则|c |的取值范围是(A . 22C . 24 ••• AP BP =••• AB AD = 22. 10.已知a, b 是两个单位向量,A . [ 2 -1, , 2+ 1] C . [1 , .2+ 1] 2 X 1 X 2=- 4.B . 23解析•/ AP BP = AD+T —4AB =2, 1 1 f +4AB 3 f 4AB4B . [ .2 - 1 , 2 + 2]D . [1 , . 2+ 2]答案A解析条件|c—a—b|= 1可理解成如图的情况.*|a+ b|= 2,向量c的终点在单位圆上,故|c|的最大值为,2+ 1,最小值为.2— 1.二、填空题11. 在平行四边形ABCD中,AD = 2,Z BAD = 60° E为CD的中点,若AD BE= 1,贝V AB的长为_________ .答案6解析如图所示,由题意可得,-> -> -> -> -> -> -> -> -> -> 2 1 ~> -> 2 1 ~>AD BE = AD ( BC+ CE) = AD BC + AD CE = AD —?AD AB= 2 — "X 2X |AB|x cos 60°= 1,••jAB|= 6,即AB 的长为 6.12. 已知正三角形ABC的边长为1.设AB= a,BC= b,AC = c,那么a b+ b c+ c a的值为1答案2解析由题意可知,a,b的夹角为120°b,c的夹角为60° a,c的夹角为60°1 所以a b+ b c+ c a= 1 X 1 X cos 120 + 1 X 1X cos 60 + 1 X 1X cos 60 = ?.13. 在等腰三角形ABC中,AB = AC= 1,Z BAC = 90°点E为斜边BC的中点,点M在线段AB上运动,则IME M I C的取值范围是_________ .答案_W,11 1 7 1 i —> —> 7 —> —> +2 = m -4 + 16,由于4 € [0,1],所以当m = 4时,ME MC 取得最小值 石;当m = 1时,ME MC 取得最大值1.所以ME MC 的取值范围是£, 1〔14. (2016 年 10 月学考)如图,在厶 ABC 中,AB = 2, AC = 3, AB AC = 2,右点 P 满足 BP = 2PC , 贝U AP BC= ____答案 4解析 依题意得 AP = AB + BP = AB + |EB C = AB + |(E3A + AC) = AB + |AC ,贝U A P BC = 3 3 3 3 -|AB 2- ^AC AB + |AC 2=- I -1+ 6 = 4.15. (2017年4月学考)设点P 是边长为2的正三角形ABC 的三边上的动点,贝U PA (PB + PC ) 的取值范围为 __________答案 -9, 2 I解析取AB 的中点0.解析 如图,以A 为坐标原点,AC , AB 所在直线分别为x 轴,y 轴建立平面直角坐标系,则 A(0,0),B(0,1),C(1,0),E 1, 1.设 M(0, m)(0 w m W 1),则 ME = 2,^AB + |AC (AC - AB) =m).ME m 2-gm学习-----好资料AB边所在直线为x轴,AB边高线为y轴建立如图所示的平面以AB的中点0为坐标原点,直角坐标系,可得A(- 1,0), B(1,0) , C(0, 一3).当点P在线段AB上时,设P(t,0)(- K t< 1),PA= (- 1 - t,0), PB = (1 - t,0), PC= (- t, 3),即有PA (PB + PC) = (- 1-1,0) (1 - 2t, ,3)=(-1-1)(1 - 2t)+ 0X 3 = 2t2+ t- 11 -> -> -> 9 ~》-> -> 由一K t< 1可得,当t=- 4时,PA(PB+ PC)取得最小值一8,当t= 1时,PA (PB + PC)取得最大值2;当点P在线段CB上时,设P(m, .3(1 - m))(0 < m w 1),P A= (- 1 - m, . 3(m- 1)), PB = (1 - m, 3(m- 1)),PC= (- m, , 3m),即有P A (PB + PC) = (- 1-m, ,3(m- 1)) (1 -2m, 3(2m- 1))=(-1-m)(1 - 2m) + , 3(m- 1) x 3(2m-1)=2(2m- 1)2,由0w m W 1可得,当m= 丁时,PA (PB + PC)取得最小值0,当m= 0或1时,PA (PB+ PC)取得最大值2;当点P在线段AC上时,设P(n, .3(1 + n))( - 1W n w 0),PA = (— 1 — n ,— 3(1 + n)), PB = (1 — n ,— 3(1 + n)), PC = (— n ,— 3n),即有 PA (PB + PC) = (— 1 — n ,— .3(1+ n))(1 — 2n ,— .3(1 + 2n)) =(—1 — n)(1 — 2n)+ 3(1 + n) x 3(1 + 2n) = 8n 2+ 10n + 2 = 8n +1 2— |,5 ~> -> -> 9 ~> -> ->由一1w n w 0可得,当n = — 8时,PA (PB + PC)取得最小值一@当n = 0时,PA (PB + PC) 取得最大值2. 2 (2)f(x)= 2a b + 1 = 2( — cos x + sin xcos x) + 1=2sin xcos x — (2cos 2x — 1)=sin 2x — cos 2x综上可得,PA (PB + PC)的取值范围是29 -学习-----好资料更多精品文档三、解答题 16. 已知向量 a = (cos x , sin x), b = (— cos x , cos x), c = (—1,0). n (1)若x = 6,求向量a , c 的夹角; ;,尹时,求函数f") = 2a b + 1的最大值.—cos x5 n 0 w 〈 a , c > < n ••• 〈 a , c >=— 6(2)当 x € 解(1)cos 〈 a , c > a c a i c i ,—12+02 =—cos x =— n 5n 6=cos 孑 2 2 x + sin x x学习-----好资料 更多精品文档故 sin 2x — •••当 2x — 4= 3j-n 即 x =扌时寸,f(x)max = 1■/ x € -n 9 n 2,8_ —1,。
浙江201510月_2017年11月数学学考题分类汇编
学考复习题分类练习1——集合与常用逻辑用语2015年10月1、(20.)设全集U={2,3,4},集合A={2,3},则A 的补集 U A=2、(12.)设a>0,且a≠1,则“a>1”是“log a 12<1”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件2016年4月3、(1.)已知集合{}1,2A =,.若,则的值为( )A. B. C. D. 4、(13.)在空间中,设为三条不同的直线,为一平面.现有:命题若,,且∥,则∥命题若,,且⊥,⊥,则⊥.则下列判断正确的是( )A.,都是真命题B.,都是假命题C.是真命题,是假命题 D.是假命题,是真命题5、(14.)设,则“数列为等比数列”是“数列为等比数列”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件2016年10月 6、(1.)已知集合}6,5,4,3{=A ,}{a B =,若}6{=⋂B A ,则=aA .3B .4C .5D .67、(8.)已知向量,,则“//”是“||||||b a b a -=-”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2017年4月8、(1.)已知全集{}1,2,3,4U =,若{}1,3A =,则U A =ð( )A .{}1,2B .{}1,4C .{}2,3D .{}2,49、(13.)设实数a ,b 满足||||a b >,则“0a b ->”是“0a b +>”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件{}(1)()0,B x x x a a R =--=∈A B =a 211-2-,,a b c α:p a α⊄b α⊂a b a α:q a α⊂b α⊂c a c b c αpq pqpq pq*n N ∈{}n a 21n a ⎧⎫⎨⎬⎩⎭2017年11月 10、(1.)已知集合A={1,2,3},B={1,3,4},则A ∪B=( )A. {1,3}B. {1,2,3}C. {1,3,4}D. {1,2,3,4,}11、(13.)已知a,b 是实数,则“|a|<1且|b|<1”是“a 2+b 2<1”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D.既不充分也不必要条件学考复习分类练习2——函数2015年10月 1、(1.)函数()f x =A.(-∞,0)B.[0,+∞)C. [2,+∞)D. (-∞,2)2、(22.)已知函数f(x)=||2x a x a ++-,g(x)=ax+1,其中a>0。
(完整版)浙江省学考真题专题汇总-----必修4---第一章三角函数定义
浙江省学考真题专题汇总-----必修4---第一章三角函数定义【2013-7】4.函数R))(3π2sin()(∈+=x x x f 的最小正周期为 ( ) (A)2π(B) π (C) π2 (D) 4π31.(本题7分) 已知,54sin ),π,2π(=∈θθ求θcos 及)3πsin(+θ的值.【2014-1】5、与角-6π终边相同的角是( )A.56πB.3πC.116πD.23π31、(本题7分)已知3sin ,052παα=<<,求cos α和sin()4πα+的值.【2014-7】7.)cos(απ+=( )A. αcosB. αcos -C. αsinD. αsin -11.将函数)4sin()(π-=x x f 图象上的所有点向左平移4π个单位长度,则所得图象的函数解析式是( )A. x y sin =B. x y cos =C. x y sin -=D. x y cos -=15.设函数),23,23(,tan )(ππ-∈=x x x x f 且2π±≠x ,则该函数的图像大致是( )28.已知函数)0)(3sin(2)(>+=ωπωx x f 的最小正周期为π,则=ω .【2015-1】 31、(本题7分)已知1cos ,032x x π=<<,求sinx 与sin2x 的值.【2015-10】5.要得到余弦曲线y=cosx ,只需将正弦曲线y=sinx 向左平移 ( ) A.个单位2πB.个单位3πC.个单位4πD.个单位6π【2016-1】5. =-∈)sin(απα,则设RA.αcosB.αcos -C.αsinD.αsin - 13. 将函数cos ,y x x R =∈图像上的每个点向右平移3π个单位,再向上平移2个单位,得到的图像对应的函数解析式为 A. cos()23y x π=+- B. cos()23y x π=++ C. cos()23y x π=-- D. cos()23y x π=-+ 31.(本题7分)).4sin(sin ),2,0(,53cos πααπαα+∈=及求已知【2016-4】2. 已知角α的终边经过点P (3,4),则=αsin ( ) A.53B. 43C. 54D.34【2016-10】4.若点P (-3,4)在角α的终边上,则cos α= ( ) A.53-B.53C.54-D.54【2017-4】8. 已知θ为锐角,且sinθ=53,则sin (θ+4π)= ( )A.1027 B.1027- C.102 D.102-【2017-11】3.设θ为锐角,sin θ=31,则cos θ= A.32 B.32 C.36 D.3225.下面函数中,最小正周期为π的是A.y=sin xB.y=cos xC.y=tan xD.y=sin 2x【2018-1】7.下列角中,终边在y 轴正半轴上的是 ( )A. 4πB. 2πC. πD.23π 31.(本题7分)的值。
浙江省 学考 选考三年 真题 分题 逐题解析
【经典考题】(2015年10月浙江省普通高中招生选考科目试题) 1.驱动水循环的能量主要来自A、地球内能B、太阳辐射C、地表径流D、大气环流【答案】【解析】驱动水循环的能量主要是太阳能和地球重力。
【经典考题】(2015年10月浙江省普通高中招生选考科目试题)2、霜冻往往出现于深秋至第二年早春晴朗的夜晚,因为此时A、地面辐射强,地表降温慢B、空气中水汽多,地表降温快C、大气逆辐射弱,地表降温快D、大气保温作用强,地表降温慢【答案】【解析】大气逆辐射强弱与云层厚度有关,云层越厚,大气逆辐射作用越强,晴朗的夜晚,大气逆辐射弱,大气的保温作用弱,地面降温快,当气温降至0℃以下,大气中的水汽就会凝结为霜,因降温幅度大同时也会出现冻害。
【经典考题】(2015年10月浙江省普通高中招生选考科目试题)3、我国东部地区不少城市出现了“热岛效应”,其主要原因有①城市郊区化②绿地面积增大③能源消耗加大④城市人口剧增A、①②B、③④C、②④D、①③【答案】【解析】城市“热岛效应”的形成原因主要是城市人口众多,生产、生活、交通等消耗大量燃料,排放大量的废热造成的。
【经典考题】(2015年10月浙江省普通高中招生选考科目试题)4、解决漫画中反映的环境问题,合理的措施是A、生产纯净水B、治理水体污染C、修建水利工程D、节约生产用水【答案】【解析】漫画中鱼身上太脏,需要用纯净水来洗澡,说明鱼生存的环境中水污染严重,故采取的措施是治理水污染。
【经典考题】(2015年10月浙江省普通高中招生选考科目试题)5、下列山地中,垂直方向自然带类型最多的是A、秦岭B、喜马拉雅山C、阿尔卑斯山D、阿巴拉契亚山【答案】【解析】山地垂直带普的多少取决于纬度和相对高度,选项中喜马拉雅山纬度最低,其相对高度也最高,故其自然带类型最多。
【经典考题】(2015年10月浙江省普通高中招生选考科目试题)6、GIS的数据存储采用分层技术,叠加不同图层后可以分析地理事物的相互关系。
浙江省普通高中学业水平考试数学及参考答案
2015年1月浙江省普通高中学业水平考试数学试题学生须知:1、本试卷分选择题和非选择题两部分,共6页,满分100分,考试时间110分钟.2、考生答题前,务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上.3、选择题的答案须用2B 铅笔将答题纸上对应题目的答案标号涂黑,如要改动,须将原填涂处用橡皮擦净.4、非选择题的答案须用黑色字迹的签字笔或钢笔写在答题纸上的相应区域内,作图时可先使用2B 铅笔,确定后须用黑色字迹的签字笔或钢笔描黑,答案写在本试卷上无效. 5、参考公式柱体的体积公式: V=Sh 锥体的体积公式:V=13Sh (其中S 表示底面积,h 表示高)选择题部分一、选择题(共25小题,1-15每小题2分,16-25每小题3分,共60分.每小题给出的选项中只有一个是符合题目要求的,不选、多选、错选均不得分.) 1、设集合M={0,3},N={1,2,3},则 M ∪N = ( )A. {3}B. {0,1,2}C. {1,2,3}D. {0,1,2,3} 2、函数121y x =-的定义域是 ( )A. {x|x>12}B. {x|x≠0,x ∈R }C. {x|x<12}D. {x|x≠12,x ∈R }3、向量a =(2,1),b =(1,3),则a +b = ( )A.(3,4)B.(2,4)C.(3,-2)D.(1,-2) 4、设数列{a n }(n ∈N *)是公差为d 的等差数列,若a 2=4,a 4=6,则d= ( )A.4B.3C.2D.15、直线y=2x+1在y 轴上的截距为 ( )A.1B.-1C.12D.-126、下列算式正确的是 ( )A.26+22=28B. 26-22=24C. 26×22=28D. 26÷22=237、下列角中,终边在y 轴正半轴上的是 ( )A.4πB.2π C.π D.32π8、以(2,0)为圆心,经过原点的圆方程为 ( )A.(x+2)2+y 2=4B. (x -2)2+y 2=4C. (x+2)2+y 2=2D. (x -2)2+y 2=2 9、设关于x 的不等式(ax -1)(x+1)<0(a ∈R )的解集为{x|-1<x<1},则a 的值是 ( )A.-2B.-1C.0D.110、下列直线中,与直线x -2y+1=0垂直的是 ( )A.2x -y -3=0B.x -2y+3=0C.2x+y+5=0D.x+2y -5=011、设实数x ,y 满足{02x y x y +≥-≤-,则x+2y 的最小值为( )A.-3B.-1C.1D.312、椭圆22143y x +=的离心率为( )C.12D.1413、一个几何体的三视图如图所示,则该几何体的体积为( )A.πB.2πC.4πD.8π14、在△ABC 中,设角A ,B ,C 的对边分别为a ,b ,c 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省学考真题专题汇总-----必修4---第二章向量
【2013-7】
17.若平面向量,a b 的夹角为60,且|2|=|a b |,则
( ) (A)()⊥+a b a (B)()⊥-a b a
(C)()⊥+b b a (D)()⊥-b b a
27.已知平面向量(2,3)=a ,(1,)m =b ,且//a b ,则实数m 的值为 .
【2014-1】
10、设a ,b 是两个平面向量,则“a =b ”是“|a |=|b |”的
( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
29、设P 是半径为1的圆上一动点,若该圆的弦AB=3,则AP AB ⋅的取值范围是
4.已知ABC Rt ∆的斜边AB 的长为4,设P 是以C 为圆心1为半径的圆上的任意一点,则PB PA ⋅的取值范围是 ( ) A. ]25,23[- B. ]2
5,25[- C. ]5,3[- D. ]321,321[+-
【2015-1】
3、向量a =(2,1),b =(1,3),则a +b =
( ) A.(3,4) B.(2,4) C.(3,-2)
D.(1,-2)
30、如图,已知AB ⊥AC ,AB=3,AC=3,圆A 是以A 为圆心
半径为1的圆,圆B 是以B 为圆心的圆。
设点P ,Q 分别为
圆A ,圆B 上的动点,且12AP BQ =,则CP CQ ⋅的取值
范围是 Q C B A P (第30题图)
10.若b a ,是两个单位向量,则 ( )
A.b a =
B.b a =
C.0=⋅b a
D.1=⋅b a
30.如图所示,在直角三角形AOB 中,OA=1,OB=2,M 是斜边AB 的中点,过M 的直线分别交射线OA,OB 于P,Q 两点,N 是线段PQ 的中点,则ON OM ⋅的最小值是
O A
B M。
