初一数学综合练习题集精华与答案解析(基础)
初中七下数学知识和能力综合训练题6套(有参考解答)
七年级下学期数学知识和能力训练题1一、选择题: 1、已知⎩⎨⎧==12y x 是二元一次方程组⎩⎨⎧=-=+18my nx ny mx 的解，则2m ﹣n 的值是( ) A 、4 B 、2 C 、﹣2 D 、﹣42、当x =3时，代数式3x 2﹣5ax +10的值为7，则a 等于( ) A 、2 B 、﹣2 C 、1 D 、﹣13、已知△ABC 中，∠B 是∠A 的2倍，∠C 比∠A 大20°，则∠A 等于( ) A 、40° B 、60° C 、80° D 、 90° 二、填空题1、小玉买书用48元钱，付款时恰好用了1元和5元的纸币共12张．那么1元的纸币用了 张；2、已知不等式组 的解集为﹣1＜x ＜2，则(m +n )2019= ；3、已知△ABC 中，∠A=21∠B=31∠C ，则△ABC 为 三角形。
三、解答题1、是否存在负整数k 使得关于x 的方程5x ﹣3k =9的解是非负数？若存在请求出k 的值，若不存在请说明理由．2．已知当x =﹣1时，代数式ax 3+bx +1的值为﹣2009，则当x =1时，代数式ax 3+bx +1的值为多少？3．试确定实数a 的取值范围，使不等式组 恰有两个整数解． x +2＞m+nx -1< m -1 ⎩⎨⎧312++x x ＞0⎩⎨⎧＞ 345++a x ax ++)1(34七年级下学期数学知识和能力训练题1解答参考一、选择题：1、已知⎩⎨⎧==12y x 是二元一次方程组⎩⎨⎧=-=+18my nx ny mx 的解，则2m ﹣n 的值是( ) A 、4 B 、2 C 、﹣2 D 、﹣4【主要考查学生对二元一次方程组的解的认识及用消元思想解二元一次方程组的熟练程度，难度较低.】选A. 解：将⎩⎨⎧==12y x 代入方程组，得⎩⎨⎧=-=+1282m n n m ，解得⎩⎨⎧==23n m ，故2m ﹣n =2×3﹣2=4. 2、当x =3时，代数式3x 2﹣5ax +10的值为7，则a 等于( ) A 、2 B 、﹣2 C 、1 D 、﹣1【主要考查学生对方程的解的认识及简单的解一元一次方程，难度低.】选A. 解：由题意，得3×32﹣5a ×3+10=7，解得a =2.3、已知△ABC 中，∠B 是∠A 的2倍，∠C 比∠A 大20°，则∠A 等于( ) A 、40° B 、60° C 、80° D 、 90°【主要考查学生将方程思想应用到图形问题中，及对三角形内角和定理的理解，难度不大.】选A.解：由已知，得∠B=∠A ×2，∠C=∠A+20°，又∵△ABC 中，∠A+∠B+∠C=180°，∴∠A+2∠A+∠A+20°=180°，解得∠A=40°.二、填空题：1、小玉买书用48元钱，付款时恰好用了1元和5元的纸币共12张．那么1元的纸币用了 张；【主要考查学生对方程思想在实际生活中的应用，难度不大.但可以练练“一题多解”】 解：(法一)设1元纸币有x 张，则5元纸币有(12﹣x )张.由题意，列方程x +5(12﹣x )=48，解得x =3. 故1元的纸币用了3张.(法二)设1元纸币有x 张，5元纸币有y 张.由题意，列方程组⎩⎨⎧=+=+48512y x y x ，解得⎩⎨⎧==93y x ，故1元的纸币用了3张.(法三)假设12张纸币都是5元的，则应为60元，实际少了60-48=12元，少的钱就是1元和5元之间的差距造成的，所以1元纸币有12÷(5﹣1)=3张.2、已知不等式组 的解集为﹣1＜x ＜2，则(m +n )2019= ；【主要考查学生对一元一次不等式组及其解集的理解，有一定的综合性】解：由不等式组变形，得 ，∵该不等式组的解集为﹣1＜x ＜2，∴⎩⎨⎧-=-+=122n m m ，解得⎩⎨⎧-==12n m∴(m +n )2019=(2﹣1)2019=12019=1.x +2＞m+nx -1< m -1 ⎩⎨⎧x < mx ＞m+n -2⎩⎨⎧3、已知△ABC 中，∠A=21∠B=31∠C ，则△ABC 为 三角形。
初一数学初中数学综合库试题答案及解析
初一数学初中数学综合库试题答案及解析1.若线段CD是由线段AB平移得到的，点A（﹣2，3）的对应点为C（3，6），则点B（﹣5，﹣2）的对应点D的坐标是．【答案】（0，1）【解析】略2.把命题“对顶角相等”写成“如果……，那么……”的形式为： ______ _____。
【答案】略【解析】略3.如图，小亮从点出发前进，向右转，再前进，又向右转，…，这样一直走下去，他第一次回到出发点时，一共走了 m【答案】240【解析】略4.（1） -4的相反数是▲，（2） 36的平方根是▲．（3）当x ▲时，根式有意义；（4）当x ▲时，分式的值为零．【答案】4，，【解析】略5.（本题10分）（1）解不等式：；（2）若（1）中的不等式的最小整数解是方程的解，求的值．【答案】（1）；（2）．【解析】（1）应用解不等式的方法解不等式；（2）根据（1）的解集确定x的最小整数解，把x的值代入方程，解得a的值．试题解析：解：（1）解：，5x-10+8＜6x-6+7，6x-5x＞-2-1，x＞-3，所以不等式的解集为x＞-3；（2）由x＞-3得到x的最小整数解是x=-2，把x=-2代入方程得，-4+2a=3，解得．【考点】一元一次不等式的解法；方程的解的定义；一元一次方程的解法．6.在下列各数中，去掉“0”而大小不变的是（）．A、2．00B、200C、0．05【答案】A．【解析】小数的末尾添上0或去掉0，小数的大小不变；根据小数的性质可得 2．00的去掉0，该数的大小不变；故答案选A．【考点】小数的性质．7.如下图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第（n是正整数）个图案中由个基础图形组成．【答案】3n+1【解析】第一个为：3×1+1=4，第二个为：3×2+1=7，第三个为：3×3+1=10，则第n个为3n+1个．【考点】规律题．8.下列说法：①若a为任意有理数，则总是正数；②方程是一元一次方程；③若ab＞0，a+b＜0，则a＜0，b＜0；④是分数；⑤单项式的系数是，次数是3．其中错误的有（）A．0个B．1个C．2个D．3个【答案】D．【解析】①∵≥1，∴a为任意有理数，总是正数，故本小题正确；②方程是分式方程，故本小题错误；③∵ab＞0，∴a，b同号；∵a+b＜0，∴a＜0，b＜0，故本小题正确；④是无理数，不是分数，故本小题错误；⑤单项式的系数是，次数是3，故本小题错误．故选D．【考点】1．一元一次方程的定义；2．有理数的乘法；3．有理数的乘方；4．非负数的性质：偶次方；5．整式．9.若是同类项，则．【答案】5【解析】因为是同类项，所以根据同类型的定义可得：m=1，n=4，所以5．【考点】同类型10.下列各组式子中为同类项的是（）A．5x2y与－2xy2B．4x与4x2C．－3x2y与yx2D．6x3y4与－6x3z4【答案】C．【解析】所含字母相同且相同字母的指数也相同的项是同类项，同类项与字母的顺序无关，几个常数项也是同类项．根据同类项的定义可得四个选项中只有选项C符合要求，故答案选C．【考点】同类项的定义．11.表2是从表1中截取的一部分，则a= ．【答案】18．【解析】试题解析：分析可得：表1中，第一行分别为1的1，2，3…的倍数；第二行分别为2的1，2，3…的倍数；第三行分别为3的1，2，3…的倍数；…；表2中，第一行为5的2倍，第三行为7的3倍；故a=6×3=18．【考点】规律型：数字的变化类．12.（2014秋•南京校级期末）计算：（）﹣2= ．（结果用正整数指数幂的形式表示）【答案】．【解析】首先利用负指数次幂的意义转化为正指数次幂，利用幂的乘方的性质即可求解．解：（）﹣2===．故答案是：．【考点】负整数指数幂．13.（2015秋•乳山市期末）下列结论正确的是（）A．=﹣2B．=﹣2C．=±2D．=±2【答案】B【解析】依据立方根、平方根和算术平方根的定义回答即可．解：A、=2，故A错误；B、=﹣2，故B正确；C、=2，故C错误；D、=2，故D错误．故选：B．【考点】立方根；算术平方根．14.（2015秋•乳山市期末）如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0）、（﹣3，1），AB=AC．（1）求点C的坐标；（2）比较点C的横坐标与﹣3.3的大小．【答案】（1）点C的坐标为（﹣1﹣，0）；（2）C的横坐标＞﹣3.3．【解析】（1）由勾股定理得出AB=AC==，求出OC=1+，即可得出点C的坐标；（2）由≈2.236，得出|1+|＜3.3，即可得出结果．解：（1）由勾股定理得：AB=AC==，∴OC=1+，∴点C的坐标为（﹣1﹣，0）；（2）∵≈2.236，∴|1+|＜3.3，∴﹣1﹣＞﹣3.3，即C的横坐标＞﹣3.3．【考点】勾股定理；坐标与图形性质．15.（2015秋•昌平区期末）甲班有35人，乙班有26人．现在需要从甲、乙两班各抽调一些同学去养老院参加敬老活动．如果从甲班抽调的人数比乙班多3人，那么甲班剩余的人数恰好是乙班剩余人数的2倍．问从乙班抽调了多少人参加了这次敬老活动？【答案】从乙班抽调了20人参加了这次敬老活动．【解析】设从乙班抽调了x人，那么从甲班抽调了（x﹣3）人，根据抽调之后甲班剩余人数恰好是乙班剩余人数的2倍，列方程求解．解：设从乙班抽调了x人参加了敬老活动．根据题意列方程，得35﹣（x﹣3）=2（26﹣x）．解方程得：x=20．答：从乙班抽调了20人参加了这次敬老活动．【考点】一元一次方程的应用．16. |﹣3|的相反数是．【答案】﹣3【解析】根据绝对值定义得出|﹣3|=3，再根据相反数的定义：只有符号相反的两个数互为相反数作答．解：∵|﹣3|=3，∴3的相反数是﹣3，故答案为：﹣3．【考点】相反数；绝对值．17.﹣2015的倒数是（）A．2015B．﹣2015C．D．-【答案】D．【解析】根据乘积是1的两个数互为倒数，所以﹣2015的倒数是-，故本题正确的选项是D．【考点】倒数的意义．18.（1）已知：（x+y）2+|3﹣y|=0，求的值；（2）当式子3﹣（x+y）2有最大值时，最大值是；此时x与y的关系为．【答案】（1）；（2）3；互为相反数．【解析】（1）根据非负数的性质列出方程求出x、y的值，代入所求代数式计算即可；（2）根据偶次方的非负性解答即可．解：（1）由题意得，x+y=0，3﹣y=0，解得，x=﹣3，y=3则=；（2）∵（x+y）2≥0，∴﹣（x+y）2≤0，∴3﹣（x+y）2有最大值3，x与y互为相反数，故答案为：3；互为相反数．【考点】非负数的性质：偶次方；非负数的性质：绝对值．19.用科学记数法表示：0.000000723= ．【答案】7.23×10﹣7．【解析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．解：0.000000723=7.23×10﹣7．故答案为：7.23×10﹣7．【考点】科学记数法—表示较小的数．20.如果等式=1，则x的值为____ _____．【答案】x=1，x=-2或x=0．【解析】试题解析：当2x-1≠0且x+2=0时，解得x=-2；当2x-1=1时，解得x=1；当2x-1=-1，且x+2是偶数时，解得x=0.【考点】1.零指数幂；2.有理数的乘方．21.如果（a+4）x|a+3|+8=0是关于x的一元一次方程，那么a2+a﹣1= ．【答案】1【解析】解：∵（a+4）x|a+3|+8=0是关于x的一元一次方程，∴|a+3|=1，a+4≠0．解得a=﹣2．将a=﹣2代入得：原式=（﹣2）2+（﹣2）﹣1=4﹣2﹣1=1．故答案为：1．【点评】本题主要考查的是一元一次方程的定义、求代数式的值，依据一元一次方程的定义求得a的值是解题的关键．22.计算：（﹣1）2016+|﹣|﹣+（﹣）2．【答案】+﹣．【解析】①（﹣1）2016=1，②∵＞，∴|﹣|=﹣；③是求﹣3的立方根，先把3化成假分数，再开方；④（﹣）2=（）2=9．解：（﹣1）2016+|﹣|﹣+（﹣）2，=1+﹣﹣+9，=1+﹣++9，=+﹣．【点评】本题是实数的运算，是常考题型，熟练掌握：①（）2=a（a≥0），②=|a|；③任何实数的偶次方都是正数；④二次根式被开方数越大，值越大；实数的运算和在有理数范围内一样，注意运算顺序；有时会使用运算律简化运算，提高运算速度和准确度．23.如图，已知数轴上点A表示的数为-7，点B表示的数为5，点C到点A，点B的距离相等，动点P从点A出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动的时间为（＞0）秒（1）点C表示的数是_________（2）求当等于多少秒时，点P到达点B处（3）点P表示的数是_________（用含有的代数式表示）（4）求当t等于多少秒时，PC之间的距离为2个单位长度【答案】(1)、－1；(2)、6；(3)、－7+2t；(4)、t=2或t=4.【解析】(1)、两点所表示的数的和除以2得出答案；(2)、求出两点之间的距离，然后除以速度得出答案；(3)、向右移动几个单位则加上几，将原数加上所运动的距离；(4)、根据两点之间的距离分两种情况分别进行计算得出t的值.试题解析：(1)、(－7+5)÷2=-1(2)、[5－(－7)]÷2=6(3)、-7+2t(4)、因为PC之间的距离为2个单位长度所以点P运动到-3或1即-7+2t=-3或-7+2t =1 即t=2或t=4【考点】数轴24.若a是整数，则下列四个式子中不可能是整数的是（）A．B．C．D．【答案】C【解析】试题解析：A、当a=1时，为整数；B、当a=-3时，为整数，C、无论a取何值，都不可能为整数；D、当a=-1时，为整数．故选C．【点睛】本题考查了代数式的求值，排除法是做选择题常用的方法，关键是根据式子的特点，取a的一些特殊整数值，运用排除法，逐一检验．逐一排除．25.已知x的方程2x+k="5的解为正整数，则k所能取的正整数值为（" ）A．1B．1或3C．3D．2或3【答案】B【解析】因为2x+k=5，所以 ,又因为方程2x+k=5的解为正整数，所以当k=1时x=2;当k=3时x=1；故选B。
基础卷-(全解全析)
2021-2022学年初一数学下学期期中考前必刷卷初一数学·全解全析12345678B C C C D D C D1.B【解析】解：A、0.4587是小数，属于有理数，故此选项不符合题意；B、-π是无理数，故此选项符合题意；C、17是分数，属于有理数，故此选项不符合题意；D、18是整数，属于有理数，故此选项不符合题意．故选：B．2.C【解析】解：∵π不带根号，但π是无理数，∴不带根号的数都是有理数的说法错误，∴A选项不正确；，∴两个无理数的和还是无理数的说法错误，∴B选项不正确；∵0的平方根等于0，∴平方根等于本身的数是0的说法正确，∴C选项正确；∵1的立方根等于1，-1的立方根等于-1，∴立方根等于本身的数是0或1或-1，∴D选项说法不正确．综上，说法正确的是：平方根等于本身的数是0，故选：C．3.C 【解析】解：对顶角指的是有一个公共顶点，并且一个角的两边是另一个角两边的反向延长线的两个角，所以：A、两角没有公共顶点，不符合题意；B、两角也是只有一条边互为反向延长线，另一条边没有互为反向延长线，不符合题意；C、两角有一个公共顶点，并且一个角的两边是另一个角两边的反向延长线的两个角，符合题意；D 、两角只有一条边互为反向延长线，另一条边没有互为反向延长线，不符合题意；故选：C ．4.C 【解析】解：如图，∵263Ð=°，32180Ð+Ð=°，∴3117Ð=°，∵12l l ∥，∴1=3117Ð=°∠．故选：C5.D∵AB ∥y 轴，∴A 、B 两点的横坐标相同，又∵AB ＝5，∴B 点纵坐标为：3+5＝8或3﹣5＝﹣2，∴B 点的坐标为：（﹣4，8）或（﹣4，﹣2）故选：D ．6.D 【解析】湛河北岸、电影院第2排、南偏西45°只能确定一个方向，故不符合题；东经113°，北纬33°，可以确定位置；故选：D ．7.C 【解析】解：因为,,x y z 为实数，且满足()240x z --=，所以30,30,40x y z -=+=-=，解得3,3,4x y z ==-=，则201420143443x z y æöæö×=´=ç÷ç÷-èøèø，故选：C ．8.D 【解析】解：设2x Ð=，则1336x Ð=-°，∵∠1和∠2的两边分别平行，∴12Ð=Ð或12180Ð+Ð=°，当12Ð=Ð时，有336x x =-°，解得：18x =°，此时118Ð=°；当12180Ð+Ð=°时，()336180x x +-°=°，解得：54x =°，此时118054126Ð=°-°=°；综上所述，∠1的度数是18°或126．故选：D9.5±【解析】解：225x =根据平方根的意义，得5x =±，故答案为：5±．10.()0,5【解析】解：∵点()2,3M a a -+在y 轴上，∴a -2=0，解得a =2，故a +3=2+3=5，故点M 的坐标为()0,5，故答案为：()0,5．【解析】解：∵41a +的算术平方根是5，5=，∴6a =，=，∴a ；．12.北偏西25°##北偏西25度解：如图，∵射线OB 与射线OA 构成平角，∴∠BOD =∠AOC =25°，即射线OB 所表示的方位角是北偏西25°．故答案为：北偏西25°13.110【解析】过E 作一条直线FG AB∥∵AB CD ∥，∴FG CD ∥，∵AB FG ∥，110ABE Ð=°，∴18070BEF ABE Ð=°-Ð=°，∴CEF BEF BEC Ð=Ð+Ð7040=°+°110=°又∵CD FG ∥，∴110C CEF Ð=Ð=°．故答案为：110．14.(1)3 (2)1x =或5-【解析】(1)原式223=-+3=；(2)根据题意得：23x +=±，1x \=或5-．15.(1)a =1，b =-1 (2)0(1)解：∵某正数的平方根分别是2a -7和a +4，b -7的立方根为-2，∴2a -7+a +4=0，b -7=-8，解得a =1，b =-1；(2)解：∵a =1，b =-1，∴a +b =1-1=0，∵0的算术平方根为0，∴a +b 的算术平方根为0．16.整数{2-，-3，0}；正分数{0.31，87}；无理数{2p }；【解析】22-=4=整数{2-，-3，0}；正分数{0.31，87}；无理数{2p }；17.(1)3，1；1，-1；4，-2(2)见解析(3)4【解析】(1)(),P a b 是ABC V 的边AC 上任意一点，ABC V 经过平移后得到111A B C △，点P 的对应点为()16,2P a b +-所以，平移后各点的横坐标加6、纵坐标减2，故1(3,1)A ，1(1,1)B - ，C 1（4，-2），故答案为：3，1；1，-1；4，-2(2)△A 1B 1C 1如图所示，(3)111A B C △的面积=3×3-12×2×2-12×3×1-12×1×3=9-2-1.5-1.5=4．18.EDF ；两直线平行，内错角相等；EDF ；内错角相等，两直线平行；两直线平行，同旁内角互补．【解析】因为//DE AC （已知），所以DFC EDF Ð=Ð，（两直线平行，内错角相等）因为BED DFC Ð=Ð（已知），所以BED EDF Ð=Ð（等量代换），所以//DF AB （内错角相等，两直线平行），所以180B BDF Ð+Ð=o （两直线平行，同旁内角互补）．故答案是：EDF ；两直线平行，内错角相等； EDF ；内错角相等，两直线平行；两直线平行，同旁内角互补．19. 4【解析】解：∵|2|0x +=，∴20x +=，60y -=，∴2x =-，6y =，∴264x y +=-+=.故答案为：4.20. 7【解析】解：设这个木箱的棱长为x m ，则x 3=343，解得：x =7，故答案为：7．21. 511【解析】解：∵点P (5a -7,-6a -2)在一、三象限的角平分线上，∴5a -7=-6a -2，解得511a =．故答案为：511．22. 54【解析】解：∵∠AOC ＝72°，∴∠DOB ＝72°，∵OE 平分∠BOD ，∴∠DOE ＝12∠DOB ＝36°，∵OF ⊥CD ，∴∠DOF ＝90°，∴∠EOF ＝90°﹣36°＝54°．故答案为：5423. ()1012,1010-【解析】解：由规律可得，202145051¸×××＝，∴点P 2021在第二象限，∵点P 5(-4,2)，点P 9(-6,4)，点P 13(-8,6)，∴第二象限Pn 的坐标为()1112,244n n é--ùæöæö+´-´ç÷ç÷êúèøèøëû，∴点P 2021的坐标为()202112021112,244é--ùæöæö+´-´ç÷ç÷êúèøèøëû，即为()1012,1010-，故答案为：()1012,1010-．24.(1)8a =，4b =，4c =；(2)点P 运动时间为3秒；(3)存在点Q ，坐标为()0,12或()0,4-．【解析】(1)解：∵()2840a b -+-=，∴80a -=，40b -=，40c -=，∴8a =，4b =，4c =；(2)解：由（1）得8a =，4b =，4c =，∴()8,0A ，()4,4B ，()0,4C ，∴8OA =，4OC =，4BC =，∴OABC S =四边形(48)4242+´=,∴1122COP OABCS S ==n 四边形，设运动时间t 秒，点P 运动到如图所示位置：∴2OP t =，∴COP S =n 11242422t ´´=´，∴解得：3t =，∴点P 运动时间为3秒；(3)解：设()0,Q y ，当3t =时，6OP =，∵OABC CPQ S S D =四边形，∴1146(48)42422y -´=´+´=，∴1y =12，2y =－4，∴()0,12Q 或()0,4Q -，存在点Q ，坐标为()0,12或()0,4-．25.(1)111n n -+(2)20062007(3)10034016【解析】(1)解：由题意得：()111=11n n n n -++，故答案为：111n n -+；(2)解：由题意得：原式1111111=12233420062007-+-+-+-1=12007-2006=2007，故答案为：20062007；(3)解：∵1111=24224æö-ç÷´èø，1111=46246æö-ç÷´èø，1111=68268æö-ç÷´èø，∴可以推出()1111=2222222n n n n æö-ç÷++èø∴1111++++24466820062008´´´´L 1111111...2244620062008æö=-+-++-ç÷èø 111222008æö=-ç÷èø10034016=．26.(1)见解析；(2)40ACB°Ð=【解析】(1)证明：∵∠1＋∠2＝180°，∠1＋∠FDE＝180°，∴∠FDE＝∠2，∵∠3＋∠FEC＋∠FDE＝180°，∠2＋∠B＋∠ECB＝180°，∠B＝∠3，∴∠FEC＝∠ECB，∴EF∥BC，∴∠AFE＝∠ACB；(2)解：∵∠3＝∠B，∠3＝50°，∴∠B＝50°，∵∠2＋∠B＋∠ECB＝180°，∠2＝110°，∴∠ECB＝20°，∵CE平分∠ACB，∴∠ACB＝2∠ECB＝40°。
北师大版2020-2021学年度七年级数学上册期末综合复习基础训练题1(附答案)
北师大版2020-2021学年度七年级数学上册期末综合复习基础训练题（附答案）一、单选题1．323+（-2.53）+（-235）+（+3.53）+（-23）=[323+（-23）]+[（-2.53）+（+3.53）]+（-235），这个运算应用了（）A．加法的交换律B．加法的结合律C．加法的交换律和结合律D．以上均不对2．为响应国家的新能源政策，深圳市某公司计划在海边建设风能发电站，电站年均发电量约为 216000000 度，将数据 216000000 用科学记数法表示为（）A．216×10 6B．21.6×10 7C．2.16×10 8D．2.16×10 9 3．下列这些图形的组合能围成圆柱的是( )A．圆、长方形B．圆、三角形C．长方形、正方形D．圆、扇形4．计算()()()()76894532---⨯----⨯-的结果是( )A．－13 B．139C．－1 D．195．如图是由3个完全相同的小正方体组成的立体图形，它的主视图是（）A．B．C．D．6．下面几何体的截面图可能是圆的是（）A．圆锥B．正方体C．长方体D．棱柱7．下列方程变形正确的是（）A．由3+x=5得x=5+3 B．由7x=–4得x=–7 4C．由12y=0得y=2 D．由3=x–2得x=2+38．12-的倒数为()A．12B．2C．2-D．1-9．某商店把一件商品按进价增加20%作为定价，可是总卖不出去，后来老板把定价降低20%，以48元的价格出售，很快就卖出了，则老板卖出这件商品的盈亏情况是（）10．已知方程（m ﹣2）x |m|﹣1=3 是关于 x 的一元一次方程，则 m 的值为（ ） A ．2 B ．﹣2 C ．2 或﹣2 D ．﹣1二、填空题11．-112的相反数_____，倒数是_____，绝对值是_____. 12．若2(2)a +与1b +互为相反数，则b a -的值为________．13．（1）如果a>0，b<0，那么a b _____0； （2）如果a<0，b>0，那么a b_____0； （3）如果a<0，b<0，那么a b_____0； （4）如果a ＝0，b<0，那么a b_____0. 14．1﹣|﹣3|=________．15．若，则的值是__________。
初一数学初中数学综合库试题答案及解析
初一数学初中数学综合库试题答案及解析1.在“十·一”黄金周期间，小明、小亮等同学随家人一同到净月潭游玩．下图是购买门票时，小明与他爸爸的对话：问题：（1）小明他们一共去了几个成人？几个学生？（2）请你帮小明算一算，用哪种方式买票更省钱？【答案】解（1）设有个成人，有名学生解得∴有8个成人，4名学生（2）35×60%×16＝336＜350∴按成人票的团体票购买16人的合适【解析】略2.规定，则的值为_________。
【答案】-1【解析】略3.用计算器求25的值时，按键的顺序是（）A．5、y x、2、=B．2、y x、5、=C．5、2、y x、=D．2、3、y x、=【答案】B【解析】首先确定使用的是y x键，先按底数，再按y x键，接着按指数，最后按等号即可．解答：解：在计算器中，先按2，再按y x，接着按5，最后按=即可．4.（8分）某中学计划对本校七年级10个班的480名学生按“学科”、“文体”、“手工”三个项目安排课外兴趣小组，小明从每个班中随机抽取5名学生进行问卷调查，并将统计结果制成如下所示的表和图.（1）请将统计表、统计图补充完整；（2）请以小明的统计结果来估计该校七年级480名学生参加各个项目的人数.【答案】（1）略（2）该校七年级480名学生参加“学科”、“文体”、“手工”三个项目的人数分别约为240人，96人，144人【解析】解：（1）统计表、统计图补充如下：………………………………………………5分（2）七年级480名学生参加各项目人数约为：学科：480×50%=240（人）文体：480×20%=96（人）手工：480×30%=144（人）答：该校七年级480名学生参加“学科”、“文体”、“手工”三个项目的人数分别约为240人，96人，144人. ………………………………………………8分5.吸烟有害健康！你知道吗，即使被动吸烟也大大危害健康．有消息称，我国准备从2011年元月一日起在公众场所实行“禁烟”，为配合“禁烟”行动，某校组织同学们在某社区开展了“你支持哪种戒烟方式”的问卷调查，征求市民的意见，并将调查结果整理后制成了如下统计图：根据统计图解答：（1）同学们一共随机调查了多少人？（2）请你把统计图补充完整；（3）如果在该社区随机咨询一位市民，那么该市民支持“强制戒烟”的概率是多少？假定该社区有1万人，请估计该地区大约有多少人支持“警示戒烟”这种方式．【答案】（1）300人（2）略（3）355人【解析】解：（1）设调查的人数为，则根据题意得：一共调查了300人（3分）（2）由（1）可知，完整的统计图如图所示（5分）（3）设该市民支持“强制戒烟”的概率为，由（1）可知，（7分）支持“警示戒烟”这种方式的人有(人). （8分）6.如图，下列各数中，数轴上点A表示的可能是()A．4的算术平方根B．4的平方根C．8的算术平方根D．10的算术平方根【答案】C【解析】从数轴上的点可以看出，该点所表示的数大于2并且小于3，又选项中仅有8的算术平方根在这个范围，∴选C．7.（16分）计算：（1）4﹣8×（﹣）3（2）﹣5（x2﹣3）﹣2（3x2+5）（3）﹣12011+4×（﹣3）2÷（﹣2）（4）4a2+2（3ab﹣2a2）﹣（7ab﹣1）【答案】（1）5；（2）﹣11x2+5；（3）-19；（4）﹣ab+1．【解析】（1）先算乘方，再算乘法，最后算减法；（2）去括号，再合并同类项即可；（3）先算乘方，再算乘除，最后算加法．（4）先去括号，再合并同类项即可；试题解析：（1）原式=4﹣8×（﹣）=4+1=5；（2）原式=﹣5x2+15﹣6x2﹣10=﹣11x2+5；（3）原式=﹣1+4×9÷（﹣2）=﹣1﹣18=﹣19；（4）原式=4a2+6ab﹣4a2﹣7ab+1=﹣ab+1．【考点】有理数的混合运算；整式的加减．8.有6张纸签，分别标有数字1，2，3，4，5，6.从中随机抽出一张，则抽出标有数字为偶数的概率为 .【答案】【解析】六个数中有3个数为偶数，根据概率的定义可得．【考点】概率9.（本题4分）有这样一道题目：“当时，求多项式的值”．小敏指出，题中给出的条件，是多余的，她的说法有道理吗？为什么？【答案】-3【解析】根据去括号法则，合并同类项法则，对整式化简，然后可判断．试题解析：==－3因为多项式的值为常数，与a,b的取值无关，所以小敏说法有道理【考点】整式的加减10.下列算式中，与﹣1+9的结果相同的是（）A．1+9B．﹣（9﹣1）C．﹣（1+9）D．9﹣1【答案】D．【解析】﹣1+9=8，A．1+9=10，故此选项错误；B．﹣（9﹣1）=﹣8，故此选项错误；C．﹣（1+9）=﹣10，故此选项错误；D．9﹣1=8，故此选项正确；故选D．【考点】1．有理数的加法；2．有理数的减法．11.计算（1）（2）（3）【答案】（1）-56 ；（2）-6 ；（3）．【解析】（1）将整数部分和分数部分分别结合在一起，再由乘法分配律计算即可；（2）按照有理数混合运算的顺序，先算乘方后算乘除最后算加减；（3）按照有理数混合运算的顺序，先算乘方后算乘除最后算加减，有括号的先算括号里面的．试题解析：解：（1）原式====-56；（2）原式===-6；（3）原式=====．【考点】有理数的混合运算．12.甲乙两座城市的铁路经过技术改造，列车在甲乙两城市间的运行速度从80千米/时提高到100千米/时，运行时间缩短了2．5小时，求甲乙两城市间的铁路路程是多少千米？【答案】1000千米．【解析】根据关键描述语为：运行时间缩短了2．5小时，等量关系为：速度为80千米/时走x千米用的时间-速度为100千米/时走x千米用的时间=运行缩短的时间2．5，即可列出方程求解．试题解析：设甲乙两城市间的铁路路程为千米，则根据题意，得，解这个方程得x=1000千米．答：甲乙两城市间的铁路路程是1000千米．【考点】一元一次方程的应用．13.如图，A，O，B三点在一条直线上，OM是∠AOC的平分线，ON是∠BOC的平分线．若∠1：∠2＝1：2，则∠1＝_______°．【答案】30【解析】根据角平分线的性质可得：∠1=∠BOC，∠2=∠AOC，根据∠AOC+∠BOC=180°可得：∠1+∠2=90°，根据∠1：∠2=1:2可得：∠1=30°．【考点】（1）角平分线的性质；（2）角度的计算14.已知方程组的解满足x+y=3，则k的值为．【答案】8【解析】解方程组，把解代入x+2y=k即可求解．解：解方程组，①﹣②得：x=﹣2，把x=﹣2代入②得：﹣2+y=3，解得：y=5则方程组的解是：，代入x+2y=k得：﹣2+10=k，则k=8，故答案是：8．【考点】二元一次方程组的解．15.关于x的方程（a﹣1）x2+x+a2﹣4=0是一元一次方程，则方程的解为．【答案】3【解析】由一元一次方程的定义可得出一个关于a的方程，可求得a的值，再代入解方程即可．解：因为方程为一元一次方程，所以可得a﹣1=0，解得a=1，所以方程为x+1﹣4=0，解得x=3，故答案为：3．【考点】一元一次方程的定义．16.已知3×9m×27m=321，求m的值．【答案】4【解析】试题分析:先把9m×27m分解成32m×33m，再根据同底数幂的乘法法则进行计算即可求出m 的值．解：∵3×9m×27m=3×32m×33m=31+2m+3m=321，∴1+2m+3m=21，∴m=4．【考点】幂的乘方与积的乘方；同底数幂的乘法．17.一组数2，1，3，x，7，y，23，…，如果满足“从第三个数起，若前两个数依次为a、b，则紧随其后的数就是2a﹣b”，例如这组数中的第三个数“3”是由“2×2﹣1”得到的，那么这组数中y表示的数为（）A．﹣9B．﹣1C．5D．21【答案】A【解析】根据“从第三个数起，前两个数依次为a、b，紧随其后的数就是2a﹣b”，首先建立方程2×3﹣x=7，求得x，进一步利用此规定求得y即可．解：∵从第三个数起，前两个数依次为a、b，紧随其后的数就是2a﹣b∴2×3﹣x=7∴x=﹣1则2×（﹣1）﹣7=y解得y=﹣9．故选：A．【考点】规律型：数字的变化类．18.如图，直线AB、CD相交于点O，OA平分∠EOC，∠EOC=80°，则∠BOD= ．【答案】40°．【解析】根据角平分线的定义求出∠AOC，再根据对顶角相等解答．解：∵OA平分∠EOC，∠EOC=80°，∴∠AOC=∠EOC=×80°=40°，∴∠BOD=∠AOC=40°．故答案为：40°．【考点】对顶角、邻补角；角平分线的定义．19.如图，AB⊥AC，AD⊥BC，垂足分别为A，D，则图中能表示点到直线距离的线段共有（）A．2条B．3条C．4条D．5条【答案】D.【解析】如图所示，根据点到直线的距离就是这个点到这条直线垂线段的长度，可知线段AB是点B到AC的距离，线段CA是点C到AB的距离，线段AD是点A到BC的距离，线段BD是点B到AD的距离，线段CD是点C到AD的距离，所以图中能表示点到直线距离的线段共有5条．故答案选D.【考点】点到直线的距离．20.把“同角的补角相等”改写成如果那么的形式。
初一合并同类项练习题汇总带答案
初一合并同类项练习题汇总带答案在初一数学的学习中，合并同类项是一个重要的知识点。
为了帮助同学们更好地掌握这一内容，下面为大家汇总了一些相关的练习题，并附上详细的答案解析。
一、基础练习题1、 3x ＋ 2x ＝答案：5x解析：3 个 x 加上 2 个 x 等于 5 个 x。
2、 5y 3y ＝答案：2y解析：5 个 y 减去 3 个 y 等于 2 个 y。
3、 2a ＋ 3a 5a ＝答案：0解析：2 个 a 加上 3 个 a 等于 5 个 a，再减去 5 个 a 就等于 0。
4、 4b 2b ＋ 3b ＝答案：5b解析：4 个 b 减去 2 个 b 等于 2 个 b，再加上 3 个 b 就等于 5 个 b。
5、 6x²＋ 3x²＝答案：9x²解析：6 个 x²加上 3 个 x²等于 9 个 x²。
6、 8y² 5y²＝答案：3y²解析：8 个 y²减去 5 个 y²等于 3 个 y²。
7、 5a²＋ 2a 3a²＝答案：2a²＋ 2a解析：5 个 a²减去 3 个 a²等于 2 个 a²，再加上 2 个 a 不变。
8、 7b² 4b²＋ 5b ＝答案：3b²＋ 5b解析：7 个 b²减去 4 个 b²等于 3 个 b²，5 个 b 不变。
二、提高练习题1、 3x²＋ 2xy 5x²＋ 4xy ＝答案：－2x²＋ 6xy解析：3 个 x²减去 5 个 x²等于－2 个 x²，2 个 xy 加上 4 个 xy 等于 6 个 xy 。
2、 5y² 3y ＋ 2y²＋ 5y ＝答案：7y²＋ 2y解析：5 个 y²加上 2 个 y²等于 7 个 y²，－3 个 y 加上 5 个 y 等于 2 个 y 。
最新初一数学综合练习题精华及答案基础
精品文档初一练习（易）一、选择题：1．桌上放着一个茶壶，4个同学从各自的方向观察，请指出图1右边的四幅图，从左至右）分别是由哪个同学看到的（1图．④③①②．②④①③ D B．①③②④ CA．①②③④b ba a）在数轴上的位置如图2所示，则是（2.数，．零A．正数 B．负数 D．都有可能C2图千米，每天供给地球光和热的太阳与我们的距离非常遥远，它距地球的距离约为150000003. 千米用科学记数法表示为（）将150000000798710101010 D．×1.5千米 C．15××A．0.15×千米千米千米 B．1.5/℃温度是某市一天的温度变化曲线图，通过该图可3 4．图38）知，下列说法错误的是（34 30 15点时的温度最高A．这天26 3点时的温度最低B．这天22 ℃C．这天最高温度与最低温度的差是1324 21 15 18 时时间/ 3 6 9 12℃点时的温度是30D．这天213 图,的邻补角是∠3的对顶角是∠2∠1,∠2则∠1的度数是（） 5. ,若∠3=45° 135° 45°或． C． 135° D．A．45° B 90°），∠C=60°，则∠A+∠E=（ 6.如图4，若AB//CD4图0?y?xxy?0)(xy,P P）的坐标满足，则点点7.且,必在（．第四象限 C B．第二象限．第三象限 DA第．一象限）8.下列说法错误的是（2x<5Bx>3 62x<A 、－－的解集是、－是－的解集精品文档．精品文档C、x<2的整数解有无数个D、x<3的正整数解是有限个二、填空题：ab?12ba的值等于。
＋|，则－2|＝9.已知(0＋1)10. 一组数据4，8，3，2，6，1，x的众数是4，则它的中位数是_____，平均数是________。
11.等腰三角形的一边长为3，另一边长为6，则该三角形的周长是________．ABCDABEDCEBEC＝，若∠．＝120°，∠ 12.如图5，∥＝35°，则∠“”表示两种不同的物体，现用天平称了两次，如图613.设“”所示，那么这两种物体的质量分别为．BCDE?AADE?ABC=40°，落在四边形14. 如图7，把折叠，使点的内部，若纸片沿?1??2= °则图7a ，则=___________15. 方程组的解是三、解答题：计算：16.1111????32233?42)???3?(? b。
初一数学初中数学综合库试题答案及解析
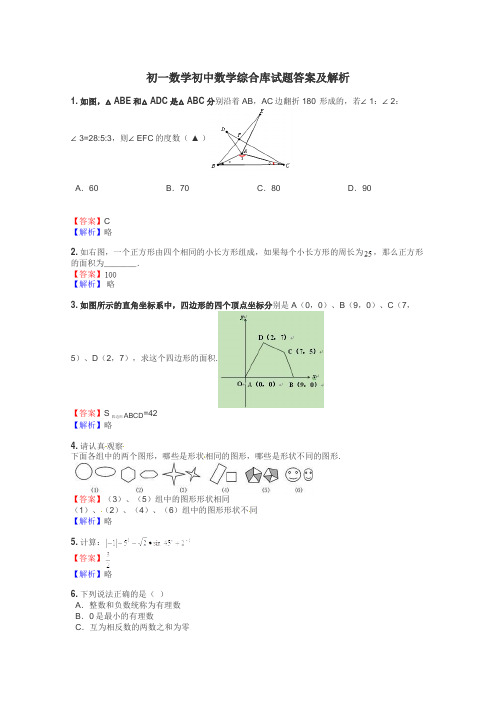
初一数学初中数学综合库试题答案及解析1.如图，△ABE和△ADC是△ABC分别沿着AB，AC边翻折180°形成的，若∠1：∠2：∠3=28:5:3，则∠EFC的度数（▲ ）A．60°B．70°C．80°D．90°【答案】C【解析】略2.如右图，一个正方形由四个相同的小长方形组成，如果每个小长方形的周长为，那么正方形的面积为_______．【答案】【解析】略3.如图所示的直角坐标系中，四边形的四个顶点坐标分别是A（0，0）、B（9，0）、C（7，5）、D（2，7），求这个四边形的面积.【答案】S四边形ABCD =42【解析】略4.请认真观察下面各组中的两个图形，哪些是形状相同的图形，哪些是形状不同的图形.【答案】（3）、（5）组中的图形形状相同（1）、（2）、（4）、（6）组中的图形形状不同【解析】略5.计算：【答案】【解析】略6.下列说法正确的是（）A．整数和负数统称为有理数B．0是最小的有理数C．互为相反数的两数之和为零D．负数就是有负号的数【答案】C【解析】因为整数和分数统称为有理数，所以选项A错误；因为0是绝对值最小的有理数，所以选项B错误；因为互为相反数的两个数之和为零，所以选项C正确；因为带有负号的数不一定是负数，如：﹣（﹣2）=2是正数，所以选项D错误．故选：C．【考点】1．有理数；2．相反数．7.某种超级计算机完成一次基本运算的时间约为0．00000000000011秒，用科学记数法表示这个数为（）A．1．1×10﹣12B．1．1×10﹣13C．11×10﹣12D．11×10﹣13【答案】B．【解析】用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．这里a=1．1，n=13，所以0．00000000000011=1．1×10﹣13，故答案选B．【考点】科学记数法表示较小的数．8.若方程组的解x、y互为相反数，则a= ．【答案】8．【解析】∵x、y互为相反数，∴x=-y．解方程组把③分别代入①、②可得解得a=8，【考点】二元一次方程组的解．9.如果有理数满足∣－2∣+（1－b）2=0试求+…+的值。
青岛版2020七年级数学下册期末综合复习基础训练题2(附答案)
青岛版2020七年级数学下册期末综合复习基础训练题2（附答案）1．某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为扩大销售，尽快减少库存，商场决定釆取降价措施，调查发现，每件衬衫，每降价1元，平均每天可多销售2件，若商场每天要盈利1200元，每件衬衫应降价（ ）A ．5元B ．10元C ．20元D ．10元或20元2．如图，在△ABC 中，CD 平分∠ACB 交AB 于点D ，过点D 作DE ∥BC交AC 于点E,若∠A=54°，∠B=48°，则∠CDE 的大小为（ ）A ．44°B ．40°C ．39°D ．38°3．下列式子中，计算结果为2215x x +-的是（ ）A ．(5)(3)x x +-B ．(5)(3)x x -+C ．(5)(3)x x ++D ．(5)(3)x x -- 4．（2011•恩施州）下列运算正确的是（ ）A ．a 6÷a 2=a 3B ．a 5﹣a 3=a 2C ．（3a 3）2=6a 9D ．2（a 3b ）2﹣3（a 3b ）2=﹣a 6b 25．(x +3ab )(x -3ab )等于（ ）A ．x 2 -9a 2b 2B ．x 2 -9ab 2C ．x 2 -ab 2D ．x 2 -a 2b 26．下列说法正确的个数（ ）①线段有两个端点，直线有一个端点；②点A 到点B 的距离就是线段AB ；③两点之间线段最短；④ 若AB=BC ，则点B 为线段AC 的中点；⑤同角（或等角）的余角相等．A ．4个B ．3个C ．2个D ．1个7．平面直角坐标系内AB ∥y 轴，AB=5，点A 的坐标为（﹣5，3），则点B 的坐标为（ ）A ．（﹣5，8）B ．（0，3）C ．（﹣5，8）或（﹣5，﹣2）D ．（0，3）或（﹣10，3）8．如图，将一张正方形纸片剪出一个边长为m 的正方形之后，剩余部分可剪拼成一个矩形(不重叠无缝隙)，若拼成的矩形一边长为3，另一边为23m +，则原正方形边长是 （ ）A ．6m +B ．3m +C ．23m +D ．26m +9．若12512'∠=o ，225.12∠=o ，325.2∠=o ，则下列结论正确的是（ ）A．∠1=∠2 B．∠2=∠3 C．∠1=∠3 D．∠1=∠2=∠3 10．下列各方程组中，不是二元一次方程组的是()A．2583x yx y-=⎧⎨+=⎩B．113x zx y+=⎧⎪⎨=⎪⎩C．3225x yx y-=⎧⎨+=⎩D．1122311332x yx y⎧+=⎪⎪⎨⎪-=⎪⎩11．-0.000031用科学记数法表示为：__________________________12．钟面上8 点30 分时，时针与分针的夹角的度数是________ ．13．已知一点到圆上的最短距离是2，最长距离是4，则圆的半径为____．14．已知4x=2x+3，则x=_________．32÷8n-1=2n，则n=_________．15．(x+2y-3)(x-2y-3)=_____-_____．16．有长为20m的铁栏杆，利用它和一面墙围成一个矩形花圃ABCD（如图），若花圃的面积为48m2，求AB的长．若设AB的长为xm，则可列方程为______．17．若2330x y++=，则927x y⋅＝________.18．把多项式4m2﹣16n2分解因式的结果是_____．19．已知方程132x y-=，用含x的代数式表示y=_________________________。
初一数学初中数学综合库试题答案及解析
初一数学初中数学综合库试题答案及解析1.已知：，求：的值．【答案】8【解析】略2.（6分）下面是小马虎解的一道题题目：在同一平面上，若∠BOA=70°，∠BOC=15°求∠AOC的度数．解：根据题意可画出图，∵∠AOC=∠BOA－∠BOC=70°－15°=55°，∴∠AOC=55°．若你是老师，会判小马虎满分吗？若会，说明理由．若不会，请将小马虎的的错误指出，并给出你认为正确的解法．【答案】不会给小马虎满分原因是：小马虎没有把问题考虑全面，他只考虑了OC落在∠AOB的内部，还有OC落在∠AOB的外部的情况．…………3分正确解法：当OC落在∠AOB的外部时，如右上图，∠AOC=∠AOB—∠BOC=55°．当OC落在∠AOB的外部时，如右下图，∠AOC=∠AOB+∠BOC=85°．………………3分【解析】略3.如图是一个数值运算程序，若输入x的值为2，则输出的数值为（）A．5B．6C．11D．12【答案】C【解析】略4.下图规律，在第四个方框内填入的数应为 .【答案】 -260【解析】略5.计算（－2）2004+（－2）2003的结果是（）A．－1B．－2C．22003D．－22004【答案】C【解析】此题考查指数幂的运算思路：先化为同类项，再加减答案 C点评：一定要会转化式子。
6.如图所示，直线AB, CD相交于点O, P是直线CD上一点。
①过点P画直线AB的垂线段PE;②过点P画直线CD的垂线，与直线AB相交于F点；③说明线段PE, PO, FO三者的大小关系，其依据是什么？【答案】（1）略（2）略（3）PE∠PO∠FO,依据是：垂线段最短【解析】略7.（本题满分12分）为实现区域教育均衡发展，我区计划对，两类薄弱学校全部进行改造．已知改造一所类学校和两所类学校共需资金万元；改造两所类学校和一所类学校共需资金万元．问改造一所类学校和一所类学校分别需要多少万元的资金？（1）老师让两位同学上黑板板演，其中甲同学设了一个未知数，请你帮他写出完整的解答过程．（2）另一位乙同学设了两个未知数，却没法做下去，老师说也可以做，但需要列两个不同的方程，爱动脑的你能帮助她列出方程吗？解：设改造一所类学校需要万元资金；改造一所类学校需要万元资金，根据题意可得方程①：方程②：（3）丙同学说我一个未知数也没有设，也可以求出答案来．请聪明的你写出丙同学的方法．【答案】（1）参见解析；（2）x+2y=230，2x+y=205；（3）参见解析．【解析】（1）此题是列一元一次方程求解，设改造一所M类学校需要x万元，根据改造一所类学校和两所类学校共需资金万元，用x把改造一所N类学校的万元数表示出来，再根据改造两所类学校和一所类学校共需资金万元，列一元一次方程求解；（2）根据改造一所类学校和两所类学校共需资金万元；改造两所类学校和一所类学校共需资金万元．找等量关系列方程．（3）不设未知数，可以先用230+205=435万元，是三所M学校和三所N类学校的总价钱，再用435÷3=145万元，是一所M学校和一所N类学校的总价钱，然后用230-145=85万元，正好是一所N类学校需要的资金，用205-145=60万元，正好是一所M类学校需要的资金．试题解析：（1）设改造一所M类学校需要x万元，则根据1个M学校+2个N学校=230，改造一所N类学校就需要万元．根据题意可得方程：，解得：，∴，∴改造一所M类学校和一所N类学校分别需要万元和万元资金．（2）∵改造一所类学校和两所类学校共需资金万元，∴方程①：x+2y=230；∵改造两所类学校和一所类学校共需资金万元，∴方程②：2x+y=205；（3）用230+205="435" 万元，是三所M学校和三所N类学校的总价钱，则一所M学校和一所N类学校的总价钱是435÷3=145万元，∵改造一所类学校和两所类学校共需资金万元；∴230-145=85万元，是一所N类学校需要的资金，∵改造两所类学校和一所类学校共需资金万元，∴用205-145=60万元，是一所M类学校需要的资金．【考点】一元一次方程与二元一次方程组的实际应用．8.某市股票在七个月之内增长率的变化状况如图所示．从图上看出，下列结论不正确的是（）A．2～6月份股票月增长率逐渐减少B．7月份股票的月增长率开始回升C．这七个月中，每月的股票不断上涨D．这七个月中，股票有涨有跌【答案】D．【解析】由折线统计图可知2～6月份股票月增长率逐渐减少，7月份股票的月增长率开始回升，这七个月中，股票的增长率始终是正数，则每月的股票不断上涨，所以A、B、C都正确，错误的只有D．故选D．【考点】折线统计图．9.在数轴上表示下列各数，并用“＜”号连接：-（-5），-|-2.5|，-，.【答案】作图见解析；-22＜＜-|-2.5|＜-（-5）.【解析】本题考查的是有理数的大小比较，引进了数轴，我们把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想. 先画出数轴并表示出各数，根据数轴的特点用“＜”把各数连接起来. 试题解析：解：画出数轴并表示出各数如图：用“＜”把各数连接起来为：-22＜＜-|-2.5|＜-（-5）.【考点】有理数大小比较；数轴.10.方程移项后，正确的是（）A．B．C．D．【答案】C【解析】在等式中，将左边的移到右边需要进行变号，将右边的移到左边也需要变号．则3x－2x=－8－6．【考点】移项的方法11.（2014秋•台州校级期末）已知，如图，B，C两点把线段AD分成2：5：3三部分，M为AD的中点，BM=6cm，求CM和AD的长．【答案】20 cm【解析】由已知B，C两点把线段AD分成2：5：3三部分，所以设AB=2xcm，BC=5xcm，CD=3xcm，根据已知分别用x表示出AD，MD，从而得出BM，继而求出x，则求出CM和AD的长．解：设AB=2xcm，BC=5xcm，CD=3xcm所以AD=AB+BC+CD=10xcm因为M是AD的中点所以AM=MD=AD=5xcm所以BM=AM﹣AB=5x﹣2x=3xcm因为BM="6" cm，所以3x=6，x=2故CM=MD﹣CD=5x﹣3x=2x=2×2=4cm，AD="10x=10×2=20" cm．【考点】两点间的距离．12.命题“同角的余角相等”的题设是_______ ，结论是 ________ .【答案】同角的余角;相等.【解析】命题由题设和结论两部分组成．其中题设是已知的条件，结论是由题设推出的结果.【考点】⒈命题；⒉定理.13.如图，AB交CD于O，OE⊥AB．（1）若∠EOD=20°，求∠AOC的度数；（2）若∠AOC：∠BOC=1：2，求∠EOD的度数．【答案】(1)、70°；(2)、30°【解析】(1)、首先根据垂直得出∠AOE=90°，根据∠AOC=180°－∠AOE－∠EOD得出答案；(2)、首先设∠AOC=x，则∠BOC=2x，根据平角的性质得出x的值，根据∠EOD=180°－AOE－∠AOC得出答案.试题解析：(1)、∵OE⊥AB，∴∠AOE=90°，∵∠EOD=20°，∴∠AOC=180°﹣90°﹣20°=70°；(2)、设∠AOC=x，则∠BOC=2x，∵∠AOC+∠BOC=180°，∴x+2x=180°，解得：x=60°，∴∠AOC=60°，∴∠EOD=180°﹣90°﹣60°=30°．【考点】角度的计算14.九台全区7年级学生大约有10200人，10200这个数用科学记数法表示为（）A．B．C．D．【答案】B【解析】科学计数法是指a×，且，n为原数的整数位数减一.【考点】科学计数法15.两个有理数相除，其商是负数，则这两个有理数（）A．都是负数B．都是正数C．一个正数一个负数D．有一个是零【答案】C【解析】两数相除，同号得正，异号得负.商为负数，则说明两数异号.【考点】有理数的除法计算16.已知代数式2x－y的值是，则代数式－6x + 3y－1的值是；【答案】【解析】原式=－3(2x－y)－1=－3×－1=－.【考点】整体思想求解17.如图中的俯视图是（）A．B．C．D．【答案】C【解析】根据三视图的法则可得：A为主视图；B为左视图；C为俯视图.【考点】简单图形的三视图18.下列算式正确的是（）A．-1-1=0B．2－2÷(－)=0C．|5－2|=－(5－2)D．【答案】D【解析】A、原式=－1+(－1)=－2；B、原式=2－(－6)=2+6=8；C、原式=3；D、计算正确.【考点】有理数的计算19.已知数轴上有A、B、C三点，分别表示有理数-26，-10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒．（1）用含t的代数式表示P点对应的数：___________;用含t的代数式表示点P和点C的距离：PC=_____________（2）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C 点后，再立即以同样的速度返回点A，①点P、Q同时运动运动的过程中有__________处相遇，相遇时t=_______________秒。
初一数学初中数学综合库试题答案及解析
初一数学初中数学综合库试题答案及解析1.掷一枚普通的正方体骰子，事件：①点朝上；②朝上的点数是两位数；③偶数点朝上；④朝上的点数小于7．将以上事件按发生的可能性从大到小排序：．（只填序号）【答案】【解析】略2.现规定一种新型的运算“*”：，如，则等于（）A．8B．6C．－8D．－6【答案】C．【解析】根据题目中的规定可得，故答案选C．【考点】有理数的运算．3.如图，直线a∥b，直线c分别与a，b相交，若∠1=60°，则∠2= °．【答案】120．【解析】∵∠1=60°，∴∠1的对顶角也是60度，∵a∥b，∴∠2与∠1的对顶角互补，∴∠2=120º．【考点】平行线的性质．4.如图，AB=10cm，AC=6cm，且D是AC的中点，则BD= cm【答案】7．【解析】，可得AD的长，根据线段的和差，可得BD的长．已知D是AC的中点，AC=6cm，根据线段中点的性质可得AD=AC=×6=3cm．所以BD=AB﹣AD=10﹣3=7cm，【考点】线段中点的性质.5.二元一次方程x﹣2y=1有无数多个解，下列四组值中不是该方程的解的是（）A．B．C．D．【答案】B【解析】本题考查二元一次方程的解的定义，要求理解什么是二元一次方程的解，并会把x，y的值代入原方程验证二元一次方程的解．A、当x=0，y=﹣时，x﹣2y=0﹣2×（﹣）=1，是方程的解；B、当x=1，y=1时，x﹣2y=1﹣2×1=﹣1，不是方程的解；C、当x=1，y=0时，x﹣2y=1﹣2×0=1，是方程的解；D、当x=﹣1，y=﹣1时，x﹣2y=﹣1﹣2×（﹣1）=1，是方程的解；【考点】二元一次方程的解6.下列各数2，π，，﹣，中，无理数的个数是（）个．A．1B．2C．3D．4【答案】B【解析】无理数有：π，﹣共2个．故选B．【考点】无理数．7.下列图形中，∠1与∠2是对顶角的是（）【答案】D．【解析】A、∠1与∠2不是对顶角，故本选项错误；B、∠1与∠2不是对顶角，故本选项错误；C、∠1与∠2不是对顶角，故本选项错误；D、∠1与∠2是对顶角，故本选项正确；故选D．【考点】对顶角、邻补角．8.的算术平方根是．【答案】3．【解析】=9,根据算数平方根的定义可得9的算术平方根是3．【考点】算数平方根的定义．9.从数轴上表示﹣1的点开始，向右移动6个单位长度，再向左移动5个单位长度，最后到达的终点所表示的数是．【解析】-1+6-5=0，故最后到达的终点所表示的数是0．【考点】1．数轴；2．有理数的加减法．10.在、、、这四个数中，最大的数比最小的数要大（）A．25B．20C．19D．12【答案】B【解析】因为=-1，=1，=-4，=16，所以最大的数16比最小的数-4要大16-（-4）=16+4=20，故选：B．【考点】有理数的大小比较．11.如果有理数满足∣－2∣+（1－b）2=0试求+…+的值。
北师大版2020七年级数学期末复习综合练习题(基础部分 含答案)
北师大版2020七年级数学期末复习综合练习题（基础部分 含答案）1．一辆汽车在笔直的公路上行驶，在两次转弯后，前进的方向仍与原来相同，那么这两次转弯的角度可以是（ ）A ．先右转 60°，再左转 120°B ．先左转 120°，再右转 120°C ．先左转 60°，再左转 120°D ．先右转 60°，再右转 60°2．(济南中考)下列图案中既是轴对称图形又是中心对称图形的是( )A ．AB ．BC ．CD ．D3．计算（a+1）(-a-1)的结果是（ ）A ．-a 2-2a-1B ．a 2 -1C ．-a 2-1D ．-a 2+2a-14．下列运算正确的A ．45()?()a a a --=-B ．(a-b)2=a 2-b 2C ．325a )a =（D ．a 3+a 3=2a 6 5．下列事件中，是必然事件的为 ( )A ．明天会下雨B ．打开电视机，正在播放动画片C ．三角形内角和为180°D ．经过一个路口，信号灯刚好是红灯6．如图，已知AC ∥BD ，∠CAE =30°，∠DBE =45°，则∠AEB 等于（ ）A ．30°B ．45°C ．60°D ．75°7．计算的结果为（ ）． A ． B ． C ． D ．8．由图所示的地板砖各两块所铺成的下列图案中,既是轴对称图形,又是中心对称图形的是（ ） A ． B ． C ． D ．9．下列说法不正确的有（ ）个①从直线外一点到这条直线的垂线段，叫做点到直线的距离②内错角相等,③过一点有且只有一条直线与已知直线垂直④相等的角是对顶角A ．0B ．2C ．3D ．410．如图，观察下列各正方形图案，每条边上有n （n≥2）个圆点，每个图案圆点的总数是S ，按此规律推断S 与n 的关系式是_______．11．如图，△ABC 的内部有一点P ，且D ，E ，F 是点P 分别以AB ，BC ，AC 为对称轴的对称点，则∠ADB ＋∠BEC ＋∠CF A ＝___．12．如图，将三角板的直角顶点放在直尺的一边上，若∠1=60°，则∠2的度数为____o ．13．33()()()n n x y x y x y -+---=________；15．已知，如图：∠ABC=∠DEF ，AB=DE ，要说明△ABC ≌△DEF ，若以“ASA”为依据，还要添加的条件为__________．16．如图，已知∠1=∠2，请你添加一个条件使△ABC ≌△BAD ，你的添加条件是_______（填一个即可）。
初一数学初中数学综合库试题答案及解析
初一数学初中数学综合库试题答案及解析1.（1） -4的相反数是▲，（2） 36的平方根是▲．（3）当x ▲时，根式有意义；（4）当x ▲时，分式的值为零．【答案】4，，【解析】略2.已知方程3x＋1＝2x＋2与方程3x＋5a＝8有相同的解，,求a的值.【答案】x = 1，a = 1。
【解析】略3.计算：-2+5的结果是（）A．－7B．－3C．3D．7【答案】 C【解析】略4.（6分）图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为：1+2+3+…+n=图１图2图3图4如果图1中的圆圈共有12层，（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1， 2，3，4…，则最底层最左边这个圆圈中的数是；（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数−40，−39，−38，…，求图4中所有圆圈中各数的和．【答案】（1）67；（2）(-40)+(-39)+(-38)+…+(-1)+0+1+…+36+37= -117．【解析】略5. 1. 下列说法不正确的是（）A．位似图形一定是相似图形B．相似图形不一定是位似图形C．位似图形上任意一对对应点到位似中心的距离之比等于位似比D．位似图形中每组对应点所在的直线必相互平行【答案】D【解析】略6.一只蚂蚁由（0，0）先向上爬4个单位长度，再向右爬3个单位长度，再向下爬2个单位长度后，它所在位置的坐标是________【答案】（3,2）【解析】略7.线段CD是由线段AB平移得到的，点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标【答案】（1,2）【解析】略8.已知：如图，线段AB＝10cm，点O是线段AB的中点，线段BC＝3cm，则线段OC＝ cm【答案】2【解析】略9. 9的算术平方根是（）A．±3B．3C．﹣3D．【答案】B.【解析】一个正数的正的平方根是这个数的算术平方根，根据算术平方根的定义可得9的算术平方根是3，故答案选B.【考点】算术平方根的定义.10.将一张完好无缺的报纸对折n次后，数了一下共有128层，则n=_____________。
初一数学综合练习题精华及答案基础
初一数学综合练习题精华及答案基础第一节：有理数与整式1. 下面的有理数中，哪一个数是整数？A. 2/7B. 0C. √3D. -4/5答案：B. 02. 将-12/5化为带分数。
答案：-12/5 = -2 2/53. 计算：(-2/3) + (-5/6)。
答案：(-2/3) + (-5/6) = -4/6 = -2/34. 将2x - 4y + 3(x - y)化简。
答案：2x - 4y + 3(x - y) = 2x - 4y + 3x - 3y = 5x - 7y5. 用x表示5的三倍与7的差的一半。
答案：5的三倍是15，7的差是0，一半是0/2=0，用x表示为0。
6. 计算：2x(x + 3) - 3(x - 2)(x + 1)。
答案：2x(x + 3) - 3(x - 2)(x + 1) = 2x^2 + 6x - 3(x^2 - x - 2x + 2)= 2x^2 + 6x - 3x^2 + 3x + 6 = -x^2 + 12x + 6第二节：方程与不等式1. 解方程3(x + 1) - 2 = 5x - 7。
答案：3(x + 1) - 2 = 5x - 73x + 3 - 2 = 5x - 73x + 1 = 5x - 7-2x = -8x = 42. 解不等式2x - 5 > 3x + 1。
答案：2x - 5 > 3x + 12x - 3x > 1 + 5-x > 6x < -63. 求方程组的解：{2x + 3y = 8，3x - y = 5}。
答案：通过消元法解方程组：3(2x + 3y) = 3(8) --> 6x + 9y = 242(3x - y) = 2(5) --> 6x - 2y = 10将两式相加消去x：(6x + 9y) + (6x - 2y) = 24 + 1012x + 7y = 34将y代入6x + 9y = 24：6x + 9(1) = 246x + 9 = 246x = 15x = 15/6 = 2.5所以方程组的解为{x = 2.5，y = 1}。
初一数学综合练习题集精华与答案解析(基础)(最新整理)
初一练习（易）一、选择题：1．桌上放着一个茶壶，4个同学从各自的方向观察，请指出图1右边的四幅图，从左至右分别是由哪个同学看到的（ ）A ．①②③④B ．①③②④C ．②④①③D ．④③①②2.数，在数轴上的位置如图2所示，则是（ ）a b b a +A ．正数 B ．零 C ．负数 D ．都有可能3. 每天供给地球光和热的太阳与我们的距离非常遥远，它距地球的距离约为15000000千米，将150000000千米用科学记数法表示为（ ）A ．0.15×千米B ．1.5×千米C ．15×千米D ．1.5×千米9108107107104．图3是某市一天的温度变化曲线图，通过该图可知，下列说法错误的是（ ）A ．这天15点时的温度最高B ．这天3点时的温度最低C ．这天最高温度与最低温度的差是13℃D ．这天21点时的温度是30℃5. ∠1的对顶角是∠2,∠2的邻补角是∠3,若∠3=45°,则∠1的度数是（ ）A ．45° B ． 90° C ． 135° D ． 45°或135°6.如图4，若AB//CD ，∠C=60°，则∠A+∠E=（）图47.点的坐标满足,且，则点必在（ ）(,)P x y 0xy >0x y +>P A 第．一象限 B ．第二象限 C ．第三象限 D ．第四象限8.下列说法错误的是（ ）A 、－2x<－6的解集是x>3B 、－5是x<－2的解集C 、x<2的整数解有无数个D 、x<3的正整数解是有限个图1温度/℃3 6 9图3图2二、填空题：9.已知(a ＋1)2＋|b －2|＝0，则的值等于。
1+ab 10. 一组数据4，8，3，2，6，1，x 的众数是4，则它的中位数是_____，平均数是________。
11.等腰三角形的一边长为3，另一边长为6，则该三角形的周长是________．12.如图5，AB ∥CD ，若∠ABE ＝120°，∠DCE ＝35°，则∠BEC ＝ ．13.设表示两种不同的物体，现用天平称了两次，如图6所示，那么这两种物体的质量分别为．14. 如图7，把纸片沿折叠，使点落在四边形的内部，若=40°，∆ABC DE A BCDE ∠A 则=°∠+∠12图715. 方程组 的解是 ，则a b =___________。
青岛版2020七年级数学下册期末综合复习基础训练题1(附答案)
【详解】
x 1
3x 2y a 3-4 a
把
y
2
代入二元一次方程组
bx
y
5
得 b 2 5 ，解得 a=-1,b=3，
∴b-a=4
故选 D.
【点睛】
此题主要考查二元一次方程组的解，解题的关键是把方程组的解代入求解.
4．C
【解析】
【分析】
根据两直线的位置即可判断求解.
【详解】
①如果两条直线都与第三条直线平行，那么这两条直线也互相平行，正确；
【详解】
解：：直线 a//b，
∵∠ACB=∠2，AC⊥BA，
∴∠BAC=90°，
∴∠2=∠ACB=180°-∠1-∠BAC=50°，
.∠1=50°，故选：C
【点睛】 本题考查了对平行线的性质和三角形内角和定理的应用，注意：⑥两直线平行，同位角相等， @两直线平行，内错角相等，@两直线平行，同旁内角互补 11．19 或－17 【解析】 【分析】 这里首末两项是 2x 和 9y 这两个数的平方，那么中间一项为加上或减去 2x 和 9y 积的 2 倍． 【详解】
根据任何非 0 数的零次幂等于 1，1 的任何次幂等于 1，-1 的偶数次幂等于 1 解答．
【详解】
当 3-2t=0 时，t= 3 ，此时 t-3= 3 -3=- 3 ，（- 3 ）0=1，
2
22 2
当 t-3=1 时，t=4，此时 3-2t=2-3×4=-6，1-6=1，
当 t-3=-1 时，t=2，此时 3-2t=3-2×2=-1，（-1）-1=-1，不符合题意，
x 2y 8, 3x 2y 12,
27．如图，在△ ABC 中，∠ABC 与∠ACB 的角平分线交于点 I．根据下列条件求∠BIC
七年级上册数学综合复习基础题(含答案)
七年级数学全册暑期大练兵——综合复习基础练习试卷简介:全卷共6个选择题，8个填空题，5个计算题，分值100，测试时间60分钟。
本套试卷是七年级上册综合复习测试题。
整套试卷难度都不大，主要考察了学生对课本基础知识的理解和掌握。
但是有些题目需要一定的计算量，这个是比较容易出错的。
学生在做题过程中可以回顾本学期知识点，做到认真细心，提高正确率。
学习建议:本卷是综合测试卷，考的不是某一方面的知识点，而是整个一本书的知识点。
这就要求学生在平时的学习过程中注意积累和复习，每一节都学踏实了，做起综合题才不会困难。
同学们在做完题之后，要根据各个题目涉及到的知识点，回头看课本，做到查漏补缺。
一、单选题(共6道，每道5分)1.一个正方体的表面展开图可以是（）A.B.C.D.答案：C解题思路：A、B、D项都不能构成正方体易错点：对正方体的十一种展开图没有掌握试题难度：二颗星知识点：几何体的展开图2.由一些大小相同的小正方体搭成的几何体的俯视图如图所示，其中正方形中的数字表示该位置上的小正方体的个数，那么该几何体的左视图是（）A.B.C.D.答案：B解题思路：从俯视图分析，该几何体的左视图共有3列，第一列最高为2个小正方体，第二列最高为3个小正方体，第三列最高为1个小正方体，故选B易错点：对几何体的三视图掌握不牢固试题难度：三颗星知识点：简单组合体的三视图3.如图，已知C 是线段AB的中点，D 是BC的中点，E 是AD的中点，F 是AE的中点，那么线段AF是线段AC 的（）A.B.C.D.答案：C解题思路：由已知条件可知，AF=AE=AD=(AC+AD)=AC+×AC=AC易错点：不会进行线段之间的转换试题难度：三颗星知识点：两点间的距离4.已知在数轴上a、b的对应点如图所示，则下列式子正确的是（）A.ab＞0B.|a|＞|b|C.a—b＞0D.a + b＞0答案：C解题思路：从数轴上可以看出，0＜a＜1，b＜-1，答案选C易错点：不会根据数轴比较数的大小试题难度：三颗星知识点：有理数大小比较5.代数式xa+bya-1与3x2y是同类项，则a-b的值为（）A.2B.0C.-2D.1答案：A解题思路：由题意知，a+b=2，a-1=1，解得a=2，b=0易错点：对同类项的特点不熟悉试题难度：三颗星知识点：同类项6.有理数x，y在数轴上的位置如图所示，则（）A.y＞x＞0B.x＞y＞0C.x＜y＜0D.y＜x＜0答案：A解题思路：观察数轴，可以得出y＞x＞0易错点：不会比较数轴上数的大小试题难度：二颗星知识点：有理数大小比较二、填空题(共8道，每道5分)1.如图，∠AOC=90°，∠COB=α，OD平分∠AOB，则∠COD等于______答案：45°-解题思路：∠COD=∠BOD-∠BOC=∠AOB-α=（90°+α）-α=45°-易错点：不会根据角之间的关系进行转化试题难度：三颗星知识点：角的计算2.若|a|=1，|b|=4，且ab＜0，则a+b＝______答案：3或-3解题思路：由题意可知，a=1，b=-4或a=-1，b=4，则a+b=-3或3易错点：对绝对值的知识点掌握不牢试题难度：三颗星知识点：绝对值3.a是不为1的有理数，我们把称为a的差倒数．如：2的差倒数是，-1的差倒数是．已知，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数，……，依此类推，则a2011=______答案：解题思路：，，，,……，由此可以发现，，，，而2011=3×670+1，所以易错点：不能发现各项之间的规律试题难度：四颗星知识点：开放探究型问题4.据报道，全球观看北京奥运会开幕式现场直播的观众达到2 300 000 000人，创下全球直播节目收视率的最高纪录．该观众人数可以用科学计数法表示为______人答案：2.3×109易错点：对科学记数法掌握不熟练试题难度：二颗星知识点：科学计数法5.在“2008北京”奥运会国家体育场的“鸟巢”钢结果工程施工建设中，首次使用了我国科研人员自主研制的强度为4.6×108帕的钢材，那么4.6×108的原数为______答案：460 000 000易错点：对科学记数法掌握不熟练试题难度：二颗星知识点：科学计数法6.典典同学学完统计知识后，随机调查了她所在辖区若干名居民的年龄，将调查数据绘制成扇形和条形统计图，如图所示．（1）典典同学共调查了___名居民的年龄，扇形统计图中a=_____，b=_____；（2）补全条形统计图．（3）若该辖区年龄在0～14岁的居民约有3人，请估计年龄在15～59岁的居民的人数．答案：（1）500,20%，12%；（2）如图：（3）10解题思路：（1）共调查了居民230÷46%=500名居民，a=100÷500=20%，b=60÷500=12% （2）41~59岁之间有500-100-230-60=110个人（3）3÷100×（230+110）≈10人易错点：对各种统计图掌握不牢固试题难度：四颗星知识点：条形统计图7.-a+2b-3c的相反数是______答案：a-2b+3c易错点：对相反数的概念理解不清楚试题难度：二颗星知识点：相反数8.已知，，，，则a+b=_______答案：109解题思路：观察规律可以发现：，所以a=10，b=102-1=99，a+b=109易错点：不能发现各项等式中数字之间的关系和规律试题难度：三颗星知识点：规律探索型问题三、计算题(共5道，每道6分)1.计算：0.25×（-2）3-答案：-13解题思路：原式==-2-10-1=-13易错点：计算错误试题难度：三颗星知识点：有理数的混合运算2.解方程：答案：解题思路：去分母：4（2x-1）-3（5x+1）=24,去括号：8x-4-15x-3=24，-7x=31，易错点：计算容易出现错误试题难度：三颗星知识点：解一元一次方程3.化简求值：,其中x=3，答案：xy2+xy，解题思路：原式=3x2y-（2xy2-2xy+3x2y+xy）+3xy2=3x2y-2xy2+2xy-3x2y-xy+3xy2=xy2+xy，把x和y的值代入上式得：原式=易错点：计算容易出现错误试题难度：三颗星知识点：代数式求值4.甲、乙两人做如下的游戏：一个均匀的骰子，它的每个面上分别标有数字1，2，3，4，5，6，任意掷出骰子后，若朝上的数字是6，则甲获胜；若朝上的数字不是6，则乙获胜. 你认为这个游戏对甲、乙双方公平吗？答案：不公平解题思路：朝上的数字是6的概率为，而朝上的数字不是6的概率为，所以这个游戏对甲、乙双方不公平易错点：不会计算概率试题难度：三颗星知识点：游戏公平性5.化简求值：4x2-4xy+y2-2（x2-2xy+y2），其中，y=-2答案：2x2-y2，解题思路：原式=4x2-4xy+y2-2x2+4xy-2y2=2x2-y2，把x和y的值代入上式，得：原式=易错点：计算易出错试题难度：三颗星知识点：整式的加减众享课程主页/curriculum/index.jsp?do=ok 东区总校：郑州市文化路与黄河路交叉口中孚大厦7楼B室电话：65335902 西区总校：郑州市陇海路与桐柏路交叉口凯旋门大厦B座405室电话：68856662。
初一数学初中数学综合库试题答案及解析
初一数学初中数学综合库试题答案及解析1.如图，图中与是同位角的有（）.个．个．个．个【答案】B【解析】略2.下列各式中，不是方程的是（）A．= 1；B．3= 2+5C．=" 0"D．2－3+ 1【答案】D【解析】略3.绝对值小于3的整数有个，它们的积是【答案】 5,0【解析】略4.若x=1是关于x的方程ax+1=2的解，则a是（）A．1B．2C．-1D．-2【答案】 A【解析】略5.分解因式:xy-x-y+1=__________________.【答案】【解析】略6.地球上的陆地面积约为149 000 000千米2，用科学记数法表示为 ( )A．149×106千米2B．14.9×107千米2C．1.49×108千米2D．0.149×109千2【答案】C【解析】略7.有下列说法：①任何无理数都是无限小数；②有理数与数轴上的点一一对应；③在1和3之间的无理数有且只有，，，这4个；④是分数，它是有理数.⑤近似数7.30所表示的准确数的范围是：7.2957.305.其中正确的有（填“序号”）【答案】①⑤【解析】略8.下列说法正确的是（）．A．x=1是不等式＜1的解B．x=3是不等式＜1的解集C．x＞－1是不等式＜1的解集D．x＞－1是不等式＜1的解集【答案】D【解析】略9.下列说法正确的是（）A．两点之间，直线最短；B．过一点有一条直线平行于已知直线；C．和已知直线垂直的直线有且只有一条；D．在平面内过一点有且只有一条直线垂直于已知直线．【答案】D【解析】略10.若∠1与∠2是对顶角，∠3与∠2互补，又知∠3=60°，则∠1=" "【答案】120°【解析】略11. (2014四川凉山州)在实数、、0、、、－1.414中，有理数有( )A．1个B．2个C．3个D．4个【答案】D【解析】、0、、－1.414是有理数，共4个．12.观察探索：……（1）按规律请写出：（4分）=（2）用上述规律计算：（2分）……【答案】（1），；（2）．【解析】从题意得等式的左右两边乘号或减号前的整数等于乘号或减号后的分数的分子，而分母加1，从而得到规律．试题解析：（1）（2）……=……==．【考点】规律型：数字的变化类．13.（8分）如图，已知点在线段上，BE=CF，AB∥DE，∠ACB=∠F．求证：．【答案】见解析【解析】根据AB∥DE得出∠B=∠DEF，再由BE=CF得出BC=EF，利用ASA可证．试题解析：证明：∵AB∥DE，∴∠B=∠DEF，∵BE=CF，∴BE+CE=CF+CE，即BC=EF，∵∠ACB=∠F，∴△ABC≌△DEF（ASA）【考点】全等三角形的判定14.若代数式的值是7，则代数式的值是．【答案】4．【解析】试题解析：∵代数式x2+3x+5的值是7，∴x2+3x+5=7，∴x2+3x=2，∴3x2+9x-2=3（x2+3x）-2=3×2-2=6-2=4．【考点】代数式求值．15.学校阶梯教室的第一排有个座位，后面每排都比前一排多2个座位，那么第排的座位数有（）个．A．B．C．D．【答案】A【解析】根据题意可得：第二排有（m+2）个座位，第三排有（m+4）个座位，第四排有（m+6）个座位，则第n排有[m+2（n－1）]个座位．【考点】代数式16.若代数式4x与的值相等，则x的值是__________．【答案】-．【解析】试题解析：根据题意得；4x=，去分母得：8x=2x-1移项得：8x-2x=--1，合并同类项得：6x=-1，系数化为1得；x=-．【考点】解一元一次方程．17.把3．1415取近似数（精确到0．01）为__________．【答案】3．14【解析】根据四舍五入法、精确数和近似数的表示，可知3．1415精确到0．01为3．14．【考点】近似数与精确数18.已知：如图∠1=∠2，当DE与FH有什么位置关系时，CD∥FG？并说明理由．【答案】当DE∥FH时，CD∥FG．理由见解析.【解析】欲证CD∥FG,只需证明内错角∠CDF=∠GFD;所以从两直线ED∥FG知内错角∠EDF=∠HFD然后根据已知条件∠1=∠2和等量代换求得内错角∠CDF=∠GFD，从而判定两直线CD∥FG.试题解析：当DE∥FH时，CD∥FG．理由如下：∵ED∥FH，∴∠EDF=∠HFD（两直线平行，内错角相等），∴∠EDF﹣∠1=∠HFD﹣∠1=∠HFD﹣∠2，∴∠CDF=∠GFD，∴CD∥FG（内错角相等，两直线平行）．【考点】平行线的判定.19.如图，将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上，如果∠1=27°，那么∠2的度数为（）A．53°B．55°C．57°D．60°【答案】C【解析】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠3，再根据两直线平行，同位角相等可得∠2=∠3．解：由三角形的外角性质，∠3=30°+∠1=30°+27°=57°，∵矩形的对边平行，∴∠2=∠3=57°．故选：C．20.如果|a﹣1|+|b+2|=0，那么a+b= ．【答案】﹣1【解析】先根据绝对值的性质求出a、b的值，进而可得出结论．解：∵|a﹣1|+|b+2|=0，∴a﹣1=0，b+2=0，解得a=1，b=﹣2，∴a+b=1﹣2=﹣1．故答案为：﹣1．【点评】本题考查的是非负数的性质，熟知任意一个数的绝对值都是非负数是解答此题的关键．21.如图，已知：∠AOB=60°，点A、B分别在∠AOB两边上，直线l、m、n分别过A、O、B三点，且满足直线l∥m∥n，OB与直线n所夹的角为25°，则∠α的度数为（）A．25° B．45° C．35° D．30°【答案】C【解析】先根据m∥n求出∠BCD的度数，再由△ABC是等边三角形求出∠ACB的度数，根据l∥m即可得出结论．解：∵m∥n，边BO与直线n所夹的角为25°，∴∠1=25°．∵∠AOB=60°，∴∠2=60°﹣25°=35°．∵l∥m，∴∠α=∠2=35°．故选C．【点评】本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．22.某校师生积极为汶川地震灾区捐款，在得知灾区急需账篷后，立即到当地的一家账篷厂采购，帐篷有两种规格：可供3人居住的小账篷，价格每顶160元；可供10人居住的大账篷，价格每顶400元．学校花去捐款96000元采购这两种帐篷，正好可供2300人临时居住．（1）求该校采购了多少顶3人小帐篷，多少顶10人大帐篷；（2）学校现计划租用甲、乙两种型号的卡车共20辆将这批帐篷紧急运往灾区，已知甲型卡车每辆可同时装运4顶小帐篷和11顶大账篷，乙型卡车每辆可同时装运12顶小帐篷和7顶大帐篷．如何安排甲、乙两种卡车可一次性将这批帐篷运往灾区有哪几种方案？【答案】（1）100顶3人小帐篷，200顶10人大帐篷．（2）3种方案【解析】（1）首先设采购了x顶3人小帐篷，y顶10人大帐篷，列出二元一次方程组．（2）设甲型卡车安排了a辆，则乙型卡车安排了（20﹣a）辆，列出不等式组解答即可．解：（1）设采购了x顶3人小帐篷，y顶10人大帐篷．由题材意得．解得．答：采购了100顶3人小帐篷，200顶10人大帐篷．（2）设甲型卡车安排了a辆，则乙型卡车安排了（20﹣a）辆，则．解得15≤a≤17.5∵a为整数，∴a=15、16、17则乙型卡车：20﹣a=5、4、3答：有3种方案：①甲型卡车15辆，乙型卡车5辆．②甲型卡车16辆，乙型卡车4辆．③甲型卡车17辆，乙型卡车3辆．点评：本题考查一元一次不等式组的应用，将现实生活中的事件与数学思想联系起来，读懂题列出不等式关系式即可求解．23.下面每个表格中的四个数都是按相同规律填写的：根据此规律确定x的值为．新-【答案】209【解析】根据规律可得：b=20÷2=10，a=10－1=9，则x=20b+a=20×10+9=209.【考点】规律题24.苏宁电器商场计划用9万元从生产厂家购进50台电视机．已知该厂家生产3•种不同型号的电视机，出厂价分别为A种每台1500元，B种每台2100元，C种每台2500元．（1）若苏宁电器商场同时购进两种不同型号的电视机共50台，用去9万元，请你研究一下商场的进货方案．（2）若商场销售一台A种电视机可获利150元，销售一台B种电视机可获利200元，•销售一台C种电视机可获利250元，在同时购进两种不同型号的电视机方案中，为了使销售时获利最多，你选择哪种方案？【答案】(1)、一是购A，B两种电视机25台；二是购A种电视机35台，C种电视机15台；(2)、方案二.【解析】(1)、按购A，B两种，B，C两种，A，C两种电视机这三种方案分别计算，设购A种电视机x台，则B种电视机y台.按照每种情况分别列出一元一次方程，从而分别求出每种情况的答案；(2)、分别求出每种方案所能获得的利润，然后选择利润最大的方案.试题解析：按购A，B两种，B，C两种，A，C两种电视机这三种方案分别计算，设购A种电视机x台，则B种电视机y台．(1)、①当选购A，B两种电视机时，B种电视机购（50－x）台，可得方程1500x+2100（50－x）=90000 即5x+7（50－x）=3002x=50 x=25 50－x=25②当选购A，C两种电视机时，C种电视机购（50－x）台，可得方程1500x+2500（50－x）=900003x+5（50－x）=1800 x=35 50－x=15③当购B，C两种电视机时，C种电视机为（50－y）台．可得方程2100y+2500（50－y）=9000021y+25（50－y）=900，4y=350，不合题意由此可选择两种方案：一是购A，B两种电视机25台；二是购A种电视机35台，C种电视机15台．(2)、若选择（1）中的方案①，可获利150×25+250×15=8750（元）若选择（1）中的方案②，可获利150×35+250×15=9000（元）9000>8750故为了获利最多，选择第二种方案．【考点】一元一次方程的应用25.小李解关于x的方程5a-x=12时，误将-x看作+x，得方程的解为x=-3，则原方程的解是【】A．x=-2B．x=1C．x=3D．x=2【答案】C【解析】试题解析：把x=-3代入5a+x=12得：5a-3=12，解得：a=3，方程为15-x=12，解得：x=3，故选C．26.在下列各数：，，，，，中，负有理数的个数是（）A．个B．个C．个D．【答案】C【解析】首先根据计算的法则将各数进行计算，然后进行判断.-(+2)=-2；-=-9；=-；=-；=1；=3，则负有理数有4个.27.纽约与北京的时差是小时，如果现在是北京时间月日时，那么现在的纽约时间是__________.【答案】月日时【解析】分析：由有理数的加法计算得出即可；解：纽约时间=15：00+（-13）=2：00．故答案是9月11日2时。
浙教版2020七年级数学期末复习综合练习题(基础部分 含答案)
）
A．100 2 +1
B．101×2
C．100 2 +100×1+1 D．100 2 +2×100+1
5．某同学为了解梅州市火车站今年“五一”期间每天乘车人数,随机抽查了其中 2 天的乘
车人数,所抽查的这 2 天中每天乘车人数是这个问题的 ( )
A．总体 B．个体 C．样本 D． 以上都不对
6．已知 a+b=3，ab=2，则 a2+b2 的值为（
22． 2x 1;0
【解析】 试题分析： 先去括号、再合并同类项，最后代值计算即可；
试题解析：
原式＝ 2x 12 2x 2x 1
＝ 4x2 4x 1 4x2 2x
＝ 2x 1
当 x 1 时， 2
原式= 2x 1
2
1 2
1
0.
23．（1）1；（2） BF 3 10
【解析】 试题分析：（1）由矩形的性质和角平分线的定义得出∠DAE=∠EAB=∠BEA，推出 BE=BA=5；利用勾股定理可求出 CE=4，故可求出 DE=1； （2）在矩形 ABCD 中，在 CD 边上取点 E，使 CE=4，则 DE=1，沿 BE 剪下，则 BE=5， 再将△ BCE 平移，使 BC 与 AD 重合，所得四边形即为菱形，即可求解.
A.第一项 3 没有乘以公分母 4;
B.等号右边去括号未变号;
C.正确;
D. 等号左边去括号未变号.
故选 C.
点睛: 本题主要考查一元一次方程的解法，去分母时，方程两端同乘各分母的最小公倍数时，
不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．
4．D
【解析】
解：1012=（100+1）2=1002+2×100+1．故选 D．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初一练习（易）
一、选择题：
1．桌上放着一个茶壶，4个同学从各自的方向观察，请指出图1右边的四幅图，从左至右分别是由哪个同学看到的（ ）
A ．①②③④
B ．①③②④
C ．②④①③
D ．④③①② 2.数a ，b 在数轴上的位置如图2所示，则b a +是（ ）
A ．正数
B ．零
C ．负数
D ．都有可能
3. 每天供给地球光和热的太阳与我们的距离非常遥远，它距地球的距离约为千米，将0千
米用科学记数法表示为（ ）
A ．×910千米
B ．×810千米
C ．15×710千米
D ．×710千米
4．图3是某市一天的温度变化曲线图，通过该图可
知，下列说法错误的是（ ） A ．这天15点时的温度最高 B ．这天3点时的温度最低
C ．这天最高温度与最低温度的差是13℃
D ．这天21点时的温度是30℃
5. ∠1的对顶角是∠2,∠2的邻补角是∠3,若∠3=45°,则∠1的度数是（ ） A ．45° B． 90° C． 135° D． 45°或135°
6.如图4，若AB (,)P x y 的坐标满足0xy >,且0x y +>，则点P
必在（ ）
A 第．一象限
B ．第二象限
C ．第三象限
D ．第四象限 8.下列说法错误的是（ ）
图1
温度/℃
3 6 9 12 时间/时 38 3
4 26 22 1
5 18 21 24 图2
A 、－2x<－6的解集是x>3
B 、－5是x<－2的解集
C 、x<2的整数解有无数个
D 、x<3的正整数解是有限个 二、填空题：
9.已知(a ＋1)2
＋|b －2|＝0，则1+ab 的值等于。
10. 一组数据4，8，3，2，6，1，x 的众数是4，则它的中位数是_____，平均数是________。
11.等腰三角形的一边长为3，另一边长为6，则该三角形的周长是________． 12.如图5，AB ∥CD ，若∠ABE ＝120°，∠DCE ＝35°，则∠BEC ＝ ．
13.设“ ”“ ”表示两种不同的物体，现用天平称了两次，如图6所示，那么这两种物
体的质量分别为．
14. 如图7，把∆ABC 纸片沿DE 折叠，使点A 落在四边形BCDE 的内部，若∠A =40°，则∠+∠12=°
图7
15. 方程组 的解是 ，则a b
=___________。
三、解答题： 16.计算：
（1）()23
3(2)4---⨯-÷14⎛⎫-
⎪⎝⎭
（2）42×1(4)2+︱2︱3
×(12)3+错误!
17.（1）解方程组⎩
⎨⎧=-=+24632
47y x y x （4）解不等式组
18. 先化简，再求值： )441()34(2
2
a a a a +--- 其中a =－2。
北
东
A
B
20. 下面有8个算式，排成4行2列
2＋2， 2×2
3＋
23， 3×23 4＋34， 4×34
5＋45， 5×4
5
……， ……
（1）同一行中两个算式的结果怎样 （2）算式2005＋
20042005和2005×2004
2005
的结果相等吗 （3）请你试写出算式，试一试，再探索其规律，并用含自然数n 的代数式表示这一规律。
21. 如图，AD
即∠__________=∠__________. ∴ AB 方程解应用题
用3元5角买了10分、20分、50分三种邮票共18枚，10分邮票
与20分邮票的总面值相同，求三种邮票各买了多少枚。
23. 如图，宽为50 cm的长方形图案由10个相同的小长方形拼成，求每块长方形的长和宽分别是多少
24. 如图，平面直角坐标系的单位长度为小正方形的边长，△ABC在平面直角坐标系中．（1）请你写出△ABC各点的坐标；
（2）求△ABC的面积；
（3）若把△ABC向左平移3个单位，向上平移2个单位，得C
B
A'
'
'
∆，请你画出C
B
A'
'
'
∆，并写出C
B
A'
'
'
∆各点的坐标．
A
B
x
C
y
Ｏ
答案
一、选择题：
二、填空题：9. -1 10. 2,4 11. 15 12. 95° 13. 30和40 14. 80° 15. -8 三、解答题：16.（1）119 （2）-102 17.（1
） 2x =
（2）38x -<≤
18. 解：)441()34(2
2
a a a a +---=2244134a a a a -+
--………………2分
=1-a …………………………………… 4分 6分
3
y =-
说明：只要能比较准确的画出题中所述的两个角，并标出C 点位置即可得全分（5分）。
20. 解（1）处在同一行的两个算式，计算结果相等。
………………………… 3分 （2）相等…………………………………………………………………… 5分 （3）n
n n n n n 1
)1(1)1(+⨯
+=++
+…………………………………… 8分 21. ∠BCA ，（两直线平行，内错角相等） ∠BCA ， ∠BAC ，∠DCA ，
DC ，（内错角相等，两直线平行）
22. 解：设10分邮票买了x 枚，20分邮票买了y 枚，50分邮票买了z 枚。
则
解之得
答：10分邮票买了10枚，20分邮票买了5枚，50分邮票买了3枚。
23. 分别是40 ，10
24.(1) A(-2,1) B(5,1) C(1,3)
(2) S ABC ∆=11 (3)A ′(-5,3) B ′(2,3) C ′(-2,5)。