最大公约数和最小公倍数怎么求
利用递归求最大公约数和最小公倍数
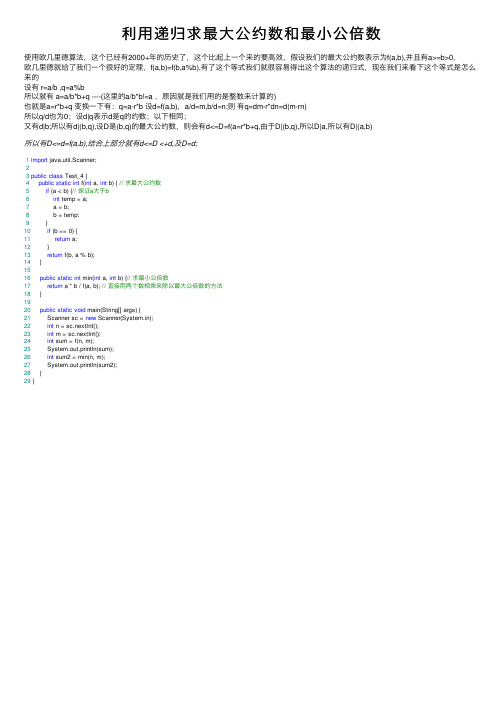
利⽤递归求最⼤公约数和最⼩公倍数使⽤欧⼏⾥德算法,这个已经有2000+年的历史了,这个⽐起上⼀个来的要⾼效,假设我们的最⼤公约数表⽰为f(a,b),并且有a>=b>0,欧⼏⾥德就给了我们⼀个很好的定理,f(a,b)=f(b,a%b),有了这个等式我们就很容易得出这个算法的递归式,现在我们来看下这个等式是怎么来的设有 r=a/b ,q=a%b所以就有 a=a/b*b+q ----(这⾥的a/b*b!=a ,原因就是我们⽤的是整数来计算的)也就是a=r*b+q 变换⼀下有:q=a-r*b 设d=f(a,b),a/d=m,b/d=n;则有q=dm-r*dn=d(m-rn)所以q/d也为0;设d|q表⽰d是q的约数;以下相同;⼜有d|b;所以有d|(b,q),设D是(b,q)的最⼤公约数,则会有d<=D=f(a=r*b+q,由于D|(b,q),所以D|a,所以有D|(a,b)所以有D<=d=f(a,b),结合上部分就有d<=D <+d,及D=d;1import java.util.Scanner;23public class Test_4 {4public static int f(int a, int b) { // 求最⼤公约数5if (a < b) {// 保证a⼤于b6int temp = a;7 a = b;8 b = temp;9 }10if (b == 0) {11return a;12 }13return f(b, a % b);14 }1516public static int min(int a, int b) {// 求最⼩公倍数17return a * b / f(a, b); // 直接⽤两个数相乘来除以最⼤公倍数的⽅法18 }1920public static void main(String[] args) {21 Scanner sc = new Scanner(System.in);22int n = sc.nextInt();23int m = sc.nextInt();24int sum = f(n, m);25 System.out.println(sum);26int sum2 = min(n, m);27 System.out.println(sum2);28 }29 }。
辗转相除法求最大公约数和最小公倍数

辗转相除法求最大公约数和最小公倍数1: /*辗转相除法基于如下原理:两个整数的最大公约数等于其中较小的数和两数的差的最大公约数。
2: 例如,252和105的最大公约数是21(252 = 21 ×12;105 = 21 ×5);3: 因为252 ? 105 = 147,所以147和105的最大公约数也是21。
在这个过程中,较大的数缩4: 小了,所以继续进行同样的计算可以不断缩小这两个数直至其中一个变成零。
这时,所剩下的5: 还没有变成零的数就是两数的最大公约数。
6: */7: #include <stdio.h>8:9: int getGCDAndLCM(int a,int b){10: int max=a>b?a:b;//将较大的数赋给max11: int min=(max=a)?b:a;//将较小的数赋给min12: int temp;//暂时存储变量13: while(max!=0){14: temp=min%max;15: min=max;16: max=temp;17: }18: printf("最大公约数为%d\n",min);19: printf("最小公倍数为%d\n",a*b/min);20: }21:22: int main(){23: printf("输入两个数整数值\n");24: int a,b;25: scanf("%d",&a);26: scanf("%d",&b);27: getGCDAndLCM(a,b);28: return 0;29: }C语言水仙花数算法打印出所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其各位数字立方和等于该数本身。
例如:153是一个“水仙花数”,因为153=1的三次方+5的三次方+3的三次方。
求最大公约数和最小公倍数的方法探析

求最大公约数和最小公倍数的方法探析郑州市惠济区东风路小学吕绣娟求最大公约数和最小公倍数的方法多样,按照教材由基本到最优化的计算方法步步探讨,看看各自的利弊和特点。
例如求12和9的最大公约数和最小公倍数.通常有以下4种方法:1、集合圈法: 12的约数9的约数12的倍数9的倍数2、4 1 9 12、24、9、18、12、6、3、48、60 36、27、45...... ...... ......它们的公约数它们的公倍数它们的最大公约数和最小公倍数分别是3和362、分解质因数法:12=3×2 ×2 9=3×3它们的最大公约数是3。
最小公倍数是3×2×2×3=363、短除法:3 12 94 3它们的最大公约数是3最小公倍数是3×4×3=364、特殊情况法1)两数互质时:例如8和11 它们的最大公约是1最小公倍数是两数积882)一个数是另一个数的倍数时:例如3和12 它们的最大公约是较小数3最小公倍数是较大数12。
5、求最小公倍数的方法:大数翻倍法。
例如:6和8 8的1倍、2倍......倍,其中最先同时是6的倍数的24即是它们的最小公倍数.尽管在初学时我们是按照有繁到简、有难到易的这种逐步抽象顺序来学的,总结的短除法非常方便,而且相当多数同学,也常认为在使用了方法5、4或方法3时似乎就掌握了一把万能钥匙,足以解决所有相关题目,其实有时候的确如此。
但实际上,仍然会遇到问题障碍。
例如:求65与117的最大公约数和最小公倍数。
利用法5显然数比较大,简单的几倍过后,没有收获;利用法4,不是倍数关系,但也同时不易辨别它们是否互质关系。
利用法3,同样我们也不易找到它们的公约数。
于是部分学生转而就把它当成了互质数来计算,这样就错了。
这时全面了解所有方法的显得尤其重要。
所以通常在求最小公倍数和最大公约数的时候,我们选择的方法依次是5-4-3-2-1,直到问题被解决。
最大公倍数和最小公倍数求法

一、观察法.运用能被2、3、5整除的数的特征进行观察.例如,求225和105的最大公约数.因为225、105都能被3和5整除,所以225和105至少含有公约数(3×5)15.因为225÷15=15,105÷15=7.15与7互质,所以225和105的最大公约数是15.二、查找约数法.先分别找出每个数的所有约数,再从两个数的约数中找出公有的约数,其中最大的一个就是最大公约数.例如,求12和30的最大公约数.12的约数有:1、2、3、4、6、12;30的约数有:1、2、3、5、6、10、15、30.12和30的公约数有:1、2、3、6,其中6就是12和30的最大公约数.三、分解因式法.先分别把两个数分解质因数,再找出它们全部公有的质因数,然后把这些公有质因数相乘,得到的积就是这两个数的最大公约数.例如:求125和300的最大公约数.因为125=5×5×5,300=2×2×3×5×5,所以125和300的最大公约数是5×5=25.四、关系判断法.当两个数关系特殊时,可直接判断两个数的最大公约数.例如,两个数互质时,它们的最大公约数就是这两个数的乘积;两个数成倍数关系时,它们的最大公约数就是其中较小的那个数.五、短除法.为了简便,将两个数的分解过程用同一个短除法来表示,那么最大公约数就是所有除数的乘积.例如:求180和324的最大公约数.因为:5和9互质,所以180和324的最大公约数是4×9=36.六、除法法.当两个数中较小的数是质数时,可采用除法求解.即用较大的数除以较小的数,如果能够整除,则较小的数是这两个数的最大公约数.例如:求19和152,13和273的最大公约数.因为152÷19=8,273÷13=21.(19和13都是质数.)所以19和152的最大公约数是19,13和273的最大公约数是13.七、缩倍法.如果两个数没有之间没有倍数关系,可以把较小的数依次除以2、3、4……直到求得的商是较大数的约数为止,这时的商就是两个数的最大公约数.例如:求30和24的最大公约数.24÷4=6,6是30的约数,所以30和24的最大公约数是6.八、求差判定法.如果两个数相差不大,可以用大数减去小数,所得的差与小数的最大公约数就是原来两个数的最大公约数.例如:求78和60的最大公约数.78-60=18,18和60的最大公约数是6,所以78和60的最大公约数是6.如果两个数相差较大,可以用大数减去小数的若干倍,一直减到差比小数小为止,差和小数的最大公约数就是原来两数的最大公约数.例如:求92和16的最大公约数.92-16=76,76-16=60,60-16=44,44-16=28,28-16=12,12和16的最大公约数是4,所以92和16的最大公约数就是4.九、辗转相除法.当两个数都较大时,采用辗转相除法比较方便.其方法是:以小数除大数,如果能整除,那么小数就是所求的最大公约数.否则就用余数来除刚才的除数;再用这新除法的余数去除刚才的余数.依此类推,直到一个除法能够整除,这时作为除数的数就是所求的最大公约数.例如:求4453和5767的最大公约数时,可作如下除法.5767÷4453=1余13144453÷1314=3余5111314÷511=2余292511÷292=1余219292÷219=1余73219÷73=3最大公约数和最小公倍数的求法一、观察法.运用能被2、3、5整除的数的特征进行观察.例如,求225和105的最大公约数.因为225、105都能被3和5整除,所以225和105至少含有公约数(3×5)15.因为225÷15=15,105÷15=7.15与7互质,所以225和105的最大公约数是15.二、查找约数法.先分别找出每个数的所有约数,再从两个数的约数中找出公有的约数,其中最大的一个就是最大公约数.例如,求12和30的最大公约数.12的约数有:1、2、3、4、6、12;30的约数有:1、2、3、5、6、10、15、30.12和30的公约数有:1、2、3、6,其中6就是12和30的最大公约数.三、分解因式法.先分别把两个数分解质因数,再找出它们全部公有的质因数,然后把这些公有质因数相乘,得到的积就是这两个数的最大公约数.例如:求125和300的最大公约数.因为125=5×5×5,300=2×2×3×5×5,所以125和300的最大公约数是5×5=25.四、关系判断法.当两个数关系特殊时,可直接判断两个数的最大公约数.例如,两个数互质时,它们的最大公约数就是这两个数的乘积;两个数成倍数关系时,它们的最大公约数就是其中较小的那个数.五、短除法.为了简便,将两个数的分解过程用同一个短除法来表示,那么最大公约数就是所有除数的乘积.例如:求180和324的最大公约数.5和9互质,所以180和324的最大公约数是4×9=36.六、除法法.当两个数中较小的数是质数时,可采用除法求解.即用较大的数除以较小的数,如果能够整除,则较小的数是这两个数的最大公约数.例如:求19和152,13和273的最大公约数.因为152÷19=8,273÷13=21.(19和13都是质数.)所以19和152的最大公约数是19,13和273的最大公约数是13.七、缩倍法.如果两个数没有之间没有倍数关系,可以把较小的数依次除以2、3、4……直到求得的商是较大数的约数为止,这时的商就是两个数的最大公约数.例如:求30和24的最大公约数.24÷4=6,6是30的约数,所以30和24的最大公约数是6.八、求差判定法.如果两个数相差不大,可以用大数减去小数,所得的差与小数的最大公约数就是原来两个数的最大公约数.例如:求78和60的最大公约数.78-60=18,18和60的最大公约数是6,所以78和60的最大公约数是6.如果两个数相差较大,可以用大数减去小数的若干倍,一直减到差比小数小为止,差和小数的最大公约数就是原来两数的最大公约数.例如:求92和16的最大公约数.92-16=76,76-16=60,60-16=44,44-16=28,28-16=12,12和16的最大公约数是4,所以92和16的最大公约数就是4.九、辗转相除法.当两个数都较大时,采用辗转相除法比较方便.其方法是:以小数除大数,如果能整除,那么小数就是所求的最大公约数.否则就用余数来除刚才的除数;再用这新除法的余数去除刚才的余数.依此类推,直到一个除法能够整除,这时作为除数的数就是所求的最大公约数.例如:求4453和5767的最大公约数时,可作如下除法.5767÷4453=1余13144453÷1314=3余5111314÷511=2余292511÷292=1余219292÷219=1余73219÷73=3于是得知,5767和4453的最大公约数是73.辗转相除法适用比较广,比短除法要好得多,它能保证求出任意两个数的最大公约数.つないだ手。
最大公约数与最小公倍数

最大公约数与最小公倍数【知识导引】一、约数的概念与最大公约数约数又叫因数(在正整数范围内)整数a 能被整数b 整除,a 叫做b 的倍数,b 就叫做a 的约数。
最大公约数:如果一个数既是数a 的约数,又是数b 的约数,称为[a,b]的约数。
几个数公有的因数,叫做这几个数的公因数,其中最大的一个叫做这几个数的最大公因数。
1. 求最大公约数的方法①分解质因数法:先分解质因数,然后把相同的因数连乘起来。
例如:2313711=⨯⨯,22252237=⨯⨯,所以(231,252)3721=⨯=;②短除法:先找出所有共有的约数,然后相乘。
例如:2181239632,所以(12,18)236=⨯=;③辗转相除法:每一次都用除数和余数相除,能够整除的那个余数,就是所求的最大公约数。
用辗转相除法求两个数的最大公约数的步骤如下:先用小的一个数除大的一个数,得第一个余数;再用第一个余数除小的一个数,得第二个余数;又用第二个余数除第一个余数,得第三个余数;这样逐次用后一个余数去除前一个余数,直到余数是0为止。
那么,最后一个除数就是所求的最大公约数(如果最后的除数是1,那么原来的两个数是互质的)。
例如,求600和1515的最大公约数:151********÷=;6003151285÷=;315285130÷=;28530915÷=;301520÷=;所以1515和600的最大公约数是15。
2. 最大公约数的性质①几个数都除以它们的最大公约数,所得的几个商是互质数;②几个数的公约数,都是这几个数的最大公约数的约数;③几个数都乘以一个自然数n ,所得的积的最大公约数等于这几个数的最大公约数乘以n 。
3. 求一组分数的最大公约数先把带分数化成假分数,其他分数不变;求出各个分数的分母的最小公倍数a ;求出各个分数的分子的最大公约数b ;b a即为所求。
二、倍数的概念与最小公倍数对于整数m ,能被n 整除(n/m ),那么m 就是n 的倍数。
求最大公约数和最小公倍数的c语言

【题目】求最大公约数和最小公倍数的c语言【正文】1. 导言在数学中,最大公约数和最小公倍数是非常基础且重要的概念,它们在我们日常生活和工程技术中都有着广泛的应用。
而在计算机编程中,我们可以通过C语言来求解最大公约数和最小公倍数,本文将从简单到复杂,由浅入深地介绍如何用C语言来求解最大公约数和最小公倍数。
2. 最大公约数的求解最大公约数(Greatest Common Divisor, GCD)指的是一组数中能够整除它们的最大正整数。
求解最大公约数有多种方法,其中辗转相除法是其中最常用的一种。
下面我们就通过C语言来实现辗转相除法求解最大公约数。
```c#include <stdio.h>// 辗转相除法求最大公约数int gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);}int main() {int num1, num2;printf("请输入两个整数:\n");scanf("%d %d", &num1, &num2);printf("%d 和 %d 的最大公约数是:%d\n", num1, num2,gcd(num1, num2));return 0;}```在这段代码中,我们定义了一个gcd函数来使用辗转相除法求解最大公约数,并在主函数中进行了输入和输出。
通过这个简单的例子,我们可以看到C语言是如何轻松地求解最大公约数的。
3. 最小公倍数的求解最小公倍数(Least Common Multiple, LCM)指的是一组数中的公共倍数中最小的一个数。
求解最小公倍数也有多种方法,例如可以利用最大公约数来求解。
下面我们就通过C语言来实现利用最大公约数来求解最小公倍数。
```c#include <stdio.h>// 求最小公倍数int lcm(int a, int b) {return a * b / gcd(a, b);}int main() {int num1, num2;printf("请输入两个整数:\n");scanf("%d %d", &num1, &num2);printf("%d 和 %d 的最小公倍数是:%d\n", num1, num2,lcm(num1, num2));return 0;}```在这段代码中,我们定义了一个lcm函数来利用最大公约数来求解最小公倍数,并在主函数中进行了输入和输出。
小学五年级数学上册《最小公倍数》教案:最小公倍数和最大公约数的应用场景有哪些?

小学五年级数学上册《最小公倍数》教案:最小公倍数和最大公约数的应用场景有哪些?最小公倍数和最大公约数是小学数学中的重要概念之一。
在小学五年级数学上册中,我们学习了最小公倍数的概念、求法及其应用。
最小公倍数和最大公约数的应用场景有哪些呢?本篇文章将为大家详细介绍。
一、最小公倍数的概念和求法我们来了解一下最小公倍数的概念和求法。
最小公倍数,简称最小倍数,是若干个正整数公有的倍数中最小的一个。
比如,6和8的公倍数有6、8、12、24等,其中最小的是24,6和8的最小公倍数为24。
求最小公倍数有两种常用方法:1. 分解质因数法将所给的几个数都分解质因数,把每个质因数的最高次幂相乘即可。
比如,求12和20的最小公倍数,将它们分解质因数:12=2×2×320=2×2×5把每个质因数的最高次幂相乘:最小公倍数=2×2×3×5=6012和20的最小公倍数为60。
2. 倍数相乘法将所给的几个数分别乘以一个相同的数,直到它们的倍数相等,把这个相同的数作为最小公倍数即可。
比如,求6和9的最小公倍数,分别将它们乘以2和3:6×2=129×3=27此时,它们的最小公倍数为12×3=36。
二、最小公倍数的应用场景最小公倍数不仅在数学运算中有应用,也经常出现在日常生活中,例如:1. 分糖果和瓜果小学生分糖果或瓜果时,如果每个人分到的个数要一样多,就需要求出糖果或瓜果数的最小公倍数。
比如,班级里有24个学生,老师给他们分糖果,每个学生分到的个数相同且最多为6个,需要求出24和6的最小公倍数,即24÷6=4,每个学生最多分4个糖果。
2. 日历要知道某几个日期中所有日期的排列顺序,就需要使用最小公倍数。
比如,如果要知道在2024年中每隔4天出现的是星期几,就需要求出4和7(一周有7天)的最小公倍数,即28,每隔28天后就是重复的星期几。
质数合数偶数奇数最大公约数及最小公倍数求法讲解

什么是质数?就是在所有比1大的整数中,除了1和它本身以外,不再有别的约数,这种整数叫做质数,质数又叫做素数。
最小的质数是2.合数是自然数中除能被1和本数整除外,还能被其他的数整除数。
如:6能被1和6整除,也能被2和3整除.最小的合数是4.约数和倍数是相对而言,约数是能整除某数的,倍数是能被某数整除的例,6和3都是12的约数, 12是3和6的倍数8的约数包括1,2,4和8能被2整除的数叫做偶数(包括0,0是最小的偶数),不能被2整除的数叫做奇数,最小的奇数是1.1.公约数和最大公约数几个数公有的约数,叫做这几个数的公约数;其中最大的一个,叫做这几个数的最大公约数。
例如:12的约数有:1,2,3,4,6,12;18的约数有:1,2,3,6,9,18。
12和18的公约数有:1,2,3,6.其中6是12和18的最大公约数,记作(12,18)=6。
2.公倍数和最小公倍数几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
例如:12的倍数有:12,24,36,48,60,72,84,…18的倍数有:18,36,54,72,90,…12和18的公倍数有:36,72,….其中36是12和18的最小公倍数,这样求最小公倍数首先把两个数的质因数写出来,最小公倍数等于它们所有的质因数的乘积(如果有几个质因数相同,则比较两数中哪个数有该质因数的个数较多,乘较多的次数)。
比如求45和30的最小公倍数。
45=3*3*530=2*3*5不同的质因数是2,3,5。
3是他们两者都有的质因数,由于45有两个3,30只有一个3,所以计算最小公倍数的时候乘两个3.最小公倍数等于2*3*3*5=90又如计算36和270的最小公倍数36=2*2*3*3270=2*3*3*3*5不同的质因数是5。
2这个质因数在36中比较多,为两个,所以乘两次;3这个质因数在270个比较多,为三个,所以乘三次。
最小公倍数等于2*2*3*3*3*5=540这样求最大公约数法一、短除法求最大公因数的一种方法,也可用来求最小公倍数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最大公约数和最小公倍数怎么求?
首先把两个数的质因数写出来,最小公倍数等于它们所有的质因数的乘积(如果有几个质因数相同,则比较两数中哪个数有该质因数的个数较多,乘较多的次数)。
比如:求45和30的最小公倍数。
45=3*3*5
30=2*3*5
不同的质因数是2,3,5。
3是他们两者都有的质因数,由于45有两个3,30只有一个3,所以计算最小公倍数的时候乘两个3.
最小公倍数等于2*3*3*5=90
又如:计算36和270的最小公倍数。
36=2*2*3*3
270=2*3*3*3*5
不同的质因数是5。
2这个质因数在36中比较多,为两个,所以乘两次;3这个质因数在270个比较多,为三个,所以乘三次。
最小公倍数等于2*2*3*3*3*5=540
最大公约数和最小公倍数<练习题>
1.有一级茶叶96克,二级茶叶156克,三级茶叶240克,价值相等.现将这三种茶叶分别等分装袋(均为整数克),每袋价值相等,要使每袋价值最低应如何装袋?
2.a、b两数的最大公约数是12,已知a有8个约数,b有9个约数,求a与b.
3.两个数的积是6912,最大公约数是24,求:(1)它们的最小公倍数;(2)满足已知条件的自然数是哪几组?
4.甲、乙、丙三个学生定期向某老师求教,甲每4天去一次,乙每6天去一次,丙每9天去一次,如果这一次他们三人是3月23日都在这个老师家见面,那么下一次三人都在这个老师家见面的时间是几月几日?
5.求被5除余2,被6除余3,被7除4的大于1000、小于1500的所有自然数.
6.某个数与36的最大公约数是12,与36的最小公倍数是180,求这个数.
7.有三个自然数a、b、c,a与b的最大公约数是2;b和c的最大公约数是4;a和c的最大公约数是6;a、b、c三个数的最小公倍数是60,求这三个数的最小的和是多少?
答案仅供参考:
1.三种数量不等的茶叶价值相等,等分装袋后,每袋价值仍相等,由于每种茶叶的总价值相等,每袋价值也要相等,所以这三种茶叶分装的袋数也一定相同.为了使每袋价值最低,就应使袋数尽可能多,
因此,每种茶叶应装的袋数是96,156,240的最大公约数.
(96,156,240)=4×3=12
96÷12=8,156÷12=13,240÷12=20
所以三种茶叶各自等分成12袋,并依次装8克,13克,20克.
2.因为(a,b)=12=22×3,所以a和b只有质因数2和3,又因为a有8个约数,8=2×2×2=2×4=8×1,所以a=23×3=24,同理b有9个约数,9=3×3=9×1,b=22×32=36.
3.(1)因为两个数的最大公约数与最小公倍数的乘积等于这两个数的积,所以这两个数的最小公倍数是6912÷24=288.
(2)因为两个数的最大公倍数除以它们的最大公约数等于这两个数分别除以它们的最大公约数所得商的乘积,且得到的这两个商是互质数.288÷24=12,12只能分解成12×1和4×3两组质因数的积,所以满足条件的有两组:
24×12=288,24×1=24;
24×4=96,24×3=72.
即这两组数为288和24,96和72.
4.他们下一次都在这个老师家见面的天数一定是4,6和9的最小公倍数.[4,6,9]≈36,经过36天,他们三人又要见面,那么3月23日开始,又经过36天,是4月28日,所以下一次三人都在这个老师家见面的时间是4月28日.
5.这个数被5除余2,被6除余3,被7除余4,尽管余数不同,但如果这个数加上3以后,恰好能被5,6,7整除,也就是说符合被5除余2,被6除余3,被7除余4的数等于5,6,7的公倍数减去3.[5,6,7]=210,符合条件的数可表示为210m-3,m是自然数.又因为所求数在1000到1500之间,当m=5时210×5-3=1047;当m=6时,210×6-3=1257;当m=7时,210×7-3=1467.所以所求的数为1047,1257,1467.6.设所求数为a,已知(a,36)=12,有a=12n,n是自然数.又因为36=12×3,所以n与3互质,又已知[a,36]=180,180=12×3×5,所以n=5,故a=12×5=60.
7.因为a与c的最大公约数是6,因此a必有质因数2和3;由b与c的最大公约数是4,知b必有2个质因数2;由前两个条件知c必有2个质因数2和1个质因数3;要满足[a,b,c]=60=22×3×5,必有一个数含有质因数5;要使三个数的和最小,应b含有质因数5;所以这三个数为:a=2×3=6,b=2×2×5=20,c=2×2×3=12,它们的和是6+20+12=38.。
