九年级小题训练五
新目标九年级上英语听力专项训练五（含听力音频mp3，听力材料及听力试题PPT）
九年级上英语听力专项训练五一、听力测试（本大题共20分，每小题1分）A. 听对话，选出与所听意思相符的图画。
听两遍。
1．What will the boy probably give his mother?2．What do we know about the man?3．What is the man doing?4．What is the woman?B. 听对话，从所给选项中选出最佳答案回答问题。
听两遍。
5. Which subject does David like best?A. Geography.B. Music.C. Science.6. Where are the speakers?A. In a hospital.B. On a beach.C. In a street.7. When will the film begin?A. At 6:30.B. At 7:00.C. At 7:30.8. What are the speakers doing?A. They’re climbing a mountain.B. They’re celebrating the man's birthday.C. They’re celebrating the woman's birthday.9. What does the man want to do?A. Buy a new car.B. Drive his car to work at once.C. Change a wheel (轮子) for his car.10. What is the man looking for?A. A market.B. A cinema.C. A bookshop.C．听下面的对话和短文，回答问题。
听两遍。
听下面一段材料，回答第11-12题。
听两遍。
11. Why does the woman call the man?A. To book (预订) tickets.B. To check the date.C. To invite him to a show.12. When will the woman go to see the show?A. On Friday.B. On Saturday.C. On Sunday.听下面一段材料，回答第13-15题。
初中历史九年级下册同步训练及答案第五单元测评
第五单元测评(时间:60分钟满分:100分)一、选择题(本大题共15小题,每小题4分,共60分。
下列各题给出的四个选项中,只有一项符合题意)1.这是一场特殊的战争,它存在于两种不同的社会制度之间,既威胁了世界和平又维持了世界相对的和平。
这场特殊的战争开始于()A.杜鲁门主义的出台B.马歇尔计划的实施C.北约成立D.华约成立2.1945年5月18日,美国驻苏联参赞凯南说:“他们以为战争结束了,而战争才刚刚开始。
”这里的两个“战争”分别是()A.第一次世界大战、第二次世界大战B.第二次世界大战、美苏冷战C.第二次世界大战、科索沃战争D.第二次世界大战、中东战争3.美国推行冷战政策的表现有()①杜鲁门主义出台,宣称美国将领导和帮助所有选择“自由制度”,抵抗极权统治的力量②推动万隆会议成功召开③经济上实施马歇尔计划④成立北大西洋公约组织A.①②③B.①②③④C.①③④D.①②④4.两极格局结束后,下列冷战的产物至今依然存在的是()A.杜鲁门主义B.马歇尔计划C.华沙条约组织D.北大西洋公约组织5.据此可知主要资本主义国家()A.经济持续发展B.受到通货膨胀的困扰C.出现“新经济”D.经济发展衰退6.近代以来欧洲有三次统一的尝试和努力:第一次是法国主导,结果失败;第二次是德国主导,也以失败告终;第三次是法德和解促成统一。
“法德和解促成统一”是指()A.拿破仑帝国的建立B.第一次世界大战后凡尔赛体系的建立C.第二次世界大战中德国的侵略D.第二次世界大战后欧洲的联合7.数据图表能给我们提供很多重要的信息。
分析右面的《20世纪50—70年代主要资本主义国家经济年平均增长率柱状图》,我们不能．．得出的信息是()A.日本是四个国家中经济年平均增长率最高的国家B.联邦德国的经济年平均增长率比英国高C.英国是四个国家中经济年平均增长率最低的国家D.美国丧失了资本主义世界头号经济强国的地位8.有学者评论某次改革时说:“天冷,本想弄点木材烤烤手,想不到竟将整个房子烧了。
英语九年级全一册组合训练小题狂做
英语九年级全一册组合训练小题狂做1、—______some nice crayons. I think they are ______.（）[单选题] *A. Here is; Betty’sB. Here are; BettyC. Here is; BettyD. Here are; Betty’s(正确答案)2、Nick got out of bed and _______ a shower. [单选题] *A. practicedB. took(正确答案)C. didD. made3、58．—How much is Lucy's skirt?—She________320 yuan for it. I think it's a little dear. [单选题] *A．tookB．paid(正确答案)C．spentD．bought4、Mary _______ Math. [单选题] *A. is good at(正确答案)B. do well inC. is good forD. is good with5、English is very important in our daily life. Never _______. [单选题] *A. give up itB. give it up(正确答案)C. give away itD. give it away6、They all choose me ______ our class monitor.（）[单选题] *A. as(正确答案)B. inC. withD. on7、21．Design a travel guide for Shanghai! ________ the competition and be the winner! [单选题] *A．JoinB．AttendC．EnterD．Take part in (正确答案)8、2．The villagers want to have a bridge. Can this dream ________? [单选题] * A．come outB．get awayC．come true(正确答案)D．get out9、While they were in discussion, their manager came in by chance. [单选题] *A. 抓住时机B. 不时地C. 碰巧(正确答案)D. 及时10、25．A watch is important in our life. It is used for ______ the time. [单选题] * A．telling (正确答案)B．sayingC．speakingD．holding11、Have you done something _______ on the weekends? [单选题] *A. special(正确答案)B. soreC. convenientD. slim12、1．________my father ________ my mother is able to drive a car. So they are going to buy one. [单选题] *A．Neither; norB．Both; andC．Either; orD．Not only; but also(正确答案)13、28．The question is very difficult. ______ can answer it. [单选题] *A．EveryoneB．No one(正确答案)C．SomeoneD．Anyone14、--All of you have passed the test!--_______ pleasant news you have told us! [单选题] *A. HowB. How aC. What(正确答案)D. What a15、34．My mother usually_______ much time shopping in the supermarkets on weekends. [单选题] *A．spends (正确答案)B．costsC．takesD．pays16、My brother is _______ actor. He works very hard. [单选题] *A. aB. an(正确答案)C. theD. one17、John Smith is _______ of the three young men. [单选题] *A. strongB. strongerC. the strongerD. the strongest(正确答案)18、—What’s wrong with you, Mike?—I’m really tired because I studied for today’s test ______ midnight last night. （）[单选题] *A. althoughB. unlessC. until(正确答案)D. so that19、85．You’d better? ? ? ? ? a taxi, or you’ll be late. [单选题] *A．take(正确答案)B．takingC．tookD．to take20、55．There is a ________ on in the bookshop. Let's go to buy some books. [单选题] *A．movieB．matchC．sale(正确答案)D．concert21、I _______ seeing you soon. [单选题] *A. look afterB. look forC. look atD. look forward to(正确答案)22、Jim will _______ New York at 12 o’clock. [单选题] *A. get onB. get outC. get offD. get to(正确答案)23、Nowadays schools should care for the full _______ of a student’s talents. [单选题] *A. satisfactionB. development(正确答案)C. communicationD. preparation24、The manager was quite satisfied with his job. [单选题] *A. 担心的B. 满意的(正确答案)C. 高兴的D. 放心的25、My home is about _______ away from the school. [单选题] *A. three hundred metreB. three hundreds metresC. three hundred metres(正确答案)D. three hundreds metre26、Leave your key with a neighbor ___ you lock yourself out one day [单选题] *A. ever sinceB. even ifC. soon afterD. in case(正确答案)27、33．Body language is even___________ and ___________ than any other language. [单选题] *A．stronger, loudB．strong, louderC．strong, loudD．stronger, louder (正确答案)28、Guilin is _______ its beautiful scenery. [单选题] *A. famous for(正确答案)B. interested inC. fond ofD. careful with29、—Why is Mary asking Bob about the school trip? —Because she wants to know ______.（）[单选题] *A. how does he think of the tripB. what does he think of the tripC. what he likes the tripD. how he likes the trip(正确答案)30、Julia’s on holiday in Shanghai _______. [单选题] *A. in a momentB. after a momentC. at the moment(正确答案)D. at any moment。
人教版九年级化学第二单元 我们周围的空气 提高训练题 (5)(含答案解析)
第二单元我们周围的空气提高训练题 (5)一、单选题（本大题共6小题，共12.0分）1.下列实验操作正确的是()A塞紧胶塞 B贮存氧气 C熄灭酒精灯D称量腐蚀性药品A. AB. BC. CD. D2.某同学利用如图装置测定空气中氧气的含量，红磷燃烧后恢复到室温，打开弹簧夹发现进入广口瓶中的水的高度大于广口瓶容积的15，造成这一现象的原因可能的是()A. 实验时，将木炭代替红磷B. 实验中所取的红磷不足，瓶中氧气未反应完C. 实验时，没有塞紧瓶塞D. 插入燃烧匙太慢，塞紧瓶塞之前，瓶内已有部分空气受热逸出3.下列关于氧气用途的叙述，错误的是()A. 用于钢铁工业，提高钢铁的质量和产量B. 氧炔焰用来焊接或切割金属C. 液氧制成炸药，用来开山采矿D. 液氧可用作宇宙火箭的燃料4.下列关于催化剂的说法正确的是()A. 化学反应前后，催化剂的质量和化学性质都不变B. 催化剂可以提高化学反应的速率C. 催化剂可以增加生成物的质量D. 任何化学反应都需要催化剂5.某化学兴趣小组用如图所示的装置来制取干燥的氧气。
装置气密性良好，图中的锥形瓶内盛有质量为m的H2O2溶液，燃烧匙内装有二氧化锰，燃烧匙可以上下移动，干燥管内装有足量碱石灰(CaO和NaOH的混合物，可吸收水蒸气)。
下列说法正确的是()①将装置Ⅰ分别与装置Ⅱ、Ⅲ、Ⅳ、V连接，均能达到实验目的②称量装置Ⅰ反应前和完全反应冷却后的质量，可计算出生成O2的质量③若用装置Ⅳ收集氧气，氧气应从a导管口进入④若用装置V测量生成氧气的体积，集气瓶上方原有的空气不会影响测量结果⑤通过燃烧匙的上下移动可以控制反应的发生⑥V中植物油的作用是使氧气与水隔绝，保证氧气的干燥A. ②③④⑤⑥B. ①②④⑤⑥C. ①②③④⑤⑥D. ②④⑤⑥6.下列说法正确的是()A. 在空气中不燃烧的物质，在氧气中也一定不燃烧B. 化合反应是由两种物质生成一种物质的反应C. 不使用催化剂，加热双氧水就也能分解出氧气D. 使用催化剂可以使双氧水分解出比理论值更多的氧气二、简答题（本大题共9小题，共72.0分）7.多种因素对化学反应速率有影响．(1)硫在氧气中燃烧比在空气中燃烧更剧烈，说明其影响因素是什么？(2)反应物之间的接触面积会影响化学反应速率，请举例说明．8.空气是一种用途很多的自然资源，可用于工业上制取氧气，其流程如下：【查阅资料】常温下，氧气的沸点是−183℃，氮气的沸点是−196℃。
北师大版九年级数学上册第一章特殊平行四边形《矩形的性质与判定》同步练习(解析版) (5)
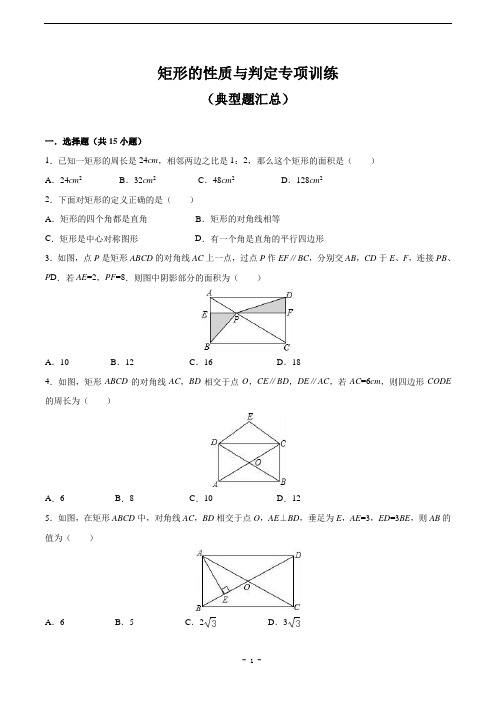
矩形的性质与判定专项训练（典型题汇总）一．选择题（共15小题）1．已知一矩形的周长是24cm，相邻两边之比是1：2，那么这个矩形的面积是（）A．24cm2B．32cm2C．48cm2D．128cm22．下面对矩形的定义正确的是（）A．矩形的四个角都是直角B．矩形的对角线相等C．矩形是中心对称图形D．有一个角是直角的平行四边形3．如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于E、F，连接PB、P D．若AE=2，PF=8．则图中阴影部分的面积为（）A．10 B．12 C．16 D．184．如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，DE∥AC，若AC=6cm，则四边形CODE 的周长为（）A．6 B．8 C．10 D．125．如图，在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD，垂足为E，AE=3，ED=3BE，则AB的值为（）A．6 B．5 C．2D．36．如图，在矩形ABCD中，对角线AC，BD相交于点O，AE垂直平分BO，AE=cm，则OD=（）A．1cm B．1.5cm C．2cm D．3cm7．下列命题中正确的是（）A．对角线相等的四边形是矩形；B．对角线互相垂直的四边形是矩形；C．对角线相等的平行四边形是矩形；D．对角线互相垂直的平行四边形是矩形8．如图，在平行四边形ABCD中，AC、BD是它的两条对角线，下列条件中，能判断这个平行四边形是矩形的是（）A．∠BAC=∠ACB；B．∠BAC=∠ACD；C．∠BAC=∠DAC；D．∠BAC=∠ABD9．如图，平行四边形ABCD的对角线AC与BD相交于点O，要使它成为矩形，需再添加的条件是（）A．AO=OC B．AC=BD C．AC⊥BD D．BD平分∠ABC10．如图，为了检验教室里的矩形门框是否合格，某班的四个学习小组用三角板和细绳分别测得如下结果，其中不能判定门框是否合格的是（）A．AB=CD，AD=BC，AC=BD B．AC=BD，∠B=∠C=90°C．AB=CD，∠B=∠C=90°D．AB=CD，AC=BD11．在△ABC中，点D是边BC上的点（与B，C两点不重合），过点D作DE∥AC，DF∥AB，分别交AB，AC于E，F两点，下列说法正确的是（）A．若AD⊥BC，则四边形AEDF是矩形B．若AD垂直平分BC，则四边形AEDF是矩形C．若BD=CD，则四边形AEDF是菱形D．若AD平分∠BAC，则四边形AEDF是菱形12．如图，在Rt△ABC中，AC=3，BC=4，D为斜边AB上一动点，DE⊥BC，DF⊥AC，垂足分别为E、F．则线段EF的最小值为（）A．B．C．D．13．如图，在矩形COED中，点D的坐标是（1，3），则CE的长是（）A．3 B．C．D．414．如图，D、E、F分别是△ABC各边的中点．添加下列条件后，不能得到四边形ADEF是矩形的是（）A．∠BAC=90°B．BC=2AE C．DE平分∠AEB D．AE⊥BC15．已知四边形ABCD中，对角线AC与BD相交于点O，AD∥BC，下列判断中错误的是（）A．如果AB=CD，AC=BD，那么四边形ABCD是矩形B．如果AB∥CD，AC=BD，那么四边形ABCD是矩形C．如果AD=BC，AC⊥BD，那么四边形ABCD是菱形D．如果OA=OC，AC⊥BD，那么四边形ABCD是菱形二．填空题（共6小题）16．矩形ABCD中，AB=3，BC=4，则AC=，矩形的面积为．17．如图，在▱ABCD中，再添加一个条件（写出一个即可），▱ABCD是矩形（图形中不再添加辅助线）18．如图，设矩形ABCD和矩形AEFC的面积分别为S1、S2，则二者的大小关系是：S1S2．19．如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=5cm，BC=12cm，则EF=cm．20．如图，连接四边形ABCD各边中点，得到四边形EFGH，还要添加条件，才能保证四边形EFGH 是矩形．21．如图，在△ABC中，AB=3，AC=4，BC=5，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为．三．解答题（共5小题）22．如图，在矩形ABCD中，对角线AC与BD相交于点O，∠AOD=120°，BD=6，求矩形ABCD的面积．23．如图，DB∥AC，且DB=AC，E是AC的中点．（1）求证：BC=DE；（2）连接AD、BE，若∠BAC=∠C，求证：四边形DBEA是矩形．24．已知：如图，菱形ABCD，分别延长AB，CB到点F，E，使得BF=BA，BE=BC，连接AE，EF，FC，C A．（1）求证：四边形AEFC为矩形；（2）连接DE交AB于点O，如果DE⊥AB，AB=4，求DE的长．25．如图，四边形ABCD为平行四边形纸片．把纸片ABCD折叠，使点B恰好落在CD边上，折痕为AF．且AB=10cm、AD=8cm、DE=6cm．（1）求证：平行四边形ABCD是矩形；（2）求BF的长；（3）求折痕AF长．26．已知矩形ABCD和点P，当点P在图1中的位置时，则有结论：S△PBC=S△PAC+S△PCD理由：过点P作EF垂直BC，分别交AD、BC于E、F两点．∵S△PBC+S△PAD=BC•PF+AD•PE=BC（PF+PE）=BC•EF=S矩形ABC D．（1）请补全以上证明过程．（2）请你参考上述信息，当点P分别在图1、图2中的位置时，S△PBC、S△PAC、S PCD又有怎样的数量关系？请写出你对上述两种情况的猜想，并选择其中一种情况的猜想给予证明．参考答案一．选择题（共15小题）1．B．2．D．3．C．4．D．5．C．6．C．7．C．8．D．9．B．10．D．11．D．12．D．13．C．14．D．15．A．二．填空题（共6小题）16．5，12．17．AC=BD18．=．19．．20．AC⊥B D．21．．三．解答题（共5小题）22．解：∵四边形ABCD是矩形，∴∠BAD=90°，AC=BD，OA=AC，OD=BD，∴OA=OD，∵∠AOD=120°，∴∠ADO=30°∴AB=B D．在直角三角形ABD中，由勾股定理，得AD===3∴S=AB•AD=3×3=9．矩形ABCD23．（1）证明：∵E是AC中点，∴EC=A C．∵DB=AC，∴DB=E C．又∵DB∥EC，∴四边形DBCE是平行四边形．∴BC=DE．（2）证明：∵DB∥AE，DB=AE，∴四边形DBEA是平行四边形．∵∠BAC=∠C，∴BA=BC，∵BC=DE，∴AB=DE．∴▭ADBE是矩形．24．证明：（1）∵BF=BA，BE=BC，∴四边形AEFC为平行四边形，∵四边形ABCD为菱形，∴BA=BC，∴BE=BF，∴BA+BF=BC+BE，即AF=EC，∴四边形AEFC为矩形；（2）连接DB，由（1）可知，AD∥EB，且AD=EB，∴四边形AEBD为平行四边形，∵DE⊥AB，∴四边形AEBD为菱形，∴AE=EB，AB=2AG，ED=2EG，∵矩形ABCD中，EB=AB，AB=4，∴AG=2，AE=4，∴在Rt△AEG中，EG=2，∴ED=4．25．（1）证明：∵把纸片ABCD折叠，使点B恰好落在CD边上，∴AE=AB=10，AE2=102=100，又∵AD2+DE2=82+62=100，∴AD2+DE2=AE2，∴△ADE是直角三角形，且∠D=90°，又∵四边形ABCD为平行四边形，∴平行四边形ABCD是矩形（有一个角是直角的平行四边形是矩形）；（2）解：设BF=x，则EF=BF=x，EC=CD﹣DE=10﹣6=4cm，FC=BC﹣BF=8﹣x，在Rt△EFC中，EC2+FC2=EF2，即42+（8﹣x）2=x2，解得x=5，故BF=5cm；（3）解：在Rt△ABF中，由勾股定理得，AB2+BF2=AF2，∵AB=10cm，BF=5cm，∴AF==5cm．26．证明：（1）∵S△PAC+S△PCD+S△PAD=S矩形ABCD∴S△PBC+S△PAD=S△PAC+S△PCD+S△PAD，∴S△PBC=S△PAC+S△PCD；（2）猜想结果：图2结论S△PBC=S△PAC+S△PCD；图3结论S△PBC=S△PAC﹣S△PC D．证明：如图，过点P作EF垂直AD，分别交AD、BC于E、F两点．∵S△PBC=BC•PF=BC•PE+BC•EF=AD•PE+BC•EF=S△PAD+S矩形ABCDS△PAC+S△PCD=S△PAD+S△ADC=S△PAD+S矩形ABCD∴S△PBC=S△PAC+S△PC D．矩形的性质与判定专项训练（典型题汇总）一、填空题：1．矩形的对边，对角线且，四个角都是，即是图形又是图形。
人教版九年级化学下册作业课件 第十二单元 化学与生活 专题训练(五) 实验探究题
(5)【反思评价】如图2是小红将一根铝丝与过量的稀盐酸混合在一密闭容器内反应， 利用压强和温度传感器测出的反应变化过程。那么，在______(C填字母)点时铝与酸反 应结束；请你解释压强曲线AB段、BC段、CD段的变化原因。
①__A__B_段__是__稀__盐__酸__和__氧__化__铝__反__应__，__没__有__生__成__气__体__，__不__放__热__，__气__压__几__乎__不__变___。 ②__B__C_段__是__稀__盐__酸__和__铝__反__应__，__生__成__氢__气__，__放__热__，__气__压__增__大_________________。 ③__C__D_段__没__有__反__应__，__温__度__降__低__，__气__压__减__小_______________________________。
②资料显示：Fe3O4与稀盐酸混合无气体生成且不与CuSO4溶液反应。故小嘉同学 猜想乙组的生成物为Fe3O4，她又发现m2恰好为___4_.6_4__，这可以成为支持上述猜想 的新证据。则乙中硬质玻璃管内发生反应的化学式方程式为
________C__O_＋__3_F_e_2_O_3_=_=_△=_=_=__2_F__e_3O__4＋__C__O_2_____________。 (4)两组实验说明：CO具有还原性且温度越__高____，CO越有可能将Fe2O3还原为单 质铁。
(3)实验过程中通N2的作用是____排__除__内__部__残__留__的__空__气_____。 (4)测得装置C中餐具碎片的起始质量为0.72 g，反应后装置C中硬质玻璃管内无固体 残留。装置D增重0.36 g，装置E和F一共增重1.32 g。经计算确认猜想______2_成立。 (不考虑空气中成分进入F中)
人教九年级化学同步练习及答案第五单元综合训练
第五单元综合训练一、快乐点击(下列每小题给出的四个选项中,只有一项是符合题目要求的)1.在化学变化中,下列说法正确的是()①原子的种类、元素的种类、分子的种类均不变②原子的数目、分子的数目均不变③原子的质量、元素的质量、物质的总质量均不变④原子核的种类、数量、质量均不变A.①②B.①③C.③④D.②④2.化学是以实验为基础的学科,当你走进化学实验室时,会发现有些药品装在棕色瓶中,这是因为这些药品见光后在紫外线作用下容易分解,你预测硝酸银见光分解不可能得到的产物是()A.N2B.NOC.NO2D.NH33.四位同学正在讨论某一个化学方程式的意义,他们所描述的化学方程式是()A.C+O2CO2B.2CO+O22CO2C.H2+Cl22HClD.2Mg+O22MgO4.4.6 g某化合物在足量氧气中充分燃烧,生成8.8 g二氧化碳和5.4 g水。
下列对该化合物组成的判断中,正确的是()A.由碳、氢两种元素组成B.由碳、氧两种元素组成C.由碳、氢、氧三种元素组成D.一定含有碳、氢两种元素,可能含有氧元素5.下列化学方程式书写正确的是()A.硫在空气中燃烧:S+O2↑SO2↑B.加热氯酸钾制取氧气:2KClO32KCl+3O2↑C.锌与稀硫酸反应:Zn+H2SO4ZnSO4+H2↑D.熟石灰与盐酸反应:Ca(OH)2+2HCl CaCl2+HO26.一种焰火火药中所含的硝酸铜在燃放时产生绿色火焰,发生如下反应:2Cu(NO3)22CuO+O2↑+4X↑。
下列有关说法错误的是()A.根据质量守恒定律可知X的化学式为NO2B.该反应的基本反应类型为分解反应C.Cu(NO3)2中铜元素的化合价为+1价D.产物中CuO属于氧化物7.一定温度下,在下图所示装置中,固体X与气体Y反应,生成气态产物,当改变温度时该气态产物发生逆向反应,重新生成X和Y。
利用上述反应原理和装置,对含杂质的固体Co进行提纯(杂质不参加反应),发生的化学反应为Co(固)+2HCl(气)CoCl2(气)+H2(气)。
九年级数学二次函数专题训练含答案解析-精选5份
九年级数学上册《二次函数》专题测试题（附答案）一．选择题（共8小题，满分32分）1．若y＝（a+1）x|a+3|﹣x+3是关于x的二次函数，则a的值是（）A．1B．﹣5C．﹣1D．﹣5或﹣12．下列关于二次函数y＝﹣（x﹣m）2+m2+1（m为常数）的结论错误的是（）A．当x＞0时，y随x的增大而减小B．该函数的图象一定经过点（0，1）C．该函数图象的顶点在函数y＝x2+1的图象上D．该函数图象与函数y＝﹣x2的图象形状相同3．已知：抛物线的解析式为y＝﹣3（x﹣2）2+1，则抛物线的对称轴是直线（）A．x＝﹣1B．x＝1C．x＝2D．x＝﹣24．将二次函数y＝2x2向左平移5个单位，再向上平移3个单位，所得新抛物线表达式为（）A．y＝2（x+5）2﹣3B．y＝2（x+5）2+3C．y＝2（x﹣5）2﹣3D．y＝2（x﹣5）2+35．二次函数y＝ax2+bx+c的图象如图所示，下列结论：（1）4ac＜b2；（2）abc＜0；（3）2a+b＜0；（4）（a+c）2＜b2其中正确的个数是（）A．1B．2C．3D．46．已知抛物线y＝ax2+4ax﹣8与直线y＝n相交于A，B两点（点A在点B左侧），AB＝4，且抛物线与x轴只有一个交点，则n的值为（）A．﹣8B．﹣4C．4D．87．已知二次函数y＝ax2+bx+c的图象经过（﹣3，0）与（1，0）两点，关于x的方程ax2+bx+c+m ＝0（m＞0）有两个整数根，其中一个根是3，则另一个根是（）A．﹣5B．﹣3C．﹣1D．38．物理课上我们学习了竖直上抛运动，若从地面竖直向上抛一小球，小球的高度h（单位：m）与小球运动时间t（单位：s）之间的函数关系如图所示，下列结论：①小球在空中经过的路程是40m②小球抛出3s后，速度越来越快③小球抛出3s时速度为0④小球的高度h＝30m时，t＝1.5s其中正确的是（）A．①②③B．①②C．②③④D．②③二．填空题（共8小题，满分32分）9．已知抛物线y＝x2+bx+c关于直线x＝2对称，设x＝1，2，4时对应的函数值依次为y1，y2，y4，那么y1，y2，y4的大小关系是．（用“＜”连接）10．已知抛物线y＝ax2﹣2ax﹣1（a＜0）（I）抛物线的对称轴为；（2）若当﹣2≤x≤2时，y的最大值是1，求当﹣2≤x≤2时，y的最小值是．11．已知二次函数y＝ax2﹣2ax+c（a≠0）的图象与x轴的一个交点为（﹣1，0），则关于x 的一元二次方程ax2﹣2ax+c＝0的两根之积是．12．已知二次函数y＝﹣x2+4x+5及一次函数y＝﹣x+b，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象（如图所示），当直线y＝﹣x+b与新图象有4个交点时，b的取值范围是．13．将抛物线y＝﹣（x﹣3）2﹣1向右平移5个单位，再向上平移2个单位，所得的抛物线的解析式为．14．如图，抛物线y＝ax2与直线y＝bx+c的两个交点坐标分别为A（﹣3，9），B（1，1），则方程ax2﹣bx﹣c＝0的解是．15．抛物线y＝ax2+bx+tc（a＜0）交x轴于点A、B，交y轴于点C（0，3），其中点B坐标为（1，0），同时抛物线还经过点（2，﹣5）．（1）抛物线的解析式为；（2）设抛物线的对称轴与抛物线交于点E，与x轴交于点H，连接EC、EO，将抛物线向下平移n（n＞0）个单位，当EO平分∠CEH时，则n的值为．16．某食品零售店新上架一款冷饮产品，每个成本为8元，在销售过程中，每天的销售量y （个）与销售价格x（元/个）的关系如图所示，当10≤x≤20时，其图象是线段AB，则该食品零售店每天销售这款冷饮产品的最大利润为元（利润＝总销售额﹣总成本）．三．解答题（共6小题，满分56分）17．已知二次函数y＝x2+mx+m2﹣3（m为常数，m＞0）的图象经过点P（2，4）．（1）求m的值；（2）判断二次函数y＝x2+mx+m2﹣3的图象与x轴交点的个数，并说明理由．18．对于向上抛的物体，如果空气阻力忽略不计，有下面的关系式：h＝v0t﹣gt2（h是物体离起点的高度，v0是初速度，g是重力系数，取10m/s2，t是抛出后经过的时间）．杂技演员抛球表演时，以10m/s的初速度把球向上抛出．（1）球抛出后经多少秒回到起点？（2）几秒后球离起点的高度达到1.8m？（3）球离起点的高度能达到6m吗？请说明理由．19．在平面直角坐标系中，已知二次函数y＝ax2+（a﹣1）x﹣1．（1）若该函数的图象经过点（1，2），求该二次函数图象的顶点坐标．（2）若（x1，y1），（x1，y2）为此函数图象上两个不同点，当x1+x2＝﹣2时，恒有y1＝y2，试求此函数的最值．（3）当a＜0且a≠﹣1时，判断该二次函数图象的顶点所在象限，并说明理由．20．某商场新进一批拼装玩具，进价为每个10元，在销售过程中发现，日销售量y（个）与销售单价x（元）之间满足如图所示的一次函数关系．（1）求y与x的函数关系式（不要求写出自变量x的取值范围）；（2）若该玩具某天的销售利润是600元，则当天玩具的销售单价是多少元？（3）设该玩具日销售利润为w元，当玩具的销售单价定为多少元时，日销售利润最大？最大利润是多少元？21．如图，抛物线y＝﹣x2+bx+c过点A（4，0），B（0，2）．M（m，0）为线段OA上一个动点（点M与点A不重合），过点M作垂直于x轴的直线与直线AB和抛物线分别交于点D、N．（1）求直线AB的表达式和抛物线的表达式；（2）若DN＝3DM，求此时点N的坐标；（3）若点P为直线AB上方的抛物线上一个动点，当∠ABP＝2∠BAC时，求点P的坐标．22．如图，已知二次函数y＝x2+bx+c（b，c为常数）的图象经过点A（3，﹣2），点C（0，﹣5），顶点为点M，过点A作AB∥x轴，交y轴于点D，交二次函数y＝x2+bx+c的图象于点B，连接BC．（1）求该二次函数的表达式及点M的坐标；（2）若将该二次函数图象向上平移m（m＞0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包括△ABC的边界），求m的取值范围；（3）若E为线段AB上一点，且BE：EA＝3：1，P为直线AC上一点，在抛物线上是否存在一点Q，使以B、P、E、Q为顶点的四边形是平行四边形？若存在，请直接写出点Q的横坐标；若不存在，请说明理由．参考答案一．选择题（共8小题，满分32分）1．解：∵函数y＝（a+1）x|a+3|﹣x+3是关于x的二次函数，∴|a+3|＝2且a+1≠0，解得a＝﹣5，故选：B．2．解：A．∵y＝﹣（x﹣m）2+m2+1（m为常数），∴抛物线开口向下，对称轴为直线x＝m，∴x＞m时，y随x增大而减小，故A错误，符合题意；∵当x＝0时，y＝1，∴该函数的图象一定经过点（0，1），故B正确，不合题意；∵y＝﹣（x﹣m）2+m2+1，∴抛物线顶点坐标为（m，m2+1），∴抛物线顶点在抛物线y＝x2+1上，故C正确，不合题意；∵y＝﹣（x﹣m）2+m2+1与y＝﹣x2的二次项系数都为﹣1，∴两函数图象形状相同，故D正确，不合题意．故选：A．3．解：∵y＝﹣3（x﹣2）2+1，∴抛物线对称轴为直线x＝2．故选：C．4．解：将二次函数y＝2x2向左平移5个单位，再向上平移3个单位，所得新抛物线表达式为y＝2（x+5）2+3，故选：B．5．解：根据图象知道抛物线与x轴有两个交点，∴b2﹣4ac＞0，即4ac＜b2，故（1）正确．∵抛物线开口朝下，∴a＜0，∵对称轴在y轴右侧，∴b＞0，∵抛物线与y轴的交点在x轴的上方，∴c＞0，∴abc＜0，故（2）正确；∵对称轴x＝﹣＞1，∴2a+b＞0，故（3）错误；根据图象知道当x＝1时，y＝a+b+c＞0，根据图象知道当x＝﹣1时，y＝a﹣b+c＜0，∴（a+c）2﹣b2＝（a+c+b）（a+c﹣b）＜0，故（4）正确；故选：C．6．解：∵抛物线与x轴只有一个交点，∴a≠0且Δ＝16a2﹣4a×（﹣8）＝0，∴a＝﹣2，∴抛物线解析式为y＝﹣2x2﹣8x﹣8，∵抛物线的对称轴为直线x＝﹣＝﹣2，而AB平行x轴，AB＝4，∴A点的横坐标为﹣4，B点的横坐标为0，当x＝0时，y＝﹣8，∴n的值为﹣8．故选：A．7．解：∵二次函数y＝ax2+bx+c的图象经过（﹣3，0）与（1，0）两点，∴函数y＝ax2+bx+c的对称轴是直线x＝﹣1，又∵关于x的方程ax2+bx+c+m＝0（m＞0）有两个根，其中一个根是3．∴二次函数y＝ax2+bx+c的图象与直线y＝﹣m的一个交点的横坐标为3，∵对称轴是直线x＝﹣1，∴二次函数y＝ax2+bx+c的图象与直线y＝﹣m的另一个交点的横坐标为﹣5，∴关于x的方程ax2+bx+c+m＝0（m＞0）的另一个根是﹣5，故选：A．8．解：①由图象知小球在空中达到的最大高度是40m；故①错误；②小球抛出3秒后，速度越来越快；故②正确；③小球抛出3秒时达到最高点即速度为0；故③正确；④设函数解析式为：h＝a（t﹣3）2+40，把O（0，0）代入得0＝a（0﹣3）2+40，解得，∴函数解析式为，把h＝30代入解析式得，，解得：t＝4.5或t＝1.5，∴小球的高度h＝30m时，t＝1.5s或4.5s，故④错误；故选D．二．填空题（共8小题，满分32分）9．解：∵抛物线y＝x2+bx+c的开口向上，对称轴是直线x＝2，∴当x＝2时取最小值，又|1﹣2|＜|4﹣2|，∴y1＜y4，故答案为：y2＜y1＜y4．10．解：（1）抛物线的对称轴为：直线x＝﹣＝1，故答案为：直线x＝1；（2）∵抛物线y＝ax2﹣2ax﹣1＝a（x﹣1）2﹣a﹣1（a＜0），∴该函数图象的开口向下，对称轴是直线x＝1，当x＝1时，取得最大值﹣a﹣1，∵当﹣2≤x≤2时，y的最大值是1，∴x＝1时，y＝﹣a﹣1＝1，得a＝﹣2，∴y＝﹣2（x﹣1）2+1，∵﹣2≤x≤2，∴x＝﹣2时，取得最小值，此时y＝﹣2（﹣2﹣1）2+1＝﹣17，故答案为：﹣17．11．解：∵二次函数y＝ax2﹣2ax+c（a≠0）的图象与x轴的一个交点为（﹣1，0），∴该函数的对称轴是直线x＝﹣＝1，∴该函数图象与x轴的另一个交点坐标为（3，0），∴关于x的一元二次方程ax2﹣2ax+c＝0的两实数根是x1＝﹣1，x2＝3，∴两根之积为﹣3，故答案为：﹣3．12．解：如图，当y＝0时，﹣x2+4x+5＝0，解得x1＝﹣1，x2＝5，则A（﹣1，0），B（5，0），将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的解析式为y＝（x+1）（x﹣5），即y＝x2﹣4x﹣5（﹣1≤x≤5），当直线y＝﹣x+b经过点A（﹣1，0）时，1+b＝0，解得b＝﹣1；当直线y＝﹣x+b与抛物线y＝x2﹣4x﹣5（﹣1≤x≤5）有唯一公共点时，方程x2﹣4x﹣5＝﹣x+b有相等的实数解，解得b＝﹣，所以当直线y＝﹣x+b与新图象有4个交点时，b的取值范围为﹣＜b＜﹣1．故答案为：﹣＜b＜﹣1．13．解：将抛物线y＝﹣（x﹣3）2﹣1向右平移5个单位，再向上平移2个单位，所得的抛物线的解析式为y＝﹣（x﹣3﹣5）2﹣1+2，即y＝﹣（x﹣8）2+1，故答案为：y＝﹣（x﹣8）2+1．14．解：∵抛物线y＝ax2与直线y＝bx+c的两个交点坐标分别为A（﹣3，9），B（1，1），∴方程ax2＝bx+c的解为x1＝﹣3，x2＝1，∴ax2﹣bx﹣c＝0的解是x1＝﹣3，x2＝1，故答案为：x1＝﹣3，x2＝1．15．解：（1）将点C（0，3）、B（1，0）、（2，﹣5）代入抛物线y＝ax2+bx+tc中，得：a+b+c＝0，c＝3，4a+2b+c＝﹣5；解得：a＝﹣1，b＝﹣2，c＝3，∴抛物线的解析式为y＝﹣x2﹣2x+3．（2）抛物线向下平移n个单位后，E为（﹣1，4﹣n），C为（0，3﹣n），∴EC＝，∵CO∥EH，∴当CO＝CE＝时，∠CEO＝∠COE＝∠OCH，∴3﹣n＝或n﹣3＝，即n＝3﹣或3+．16．解：当10≤x≤20时，设y＝kx+b，把（10，20），（20，10）代入可得：，解得，∴每天的销售量y（个）与销售价格x（元/个）的函数解析式为y＝﹣x+30，设该食品零售店每天销售这款冷饮产品的利润为w元，w＝（x﹣8）y＝（x﹣8）（﹣x+30）＝﹣x2+38x﹣240＝﹣（x﹣19）2+121，∵﹣1＜0，∴当x＝19时，w有最大值为121，故答案为：121．三．解答题（共6小题，满分56分）17．解：（1）将（2，4）代入y＝x2+mx+m2﹣3得4＝4+2m+m2﹣3，解得m1＝1，m2＝﹣3，又∵m＞0，∴m＝1．（2）∵m＝1，∴y＝x2+x﹣2，∵Δ＝b2﹣4ac＝12+8＝9＞0，∴二次函数图象与x轴有2个交点．18．解：∵初速度为10m/s，g取10m/s2，∴h＝10t﹣×10t2＝10t﹣5t2，（1）当h＝0时，10t﹣5t2＝0，解得t＝0或t＝2，∴球抛出后经2秒回到起点；（2）当h＝1.8时，10t﹣5t2＝1.8，解得t＝0.2或t＝1.8，∴0.2秒或1.8秒后球离起点的高度达到1.8m；（3）球离起点的高度不能达到6m，理由如下：若h＝6，则10t﹣5t2＝6，整理得5t2﹣10t+6＝0，Δ＝（﹣10）2﹣4×5×6＝﹣20＜0，∴原方程无实数解，∴球离起点的高度不能达到6m．19．解：（1）∵函数图象过点（1，2），∴将点代入y＝ax2+（a﹣1）x﹣1，解得a＝2，∴二次函数的解析式为y＝2x2+x﹣1，∴x＝﹣＝﹣，∴y＝2×﹣﹣1＝﹣，∴该二次函数的顶点坐标为（﹣，﹣）；（2）函数y＝ax2+（a﹣1）x﹣1的对称轴是直线x＝﹣，∵（x1，y1），（x2，y2）为此二次函数图象上的两个不同点，且x1+x2＝﹣2，则y1＝y2，∴﹣＝＝＝﹣1，∴a＝﹣1，∴y＝﹣x2﹣2x﹣1＝﹣（x+1）2≤0，∴当x＝﹣1时，函数有最大值0；（3）∵y＝ax2+（a﹣1）x﹣1，∴由顶点公式得：x＝﹣＝﹣+，y＝＝﹣，∵a＜0且a≠﹣1，∴x＜0，y＞0，∴该二次函数图象的顶点在第二象限．20．解：（1）设一次函数的关系式为y＝kx+b，由题图可知，函数图象过点（25，50）和点（35，30）．把这两点的坐标代入一次函数y＝kx+b，得，解得，∴一次函数的关系式为y＝﹣2x+100；（2）根据题意，设当天玩具的销售单价是x元，由题意得，（x﹣10）×（﹣2x+100）＝600，解得：x1＝40，x2＝20，∴当天玩具的销售单价是40元或20元；（3）根据题意，则w＝（x﹣10）×（﹣2x+100），整理得：w＝﹣2（x﹣30）2+800；∵﹣2＜0，∴当x＝30时，w有最大值，最大值为800；∴当玩具的销售单价定为30元时，日销售利润最大；最大利润是800元．21．解：（1）设直线AB的解析式为y＝px+q，把A（4，0），B（0，2）代入得，，解得，∴直线AB的解析式为y＝﹣x+2；把A（4，0），B（0，2）代入y＝﹣x2+bx+c得，，解得；∴抛物线解析式为y＝﹣x2+x+2；（2）∵MN⊥x轴，M（m，0），点D在直线AB上，点N在抛物线上，∴N（m，﹣m2+m+2），D（m，﹣m+2），∴DN＝﹣m2+2m，DM＝﹣m+2，∵DN＝3DM，∴﹣m2+2m＝3（﹣m+2），解得m＝3或m＝4（舍），∴N（3，2）．（3）如图，作点B关于x轴的对称点B′，∴OB＝OB′，B′（0，﹣2），∵∠AOB＝∠AOB′＝90°，OA＝OA，∴△AOB≌△AOB′，∴∠OAB′＝∠OAB，∴∠BAB′＝2∠BAC，∵A（4，0），B′（0，﹣2），∴直线AB′的解析式为：y＝x﹣2，过点B作BP∥AB′交抛物线于点P，则∠ABP＝∠BAB′＝2∠BAC，即点P即为所求，∴直线BP的解析式为：y＝x+2，令x+2＝﹣x2+x+2，解得x＝2或x＝0（舍），∴P（2，3）．22．解：（1）将点A（3，﹣2），点C（0，﹣5）代入y＝x2+bx+c，∴，解得，∴y＝x2﹣2x﹣5，∴M（1，﹣6）；（2）平移后的函数解析式为y＝（x﹣1）2﹣6+m，∴平移后的顶点坐标为（1，m﹣6），∴抛物线的顶点在x＝1的直线上，设直线CA的解析式为y＝kx+b，∴，∴，∴y＝x﹣5，当x＝1时，y＝﹣4，∴﹣4＜m﹣6＜﹣2，解得2＜m＜4；（3）存在一点Q，使以B、P、E、Q为顶点的四边形是平行四边形，理由如下：当y＝﹣2时，x2﹣2x﹣5＝﹣2，解得x＝﹣1或x＝3，∴B（﹣1，﹣2），∴AB＝4，∵BE：EA＝3：1，∴AE＝1，∴E（2，﹣2），设P（t，t﹣5），Q（x，x2﹣2x﹣5），①当BE为平行四边形的对角线时，，解得或，∴Q（，）或（，）；②当BP为平行四边形的对角线时，，解得或，∴Q（，）或（，）；③当BQ为平行四边形的对角线时，，此时无解；综上所述：Q点坐标为（，）或（，）或（，）或（，）．九年级数学上册二次函数的图象与性质练习题（附答案）一．选择题1．如果在二次函数的表达式y＝ax2+bx+c中，a＞0，b＜0，c＜0，那么这个二次函数的图象可能是（）A．B．C．D．2．已知y＝（m+2）x|m|+2是关于x的二次函数，那么m的值为（）A．﹣2B．2C．±2D．03．已知A（，y1），B（2，y2），C（﹣，y3）是二次函数y＝3（x﹣1）2+k图象上三点，则y1、y2、y3的大小关系为（）A．y1＞y2＞y3B．y2＞y1＞y3C．y3＞y2＞y1D．y2＞y3＞y1 4．二次函数的部分图象如图所示，对称轴是直线x＝﹣1，则这个二次函数的表达式为（）A．y＝﹣x2+2x+3B．y＝x2+2x+3C．y＝﹣x2+2x﹣3D．y＝﹣x2﹣2x+35．在同一平面直角坐标系中，一次函数y＝ax+b和二次函数y＝ax2+bx+c的图象可能为（）A．B．C．D．6．关于抛物线y＝﹣x2+2x﹣3的判断，下列说法正确的是（）A．抛物线的开口方向向上B．抛物线的对称轴是直线x＝﹣1C．抛物线对称轴左侧部分是下降的D．抛物线顶点到x轴的距离是27．已知二次函数y＝x2﹣4x+5（0≤x≤3），则它的最大值是（）A．1B．2C．3D．58．如图为二次函数y＝ax2+bx+c的图象，给出下列说法：①ab＜0；②方程ax2+bx+c＝0的根为x1＝﹣1，x2＝3；③a+b+c＞0；④当x＜1时，y随x值的增大而增大；⑤当y＞0时，x＜﹣1或x＞3．其中，正确的说法有（）A．①②④B．①②⑤C．①③⑤D．②④⑤9．已知函数y＝2（x+1）2+1，则（）A．当x＜1 时，y随x的增大而增大B．当x＜1 时，y随x的增大而减小C．当x＜﹣1 时，y随x的增大而增大D．当x＜﹣1 时，y随x的增大而减小10．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论中不正确的有（）个．①abc＞0；②2a+b＝0；③9a+3b+c＜0；④4ac﹣b2＜0；⑤a+b≥m（am+b）（m为任意实数）．A．3B．2C．1D．0二．填空题11．已知四个二次函数的图象如图所示，那么a1，a2，a3，a4的大小关系是．（请用“＞”连接排序）12．抛物线y＝3x2+6x+11的顶点坐标为．13．二次函数y＝3（x﹣1）2+5的最小值为．14．已知二次函数y＝2x2+bx+4顶点在x轴上，则b＝．15．二次函数y＝x2﹣2x+1在2≤x≤5范围内的最小值为．16．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：①2a+b＝0；②a+c＞b；③抛物线与x轴的另一个交点为（3，0）；④abc＞0．其中正确的结论是（填写序号）．三．解答题17．已知二次函数的顶点坐标为A（1，﹣4），且经过点B（3，0）．（1）求该二次函数的解析式；（2）判断点C（2，﹣3）是否在该函数图象上，并说明理由．18．如图，已知直线l过点A（4，0），B（0，4）两点，它与二次函数y＝ax2的图象在第一象限内交于点P，若S△AOP＝4，试求二次函数的表达式．19．如图，直线L1：y＝bx+c与抛物线L2：y＝ax2的两个交点坐标分别为A（m，4），B （1，1）．（1）求m的值；（2）过动点P（n，0）且垂直于x轴的直线与L1，L2的交点分别为C，D，当点C 位于点D上方时，请直接写出n的取值范围．20．已知二次函数y＝a（x+a）（x+a﹣1）．（1）当a＝2时，求该二次函数图象的对称轴．（2）当a＜0时，判断该二次函数图象的顶点所在的象限，并说明理由．（3）当0＜x＜3时，y随着x增大而增大，求a的取值范围．21．已知二次函数y＝ax2（a≠0）与一次函数y＝kx﹣2的图象相交于A、B两点，如图所示，其中A（﹣1，﹣1），求△OAB的面积．22．抛物线y＝﹣x2+bx+c经过点A（3，0）和点B（0，3），且这个抛物线的对称轴为直线l，顶点为C．（1）求抛物线的解析式；（2）连接AB、AC、BC，求△ABC的面积．23．如图，在平面直角坐标系中，直线AB与抛物线y＝﹣x2+bx+c交于A（﹣1，0）和B（2，3）两点，抛物线与y轴交于点C．（1）求一次函数和二次函数的解析式；（2）求△ABC的面积．参考答案一．选择题1．解：∵a＞0，b＜0，c＜0，∴﹣＞0，∴抛物线的图象开口向上，对称轴在y轴的右边，交y轴于负半轴，故选：C．2．解：∵y＝（m+2）x|m|+2是y关于x的二次函数，∴|m|＝2且m+2≠0．解得m＝2．故选：B．3．解：∵二次函数y＝3（x﹣1）2+k图象的对称轴为直线x＝1，而A（，y1）到直线x＝1的距离最近，C（﹣，y3）到直线x＝1的距离最远，∴y3＞y2＞y1．故选：C．4．解：由图象知抛物线的对称轴为直线x＝﹣1，设抛物线解析式为y＝a（x+1）2+k，将（﹣3，0）、（0，3）代入，得：，解得：，则抛物线解析式为y＝﹣（x+1）2+4＝﹣x2﹣2x+3，故选：D．5．解：A、由抛物线可知，a＜0，x＝﹣＜0，得b＜0，由直线可知，a＜0，b＜0，故本选项正确；B、由抛物线可知，a＞0，由直线可知，a＜0，故本选项错误；C、由抛物线可知，a＞0，x＝﹣＞0，得b＜0，由直线可知，a＞0，b＞0，故本选项错误；D、由抛物线可知，a＞0，由直线可知，a＜0，故本选项错误．故选：A．6．解：∵y＝﹣x2+2x﹣3＝﹣（x﹣1）2﹣2，∴抛物线开口向下，对称轴为x＝1，顶点坐标为（1，﹣2），在对称轴左侧，y随x的增大而增大，∴A、B、C不正确；∵抛物线顶点到x轴的距离是|﹣2|＝2，∴D正确，故选：D．7．解：y＝x2﹣4x+5＝（x﹣2）2+1，由于0≤x≤3，所以当x＝2时，y有最小值1，当x＝0时，y有最大值5．故选：D．8．解：根据图象可知：①对称轴﹣＞0，故ab＜0，正确；②方程ax2+bx+c＝0的根为x1＝﹣1，x2＝3，正确；③x＝1时，y＝a+b+c＜0，错误；④当x＜1时，y随x值的增大而减小，错误；⑤当y＞0时，x＜﹣1或x＞3，正确．正确的有①②⑤．故选：B．9．解：∵y＝2（x+1）2+1，∴当x＞﹣1时，y随x的增大而增大，故选项A错误，当x＜﹣1时，y随x的增大而减小，故选项B错误、选项C错误、选项D正确；故选：D．10．解：∵抛物线开口向下，∴a＜0，∵抛物线的对称轴为直线x＝﹣＝1，∴b＝﹣2a＞0，∵抛物线与y轴的交点坐标在x轴上方，∴c＞0，∴abc＜0，所以①错误；∵b＝﹣2a，∴2a+b＝0，所以②正确；∵x＝3时，y＜0，∴9a+3b+c＜0，所以③正确．∵抛物线与x轴有2个交点，∴Δ＝b2﹣4ac＞0，即4ac﹣b2＜0，所以④正确；∵抛物线的对称轴为直线x＝1，∴函数的最大值为a+b+c，∴a+b+c≥am2+bm+c（m为任意实数），即a+b≥m（am+b），所以⑤正确．故选：C．二．填空题11．解：如图所示：①y＝a1x2的开口小于②y＝a2x2的开口，则a1＞a2＞0，③y＝a3x2的开口大于④y＝a4x2的开口，开口向下，则a4＜a3＜0，故a1＞a2＞a3＞a4．故答案为：a1＞a2＞a3＞a412．解：∵y＝3x2+6x+11＝3（x+1）2+8，∴抛物线y＝3x2+6x+11的顶点坐标为（﹣1，8），故答案为（﹣1，8）．13．解：由于二次函数y＝3（x﹣1）2+5中，a＝3＞0，所以当x＝1时，函数取得最小值为5，故答案为5．14．解：∵二次函数y＝2x2+bx+4顶点在x轴上，∴＝0，解得b＝，故答案为：±4．15．解：∵二次函数y＝x2﹣2x+1＝（x﹣1）2，∴当x＞1时，y随x的增大而增大，∴在2≤x≤5范围内，当x＝2时，y取得最小值，此时y＝（2﹣1）2＝1，故答案为：1．16．解：∵抛物线的对称轴为直线x＝﹣＝1，∴2a+b＝0，所以①正确；∵x＝﹣1时，y＜0，∴a﹣b+c＜0，即a+c＜b，所以②错误；∵抛物线与x轴的一个交点为（﹣2，0）而抛物线的对称轴为直线x＝1，∴抛物线与x轴的另一个交点为（4，0），所以③错误；∵抛物线开口向上，∴a＞0，∴b＝﹣2a＜0，∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＞0，所以④正确．故答案为①④．三．解答题17．解：（1）设二次函数的解析式是y＝a（x﹣h）2+k，∵二次函数的顶点坐标为A（1，﹣4），∴y＝a（x﹣1）2﹣4，∵经过点B（3，0），∴代入得：0＝a（3﹣1）2﹣4，解得：a＝1，∴y＝（x﹣1）2﹣4，即二次函数的解析式为y＝x2﹣2x﹣3；（2）点C（2，﹣3）在该函数图象上，理由是：把C（2，﹣3）代入y＝x2﹣2x﹣3得：左边＝﹣3，右边＝4﹣4﹣3＝﹣3，即左边＝右边，所以点C在该函数的图象上．18．解：设直线l的解析式为y＝kx+b，把A（4，0），B（0，4）分别代入得，解得，∴直线l的关系式为y＝﹣x+4，设P（t，﹣t+4），∵S△AOP＝4，∴×4×（﹣t+4）＝4，解得t＝2，∴P（2，2），把P（2，2）代入y＝ax2得4a＝2，解得a＝，∴二次函数的表达式为y＝x2．19．解：（1）把B（1，1）代入y＝ax2得：a＝1，∴抛物线解析式为y＝x2．把A（m，4）代入y＝x2得：4＝m2，∴m＝±2．∵点A在二象限，∴m＝﹣2．（2）观察函数图象可知：当﹣2＜x＜1时，直线在抛物线的上方，∴n的取值范围为：﹣2＜n＜1．20．解：（1）当a＝2时，y＝2（x+2）（x+1），∴二次函数的对称轴为x＝．（2）由题知二次函数与x轴的交点坐标为（﹣a，0），（1﹣a，0）；∵a＜0，∴二次函数的开口方向向下；又﹣a＞0，1﹣a＞0，所以对称轴所在直线为x＝＝＞0，当x＝时，y＝﹣＞0，所以顶点坐标（，﹣）在第一象限．（3）由（2）知，二次函数的对称轴为直线x＝，∵当0＜x＜3时，y随着x增大而增大，∴当a＞0时，≤0，解得a≥；当a＜0，≥3，解得a≤﹣．∴a的取值范围为a≥或a≤﹣．21．解：∵一次函数y＝kx﹣2的图象相过点A（﹣1，﹣1），∴﹣1＝﹣k﹣2，解得k＝﹣1，∴一次函数表达式为y＝﹣x﹣2，∴令x＝0，得y＝﹣2，∴G（0，﹣2），∵y＝ax2过点A（﹣1，﹣1），∴﹣1＝a×1，解得a＝﹣1，∴二次函数表达式为y＝﹣x2，由一次函数与二次函数联立可得，解得，，∴S△OAB＝OG•|A的横坐标|+OG•点B的横坐标＝×2×1+×2×2＝1+2＝3．22．解：（1）∵抛物线经过A、B（0，3）∴由上两式解得∴抛物线的解析式为：；（2）由（1）抛物线对称轴为直线x＝把x＝代入，得y＝4则点C坐标为（，4）设线段AB所在直线为：y＝kx+b，则有，解得∴AB解析式为：∵线段AB所在直线经过点A、B（0，3）抛物线的对称轴l于直线AB交于点D∴设点D的坐标为D将点D代入，解得m＝2∴点D坐标为，∴CD＝CE﹣DE＝2过点B 作BF ⊥l 于点F ∴BF ＝OE ＝∵BF +AE ＝OE +AE ＝OA ＝∴S △ABC ＝S △BCD +S △ACD ＝CD •BF +CD •AE ∴S △ABC ＝CD （BF +AE ）＝×2×＝23．解：（1）∵抛物线y ＝﹣x 2+bx +c 交于A （﹣1，0）和B （2，3）两点 ∴，解得：， ∴抛物线解析式为y ＝﹣x 2+2x +3，设直线AB 的解析式为y ＝mx +n （m ≠0），则，解得，∴直线AB 的解析式为y ＝x +1； （2）令x ＝0，则y ＝﹣x 2+2x +3＝3， ∴C （0，3），则OC ＝3，BC ＝2，BC ∥x 轴， ∴S △ABC ＝×BC ×OC ＝＝3．九年级数学二次函数专题精练含答案一、单选题1．关于二次函数22(4)6y x =-+的最大值或最小值，下列说法正确的是（ ） A ．有最大值4B ．有最小值4C ．有最大值6D ．有最小值62．已知抛物线24y x x c =-++经过点(4,3)，那么下列各点中，该抛物线必经过的点是（ ） A ．(0,2)B ．(0,3)C ．(0,4)D ．(0,5)3．在平面直角坐标系中，已知抛物线245y x x =-+，将该抛物线沿y 轴翻折所得的抛物线的表达式为（ ） A ．245y x x =--+B ．245y x x =++C ．245y x x =-+-D ．245y x x =---4．正方形的边长为4，若边长增加x ，那么面积增加y ，则y 关于x 的函数表达式为( ) A ．216y x =+B ．2(4)y x =+C ．28y x x =+D ．2164y x =-5．把抛物线22y x =向右平移2个单位，然后向下平移1个单位，则平移后得到的抛物线解析式是（ ） A ．22(2)1y x =-+- B ．22(2)1y x =--+ C ．22(2)1y x =++D ．22(2)1y x =--6．如图，二次函数2y ax bx c =++的图象关于直线1x =对称，与x 轴交于1(,0)A x ，2(,0)B x 两点，若121x -<<-，则下列四个结论：①234x <<，②320a b +>，③24b a c ac >++，④a c b >>．正确结论的个数为（ ） A ．1个B ．2个C ．3个D ．4个7．对于抛物线23(1)2y x =-+-，下列说法正确的是（ ） A ．抛物线开口向上B ．当1x >-时，y 随x 增大而减小C ．函数最小值为﹣2D ．顶点坐标为（1，﹣2）8．关于二次函数()215y x =-+，下列说法正确的是（ ）A ．函数图象的开口向下B ．函数图象的顶点坐标是()1,5-C ．该函数有最大值，是大值是5D ．当1x >时，y 随x 的增大而增大9．已知A (−3，−2) ，B (1，−2)，抛物线y =ax 2+bx +c (a >0)顶点在线段AB 上运动，形状保持不变，与x 轴交于C ，D 两点（C 在D 的右侧），下列结论： ①c ≥−2 ；②当x >0时，一定有y 随x 的增大而增大；③若点D 横坐标的最小值为−5，点C 横坐标的最大值为3； ④当四边形ABCD 为平行四边形时，a =12．其中正确的是（ ） A ．①③B ．②③C ．①④D ．①③④10．已知二次函数2243y mx m x =--（m 为常数，0m ≠），点(),p p P x y 是该函数图象上一点，当04p x ≤≤时，3p y ≤-，则m 的取值范围是（ ） A ．m 1≥或0m < B ．m 1≥ C ．1m ≤-或0m >D ．1m ≤-11．已知函数()211y ax a x =-++，则下列说法不正确的个数是（ ）①若该函数图像与x 轴只有一个交点，则1a =②方程()2110ax a x -++=至少有一个整数根③若11x a<<，则()211y ax a x =-++的函数值都是负数 ④不存在实数a ，使得()2110ax a x -++≤对任意实数x 都成立A ．0B ．1C ．2D ．312．如图，在正方形ABCD 中，4AB =，点P 从点A 出发沿路径A B C →→向终点C 运动，连接DP ，作DP 的垂直平分线MN 与正方形ABCD 的边交于M ，N 两点，设点P 的运动路程为x ，PMN 的面积为y ，则下列图象能大致反映y 与x 函数关系的是（ ）A ．B ．C ．D ．二、填空题13．已知点（3，a ）在抛物线y =-2x 2+2x 上，则=a ______．14．如图是二次函数21y ax bx c =++ 和一次函数y 2＝kx +t 的图象，当y 1≥y 2时，x 的取值范围是_____．15．小亮同学在探究一元二次方程2ax bx c 0++=的近似解时，填好了下面的表格：根据以上信息请你确定方程2ax bx c 0++=的一个解的范围是________． 16．已知二次函数223y x x =--+，当12a x 时，函数值y 的最小值为1，则a 的值为_______． 17．已知抛物线2122y x bx =+-与x 轴交于A ，B 两点，与y 轴交于C 点． （1）若(1,0)A -，则b =______． （2）若(1,0)M -，(1,0)N ，抛物线2122y x bx =+-与线段MN 没有交点，则b 的取值范围为______． 三、解答题18．已知抛物线经过点()1,0A -，()5,0B ，()0,5C ，求该抛物线的函数关系式19．如图，抛物线212y x bx c =++与直线132y x =+分别相交于A 、B 两点，其中点A 在y 轴上，且此抛物线与x 轴的一个交点为()3,0C -．（1）求抛物线的解析式（2）在抛物线对称轴l 上找一点M ，使MBC ∆的周长最小，请求出这个周长的最小值．20．如图，一次函数y =A 、B ，二次函数2y bx c ++图象过A 、B 两点．（1）求二次函数解析式；（2）点B 关于抛物线对称轴的对称点为点C ，点P 是对称轴上一动点，在抛物线上是否存在点Q ，使得以B 、C 、P 、Q 为顶点的四边形是菱形？若存在，求出Q 点坐标；若不存在，请说明理由．21．如图，二次函数y ＝ax 2+bx +c 的图象与x 轴交于点A (﹣2，0)和点B (8，0)，与y 轴交于点C (0，﹣8)，连接AC ，D 是抛物线对称轴上一动点，连接AD ，CD ，得到△ACD ．（1）求该抛物线的函数解析式．（2）△ACD 周长能否取得最小值，如果能，请求出D 点的坐标；如果不能，请说明理由．（3）在（2）的条件下，在抛物线上是否存在点E ，使得△ACE 与△ACD 面积相等，如果存在，请求出点的坐标；如果不存在，请说明理由．参考答案1--10DBCCD BBDDA 11--12CA13．-1214．﹣1≤x ≤215．3.24x 3.25<<16．1-17． 32- 3322b -<< 18．解：△抛物线经过点()1,0A -，()5,0B ，()0,5C ，△设抛物线的表达式为()()15y a x x =+-，将点()0,5C 代入得：55a =-，解得：1a =-，△()()21545y x x x x =-+-=-++．△该抛物线的函数关系式为245y x x =-++．19．.解：（1）抛物线212y x bx c =++与直线132y x =+交于y 轴上一点A ， 令0,x = 则3,y =∴ 点()0,3A把()0,3A ，()3,0C -代入212y x bx c =++得： 39302c b c =⎧⎪⎨-+=⎪⎩， 解得：523b c ⎧=⎪⎨⎪=⎩， ∴抛物线的解析式是215322y x x =++； （2）将直线132y x =+与二次函数215322y x x =++联立得方程组： 213215322y x y x x ⎧=+⎪⎪⎨⎪=++⎪⎩ 215133,222x x x ∴++=+ 240,x x ∴-=解得：0x =或4x =-，04,,31x x y y ==-⎧⎧∴⎨⎨==⎩⎩()0,3A ，()4,1B ∴-BC ∴==如图，要使MBC △的周长最小，则MB MC +最小，设二次函数215322y x x=++与x 轴的另一交点为D ， 抛物线的对称轴为：552,1222x =-=-⨯ ()3,0C -∴ 点()2,0D -，连接,BD 交对称轴于,MMD MC ∴=，此时，MB MC MB MD BD +=+=最小，此时：BD =MBC ∴20．解：（1）对于y =x =0时，y =当y =0时，03x -=，妥得，x =3 △A （3，0），B （0，把A （3，0），B （0，2y bx c++得：+=0b c c ⎧⎪⎨=⎪⎩解得，b c ⎧=⎪⎨⎪=⎩△抛物线的解析式为：2y =（2）抛物线的对称轴为直线12b x a =-== 故设P （1，p ），Q （m ，n ）①当BC 为菱形对角线时，如图，△B ，C 关于对称没对称，且对称轴与x 轴垂直，△△BC 与对称轴垂直，且BC //x 轴△在菱形BQCP 中，BC △PQ△PQ △x 轴△点P 在x =1上，△点Q 也在x =1上，当x =1时，211y△Q （1，）； ②当BC 为菱形一边时，若点Q 在点P 右侧时，如图，△BC //PQ ，且BC =PQ△BC //x 轴，△令y =2y 解得，120,2x x ==△(2,C△PQ=BC=22=△PB=BC=2△迠P在x轴上，△P(1,0)△Q(3，0)；若点Q在点P的左侧，如图，同理可得，Q（-1，0）综上所述，Q点坐标为（1，）或(3，0)或（-1，0）21．解：（1）由题意可得：0=4206488a b ca b cc-+⎧⎪=++⎨⎪=-⎩，解得：1238abc⎧=⎪⎪=-⎨⎪=-⎪⎩，△抛物线的解析式为：y＝12x2﹣3x﹣8；（2）△ACD周长能取得最小值，△点A（﹣2，0），点B（8，0），△对称轴为直线x＝3，△△ACD周长＝AD+AC+CD，AC是定值，△当AD+CD取最小值时，△ACD周长能取得最小值，△点A，点B关于对称轴直线x＝3对称，△连接BC交对称轴直线x＝3于点D，此时AD+CD有最小值，设直线BC 解析式为：y ＝kx ﹣8，△0＝8k ﹣8，△k ＝1，△直线BC 解析式为：y ＝x ﹣8，当x ＝3，y ＝﹣5，△点D （3，﹣5）；（3）存在，△点A （﹣2，0），点C （0，﹣8），△直线AC 解析式为y ＝﹣4x ﹣8，如图，△△ACE 与△ACD 面积相等，△DE △AC ，△设DE 解析式为：y ＝﹣4x +n ，△﹣5＝﹣4×3+n ，△n ＝7，△DE 解析式为：y ＝﹣4x +7， 联立方程组可得：2471382y x y x x =-+⎧⎪⎨=--⎪⎩，解得：12111x y ⎧=⎪⎨=-⎪⎩，22111x y ⎧=⎪⎨=⎪⎩， △点E1，﹣1，）．九年级上册数学二次函数同步练习一、单选题1．下列函数中，是二次函数的是（ ）A ．y ＝（2x ﹣1）2B ．y ＝（x +1）2﹣x 2C ．y ＝ax 2D ．y ＝2x +3 2．若抛物线258(3)23mm y m x x -+=-+-是关于x 的二次函数，那么m 的值是（ ） A ．3 B ．2-C ．2D ．2或3 3．若抛物线y =x 2-x -2经过点A （3，a ），则a 的值是（ ）A ．2B ．4C ．6D ．84．已知二次函数2135y x x =-+，则其二次项系数a ，一次项系数b ，常数项c 分别是（ ）A ．1,3,5a b c ==-=B ．1,3,5a b c ===C ．5,3,1a b c ===D ．5,3,1a b c ==-= 5．如果函数2(2)25y a x x =-+-是二次函数，则a 的取值范围是（ ）A ．2a ≠B ．a≥0C ．a=2D ．a>0 6．下列函数中①31y x ；②243y x x =-；③1y x =；④225=-+y x ，是二次函数的有（）A ．①②B ．②④C ．②③D ．①④ 7．若抛物线2y x bx c =-++经过点()2,3-，则247c b --的值是（ ）A ．6B ．7C ．8D ．208．函数y=ax2+bx+c(a ，b ，c 是常数)是二次函数的条件是( )A ．a≠0，b≠0，c≠0B ．a<0，b≠0，c≠0C ．a>0，b≠0，c≠0D ．a≠0 二、填空题9．若()2321mm y m x --=+是二次函数，则m 的值为______． 10．若22a y x -=是二次函数，则=a ________．11．在二次函数21y x =-+中，二次项系数、一次项系数、常数项的和为_____． 12．下列函数一定是二次函数的是__________．①2y ax bx c =++；②3y x=-；③2431y x x =-+；④2(1)y m x bx c =-++；⑤y =(x -3)2-x 213．当常数m ≠______时，函数y =（m 2﹣2m ﹣8）x 2+（m +2）x +2是二次函数；当常数m =___时，这个函数是一次函数．14．已知函数2135m y x -=-① 当m ＝ _________时，y 是关于x 的一次函数；② 当m ＝_________时，y 是关于x 的二次函数 ．15．二次函数()22339y m x x m =+++-的图象经过原点，则m =__________．16．已知二次函数2y x bx 3=-++，当x 2=时，y 3=．则这个二次函数的表达式是________．三、解答题17．下列函数中（x ，t 是自变量），哪些是二次函数？22322113,25,22,1522y x y x x y x s t t =-+=-+=+=++．18．已知函数y =（m 2-2）x 2+（m ）x +8．（1）若这个函数是一次函数，求m 的值；（2）若这个函数是二次函数，求m 的取值范围.19．若函数y=（a -1）x b+1+x 2+1是二次函数，试讨论a 、b 的取值范围.20．篱笆墙长30m ，靠墙围成一个矩形花坛，写出花坛面积y(m 2)与长x 之间的函数关系式，并指出自变量的取值范围.参考答案：1．A2．C3．B4．D5．A6．B7．B8．D9．410．2±11．012．③13． 4，-2 414． 13215．316．2y x 2x 3=-++17．2132y x =-+和215s t t =++是二次函数 18．（1）m =（2）m ≠m ≠19．①a≠0；②b=0或-1，a 取全体实数③当a=1，b 为全体实数时，y=x 2+1是二次函数 20．y= 21152x x -+, x 的取值范围为0<x<30.九年级数学上册二次函数单元综合测试卷一．选择题（共10小题）1．下列各式中，是y 关于x 的二次函数的是（ ）A ．y ＝4xB ．y ＝3x ﹣5C ．y ＝D ．y ＝2x 2+12．已知：a ＞b ＞c ，且a +b +c ＝0，则二次函数y ＝ax 2+bx +c 的图象可能是下列图象中的（ ）A．B．C．D．3．二次函数y＝（x﹣2）（x﹣4）+6的顶点坐标是（）A．（2，6）B．（4，6）C．（3，﹣5）D．（3，5）4．将二次函数y＝x2+2x﹣1转化为y＝a（x﹣h）2+k的形式，结果为（）A．y＝（x﹣1）2B．y＝（x+1）2C．y＝（x+1）2﹣1D．y＝（x+1）2﹣2 5．已知0≤x≤，则函数y＝﹣2x2+8x﹣6的最大值是（）A．﹣10.5B．2C．﹣2.5D．﹣66．顶点坐标为（3，1），形状与函数y＝的图象相同且开口方向相反的抛物线的解析式为（）A．y＝+1B．y＝+1C．y＝﹣+1D．y＝﹣+17．已知点A（﹣1，y1），B（1，y2），C（2，y3）都在二次函数y＝（x﹣1）2的图象上，则y1，y2，y3的大小关系正确的是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y2＜y3＜y1D．y3＜y2＜y1 8．抛物线y＝ax2+bx+c纵坐标y的对应值如下表：x…﹣2﹣1012…y…04664…则下列说法中正确的个数是（）①方程ax2+bx+c＝0，有两根为x1＝﹣2，x2＝3；②抛物线与y轴的交点为（0，6）；③抛物线的对称轴是直线x＝1；④抛物线开口向上．A．1B．2C．3D．49．如图，在正方形ABCD中，AB＝4，AC与BD交于点O，E，F分别为边BC，CD上的点（点E，F不与线段BC，CD的端点重合），BE＝CF，连接OE，OF，EF．关于以下三个结论，下列判断正确的是（）结论Ⅰ：∠BOF始终是90°；结论Ⅱ：△OEF面积的最小值是2；结论Ⅲ：四边形OECF的面积始终是8．A．结论Ⅰ和Ⅱ都对，结论Ⅲ错B．结论Ⅰ和Ⅱ都对，结论Ⅱ错C．结论Ⅱ和Ⅲ都对，结论Ⅰ错D．三个结论都对10．使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m3）与旋钮的旋转角度x（单位：度）（0＜x≤90）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（）A．37.5°B．40°C．42.5°D．45°二．填空题（共6小题）11．函数是二次函数，则m的值为．12．已知抛物线y＝x2﹣4x+c．与直线y＝m相交于A，B两点，若点A的横坐标；x A＝﹣1，。
九年级数学训练试题
九年级数学试卷一、选择题（每小题3分，共15分） 1、下列计算中，正确的是（ ） A=B、2+=C、= D321==-=2、= ） A 、3x ≥ B 、3x > C 、1x >- D 、1x ≥- 3、方程22x x =的解是（ ）A 、2x =B 、0x = C、1x =2x = D 、 10x =,22x = 4、关于x 的一元二次方程230x ax a --=有一个根是6，则另一个根为（ ） A 、2- B 、2 C 、2-或6 D 、2或6- 5、直角体系中，点P （2，-6）与点Q （-2，6）（ ）A 、关于X 轴对称B 、关于Y 轴对称C 、关于原点对称D 、以上都不对 二、填空题（每小题4分，共20分） 6、+= 。
7、1011(1(1-+= 。
8、以2和3为根的一元二次方程是 。
9、26x x ++ =（x + ）210、已知方程220x kx ++=的一个根是2-，则另一个根是 ，k 的值是 。
三、解答题（每小题6分，共30分）11、化简：（1（212、计算：（1） （2）÷13、解方程：(2)20x x x -+-=14、画出△ABC 关于点O 对称的三角形。
OCBA15、n 的值。
四、解答题（每小题7分，共28分） 16、已知1x =+，1y =，求下列各式的值。
（1）222x xy y ++ （2）22x y -17、计算：2001001)(3•+18、根焊接一个如图所示的钢架，大约需要多少米钢材（精确到0.1m ）2m1m4mD C B A19、两个数的差等于4，积等于45，求这两个数。
五、解答题（每小题9分，共27分）20、如图，正方形ABCD 中，E 在BC 上，F 在AB 上，∠FDE=45°，△DEC 按顺时针方向转动一个角度后得到△DGA 。
（1）图中哪一个点是旋转中心？ （2）旋转了多少度？ （3）求∠GDF 的度数。
342545︒1D C EF BGA21、已知关于x 的方程22(1)0x m x m -++=； （1）当m 为何值时，方程有两个实数根？ （2）为m 选取一个合适的整数，使方程有两个不相等的实数根，并求出这两个实数根。
人教新目标英语九年级上册Unit 5单元训练题(含答案)
人教新目标英语九年级上册Unit 5 What are the shirts made of单元训练题(含答案)一、单项选择(每小题1分，共15分)。
( )1.This and this pair of are made of .A. glass；glasses；glassesB. glasses；glass；glassC. glasses；glasses；glassD. glass；glasses；glass( )2.Miss Zhang by all of us because her classes are always and interesting.A. loves；lovelyB. loves；livingC. is loved；livelyD. is loved；lovely( )3.—What is the fork made of?—It's made of ．A．silk B．cotton C．steel D．grass( )4.It's necessary for human beings to breathe O2 and plants can it.A．develop B．produce C．improve D．introduce( )5.—Tom，you look tired this morning. What's wrong?—I was so busy that I didn't go to bed 12 o'clock last night.A. untilB. whenC. thoughD. unless( )6. — Mary, will you invite your friends to your birthday party?— Yes, Mom. I have many invitations to my friends.A. given awayB. taken awayC. worked outD. sent out( )7. China has many special forms of traditional art, sky lanterns, paper cutting and Chinese clay art.A. such asB. instead ofC. except forD. because of( )8.—Do you believe that paper is made wood?—Yes, I do. And you can see that books are made paper.A. from；fromB. from；ofC. of；fromD. of；of( )9.If you want to improve your ________ English,you should practice it .A. everyday；every dayB. every day；everydayC. everyday；everydayD. every day；every day( )10.Each different part of China has forms of traditional art.A. own specialB. special ownC. its own specialD. own special its( )11. I’ll finish the job, _______ how long it takes.A. untilB. unlessC. no matterD. even though( )12. — Our English teacher always keeps his lessons .—That’s why he is so popular among his students.A. happilyB. livelyC. freelyD. friendly( )13. In those days bikes were not used because few people could afford (负担起) to buy one.A. quicklyB. hardlyC. widelyD. nearly( )14. — Where did Jane go just now?—I don’t know. When I asked her, she tried to avoid me.A. answeredB. answeringC. answerD. to answer( )15. — The house prices in the city a lot last year.—That’s true. But houses don’t sell well this year.A. roseB. are risenC. have risenD. would rise二、完形填空(每小题1分，共10分)。
九年级数学综合测试卷五
九年级数学综合测试卷五一、选择题（本大题共10小题，每小题4分，满分40分）1． 12的相反数是( )（A ）12 （B ）12- （C ）2 （D ）–22．下列运算正确．．的是（ ） A ．43x x x =⋅B ．532)(x x =C ．326x x x =÷D ．532x x x =+3．代数式221x x --的最小值是（ ）A ．1B ．－1C ．2D ．2- 4．某种生物孢子的直径是0.00063m ，用科学记数法表示为（ ） A ．36.310-⨯ B ．46.310-⨯ C ．30.6310-⨯ D ．56310-⨯5．若a ＞0，b ＜-2，则点（a ，b+2）应在 ( )（A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限6．已知在一个不透明的口袋中有4个形状、大小、材质完全相同的球，其中1个红色球，3个黄色球．从口袋中随机取出一个球（不放回），接着再取出一个球，则取出的两个都是黄色球的概率为( )（A ）34 （B ）23 （C ）916 （D ）12 7. 如图所示是由几个小立方块所搭成的几何体，那么 这个几何体的主视图是（ ）8. 在Rt △ABC 中，∠C ＝90º，b ＝35c ，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，则sinB 的值是（ ）（A ）35 （B ）45 （C ）34（D ）439．若b ＜0，则一次函数y=ax+b 与二次函数y=ax 2+bx+c 在同一坐标系内的图象可能是( )第10题10.如图所示，已知直线l 的解析式是434-=x y ，并且与x 轴、y 轴分别交于A 、B 两点。
一个半径为1.5A ．B ．C ．D ．第7题的⊙C,圆心C 从点（0，1.5）开始以每秒0.5个单位的速度沿着y 轴向下运动,当⊙C 与直线l 相切时,则该圆运动的时间为（ ▲ ）A.3秒或6秒B.6秒或10秒C.3秒或16秒D.6秒或16秒二、填空题（本大题共4小题，每小题5分，满分20分）11．已知甲、乙两名同学5次数学检测成绩的平均分都是90.5分，老师又算得甲同学5次数学成绩的方差是 2.06，乙同学5次数学成绩的方差是16.8，根据这些数据，说一说你可以从中得出怎样的结论： .12．将382x x -分解因式得：13. 如图所示，△ABC 是⊙O 的内接三角形，AD ⊥BC 于D 点，且AC =5，DC =3，AB =24，则⊙O 的直径等于 。
九年级(下)数学教学目标检测题(五)
九年级（下）数学教学目标检测题（五）《综合训练题》一、选择题：（每小题3分，共30分）1、－（ ）的算术平方根是（ ）。
A 、 B 、 C 、 D 、以上都不对2、将1700000用科学记数法表示，应该是（ ）A 、17×105B 、0.17×107C 、1.7×106D 、1.7×1073、 如图是由若干个小立方体搭成的几何体的三视图，则该几何体中小立方体的个数是（ ）。
A 、4B 、5C 、6D 、74、小明的爸爸想对小明中考前的5次数学考试成绩进行统计分析，判断他的成绩是否稳定，则小明的爸爸需要知道小明这5次考试成绩的（ ）A 、平均数或中位数B 、频数或众数C 、频率或中位数D 、方差或标准差 5、下列四个点：P （-3，2），Q （3，-2），M （6，1），N （ ），其中有三个点在同一反比例函数的图象上，那么不在这个反比例函数图象上的点是（ ）A 、点PB 、点QC 、点MD 、点N6、已知△ABC 的面积为5，则它的一边的长y 与这条边上的高x 之间的函数关系用图象大致可表示为（ ）7、如图，量角器外缘上有A 、B 两点，它们的读数分别是80°、50°，则∠1的度数应为（ ）A 、50°B 、30°C 、25°D 、15°8、已知m 是方程x 2＋2x －1=0的一个根，那么代数式3m 2＋6m －1的值是（ ）A 、3B 、2C 、1D 、09、等腰梯形ABCD 中，AD ∥BC ，AB=DC ，∠B=60°，AE ∥DC 交BC 于E ，若BC=3，且△ABE 的周长为6，则该等腰梯形的周长是（ ）。
A 、12B 、10C 、810、两圆的半径分别是5和6，圆心距x 满足不等式组 ，则两圆的位置关系是（ ）。
A 、相交 B 、外离 C 、外切 D 41-1612121±34,29-11、分解因式：x 3y －9xy 3= 。
九年级英语全册专题训练五任务型阅读作业课件新版人教新目标版
Passage 2(黑龙江牡丹江) 阅读短文，根据其内容完成文后的表格。 What would the world be like if cars could drive themselves? Imagine seeing an empty car passing by on its way to pick up its owner, or a car full of passengers who are reading, listening to music or even sleeping. But none of them are worried about the road ahead. Well, all of this could be the future of driving. There are several companies, including Google, working on driverless cars. So far, no Google selfdriven cars have gotten a traffic ticket (罚单), but some of them have been in accidents when other cars hit them.
Learn to understand his teaching method. Sometimes, the reason why you don't like your teacher is the way he runs the classroom. If you're used to a very relaxing class, learning to develop in a strict environment is difficult. In fact, giving yourself time to accept this new style of teaching is possible.
滑集中学九年级数学分层辅导测试卷(五)
滑集中学九年级数学分层辅导测试卷（五）一、选择题（本题共10 小题，每小题4 分，满分40分）1.在天气预报图上，有各种各样表示天气的符号，下列表示天气符号的图形中，既是中心对称图形又是轴对称图形的是（ ）A B C D2、向上发射一枚炮弹，经x 秒后的高度为y 公尺，且高度与时间关系为y =ax 2+bx 。
若此炮弹在第6秒与第14秒时的高度相等，则再下列哪一个时间的高度是最高的？（ ）A 第8秒B 第10秒C 第12秒D 第15秒3、已知△ABC 中，∠C ＝90°，∠A 、∠B 、∠C 所对的边分别为a 、b 、c ，且c ＝3b ，则cosA 等于（ ） A ．31 B ．32 C ．332 D ．310 4、在△ABC 中，∠A=60°，AC=1，BC=3，那么∠B 为（ ）A ．60°B ．60°或120°C ．30°或150°D ．30°5、已知二次函数c bx ax y ++=2的y 与x 的部分对应值如下表：则下列判断中正确的是（ ）A ．抛物线开口向上；B ．抛物线与y 轴交于负半轴；C ．当x ＝3时，y <0； D ．方程02=++c bx ax 有两个相等实数根．6、若把函数y=x 的图象用E （x ，x ）记，函数y=2x+1的图象用E （x ，2x+1）记，……则E （x ，122+-x x ）可以由E （x ，2x ）怎样平移得到？（ ）A ．向上平移１个单位B ．向下平移１个单位C ．向左平移１个单位D ．向右平移１个单位7、如图，已知E 是矩形ABCD 边AD 的中点，F 是边AB 上一点，EF ⊥CE.若AB:BC=3:2,则图中相似三角形的对数有（ ）A. 2B. 3C. 4D. 68、如图，在矩形ABCD 中，DE ⊥AC 于E ，设∠ADE=α，且cos α=0.6，AB=4，则AD 的长为（ ） A.320 B.310 C.3 D.3169、如图，阴影部分组成的图案既是关于x 轴成轴对称的图形又是关于坐标原点O 成中心对称的图形．若点A 的坐标是（1，3），则点M 和点N 的坐标分别是（ ）A.M （1，-3），N （-1，-3）B.M （-1，-3），N （1，-3）C.M （-1，-3），N （-1，3）D.M （-1，3），N （1，-3）x … 1-0 1 2 … y…5-131…第7题图BCA EDF第10题图10、已知函数y =x 2-2x -2的图象如图所示，关于x 的一元二次方程2220x x m ---=两根为1x 和2x ,且1x ＜0，2x ＞0.则m 的取值范围是（）A.-3≤m ≤-2 B.-3＜m ＜0 C.-3＜ m D.-2 ＜m二、填空题（本题共 5小题，每小题 5 分，满分 25 分）11、一束光线从y 轴上一点A （0,1）出发，经过x 轴上的点C 反射后经过点B(3,3),则光线从点A 到点B 经过的路程长为 .12、将量角器按如图所示的方式放置在三角形纸板上，使点C 在半圆上．点A 、B 的读数分别为86°、30°，则∠ACB = . 13、因为cos 30°= 3 2 ，cos 210°=﹣ 3 2 ，所以cos 210°=cos （180°+30°）＝﹣cos 30°＝﹣ 3 2 ，因为cos 45°= 22，cos 225°＝﹣2 2 ，所以cos 225°＝cos （180°+45°）＝﹣ 2 2，猜想：一般地，当α为锐角时，有cos （180°+α）＝ ，由此可知cos 240°的值等于 ．14、长为4m 的梯子搭在墙上与地面成45°角，作业时调整为60°角（如图所示），则梯子的顶端沿墙面升高了 15、如图，点A 、B 是双曲线3yx=上的点，分别经过A 、B 两点向x 轴、y 轴作垂线，若1=阴影S ，则12S S +=第1８题图 三、（本题共 2 小题，每小题 ６分，满分 １２分）16、计算: 00203tan60|3sin30|cos 45+-- +(75tan 118sin -)0-(-cos60o)-2.17、前不久，某市进行了城市亮化工程建设，施工过程中，工人师傅遇到这样一个问题：墙面的花色壁纸中间有一个“三角形的洞”（如图）需要修补完整，现有一块与三角形全等且花色相同的三角形壁纸（如图），但由于正反面的原因不能直接补上，请你帮助工人师傅用笔画出裁剪图和贴补方案（裁剪损耗忽略不计） 四、（本题共 2 小题，第1８小题７分，第17小题９分，满分 １６分） 18、一个长方形如下图所示，恰分成六个正方形，其中最小的正方形面积为1cm 2，求长方形的面积。
人教版九年级数学上册21.3 实际问题与一元二次方程 提分专项解答题训练 (五)
人教版九年级数学实际问题与一元二次方程提分专项解答题训练（五）1．新苑小区的物业管理部门为了美化环境，在小区靠墙的一侧设计了一处长方形花圃（墙长25m），三边外围用篱笆围起，栽上蝴蝶花，共用篱笆40m，（1）花圃的面积能达到180m2吗？（2）花圃的面积能达到250m2吗？如果能，请你给出设计方案；如果不能，请说明理由．2．学校课外生物小组的试验园地是长20米宽15米的长方形．为了便于管理，现要在中间开辟一横两纵等宽的小道（如图），要使种植面积为252平方米，求小道的宽．3．如图①，要设计一幅宽20cm、长30cm的矩形图案，其中有两横两竖的彩条，横、竖彩条的宽度比为2：3，如果要使所有彩条所占面积为原矩形图案面积的三分之一，应如何设计每个彩条的宽度？分析：由横、竖彩条的宽度比为2：3，可设每个横彩条的宽为2x，则每个竖彩条的宽为3x．将横、竖彩条分别集中，则原问题转化为如图②的情况，得到矩形ABCD．结合以上分析完成填空：如图②，用含有x的代数式表示：AB＝cm，AD＝cm．列出方程并完成本题解答．4．某厂工业废气的年排放量为450万立方米，为改善大气质量环境，决定分两期投入治理，使废气的年排气量减少到288万立方米，如果每期治理中废气减少的百分率相同．（1）求每期减少的百分率是多少？（2）预计第一期治理中每减少1万立方米需投入3万元，第二期治理中每减少1万立方米废气需投入2.5万元．问两期治理完成后共需投入多少万元？5．我县某单位于五一期间组织职工到景洪森林公园旅游，下面是领队与旅行社导游就收费标准的一段对话：领导：组团去辽河源森林公园旅游每人收费是所少？导游：如果人数不超过25人，人均旅游费用为100元．领导：超过25人怎样优惠呢？导游：如果超过25人，每增加1人，人均旅游费用降低2元，但人均旅游费用不得低于70元．该单位按旅行社的收费标准组团游览景洪森林公园结束后，共支付给旅行社2700元．请你根据上述信息，求该单位这次到景洪森林公园旅游共有多少人？6．小亮家想利用房屋侧面的一面墙，再砌三面墙，围成一个矩形猪圈，如图所示，在平行墙的一边开一个1米宽的小门．现在已备足可以砌11米长的墙的材料．（1）如果小亮家想围成面积为16m2的矩形猪圈，你能够教他们怎么围吗？（2）如果小亮家想围成面积为20m2的矩形猪圈，你认为可能吗？说明理由．7．如图，利用12米长的墙为一边，用篱笆围成一个长方形菜地，并在中间用篱笆分割成四个小长方形，总共用去篱笆48米．如果围成的菜地面积是90米2，求菜地的宽AB的长．8．某工程队在季梁公园建设过程中承包了一项拆迁工程，原计划每天拆迁1250m2，因为准备工作不足，第一天少拆迁了20%，从第二天开始，不断增加工人，加快了拆迁速度，第三天拆迁了1440m2．如果从第一天之后，每天的拆迁面积比前一天增长的百分数相同，请预测一下该工程队第四天可能要拆迁多少平方米？9．如图，在Rt△ABC中，∠C＝90°，AB＝10cm，AC＝8cm，点P从A出发向C以1cm/s的速度运动、点Q同时从C出发向B以1cm/s的速度运动，当一个点运动到终点时，该点停止运动，另一个点继续运动，当两个点都到达终点时也停止运动．（1）几秒后，△CPQ的面积为Rt△ABC的面积的？（2）填空：①点经过秒，点P在线段AB的垂直平分线上．②点Q经过秒，点Q在∠BAC的平分线上．10．某商店经销一种成本为每千克20元的水产品，据市场分析，若按每千克30元销售，一个月能售出500kg，销售单价每涨1元，月销售量就减少10kg，解答以下问题．（1）当销售单价定位每千克35元时，计算销售量和月销售利润；（2）设销售单价为x元，月销售收入为y元，请求出y与x的函数关系；（3）商店想在月销售成本不超过6000元的情况下，使得月销售利润达到8000元，销售单价应为多少？参考答案1．解：（1）设BC ＝xm ，则AB ＝（40﹣x ）＝（20﹣x ）m①由题意得：x （20﹣x ）＝180，x 2﹣40x +360＝0，△＝402﹣4×360＝0，解之得，x ＝20m答：能达到200m 2．（2）x （20﹣x ）＝250，x 2﹣40x +500＝0，△＝402﹣4×500＝﹣400＜0，即：此方程无解，答：不能达到250m 22．解：设该小道的宽为x 米，依题意得（20﹣2x ）（15﹣x ）＝252，整理得x 2﹣25x +24＝0，即：（x ﹣24）（x ﹣1）＝0，解得x 1＝24（舍去），x 2＝1．答：该小道的宽为1米．3．解：（1）AB ＝（20﹣6x ）cm ，（30﹣4x ）cm ；（2）根据题意，得24x 2﹣260x +600＝（1﹣）×20×30，整理，得6x 2﹣65x +50＝0，解方程，得x 1＝，x 2＝10（不合题意，舍去），则2x ＝，3x ＝． 答：每个横条的宽度为cm ，竖彩条的宽度为cm ．故答案为：（20﹣6x ），（30﹣4x ）．4．解：（1）设每期减少的百分率是x ，450×（1﹣x ）2＝288，解得：x 1＝1.8（舍去），x 2＝0.2解得x ＝20%．答：每期减少的百分率是20%．（2）两期治理共需投入资金＝450×20%×3+（450﹣450×20%）×20%×2.5＝450（万元）． 答：两期治理共需投入450万元．5．解：设该单位这次到景洪森林公园旅游共有x 人．因为100×25＝2500＜2700，所以员工人数一定超过25人．可得方程[100﹣2（x ﹣25）]x ＝2700，整理得x 2﹣75x +1350＝0，解得x 1＝45，x 2＝30，当x 1＝45时，100﹣2（x ﹣25）＝60＜70，故舍去x 1；当x 2＝30时，100﹣2（x ﹣25）＝90＞70，符合题意．答：该单位这次到景洪森林公园旅游共有30人．6．解：（1）设垂直于墙的边长为xm ，则x （12﹣2x ）＝16，解得x 1＝2，x 2＝4，当x ＝2时，12﹣2x ＝8，当x ＝4时，12﹣2x ＝4，所以垂直于墙的边长为2米或4米；（2）设垂直于墙的边长为ym ，则y （12﹣2y ）＝20，整理得，﹣2y2+12y﹣20＝0，△＝144﹣4×（﹣2）×（﹣20）＝﹣16＜0，∴此方程无解，所以不能够围成．7．解：设AB的长为x米，根据题意得：，x2﹣16x+60＝0，（x﹣6）（x﹣10）＝0，解得：x1＝6，x2＝10，当x1＝6时，＞12，∴x1＝6舍去，当x2＝10时，＜12，∴x2＝10符合题意答：菜地的宽AB的长为10米．8．解：设该工程队第一天之后每天的拆迁面积比前一天增长百分数为x，根据题意列方程为1250×（1﹣20%）×（1+x）2＝1440解得x1＝0.2 x2＝﹣2.2 （舍去）∴第四天可能拆迁面积为1440×（1+20%）＝1728（m2）答：该工程队第四天可能要拆迁1728m2．9．解；（1）设经过x秒．在Rt△ABC中，根据题意得；当x≤6时，（8﹣x）x＝××8×6解得：当6＜x≤8时，（8﹣x）×6＝37解得：x＝7答：经过7秒或秒．（2）当点P在线段AB的垂直平分线上时，PA＝PB，∵设经过x秒后点P在线段AB的垂直平分线上，∴x2＝（8﹣x）2+62解得：x＝，∴经过秒，点P在线段AB的垂直平分线上②如图，作QD⊥AB于点D，∵点Q在∠BAC的平分线上，∴QD＝QC，设经过x秒，则CQ＝x，则QD＝（6﹣x），∴x＝（6﹣x），解得：x＝，∴点Q经过秒，点Q在∠BAC的平分线上．10．解：（1）销售量：500﹣5×10＝450（kg）；销售利润：450×（35﹣20）＝450×15＝6750元（2）y＝（x﹣20）[500﹣10（x﹣30）]＝﹣10x2+1000x﹣16000 （3）由于水产品不超过10000÷40＝250kg，定价为x元，则（x﹣20）[500﹣10（x﹣30）]＝8000解得：x1＝40，x2＝60当x1＝40时，进货500﹣10（40﹣30）＝400kg＞250kg，舍去，当x2＝60时，进货500﹣10（60﹣30）＝200kg＜250kg，符合题意．。
化学训练题(五)
九年级化学模拟训练题（五）姓名成绩本卷满分50分。
答题时可能用到的相对原子质量：H-1 O-16 C-12 K-39 Cl-35.5 Na-23 Ag-108一.选择题（共7小题，16分）1.下列广告用语从化学角度看，没有科学错误的是A “K”牌咖啡，滴滴香浓，决不含任何化学物质B “雪山牌”矿泉水，真正的纯正C “大自然”蔬菜，天然种植，不含任何元素，真正的“绿色”食品D 食用合格“碘盐”，可预防某种甲状腺疾病2.下列物质中均含有氯元素，它们按下列顺序排列：①KCl ②Cl2③HClO ④X ⑤NaClO4.根据这种排列规律,X不可能是A AgClB KClO3C HClO2D Cl2O53.一些可溶性重金属离子如Ag+、Cu2+、Ba2+、Pb2+等能使蛋白质丧失生理功能,使生命中毒.人体胃液含有盐酸,误服含有下列物质的药剂不会引起中毒的是A CuCO3B CuSO4C BaSO4D BaCO34.溶液的酸碱性强弱与溶液中的OH—数目有关.一定体积的溶液中OH-数目越多,则溶液碱性越强.10%的NaOH溶液(密度为1.1g/cm3)与10%的KOH溶液(密度为1.1g/cm3)相比较,碱性更强的是A NaOHB KOHC 一样多D 无法比较5.向下表的甲物质中逐渐滴加相应的乙溶液至过量,反应过程中生成气体或沉淀的质量加入乙的质量关系能用右A ①②B ②④C ③④D ④第5题图6.金属La(镧)的活动性比锌强,它的氧化物为La2O3,其对应的碱为La(OH)3,La(OH)3难溶于水.下列各组中的物质难以直接反应而制得LaCl3的是A La + HClB La2O3 + HClC La(OH)3 + HClD La(OH)3 + MgCl27.学习化学时会遇到许多“相等”，下列关于“相等”的说法中错误的是A 原子中核内质子数和核外电子数一定相等B 中和反应中参加反应的酸和碱质量一定相等C 溶液稀释前后溶质的质量一定相等D 物质发生化学反应前后质量总和一定相等8.小亮的家庭实验室有以下物品：a试管；b导管与橡皮塞；c干电池；d导线；e小灯泡；f6B铅笔；g牙膏；h肥皂水；i铁钉；j石灰水；k水样；l食醋。
辽宁省2024九年级语文上册期末专题训练五古诗文默写与古诗词鉴赏课件新人教版
D. “千淘万漉虽辛苦，吹尽狂沙始到金”告诉我们尽管“千淘万 漉”，历尽辛苦，但是终究会“吹尽狂沙”，是金子迟早是要 发光的，揭示了经受住磨难迟早会显出英雄本色的道理。
一二三
点拨：B. 联系“千淘万漉虽辛苦，吹尽狂沙始到金”可 知，诗人在遭受挫折后，依然坚强不屈，相信经历“千淘 万漉”终究会被发现；本项“迁客必成‘沙沉’，遭受不 公正待遇的人也都会如泥沙一样沉入江底”鉴赏有误。
因望月有感，聊书所怀，寄上浮梁大兄、於潜七兄、乌江十 五兄，兼示符离及下 (guī)
弟妹 白居易 时难年荒世业①空，弟兄羁旅②各西东。 田园寥落③干戈④后，骨肉流离道路中。 吊影分为千里雁⑤，辞根散作九秋蓬⑥。 共看明月应垂泪，一夜乡心五处同。
一二三
【注释】①世业：世代传下的产业。②羁旅：指漂泊。③寥 落：冷落，空寂。④干戈：本是两种兵器，这里指战争。⑤ 千里雁：离群孤雁。⑥九秋蓬：深秋时节随风飘转的蓬草。
3. 对两首诗词的理解和分析不恰当的一项是( D )
A. 《行路难》(其一)开头以极为夸张的笔法领起，写“金樽清 酒”“玉盘珍羞”，仿佛在营造欢乐的气氛，但三四句急转直 下，忽说“停杯投箸不能食，拔剑四顾心茫然”，强烈的反差 衬托出诗人内心的悲苦。
B. 《鹧鸪天·送人》中“浮天水送无穷树，带雨云埋一半山”寓情 于景，烘托了词人与朋友分别之际的黯然与惆怅。
一二三
4. 下列选项正确的一项是( D )
A. 【甲】词作者苏轼，号子瞻，“唐宋八大家”之一。【乙】 诗作者白居易，号香山居士，唐代伟大的现实主义诗人。
B. 【甲】词上片写词人对天上宫阙的向往和对人间生活的热 爱，下片写词人在月下对亲人的怀念和祝福，全词始终洋溢 着乐观旷达的情绪。
九年级英语限时训练(附参考答案)
九年级英语限时训练（附参考答案）（满分35分时间25分钟）一、单词拼写（共5小题；每小题2分，满分10分）1.He was one of the finest writers of the__________ (twenty)century.2.She _________ (gradual)knows what her parents did for her.3.---COVID-19 is spreading wildly in India.Take care!----Yes.More than 300,000 people_________ (die) there.4.M_________ is the day after Sunday and before Tuesday.5.On February 25,President Xi Jinping announced that China has made a “complete_________(胜利）” in its fight against poverty(贫困).二、完形填空（共10小题；每小题1分，满分10分）阅读下面短文，掌握其大意，然后从每题所给的A、B、C三个选项中，选出能填入短文相应空白处的最佳选项，并在答题卡上将该项涂黑。
Dr. Zhong Nanshan was born in October 1936 in Nanjing,Jiangsu Province. He is one of the most famous medical 1 in the 21st century. He studied in Guangdong Experimental High School in 1953 and graduated 2Beijing Medical College in 1960. In the first Chinese National Games, Zhong 3the first place in men's 400- meter hurdles(跨栏赛)and set up a new national record at that time.In the spring of 2003, SARS broke out in China and all over the world. 4it is dangerous and hard, Zhong not only led but also took active part in the battle 5SARS. People at that time knew 6 about SARS. Zhong and his team worked day and night treating patients. Through their hard work for several , 7they made remarkable results and SARS was stopped 8Zhong 9as one of the top ten people touching China in 2004. He has been working in the medical field for over 60 years.And now he is still working in Wuhan along with young doctors. He 10most of his time on the medical research and treating patients. He is a good doctor in countrymen's eyes and respected by all the people in China.1.A.scientists B.engineers C.officers2.A.of B.in C.from3.A.beat B.won C.lost4.A.Unless B.But C.Although5.A.against B.with C.about6.A.few B.little C.much7.A.days B.years C.months8.A.in the end B.by the end C.at the end9. A.considered B.is considered C.was considered10. A.pays B.spends C.takes三、阅读表达（共5小题，每小题3分，满分15分）Online classes at homeSun Jiayi, a student from Shanghai, has to take online classes at home. Her school is closed due to the novel coronavirus."Studying at home is not easy as there are some distractions( 使人分心的事物) such as snack foods and the mobile phone. I usually put them away when l am having lessons,"Shanghai has chosen over 1,000 teachers to pre-record online lessons. Wu Wentao is one of them. He is an English teacher."We teachers are quite used to the physical environment of classrooms, but now we have to adapt to (适应)online teaching. In this situation, I can't see how students react to my lessons. It seems like I'm just talking to a camera," he said.Besides, online teaching possibly needs more preparation time. Zhang Ju, a music teacher, said,“I need to prepare pictures, sounds and videos in advance to present my lessons. Teachers need more time to search and handle multimedia(多媒体的)resources."Each of these online classes usually lasts for about 20 to30 minutes. Students have five or six classes a day in order to limit(限制)screen time to about two hours a day.While taking online classes might be easy for students from cities, it might not be easy for those from less developed areas. Not all families in the rural areas can afford a computer and Internet connection needed for online lessons every day.After such a long holiday, most students and teachers can't wait to return to their classrooms. We just hope that the fight against the novel coronavirus ends soon and that life can go back to normal.1. Why does Sun Jiayi have to take online classes at home?___________________________________________________2. What does Wu Wentao feel like when he is teaching online?____________________________________________________3.What kind of teaching needs more preparation time, traditional teaching or online teaching?_______________________________________________________4.Please show the reason that taking online classes might be difficult for those from less-developed areas._______________________________________________________5.将画线部分的英语译成汉语。
(最新)人教版九年级英语全一册 优化训练 第五单元检测
第五单元检测(时间:45分钟满分:100分)Ⅰ.单项选择(每小题1分,共15分)1.The old bridge is made C more than 1,000 stones.A.byB.fromC.ofD.with2.Each of us may meet problems in our D life,but we should learn to be active and happy .A.everyday;everydayB.every day;everydayC.every day;every dayD.everyday;every day3.This town is known C making all kinds of kites.A.asB.withC.forD.in4.They must arrive there before 10 a.m.,according A the plan.A.toB.withC.inD.as5.—Why did you get up so early to work?—In order to A the heavy traffic in the city.A.avoidB.stopC.keepD.solve6.—In Chinese culture,children born in the Year of the Monkey are said to be smart. —Yes.They are always full of energy,so I think they are also C.A.honestB.dangerousC.livelyD.funny7.You can hardly avoid B her if you both work in the same office.A.meetB.meetingC.to meetD.to meeting8.We are going to take the high-speed train to Xi an tomorrow,so an early arrival at the station B.A.advisesB.is advisedC.is advisingD.was advised9.I D the good news to all my good friends by WeChat.A.send awayB.sent forC.sent upD.sent out10.Learn to be calm no matter D happens.A.howB.whereC.whyD.what11.(2016湖北随州)—Waiter,I d like some Ningbo Dumplings.—Sorry,sir.Ningbo Dumplings C only for lunch and dinner.A.serveB.servedC.are servedD.are serving12.The window C by the students every day.A.cleanB.cleansC.is cleanedD.was cleaned13.— Why does the earth look blue in space?—Because most of the earth s surface B by water.A.coversB.is coveredC.coverD.are covered14.When the lantern slowly B into the sky,we all felt very excited.A.risedB.roseC.risenD.raised15.—Jeff,could you tell me how to order a taxi through “Didi”?—B.A.You re welcomeB.SureC.Take it easyD.It doesn t matterⅡ.完形填空(每小题1分,共10分)导学号12064048The umbrella is a very common object.It keeps the 16.A and the sun off the people.Most umbrellas can be folded up (折叠) so it is 17.D to carry them.However,the umbrella has not always been as 18.C as it is now.In the past,it was a symbol of importance.Some African countries still use umbrellas in this 19.A.Someone carries an umbrella and walks behind a king or an important person.People in different parts of the world began to 20.B umbrellas at different times.The Chinese had them more than 3,000 years ago.From there,umbrellas 21.B to India and Egypt.In Greece and Rome,22.C wouldn t use them.They believed umbrellas were only for women.England was 23.A the first country in Europe where common people used umbrellas against rain.The weather there is 24.B and umbrellas are very useful.Everybody uses umbrellas today.So next time you 25.D one,thinking that for centuries only great men and women use them,you ll feel you are an importantperson,too.16.A.rain B.cloud C.air D.water17.A.lovely B.cheap C.hard D.easy18.A.light B.heavy mon D.special19.A.way B.size C.reason D.place20.A.discover eC.examineD.discuss21.A.walked B.traveled C.rode D.flew22.A.children B.parentsC.menD.women23.A.probably B.alreadyC.suddenlyD.quickly24.A.sunny B.rainy C.snowy D.windy25.A.sell B.return C.borrow D.carryⅢ.阅读理解(每小题2分,共20分)A导学号12064049Most of us probably live without vegetables,but a world without chocolate?Now that would be hard! According to chocolate makers it could happen if we don t act soon.There are two main causes of the chocolate shortage(短缺)—chocolate s growing popularity and less production of cocoa,the plant from which chocolate is made.Withmore and more people in India and China loving chocolate,not much can be done aboutthe first cause.Therefore(所以),the only thing we can do is to increase cocoaproduction.However,because new plant diseases and little rain in Ivory Coast and Ghana,the world s largest producers have reduced cocoa production by 40 percent inthe past 10 years.What s worse,many cocoa farmers in Africa and other cocoa-producing countries like Indonesia and Venezuela are changing to easier-to-grow crops such as corn and rubber.This way,the farmers can make more money.To prevent more farmers from changing,researchers at the newly-openedInternational Cocoa Control Centre,in the UK,are trying to create new cocoa plants that grow faster and more strongly.But first they must make sure the new plants are safe to grow.This takes a long time.First,each new plant is stored at the Control Centre for six months to make sureit is healthy.It is then planted in the Centre s fields,studied and tested for another two years.Only after scientists are certain that it s disease-free will the plant be sent to farmers in West Africa or wherever else it is needed.To create new stronger types of cocoa,scientists at the Centre are combining the best parts from different cocoa plants.Though the world is facing a serious chocolate shortage,there is now hope!26.The first paragraph tells us that B.A.chocolate is healthier than vegetablesB.the world could soon be without chocolateC.people love vegetables more than chocolateD.it s not necessary to eat so much chocolate27.In which countries has chocolate become more popular in recent years?DA.Venezuela and Indonesia.B.Ivory Coast and Ghana.C.Indonesia and China.D.China and India.28.Cocoa farmers are choosing to grow rubber and corn because these crops A.A.can let farmers make more moneyB.need less rain to growC.can be planted more times each yearD.are not damaged by plant diseases29.How long does it take scientists at the Centre to make sure a cocoa plant is safe to grow?DA.6 months.B.12 months.C.24 months.D.30 months.30.What is one of the purposes of the Cocoa Control Centre?CA.To introduce cocoa production to more countries.B.To provide more chocolate for British people.C.To create stronger types of cocoa plants.D.To make sure that cocoa is healthy to eat.B导学号12064050Have you ever had the feelings that no one can understand you?Well,here comes “Pepper”.It could be about to change all that.Pepper is the first robot to read human ing its emotion recognition functions (情感识别功能),Pepper can make jokes,dance and even sing to people when they are around it.The robot looks like a lovely girl.It is four feet tall with a tablet computer in its chest.It has human-like hands,a girl-like body and a baby-like voice.It is shown to attract people at stores.Pepper can tell facial expressions,human voice and signs,and then make an answer.Pepper is designed to be a family robot,but it isn t like the household robot on the cartoon.Pepper is used at home or stores,where we enjoy pleasure and entertainment.At home,not only can it tell jokes,it also helps people in trouble.If a natural accident happens,it can encourage them,make them laugh and feel relaxed.At present,several Peppers are on show at stores for people to visit.Before selling Peppers,the creators want them to store more knowledge in order to get better along with human beings.根据短文内容完成所缺信息。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
胡集初中九年级小题训练五命题：李国芹( )1. （·北京）—Can you tell me ?—He lives in Shanghai.A. where Mark livesB. where does Mark liveC. where Mark livedD. where did Mark live ( )2. （·北京）—Can you tell me to London?—Sure. Next month.A. when you will travelB. when will you travelC. when you travelledD. when did you travel ( )3. （·顺义）Tom knew nothing about it his sister told him.A. sinceB. ifC. untilD. after ( )4. （·重庆）—Your book is very interesting. Could you tell me ? —In Xinhua Bookstore next to our school.A. where did you buy itB. why did you buy itC. where you bought itD. why you bought it( )5. （·平谷）—Your French is so good. How long have you been in France?—I was five.A. UntilB. SinceC. WhenD. While ( )6. （·天津）—Do you know ?—For a month.A. how long will she be awayB. how long she will be awayC. how often will she go thereD. how often she will go there ( )7. （·三亚）—Do you know ?—Yes. It’s on your table.A. where my dictionary isB. where is my dictionaryC. where my dictionary wasD. where was my dictionary ( )8. （·苏州）I didn’t hear clearly. Could you say it again, please? A. what you said B. what did you sayC. what you sayD. what do you say( )9. （·宜宾）Frank asked me for the violin.A. how much do I payB. how much I paidC. how much did I payD. how much I pay ( )10. （·朝阳期末）—What was your brother doing at this time yesterday? —He was reading I was writing an email.A. as soon asB. afterC. untilD. while ( )11.（·石景山）—Do you know the map yesterday?—In the bookstore on the corner.A. where Mike boughtB. where did Mike buyC. where will Mike buyD. where Mike will buy( )12.（·通州）—Can you tell me in Beijing?—Yes. At 7 o’clock tomorrow evening.A. when they will arriveB. when will they arriveC. when they arrivedD. when did they arrive ( )13.（·海淀）—Jack, can you tell me ?—I want to study computer science.A. what is your future planB. what your future plan isC. what was your future planD. what your future plan was ( )14. （·朝阳）—Can you tell me ?—Next week.A. when we had a meetingB. when will we have a meetingC. when did we have a meetingD. when we will have a meeting ( )15. （·西城）—Excuse me, can you tell me?—Take the No. 22 bus. It will take you right there.A. how can I get to Laoshe TeahouseB. how I can get to Laoshe TeahouseC. which bus did I take to Laoshe TeahouseD. which bus I took to Laoshe Teahouse( )16. （·东城）—Do you know our school?—The day after tomorrow.A. when the American students visitB. when the American students will visitC. when do the American students visitD. when will the American students visit( )17. Don’t forget to wash your hands you have meals.A. untilB. beforeC. whenD. while ( )18. （·海淀）—Could you tell me at the station?—At 9:00 tomorrow morning.A. when we metB. when did we meetC. when we will meetD. when will we meet( )19. （·朝阳）—Excuse me, could you tell me ?—My name is Kate Green.A. what is your nameB. what was your nameC. what your name isD. what your name was( )20. （·丰台）—Do you know for her mother tomorrow?—She will buy a skirt.A. what Kate will buyB. what will Kate buyC. what did Kate buyD. what Kate bought( )21. （·燕山）—Excuse me! We’d like to buy some bottles of water.—Oh, I know a store near here. Let me show you .A. what it isB. what it wasC. where it isD. where it was ( )22. （·丰台）—Can you tell me ?—Last month.A. when they cameB. when did they comeC. when they will comeD. when will they come23. I will write to you I get to Beijing.A. soB. as soon asC. becauseD. though ( )24. （·顺义）—Could you tell me yesterday?—Because my bike was broken on my way here.A. why you came lateB. why do you come lateC. why you come lateD. why did you come late( )25. （·石景山）—Sam, do you know for the holiday next month?—To Australia, I suppose.A. where did we goB. where will we goC. where we will goD. where we went( )26. （·石景山）I’m going to Flower Bookstore. Could you please tell me ?A. where is itB. where it wasC. where it isD. where was it ( )27. （·顺义）—Could you tell me your grandparents?—Every week.A. how often you visitB. how often do you visitC. how often did you visitD. how often you visited( )28. （·通州）Linda, could you tell me this book?A. where you buyB. where do you buyC. where you boughtD. where did you buy ( )29. （·怀柔）—Do you know every year, Jack?—Sorry, I don’t know.A. when the School Day isB. when is the School DayC. when the School Day wasD. when was the School day( )30. （·平谷）—Do you know for England last night?—At 9:00.A. when she leavesB. when she leftC. when does she leaveD. when did she leave31. —Could you tell me the Dragon Boat Festival in China?—Sure. People usually watch the dragon boat race and eat zongzi.A. how people celebrateB. how do people celebrateC. when people celebrateD. when do people celebrate ( )32. —Excuse me, can you tell me tomorrow?—At 8:00.A. what time the plane arrived in BeijingB. what time did the plane arrive in BeijingC. what time the plane will arrive in BeijingD. what time will the plane arrive in Beijing( )33. Could you tell me a moment ago?A. what they were talking aboutB. what were they talking aboutC. what they are talking aboutD. what are they talking about( )34. They arrived we were having dinner.A. ifB. whileC. sinceD. for ( )35. The policeman asked the lost boy .A. where his mother isB. where is his motherC. where his mother wasD. where was his mother ( )36. —What did the teacher ask the students just now?—He asked .A. if they are interested in the lessonB. if are they interested in the lessonC. if they were interested in the lessonD. if were they interested in the lesson( )37. —Could you tell me yesterday?—The Summer Palace.A. where you goB. where do you goC. where you wentD. where did you go( )38. she works harder, she will pass the exam.A. ThoughB. IfC. SoD. For39. Excuse me, can you tell me ?A. how I can improve my mathB. how can I improve my mathC. how I could improve my mathD. how could I improve my math( )40. —Can you tell me the Science Museum?—Next week.A. when we will visitB. when will we visitC. when we visitedD. when did we visit( )41. （·北京）I got home, my sister was doing her homework.A. WhenB. BecauseC. IfD. Though( )42. （·襄樊）We won’t start the meeting our teacher arrives.A. thoughB. untilC. whileD. or( )43. （·上海）I’ll send you an email as soon as I in Canada.A. arriveB. arrivedC. am arrivingD. will arrive( )44. （·益阳）She is a nice girl we all like her.A. so；thatB. such；thatC. too；toD. very；that( )45. （·长沙）Making friends is not easy. Sometimes it can take years you become true friends with someone.A. beforeB. afterC. becauseD. since( )46. （·洛阳）it was very cold yesterday, he had a swim in the river as usual.A. BecauseB. AlthoughC. ButD. For( )47. （·襄樊）—What shall we do now?—it’s raining very hard, let’s stay at home.A. SoB. SinceC. ThoughD. If( )48. （·新疆）Nobody knows if he . If he here, I’ll call you at once.A. will come；will arriveB. will come；arrivesC. comes；will arriveD. comes；arrives( )49. （·东城）I’m waiting for my mother. , I’ll go shopping with her. A. If she doesn’t come B. If she comesC. If she will comeD. If she won’t come( )50. （·东城）The film Kung Fu Panda is interesting I would like to see it again.A. such；thatB. too;toC. as;asD. so; that。