3月(人教A版必修三)高一数学第一次月考试题及答案
最新版高一数学上学期第一次月考试题及答案(新人教A版 第115套)

抚州一中高一上学期第一次月考数学试卷一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知A={}R x x x ∈≤,32|,a=14,b=22,则 ( )A .a ∈A ,且b ∉AB .a ∉A ,且b ∈AC .a ∈A ,且b ∈AD .a ∉A ,且b ∉A2.已知A={}Z x x x x ∈≤--,0103|2,B={}Z x x x x ∈>--,062|2,则A ∩B 的非空真子集的个数为 ( ) A .16 B .14 C .15 D .323.已知A={}2,2-,B={}1|=ax x ,且A ∪B=A ,则a 的取值集合为 ( )A .⎭⎬⎫⎩⎨⎧21B .⎭⎬⎫⎩⎨⎧-21 C .⎭⎬⎫⎩⎨⎧-21,21 D .⎭⎬⎫⎩⎨⎧-0,21,21 4.下列各组函数中表示同一函数的是 ( )A .()()0,1x x g x f == B .()()39,32--=+=x x x g x x fC .()()||,2x x g x x f ==D .()()2,x x g x x f ==5.已知全集{}2,1,0,1-=U ,集合{}2,1-=A ,{}2,0=B ,则=A B C U )(( ) A.{}0B. {}1-C. {}12-,D.∅ 6..函数|2|2x y x x=+的图象是( )A B C D 7.下列函数中,在区间)2,0(上为增函数的是( )A.x y -=3B.12-=x y C.xy 1=D.2)1(-=x y8.若()2)1(22+-+=x a x x f 在[-1,2]上是单调函数,则a 的范围为 ( ) A .1≤a B .2≥a C .21≥-≤a a 或 D .21>-<a a 或9.“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…用S1、S2分别表示乌龟和兔子所行的路程,t 为时间,则与故事情节相吻合是 ( )10.A={}01)2(|2=+++x m x x ,若φ=⋂+R A ,则m 的范围为 ( )A .0≥mB .04<<-mC .4-≥mD .4->m 二、填空题(本大题共5小题,每小题5分,共25分)11.已知元素(,)x y 在映射f 下的象是(2,2)x y x y +-,则(3,1)在f 下的原象..是 。
新人教A版高一上学期数学第一次月考试卷(附答案解析))

新人教A 版高一上学期摸底试卷数 学 试 卷 (六)B 卷考生注意: 1.本试卷分第Ⅰ卷(选择题)和第二卷(非选择题)两部分,共150分,考试时间120分钟.2.请将各题答案填写在答题卡上.第Ⅰ卷(选择题 共60分)一、单项选择题(每小题5分,共40分)1. 下列元素与集合的关系表示正确的是 【 】 (A )∈-1N* (B )∈2Z (C )∈23Q (D )∈πQ2. 已知集合{}m m m A ,2-=,{}12,0-=m B ,若B A =,则m 的值为 【 】 (A )0 (B )0或1 (C )1 (D )1-3. 设集合{}4,2,1=A ,{}042=+-=m x x x B ,若{}1=B A ,则集合B 的子集个数为 【 】 (A )1 (B )2 (C )3 (D )44. 设集合{}12≤=x x A ,{}m x x B <=,若⊆A (C R B ),则实数m 的取值范围是 【 】 (A )()+∞,1 (B )()1,-∞- (C )[)+∞-,1 (D )(]1,-∞-5. 在△ABC 中,“内角A 是锐角”是“△ABC 是锐角三角形”的 【 】 (A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件 6. 已知正数b a ,满足1=+b a ,则baa +4的最小值为 【 】(A )6 (B )8 (C )9 (D )127. 不等式0342>+-x x 的解集是 【 】 (A ){}1<x x (B ){}31><x x x 或 (C ){}31<<x x (D ){}3>x x8. 《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形证明,也称之为无字证明.现有如图所示的图形,点F 在半圆O 上,点C 在直径AB 上,且AB OF ⊥,设a AC =,b BC =,则该图形可以完成的无字证明为 【 】(A )2ba +≥ab (0,0>>b a ) (B )22b a +≥ab 2(0,0>>b a ) (C )b a ab +2≤ab (0,0>>b a ) (D )2ba +≤222b a +(0,0>>b a )二、多项选择题(每小题5分,共20分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)9. 设全集{}4,3,2,1,0=U ,集合{}4,1,0=A ,{}3,1,0=B ,则下列结论正确的有 【 】 (A ){}1,0=B A (B )C U B {}4=(C ){}4,3,1,0=B A (D )集合A 的真子集个数为810. 下列说法中,正确的有 【 】 (A )在数学中,可判断真假的句子叫做命题 (B )1>a 且1>b 是1>ab 成立的充分条件 (C )命题:p ∈∀x R ,02>x ,则∈∃⌝x p :R ,02<x (D )命题“若0>>b a ,则ba 110<<”的否定是假命题 11. 已知二次函数c bx ax y ++=2(c b a ,,为常数,且a 的部分图象大致如图所示,则下列结论正确的是 【 (A )0,0<>b a (B )02>+b a (C )024>++c b a (D )0>++c b a12. 若0,0>>q p 且2=+q p ,则下列不等式恒成立的是 【 】 (A )q p +≤2 (B )pq ≤1 (C )qp 11+≤2 (D )22q p +≥2第Ⅱ卷 非选择题(共90分)三、填空题(每小题5分,共20分)13. 命题“1>∃x ,使得x⎪⎭⎫ ⎝⎛21≥21成立”的否定是________________.14. 某小型服装厂生产的一种风衣日销售量x 件与售价P 元/件之间的关系为x P 2150-=,生产x 件风衣所需成本为x C 3050+=元,要使日获利不少于1 300元,则该厂日产量x 的取值范围为__________.(日产量=日销售量).15. 已知∈∀x p :R ,012>+mx ,∈∀x q :R ,函数12++=mx x y 的图象在x 轴的上方,若q p 、均为真命题,则实数m 的取值范围是__________.16. 在R 上定义运算:bc ad d c b a -=,若不等式xa a x 121+--≥1对任意∈x R 恒成立,则实数a 的最大值为__________.四、解答题(共70分,解答应写出文字说明,证明过程或演算步骤) 17.(本题满分10分)已知集合{}12≤<-=x x A ,{}212≤-=x x B . (1)求B A ,B A ; (2)求(C R A ) (C R B ).设全集=U R ,集合{}51≤≤=x x A ,集合{}a x a x B 212+≤≤-=(0>a ). (1)若A x ∈是B x ∈的充分条件,求实数a 的取值范围; (2)若A x ∈是B x ∈的必要条件,求实数a 的取值范围.19.(本题满分12分)已知关于x 的方程062=-+mx x (0>m )的两个根为21,x x ,且512=-x x . (1)求函数62-+=mx x y (0>m )的解析式; (2)解关于x 的不等式x y 24-<.2020年10月1日是新中国成立71周年纪念日,是全国各族人民的共同节日,各地举行了丰富多彩的庆祝活动,某校为丰富校园文化生活,展示学生风采,增强同学们的爱国情怀和爱国意识,激发同学们的爱国热情,组织开展了庆祝国庆节系列活动.要求各班设计如图所示的一张矩形画报,并在画报内设计一个矩形图案,且该图案的面积为 2 m 2.要求图案在画报内左右留白20 cm,上下各留白10 cm,试问怎样设计画报内图案长与宽的尺寸,能使整个画报面积最小,面积最小值是多少?21.(本题满分12分)已知集合⎭⎬⎫⎩⎨⎧<-=112x x x A ,集合(){}01222<+++-=m m x m x x B .(1)求集合A 、B ;(2)若A B ⊆,求实数m 的取值范围.(1)已知0,0>>b a ,试比较ab b a 22-与b a -的大小; (2)用反证法证明:若∈c b a ,,R ,且542+-=b a x ,862+-=c b y ,122+-=a c z ,则z y x ,,中至少有一个不小于0.新人教A 版高一上学期摸底试卷数 学 试 卷 (六)B 卷 答 案 解 析考生注意: 1.本试卷分第Ⅰ卷(选择题)和第二卷(非选择题)两部分,共150分,考试时间120分钟.2.请将各题答案填写在答题卡上.第Ⅰ卷(选择题 共60分)一、单项选择题(每小题5分,共40分)1. 下列元素与集合的关系表示正确的是 【 】 (A )∈-1N* (B )∈2Z (C )∈23Q (D )∈πQ 答案 【 C 】解析 本题考查元素与集合之间的关系. 选择答案【 C 】.2. 已知集合{}m m m A ,2-=,{}12,0-=m B ,若B A =,则m 的值为 【 】 (A )0 (B )0或1 (C )1 (D )1- 答案 【 C 】解析 本题考查集合的相等与集合元素的性质. 若0=m ,则{}0,0=A ,不满足集合元素的互异性,舍去.∴⎩⎨⎧=--=0122m m m m ,解之得:1=m .∴选择答案【 C 】.3. 设集合{}4,2,1=A ,{}042=+-=m x x x B ,若{}1=B A ,则集合B 的子集个数为 【 】 (A )1 (B )2 (C )3 (D )4 答案 【 D 】解析 本题考查集合的基本运算和集合子集个数的确定. ∵{}1=B A ,∴B ∈1.把1=x 代入方程042=+-m x x 得:041=+-m ,解之得:3=m .∴0342=+-x x ,解之得:3,121==x x . ∴{}3,1=B ,满足{}1=B A . ∴集合B 的子集个数为422=. ∴选择答案【 D 】.4. 设集合{}12≤=x x A ,{}m x x B <=,若⊆A (C R B ),则实数m 的取值范围是 【 】 (A )()+∞,1 (B )()1,-∞- (C )[)+∞-,1 (D )(]1,-∞- 答案 【 D 】解析 本题考查根据集合之间的基本关系确定参数的值或取值范围. 解不等式2x ≤1得:1-≤x ≤1,∴{}11≤≤-=x x A . ∵{}m x x B <=,∴C R B {}m x x ≥=. ∵⊆A (C R B ),∴m ≤1-. ∴实数m 的取值范围是(]1,-∞-. ∴选择答案【 D 】.5. 在△ABC 中,“内角A 是锐角”是“△ABC 是锐角三角形”的 【 】 (A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件 答案 【 B 】解析 本题考查充分必要条件的判断.显然,由“内角A 是锐角”不能推出“△ABC 是锐角三角形”;但是由“△ABC 是锐角三角形”一定能推出“内角A 是锐角”.∴“内角A 是锐角”是“△ABC 是锐角三角形”的必要不充分条件. ∴选择答案【 B 】.6. 已知正数b a ,满足1=+b a ,则baa +4的最小值为 【 】(A )6 (B )8 (C )9 (D )12 答案 【 B 】解析 本题考查利用基本不等式求最值. ∵正数b a ,满足1=+b a∴()baa b b a a b a b a a ++=++=+4444≥8424=⋅+b a a b . 当且仅当baa b =4,即31,32==b a 时,等号成立.∴baa +4的最小值为8. ∴选择答案【 B 】.7. 不等式0342>+-x x 的解集是 【 】 (A ){}1<x x (B ){}31><x x x 或 (C ){}31<<x x (D ){}3>x x 答案 【 B 】解析 本题考查一元二次不等式的解法.解一元二次不等式的一般步骤是:(1)利用不等式的性质,将二次项系数化为正数; (2)计算ac b 42-=∆的值,并判断∆的符号; (3)当∆≥0时,求出相应的一元二次方程的根; (4)画出对应的二次函数的简图;(5)根据一元二次不等式的形式,结合简图,写出其解集.注意 一元二次不等式的解集结构与二次项系数的符号有着直接的关系.0342>+-x x ,即()()031>--x x ,解之得:3>x 或1<x .∴不等式0342>+-x x 的解集是{}31><x x x 或. ∴选择答案【 B 】.8. 《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形证明,也称之为无字证明.现有如图所示的图形,点F 在半圆O 上,点C 在直径AB 上,且AB OF ⊥,设a AC =,b BC =,则该图形可以完成的无字证明为 【 】(A )2ba +≥ab (0,0>>b a ) (B )22b a +≥ab 2(0,0>>b a ) (C )b a ab +2≤ab (0,0>>b a ) (D )2ba +≤222b a +(0,0>>b a )答案 【 D 】解析 本题考查不等式的证明.由题意可知:2ba OB OA OF +===. ∴22ba b b a BC OB OC -=-+=-=(当点C 在半径OB 上时). 在Rt △COF 中,由勾股定理得:222222222b a b a b a OC OF FC +=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+=+=. ∵FC ≤OF ,∴2ba +≤222b a +(0,0>>b a ),当且仅当点C 与点O 重合,即b a =时,等号成立.∴选择答案【 D 】.二、多项选择题(每小题5分,共20分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)9. 设全集{}4,3,2,1,0=U ,集合{}4,1,0=A ,{}3,1,0=B ,则下列结论正确的有 【 】 (A ){}1,0=B A (B )C U B {}4=(C ){}4,3,1,0=B A (D )集合A 的真子集个数为8 答案 【 AC 】解析 本题考查集合的基本运算.∵{}4,3,2,1,0=U ,集合{}4,1,0=A ,{}3,1,0=B ∴{}1,0=B A ,{}4,3,1,0=B A , C U B {}4,2=. ∴(A )、(C )正确,(B )错误;对于(D ),集合A 的真子集个数为7123=-.故(D )错误. ∴选择答案【 AC 】.10. 下列说法中,正确的有 【 】(A )在数学中,可判断真假的句子叫做命题 (B )1>a 且1>b 是1>ab 成立的充分条件 (C )命题:p ∈∀x R ,02>x ,则∈∃⌝x p :R ,02<x (D )命题“若0>>b a ,则ba 110<<”的否定是假命题 答案 【 BD 】解析 本题考查与命题有关的知识点.对于(A ),一般地,我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.故(A )错误; 对于(B ),正确;对于(C ),∈∃⌝x p :R ,2x ≤0.故(C )错误;对于(D ),一个命题和它的否定只能是一真一假,不能同真同假.根据不等式性质的倒数法则,可知命题“若0>>b a ,则ba 110<<”是真命题,所以它的否定是假命题.故(D )正确. ∴选择答案【 BD 】.11. 已知二次函数c bx ax y ++=2(c b a ,,为常数,且a 的部分图象大致如图所示,则下列结论正确的是 【 (A )0,0<>b a (B )02>+b a (C )024>++c b a (D )0>++c b a 答案 【 ABC 】解析 本题考查二次函数的图象.对于(A ),函数的图象开口向上,可得0>a ,对称轴在y 轴的右侧,所以b a ,异号,即0<b .故(A )正确;对于(B ),由函数的图象可知,12<-ab,结合0>a 可得:02>+b a .故(B )正确; 对于(C ),点()c b a ++24,2在函数位于第一象限的图象上,所以024>++c b a .故(C )正确;对于(D ),点()c b a ++,1在函数位于第四象限的图象上,所以0<++c b a .故(D )错误.∴选择答案【 ABC 】.12. 若0,0>>q p 且2=+q p ,则下列不等式恒成立的是 【 】 (A )q p +≤2 (B )pq ≤1 (C )qp 11+≤2 (D )22q p +≥2 答案 【 ABD 】解析 本题考查基本不等式的应用. 对于(A ),∵0,0>>q p ,2=+q p ∴()pq q p qp 22++=+≤()42=+=+++q p q p q p .∴q p +<0≤2.当且仅当1==q p 时,等号成立.故(A )正确;对于(B ),∵0,0>>q p ,2=+q p∴pq ≤122=⎪⎭⎫ ⎝⎛+q p ,当且仅当1==q p 时,等号成立.故(B )正确;对于(C ),∵0,0>>q p ,2=+q p ∴()⎪⎭⎫ ⎝⎛++=⎪⎭⎫⎝⎛++=+p q q p q p q p q p 211112111≥22211=⋅⨯+p q q p . 当且仅当pqq p =,即1==q p 时,等号成立. 故(C )错误;对于(D ),∵0,0>>q p ,2=+q p∴222q p +≥122=⎪⎭⎫ ⎝⎛+q p ,∴22q p +≥2. 当且仅当1==q p 时,等号成立. 故(D )正确.∴选择答案【 ABD 】.第Ⅱ卷 非选择题(共90分)三、填空题(每小题5分,共20分)13. 命题“1>∃x ,使得x⎪⎭⎫ ⎝⎛21≥21成立”的否定是________________.答案 1>∀x , 2121<⎪⎭⎫ ⎝⎛x解析 本题考查含有一个量词的命题的否定.对含有一个量词的命题进行否定的方法是:改变量词,否定结论.该命题的否定:1>∀x , 2121<⎪⎭⎫ ⎝⎛x.14. 某小型服装厂生产的一种风衣日销售量x 件与售价P 元/件之间的关系为x P 2150-=,生产x 件风衣所需成本为x C 3050+=元,要使日获利不少于1 300元,则该厂日产量x 的取值范围为__________.(日产量=日销售量). 答案 []45,15解析 本题考查一元二次不等式的应用. 设该厂日获利为y 元,则有:()()501202305021502-+-=+--=x x x x x y .∵要使日获利不少于1 300元∴y ≥1 300,即5012022-+-x x ≥1 300. ∴675602+-x x ≤0,解之得:15≤x ≤45. ∴该厂日产量x 的取值范围为[]45,15.15. 已知∈∀x p :R ,012>+mx ,∈∀x q :R ,函数12++=mx x y 的图象在x 轴的上方,若q p 、均为真命题,则实数m 的取值范围是__________.答案 [)2,0解析 本题考查根据真假命题确定参数的值或取值范围.若命题p 为真命题,则有0=m 或⎩⎨⎧<-=∆>040m m ,解之得:m ≥0;若命题q 为真命题,则有042<-=∆m ,解之得:22<<-m . ∴当q p 、均为真命题时,实数m 的取值范围是[)2,0.16. 在R 上定义运算:bc ad d c b a -=,若不等式xa a x 121+--≥1对任意∈x R 恒成立,则实数a 的最大值为__________. 答案23解析 本题考查定义新运算以及与一元二次不等式有关的恒成立问题,注意分离参数法的应用. ∵bc ad dc ba -= ∴()()()211121-+--=+--a a x x xa a x ≥1.∴a a -2≤12+-x x .设()12+-=x x x f ,只需a a -2≤()min x f 即可.∵()4321122+⎪⎭⎫ ⎝⎛-=+-=x x x x f ,∴()43min=x f . ∴a a -2≤43,即3442--a a ≤0,解之得:21-≤a ≤23. ∴实数a 的最大值为23.四、解答题(共70分,解答应写出文字说明,证明过程或演算步骤) 17.(本题满分10分)已知集合{}12≤<-=x x A ,{}212≤-=x x B . (1)求B A ,B A ; (2)求(C R A ) (C R B ).解:(1)不等式12-x ≤2即2-≤12-x ≤2,解之得:21-≤x ≤23.∴⎭⎬⎫⎩⎨⎧≤≤-=2321x x B .∴⎭⎬⎫⎩⎨⎧≤≤-=121x x B A ,⎭⎬⎫⎩⎨⎧≤<-=232x x B A ; (2)(C R A ) (C R B )= C R (B A )⎭⎬⎫⎩⎨⎧>-≤=232x x x 或.18.(本题满分12分)设全集=U R ,集合{}51≤≤=x x A ,集合{}a x a x B 212+≤≤-=(0>a ). (1)若A x ∈是B x ∈的充分条件,求实数a 的取值范围; (2)若A x ∈是B x ∈的必要条件,求实数a 的取值范围. 解:(1)∵A x ∈是B x ∈的充分条件,∴B A ⊆.根据题意则有⎪⎪⎩⎪⎪⎨⎧≥+≤-+<->521122120a a a a a ,解之得:a ≥2.∴实数a 的取值范围是[)+∞,2;(2)∵A x ∈是B x ∈的必要条件,∴A B ⊆.当∅=B 时,则有⎩⎨⎧+>->a a a 2120,解之得:310<<a ;当∅≠B 时,则有⎪⎪⎩⎪⎪⎨⎧≤+≥-+≤->521122120a a aa a ,解之得:31≤a ≤1.综上所述,实数a 的取值范围是(]1,0. 19.(本题满分12分)已知关于x 的方程062=-+mx x (0>m )的两个根为21,x x ,且512=-x x . (1)求函数62-+=mx x y (0>m )的解析式; (2)解关于x 的不等式x y 24-<.解:(1)由根与系数的关系定理可得:6,2121-=-=+x x m x x . ∵512=-x x∴()()25244221221212=+=-+=-m x x x x x x ,解之得:1±=m . ∵0>m ,∴1=m .∴函数62-+=mx x y (0>m )的解析式为62-+=x x y ; (2)x y 24-<即x x x 2462-<-+.整理得:01032<-+x x ,解之得:25<<-x . ∴不等式x y 24-<的解集为{}25<<-x x . 20.(本题满分12分)2020年10月1日是新中国成立71周年纪念日,是全国各族人民的共同节日,各地举行了丰富多彩的庆祝活动,某校为丰富校园文化生活,展示学生风采,增强同学们的爱国情怀和爱国意识,激发同学们的爱国热情,组织开展了庆祝国庆节系列活动.要求各班设计如图所示的一张矩形画报,并在画报内设计一个矩形图案,且该图案的面积为 2 m 2.要求图案在画报内左右留白20 cm,上下各留白10 cm,试问怎样设计画报内图案长与宽的尺寸,能使整个画报面积最小,面积最小值是多少?解: 设画报内矩形图案的长为x m,则图案的宽为x2m,则画报的长为()4.0+x m,画报的宽为⎪⎭⎫ ⎝⎛+2.02x m,设画报的面积为y m 2. ∴()x x x x y 8.02.008.22.024.0++=⎪⎭⎫ ⎝⎛++=≥88.28.02.0208.2=⋅+x x . 当且仅当xx 8.02.0=,即2=x 时,等号成立.122=(m ).答:当矩形图案的长为2 m,宽为1 m 时,可使画报的面积最小,面积最小值是2. 88 m 2. 21.(本题满分12分)已知集合⎭⎬⎫⎩⎨⎧<-=112x x x A ,集合(){}01222<+++-=m m x m x x B .(1)求集合A 、B ;(2)若A B ⊆,求实数m 的取值范围. 解:(1)112<-x x 即011<-+x x ,同解于()()011<-+x x ,解之得:11<<-x . ∴{}11<<-=x x A .()01222<+++-m m x m x 即()()[]01<+--m x m x ,解之得:1+<<m x m .∴{}1+<<=m x m x B ;(2)∵A B ⊆∴⎩⎨⎧≤+-≥111m m ,解之得:1-≤m ≤0.∴实数m 的取值范围为[]0,1-. 22.(本题满分12分)(1)已知0,0>>b a ,试比较ab b a 22-与b a -的大小; (2)用反证法证明:若∈c b a ,,R ,且542+-=b a x ,862+-=c b y ,122+-=a c z ,则z y x ,,中至少有一个不小于0.(1)解: ()()()abb a b a b a a b b a 2222+-=---. ∵0,0>>b a∴当b a >时,()()022>+-ab b aa b a ,∴b a ab b a ->-22;当b a =时,()()022=+-ab b aa b a ,∴b a a b b a -=-22;当b a <时,()()022<+-ab b aa b a ,∴b a ab b a -<-22.综上所述,若0,0>>b a ,当b a >时,b a a b b a ->-22;当b a =时,b a ab b a -=-22;当ba <时,b a ab b a -<-22.(2)证明: 假设z y x ,,均小于0,∴0<++z y x . ∵128654222+-++-++-=++a c c b b a z y x()()()()()()222222321964412-+-+-=+-++-++-=c b a c c b b a a ≥0∴这与假设矛盾,即假设不成立. ∴z y x ,,中至少有一个不小于0.。
最新版高一数学第一次月考试题及答案(新人教A版第41套)

A {1} B {0,1} C {0,1,4} D {0,1,2,3,4}
2、在如图所示的对应中是 A 到 B 的映射的是(
)
a
1
b
c
3
1
a
b
3
c
1
a
2
3
b
a
1
b
2
c
3
(1) A (2) B (3)
(2) C (3)
、 (4)
(3) D (4)
3、下列四组中,f ( x ) 与g ( x ) 表示同一函数的是(
A 2,4 B 2,-4 C-2,4 D -2,-4
10、函数 f(x)= ax 1 2 (a>0,a ≠1) 的图像恒过定点 P,则定点 P 的坐标为 ( )
A (1,3) B (1,2) C (0,3) D (0,2) 11、若 f(x) 满足 f(ab)=f(a)+f(b) 且 f(2)=p,f(3)=q ,则 f(144)=( )
A. f : x→ y= 1 x
B. f
2
: x→ y= 1 x 3
C. f : x→ y= 2 x
D. f
3
:x→ y= x
5、若 f(x)=ax 2+bx+c 是偶函数,则 g(x)=ax 3+bx2+cx 是( )
A 奇函数 B 偶函数 C 非奇非偶函数 D 既是奇函数又是偶函数
6、函数 y= 1 x x 的定义域为(
B . f ( 1) D . f (2)
3 f( )
2 3 f( ) 2
f (2) f ( 1)
8、若函数 f (x) 4x2 kx 8 在 [5,8] 上是单调函数,则 k 的取值范围是(
2013-2014学年高一数学上学期第一次月考试题及答案(新人教A版 第32套)

高一上学期第一次月考数学试题一、选择题(本大题共12小题,每小题5分,共60分.)1、集合A ={x |-1≤x ≤2},B ={x |x <1},则A ∩(∁R B )=( ) A .{x |x >1} B .{x |x ≥1}C.{x |1<x ≤2} D.{x |1≤x ≤2}2、下列函数完全相同的是( )A .f (x )=|x |,g (x )= (x )2B .f (x )=|x |,g (x )=x 2C .f (x )=|x |,g (x )=x 2xD .f (x )=x 2-9x -3,g (x )=x +33、下列函数是奇函数的是( )A .x y =B .322-=x y C .21x y = D .]1,0[,2∈=x x y 4、设31log 21=y ,1420.6y =,1530.6y =则( ) A.321y y y << B.123y y y << C.132y y y << D.231y y y <<5.已知函数4log ,0()2,0xx x f x x >⎧=⎨≤⎩,则1[()]4f f = ( ) A .2 B .-2 C .12 D .-126、函数2()(31)2f x x a x a =+++在(,4)-∞上为减函数,则实数a 的取值范围是( ) A .3a ≤- B .3a ≤ C . 5a ≤ D .3-≥a7、函数()f x 是定义域为R 的奇函数,当0x >时()1f x x =-+,则当0x <时,()f x 的表达式为( )A .()1f x x =-+B .()1f x x =--C .()1f x x =+D .()1f x x =-8、在同一坐标系中,函数1()xy a =与log ()a y x =-(其中0a >且1a ≠)的图象只可能是()9、若31log a y x -=在(0,+∞)内为减函数,且xay )21(=为增函数,则a 的取值范围是( ) A. 1)B.1(0,)3C.(0,D. )21,31(10、若函数242--=x x y 的定义域为[]m ,0,值域为[]2,6--,则m 的取值范围是( )A .(]4,0B .[]4,2C . (]2,0D .()4,211、已知定义在R 上的函数()f x 为奇函数,且有3()()2f x f x +=-,则)3()2()1(-+-+-f f f 的值为( )A .2B .1C .0D .1-12、下列四个命题:(1)函数f x ()在0x >时是增函数,0x <也是增函数,所以)(x f 是增函数;(2)若函数2()2f x ax bx =++与x 轴没有交点,则280b a -<且0a >;(3) 223y x x =--的递增区间为[)1,+∞;(4) 1y x =+和y =表示相等函数。
人教A版高中数学必修三试卷高一下学期第一次月考考卷.docx

马鸣风萧萧高中数学学习材料马鸣风萧萧*整理制作高一下学期第一次月考数学考卷一、选择题(共12题,每题5分,共60分)1.下列给出的赋值语句中正确的是( )A.A =3B.M M -=C.2==B AD.0=+y x2.把89化成五进制数的末位数字为( )A.1B.2C.3D.43.阅读下图中的算法,其功能是( ).第一步,m = a .第二步,b <m ,则m = b .第三步,若c <m ,则m = c .第四步,输出m .A .将a ,b ,c 由小到大排序B .将a ,b ,c 由大到小排序C .输出a ,b ,c 中的最小值D .输出a ,b ,c 中的最大值4.总体由编号为01,02, ,19,20的20个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为( )7816 6572 0802 6314 0702 4369 1128 05983204 9234 4935 8200 3623 4869 6938 7481A .11B .02C .05D .045.已知样本数据1,2,4,3,5,下列说法不正确...的是 ( ) A 、平均数是3 B 、中位数是4 C 、极差是4 D 、方差是2马鸣风萧萧6.某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件、80件、60件.为了解它们的产品质量是否存在显著差别,用分层抽样方法抽取了一个容量为n 的样本进行调查,其中从丙车间的产品中抽取了3件,则n =( )A .9B .10C .12D .137.下列说法一定正确的是( )A .一名篮球运动员,号称“百发百中”,若罚球三次,不会出现三投都不中的情况B .一枚硬币掷一次得到正面的概率是21,那么掷两次一定会出现一次正面的情况 C .如买彩票中奖的概率是万分之一,则买一万元的彩票一定会中奖一元D .随机事件发生的概率与试验次数无关8.从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品至少有一件是次品”,则下列结论正确的是( )A.A 与C 对立B.任何两个均互斥C.B 与C 互斥D.任何两个均不互斥9.若将一个质点随机投入如图所示的长方形ABCD 中,其中AB=2,BC=1,则质点落在以AB 为直径的半圆内的概率是( )A .2πB .4πC .6πD .8π10.下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y 关于x 的线性回归方程为y ^=0.7x +0.35,那么表中m 值为( ).x 3 4 5 6y 2.5 m 4 4.5A. 3 B .3.15 C .4 D .4.511.先后抛掷质地均匀的硬币三次,则至少一次正面朝上的概率是( )A.81B.83C.85D.87 12.阅读如下程序框图,如果输出4i =,那么空白的判断框中应填人的条件是 ( )A .S<8?B .S<12?C .S<14?D .S<16?马鸣风萧萧二.填空题(共4题,每题4分,共16分)13.用辗转相除法求得数98与63的最大公约数是____________;14.已知函数532)(2345-+-++=x x x x x x f ,用秦九韶算法计算,当X =5时,V 3=_______;15.某单位有职工200名,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第5组抽出的号码为22,则第10组抽出的号码应是_________.16.已知点E 在正△ABC 的边AB 上,AE = 2EB ,在边AC 上任意取一点P ,则“△AEP 的面积恰好小于△ABC 面积的一半”的概率为 .三.解答题(共6题,满分74分)17.(本小题满分12分)已知一组数据的频率分布直方图如下.求(1)众数;(2)中位数;(3)平均数.18.(本小题满分12分)如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以a 表示.已知甲、乙两个小组的数学成绩的平均分相同.(1)求a 的值;(2)求甲、乙两个小组数学成绩的方差,并说明哪个小组的成绩相对比较稳定;马鸣风萧萧参考公式:])()()[(1222212x x x x x x ns n -++-+-= 19.(本小题满分12分)口袋中装有除编号外其余完全相同的5个小球,编号依次为1,2,3,4,5.现从中同时取出两个球,分别记录下其编号为m,n(其中m<n).(1) 用(m,n )表示抽取结果,列出所有可能的抽取结果;(2)求“5+=m n ”的概率;(3)求“5≥mn ”的概率.20.(本小题满分12分)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作四次试验,得到的数据如下:零件的个数x (个)2 3 4 5 加工的时间y (小时) 2.5 3 4 4.5(1)已知零件个数与加工时间线性相关,求出y 关于x 的线性回归方程;(2)试预测加工10个零件需要多少时间?1221ˆˆˆni ii n i i x y nx y b a y bx xnx ==-⋅==--∑∑参考公式:, 21.(本小题满分12分)如下图,给出了一个程序框图,其作用是输入x 的值,输出相应的y 的值,(I )请指出该程序框图所使用的逻辑结构;(Ⅱ)若视x 为自变量,y 为函数值,试写出函数()y f x =的解析式;(Ⅲ)若要使输入的x 的值与输出的y 的值相等,则输入x 的值的集合为多少? 甲组乙组 8 9 7 a 3 5 79 66马鸣风萧萧 开始y输出结束2x ≤?x输入2y x =5x ≤?23y x =-1y x=1图是否是否22.(本小题满分14分)某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.(1)求应从小学、中学、大学中分别抽取的学校数目;(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析.(ⅰ)列出所有可能的抽取结果;(ⅱ)求抽取的2所学校均为小学的概率.马鸣风萧萧 高一下学期第一次月考数学参考答案一、选择题:1—12 BDCCB DDABA DB二、填空题:13、 7 14、179 15、 47 16、34三、解答题(以下评分标准仅供参考,最终由备课组统一确定):17解:(1)由频率分布直方图可知,众数为65. …………2分(2)由10×0.03+5×0.04=0.5,所以面积相等的分界线为65,即中位数为65。
人教A版高中数学必修三试卷高一(下)3月月考数学试卷.doc

马鸣风萧萧马鸣风萧萧高中数学学习材料马鸣风萧萧*整理制作高一(下)3月月考数学试卷参考答案与试题解析一、选择题1.(5分)设A,B为两个事件,且P(A)=0.3,则当()时一定有P(B)=0.7.A.A与B互斥B.A与B对立C.A BD.A不包含B考点:互斥事件与对立事件.专题:阅读型.分析:根据题意,依次分析选项可得:对于A、由互斥事件的概率性质,可得P(B)=0.7不一定成立,则A错误;对于B、根据对立事件的性质,易得P(B)=1﹣0.3=0.7,B正确;对于C、D,事件相互包含时,事件A、B的概率没有明确的关系,均错误,即可得答案.解答:解:根据题意,依次分析选项可得:对于A、若A与B互斥,不一定有P(A)+P(B)=1成立,即P(B)=0.7不一定成立,则A错误;对于B、当A、B对立时,根据对立事件的性质,易得P(B)=1﹣0.3=0.7,B正确;对于C、若A⊆B,则P(A)<P(B),即P(B)=0.7不一定成立,则C错误;对于D、A不包含B,事件A、B的概率没有明确的关系,则D错误;故选B.点评:本题考查随机事件的概率的基本性质,解题的关键要了解对立、互斥事件的概率性质.2.(5分)计算机执行如图的程序段后,输出的结果是()A.1,3 B.4,1 C.0,0 D.6,0考点:程序框图.专题:操作型.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用顺序结构计算变量a,b的值,并输出,逐行分析程序各语句的功能不难得到结果.解答:解:∵a=1,b=3∴a=a+b=3+1=4,∴b=a﹣b=4﹣3=1.故输出的变量a,b的值分别为:4,1故选B点评:根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.3.(5分)(2011•宁波模拟)某篮球运动员在一个赛季的40场比赛中的得分的茎叶图如右图所示,则中位数与众数分别为()A.23,21 B.23,23 C.23,25 D.25,25考点:众数、中位数、平均数;茎叶图.专题:计算题.分析:有茎叶图知这些数据是按照大小顺序排列的,中位数是最中间两个数字的平均数23,在这组数据中出现的次数最多的是23,得到结果.解答:解:由茎叶图知这里有40个数据,这些数据是按照大小顺序排列的,中位数是最中间两个数字的平均数23,在这组数据中出现的次数最多的是23,故选B.点评:本题考查中位数,平均数,考查茎叶图,这组数据的个数比较多,在个数上容易出错,本题的茎叶图帮我们标出了每个茎上的数据个数,注意观察.4.(5分)为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第1小组的频数为6,则报考飞行员的学生人数是()马鸣风萧萧A.36 B.40 C.48 D.50考点:频率分布直方图.专题:阅读型.分析:设报考飞行员的人数为n,根据前3个小组的频率之比为1:2:3设出频率,再根据所有频率和为1,解之即可求出第一组频率,根据第1小组的频数为6,即可求得结论.解答:解:设报考飞行员的人数为n,根据前3个小组的频率之比为1:2:3,可设前三小组的频率分别为x,2x,3x;由题意可知所求频率和为1,即x+2x+3x+(0.037+0.013)×5=1解得x=0.125则0.125=,解得n=48故选C.点评:本题主要考查了频率分布直方图,同时考查了学生的读图能力,属于基础题.5.(5分)在面积为S的△ABC的边AB上任取一点P,则△PBC的面积不小于的概率是()A.B.C.D.考点:几何概型.专题:计算题.分析:首先分析题目求在面积为S的△ABC的边AB上任取一点P,则△PBC的面积不小于的概率,即可考虑画图求解的方法,然后根据图形分析出基本的事件空间与事件的几何度量是什么.再根据几何关系求解出它们的比例即可.解答:解:记事件A={△PBC的面积大于等于},基本事件空间是线段AB的长度,(如图)因为,则有;化简记得到:,因为PE平行AD则由三角形的相似性;所以,事件A的几何度量为线段AP的长度,因为AP=,所以P(A)=.故选A.点评:由这个题目可以看出,解决有关几何概型的问题的关键是认清基本事件空间是指面积还是长度或体积,同学们需要注意.6.(5分)为了在运行下面的程序之后得到输出16,键盘输入x应该是()INPUT xIF x<0 THENy=(x+1)(x+1)ELSEy=(x﹣1)(x﹣1)END IFPRINT yEND.A.3或﹣3 B.﹣5 C.5或﹣3 D.5或﹣5考点:选择结构.专题:阅读型.分析:本题考查条件语句,先根据算法语句写出分段函数,然后讨论x的正负,根据函数值求出自变量即可.解答:解:根据条件语句可知是计算y=当x<0,时(x+1)*(x+1)=16,解得:x=﹣5当x≥0,时(x﹣1)*(x﹣1)=16,解得:x=5故答案为:﹣5或5.点评:本题主要考查了条件语句,以及分段函数和根据函数值求出自变量的问题,如果将程序摆在我们的面前时,我们要从识别逐个语句,整体把握,概括程序的功能,同时考查了分类讨论的思想,属于基础题.马鸣风萧萧7.(5分)如图,程序运行后输出的结果为()A.50 B.5C.25 D.0考点:伪代码.专题:计算题.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算并输出a的值,模拟程序的循环过程,并用表格对程序运行过程中的数据进行分析,不难得到正确的答案.解答:解:根据伪代码所示的顺序,逐框分析程序中各变量、各语句的作用可知:程序在运行过程中各变量的值如下表示:是否继续循环 a j循环前/0 1第一圈是 1 2第二圈是 3 3第三圈是 1 4第四圈是0 5第五圈是0 6第四圈否故最后输出的值为:0故选D.点评:根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.8.(5分)若某程序框图如图所示,则该程序运行后输出的值是()A.4B.5C.6D.7考点:程序框图.专题:图表型.分析:根据所给数值判定是否满足判断框中的条件,然后执行循环语句,一旦不满足条件就退出循环,执行语句输出i,从而到结论.解答:解:当输入的值为n=12时,n不满足判断框中的条件,n=6,i=2,n不满足判断框中的条件,n=3,i=4n满足判断框中的条件,n=10,i=5,n不满足判断框中的条件,n=5,i=6n满足下面一个判断框中的条件,退出循环,即输出的结果为i=6,故选C.点评:本题主要考查了循环结构,是当型循环,当满足条件时,执行循环,属于基础题.9.(5分)函数f(x)=x2﹣x﹣2,x∈[﹣5,5],在定义域内任取一点x0,使f(x0)≤0的概率是()A.B.C.D.马鸣风萧萧考点:几何概型;一元二次不等式的解法.专题:计算题.分析:先解不等式f(x0)≤0,得能使事件f(x0)≤0发生的x0的取值长度为3,再由x0总的可能取值,长度为定义域长度10,得事件f(x0)≤0发生的概率是0.3解答:解:∵f(x)≤0⇔x2﹣x﹣2≤0⇔﹣1≤x≤2,∴f(x0)≤0⇔﹣1≤x0≤2,即x0∈[﹣1,2],∵在定义域内任取一点x0,∴x0∈[﹣5,5],∴使f(x0)≤0的概率P==故选C点评:本题考查了几何概型的意义和求法,将此类概率转化为长度、面积、体积等之比,是解决问题的关键10.(5分)将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区.三个营区被抽中的人数依次为()A.25,17,8 B.25,16,9 C.26,16,8 D.24,17,9考点:系统抽样方法.专题:计算题.分析:由于是系统抽样,故先随机抽取第一数,再确定间隔,可知样本组成以3为首项,12为公差的等差数列,由此可得结论.解答:解:由题意,在随机抽样中,首次抽到003号,以后每隔12个号抽到一个人,则分别是003、015、027、039构成以3为首项,12为公差的等差数列,故可分别求出在001到300中有25人,在301至495号中共有17人,则496到600中有8人.故选A.点评:本题考查系统抽样,解题的关键是随机抽取第一数,再确定间隔,从而得到样本组成等差数列.11.(5分)在三棱锥的六条棱中任意选择两条,则这两条棱是一对异面直线的概率为()A.B.C.D.考点:等可能事件的概率.专题:计算题.分析:所有的选法共有C62=15 种,这两条棱是一对异面直线的选法有3种,即三棱锥的3对对棱,由古典概型公式可得所求事件的概率.解答:解:在三棱锥的六条棱中任意选择两条,所有的选法共有C62=15 种,其中,这两条棱是一对异面直线的选法有3种,即三棱锥的3对对棱,故所求事件的概率等于=,故选C.点评:本题考查等可能事件的概率的求法,判断这两条棱是一对异面直线的有3种,即三棱锥的3对对棱,是解题的关键.12.(5分)两人约定在20:00到21:00之间相见(两人出发是各自独立,且在20:00到21:00各时刻相见的可能性是相等的),并且先到者必须等迟到者40分钟方可离去,则两人在约定时间内能相见的概率是()A.B.C.D.考点:几何概型.专题:概率与统计.分析:由题意设事件A为“甲乙两人能会面”,求出试验包含的所有事件,并且事件对应的集合表示的面积是s=1,再求出满足条件的事件,并且得到事件对应的集合表示的面积是,进而根据几何概率模型的计算公式可得答案.解答:解:由题意知本题是一个几何概型,设事件A为“甲乙两人能会面”,试验包含的所有事件是Ω={(x,y)|20<x<21,20<y<21},并且事件对应的集合表示的面积是s=1,满足条件的事件是A={(x,y)|20<x<21,20<y<21,|x﹣y|<=}所以事件对应的集合表示的面积是1﹣2×××=,根据几何概型概率公式得到P=.则两人在约定时间内能相见的概率是.故选B.点评:解决此类问题的关键是熟练掌握几何概型的定义与概率计算公式,而几何概率模型一般通过事件的长度、面积或者体积之比来求事件发生的概率,因此只要根据题意判断出题目是属于那种类型即可,此题属于中档题,是根据面积之比来计算事件发生的概率.二、填空题13.(5分)从1,2,3,4,5这5个数中任取两个,则这两个数正好相差1的概率是.考点:古典概型及其概率计算公式.马鸣风萧萧 专题: 计算题.分析: 由题意可得:从1,2,3,4,5这5个数中任取两个共有10个基本事件,而符合条件的共有4个,由古典概型的公式可得答案.解答: 解:由题意可得:从1,2,3,4,5这5个数中任取两个共有10个基本事件,即(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5);而符合条件的共有(1,2),(2,3),(3,4),(4,5)共4个,故所求概率为:=, 故答案为:点评: 本题考查古典概型的求解,利用列举法求对基本事件数十解决问题的关键,属基础题.14.(5分)在Rt △ABC 中,∠A=60°,∠C=90°,过点C 做射线交斜边AB 于P ,则CP <CA 的概率是 .考点: 几何概型.专题: 概率与统计.分析: 由于过直角顶点C 在∠ACB 内部任作一射线CP ,故可以认为所有可能结果的区域为∠ACB ,可将事件A 构成的区域为∠ACC',以角度为“测度”来计算.解答: 解:在AB 上取AC'=AC ,则∠ACC ′=60°.记A={在∠ACB 内部任作一射线CP ,与线段AB 交于点P ,CP <CA},则所有可能结果的区域为∠ACB ,事件A 构成的区域为∠ACC'.又∠ACB=90°,∠ACC'=60°.∴P (A )==.故答案为:.点评: 本题主要考查了概率里的几何概型,在利用几何概型的概率公式来求其概率时,几何“测度”可以是长度、面积、体积、角度等,属于基础题.15.(5分)(2008•湖南)从某地区15000位老人中随机抽取500人,其生活能否自理的情况如下表所示: 性别 人数生活能否自理男 女能178 278 不能23 21 则该地区生活不能自理的老人中男性比女性约多 60 人.考点: 简单随机抽样.分析: 在抽取的500人的样本中,有23名男性不能自理,有21名女性不能自理,所以500人中,男性比女性多2人,而总人数是15000,是样本的30倍,所以男性比女性多60人.解答:解:由表得.故答案为:60点评:在抽样过程中,每个个体被抽到的概率相等,在调查某一事件时,若总体的个体较多,不能一一考查,通常采用抽取样本来调查.16.(5分)执行如图所示的程序,输出的结果为48,则判断框中应填入的条件为i>3?(或者i>=4?).考点:程序框图.专题:图表型.分析:根据程序框图,写出运行结果,根据程序输出的结果是48,可得结论.解答:解:根据程序框图,运行结果如下:S i第一次循环2×2=4 2第二次循环4×3=12 3第三次循环12×4=48 4退出循环,故判断框内应填入的条件是i>3?(或者i>=4?).故答案为:i>3?(或者i>=4?).点评:本题考查程序框图,尤其考查循环结构.对循环体每次循环需要进行分析并找出内在规律.本题属于基础题.三、解答题17.(10分)已知有一列数,设计框图实现求该列数前20项的和.考点:设计程序框图解决实际问题.专题:图表型.分析:根据已知条件累加求和,利用循环结构S=S+,画出程序框图.解答:解:因为S=,利用循环结构S=S+,程序框图如图(左图或右图):马鸣风萧萧点评:本题考查程序框图以及计算机语言,画程序框图首先要弄清各种图形符号的意义,明确每个图形符号的使用环境,图形符号间的连接方式,18.(12分)不透明袋中有3个白球,3个黑球,从中任意摸出3个,求下列事件发生的概率:(1)摸出1个或2个白球;(2)至少摸出1个白球.考点:古典概型及其概率计算公式;互斥事件与对立事件.专题:概率与统计.分析:(1)所有的摸球方法共有种,摸出1个或2个白球的摸球方法有•+•种,由此求得故摸出1个或2个白球概率.(2)至少摸出一个白球的对立事件为:“摸出的3个球都是黑球”,求得其对立事件的概率为,从而求得至少摸出1个白球的概率.解答:解:(1)所有的摸球方法共有=20种,摸出1个或2个白球的摸球方法有•+•=18 种,故摸出1个或2个白球概率为=.(2)至少摸出一个白球的对立事件为摸出的3个球都是黑球,故其对立事件的概率为,故至少摸出1个白球的概率等于1﹣=.点评:本题考查古典概型及其概率计算公式的应用,所求的事件与它的对立事件概率间的关系,属于基础题.19.(12分)根据下面的要求,求满足1+2+3+…+n>500的最小的自然数n.(1)画出执行该问题的程序框图;(2)以下是解决该问题的一个程序,但有3处错误,请找出错误并予以更正.考点:设计程序框图解决实际问题;伪代码.专题:图表型.分析:(1)分析题目中的要求,发现这是一个累加型的问题,故可能用循环结构来实现,在编写算法的过程中要注意,计数的初始值为1,计数值每一次增加1,退出循环的条件是累加结果S≤500,即可得到流程图;(2)有三处错误:①直到型循环结构是直到满足条件退出循环,则S≤500,改为S>500,;②,根据循环次数可知输出结果为i﹣1;③,S的初始值改为S=0.解答:解:(1)程序框图如图所示:…..(6分)(两者选其一即可)(2)①S<=500应改为S>500;②输出i 应改为输出i﹣1;③S=1应改为S=0.…(每个2分)点评:本题主要考查了循环结构,以及利用循环语句来实现数值的累加(乘),同时考查了流程图的应用,属于中档题.算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.20.(12分)设函数f(x)=x2+2ax+b2(1)将一枚骰子抛掷两次,若先后出现的点数分别为a、b,求函数f(x)无零点的概率.(2)若a是从区间[0,2]任取的一个数,b是从区间[0,3]任取的一个数,求函数f(x)有零点的概率.马鸣风萧萧考点:古典概型及其概率计算公式;几何概型.专题:概率与统计.分析:(1)为古典概型,可得总的基本事件数为36,符合条件的由15个,可求概率;(2)为几何概型,作图可得面积,作比值可得答案.解答:解:(1)设事件A为“函数f(x)=x2+2ax+b2无零点”,当a≥0,b≥0时,方程x2+2ax+b2=0无实根的条件为△=4a2﹣4b2<0,即a<b …..(2分)将一枚骰子抛掷两次,若先后出现的点数分别为a、b,总的基本事件共有6×6=36个….(4分)其中15个满足a<b,15个满足a>b,6个满足a=b,故事件A发生的概率为P(A)==….(6分)(2)试验的全部结果所构成的区域为{(a,b)|0≤a≤2,0≤b≤3} …(8分)构成事件B=“函数f(x)有零点”的区域为{(a,b)|0≤a≤2,0≤b≤3,a≥b}即如图的阴影区域所示,….(10分)所以所求的概率为P(B)==…..(12分)点评:本题考查古典概型和几何概型的求解,属基础题.21.(12分)为了分析某个高二学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前7次考试的数学成绩x、物理成绩y进行分析.下面是该生7次考试的成绩.数学88 83 117 92 108 100 112物理94 91 108 96 104 101 106(1)他的数学成绩与物理成绩哪个更稳定?请给出你的证明;(2)已知该生的物理成绩y与数学成绩x是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.考点:线性回归方程;极差、方差与标准差.专题:计算题.分析:(1)做出物理和数学成绩的平均数,进而做出两门成绩的方差,把两个方差进行比较,得到物理的方差小于数学的方差,所以物理成绩更稳定.(2)根据上一问做出的平均数,利用最小二乘法做出线性回归方程的系数,把样本中心点代入求出a的值,写出线性回归方程,把所给的物理的成绩代入预报出数学的成绩.解答:解:(1)=100,=100,∴数学的方差是=142物理的方差是=从而物理的方差小于数学的方差,所以物理成绩更稳定.(2)由于x与y之间具有线性相关关系,∴b==0.5,a=100﹣0.5×100=50∴线性回归方程为y=0.5x+50当y=115时,x=130即该生物理是115分时,数学成绩是130.物理和数学的关系非常密切,要学好物理需要有好的数学做基础点评:本题考查线性回归方程的求法和应用,考查判断两组数据的稳定性的方法,本题解题的关键是正确运算出结果,本题是一个基础题.22.(12分)若a是从1,2,3三个数中任取的一个数,b是从2,3,4,5四个数中任取的一个数,(1)有序数对(a,b)共有多少个?将结果列举出来.(2)求成立的概率.(3)设函数,求f(x)>b恒成立的概率.考点:古典概型及其概率计算公式.专题:概率与统计.分析:(1)利用分步乘法原理和列举法即可得出;(2)验证条件“”即可找出;(3)利用基本不等式可得:成立.经验证即可得出要求事件包括的基本事件,再利用古典概型的概率计算公式即可得出.解答:解:(1)基本事件总数==12个,即(1,2),(1,3),(1,4),(1,5);(2,2),(2,3),(2,4),(2,5);(3,2),(3,3),(3,4),(3,5);(2)设事件A为“”,事件A包含事件:(1,4),(1,5).由古典概型得P==.(3)设事件B:“f(x)>b恒成立”,则x>1,a>0,=,∴,于是成立.则事件B包含事件:(1,2),(1,3);(2,2),(2,3),(2,4),(2,5);(3,2),(3,3),(3,4),马鸣风萧萧(3,5)共10个.由古典概型得.点评:熟练掌握分步乘法原理、列举法、古典概型的概率计算公式及利用基本不等式把问题正确等价转化是解题的关键.。
人教A版高中数学必修三试卷高一下学期第一次月考.doc

高一下学期第一次月考一、选择题(每小题5分,10小题,共计50分)1、在ABC ∆中,ο45=A ,2=a ,2=b ,则角B 为( )A. ο30B. ο60C. οο15030或D. οο12060或4、在ABC ∆中,有ab c b a =-+222,则角C 为( )A. ο60B. ο120C. ο30D. οο13545或5、若实数a 、b 、c 成等比数列,则函数2y ax bx c =++与x 轴的交点的个数 为( )A. 0B. 1C. 2D. 无法确定6、在一幢20m 高的楼顶测得对面一塔顶的仰角为ο60,塔基的俯角为ο45,那么这座塔的高度是( )m 。
A. )331(20+ B. )31(20+ C. )26(10+ D. )26(20+ 7、数列{}n a 的通项公式11++=n n a n ,则该数列的前( )项之和等于9。
A .98B .99C .96D .978、数列}{n a 的首项为3,}{n b 为等差数列且n n n a a b -=+1(*N n ∈).若23-=b , 1210=b ,则=8a ( )A. 0B. 11C. 8D. 39、在ABC ∆中,tan A 是以4-为第三项,4为第七项的等差数列的公差,tan B 是以13为第三项,9为第六项的等比数列的公比,则这个三角形是( ) A .钝角三角形 B .锐角三角形 C .等腰直角三角形 D .等腰三角形10、设ABC ∆的内角A ,B ,C 所对的边分别为a ,b ,c .若三边的长为连续的三个正整数,且C B A >>,A a b cos 203=,则A sin :B sin :C sin 为( )A. 4:3:2B. 5:6:7C. 5:4:3D. 6:5:4二、填空题(每小题5分,5小题,共计25分)11、等比数列{}n a 中, ,16,252==a a 则{}n a 的公比为_______。
高一下学期第一次月考数学试题3(必修3)(含答案)
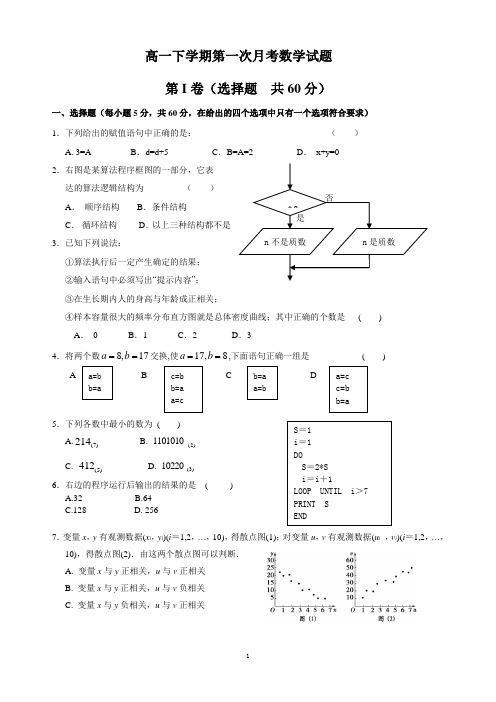
高一下学期第一次月考数学试题第I 卷(选择题 共60分)一、选择题(每小题5分,共60分,在给出的四个选项中只有一个选项符合要求)1.下列给出的赋值语句中正确的是: ( )A. 3=A B .d=d+5 C .B=A=2 D . x+y=02.右图是某算法程序框图的一部分,它表达的算法逻辑结构为 ( )A . 顺序结构B .条件结构C . 循环结构D .以上三种结构都不是3.已知下列说法:①算法执行后一定产生确定的结果;②输入语句中必须写出“提示内容”;③在生长期内人的身高与年龄成正相关;④样本容量很大的频率分布直方图就是总体密度曲线;其中正确的个数是 ( )A . 0B .1C .2D .34.将两个数8,17a b ==交换,使17,8a b ==,下面语句正确一组是 ( )AB C D5.下列各数中最小的数为 ( ) A.)7(214 B. )2(1101010 C. )5(412 D. )3(10220 6.右边的程序运行后输出的结果的是 ( ) A.32 B.64 C.128 D. 2567.变量x ,y 有观测数据(x i ,y i )(i =1,2,…,10),得散点图(1);对变量u ,v 有观测数据(u i ,v i )(i =1,2,…,10),得散点图(2).由这两个散点图可以判断.A. 变量x 与y 正相关,u 与v 正相关B. 变量x 与y 正相关,u 与v 负相关C. 变量x 与y 负相关,u 与v 正相关D. 变量x 与y 负相关,u 与v 负相关8则图中判断框内(1)处和执行框中的(2)处应填的语句是 ( )A .1,100+=>n n iB .2,100+=>n n iC .2,50+=>n n iD .2,50+=≤n n i9.若某高校共有在校大学生16050名,其中专科生4500人,本科生9750人,研究生1800人,现在需要采用分层抽样的方法调查学生的家庭情况,已知从专科生抽取了60人,则需要从本科生、研究生两类学生分别抽取多少人 ( )A .130 ,24B .260,24C .390,48D .130,3610.某产品的广告费用x 与销售额y 的统计数据如下表根据上表可得回归方程ˆˆy b x a =+中的ˆb为4.9,据此模型预报广告费用为7万元时销售额 ( )A .63.6万元B .65.5万元C .77.9万元D .74.9万元11.若样本1x +2,2x +2,……,n x +2的平均数为10,方差为3,则样本21x +3,22x +3,…,2n x +3,的平均数、方差、标准差是 ( )A .19,12,32B .23,12,32C .23,18,23D .19,18,2312.在刚召开的十二届全国人大一次会上,为了调查人大代表对“反腐倡廉”的意见,现从1000名代表中使用系统抽样,按以下规定获取样本编号:如果在起始组中随机抽取的号码为M ,那么第K 组(组号K 从0开始,K=0,1,2,…,9)抽取的号码的百位数为组号,后两位数为M+32K 的后两位数,若M=16,则4,7K K ==时所抽取的样本编号为:( )A .444 ,740B .416,716C .444,726D .423,726第Ⅱ卷(非选择题 共90分)二、填空题(每小题5分,共20分)13.在学校的生物园中,甲同学种植了9株花苗, 乙同学种植了10株花苗.测量出花苗高度的数 据(单位:cm),并绘制成如图所示的茎叶图,则 第8题 甲 乙9 1 0 4 0 4 3 1 0 2 6 41 2 3 7 3 04 4 6 6 7。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D.自变量取x。时,n个代数式的值
二、填空题(每小题5
分,共20分)
13.右边程序框图输出d的含义是
14.INPUT x
IF 9<x AND x<100 THEN
a=x\10
b=பைடு நூலகம் MOD 10
x=10※b+a
PRINT x
ENDIF
END
(注:“\”是x除以10的商,“MoD”是x 除以10的余数)
A B
C D
10 用样本频率分布估计总体频率分布的过程中,下列说法正确的是()
A 总体容量越大,估计越精确 B 总体容量越小,估计越精确
C 样本容量越大,估计越精确 D 样本容量越小,估计越精确
11.读程序
甲:INPUT i=1乙:INPUT I=1000
S=0S=0
WHILE i≤1000DO
S=S+iS=S+i
第二步 如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);
否则 y=25+0.1(x-1300)
第三步 输出税款y, 结束。
请写出该算法的程序框图和程序。(注意:程序框图与程序必须对应)
21(本小题满分12分)求方程 在[0,1]上的近似解,精度为0.01画出框图写出程序。
If f(a)*f(m)<0 THEN
b=m
ELSE
a=m
END IF
LOOP UNTIL ABS(a-b)<d OR f(m)=0
PRINT m
END
22.(本小题满分14分)给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先将下面给出的程序框图补充完整,再根据程序框图写出程序.
A.1个 B.2个 C.3个 D.4个
5. 用秦九韶算法计算多项式 当 时的值时,需要做乘法和加法的次数分别是( )
A. 6 , 6 B. 5 ,6 C. 5 , 5 D. 6 , 5
6. 用秦九韶算法计算多项式 在 时的值时, 的值为 ( )
A. -845 B.220 C. -57 D. 34
7 容量为 的样本数据,按从小到大的顺序分为 组,如下表:
1. 把程序框图补充完整:
(1)________________________ (3分)
(2)________________________ (4分)
2. 程序:(7分)
(1)_____i < = 50___(2)_____p= p + i____
2. 程序:
i=1
p=1
s=0
WHILE i<=50
A 1 B2 C3 D 4
3.如右图,是某算法流程图的一部分,其算法的逻辑结构为()
A. 顺序结构 B. 判断结构
C.条件结构 D. 循环结构
4.我们已学过的算法有求解一元二次方程的求根公式,加减消元法求二元一次方程组解,二分法求函数零点等.对算法的描述有①对一类问题都有效;②对个别问题有效;③计算可以一步步地进行,每一步都有惟一的结果;④是一种通法,只要按部就班地做,总能得到结果.以上正确描述算法的有 ( )
22.(本小题满分12分)给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先将下面给出的程序框图补充完整,再根据程序框图写出程序.
1. 把程序框图补充完整:
(1)________________________ (2分)
高一数学月考测试题(人教A版)
限时:100分钟
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分,
第I卷
作者:吕清亮老师 整理上传者:孟凡洲老师
一、选择题(每小题5分,共60分)
1.下列给出的赋值语句中正确的是:( )
A、3=A B、M=—M C、B=A=2 D、x+y=0
2.把119化成五进制数的末位数字为()
19.(本小题满分12分)根据下面的要求,求满足1+2+3+…+n > 500的最小的自然数n。
(1)画出执行该问题的程序框图;
(2)以下是解决该问题的一个程序,但有几处错误,
请找出错误并予以更正,并把正确的程序写下来。
20.(本小题满分12分)下面是计算应纳税所得额的算法过程,其算法如下:
第一步 输入工资x(注x<=5000);
组号
1
2
3
4
5
6
7
8
频数
10
13
x
14
15
13
12
9
第三组的频数和频率分别是()
A 和 B 和 C 和 D 和
8 某企业有职工 人,其中高级职称 人,中级职称 人,一般职员 人,
现抽取 人进行分层抽样,则各职称人数分别为()
A B C D
9 有 件产品编号从 到 ,现在从中抽取 件检验,用系统抽样
确定所抽取的编号可以为( )
i=i+lI=i一1
WENDLoopUNTIL i<1
PRINT SPRINT S
ENDEND
对甲乙两程序和输出结果判断正确的是 ( )
A.程序不同结果不同B.程序不同,结果相同C.程序相同结果不同D.程序同,结果同
12.如下程序框图是古代一数学家的算法程序框图,它输出的结果S代表
A.一个数列的和
B.一个n次多项式系数的和
(2)估计这次环保知识竞赛的及格率( 分及以上为及格)
1 解:(1)频率为: ,频数:
(2)
19.(本小题满分14分)根据下面的要求,求满足1+2+3+…+n > 500的最小的自然数n。
(1)画出执行该问题的程序框图;
(2)以下是解决该问题的一个程序,但有几处错误,
请找出错误并予以更正。
解:(1)程序框图如图所示:或者:
(2)________________________ (3分)
2. 程序:(7分)
一.选择:
1-5 .BDCCA 6-10.CABDC 11—12.BC
二.填空:
13.点p(x0,y0)到直线AX+BY+C=0的距离
14.交换这个数的各位与十位数字
15. 64 118
16.A=30
B=57
19/2
否则 y=25+0.1(x-1300)
第三步 输出税款y, 结束。
请写出该算法的程序框图和程序。(注意:程序框图与程序必须对应)
解:框图7分,程序6分(不对应扣3-4分)
21
a =0
b =1
d =0.01
f(x)=x^3+x^2—1
Do
m=(a+b)/2
f(a)=a^3+a^2—1
f(m)=m^3+m^2—1
s= s + p
p= p + i
i=i+1
WEND
PRINT s
END
上述程序输出x的含义是:
15.图一的输出结果是:
图二的输出结果是:
13题图
图一图二
16 A=3 a=2
B=A^3 b=4
A=A+B c=SQR(b)+a*b
B=A+B s=a/b+c/a
PRINT“A,B=”; A,B PRINT s
输出结果为___________输出结果为____________
8分
(2)①DO应改为WHILE;10分
②PRINT n+1应改为PRINT n;12分
③S=1应改为S=014分
20.(13分)下面是计算应纳税所得额的算法过程,其算法如下:
第一步 输入工资x(注x<=5000);
第二步 如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);
17.
INPUT a,b
IF a<>0 THEN
x=-b/a
ELSE
IF b=0 THEN
X=0
ELSE
PRINT“方程无解”
END IF
END IF
PRINT x
END
18 如图,从参加环保知识竞赛的学生中抽出 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1)79.5—89.5这一组的频数、频率分别是多少?
17.(本小题满分10分)设计算法,求出方程 的解,画出算法流程图并写出程序.
18 (本小题满分12分)如图,从参加环保知识竞赛的学生中抽出 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1)79.5—89.5这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率( 分及以上为及格)
