原子物理学总复习
原子物理学总复习
段正路
2014年
1
第一章 原子的基本状况
重点： 1，原子的核式结构 2，α粒子散射实验的意义
2
1、卢瑟福的原子核式模型
原子中的全部正电荷和几乎全部质量都集中在原子中央一 个很小的体积内，称为原子核。原子中的电子在核的周围 绕核运动。
2. α粒子的散射实验：
α粒子被静止核的库仑场散射的角度θ由下式决定
• Z：质子数 • A: 质量数
C4 0
20
a
原子核的角动量
P 核 LnSnLpSp
P核 I(I1)h
原子核的磁矩
I g
I(I1) he 2M
38
原子核的统计性：A为奇数的原子核属于费米子；A为偶 数的原子核属于玻色子。
原子核的结合能
E [Z m p (A Z )m n m 核 ]C 2 或 E [Z m H (A Z )m n m 原 子 ]C 2
r rr 总角动量 JLS JLS,LS 1 ,......,LS
L LS耦合下的原子态符号表示:
2S 1
s=0，单重态
J s=1，三重态
能级排布规则
洪特定则 朗德间隔定则
17
j-j 耦合
rjrj21 rrll12srsr12 rr r Jj1j2
j1 l1 s 1 ,l1 s 1 1 ,....,l1 s 1 j2 l2 s 2 ,l2 s 2 1 ,....,l2 s 2 Jj1j2,j1j2 1 ,....,j1j2
% 1R (m 12n 1 2)Tm Tn
R — 里德堡常数；T(m) —光谱项。
光谱线系 m = 1，n = 2、3、4…，赖曼系（紫外） m = 2，n = 3、4、5…，巴尔末系（可见光） m = 3，n = 4、5、6…，帕邢系（红外） m = 4，n = 5、6、7…，布喇开系（远红外）
原子物理学复习总结提纲
第一章 原子的位形：卢瑟福模型一、学习要点1、原子的质量和大小R ~10-10 m , N A =6.022⨯1023mol -1,1u=1.6605655⨯10-27kg2、原子核式结构模型(1)汤姆孙原子模型(2)α粒子散射实验：装置、结果、分析(3)原子的核式结构模型(4)α粒子散射理论： 库仑散射理论公式：221212200cot cot cot 12422242C Z Z e Z Z e a b E m v θθθπεπε===⋅'⋅ 卢瑟福散射公式：222124401()4416sin sin 22Z Z e a d d dN N nAt ntN E A θθπεΩΩ'== 2sin d d πθθΩ=实验验证:1422sin ,,Z , ,2A dN t E n N d θρμ--'⎛⎫∝= ⎪Ω⎝⎭，μ靶原子的摩尔质量 微分散射面的物理意义、总截面 24()216sin 2a d d b db σθπθΩ==()022212244()114416sin 22Z Z e d a d E Sin σθσθθθπε⎛⎫≡== ⎪Ω⎝⎭ (5)原子核大小的估计: α粒子正入射（0180θ=）：：2120Z Z 14m c e r a E πε=≡ ,m r ～10－15－10－14m第一章自测题1. 选择题(1)原子半径的数量级是：A ．10－10cm; B.10-8m C. 10-10m D.10-13m(2)原子核式结构模型的提出是根据α粒子散射实验中：A.绝大多数α粒子散射角接近180︒B.α粒子只偏2︒～3︒C.以小角散射为主也存在大角散射D.以大角散射为主也存在小角散射（3）进行卢瑟福理论实验验证时发现小角散射与实验不符这说明：A.原子不一定存在核式结构B.散射物太厚C.卢瑟福理论是错误的D.小角散射时一次散射理论不成立(4)用相同能量的α粒子束和质子束分别与金箔正碰，测量金原子核半径的上限. 问用质子束所得结果是用α粒子束所得结果的几倍？ A. 1/4 B . 1/2 C . 1 D. 2(5)动能E K =40keV 的α粒子对心接近Pb(z=82)核而产生散射,则最小距离为（m ）：A.5.91010-⨯B.3.01210-⨯C.5.9⨯10-12D.5.9⨯10-14 (6)如果用相同动能的质子和氘核同金箔产生散射,那么用质子作为入射粒子测得的金原子半径上限是用氘核子作为入射粒子测得的金原子半径上限的几倍？ A.2 B.1/2 C.1 D .4(7)在金箔引起的α粒子散射实验中,每10000个对准金箔的α粒子中发现有4个粒子被散射到角度大于5°的范围内.若金箔的厚度增加到4倍,那么被散射的α粒子会有多少？ A. 16 B.8 C.4 D.2(8）在同一α粒子源和散射靶的条件下观察到α粒子被散射在90°和60°角方向上单位立体角内的粒子数之比为：A ．4:1 B.2:2 C.1:4 D.1:8（9）在α粒子散射实验中,若把α粒子换成质子,要想得到α粒子相同的角分布,在散射物不变条件下则必须使：A ．质子的速度与α粒子的相同；B ．质子的能量与α粒子的相同；C ．质子的速度是α粒子的一半；D ．质子的能量是α粒子的一半2. 填空题（1）α粒子大角散射的结果证明原子结构为 核式结构 .（2）爱因斯坦质能关系为 2E mc = .（3）1原子质量单位（u ）= 931.5 MeV/c 2. (4) 24e πε= 1.44 fm.MeV. 3．计算题习题1-2、习题1-3、习题1-5、习题1-6.4．思考题1、什么叫α粒子散射？汤姆孙模型能否说明这种现象？小角度散射如何？大角度散射如何？2、什么是卢瑟福原子的核式模型？用原子的核式模型解释α粒子的大角散射现象。
原子物理学期末总复习
能级跃迁选择定则:
即 li 奇数 l’ i 偶数
对L S耦合：S 0; L 0,1; J 0,1( J 0 J ' 0除外) J 0,1( J 0 J ' 0除外) 对j j耦合：j 0,1;
跃迁还需满足初末态宇 称相反，
11. 碱金属原子能级的双重结构是由于下面的原因产生 : [ D] （A)相对论效应; （ B) 原子实极化; （C) 价电子的轨道贯穿; （D) 价电子自旋与轨道角动量相 互作用。
12.在（1）α粒子散射实验，（2）弗兰克－赫兹实验， （3）史特恩－盖拉实验，（4）反常塞曼效应中， 证实电子存在自旋的有：[ B ] （A）（1），（2）; （B）（3）,（4）; （C）（2）,（4）; （D）（1）,（3）.
多电子原子
电子组态: n1l1n2l2原子态(n1l1n2l2)2s+1Lj 电子组态的耦合方式:L-S耦合, j-j耦合 核外电子排布规则:泡利原理和能量最低原理 泡利不相容原理：在一个原子中不可能有两个或者两个 以上的电子具有完全相同的四个量子数（n,l,ml,ms）。 换言之，原子中的每一个状态只能容纳一个电子.
5. 一次电离的氦离子（ He+ ）处于 n=2 的激发态，根据波 尔理论，能量E为 [ C ] (A)-3.4eV ( B) -6.8eV ( C) -13.6eV (D) -27.2eV
6．夫兰克—赫兹实验证明了[ B ] (A)原子内部能量连续变化 (B)原子内存在能级 (C)原子有确定的大小 (D)原子有核心
16.处于L=3, S=2原子态的原子,其总角动量量子数J的可能 取值为:[ B ] (A) 3, 2,1; (B) 5, 4, 3, 2, 1; (C) 6, 5, 4, 3; (D) 5/2, 4/2, 3/2, 2/2, 1/2。
原子物理总复习
E = En,l + El ,s
En , l R = − hc 2 (n − ∆ l )
2 *4
Rhcα Z j ( j + 1) − l (l + 1) − s(s + 1) El ,s = 1 2 3 n l (l + )(l + 1) 2
5、碱金属原子态符号 、
n
2
2s+1
L
j
j=l+1/2 l j=l-1/2 l
锂原子能级图
光谱符号
主 线 系： 第二辅线系： 第二辅线系： 第一辅线系： 第一辅线系： 柏格曼系： 柏格曼系：
~ =2S − nP ν
~ = 2P − nS ν ~ = − nD ν
~ = 3D − nF ν
n = 2, 3, 4… n =3,4,5… n =3,4,5… n =4,5,6…
第一章
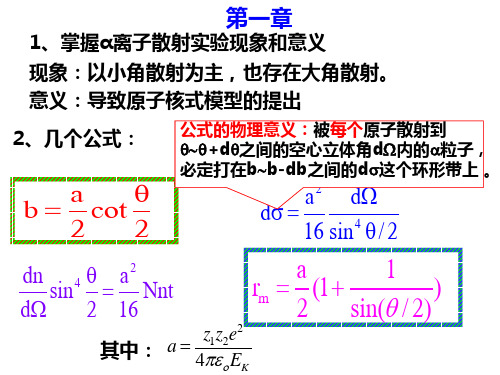
掌握α 1、掌握α离子散射实验现象和意义 现象：以小角散射为主，也存在大角散射。 现象：以小角散射为主，也存在大角散射。 意义： 意义：导致原子核式模型的提出 几个公式： 2、几个公式：
公式的物理意义：被每个原子散射到 公式的物理意义： 每个原子散射到 θ∼θ+d 之间的空心立体角d 内的α粒子， +dθ θ∼θ+dθ之间的空心立体角dΩ内的α粒子， 必定打在b db之间的 之间的d 必定打在b∼b-db之间的dσ这个环形带上 。
2
n r = rn = a1 Z
3、玻尔三个假设
定态假设 频率条件 角动量量子化
4、类氢离子能级和轨道半径公式
Z E n = E1 ⋅ 2 n
2
n r = rn = a1 Z
2
原子物理学复习资料
原子物理学总复习指导名词解释：光谱，氢原子线系，类氢离子，电离电势，激发电势，原子空间取向量子化，原子实极化，轨道贯穿，有效电荷数，电子自旋，磁矩，旋磁比，拉莫尔进动，拉莫尔频率，朗德g因子，电子态，原子态，塞曼效应，电子组态，LS耦合，jj耦合，泡利原理，同科电子，元素周期表，壳层，原子基态，洪特定则，朗德间隔定则数据记忆：电子电量，质量，普朗克常量，玻尔半径，氢原子基态能量，里德堡常量，hc，ħc，玻尔磁子，精细结构常数，拉莫尔进动频率著名实验的内容、现象及解释：α粒子散射实验，光电效应实验，夫兰克—赫兹实验，施特恩—盖拉赫实验，碱金属光谱的精细结构，塞曼效应，反常塞曼效应，理论解释：（汤姆逊原子模型的不合理性），卢瑟福核式模型的建立、意义及不足，玻尔氢原子光谱理论的建立、意义及不足，元素周期表计算公式：氢原子光谱线系，玻尔理论能级公式、波数公式，角动量表达式及量子数取值（l，s，j），LS耦合原子态，jj耦合原子态，朗德间隔定则，g因子，塞曼效应，原子基态谱线跃迁图：精细结构，塞曼效应；电子态及组态、原子态表示，选择定则，1.同位素：一些元素在元素周期表中处于同一地位，有相同原子序数，这些元素别称为同位素。
2.类氢离子：原子核外只有一个电子的离子，这类离子与氢原子类似，叫类氢离子。
3.电离电势：把电子在电场中加速，如使它与原子碰撞刚足以使原子电离，则加速时跨过的电势差称为电离电势。
4.激发电势：将初速很小的自由电子通过电场加速后与处于基态的某种原子进行碰撞，当电场电压升到一定值时，发生非弹性碰撞，加速电子的动能转变成原子内部的运动能量，使原子从基态激发到第一激发态，电场这一定值的电压称为该种原子的第一激发电势5.原子空间取向量子化：在磁场或电场中原子的电子轨道只能取一定的几个方向，不能任意取向，一般的说，在磁场或电场中，原子的角动量的取向也是量子化的。
6.原子实极化：当价电子在它外边运动时，好像是处在一个单位正电荷的库伦场中，当由于价电子的电场的作用，原子实中带正电的原子核和带负电的电子的中心会发生微小的相对位移，于是负电的中心不再在原子核上，形成一个电偶极子，这就是原子实的极化。
高考物理原子物理总复习.ppt陈
疑难辨析：
疑难辨析：
hν=E初－E终适用于光子和原子作用而使原子在各定 态之间跃进迁的情况，对于光子和原子作用而使原子电离 和实物粒子与原子作用而使原子激发的情况，则不受此条 件的限制。
疑难辨析：
hν=E初－E终适用于光子和原子作用而使原子在各定 态之间跃进迁的情况，对于光子和原子作用而使原子电离 和实物粒子与原子作用而使原子激发的情况，则不受此条 件的限制。
1.玻尔理论的主要内容
⑴原子只能处于一系列不连续的能量状态中，在这些 状态中原子是稳定的，电子虽然绕核运动，但并不向外辐 射能量。这些状态叫做定态。——定态假设
⑵原子从一种定态跃迁到另一种定态时，它辐射或吸 收一定频率的光子，光子的能量由这两定态的能量差决定， 即hν=E初－E终。——跃迁假设 疑难辨析
在此跃迁过程中，电场力对电子做了正功，因而电势能应减小。
解析：该题主要考查：
⑴玻尔理论，⑵库仑定律和向心力，⑶电势能
正确的思路为： 由玻尔理论可知，氢原子辐射光子后，应从离核较远的轨道跃 迁到离核较近的轨道。 另由经典电磁理论，电子绕核做匀速圆周运动的向心力即为氢 核对电子的库仑力：
在此跃迁过程中，电场力对电子做了正功，因而电势能应减小。
解析：该题主要考查：
⑴玻尔理论，⑵库仑定律和向心力，⑶电势能
解析：该题主要考查：
⑴玻尔理论，⑵库仑定律和向心力，⑶电势能
正确的思路为： 由玻尔理论可知，氢原子辐射光子后，应从离核较远的轨道跃 迁到离核较近的轨道。
解析：该题主要考查：
⑴玻尔理论，⑵库仑定律和向心力，⑶电势能
正确的思路为： 由玻尔理论可知，氢原子辐射光子后，应从离核较远的轨道跃 迁到离核较近的轨道。
⑶原子的不同能量状态跟电子沿不同轨道绕核运动相 对应。原子的定态是不连续的，因此电子的可能轨道也是 不连续的。——轨道能级化假设
原子物理学总复习
原子物理学总复习量子物理卢瑟福微分截面d dN c ( ) d Nntd 散射在某个范围内(θ1到θ2)的几率有效散射截面2d 2 b dba 2 d 16 Sin42dN ' 2 d nt d nt N 3 1 1 4 si n 22a 2 cos第十九章Ch2 原子的量子态量子物理玻尔理论：三步曲1.定态条件(量子态概念); 2.频率条件(量子跃迁); h 3.角动量量子化。
Ln nEn Em实验验证：1.夫兰克-赫兹实验：证实了量子态的存在；2.光谱：三类单电子体系~ 1 Z 2R 1 1 T( m ) T( n ) H 2 n2 m第十九章量子物理~ 1 Z 2R 1 1 T( m ) T( n ) H m 2 n2光谱项R T , E hcT 2 n*n , 碱金属n* n l Z对氢n* n, 类氢n*~ hc 物理量的关系E h hc第十九章量子物理氢光谱rn r1n2 , r1 0.053nm(n 1,2,3, )E1 13.6eVEn E1 n能量E2类氢离子光谱:n2 半径rn a1 ZhcR 2 Z 2 n线系n 4 n 3 n 2n第十九章量子物理E 0帕邢系巴耳末系莱曼系布拉开系n 1E碱金属光谱Li四个线系主线系，nP→2S, T2 s Tnp 主线系~ R R 2 (2 s ) (n p )2第十九章量子物理n 2, 3, 4, 基线系锐线系，nS→2P,又称第二辅线系线系T2 p Tnsn 3, 4, 5, n 3, 4, 5,锐线系漫线系漫线系，nD→2P,又称第一辅线系；线系T2 p Tnd基线系，nF→3D 又称柏格曼线系主线系系T3d Tnfn 4, 5, 6,第十九章量子物理mM Δ 几个光谱名词二体问题me→ M mRA线系限共振线主线rm Mme M r1 r1 (基态) M meR m 1 e M.典型题目：三种体系的光谱计算2-6~2-10,2-13~2-14第四章原子的精细结构第十九章量子物理碱金属精细结构史特恩―盖拉赫实验塞曼效应电子的自旋S基础：原子磁矩，空间量子化1.一个假设(核心)――电子的自旋第十九章量子物理它是与粒子运动状态无关的、粒子的内禀性特性。
原子物理复习总结
原子物理学总复习总结一、原子物理学发展中重大事件1.1897年汤姆孙通过阴极射线管实验发现电子，从而打破了原子不可分的神话，并提出关于原子结构的“葡萄干面包”模型。
2.1900年普朗克提出能量量子化假说，解释黑体辐射问题。
3.1905年爱因斯坦提出光量子假说，并用以解释光电效应。
4.1910年密立根采用“油滴实验”方法精确地测定了电子的电荷，并发现电荷是量子化的。
5.1908年卢瑟福的学生盖革-马斯顿在 粒子散射实验中发现大角度散射现象，1911年卢瑟福基于此实验提出原子的核式结构模型，从而否认了汤姆孙的模型。
但是这种核式结构模型不能解释原子的稳定性、同一性和再生性。
6.1913年波尔为了解释氢原子光谱提出氢原子理论模型，提出三个基本假设：定态理论、能级跃迁条件和轨道量子化条件，可以解释氢原子和类氢原子的光谱。
7.1914年为了验证波尔的能级理论，弗兰克-赫兹实验用电子轰击汞原子，证明了能级的存在，即原子内部定态的能量是量子化的。
8.1916年索末菲将波尔的圆形轨道推广为椭圆轨道理论，并引入相对论修正.9.1921年施特恩-盖拉赫提出一个能直接显示原子轨道角动量空间量子化的实验方案，用银原子束通过不均匀磁场，原子磁矩在不均匀磁场中受磁力，力的大小和方向与原子磁矩空间取向有关。
10.1925年乌伦贝克和古兹密特提出电子自旋假设，电子自旋的引入可以解释碱金属双线结构、赛曼效应和施特恩-盖拉赫实验。
11.1925年泡利提出泡利不相容原理。
提出了多电子原子中电子的排列规则问题。
此定理对费米子系统成立，但是对于玻色子系统不成立。
二、 基本物理规律、定理和公式1.库仑散射公式：,22θctg a b = 为库仑散射因子其中Ee Z Z a 02214πε≡，为散射角参数，为瞄准距离，或者碰撞θb 2.卢瑟福公式：微分散射截面：2sin 16')()(42θθσθσa Nntd dN d d C =Ω=Ω=物理意义：α粒子散射到θ方向单位立体角内每个原子的有效散射截面.3.原子核大小的估计（即入射粒子与原子核的最小距离）：a r =min4.光电效应：221m mv h +=φν 其中00λνφc h h ==为金属的结合能（脱出功），0ν和0λ分别为金属的红限频率和波长，2021m mv eV =，0V 为遏制电压。
原子物理学复习总结提纲
原子物理学复习总结提纲I.引言
A.原子物理学概述
B.原子结构的发现历程
II.原子结构
A.原子的基本组成
B.原子的大小和质量
C.原子核的结构
1.质子和中子
2.原子核的稳定性和不稳定性
D.原子壳层结构
1.电子的概念和特性
2.原子层能级
3.壳层填充规则
III.原子光谱
A.光的性质和特性
B.原子光谱的产生机制
C.原子发射光谱
1.电子激发
2.原子的激发态和基态
3.能级跃迁和发射光谱
D.原子吸收光谱
1.光的吸收和衰减
2.能级跃迁和吸收光谱IV.原子核物理学
A.原子核的性质和特性
B.原子核的稳定性和放射性
1.放射性的概念和分类
2.放射性衰变的过程和特征
C.核反应和核能
1.核反应的概念和条件
2.核能及其应用
V.原子物理学的应用
A.核技术与核工程
1.核裂变与核聚变
2.核电站和核燃料循环
B.医学影像学和放射治疗
1.X射线和CT扫描
2.放射治疗的原理和应用
C.等离子体物理学
1.等离子体的概念和性质
2.等离子体的应用和研究VI.总结
A.原子物理学的重要性和意义
B.原子物理学的发展前景
C.总结复习要点。
原子物理学复习资料讲解
原子物理学复习资料讲解1 原子物理学总复习指导名词解释：光谱，氢原子线系，类氢离子，电离电势，激发电势，原子空间取向量子化，原子实极化，轨道贯穿，有效电荷数，电子自旋，磁矩，旋磁比，拉莫尔进动，拉莫尔频率，朗德g因子，电子态，原子态，塞曼效应，电子组态， LS耦合，jj耦合，泡利原理，同科电子，元素周期表，壳层，原子基态，洪特定则，朗德间隔定则数据记忆：电子电量，质量，普朗克常量，玻尔半径，氢原子基态能量，里德堡常量，hc，?c，玻尔磁子，拉莫尔进动频率著名实验的内容、现象及解释：α粒子散射实验，夫兰克—赫兹实验，施特恩—盖拉赫实验，碱金属光谱的精细结构，塞曼效应，反常塞曼效应，康普顿效应理论解释：（汤姆逊原子模型的不合理性），卢瑟福核式模型的建立、意义及不足，玻尔氢原子光谱理论的建立、意义及不足，元素周期表计算公式：氢原子光谱线系，玻尔理论能级公式、波数公式，角动量表达式及量子数取值（l，s，j），LS耦合原子态，朗德间隔定则，g因子，塞曼效应，原子基态谱线跃迁图：氢原子谱线跃迁、类氢原子谱线跃迁，碱金属原子能级跃，精细结构，塞曼效应；电子态及组态、原子态表示，选择定则， 1. 同位素：一些元素在元素周期表中处于同一地位，有相同原子序数，这些元素别称为同位素。
2. 类氢离子：原子核外只有一个电子的离子，这类离子与氢原子类似，叫类氢离子。
3. 电离电势：把电子在电场中加速，如使它与原子碰撞刚足以使原子电离，则加速时跨过的电势差称为电离电势。
4. 激发电势：将初速很小的自由电子通过电场加速后与处于基态的某种原子进行碰撞，当电场电压升到一定值时，发生非弹性碰撞，加速电子的动能转变成原子内部的运动能量，使原子从基态激发到第一激发态，电场这一定值的电压称为该种原子的第一激发电势2 5. 原子空间取向量子化：在磁场或电场中原子的电子轨道只能取一定的几个方向，不能任意取向，一般的说，在磁场或电场中，原子的角动量的取向也是量子化的。
原子物理学总复习大纲
原子物理学总复习大纲第一章 原子模型 纲要1．原子的大小和质量原子的线度r 约在10-10米数量级.原子的质量使用原子质量单位u,1u 为1个碳原子12C 质量的1/12,1u=1.6605402×10-27千克.2．卢瑟福核式结构几种结构模型：汤姆逊枣糕模型（西瓜模型）、长冈半太郎土星模型、卢瑟福核式结构模型。
卢瑟福核式结构模型：原子是由原子核和核外电子组成的,原子核带正电荷Ze ,几乎集中了原子的全部质量,核外电子在核的库存仑场中绕核运动.与实验结果符合最好。
原子核的线度r 为10-14～10-15米的数量级.3.α粒子散射理论（验证模型的理论） 偏转角与瞄准距离的关系:22θcot a b = 或 ctg θ/2=4πεоMv ²/(2Ze ²)b卢瑟福散射公式: 原子核半径大小的估算公式:)2(12θcsc +=a r m或 )21(1241220θπεsi n +=Mv Ze r m 第二章玻尔模型 纲 要1．里德伯(J.R.Rydberg)方程:（1）氢、类氢离子的里德伯方程的波数表示形式⎥⎦⎤⎢⎣⎡-=≡22111n m R H λν~ ⎥⎦⎤⎢⎣⎡-=≡22111n m R Z A λν~ （2）里德伯方程的光谱项表示形式ν~=T (m)-T (n),（3）氢、类氢离子里德伯方程的能量表示形式 []2211n m hcR Z c h h A -==λν 2n Rhc Z E n -= eV Rhc 613.=2. 里德伯公式对应的轨道跃迁、能级跃迁两种形象表示21)441()(422210θπεθσsin E e Z Z c =3．其他一些相关量 （1）氢、类氢原子的里德伯常量M m R R A +=∞11（2）能级间跃迁两能级能量差E 和波长、波数的关系E n m K e V 241.=λ nmKeV E 2411.~==λν（3）氢原子、类氢原子轨道半径公式 n a r n 1= a 1=0.053nm（4）氢原子电子速度公式n c V n α= α=1/1374．一些相关思想（1） 普朗克为了解释黑体辐射实验，引入了能量交换量子化的假说：E =h ν:普朗克常量h 的物理意义是：h 是能量量子化的量度，即能量分立性的量度。
原子物理总复习-2
n l 1
3、能量状态：
E nl
Z Rhc
2
*2
n Rhc 2 (n l )
Rhc n
*2
Ens Enp End Enf En
跃迁选择定则 碱金属光谱的解释
二.考虑精细结构 主线系双线、锐线系双线、漫线系三线、基线系三线
1.运动状态 电子绕原子实作椭圆轨道运动 ＋电子自旋运动
1 hc / mv 2 2 h h p mv
1 hc / m0 v 2 2
h h p m0 v
2.4 基于德布罗意假设得出的公式 用条件是： A.自由电子，非相对论近似； B.一切实物粒子，相对论近似； C.被电场束缚的电子，相对论结果； D.带电的任何自由粒子，非相对论近似。
8.如果对碱金属原子仅考虑轨道运动，其状态应该用哪几个 量子数完整的描述？ A.n,l B.n,l,j C.n,l,ml D.n,l,ms 9.把3Li++电离成3Li+++，需多少电子伏的能量？ A.40.7 B.196 C.5.39 D.122 10.碱金属原子能级的双重结构是由于下列哪一项产生的？ A．相对论效应 B原子实的极化 C 价电子的轨道贯穿 D 价电子的自旋轨道相互作用 11.产生钠的两条黄谱线的跃迁是： A.3P1/2 → 3S1/2, 3P3/2 → 3S1/2, B. 4S1/2,→ 3P1/2 4S1/2, →2P3/2 C.4D3/2 → 3P1/2 4D3/2 →3P3/2 D.4D5/2 → 2P1/2 4D3/2 → 2P3/2
l 0， 2，， ， 1)— 角量子数 1， 3 ( n 表示这些状态) (用s、p、d、f、
(3)角动量在空间取向的量子化 电子“轨道”角动量L在 z 方向(外磁场方向)的分量：
2023高考总复习讲义—— 原子物理
专题十五原子物理一、黑体辐射与能量子（了解）1.一切物体都在辐射电磁波，这种辐射与物体的温度有关，叫热辐射。
热辐射：一切物体都在辐射电磁波，这种辐射与物体的温度有关。
物体在室温时，热辐射的主要成分是波长较长的电磁波，不能引起人的视觉。
当温度升高时，热辐射中较短波长的成分越来越强。
常温下我们看到的物体的颜色就是反射光所致。
一些物体在光线照射下看起来比较黑，那是因为它吸收电磁波的能力较强，而反射电磁波的能力较弱。
2.黑体：某种物体能够完全吸收入射的各种波长的电磁波而不发生反射，这种物体叫黑体。
3．黑体辐射的实验规律①一般材料的物体，辐射的电磁波除与温度有关外，还与材料的种类及表面状况有关．②黑体辐射电磁波的强度按波长的分布只与黑体的温度有关．a．随着温度的升高，各种波长的辐射强度都增加．b．随着温度的升高，辐射强度的极大值向波长较短的方向移动．4．★★★普朗克能量子：带电微粒辐射或者吸收能量时，只能辐射或吸收某个最小能量值的整数倍．即能量的辐射或者吸收只能是一份一份的．这个不可再分的最小能量值ε叫做能量子．能量子的大小：ε＝hν，其中ν是电磁波的频率，h称为普朗克常量．爱因斯坦光子说：空间传播的光本身就是一份一份的，每一份能量子叫做一个光子．光子的能量为ε＝hν。
二、光电效应规律(1)每种金属都有一个极限频率．(2) 光电流的强度与入射光的强度成正比．(3)光照射到金属表面时，光电子的发射几乎是瞬时的．(4) 光子的最大初动能与入射光的强度无关，随入射光的频率增大而增大． 理解：（1）光照强度（单色光） 光子数 光电子数 饱和光电流 （2）光子频率ν 光子能量 ε＝hν爱因斯坦光电效应方程（密立根验证） E k ＝hν－W 0 遏制电压 U c e=E k 【例1】光电效应实验中，下列表述正确的是( )A ．光照时间越长光电流越大B ．入射光足够强就可以有光电流C ．遏止电压与入射光的频率有关D ．入射光频率大于极限频率才能产生光电子【解析】 各种金属都存在着极限频率，低于极限频率的任何入射光强度再大、照射时间再长都不会发生光电效应；发生光电效应时，光电流的强度与入射光的强度成正比；遏止电压随入射光的频率增大而增大，故CD 选项正确．【例2】某种金属逸出光电子的最大初动能E km 与入射光频率ν的关系如图1－13所示，其中ν0为极限频率．从图中可以确定的是________．(填选项前的字母)A ．逸出功与ν有关B ．E km 与入射光强度成正比C ．当ν<ν0时，会逸出光电子D ．图中直线的斜率与普朗克常量有关【解析】 由爱因斯坦光电方程E k ＝hν－W 和W ＝hν0(W 为金属的逸出功)可得，E k ＝hν－hW 00=νhν0，可见图象的斜率表示普朗克常量，D正确；只有ν≥ν0时才会发生光电效应，C错；金属的逸出功只和金属的极限频率有关，与入射光的频率无关，A错；最大初动能取决于入射光的频率，而与入射光的强度无关，B错．【例3】在光电效应实验中，某金属的截止频率相应的波长为λ0，该金属的逸出功为________．若用波长为λ(λ<λ0)的单色光做实验，则其遏止电压为________．已知电子的电荷量、真空中的光速和普朗克常量分别为e、c和h.【答案】h cλ0hce·λ0－λλ0λ【解析】截止频率即刚好发生光电效应的频率，此时光电子的最大初动能为零，由爱因斯坦光电效应方程E k＝hν－W0和c＝λ0ν得：W0＝h cλ0.若用波长为λ的单色光做实验，光电子的最大初动能E k＝hν－W0＝h cλ－hcλ0，设其截止电压为U，则eU＝E k，解得：U＝hce·λ0－λλ0λ.三、光的波粒二象性与物质波光电效应是指物体在光的照射下发射出电子的现象，发射出的电子称为光电子。
原子物理学总复习指导
原子物理学总复习指导原子物理学总复习指导名词解释：光谱，氢原子线系，类氢离子，电离电势，激发电势，原子空间取向量子化，原子实极化，轨道贯穿，有效电荷数，电子自旋，磁矩，旋磁比，拉莫尔进动，拉莫尔频率，朗德g因子，电子态，原子态，塞曼效应，电子组态，LS耦合，jj耦合，泡利原理，同科电子，元素周期表，壳层，原子基态，洪特定则，朗德间隔定则数据记忆：电子电量，质量，普朗克常量，玻尔半径，氢原子基态能量，里德堡常量，hc，?c，玻尔磁子，精细结构常数，拉莫尔进动频率著名实验的内容、现象及解释：α粒子散射实验，光电效应实验，夫兰克—赫兹实验，施特恩—盖拉赫实验，碱金属光谱的精细结构，塞曼效应，反常塞曼效应，理论解释：（汤姆逊原子模型的不合理性），卢瑟福核式模型的建立、意义及不足，玻尔氢原子光谱理论的建立、意义及不足，元素周期表计算公式：氢原子光谱线系，玻尔理论能级公式、波数公式，角动量表达式及量子数取值（l，s，j），LS 耦合原子态，jj耦合原子态，朗德间隔定则，g因子，塞曼效应，原子基态谱线跃迁图：精细结构，塞曼效应；电子态及组态、原子态表示，选择定则，1.同位素：一些元素在元素周期表中处于同一地位，有相同原子序数，这些元素别称为同位素。
2.类氢离子：原子核外只有一个电子的离子，这类离子与氢原子类似，叫类氢离子。
3.电离电势：把电子在电场中加速，如使它与原子碰撞刚足以使原子电离，则加速时跨过的电势差称为电离电势。
4.激发电势：将初速很小的自由电子通过电场加速后与处于基态的某种原子进行碰撞，当电场电压升到一定值时，发生非弹性碰撞，加速电子的动能转变成原子内部的运动能量，使原子从基态激发到第一激发态，电场这一定值的电压称为该种原子的第一激发电势5.原子空间取向量子化：在磁场或电场中原子的电子轨道只能取一定的几个方向，不能任意取向，一般的说，在磁场或电场中，原子的角动量的取向也是量子化的。
6.原子实极化：当价电子在它外边运动时，好像是处在一个单位正电荷的库库仑场中，当由于价电子的电场的作用，原子实中带正电的原子核和带负电的电子的中心会发生微小的相对位移，于是负电的中心不再在原子核上，形成一个电偶极子，这就是原子实的极化。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n = 1、2、3…
两个实验：
1、夫兰克—赫兹实验 物理意义：为原子的量子化能级的存在给出了直接的 实验验证。 2、史特恩—盖拉赫实验 史特恩—盖拉赫实验证实了 （1）角动量空间取向量子化； （2）电子自旋假设。
第三章 量子力学基础
光的波粒二象性 微观粒子的二象性 海森堡不确定关系
h h P mv
1
2
总角动量
J L S J L S, L S 1,......, L S
2 S 1
LS耦合下的原子态符号表示:
LJ
s=0，单重态 s=1，三重态
能级排布规则 洪特定则 朗德间隔定则
j-j 耦合
j1
1
s1
j1 j2
1 2
s1, 1 s1 1,...., s2 ,
j-j 耦合
3、在外磁场中原子能级的分裂
拉莫尔旋进
在外磁场中原子能量计算公式
M J , J 1,...... J 磁量子数 在外磁场中,原子的能级分裂成 2 J 1个,间隔为 g B B
与能量变化ΔE对应的能级的光谱项变化为：
E T MgL; hc eB L 4 mc
一、基本内容
碱金属原子光谱项
R R T 2 2 (n x ) n
碱金属原子定态的能级
Enl hcT(nl) hcR hcR 1 13 . 6 ev 2 2 2 (n x ) n n
2、碱金属原子光谱规律的解释
⑴ 多电子原子结构的价电子模型 ⑵碱金属原子能级简并解除，能量不仅与n有关，还与l 有关。原因： a. 原子实极化。 b. 轨道贯穿。
2、玻尔的氢原子理论。
1、氢原子光谱的一般规律
原子发光具有线状光谱的特征，氢原子光谱的实验规律是：
1 1 R( 2 2 ) T m T n m n
R — 里德堡常数；T(m) —光谱项。 光谱线系 m = 1，n = 2、3、4…，赖曼系（紫外）
1
m = 2，n = 3、4、5…，巴尔末系（可见光） m = 3，n = 4、5、6…，帕邢系（红外）
Mv2 2E ctg 4 0 bk b 2 2 2Ze q1q2
3. 卢瑟福公式：
被散射到与粒子的初始运动方向成θ 角的元立体角dΩ 内的 相对粒子数为： 2
dn 1 2 Ze 2 d ( ) Nt ( ) 2 n 4 0 Mv sin 4 2
第二章 原子的能级和辐射
重点： 1、氢ቤተ መጻሕፍቲ ባይዱ子光谱的实验规律。
塞曼效应的解题思路： 应掌握分析塞曼效应、计算、作图的基本方法。 基本步骤 1， 计算原谱线跃迁初、末态的朗德因子g1和g2 2，列表计算可能的 M1 g1 , M 2 g 2 ; M 2 g 2 M1 g1 值 3，计算分裂后每条谱线与原谱线的频率差（或波数差）
eB ( M 2 g 2 M 1 g1 ) 4m ~ (M g M g ) L 或 2 2 1 1 eB L 4m c
Els s B 自旋与轨道角动量耦合： Pj P l P s
自旋磁矩与轨道运动产生的磁场相互作用引起的能量修正 项是：
pj
j ( j 1)
j l s, l s 1,....., l s
精细结构产生的原因：对于S态电子（l=0），j量子数取 唯一值1/2，故为单层。对于p、d、f…等电子（l≠0），j 量子数取两个可能值，故为双层。
h 自旋运动： ps s ( s 1) 2
B
he 4m
e s ps m
s s(s 1)B
原子的磁矩=电子的轨道磁矩+电子的自旋磁矩+原子核的磁矩 电子的轨道磁矩+电子的自旋磁矩
在LS耦合下原子总磁矩的计算公式 1、单电子原子的磁矩 e e l s pl
碱金属原子光谱精细结构的规律
四个线系 主线系 第二辅线系 第一辅线系 柏格曼线系
（锐线系） （漫线系） （基线系）
碱金属原子光谱精细结构产生的原因 电子自旋
轨道角动量
自旋角动量
pl l (l 1) ps s( s 1)
l 0,1,.....n -1 1 s 2
自旋 — 轨道耦合
P1
2 2
P3
2 2
2
3d
D3
2
D5
2
第五章 多电子原子
重点：
1、氦和碱土金属的光谱的一般规律 2、两个价电子的角动量耦合规律和原子态 3、泡利原理 4、多电子原子光谱的一般规律 5、跃迁选择定则
1.氦和碱土金属光谱规律
1.两套光谱线系，两套能级 2.两套能级间不产生跃迁 3.电子组态相同的，三重态能级总低于单一态相应的能级； 三重能级结构中，同一 值的三个能级， 值大的能级 低（倒转次序）
m = 4，n = 5、6、7…，布喇开系（远红外）
2、玻尔的氢原子理论
三个基本假设： ⑴ 定态假设：电子在符合量子条件的轨道上运动时，原子 具有一定能量而不发生辐射。 ⑵ 频率规则：电子从能量En的定态跃迁到Em时，原子辐射 光子，其频率 En Em
h
⑶ 角动量量子化条件：Pφ= mrv = n h/2π ，n = 1、2、3…
n=1,2,3
X射线谱由连续谱和标识谱两部分组成。
1，X射线连续谱发射机制：轫致辐射 2，X射线标识谱发射机制：内层电子跃迁 连续谱的短波限
hc
0
eV
min
1.242 nm U (kV )
各元素标识谱有相似结构，分为波长最短的K线系、L线系、 M线系等。
X射线的吸收谱
朗伯-比耳定律：
I (x) I 0e x
J ( J 1) L( L 1) S ( S 1) g 1 2 J ( J 1)
J(J 1 ) ji(ji 1 ) J P(J P 1 ) 2 J(J 1 ) J(J 1 ) J P(J P 1 ) ji(ji 1 ) gp 2 J(J 1 ) g gi
j
2.电子组态的表示
Na : 基态电子组态： 1s
2s 2p 3s 2 2 6 1 1s 2s 2p 3p
2
2
6
1
简记：3s
1
简记： 3p
1
L-S耦合
S s1 s2
S s1 s2 , s1 s2 1,......, s1 s2
L
1
L
1
2
2, 1
2
1,......,
1、元素性质的周期性变化 2、原子核外电子排布遵守两条规律：泡利不相容原理和最 低能量原理。 四个量子数：n；l；ml；ms。不能有两个电子具有完全相 同的四个量子数，即原子中的电子是分布在不同状态的。
3、原子核外电子的壳层结构
电子壳层： K、L、M、N、O、P、Q 对应量子数n： 1、2、3、4、 5、6、7 每个电子壳层能容纳的最多电子数为2n2。 次壳层： S、P、d、f … 对应量子数l：0、1、2、3 … 各次壳层能容纳的最多电子数为2(2l+1) 了解各个周期原子基态的电子组态。
— 洛仑兹单位
画出能级图和能级跃迁图。
⑵塞曼跃迁的选择定则： ∆M = 0 产生π光。 ∆M = ±1 产生σ光。
2. 镉6438.47埃的塞曼效应
这条线对应的跃迁是
1D 2 1P 1
L
1D 2
S
0 0
J
2 1
M
0，±1，± 2 0 ， ±1
g
1 1
Mg
2 1
2 1
1P
1
(
1
'
1
) M 2 g 2 M 1 g1 L (0, 1) L
2.确定原子基态光谱项的简易方法
(1)由泡利原理和能量最低原理求一定电子组态的最大S。
(2)求上述情况上的最大L。 (3)由半数法则确定J。 (4)按2s+1LJ 确定基态原子态（光谱项）。
第八章 X射线
重点：
X射线的基本性质
X射线的产生机制 与X射线相关的原子能级 康普顿散射
布拉格方程 2dsin =n ,
2
1
s1 s2
j2
2
s2
s2 1,....,
2
J j1 j2
J j1 j2 , j1 j2 1,...., j1 j2
j-j耦合下原子态标记
( j1 , j2 ) J
泡利不相容原理
在一个原子中，不可能有两个或两个以上的电子具有完全
相同的状态(完全相同的四个量子数)。
辐射跃迁的选择定则 一. 跃迁只能发生在不同宇称的原子态间
二. 看具体的耦合形式
L-S耦合跃迁选择定则: j-j耦合跃迁选择定则:
Δj1 0
ΔS 0 ΔL 0 , 1 ΔJ 0 , 1 （0
0除外）
Δj2 0 , 1 Δ J 0 , 1 （0
或对换
0除外）
第六章 在磁场中的原子
2m ps
m
e ( pl 2 ps ) 2m
单电子原子总磁矩（有效磁矩）:
j(j 1 ) l(l 1 ) s(s 1 ) g 1 2 j(j 1 )
e j gj 2m
朗德因子
2、多电子原子的磁矩
L-S 耦合
J
g
e 2m
p
J
原子态符号
2 s 1 Lj 重态数
单电子辐射跃迁的选择定则：∆l=±1，∆j=0，±1