实验2 刚体转动惯量的测定
刚体转动惯量的测量实验报告

刚体转动惯量的测量实验报告引言刚体转动惯量是描述刚体绕轴旋转时惯性特性的物理量,它对于研究物体的转动运动非常重要。
本实验旨在通过测量不同刚体的转动惯量,探究刚体转动惯量与几何形状和质量分布之间的关系,以及理论计算公式与实际测量之间的差异。
实验设备和材料1.转动惯量测量仪器:包括支架、转轴、弹簧、刻度盘等。
2.不同刚体样品:本实验使用了长方体、圆盘和圆环三种常见刚体样品。
3.实验辅助工具:包括卷尺、电子天平等。
实验步骤步骤一:准备工作1.搭建转动惯量测量仪器:将支架搭建好,并通过转轴和弹簧将测量仪器固定在支架上。
2.校准刻度盘:确保刻度盘的零点对齐并能够准确度量转动角度。
步骤二:测量不同刚体的转动惯量1.测量长方体的转动惯量:–将长方体放置在转轴上,并调整初始角度。
–施加一定的力矩,使长方体绕轴做匀速转动。
–通过刻度盘测量长方体转动的角度和力矩的大小。
–重复上述步骤,记录多组数据,以增加测量精度。
2.测量圆盘的转动惯量:–将圆盘放置在转轴上,并调整初始角度。
–施加一定的力矩,使圆盘绕轴做匀速转动。
–通过刻度盘测量圆盘转动的角度和力矩的大小。
–重复上述步骤,记录多组数据,以增加测量精度。
3.测量圆环的转动惯量:–将圆环放置在转轴上,并调整初始角度。
–施加一定的力矩,使圆环绕轴做匀速转动。
–通过刻度盘测量圆环转动的角度和力矩的大小。
–重复上述步骤,记录多组数据,以增加测量精度。
步骤三:数据处理与分析1.根据测量的角度和力矩数据,利用公式计算刚体的转动惯量。
2.利用不同质量分布和几何形状的刚体的转动惯量数据,探究其之间的关系。
3.对比理论计算公式与实际测量结果之间的差异,并对可能存在的误差进行分析和讨论。
结果与讨论不同刚体的转动惯量测量结果•长方体:–测量数据1:转动惯量= 0.25 kg·m^2–测量数据2:转动惯量= 0.26 kg·m^2•圆盘:–测量数据1:转动惯量= 0.15 kg·m^2–测量数据2:转动惯量= 0.17 kg·m^2•圆环:–测量数据1:转动惯量= 0.20 kg·m^2–测量数据2:转动惯量= 0.19 kg·m^2转动惯量与几何形状和质量分布的关系从测量数据可以看出,长方体的转动惯量较大,圆盘次之,圆环最小。
刚体转动惯量的测定实验报告

刚体转动惯量的测定实验报告一、实验目的1、学习用三线摆法测定刚体的转动惯量。
2、加深对转动惯量概念的理解。
3、掌握用游标卡尺和秒表等仪器的使用方法。
二、实验原理三线摆是由三根等长的悬线将一水平圆盘悬挂在一个固定的支架上构成的。
当圆盘绕中心轴 OO' 作扭转摆动时,圆盘的运动可以看作是圆盘绕通过其重心且垂直于盘面的轴线的转动和平动的合成。
设圆盘的质量为 m,半径为 R,对于通过其重心且垂直于盘面的轴线的转动惯量为Ic。
当圆盘扭转一个小角度θ 时,圆盘的势能变化为:ΔEp = mgh其中,h 为圆盘重心上升的高度。
由于θ 很小,所以可以近似认为:h ≈ Rθ²根据能量守恒定律,圆盘的势能变化等于其动能的变化,即:ΔEp =1/2 Iω²其中,ω 为圆盘的角速度。
又因为圆盘的摆动周期为 T,所以ω =2π/T。
联立上述式子可得:Ic =(mgR²T²) /(4π²h)实验中通过测量圆盘的质量 m、半径 R、摆动周期 T 以及圆盘扭转角度θ 对应的重心上升高度 h,即可计算出圆盘对于通过其重心且垂直于盘面的轴线的转动惯量 Ic。
三、实验仪器三线摆、游标卡尺、米尺、秒表、待测刚体(圆环、圆柱等)、托盘天平。
四、实验步骤1、用托盘天平测量圆盘和待测刚体的质量。
2、用游标卡尺测量圆盘和待测刚体的直径,分别测量多次,取平均值。
3、调整三线摆的悬线长度,使上下圆盘之间的距离约为 50cm 左右。
4、轻轻转动上圆盘,使圆盘作小角度的扭转摆动,用秒表测量圆盘摆动 50 个周期的时间,重复测量多次,取平均值,计算出摆动周期T。
5、将待测刚体放在圆盘上,使两者的中心轴线重合,按照上述方法测量系统(圆盘和待测刚体)的摆动周期 T'。
五、实验数据记录与处理1、圆盘质量 m =______ g,直径 D =______ cm,半径 R =D/2 =______ cm。
刚体转动惯量的测定实验报告

刚体转动惯量的测定实验报告实验目的:1.了解刚体转动惯量的概念和定义;2.学习利用旋转法测量刚体转动惯量;3.掌握利用平衡法测量刚体转动惯量的方法。
实验仪器:1.旋转法实验装置:圆盘、转轴、杠杆、螺旋测微器、质量砝码等;2.平衡法实验装置:平衡木、质量砝码、支撑点等。
实验原理:1.旋转法实验原理:设刚体的转动惯量为I,当刚体在转轴上匀加速转动时,在力矩M作用下,刚体产生角加速度α。
根据牛顿第二运动定律和角动量定理可得到:M=Iα(1)在角加速度恒定的情况下,转动惯量I与力矩M成正比。
2.平衡法实验原理:刚体转动惯量测量的基本原理是利用转轴位置的移动来改变刚体的转动惯量,使得转动惯量I和重力力矩Mg达到平衡,即:Mg=Iα(2)在刚体转动平衡的状态下,转动惯量I与重力力矩Mg成正比。
实验步骤:1.旋转法实验步骤:(1)将圆盘固定在转轴上,并将转轴竖直插入转台中央的孔中。
(2)将杠杆固定在圆盘上,使得杠杆能够自由转动。
(3)在杠杆上加上一定的质量砝码,使得圆盘开始匀加速转动。
(4)测量转轴上的螺旋测微器的读数,记录下圆盘旋转一定角度时的螺旋测微器的读数。
(5)记录下圆盘质量与加速度的数值,计算出实验测得的转动惯量。
2.平衡法实验步骤:(1)将平衡木放置在支撑点上,使得平衡木可以自由转动。
(2)在平衡木上加上一定的质量砝码,使得平衡木保持平衡。
(3)移动转轴的位置,直到平衡木重新平衡。
(4)记录下转轴位置与加在平衡木上的质量的数值,计算出实验测得的转动惯量。
实验数据处理:1.旋转法实验数据处理:(1)根据螺旋测微器的读数,计算出圆盘旋转的角度。
(2)根据实验测得的圆盘质量和加速度的数值,计算出实验测得的转动惯量。
2.平衡法实验数据处理:(1)根据转轴位置的变化,计算出实验测得的转动惯量。
实验结果分析:根据实验测得的数据,通过旋转法和平衡法两种方法测得的刚体转动惯量进行比较和分析。
分析实验数据的偏差和不确定度,讨论实验结果的可靠性。
实验2 刚体转动惯量的测定

实验2 扭摆法测定物体的转动惯量【实验目的】1.熟悉转动惯量测试仪的使用方法。
2.掌握测试仪常数(弹簧的扭转常数)K 的测定。
3.用扭摆法测定几种不同形状物体的转动惯量,并与理论值进行比较。
【实验仪器】转动惯量测试仪,空心金属圆柱体、实心塑料圆柱体、塑料圆球、细金属杆。
【实验原理】将物体在水平面内转过一角度θ后,在弹簧的恢复力矩作用下物体就开始绕垂直轴作往返扭转运动。
根据虎克定律,弹簧受扭转而产生的恢复力矩M 与所转过的角度θ成正比,即M =-K θ (2-1) 式中,K 为弹簧的扭转常数,根据转动定律 M =I β式中,I 为物体绕转轴的转动惯量,β为角加速度,由上式得 IM=β (2-2) 令 LK =2ω 忽略轴承的磨擦阻力矩,由(2-1)、(2-2)得θωθθβ222-=-==I Kdtd上述方程表示扭摆运动具有角简谐振动的特性,角加速度与角位移成正比,且方向相反。
此方程的解为:θ=Acos(ωt +φ)式中,A 为谐振动的角振幅,φ为初相位角,ω为角速度,此谐振动的周期为 KIT πωπ22==(2-3) 由(2-3)可知,只要实验测得物体扭摆的摆动周期,并在I 和K 中任何一个量已知时即可计算出另一个量。
本实验用一个几何形状规则的物体,它的转动惯量可以根据它的质量和几何尺寸用理论公式直接计算得到,再算出本仪器弹簧的K 值。
若要测定其它形状物体的转动惯量,只需将待测物体安放在本仪器顶部的各种夹具上,测定其摆动周期,由公式(2-3)即可算出该物体绕转动轴的转动惯量。
理论分析证明,若质量为m 的物体绕通过质心轴的转动惯量为I O 时,当转轴平行移动距离X 时,则此物体对新轴线的转动惯量变为I O +mx 2。
称为转动惯量的平行轴定理。
【实验内容】1. 测定弹簧的扭转常数,调整测试仪座底脚螺丝,使水平仪的气泡位于中心。
由于弹簧的扭转常数K 值不是固定常数,它与摆动角度略有关系,摆角在90º左右基本相同,在小角度时变小。
实验二刚体转动惯量的测量

实验二刚体转动惯量的测量梧州学院学生实验报告专业班级:学号:姓名:成绩:实验课程:物理实验实验名称:实验组号:同组成员:实验地点:实验实验时间:指导教师:实验目的:1用实验方法检验刚体绕固定轴的转动定理学习用复摆法测量刚尺的转动惯量。
学习用转动法测量圆盘和圆环的转动惯量。
实验仪器:一、复摆法测量转动惯量实验原理:复摆是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系。
复摆又称为物理摆。
图4-1是表示一个形状不规则刚体,挂于过Oθ角度后释放,它在重力力矩的作用下将绕回转轴自由摆动,这就是一个复摆。
当摆动的角度θ较小时,摆动近似为简谐振动,设刚体绕固定轴O在竖直平面内作左右摆动,G是该物体的重心,与轴O的距离为h,θ为其摆动角度。
若规定右转角为正,此时刚体所受力矩与角位移方向相反,即有若θ很小时((<5()近似有(4-1)根据转动定律,该复摆满足(4-2)其中为该物体转动惯量。
由式(4-1)和式(4-2)可得(4-3)其中。
此方程说明该复摆在小角度下作简谐振动,该复摆振动周期为(4-4)式(4-4)中h为回转轴到重心G的距离;I为刚体对回转轴O的转动惯量;m为刚体的质量;g是当地的重力加速度。
设刚体对过重心G,并且平行于水平的回转轴O的转动惯量为IG,根据平行轴定理得(4-5)将式(4-5)代入式(4-4)得(4-6)整理得(4-7)实验1.本实验所用复摆为一均匀,测量时它悬挂在固定转轴确定的重心位置。
质量均匀,重心在中心位置。
2.以转轴为支点,在竖直平面内拉开一小角度θ<50)后释放使之摆动,用通用计时器测量其摆动周期重复测量5次。
3.用天平出的质量。
4.按式4-7)计算的测量值,并对比理论值求出相对误差。
实验数据记录与处理尺长度am钢尺宽度bm钢尺质量mkg转轴到重心距离hm周期T(s)12345平均转动惯量转动惯量理论值相对误差二、转动法测量转动惯量实验原理:转动惯量仪是一架绕竖直轴转动的支架。
刚体转动惯量的测量实验报告

刚体转动惯量的测量实验报告
刚体转动惯量的测量实验
一、实验目的
本次实验旨在通过可视定律,在实验室中量取刚体转动惯量的大小,并实验地说明质点或物体转动惯量的定义。
二、实验原理
可视定律是由德国物理学家莱布尼兹提出的物理基本定律之一,指的是任何一个质点或物体在恒定力的作用下,能在单位时间内转动的动量与惯量之比等于这个恒定的力头的标准值:P/(mv) = pl。
三、实验装置
实验装置主要由小车、拨杆转厂、光栅、车间、气流罩和电源等组成。
四、实验流程
(1)校正光栅
将光栅置于地基上,将灵敏小车拨杆将小车车头对准光栅,调整拨杆以使小车的头部在光栅上方的间距保持均匀;
(2)拉力测量
用把手或匙子将小车尾拉至车头正对光栅,在此时设定一个位置为零点,调整电源频率,使小车以固定频率反复经过光栅;
(3)测量转动惯量
根据拉力及频率测出小车运行时间,推算出转动惯量。
五、实验结果
根据得到的测量数据,计算刚体转动惯量结果为:0.0018183 kg·m^2。
六、实验结论
本次实验结果与已知值吻合,说明实验装置的校正和测量流程均准确无误,实验基本上达到了预期的要求。
刚体转动惯量的测定实验报告

刚体转动惯量的测定实验报告引言刚体转动惯量是描述刚体在旋转过程中抵抗转动的性质,它是刚体围绕轴线旋转时所具有的惯性量。
在本实验中,我们通过测定刚体关于不同轴线的转动惯量,了解刚体转动惯量的概念与测定方法。
实验目的1.了解刚体转动惯量的概念与意义;2.学习刚体转动惯量的测定方法;3.实验测量刚体转动惯量,验证测定方法的正确性;4.掌握实验仪器的使用方法。
实验原理刚体转动惯量的定义为:$$I=\\Sigma m r^{2}$$其中,I为刚体的转动惯量,m为刚体质点的质量,r为质点到轴线的距离。
本实验主要使用转动盘进行转动惯量的测定。
转动盘由一个固定轴和一个可以转动的圆盘构成。
通过改变转动盘上的物体的位置,改变物体相对于固定轴的距离,可以测定不同轴线上刚体的转动惯量。
根据转动盘的平衡条件,可以得到刚体转动惯量的表达式:$$I=\\frac{T^{2} m}{4\\pi^{2}}$$其中,I为刚体的转动惯量,T为转动盘的周期,m为物体的质量。
实验步骤1.将转动盘调整到水平,固定好;2.在转动盘上放置圆柱体,使其与转动盘的轴线垂直;3.移动圆柱体,调整圆柱体相对于轴线的距离(例如:5cm、10cm、15cm等等),记录下距离;4.切换到计时功能,转动圆盘,记录下5次振动的周期;5.根据周期与距离的关系,计算刚体的转动惯量;6.将圆柱体移动到不同距离,重复步骤4-5,记录不同距离下的转动惯量;7.根据测得的数据,绘制出转动惯量与距离的曲线图。
数据处理与分析根据实验测得的数据,我们可以计算出不同距离下的刚体转动惯量。
将数据绘制成转动惯量与距离的曲线图,可以直观地观察到二者之间的关系。
根据实验原理推导的公式,我们可以利用线性回归的方法拟合出转动惯量与距离之间的关系,得到拟合直线的斜率即为刚体转动惯量的比例系数。
结论通过本实验,我们成功地测定了刚体转动惯量,并绘制了转动惯量与距离的曲线图。
实验结果与理论预期较为一致,验证了实验方法的正确性。
实验2 刚体转动惯量的测定
实验二刚体转动惯量的测定转动惯量是描述刚体转动中惯性大小的物理量,它与刚体的质量分布及转轴位置有关。
正确测定物体的转动惯量,在工程技术中有着十分重要的意义,是高校理工科物理实验教学大纲中的一个重要的基本实验。
IM-2型刚体转动惯量实验仪,应用霍尔开关传感器结合计数计时多功能毫秒仪自动记录刚体在一定转矩作用下,转过β角位移的时刻,从而测定刚体转动时的角加速度和刚体的转动惯量。
1.了解多功能计数、计时毫秒仪测量时间的基本方法;2.用刚体转动法测定物体的转动惯量;3.验证转动定律及平行轴定理;4.分析实验中误差产生的原因和实验中为降低误差应采取的实验手段。
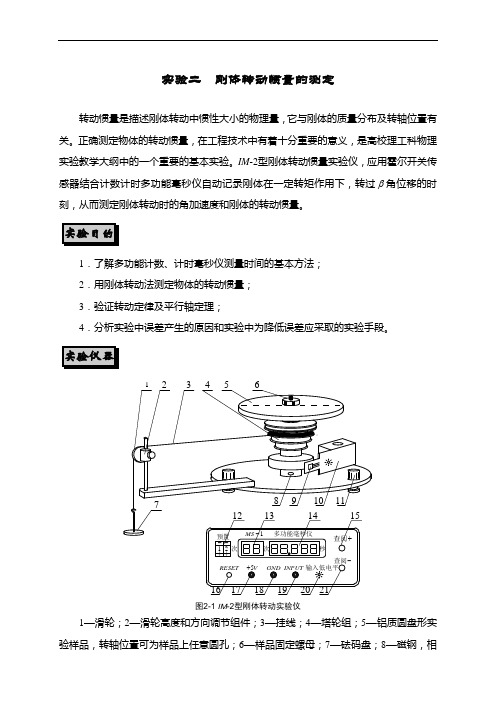
图2-1IM-2型刚体转动实验仪1—滑轮;2—滑轮高度和方向调节组件;3—挂线;4—塔轮组;5—铝质圆盘形实验样品,转轴位置可为样品上任意圆孔;6—样品固定螺母;7—砝码盘;8—磁钢,相对霍尔开关传感器时,传感器输出低电平;9—霍尔开关传感器,红线接毫秒仪V 5+接线柱,黑线接GND 接线柱,黄线接INPUT 接线柱;10—传感器固定架,装有磁钢,可任意放置于铁质底盘上;11—实验样品水平调节旋钮;12—毫秒仪次数预置拔码开关,可预设641-次;13—次数显示,00为开始计数、计时;14—时间显示,与次数相对应,时间为开始计时的累计时间;15—计时结束后,用手按+1查阅键,查阅对应次数的时间;16—毫秒仪复位键,测量前和重新测量时可按该键;17—V 5+电源接线柱;18—电源GND 接线柱;19—INPUT 输入接线柱;20—输入低电平指示;21—计时结束后,用手按次数1-查阅键,查阅对应次数的时间。
一、转动力矩、转动惯量和角加速度的关系当系统受外力作用时,系统作匀加速转动。
系统所受的外力矩有二个,一个为绳子张力T 产生的力矩r T M ⋅=,r 为塔轮上绕线轮的半径;一个是摩擦力矩μM 。
所以,2βμJ M M =+,即2βμJ M r T =+⋅ ----------------------------------------- (2-1)式中2β为系统的角加速度,此时为正值,J 为转动系统的转动惯量,μM 为摩擦力矩,数值为负。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验2 刚体转动惯量的测量[预习思考题]1.实验中的刚体转动惯量实验仪是由哪几部分组成的?2.实验中可以通过什么方法改变转动力矩?3.实验中刚体转动过程的角加速度如何测得?转动惯量是描述刚体转动中惯性大小的物理量,对于绕定轴转动的刚体,它为一恒量,以J表示,即∑=iii r mJ2式中,m i为刚体上各个质点的质量,r i为各个质点至转轴的距离。
由此可见,物体的转动惯量J与刚体的总质量、质量分布及转轴的位置有关。
对于几何形状规则、对称和质量分布均匀的刚体,可以通过积分直接计算出它绕某定轴的转动惯量。
对于形状复杂或非匀质的任意物体,则一般要通过实验来测定,例如,机械零件、电机的转子、炮弹等。
测定物体的转动惯量有多种实验方法,主要分为扭摆法和恒力矩转动法两类。
本实验介绍用塔轮式转动惯量仪测定的方法,是使塔轮以一定形式旋转,通过表征这种运动特征的物理量与转动惯量的关系,进行转换测量。
该方法属于恒力矩转动法。
转动惯量是研究、设计、控制转动物体运动规律的重要参数,实验测定刚体的转动惯量具有十分重要的意义,是高校理工科物理实验教学大纲中的一个重要基本实验。
一、实验目的1.学习用转动惯量仪测定刚体的转动惯量。
2.研究作用于刚体上的外力矩与角加速度的关系。
3.验证转动定律及平行轴定理。
二、实验仪器IM-2刚体转动惯量实验仪及其附件(霍尔开关传感器、砝码等)和MS-1型多功能数字毫秒仪。
三、仪器介绍1.滑轮 2.滑轮高度和方向调节组件 3.挂线 4.塔轮组 5.铝质圆盘承物台 6.样品固定螺母 7.砝码 8.磁钢 9.霍尔开关传感器 10.传感器固定架 11.实验样品水平调节旋钮(共3个) 12.毫秒仪次数预置拨码开关,可预设1-64次 13.次数显示屏 14.时间显示屏 l5.次数+1查阅键 16.毫秒仪复位键 17.+5V 电源接线柱 18.电源GND (地)接线柱 19.INPUT 输入接线柱 20.输入低电平指示 21.次数-1查阅键图4-3-1 IM-2刚体转动惯量实验仪和MS -1型多功能数字毫秒仪结构示意图IM-2刚体转动惯量实验仪主要由绕竖直轴转动的铝质圆盘承物台、绕线塔轮、霍尔开关传感器、磁钢、滑轮组件、砝码等组成。
样品放置在铝质圆盘承物台上,承物台上有许多圆孔,可用于改变样品的转轴位置。
绕线塔轮是倒置的塔式轮,分为四层,自上往下半径分别为3cm 、2.5cm 、2cm 、1.5cm 。
磁钢随转动系统转动,每半圈经过霍尔开关传感器一次,传感器输出低电平,通过连线送到多功能数字毫秒仪。
传感器红线接毫秒仪+5V 电源接线柱,黑线接电源GND (地)接线柱,黄线接INPUT 输入接线柱。
MS -1型多功能数字毫秒仪通过预置拨码开关预置实验所需感应次数。
每轮实验开始前通过复位键清0,直到输入低电平信号触发计时开始,次数显示屏从0次开始计时,直至达到预置次数停止。
计时停止后,方能查阅各次感应时间。
四、实验原理1. 任意样品的转动惯量测定设转动惯量仪空载(不加任何样品)时的转动惯量为J 1,称为系统的本底转动惯量,转动惯量仪负载(加上样品)时的转动惯量为J 2,根据转动惯量的可加性,则样品的转动惯量J x 为21x J J J =-2. 系统的转动惯量测定1)刚体的转动定律刚体绕定轴转动时,刚体的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比,这个关系称为刚体的转动定律。
M J β=利用转动定律,测得刚体转动时的合外力矩及该力矩作用下的角加速度,则可计算出刚体的转动惯量,这是恒力矩转动法测定转动惯量的基本原理和设计思路。
2)应用转动定律求转动惯量塔轮的转动是由挂线加上砝码通过滑轮带动的。
改变砝码的质量或改变塔轮的半径,可以获得不同的转动力矩以满足实验需要。
给系统加一个外力矩,即加适当的砝码,在重力的作用下,砝码会通过挂线带动塔轮作匀加速转动。
该系统的受力分析如图所示。
此时系统所受合外力矩有两个,一个为绳子张力T 产生的力矩M T r =⋅(r 为塔轮上绕线轮的半径),一个为摩擦力矩M μ。
由转动定律得T r M J μβ⋅+= (4-3-1)式中β为加速过程系统的角加速度,此时为正值,J 为转动系统的转动惯量,M μ为摩擦力矩,数值为负。
由牛顿第二定律可知,设砝码m 下落时的加速度为a ,则运动方程为mg T ma -=。
因为a r β=,则绳子张力T 为()T m g r β=- (4-3-2)当连接砝码的挂线脱离塔轮后,系统所受张力0T =,故外力矩0M =,此时系统只受摩擦力矩M μ的作用,作匀减速转动。
根据转动定律得M J μβ'= (4-3-3)式中β'为减速过程系统的角加速度,此时为负值。
由式(4-3-1)、式(4-3-2)、式(4-3-3)解得 βββ'--=)(r g mr J (4-3-4) 利用以上方法,分别可测得空载及负载时系统的转动惯量1J 和2J 。
式中,m 、g 、r 都是已知或是可以直接测量的物理量,关键在于如何测定角加速度β和β'。
3)β和β'的测量设转动体系统在0t =时刻初角速度为0ω,角位移为0,转动t 时间后,其角位移θ,转动中角加速度为β,则2021t t βωθ+= (4-3-5)若测得角位移1θ,2θ,与相应的时间1t ,2t ,得2110121t t βωθ+=2220221t t βωθ+= 所以 )()(2)(2122121122211222112t t t t t t t t t t t t --=--=θθθθβ (4-3-6) 实验时,角位移1θ,2θ可取为2π、4π…等,实验转动系统转过π角位移,计数计时毫秒仪的计数窗内计数次数+1。
计数为0作为角位移开始时刻,实时记录转过π角位移的时刻,计算角位移时间时应减去角位移开始时刻,应用上述公式(4-2-6),得到角加速度。
在求角加速度β'时,注意砝码挂线与绕线塔轮脱离的时刻,以下一时刻作为角位移起始时刻,计算角位移时间时,减去该角位移开始时刻,在该时间段系统角加速度为负。
4)验证平行轴定理将已知质量为M 、转动惯量为0J 的物体依次插入承物台上与轴心相距 ,2,,0a a d =的小孔,测出x J ,作2d J x -曲线,若为直线便验证了平行轴定理20Md J J += (4-3-7)五、实验内容1. 测量前的准备工作,具体操作如下:1)合理放置仪器,滑轮置于实验台外3-4cm ,调节仪器水平;2)连接传感器与计数计时毫秒仪;3)将砝码连线的一端打结,沿塔轮上开的细缝塞入(任选一层挂线,结头在下),另一端绕过定滑轮垂下砝码,调节滑轮的方向和高度,使挂线与绕线塔轮相切,挂线与绕线轮的中间呈水平;4)转动铝盘绕线(务必使得绕线整齐,减少摩擦),将砝码提升到一定高度,调整霍尔传感器探头与一磁钢相对,间距为0.3-0.5cm ,可见毫秒仪低电平指示灯亮;5)复位毫秒仪,转动铝盘缓慢放线,直到挂线与塔轮恰好脱离时即刻停止,此时次数显示屏上所显次数即为加速过程与减速过程的分界处,根据分界处设定加速过程的三个时间点(保证小于分界时刻),减速过程的三个时间点(保证大于分界时刻),根据选取的时间点设定预置次数(大于等于最大时间点),并填入表格表头部分。
2. 测量空载时转动系统的转动惯量J 1。
在空载的情况下,重复挂线→绕线→复位毫秒仪→释放砝码→查阅相应时间点→记录数据的实验过程,要求测量10组左右的数据,从中选取较为稳定的五组填入表格1。
3. 测量加载钢环时转动系统的转动惯量J 2。
将金属钢环置于承物台上,使其转动轴位于圆心位置,重复挂线→绕线→复位毫秒仪→释放砝码→查阅相应时间点→记录数据的实验过程,要求测量10组左右的数据,从中选取较为稳定的五组填入表格2。
4. (选做部分)以金属盘偏心孔d = 3.0,4.0,5.0cm 为转轴,重复以上步骤,求出相应的x J ,作2d J x -曲线,验证平行轴定理,20Md J J x +=。
六、注意事项1. 实验中,砝码置于相同的高度后释放,以利数据一致。
实验中,做好保护措施,防止砝码直接砸落地板引起磨损。
2. 挂线长度以挂线脱离绕线塔轮后,砝码离地3厘米左右为宜。
3. 实验中,砝码置于相同的高度后释放,以利数据一致。
霍尔传感器放置于合适的位置固定不动,每次绕线到相同高度,保证指示灯亮,按下RESET 键,以0初速度释放砝码。
从指示灯亮到刚灭,系统转过约π角位移后,毫秒仪开始计数计时。
4. 实验中,在砝码挂线脱离绕线塔轮前转动体系作正加速度β,在砝码挂线脱离塔轮后转动体系作负加速度β',须分清正加速度β到负加速度β'的计时分界时刻。
七、数据处理根据实验要求,将有关数据填入对应表格中,按所学的理论对数据进行处理。
选择=r ________m 进行绕线,分界处为 ;选择时间点:加速过程选 、 、 ,减速过程选 、 、 ;预置次数定为 。
=1J ______2m g ⋅, =2J ______2m g ⋅, =3J _______2m g ⋅∵理论值='3J 0.33792m g ⋅ ∴相对误差E =_______%[课后思考题]1.挂线的长度太短会如何,太长又会如何,应怎样调整?2.用该刚体转动惯量仪来测刚体的转动惯量,其主要误差有哪些?应如何消除或减小?。
