14.3 干燥速率与干 燥过程计算.
四干燥的计算公式

l —湿物料的厚度,m;
λt— 容器底面材料的热导率,W/(m·K);
λC — 湿物料的有效热导率,W/(m·K);
rw —湿球温度 tw 时水的汽化潜热,J/kg。
ܴ
ൌ
ܭሺܪ௪
െ
ܪሻ
ൌ
ఈ ಹ
ሺܪ௪
െ
ܪሻ
式中,K — 气固相间传质系数,W/(m2·h·∆;)ܪ
5
(2—4—15)
L —绝干空气的质量流率,kg/s;
GC —绝干物料的质量流率, kg/s; I1,I2 —湿空气进入及离开干燥器时的焓,kJ/ kg 绝干空气; ܫଵᇱ,ܫଶᇱ —湿物料进入及离开干燥器时的焓,kJ/ kg 绝干空气;
1
【下】功能 元件篇
化纤纺丝机械工程计算公式集锦
ܳௗ ൌ ܿܮሺݐଶ െ ݐଵሻ ܹሺݎ ܿݐଶሻ ܩܿሺߠଶ െ ߠଵሻ ܳ
cV — 湿份蒸汽的比热容,kJ/ (kg 水汽℃),水汽: cV=1.88 kJ/ (kg 水汽℃); W —单位时间内水分的蒸发量, kg/s;
cm —干燥后物料的比热容,kJ/(kg 湿物料℃) t1, t2 —湿空气进入及离开干燥器时的温度,℃; θ1,θ1 —湿物料进入及离开干燥器时的温度,℃。 Qୢ ൌ 1.01ܮሺݐଶ െ ݐଵሻ ܹሺ2490 1.88ݐଶሻ ܿܩሺߠଶ െ ߠଵሻ ܳ 3. 干燥所需风量 V
【下】功能 元件篇
化纤纺丝机械工程计算公式集锦
Hw—湿球温度 tw 时空气的饱和湿度,kg 水汽/kg 绝干空气; H —干燥介质热空气的湿度,kg 水汽/kg 绝干空气; αC — 气固相间给热系数,W/(m2·K); cH —空气的湿比热容,J/( kg 绝干空气·K),cH=αC/ K。 (3) 热空气对流和加热面传导给热干燥
干燥速度和干燥时间

言多么美丽;唯愿简单的相处,真心地付出,平淡地相守,才不负最美的人生;不负善良的自己。
己先查看一遍,把用不上的部分页面 删掉哦,当然包括最后一页,最后祝 您生活愉快!
人海茫茫,不求人人都能刻骨铭心,但求对人对己问心无愧,无怨无悔足矣。大千世界,与万千人中遇见,只是相识的 开始,只有彼此真心付出,以心交心,以情换情,相知相惜,才能相伴美好的一生,一路同行。
3、干燥总时间
1 2 3
感谢您对文章的阅读跟下载,希望本
,相互包容,相互懂得,才能走的更远。
篇文章能帮助到您,建议您下载后自
其实,世上最温暖的语言,“ 不是我爱你,而是在一起。” 所以懂得才是最美的相遇!只有彼此以诚相待,彼此尊重
相遇是缘,相守是爱。缘是多么的妙不可言,而懂得又是多么的难能可贵。否则就会错过一时,错过一世! 择一人深爱,陪一人到老。一路相扶相持,一路心手相牵,一路笑对风雨。在平凡的世界,不求爱的轰轰烈烈;不求誓
2)干燥机理 a)恒速干燥阶段 干燥速度由水的表面汽化速度所控制 b)降速干燥阶段
过程速度由水分从物料内部移动到表面的速度所控制。
c)临界含水量
临界水分随物料本身性质、厚度和干燥速率的不同而
异,通常临界水分随恒速阶段的干燥速度和物料厚度的增加 而增大。
三、干燥时间的计算
1、恒定干燥条件下干燥时间的计算
3)影响恒速干燥的因素 •空气流速的影响 •空气湿度的影响 •空气温度的影响
2、降速干燥时间的计算
Gc X1 dX 2 X 2 A U
不论干燥曲线如何,都可用图解积分法 当干燥曲线为直线或近似直线时
U kX X X
UC 0 kX X X
GC dX U C A d
固体干燥3-干燥速率与干燥过程计算

• 非等焓干燥过程 • 实际干燥过程:
ìDq > 0
îíQ损 > 0
Þ G2 (cpm1q2 - cpm2q1 ) > 0
• a、则I2<I1 • 如BD线
• 若t2不变 • HD<HC • ÞV增多
• b、若Q补>0 • 则I2>I1, 如BE线 • 若t2不变 • HE>HCÞV减少 • 求解
的) • H1 = H0 • Q损可求取,一般 Q损= 5~10%Q
• q2:实验或经验确定
• t1:选定
ì选择:t 2或j 2
求解V和Q补
Þ
ïí* 选择:Q补(Q补
=
0)或(H
2、j
2、t
)中的一个
2
ïî须对干燥过程进行简化 ,因空气出口状态不确 定)
求解V和(H
2、j
2、t
)中的另一个
2
(1)理想干燥器 (理想干燥过程,绝热干燥过程)
NA
= - GC dX
A × dt
=
KX( X
- X*)
ò ò •
•
其中:KX为系数,即CE直线的斜率 积分上式, t2 dt = GC XC dX
KX
=
(NA )恒 XC - X *
0
AK X X2 X - X *
t2
=
GC ( X - X *) A(N A)恒
ln
XC X2
-
X X
* *
三、连续干燥过程的数学描述
• b、废气带走的热量:V×I2 • c、干燥器的热损失:Q损
(3)干燥器内总热量衡算式
VI1 + GCcpm1q1 + Q补 = VI2 + GCcpm2q2 + Q损 Þ Q补 = V(I2 - I1)+ GCcp(m q2 - q1)+ Q损
干燥速率与干燥过程计算
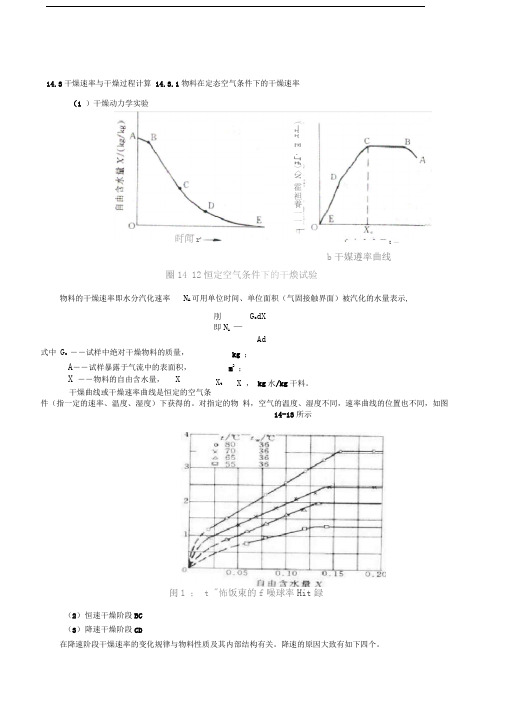
14.3干燥速率与干燥过程计算 14.3.1物料在定态空气条件下的干燥速率(1 )干燥动力学实验b 干媒遵率曲线圈14 12恒定空气条件下的干煥试验物料的干燥速率即水分汽化速率N A 可用单位时间、单位面积(气固接触界面)被汽化的水量表示,刖 G c dX 即N A —Ad式中 G c ――试样中绝对干燥物料的质量,A ――试样暴露于气流中的表面积, X ――物料的自由含水量, X干燥曲线或干燥速率曲线是恒定的空气条件(指一定的速率、温度、湿度)下获得的。
对指定的物 料,空气的温度、湿度不同,速率曲线的位置也不同,如图 14-13所示闺1 ; t "怖饭束的f 噪球率Hit 録(2) 恒速干燥阶段BC (3) 降速干燥阶段CD在降速阶段干燥速率的变化规律与物料性质及其内部结构有关。
降速的原因大致有如下四个。
X tkg ; m 2;X , kg 水/kg 干料。
时闻r(-rr E ・Jf )<N霍袒養一一X —①实际汽化表面减少;②汽化面的内移;③平衡蒸汽压下降;④固体内部水分的扩散极慢。
(4)临界含水量固体物料在恒速干燥终了时的含水量为临界含水量,而从中扣除平衡含水量后则称临界自由含水量X C (5)干燥操作对物料性状的影响1432间歇干燥过程的计算14.3.2.1恒速阶段的干燥时间i如物料在干燥之前的自由含水量阶段,恒速阶段的干燥时间1由N A X1大于临界含水量则干燥必先有一恒速阶段。
忽略物料的预热G c dX积分求出。
Ad1dG cAXC dXX1N A因干燥速率N A为一常数,G c1A 速率N A由实验决定,也可按传质或传热速率式估算,即X c N AN A S(H w H) —(t t w)「wH w为湿球温度t w下的气体的饱和湿度。
传质系数k H的测量技术不如给热系数测量那样成熟与准确,在干燥计算中常用经验的给热系数进行计算。
气流与物料的接触方式对给热系数影响很大,以下是几种典型接触方式的给热系数经验式。
干燥过程中的平衡与速率关系解读

出物料表面温度θ随τ的变化关系。图57-3 是对图57-2 采用斜率法标绘出的干
燥速率曲线(此曲线也可对实验数据采用差分法直接标绘出来)。
虽然图57-3所示干燥速率曲线的形状随物料性质不同而不同,而且还受干燥介 质状态、流速、与物料的接触方式的影响,但是,一般干燥速率曲线都明显的分 为三个阶段:第一阶段(图中AB段)为物料预热阶段;第二阶段(图中BC段) 为恒速汽化阶段;第三阶段(图中CDE段)是降速汽化阶段。第二与第三阶段的
2019/3/19 干燥过程的平衡与速率 3/21
(三)湿物料中所含水分 参考图57-1,湿物料中所含水分可按其性质作如下划分: 按在一定干燥条件下能否除去
1. 平衡水分——在一定干燥条件下,此部分水分不能除去
2. 自由水分——物料中大于平衡水分的那部分水分,这部分水分在一定干燥 条件下可以除去(非结合水+部分结合水)
2019/3/19 干燥过程的平衡与速率 4/21
的空气呈平
湿物料的相平衡关系—— ( ~ X *关系)
图57 1 物料中所含的水分
2019/3/19 干燥过程的平衡与速率 5/21
二、干燥速率
(一)干燥速率及其影响因素 干燥速率指的是单位时间从单位物料表面上所汽化的水分量,此定义
可用下面微分形式表示:
第四十八讲 干燥相平衡与干燥速率
一、干燥相平衡关系 二、干燥速率
(一)物料含水量的表示方法
(二)平衡含水率与相平衡曲线
(一)干燥速率及其影响因素
(二)恒定干燥条件下的干燥速率曲线
(三)湿物料中所含水分
(三)干燥过程分析与干燥速率关系式
பைடு நூலகம்
2019/3/19
干燥过程的平衡与速率
干燥速率与干燥过程计算
、 、 ——气体的密度、粘度和普朗特数。
14.3.2.2降速阶段的干燥时间
当 时, ↓, ↓,此阶段称为降速干燥阶段,物料从 减至 ( )所需时间 为
若有 的干燥数据可用数值积分法或图解积分法求 ,或假定在降速段 与物料的自由含水量 成正比,即采用临界点C与平衡水分点E所连结的直线CE(图中红色虚线)来代替降速段干燥速率曲线CDE,即 ,式中 ——比例系数,kg/(m2·s· ),即CE直线斜率,
kW/m2·℃
式中 为气体的质量流速,kg/(m2·s)。
上式的试验条件为 kg/(m2·s),气温 ℃。
(2)空气自上而下或自下而上穿过颗粒堆积层(图14-16b)
式中 ——气体质量流速,kg/(m2·s);
——具有与实际颗粒相同表面的球的直径,m;
——气体粘度,Pa·s。
(3)单一球形颗粒悬浮于气流中(图14-16c)
∵ ;∴
当物料干燥至 ,干燥仍由恒速和降速两阶段组成,由于干燥操作条件不变,即 值不变,所以干燥时间 为:
(2)由(1)小题可知,物料干燥至 时,所需干燥时间大于2.5h,为缩短干燥时间,可以提高湿空气的温度;因为湿空气温度提高, 、 、 等其他条件不变,那么影响干燥时间的参数只有
∵ 其中
从上式可以看出,干燥介质温度提高,使得干燥速率提高从而缩短干燥时间;
干燥过程是气、固两相的热、质同时传递过程,所以对过程设备进行数学描述时,必须列出物料衡算式、热量衡算式、气固相际传热及传质速率方程式,气固相界面参数还与物料内部的导热和扩散情况有关,其确定将变得十分复杂。固此还必须同时列出物料内部的传热、传质速率方程式。物料内部的传热、传质与物料的内部结构、水分与固体的结合方式、物料层得厚度等众多因素有关,要定量地写出这两个特征方程式是非常困难的。干燥问题之所以至今得不到较圆满的解决,原因之一就在于物料内部的传递过程难以弄清。
干燥速率与干燥过程的计算

化学化工学院 迪丽努尔
•14.3.2 间歇干燥过程的计算
一、干燥时间 • 2、降速阶段的干燥时间τ2
物料从临界含水量Xc减至X2 所需要的时间为:
2
X2
d
Gc A
dX NA
0
Xc
Xc
干
Gc dX
2
• 二、干燥结束时的物料温度
化学化工学院 迪丽努尔
•14.3.2 间歇干燥过程的计算 一、干燥时间
• 1 、恒速阶段的干燥时间τ1
由: NA GAcddX
1
Xc
d
Gc A
dX NA
0
X1
因干燥速率NA为一常数, 则:
Gc (X1Xc)
1A
NA
速率NA由实验决定,也可按传质或传热速率式估算 即:
进入干燥器空气的湿比体积为
uH(2.831034.56103H)(t273 (2.831034.561030.010)(73027)3 0.98m73/kg干气
化学化工学院 迪丽努尔
密度
1.0H10.010 1.03k2/g m 3
uH 0.987
质量流速G=ρu=1.02×6=6.12kg/(s. ㎡)
0 自X由c含水量x
化学化工学院 迪丽努尔
• 14.3.1 物料在定态空气条件下的干燥速率
•三、干燥速率曲线 2、降速干燥阶段
• 降速的原因: • ①实际汽化表面减小。
干
燥 速
B C
率
A
D
• ②汽化面的内移。
• ③平衡蒸汽压下降。
• ④固体内部水分的扩散 极慢。
化工原理下考研精品课程第三节 干燥速率与干燥时间.ppt

(3)降速干燥阶段
干燥速度降低的原因:
U=-Gc dX =-Gc X
S d
S
•实际汽化表面减小。由于物料表面水分分布不均匀,局 部表面成为干区。如CD所示,称为第一降速段。
•汽化面的内移。当物料表面都成为干区后,水分的汽化 面向物料内部迁移。热、质传递途径加长,如图中的DE
干燥速度为:
U kH HW H
此阶段空气放出的显热为:
水分汽化所需的热量为:
干燥速度为:
当空气的温度t、湿度H、 流速u等不变时,干燥速度 为一恒定值。故干燥速度与 物料的性质关系不大。
Q S t tW Q kH rW S HW H
U Q/(rWS) t tW /rW
恒速干燥速度的影响因素
a.若空气的温度t、湿度H不变,流速加快,U加快,Xc变 大,平衡含水量X*由于t、H不变而不变;
b. 若空气的湿度H、流速不变,温度t升高, U加快,Xc变 大,平衡含水量X*由于t升高降低。
c. 若空气的温度t、u不变,湿度H降低,U加快,Xc变大。
三、 间歇干燥过程的计算
递,即水分在气固间达平衡。此时物料中的水分X*称 为对应空气状态的平衡水分。而能被除去的水分(Xt- X*)称为自由水分。
常见几种物料的平衡水分
二、 恒定干燥条件下的干燥速率 (1)干燥曲线(实验测定)
UU=-SddGWSc
,dkXg
d
=m2- s
Gc S
X
A B
dW=-GcdX
C
C
B
A D
D
X
总干燥时间为:τ=4+1.04+3.98=9.04h
讨论:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福州大学化工原理电子教案固体干燥14.3 干燥速率与干燥过程计算14.3.1 物料在定态空气条件下的干燥速率(1)干燥动力学实验物料的干燥速率即水分汽化速率NA可用单位时间、单位面积(气固接触界面)被汽化的水量表示,即NA=式中 Gc——试样中绝对干燥物料的质量,kg; GcdX -AdτA——试样暴露于气流中的表面积,m2;X——物料的自由含水量,X=Xt-X*,kg水/kg干料。
干燥曲线或干燥速率曲线是恒定的空气条件(指一定的速率、温度、湿度)下获得的。
对指定的物料,空气的温度、湿度不同,速率曲线的位置也不同,如图14-13所示(2)恒速干燥阶段BC(3)降速干燥阶段CD在降速阶段干燥速率的变化规律与物料性质及其内部结构有关。
降速的原因大致有如下四个。
- 1 - 1福州大学化工原理电子教案固体干燥①实际汽化表面减少;②汽化面的内移;③平衡蒸汽压下降;④固体内部水分的扩散极慢。
(4)临界含水量固体物料在恒速干燥终了时的含水量为临界含水量,而从中扣除平衡含水量后则称临界自由含水量XC(5)干燥操作对物料性状的影响14.3.2 间歇干燥过程的计算14.3.2.1 恒速阶段的干燥时间τ1如物料在干燥之前的自由含水量X1大于临界含水量Xc,则干燥必先有一恒速阶段。
忽略物料的预热阶段,恒速阶段的干燥时间τ1由NA=GcdX积分求出。
-Adττ1GcXCdX dτ=-⎰0A⎰X1NA因干燥速率NA为一常数,τ1=GcX1-Xc ⨯ANA速率NA由实验决定,也可按传质或传热速率式估算,即NA=kH(Hw-H)=αrw(t-tw)Hw为湿球温度tw下的气体的饱和湿度。
传质系数kH的测量技术不如给热系数测量那样成熟与准确,在干燥计算中常用经验的给热系数进行计算。
气流与物料的接触方式对给热系数影响很大,以下是几种典型接触方式的给热系数经验式。
(1)空气平行于物料表面流动(图14-16a)α=0.0143G0.8kW/m2·℃式中G为气体的质量流速,kg/(m2·s)。
上式的试验条件为G=0.68~8.14kg/(m2·s),气温t=45~150℃。
(2)空气自上而下或自下而上穿过颗粒堆积层(图14-16b)G0.59α=0.0.41 dpG0.49α=0.0.41dp⎛dpG⎫⎪>350 μ⎪⎝⎭⎛dpG⎫⎪ <350 μ⎪⎝⎭式中 G——气体质量流速,kg/(m2·s);dp——具有与实际颗粒相同表面的球的直径,m;μ——气体粘度,Pa·s。
(3)单一球形颗粒悬浮于气流中(图14-16c)αdp1/2=2+0.65RepPr1/3 λdpuρ Rep=μ- 2 - 2福州大学化工原理电子教案固体干燥式中 u——气体与颗粒的相对运动速度;ρ、μ、Pr——气体的密度、粘度和普朗特数。
14.3.2.2 降速阶段的干燥时间τ2间τ2为当X<Xc时,X↓,NA↓,此阶段称为降速干燥阶段,物料从Xc减至X2(X2>X*)所需时τ2τ2=⎰*0Gdτ=-cA⎰X2XcdX NA若有NA~X的干燥数据可用数值积分法或图解积分法求τ2,或假定在降速段NA与物料的自由含水量X-X成正比,即采用临界点C与平衡水分点E所连结的直线CE(图中红色虚线)来代替降速段干燥速率曲线CDE,即NA=Kx(X-X*),式中KX——比例系数,kg/(m2·s·∆X),即CE直线斜率,KX=NA,C=NA,cXc-X* α(t-tw)=kH(Hw-H) γwGcXdXGcXdX则τ2=- =AKX⎰XX-X*AKX⎰XX-X*GcXc-X*τ2=ln*AKXX2-X2Cc2当X=0时此式还原为教材式(14-30)。
将NA,C=Kc(Xc-X)代入τ1的表达式(14-20)得 **τ1=GcX1-Xc *AKXXc-XGcX1-XcXc-X*τ=τ1+τ2=(+ln) **AKXXc-XX2-Xτ1X1-Xc=τ2Xc-X*Xc-X* ln*X2-X解题指南P367例17-9例17-9 某干燥过程干燥介质温度为363K,湿球温度307K,物料初始干基含水率为0.45,当干燥了2.5h后,物料干基含水率为0.15,已知物料临界含水率、平衡含水率分别为0.2、0.04,试求:(1)将物料- 3 - 3福州大学化工原理电子教案固体干燥'=0.1需要多少干燥时间;'=0.1且干燥时间仍维持在2.5h,将空气温度干燥至X2(2)将物料干燥至X2提高到373K(湿球温度为310K),其他条件包括空气流速保持不变,能否达到要求。
⎛T 附:恒速段的传热速率方程:Nu=CRe0.5 T⎝w⎫⎪⎪,C为常数,T、Tw单位为K。
⎭2解:(1)根据题意,这是一个恒定干燥条件下干燥时间的计算问题。
'<Xc;∴干燥过程包括恒速段与降速段,相应的干燥时间包括恒速干燥时间和降速干燥时间,∵X2在恒定干燥条件下,干燥时间可用下式计算:Gθ=θ1+θ2=CAKx式中X1、Xc、X*均已知,得:∵X2<Xc;∴2.5=⎡X1-XcXc-X*⎤ +ln⎢**⎥X2-X⎥⎢⎣Xc-X⎦GC未知,但可以通过题给条件,干燥至X2=0.15时,干燥时间为2.5h求AKxGC0.2-0.04⎤⎡0.45-0.2=1.29 +ln⇒⎢0.2-0.04⎥AK0.15-0.04⎣⎦xGCAKx'=0.1,当物料干燥至X2干燥仍由恒速和降速两阶段组成,由于干燥操作条件不变,即所以干燥时间θ为: 'GC值不变,AKx⎡X1-XcXc-X*⎤0.2-0.04⎤⎡0.45-0.2+ln=1.29⨯+ln=3.28h ⎢⎥⎢⎥**0.1-0.04⎦'-X⎥X2⎣0.2-0.04⎢Xc-X⎣⎦'=0.1时,所需干燥时间大于2.5h,为缩短干燥时间,可以(2)由(1)小题可知,物料干燥至X2Gθ'=CAKx提高湿空气的温度;因为湿空气温度提高,X1、Xc、X*等其他条件不变,那么影响干燥时间的参数只有Kx ucuα(T-Tw) =u=其中crwX-X*Xc-X*从上式可以看出,干燥介质温度提高,使得干燥速率提高从而缩短干燥时间;∵Kx=⎫⎛T⎪;∴()()K∝u∝αT-T∝NuT-T∝xcww⎪ T⎭⎝w'假设湿空气温度提高后的降速段斜率用Kx表示,所以有:'⎡⎛T'Kx =⎢ Kx⎢ T'⎣⎝w⎛T又∵Nu=CRe0.5 T⎝w22⎫⎪⎪(T-Tw) ⎭2⎫⎪T'-Tw'⎪⎭()⎤⎥⎥⎦⎡⎛T⎢⎢ T⎣⎝w⎫⎪T-Tw⎪⎭2()⎤⎥⎥⎦⎛T'⎫ = ⎪⎝T⎭2⎛Tw T'⎝w22⎫T'-Tw'373307373-310⎛⎫⎛⎫⎪=1.5 = ⎪⎪⎪T-T353310353-307⎝⎭⎝⎭w⎭2∴θ'=Kxθ=3.28÷1.5=2.19h<2.5h,即把空气温度提高到373K可以满足要求。
'Kx 14.3.3 连续干燥过程的一般特性有并流、逆流、错流流程及其他复杂的流程(1)连续干燥过程的特点以并流连续干燥为例,P341图14-20注意:连续干燥降速段NA≠Kx(X-X)- 4 - 4 *福州大学化工原理电子教案固体干燥(2)连续干燥过程的数学描述为定态过程,设备中的湿空气与物料状态沿流动途径不断变化,但流经干燥器任一确定部位的空气和物料状态不随时间而变,故应采用欧拉考虑法,在垂直于气流运动方向上取一设备微元dV作为考察对象。
干燥过程是气、固两相的热、质同时传递过程,所以对过程设备进行数学描述时,必须列出物料衡算式、热量衡算式、气固相际传热及传质速率方程式,气固相界面参数还与物料内部的导热和扩散情况有关,其确定将变得十分复杂。
固此还必须同时列出物料内部的传热、传质速率方程式。
物料内部的传热、传质与物料的内部结构、水分与固体的结合方式、物料层得厚度等众多因素有关,要定量地写出这两个特征方程式是非常困难的。
干燥问题之所以至今得不到较圆满的解决,原因之一就在于物料内部的传递过程难以弄清。
以下首先对干燥过程作物料和热量衡算,然后对干燥过程作出简化,列出传热、传质速率方程,计算设备容积。
14.3.4 干燥过程的物料衡算与热量衡算P342图14-21,物料、热量衡算是确定空气用量分析干燥过程的热效率以及计算干燥容积的基础。
(1)物料衡算W=Gc(X1-X2)=V(H2-H1)H1=H0 (空气在预热器中加热,H不变)有时物料的含水量习惯上以湿基含水量w表示,w与干基含水量的关系为w1w2,X2=,Gc=G1(1-w1)=G2(1-w2) X1=1-w11-w2w-w2,或W=Gc(X1-X2),Gc、X1、X2用上式求。
W=G1-G2=G111-w2WW V==H1-H2H2-H0H0已知,W可求出,求V关键在于确定出干燥器空气湿度H2,必须用后面的干燥器热量衡算结合才能确定H2。
实际空气(新鲜空气)质量流量V'(kg湿空气/s)=V(1+H0)空气必须用风机输送,风机的风量V''(m3湿空气/s)273+t101.3V''=VvH=V(0.773+1.244H)⨯ 273p上式中t、H是风机所在位置空气t、H,风机在装在预热器前,预热器后,甚至干燥器后。
(2)预热器的热量衡算Qp=V(I1-I0)=VcpH1(t1-t0)I1=(1.01+1.88H1)t1+2500H1I0=(1.01+1.88H0)t0+2500H0H1=H0,cpH1=cpH0(3)干燥器的热量衡算VI1+Gccpm1θ1+QD=VI2+GcCpM2θ2+Qlcpm=cps+cplX(4)物料衡算与热量衡算的联立求解在设计型问题中,Gc、θ1、X1、X2是干燥任务规定的,而H1=H0由空气初始状态决定,Ql可按传热公式求或取Q=(0.05~0.10)Qp。
θ2是干燥后期气固两相及物料内部热、质传递的必然结果,不- 5 - 5福州大学化工原理电子教案固体干燥能任意选择,应在一定条件下由实验测出或按经验判断确定(如式(14-32)确定θ2)。
气体进入干燥器的温度t1可以选定。
这样,干燥过程的物料和热量衡算常遇到以下两种情况:①选择气体出干燥器的状态(如t2及ϕ2),求V及QD;②选定QD(如许多干燥器QD=0,即不补充热量)及气体出干燥器状态的一个参数(H2、ϕ2、t2中的一个),求出V及另一个气体出口参数(如H2)。
第①种情况出口空气状态已确定,热衡及物衡简便。
在第②种情况下,由于出口气状态参数之一是未知数,联立物衡和热衡方程式的计算比较繁琐,因而常对过程作出简化,以便于初步估算。
