3控制对象的动态特性
控制对象的动态特性

双容有自平衡对象原理方框图
μ
Q0
1 h1 1
Kμ
_ F1S
R1
Q1
自平衡单容对象
1
h2
F 2S
1 R2
自平衡单容对象
2.传递函数
说 明:
❖ 双容水槽对象是二阶惯性环节,它是两个一阶惯 性环节串联而成,没有负载效应。
热工对象
第一节 概述(续)
研究对象的动态特性 实质是建立对象的数学模型, 即用数学方程描述对象各变量之间的关系。
理论建模:
基于基本的物理、化学定律和工艺参数, 推导被控对象数学模型
试验建模:
在运行条件下通过实验方法来获取
第二节 单容被控对象的动态特性
单容被控对象:
是指只有一个贮存物质或能量的容积。这 种对象用一阶微分方程式来描述。单容被控对 象可分为有自平衡单容对象和无自平衡单容对 象两大类 。
1.阶跃响应
起始的工况 :h=h0,Q1=Q10= Q2=Q20 在t=t0时刻 :
控制阀阶跃开大Δμ0
流入量Q1按比例增加ΔQ1, ΔQ2= 0
ΔQ=ΔQ1-ΔQ2=ΔQ1为一常 数
水槽液位等速(直线)上升
1.阶跃响应
0
t0
Q
0
t
Q1
0
t0
Q
0 t
Q1
Q 10 Q 20
t0
h
Ta
h0
0
t0
t Q 2 t Q 10 Q 20 0 h
3.特征参数
(2)飞升速度ε
dh dt
t0
K
1
0 F Ta
第三章控制对象的动态特性习题与参考解答

第三章控制对象的动态特性习题与参考解答3-1 什么是自衡特性?具有自衡特性被控过程的系统框图有什么特点?1)在扰动作用破坏其平衡工况后,被控过程在没有外部干预的情况下自动恢复平衡的特性,称为自衡特性。
2)被控过程输出对扰动存在负反馈。
3-2 什么是单容过程和多容过程?1)单容:只有一个储蓄容量。
2)多容:有一个以上储蓄容量。
3-3 什么是控制通道和扰动通道(干扰通道)?对于不同的通道,对象的特性参数(K、T、τ)对控制有什么不同的影响?对于一个被控对象来说,输入量是扰动量和操纵变量,而输出是被控变量。
由对象的输入变量至输出变量的信号联系称为通道。
操纵变量至被控变量的信号联系称为控制通道;扰动量至被控变量的信号联系称为扰动通道。
一般来说,对于不同的通道,对象的特性参数(K、T、τ)对控制作用的影响是不同的。
对于控制通道:放大系数K大,操纵变量的变化对被控变量的影响就大,即控制作用对扰动的补偿能力强,余差也小;放大系数K小,控制作用的影响不显著,被控变量的变化缓慢。
但K太大,会使控制作用对被控变量的影响过强,使系统的稳定性下降。
在相同的控制作用下,时间常数T大,则被控变量的变化比较缓慢,此时对象比较平稳,容易进行控制,但过渡过程时间较长;若时间常数T小,则被控变量变化速度快,不易控制。
时间常数太大或太小,在控制上都将存在一定困难,因此,需根据实际情况适中考虑。
滞后时间τ的存在,使得控制作用总是落后于被控变量的变化,造成被控变量的最大偏差增大,控制质量下降。
因此,应尽量减小滞后时间τ。
对于扰动通道:放大系数K大对控制不利,因为,当扰动频繁出现且幅度较大时,被控变量的波动就会很大,使得最大偏差增大;而放大系数K小,既使扰动较大,对被控变量仍然不会产生多大影响。
时间常数T大,扰动作用比较平缓,被控变量变化较平稳,对象较易控制。
纯滞后的存在,相当于将扰动推迟τ0时间才进入系统,并不影响控制系统的品质;而容量滞后的存在,则将使阶跃扰动的影响趋于缓和,被控变量的变化相应也缓和些,因此,对系统是有利的。
过程控制与集散系统课后习题答案

rty y )(∞y t y图1.3 过程控制系统阶跃响应曲线1-1过程控制系统中有哪些类型的被控量温度、压力、流量、液位、物位、物性、成分1-2过控系统有哪些基本单元构成,与运动控制系统有无区别被控过程或对象、用于生产过程参数检测的检测仪表和变送仪表、控制器、执行机构、报警保护盒连锁等其他部件过程控制,是一种大系统控制,控制对象比较多,可以想象为过程控制是对一条生1-4衰减比和衰减率 衰减比等于两个相邻同向波峰值之比。
衡量振荡过程衰减程度的指标。
衰减率是经过一个周期以后,波动幅度衰减的百分数。
衡量振荡过程衰减程度的另一种指标。
一般希望过程控制系统的衰减比η=4:1~10:1,相当于衰减率Ψ=0.75到0.9。
若衰减率Ψ =0.75,大约振荡两个波系统进入稳态。
1-5最大动态偏差和超调量有何异同最大动态偏差是指在阶跃响应中,被控参数偏离其最终稳态值的最大偏差量,表现在过渡 过程开始的第一个波峰(y1)。
最大动态偏差是衡量过程控制系统动态准确性的指标。
超调量为最大动态偏差占被控量稳态值的百分比。
余差是指过渡过程结束后,被控量新的稳态值与设定值的差值。
余差是过程控制系统稳态准确性的衡量指标。
调节时间ts 是从过渡过程开始到结束的时间。
理论上应该为无限长。
一般认为当被控量进入其稳态值的5%范围内所需时间 就是调节时间.调节时间是过程控制系统快速性的指标。
振荡频率β是振荡周期的倒数。
在同样的振荡频率下,衰减比越大则调节时间越短;当衰减比相同时,则振荡 频率越高,调节时间越短。
振荡频率在一定程度上也可作为衡量过程控 制系统快速性的指标。
过程控制的目标 安全性 稳定性 经济性过程工业的特点 强调实时性和整体性/全局优化的重要性/安全性要求过程控制系统的特点 / 被控过程的多样性 / 控制方案的多样性/被控过程属慢过程、多参数控制/定值控制/过程控制多种分类方法 过程控制系统的性能指标/稳定性、准确性/快速性2-1什么是对象的动态特性,为什么要研究它研究对象特性通常以某种形式的扰动输入对象,引起对象输出发生相应的变化,这种变化在时域或者频域上用微分方程或者传递函数进行描述,称为对象的动态特性。
自动控制的基本知识

七、调节过程的品质指标 调节过度过程: 1)等幅振荡 2)扩散振荡 3)衰减振荡 4)非周期过程
1。稳定性:衰减率
Ψ愈大,越稳定。 Ψ=0.75~0.98
2.准确性:准确性是指被控量的偏差大小,它包括动态偏差yM和 静态(稳态)偏差yK 动态偏差:在控制过程中,被控量与给定值之间的最大偏差称为动态偏差. 静态偏差:在控制过程结束后,被控量的稳态值y∞与给定值yg之间的残余
只包含一个容积
单容对象是最简单的热工调节对象,电厂热工生产过程中 许多储水容器,如除氧器、加热器、凝汽器等。
2)多容对象
包含两个或以上容积
(1)有自平衡能力的多容对象: 可用一个迟延时间为τ的纯迟延环节和个时间常数为Tc的惯性环节 近似。
(2)无自平衡能力的多容对象: 可用一个迟延时间为τ的纯迟延环节和一个积分环节近似。
3。阶跃响应特性:比较直观 在阶跃输入信号的作用下,系统的输出特性。 突然的扰动。 在电厂生产过程中,有许多输入信号近似于阶跃信号, 如负荷突然变化,阀门、挡板的开与关等。只要生产 过程允许,一般也比较容易通过控制机构(如控制阀 门)或扰动机构造成一个阶跃输入扰动。所以常在现 场用阶跃响应试验来检验控制系统的工作性能。
3。比例带δ对调节过程的影响
比例带: 3。比例带δ对调节过程的影响
比例带δ 小:调节作用强;
比例带δ太小:调节阀动作过频繁,不稳定。
二、积分调节规律调节器(P)
1。积分规律调节器的动态特性
U (S ) 1 WI ( S ) KP E (S ) Ti s 式中 Si——称为积分规律调节器的积分速度; Ti,——积分时间,习惯上多用积分时间来表示被调量偏差 积累的快慢。 Ti 越小表示偏差积累越快,积分作用越强。Ti是积分规律调节 器的整定参数。
过程控制3

设水槽的截面积为A ① Qi0= Qo0时,系统处于平衡状态,即静态。 这时液位稳定在ho ② 假定某一时刻,控制阀突然开大∆x,则Qi突 然增大,不再等于Qo,于是h也就开始变化。 Qi与Qo之差被囤积在水槽中,造成液位上升。 即:
(Qi Qo )dt Ad h
Qi k x x h Qo R0
TS H(S) + H(S) = KX(S)
H (s) K X ( s ) Ts 1
在过程控制中,分析各种对象动态特性最常用 的方式是阶跃信号输入时的响应。可以用突然加大 控制阀的开度,施加阶跃扰动。
输入量x作一阶跃变化Δx时 1 H ( s) K X (s) s X ( s) Ts 1 则
T R1 A1
A2 Ta kx
若对象含有纯滞后 W (s) H (s)
X ( s)
1 e 0 s Ta s(Ts 1)
对于无自平衡能力的n阶等容对象:
K W (S ) Ta s(Ts 1) n
若对象含有纯滞后
K W (S ) e 0 s Ta s(Ts 1) n
②具有纯滞后的一阶对象
y () y (0) y () a.静态放大系数K: K x x
b.时间常数T:被控量y(t)以相对值表示
Ke s Wo ( s ) Ts 1
y0 (t ) y(t ) / y()
则阶跃作用下
0 t y0 (t ) 1 e(t )/T t
第三节
时域法辨识对象的动态特性
一、阶跃响应曲线的测定 1.阶跃扰动法 当对象处于稳态时, 对输入量施加一个阶跃扰 动(如将阀门开大),并 保持不变,测定其输出量 随时间而变化的曲线(数 据),即阶跃响应曲线。
第3章 控制对象的特性

3、纯滞后时间τ
0:
(1)何谓纯滞后? 被控量变化落后于输入量变化发生 时刻的现象称为对象的纯滞后。 (2)产生纯滞后的原因: a)调节阀离调节对象太远。 b)被控参数的测量点离调节器太远。 (3)纯滞后对控制系统的影响: 稳定性 动态偏差 调节时间
§3—2多容控制对象的动态特性
一、双容水柜控制对象的阶跃响应曲线:
(3)求取容量滞后时间τ c的方法:
(4) τ c对系统过渡过程的影响: 稳定性 动态偏 调节时间
三、滞后时间τ :
滞后时间τ = 纯滞后时间τ 0+容量滞后时间 τc 总之: 单容控制对象的特性参数为 K、T、τ 0 多容控制对象的特性参数为 K、T、τ
§3-3 控制对象的自平衡能力:
一、何谓自平衡特性? 控制对象受到输入作用平衡被破坏后,不 需要外来的调节作用而依靠被控量自身的变化使 对象重新恢复平衡的特性称为对象的自平衡特性。 输入作用的变化量 二、自平衡率 : 被控量的变化量
(4)T的大小说明被调参数达到新稳态值所需时 间的长短,是表征对象惯性大小的动态特性参数。 下图中 :T1<T2<T3<T4
(5)影响时间常数T长、短的因素: a)容量系数C: 容量:对象贮存能量或工质的能力称为容量。 例如单容水柜的容量v=A×h 容量系数C:被控量变化一个单位时,对象容 量的改变量。 C=dv/dh=d( A×h )/dh=A dv=C ×dh ,可见相同的被控量变化, C大,对象贮存能力大,C小,对象贮存能力小。
2、时间常数T:
(1)何为控制对象的惯性? 被控量的变化总是落后于输入作用的变化。 (2)T的物理意义: a)在给定阶跃信号作用下,被调参数以初始 变化速度一直变化到新稳态值所需的时间。 b)控制对象受到阶跃信号后,被控参数变化 到新稳态值 的63.2%所需的时间。 (3)T 的几何意义: 以初始斜率为斜率作切线与新稳态值的交 点所对应的时间。
被控对象动态特性总结

本章重点:了解对象特性及描述方法、描述对象特性的参数等内容 。
给定值 偏差
Sv
+ -
Dev
Pv
测量值
操纵值
控制器
调节阀
Mv
干扰 D
操纵变量 被控对象
q
测量变送器
被控变量 y
被控对象是指自动控制系统中所要控制的工艺生产设备。
生产过程中常见的被控对象有各类传热设备,如换热器、加热炉、 锅炉;流体输送设备,如泵、压缩机、管道;传质设备,如精馏塔;以 及反应器等。
第一节 对象特性及描述方法
二 对象特性的描述方法 建立对象数学模型的基本方法有机理法和测试法。
(一)机理法
用机理法建模就是根据生产过程的内在机理,写出各种有关的平衡方程 如:物料平衡方程、能量平衡方程、动量平衡方程、相平衡方程等,推 导出代表对象动态特性的微分方程。
对复杂对象的机理法建模需要进行合理的假设与简化。
温度对象的时间常数T比较大。
第二节 描述对象特性的参数
由前面的推导过程知: T AR2 ,A为储槽的截面积,代表其容量大 小,R2为阀的阻力系数,即时间常数与对象的液容与液阻有关,也是由
对象本身的特性决定的。
因此,时间常数T反映了对象容量滞后的大小。
生产过程中有各种各样的对象,大部分可用放大系数K与时间常数T描
态值时,相应输出变化就大,则反应就灵敏。
由于K与输出变化过程无关,而只与过程的稳态值有关,故它是表征对
象静态特性的一个特性参数。
放大系数K的大小是由对象本身的特性确定的。
第二节 描述对象特性的参数 Q1 B
dh T dt h KQ1
0
h
(a)
第3章 控制对象的特性
C)容量系数C对控制对象时间常数的影响: 容量系数C对控制对象时间常数的影响: 若有两个单容水柜,底面积分别为A 若有两个单容水柜,底面积分别为 1和A2, 且 A2 > A 1 。 所以T 因为 T1=A1×R,T2=A2×R,所以T2>T1。 t=0: 当t=0:
dh(t) dt
=
K *∆µ T
第三章 控制对象的特性
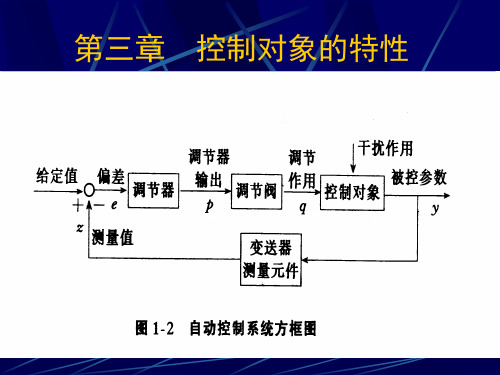
(1)何谓控制对象的特性? 何谓控制对象的特性? 是指对象在受到干扰作用或调节作用 被控参数是如何变化的, 后,被控参数是如何变化的,变化的快慢 及最终变化的数值。 及最终变化的数值。 何谓控制对象的输入、输出量? (2)何谓控制对象的输入、输出量? 干扰作用和调节作用为对象的输入量; 干扰作用和调节作用为对象的输入量; 被控参数为对象的输出量。 被控参数为对象的输出量。 干扰作用 被控参数 干扰通道 调节作用 被控参数 调节通道
(3)求取容量滞后时间τc的方法:
对系统过渡过程的影响: (4) τc对系统过渡过程的影响: 稳定性 动态偏 调节时间 三、滞后时间τ: 滞后时间τ
滞后时间τ= 纯滞后时间τ 滞后时间τ= 纯滞后时间τ0+容量滞后时 间τc 总之: 总之: 单容控制对象的特性参数为 K、T、τ0 多容控制对象的特性参数为 K、T、τ
(3)单容控制对象:只有一个储蓄容积的 单容控制对象: 控制对象 控制对象。 控制对象。其动态特性可用一阶微分方程式 表示。 表示。 多容控制对象 控制对象: 多容控制对象:有两个或两个以上 储蓄容积的控制对象。 储蓄容积的控制对象。其动态特性需用二阶 或二阶以上微分方程来表述。 或二阶以上微分方程来表述。
D)阻力系数对控制对象时间常数的影响: 阻力系数对控制对象时间常数的影响: 若有两个底面积相同的单容水柜 A1=A2), (A1=A2), >R2, R1, 但 R1 >R2,T1=A1 × R1,T2=A2 × R2 则 T1 >T2 * * * t=0: dt 当t=0: dh(t) = K * ∆ µ = K µ R R A∆ µ = K µ A∆ µ T * h(∞)= K×△u=Ku×R×△u K×△u=Ku× ×△u ×△u=Ku 可见:阻力系数越大,时间常数越大; 可见:阻力系数越大,时间常数越大; 阻力系数变,被控量初始变化速度不变; 阻力系数变,被控量初始变化速度不变; 阻力系数变,被控量稳态值变化。 阻力系数变,被控量稳态值变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fig.3-1◎
返回本章
1 Q1
h
F
2
Q2
Fig. 3-1 单容控制对象(水柜)示意图
返回最近
§3-1 单容控制对象
研究内容:
1 容量系数与阻力系数 2 自平衡率 3 纯延迟 4 单容控制对象的数学模型
第三章 控制对象的动态特性
控制对象是组成控制系统的基本环节之一, 研究控制对象的动态特性对控制系统的研究具有 重要的理论和实践意义,如判断系统的稳定性和 为控制系统选配合适的控制仪表以及控制系统的 参数调整等。
返回目录
§3-1单容控制对象
任何控制对象都具有储存物质或能量的能力。只有一个储 蓄容积的对象称为单容控制对象。依此类推,具有两个以上储 蓄容积的控制对象则称为多容控制对象。这里只讨论单容控制 对象。
0
o h
K 0
oT
t
63.2% (h)t
t
返回本节
4 单容控制对象的数学模型
分析1
h
K 0
1
2
R1 R2 C1 C2
o T1 T2
t
K k R T RC
返回本节
4 单容控制对象的数学模型
分析1
h
K1 0 K2 0
1
2
R1 R2 C1 C2
o T2 T1
t
K k R T RC
k
返回本节
§3—2多容控制对象的动态特性
• 一、双容水柜控制对象的阶跃响应曲线:
多容控制对象的数学模型
多容控制对象的传递函数
Qi(s)
G1(s)
H1(s) G2(s) Q1(s) G3(s)
H2(s)
返回本节
多容控制对象的数学模型
多容控制对象的传递函数
G1(s) H1(s) K1 Qi(s) T1s 1
G2(s) Q1(s) 1 H1(s) R1
T RC, K k R
G3(s) H 2(s) K 2 Q1(s) T 2s 1
返回本节
多容控制对象的数学模型
单容控制对象的传递函数
T dh h K
dt
T RC, K k R
Ts H(s) H (s) KM (s)
G(s) H (s) K M (s) Ts 1
一阶惯性环节
返回本节
4 单容控制对象的数学模型
单容控制对象的阶跃响应
设 0 则
M (s) 0
s
0
H (s) G(s) M (s) K 0
Q h R h
R
Q
返回本节
1 容量系数与阻力系数
阻力系数(R):推动物质或能量运动的动力与因此而产生
的物质或能量的流量之比。
液阻: R dh h dQ2 Q
对应不同的高度,阻力 系数不同。此即阻力系 数的非线性。
电阻: R du di
气阻: R dp dq
热阻: R dt dq
返回本节
0
o h
K 0
dh(t)
K 0
dt t 0 T
o
t
K
0
T
Tቤተ መጻሕፍቲ ባይዱ
K
0
T
t
返回本节
4 单容控制对象的数学模型
放大系数K和时间常数T的求法
K (h)t K 0
0
0
令t=T,则
h(t) K 0(1 et /T ) h(t) K 0 (1 e1)
63.2% K 0 63.2% (h)t
气容: C dm dp
热容: C dQ 电容: C dQ
dt
du
返回本节
1 容量系数与阻力系数
现象2:
1 Q1+ΔQ
Δh
Fh
给水量Q1增大导致液位h上升 的原因:存在阻力。
2 Q2 +ΔQ
液位h上升又将克服阻力,使 Q2增大ΔQ ,直至Q2 =Q1 。
为使流量增大ΔQ ,阻力越大, 所需增加的Δh也越大。
M (s) A s Ts
k
返回本节
4 单容控制对象的数学模型
分析2 1 k
RK
1 Q1+ΔQ Δh Fh
当R→∞时,自平衡率→0,控制 对象成为一个积分环节。
(Q1 Q2)dt C dh
Q1 dt C dh
2 k dt C dh
ΔQ2=0 G(s) H (s) 1 1 M (s) A s Ts
dh(t)
K 0 k 0
dt t 0 T
C
返回本节
4 单容控制对象的数学模型
分析2 K k R
1 k
RK
可见,控制对象之所以存 在放大系数是由于阻力系 数R所至,R越大,K也越 大,其自平衡率越小。
(Q1 Q2)dt C dh Q1 dt C dh k dt C dh G(s) H (s) 1 1
对象传递函数
返回本章
1 容量系数与阻力系数
现象1:
1 Q1
1 Q1
Fh
2 Q2
Fh
2 Q2
不同大小的水柜容纳水的能力不同。
返回本节
1 容量系数与阻力系数
容量系数(C):被控量变化一个单位时对象所容纳的物质 或能量的变化量。
(Q1 Q2)dt dv A dh
液容: C dv A dh
因此单容水柜的容积系 数就是其截面积A。
4 单容控制对象的数学模型
单容控制对象的微分方程
(Q1 Q2)dt dv A dh C dh
设进口阀开度变化Δμ,则 Δμ
(Q1 Q2)dt C dh 其中,Q1 k Q2 h / R
ΔQ1、 ΔQ2、 Δh
因此,
RC
dh
dt
h
k
R
T dh h K
dt
返回本节
4单容控制对象的数学模型
Ts 1 s
K0
(
1 s
s
1 1/T
)
o
h
K 0
t
h(t) K 0(1 et /T )
o
t
返回本节
4 单容控制对象的数学模型
放大系数K和时间常数T
h(t) K 0(1 et /T )
放大系数K:当对象达到稳态时 把输入量放大的倍数。
时间常数T:对象输出以最大变化 速度达到新稳态值所需的时间。
2 自平衡率
自平衡特性:控制对象在受到扰动后,被控量的变化将引起 物质或能量的流量产生变化,从而使自身恢复到平衡状态。
自平衡率( ):控制对象依靠被控量的变化而使自身恢复
到平衡态的能力。
自平衡率: 1
R
若将出口阀关死,则 0
没有自平衡能力。
1 Q1+ΔQ
Δh
Fh
2
Q2 +ΔQ
返回本节
3 纯延迟
纯迟延(τ):由于传输距离导致被控量的变化比控制量的
1 Q1
变化所落后的时间长度。 u Δu
0 h
t
Fh
2 0τ
Q2
t
返回本节
3 纯延迟
实际的控制对象往往存在纯迟延,通常将其视作由一个 独立的环节,即纯迟延环节,它与控制对象相串联。
Q1(s) e s Q'1(s) +
- Q2(s)
1
h
CS
1 R
返回本节
