spss主成分分析结果汇报
SPSS超详细教程:主成分分析

SPSS超详细教程:主成分分析1、问题与数据某公司经理拟招聘⼀名员⼯,要求其具有较⾼的⼯作积极性、⾃主性、热情和责任感。
为此,该经理专门设计了⼀个测试问卷,配有25项相关问题,拟从315位应聘者中寻找出最合适的候选⼈。
在这25项相关问题中,Qu3-Qu8、Qu12、Qu13测量的是⼯作积极性,Qu2、Qu14-Qu19测量的是⼯作⾃主性,Qu20-Qu25测量的是⼯作热情,Qu1、Qu9-Qu11测量的是⼯作责任感,每⼀个问题都有⾮常同意“Agree”、同意 “Agree Some”、不确定“Undecided”、不同意 “Disagree Some”和⾮常不同意 “Disagree”五个等级。
该经理想根据这25项问题判断应聘者在这四个⽅⾯的能⼒,现收集了应聘者的问卷信息,经汇总整理后部分数据如下:2、对问题的分析研究者拟将多个变量归纳为某⼏项信息进⾏分析,即降低数据结果的维度。
针对这种情况,我们可以进⾏主成分提取,但需要先满⾜2项假设:假设1:观测变量是连续变量或有序分类变量,如本研究中的测量变量都是有序分类变量。
假设2:变量之间存在线性相关关系。
经分析,本研究数据符合假设1,那么应该如何检验假设2,并进⾏主成分提取呢?3、SPSS操作(1) 在主页⾯点击Analyze→Dimension Reduction →Factor弹出下图(2) 将变量Qu1-Qu25放⼊Variables栏(3) 点击Descriptive弹出下图(4) 点选Statistics栏的Initial solution选项,并点选Correlation Matrix栏的Coefficients、KMO andBartlett’s test of sphericity、Reproduced和Anti_image选项(5) 点击Continue→Extraction(6) 点击Display栏中的Scree plot选项(7) 点击Continue→Rotation(8) 点选Method栏的Varimax选项,并点选Display栏的Rotated solution和Loading plot(s)选项(9) 点击Continue→Scores(10) 点击Save as variables,激活Method栏后点击Regression选项(11) 点击Continue→Options(12) 点击 Sorted by size和Suppress small coefficients选项,在Absolute value below栏内输⼊“.3”(13) 点击Continue→OK假设检验假设2:线性相关关系经上述操作,SPSS输出相关矩阵表如下:在变量⽐较多的时候,各变量之间的相关矩阵表会⾮常⼤。
SPSS数据的主成分分析报告

2019/9/10
4
zf
多个指标的问题:
1、指标与指标可能存在相关关系 信息重叠,分析偏误
2、指标太多,增加问题的复杂性和分析难度
如何避免?
2019/9/10
5
zf
主成分分析的基本思想
一项十分著名的工作是美国的统计学家斯通(stone)在 1947年关于国民经济的研究。他曾利用美国1929一1938 年各年的数据,得到了17个反映国民收入与支出的变量 要素,例如雇主补贴、消费资料和生产资料、纯公共支 出、净增库存、股息、利息外贸平衡等等。
运用主成分得分系数矩阵解释主成分:
王冬《我国外汇储备增长因素主成分分析》,《北京工商大学学报》, 2006年4期。
田波平等《主成分分析在中国上市公司综合评价中的作用》,《数学 的实践与认识》,2004年4期
2019/9/10
25
zf
主成分解释的案例分析
基于相关系数矩阵的主成分分析。对美国纽约上市的有关化学产业的三支股票 (Allied Chemical, du Pont, Union Carbide)和石油产业的2支股票(Exxon and Texaco )做了100周的收益率调查(1975年1月-1976年10月)。
F1
F2
F3
i
i
t
F1
1
F201源自F3001
i 0.995 -0.041 0.057 l
Δi -0.056 0.948 -0.124 -0.102 l
t -0.369 -0.282 -0.836 -0.414 -0.112 1
2019/9/10
7
zf
主成分分析:将原来具有相关关系的多个指标简化为少数几个 新的综合指标的多元统计方法。
SPSS进行主成分分析

欢呼词语的近义词有哪些欢呼词语的意思是什么呢?如何使用欢呼词语造句呢?关于欢呼词语的近义词有哪些呢?小编给大家收集了关于表达欢呼词语的解释呢,希望能帮助大家,欢迎大家学习参考!欢呼词语解释欢呼的近义词:欢庆、呐喊、呼喊、欢叫、欢乐、欢畅、喝彩基本信息拼音:huānhū释义:形容一种欢乐而振臂高呼的激情场面。
基本解释[hail;cheer;acclaim;applaud] 欢乐地喊叫他作为英雄而受到欢呼这场战争尚未正式结束,民众已在欢呼引证解释1. 欢乐地喊叫。
《东观汉记·王霸传》:“贼众欢呼,雨射营中。
” 唐元稹《辨日旁瑞气状》:“其日三将同升,万姓欢呼,四方来贺。
” 元萨都剌《将至太平驿》诗:“到驿欢呼如到家,明日舟行复如此。
” 明冯梦龙《东周列国志》第七十一回:“(齐)景公大悦,于是解衣卸冠,与梁邱据欢呼于丝竹之间,鸡鸣而返。
”毛泽东《中国人民站起来了》:“我们的革命已经获得全世界广大人民的同情和欢呼,我们的朋友遍于全世界。
”2. 懽呼:欢乐地呼喊。
唐薛用弱《集异记·李钦瑶》:“举军懽呼,声振山谷。
” 明张居正《贺瑞雪表》五:“懽呼敢效乎虫鸣,踊跃岂殊於兽舞!” 康有为《将至桂林望诸石峰》诗:“昔游燕吴读园记,每见叠石辄懽呼。
”关于欢呼造句1, 在荣誉的桂冠下面,在欢呼声的背后,便是孤独,我们的孤独!2, 收到大学录取通知书,她立刻欢呼雀跃起来。
3, 首先是50米跑,运动员们都摩拳擦脚,准备一举夺下桂冠。
随着一声令下,运动员像脱了弦的箭似的飞了出去,同学们不断为自己的班级喝彩加油打气。
观众席上欢呼声拍掌声此起彼伏,久久不断。
4, 最后一个敌人在血泊里倒下,战争胜利了,满目疮痍的战场上响起了震耳欲聋的欢呼声,只是那命悬一线的惊心动魄始终萦绕在每个人的心头。
5, 每个人都有自己的梦,都有自己的偶像,都有自己的爱好,都有自己的个性……生命中有很多事情,可能没人在乎,但说不定会有谁为你而欢呼。
spss进行主成分分析及得分分析

s p s s进行主成分分析及得分分析This manuscript was revised by the office on December 22, 2012spss进行主成分分析及得分分析1将数据录入spss1. 2数据标准化:打开数据后选择分析→描述统计→描述,对数据进行标准化,选中将标准化得分另存为变量:2.3进行主成分分析:选择分析→降维→因子分析,3.4设置描述性,抽取,得分和选项:4.5查看主成分分析和分析:相关矩阵表明,各项指标之间具有强相关性。
比如指标GDP总量与财政收入、固定资产投资总额、第二产业增加值、第三产业增加值、工业增加值的相关系数较大。
这说明他们之间指标信息之间存在重叠,适合采用主成分分析法。
(下表非完整呈现)5.6由 TotalVarianceExplained(主成分特征根和贡献率)可知,特征根λ1=9.092,特征根λ2=1.150前两个主成分的累计方差贡献率达93.107%,即涵盖了大部分信息。
这表明前两个主成分能够代表最初的11个指标来分析河南各个城市经济综合实力的发展水平,故提取前两个指标即可。
主成分,分别记作F1、F2。
6.7指标X1、X2、X3、X4、X5、X6、X7、X8、X9、X10在第一主成分上有较高载荷,相关性强。
第一主成分集中反映了总体的经济总量。
X11在第二主成分上有较高载荷,相关性强。
第二主成分反映了人均的经济量水平。
但是要注意:这个主成分载荷矩阵并不是主成分的特征向量,也就是说并不是主成分1和主成分2的系数,主成分系数的求法是:各自主成分载荷向量除以各自主成分特征值的算术平方根。
7.8成分得分系数矩阵(因子得分系数)列出了强两个特征根对应的特征向量,即各主要成分解析表达式中的标准化变量的系数向量。
故各主要成分解析表达式分别为:F1=0.32ZX11+0.33ZX12+0.31ZX13+0.31ZX14+0.32ZX15+0.32ZX16+0.32ZX17+0.32ZX 18+0.32ZX19+0.21ZX110+0.15ZX111F2=8.46ZX21+0.02ZX22-0.02ZX23-0.20ZX24-0.23Z25-0.04ZX26-0.15ZX27-0.02ZX28+0.10ZX29+0.47ZX210+0.78ZX2118.9主成分的得分是相应的因子得分乘以相应的方差的算术平方根。
统计分析软件应用SPSS-主成分分析实验报告

本科学生综合性、设计性实验报告实验课程名称统计分析软件应用开课学期2010至2011学年下学期上课时间2011 年4 月25 日辽宁师范大学教务处编印、实验方案、实验目的:掌握主成分分析的思想和具体步骤。
掌握SPSS实现主成分分析的具体操作,并对处理结果做出解释。
5、参考文献:[1]卢纹岱.SPSS for Window銃计分析[M].电子工程出版社,2006[2]郭显光.如何用SPS歎件进行主成分分析[J].统计与信息论坛,1998, (2)[3]何晓群.现代统计分析方法与应用[M].中国人民大学出版社,1998[4]余建英、何旭宏.数据统计分析与SPSS^用[M].人民邮电出版社,2003、实验报告1、 实验目的、设备与材料、理论依据、实验方法步骤见实验设计方案2、 实验现象、数据及结果表1描述性统计量表表2主成分因子荷载矩阵表表3相关系数矩阵表表4公因子方差表Descriptive Statistics图1碎石图Component U 刨乡至拜占,3 GQmponenls extrudedCommunalitiesExtraction Method: Principal Component Analysis.表总方差分解表Total Variance ExplainedCompoiieint initial EigenvaluesExtraction Sums of Squared Loadings Tota J cf Variance Cumulabv? % Total % of '/a™nee Cumulative %1 3&14 48.929 +£.929 3.914 4S929 48.92921 312 23.BSS 723271.912 23B96 72 S2? 3■1.430 17.9911.43917 曲■!&G.S1B4 S79 7.335 SB.'353 5,1441,797 9^.3506.012150 100.000 76 13E-Q13 7.66E-017 1Q0JO0S-4.2E-016-4.25E-015IQO.OOQExtraction Method: Prkicipal Component AnalysisInitial Extraction赔付率1.000 .964 净收入与总收入之比 1.000 .993 投资收益率 1.000 .923 再保险率 1.000 .968 总资产报酬率 1.000 .919 两年保费收入收益率 1.000 .659 保费收入变化率 1.000 .961 流动性比率 1.000.879Plolb1= *X1+*X2+**X4+*X5+***X8b2=*X1+**X3+***X6+*X7+*X8 b3=*X1+*X2+*X3+***X6+**X8表7Y1= *x1+*x2+**x4+*x5+***x8 Y2=*xi+*x2- **x4+*x5+***x8 Y3=*x1+*x2+*x3+*x4+**x6+**x8加权:输出结果,并从高到低进行排序:表81:人保2:平安3:太平洋4:大众5:华泰6:永安7:华安 Z 主成分综合得分Num 1 Z 主成分综合得分 | Num华泰1:人保可以如上所述计算主成分得分,还可以通过综合评价函数计算综合得分综合评价函数:Z=%*Y1+%*Y2+%*Y34、结论:表8中,综合得分出现负值,这只表明该保险公司的综合水平处于平均水平之下。
SPSS进行主成分分析报告报告材料地步骤(图文)
主成分分析的操作过程原始数据如下(部分)调用因子分析模块(Analyze―Dimension Reduction―Factor),将需要参与分析的各个原始变量放入变量框,如下图所示:单击Descriptives按钮,打开Descriptives次对话框,勾选KMO and Bartlett’s test of sphericity选项(Initial solution选项为系统默认勾选的,保持默认即可),如下图所示,然后点击Continue按钮,回到主对话框:其他的次对话框都保持不变(此时在Extract次对话框中,SPSS已经默认将提取公因子的方法设置为主成分分析法),在主对话框中点OK按钮,执行因子分析,得到的主要结果如下面几张表。
①KMO和Bartlett球形检验结果:KMO为0.635>0.6,说明数据适合做因子分析;Bartlett球形检验的显著性P 值为0.000<0.05,亦说明数据适合做因子分析。
②公因子方差表,其展示了变量的共同度,Extraction下面各个共同度的值都大于0.5,说明提取的主成分对于原始变量的解释程度比较高。
本表在主成分分析中用处不大,此处列出来仅供参考。
③总方差分解表如下表。
由下表可以看出,提取了特征值大于1的两个主成分,两个主成分的方差贡献率分别是55.449%和29.771%,累积方差贡献率是85.220%;两个特征值分别是3.327和1.786。
④因子截荷矩阵如下:根据数理统计的相关知识,主成分分析的变换矩阵亦即主成分载荷矩阵U 与因子载荷矩阵A 以及特征值λ的数学关系如下面这个公式:λiiiAU=故可以由这二者通过计算变量来求得主成分载荷矩阵U 。
新建一个SPSS 数据文件,将因子载荷矩阵中的各个载荷值复制进去,如下图所示:计算变量(Transform-Compute Variables)的公式分别如下二张图所示:计算变量得到的两个特征向量U1和U2如下图所示(U1和U2合起来就是主成分载荷矩阵):所以可以得到两个主成分Y1和Y2的表达式如下:Y1=0.456X1+0.401X2+0.428X3+0.490X4+0.380X5+0.253X6Y2=-0.367X1+0.322X2-0.323X3-0.303X4+0.453X5+0.602X6由上面两个表达式,可以通过计算变量来得到Y1、Y2的值。
主成分分析、因子分析实验报告--SPSS

主成分分析、因子分析实验报告--SPSS主成分分析、因子分析实验报告SPSS一、实验目的主成分分析(Principal Component Analysis,PCA)和因子分析(Factor Analysis,FA)是多元统计分析中常用的两种方法,旨在简化数据结构、提取主要信息和解释变量之间的关系。
本次实验的目的是通过使用 SPSS 软件对给定的数据集进行主成分分析和因子分析,深入理解这两种方法的原理和应用,并比较它们的结果和差异。
二、实验原理(一)主成分分析主成分分析是一种通过线性变换将多个相关变量转换为一组较少的不相关综合变量(即主成分)的方法。
这些主成分是原始变量的线性组合,且按照方差递减的顺序排列。
主成分分析的主要目标是在保留尽可能多的数据信息的前提下,减少变量的数量,从而简化数据分析和解释。
(二)因子分析因子分析则是一种探索潜在结构的方法,它假设观测变量是由少数几个不可观测的公共因子和特殊因子线性组合而成。
公共因子解释了变量之间的相关性,而特殊因子则代表了每个变量特有的部分。
因子分析的目的是找出这些公共因子,并估计它们对观测变量的影响程度。
三、实验数据本次实验使用了一份包含多个变量的数据集,这些变量涵盖了不同的领域和特征。
数据集中的变量包括具体变量 1、具体变量 2、具体变量 3等,共X个观测样本。
四、实验步骤(一)主成分分析1、打开 SPSS 软件,导入数据集。
2、选择“分析”>“降维”>“主成分分析”。
3、将需要分析的变量选入“变量”框。
4、在“抽取”选项中,选择主成分的提取方法,如基于特征值大于1 或指定提取的主成分个数。
5、点击“确定”,运行主成分分析。
(二)因子分析1、同样在 SPSS 中,选择“分析”>“降维”>“因子分析”。
2、选入变量。
3、在“描述”选项中,选择相关统计量,如 KMO 检验和巴特利特球形检验。
4、在“抽取”选项中,选择因子提取方法,如主成分法或主轴因子法。
SPSS进行主成分分析报告
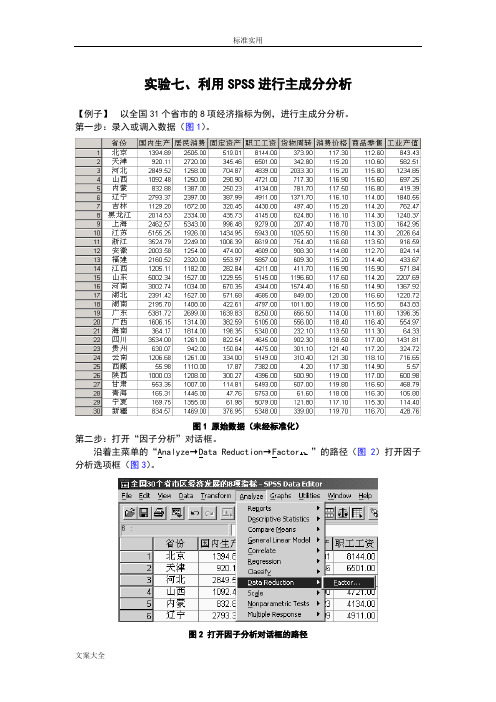
实验七、利用SPSS进行主成分分析【例子】以全国31个省市的8项经济指标为例,进行主成分分析。
第一步:录入或调入数据(图1)。
图1 原始数据(未经标准化)第二步:打开“因子分析”对话框。
沿着主菜单的“Analyze→Data Reduction→Factor ”的路径(图2)打开因子分析选项框(图3)。
图2 打开因子分析对话框的路径图3 因子分析选项框第三步:选项设置。
首先,在源变量框中选中需要进行分析的变量,点击右边的箭头符号,将需要的变量调入变量(Variables)栏中(图3)。
在本例中,全部8个变量都要用上,故全部调入(图4)。
因无特殊需要,故不必理会“Value ”栏。
下面逐项设置。
图4 将变量移到变量栏以后⒈设置Descriptives描述选项。
单击Descriptives按钮(图4),弹出Descriptives对话框(图5)。
图5 描述选项框在Statistics 统计 栏中选中Univariate descriptives 复选项,则输出结果中将会给出原始数据的抽样均值、方差和样本数目(这一栏结果可供检验参考);选中Initial solution 复选项,则会给出主成分载荷的公因子方差(这一栏数据分析时有用)。
在Correlation Matrix 栏中,选中Coefficients 复选项,则会给出原始变量的相关系数矩阵(分析时可参考);选中Determinant 复选项,则会给出相关系数矩阵的行列式,如果希望在Excel 中对某些计算过程进行了解,可选此项,否则用途不大。
其它复选项一般不用,但在特殊情况下可以用到(本例不选)。
设置完成以后,单击Continue 按钮完成设置(图5)。
⒉ 设置Extraction 选项。
打开Extraction 对话框(图6)。
因子提取方法主要有7种,在Method 栏中可以看到,系统默认的提取方法是主成分(Principal Components ),因此对此栏不作变动,就是认可了主成分分析方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实用标准文档
实验目的:原始数据中每一所高校具有20个相关性很高的变量,利用主成分分析法用较少的变量去解释原来资料中的大部分变异,将手中的众多变量转化成彼此相互独立或不相关的个数较少的变量,即所谓主成分,并用以解释资料的综合性指标,其实质的目的是降维
原始数据截屏:
操作方法:
1.描述性统计
SPSS在调用因子分析过程进行分析时,SPSS会自动对原始数据进行标准化处理,所以在得到计算结果后指的变量都是指经过标准化处理后的变量,但SPSS不会直接给出标准化后的数据,然后后期的计算需得到标准化数据,则需调用“描述”过程进行计算,为了看到标准化数据,所以采用描述性统计下的描述操作获得标准化后的变量数据
标准化数据:
文案大全
因子分析操作过程:
选取变量:
X1:科研经费得分
X2:国家人文社科重点研究基地得分
X3:院士总数得分
X4:生均图书得分
X5:研究中心数得分
X6:国家重点实验室得分
X7:生均教学科研仪器设备得分X8:生均教育事业经费得分
X9:精品课程得分
X10:优秀博士生论文总分
X11:人才得分
X12:二级学科建设得分
X13:生均固定资产得分
X14:科研论文得分
X15:博导及相关合计得分
X16:教师中博士学位比重得分X17:一级学科得分
X18:高级职称比重得分
X19:师资总分
X20:SCI数量
这里分析采用相关系数矩阵,输出选择为未旋转的因子解,并选择碎石图,抽取过程选择基于特征值(特征值大于1),最大收敛迭代次数:25,点击确定。
原数据中有较多的缺失值,选择按列表排除个案,点击继续。
分析结果:
KMO越接近1,说明变量之间的相关性越强,原有变量适合做因子分析;Bartlett的球度检验值越小于显著性水平0.05,越说明变量间存在相关关系。
本数据中KMO值为0.736,sig.值为0,符合因子分析条件,可进行因子分析,并进一步进行主成分分析
累计贡献率79.119%<80%,由反映象相关矩阵中我们可以看出(如下图所示)
反映象相关矩阵中对角线上的数值应>0.5,根据次标准,数据显示生均图书得分变量不适合做因子分析,所以删去,重新做因子分析。
去除生均图书得分变量之后的因子分析结果:
累计百分比为81.466%>80%,且特征值均大于1
结论:
初始特征根:λ1=6.901,,λ2=4.846,λ3=3.732
主成分贡献率:r1=36.32%,r2=25.506%,r3=19.640%
碎石图
旋转之后的主成分载荷矩阵,可以看出:SCI数量,国家重点实验室得分,研究中心数得分,研究中心数得分,科研经费得分,二级学科建设得分,科研论文得分,优秀博士生论文得分,一级学科得分,精品课程得分与主成分1密切相关,可将其总结归纳为软实力与资源指标;师资总分,博导及相关合计得分,人才得分,院士总数得分,高级职称比重得分,教师中博士学位比重得分与主成分2密切相关,可将其归纳总结为师资结构指标;生均教学科研仪器设备得分,生均教育事业经费得分,生均固定资产得分与主成分3密切相关,可将其归纳为学生平均资产指标。
根据主成分1得分降序排列:由主成分1可以看出,清华大学,浙江大学,北京大学,华中科技大学,西安交通大学,武汉大学,上海交通大学,中南大学,四川大学,东南大学在论文发表以及国家级实验室得分方面位列前十名,其软实力雄厚;
根据主成分2得分降序排名:可以看出北京大学,中国人民大学,复旦大学等在师资结构方面排名靠前,说明其在师资力量上占据很大竞争力
根据主成分3得分降序排名:可以看出清华大学,上海交通大学等前十名大学在学校生均资产方面具有竞争力
2> 计算主成分综合得分
Z=r1*FAC1+r2*FAC2+r3*FAC3
主成分贡献率:r1=36.32%,r2=25.506%,r3=19.640%
由综合得分可以看出:清华大学,北京大学,浙江大学,复旦大学,,,,,,等十所高校位列我国高校前十名,与武书连等国内知名统计机构结果相近,也与我国现状相似。
