初二数学代入消元法解二元一次方程组--------3月23日作业
初二数学二元一次方程组试题答案及解析

初二数学二元一次方程组试题答案及解析1.解方程组.【答案】.【解析】①+②得到方程3x=6,求出x的值,把x的值代入②得出一个关于y的方程,求出方程的解即可.试题解析:,①+②得:3x=6,解得x=2,将x=2代入②得:2﹣y=1,解得:y=1.∴原方程组的解为.【考点】解二元一次方程组.2.某工厂去年的利润(总收入-总支出)为100万元,今年总收入比去年增加了10%,总支出比去年减少了9%,今年的利润为300万元,去年的总收入、总支出各是多少万元?【答案】1100,1000.【解析】设去年的总产值为x万元,总支出为y万元,表示出今年总产值和总支出,根据两个关系列方程组求解.试题解析:设去年的总产值为x万元,总支出为y万元,根据题意得:解得:答:这个工厂去年的总收入和总支出分别为1100万元和1000万元。
考点: 二元一次方程组的应用.3.解下列二元一次方程组(1)(2)【答案】①;②.【解析】本题考查了解二元一次方程组的一般方法.解二元一次方程组的关键是消元,主要两种消元方法-代入消元法和加减消元法.(1)方程中未知数y的系数分别为5和-5,可直接用加减消元法解答;(2)先将方程①×2得到③,然后由③-②可消去未知数a,进而求解.试题解析:解:(1)①+②得:5x=10X=2把x=2代入方程①中得:6+5y=21解得:y=3∴方程组的解是.①×2-②得:15b=3解得:把代入①得:2a+1=2解得:a=1∴方程组的解是.【考点】解二元一次方程.4.小华早晨6点多钟去学校,去时看了一下手表,发现时针与分针的夹角为度(0<<180,为整数),到了学校,他又看了一下手表,发现此时还不到7点钟,且时针与分针的夹角为也为度,若小华去学校途中所用的时间是10的整数倍,那么,小华去学校途中所用的时间是多少?【答案】20分钟或40分钟【解析】设去时是6点x分,到校是6点y分,途中所用的时间为y-x.根据题意得,=(360+x)×0.5-6x=180-5.5x;=6y-(360+y)×0.5=5.5y-180.两式相加得:2=5.5(y-x),.设=10k(k为正整数),即可得到2=55k,因0<<180,所以0<55k<360,0<k<6.6,从而求得结果.设去时是6点x分,到校是6点y分,途中所用的时间为y-x.根据题意得,=(360+x)×0.5-6x=180-5.5x;=6y-(360+y)×0.5=5.5y-180.两式相加得:2=5.5(y-x),.设=10k(k为正整数) 所以2=55k,因0<<180,所以0<55k<360, 0<k<6.6.由2=55k知,k为偶数数,所以k=2或4. =55或110.=20或40.答:小华去学校途中所用的时间是20分钟或40分钟.【考点】二元一次方程的应用点评:方程的应用是初中数学的重点,是中考常见题,一般难度不大,需熟练掌握.5.已知│y-2x│+(x+y-3)2="0" 计算y-x【答案】【解析】先根据非负数的性质得到关于x、y的方程组,解出x、y的值,即可求得结果.由题意得,解得,∴【考点】本题考查的是非负数的性质点评:解答本题的关键是熟练掌握非负数的性质:几个非负数的和为0,这几个数均为0.6.解方程【答案】【解析】由①得,再代入②即可消去解得,再代入即可解得,从而得到方程组的解。
8.2.1消元-代入法解二元一次方程组

——用代入法解二元一次方程组 2课时
随堂练习:
y=2x ⑴ x+y=12 3x-2y=9 ⑶ x+2y=3
你解对了吗?
x=4
1、用代入消元法解下列方程组
x+y=11 x-y=7
⑵ y=8
x=9 y=2
x=3
yБайду номын сангаас0
用代入法解二元一次 方程组的一般步骤
讨论
4x + 5y = 4
变
用含x 的一次式表示y: y= 用含y 的一次式表示x: 代 x=
思考题:
2 x 5 y 6 3x 5 y 16 变式: 已知关于x、y的方程组 和 ax by 4 bx ay 8 的解相同,求a b的值。
例题精练
ax 6 y 3 1.若关于x,y的方程组 与 2 x 5 y 11
a = -2b - 1 ③ 由②得: 把③代入①得:
2x + ay = 3b ax - by = 1 的解,
②
把b = -4/7 代入③,得: a = -2b - 1 = -2×(-4/7)-1 a = 1/7 ∴ a = 1/7
-2 + 2(-2b – 1)= 3b -2 – 4b – 2 = 3b -4b – 3b = + 2 + 2 -7b = 4 b = -4/7
4 4x 5 4 5y 4
1、将方程组里的一个方程变 形,用含有一个未知数的一次 式表示另一个未知数 2、用这个一次式代替另一个 方程中相应的未知数,得到一 个一元一次方程,求得一个未 知数的值 3、把这个未知数的值代入一 次式,求得另一个未知数的值
求 写
4、写出方程组的解
二元一次方程组的解法-代入消元法

1.2 二元一次方程组的解法1.2.1代入消元法教学目标1.了解解方程组的基本思想是消元。
2.了解代入法是消元的一种方法。
3.会用代入法解二元一次方程组。
4.培养思维的灵活性,增强学好数学的信心。
教学重点用代入法解二元一次方程组消元过程。
教学难点灵活消元使计算简便。
教学过程一、知识回味1、如果2x+y=1.2,那么用含有x的代数式表示y的代数式是_____________;2、在方程3x+4y=16中,当x=3时,y=____________,当y=-2时,x=____________。
二、说一说在上节课的问题中,我们知道小亮家1月份共用了16m3天然气和10t 水。
现在来解决1m3天然气费多少元,1t水费多少元的问题.我们都知道二元一次方程组哪这个二元一次方程组的一个解是怎样得来的呢?把②变形得 x=20+y ③把③代人①得 (20+y )+y=60 ④解方程④得 y= 20把y 的值代人③得三、例题P 例1、例2四、 归纳代入消元法。
(简称代入法)1.基本思路:解二元一次方程组的基本思路是: (简称为 ),得到 ,然后解 .2.基本步骤:在上面的几个例子中,消去一个未知数的方法是:把其中一个方程的 用含有 的代数式表示,然后把它 ,便得到一个 .3.定义:这种解方程组的方法叫做代入消元法,简称为 .四、做一做五、作业习题1.2A 组第1题。
教学反思:⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎩⎩⎧⎧⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎩⎩ 1234 = 128 32= 5 = 4 =2 1 52= 11 31= 0 3= 7 233=0 x+y x +y x y y x x+y x y+x+y x+y ) ) ) ) ,,; . ,,; . ----((((⎧⎧⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎩⎩⎧⎧⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎩⎩ 1234 = 128 32= 5 = 4 =2 1 52= 11 31= 0 3= 7 233=0 x+y x +y x y y x x+y x y+x+y x+y )) ) ) ,,; .,,;. ---- ((((。
二元一次方程组解法-代入法练习题

二元一次方程组解法(一)—-代入法(基础)巩固练习【巩固练习】一、选择题1.用代入消元法解方程组323211x yx y-=⎧⎨+=⎩①②代入消元法正确的是()。
A .由①②得y =3x+2,代入②,得3x=11—2(3x+2)B.由②得1123yx-=,代入①,得11231123yy-=-C.由①得23yx-=,代入②,得2—y=11—2yD.由②得3x=11-2y,代入①,得11-2y-y=22.用代入法解方程组34225x yx y+=⎧⎨-=⎩①②使得代入后化简比较容易的变形是().A.由①得243yx-=B.由①得234xy-=C.由②得52yx+=D.由②得y=2x-53.对于方程3x—2y—1=0,用含y的代数式表示x,应是()。
A.1(31)2y x=-B.312xy+=C.1(21)3x y=-D.213yx+=4.已知x+3y=0,则3232y xy x+-的值为().A.13B.13-C.3 D.—35.一副三角板按如图摆放,∠1的度数比∠2的度数大50°,若设,,则可得到方程组为().A. B.C。
D.6.已知21x y =⎧⎨=⎩是二元一次方程组71ax by ax by +=⎧⎨-=⎩的解.则a -b 的值为( )。
A .-1B .1C .2D .3二、填空题7.解方程组523,61,x y x y +=⎧⎨-=⎩①②若用代入法解,最好是对方程________变形,用含_______的代数式表示________.8.如果-x+3y =5,那么7+x -3y =________.9.方程组525x y x y =+⎧⎨-=⎩的解满足方程x+y —a =0,那么a 的值是________. 10。
若方程3x -13y =12的解也是x -3y =2的解,则x =________,y =_______. 11.小刚解出了方程组332x y x y -=⎧⎨+=⎩▲的解为4x y =⎧⎨=⎩▉,因不小心滴上了两滴墨水,刚好盖住了方程组中的一个数和解中的一个数,则▲=________,▇=________。
求解二元一次方程组(知识梳理与考点分类讲解)-八年级数学上册基础知识专项突破讲与练(北师大版)
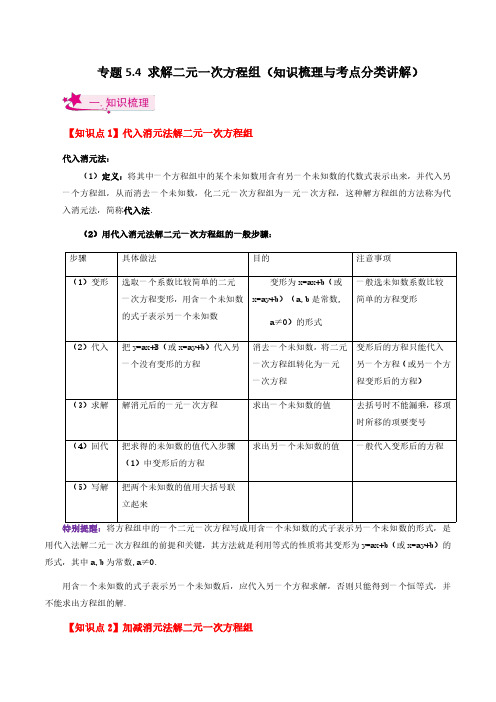
专题5.4求解二元一次方程组(知识梳理与考点分类讲解)【知识点1】代入消元法解二元一次方程组代入消元法:(1)定义:将其中一个方程组中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程组,从而消去一个未知数,化二元一次方程组为一元一次方程,这种解方程组的方法称为代入消元法,简称代入法.(2)用代入消元法解二元一次方程组的一般步骤:步骤具体做法目的注意事项(1)变形选取一个系数比较简单的二元一次方程变形,用含一个未知数的式子表示另一个未知数变形为x=ax+b(或x=ay+b)(a,b 是常数,a≠0)的形式一般选未知数系数比较简单的方程变形(2)代入把y=ax+B(或x=ay+b)代入另一个没有变形的方程消去一个未知数,将二元一次方程组转化为一元一次方程变形后的方程只能代入另一个方程(或另一个方程变形后的方程)(3)求解解消元后的一元一次方程求出一个未知数的值去括号时不能漏乘,移项时所移的项要变号(4)回代把求得的未知数的值代入步骤(1)中变形后的方程求出另一个未知数的值一般代入变形后的方程(5)写解把两个未知数的值用大括号联立起来特别提醒:将方程组中的一个二元一次方程写成用含一个未知数的式子表示另一个未知数的形式,是用代入法解二元一次方程组的前提和关键,其方法就是利用等式的性质将其变形为y=ax+b(或x=ay+b)的形式,其中a,b 为常数,a≠0.用含一个未知数的式子表示另一个未知数后,应代入另一个方程求解,否则只能得到一个恒等式,并不能求出方程组的解.【知识点2】加减消元法解二元一次方程组1.加减消元法的定义通过将两个方程相加(减)消去其中一个未知数,将二元一次方程组转化为一元一次方程来解,这种解二元一次方程组的方法叫做加减消元法,简称加减法.2.用加减消元法解二元一次方程组的一般步骤步骤具体做法目的注意事项(1)变形根据绝对值较小的未知数(同一个未知数)的系数的最小公倍数,给方程的两边都乘适当的数.使某一个未知数在两个方程中的系数相等或互为相反数.给某个方程乘一个数时,方程两边的每一项都要和这个数相乘(2)代入两个方程中同一个未知数的系数互为相反数时,将两个方程相加;同一个未知数的系数相等时,将两个方程相减.消去一个未知数,将二元一次方程组转化为一元一次方程把两个方程相加(减)时,一定要把两个方程两边分别相加(减).(3)求解解消元后的一元一次方程求出一个未知数的值(4)回代把求得的未知数的值代入方程组中某个较简单的方程求出另一个未知数的值回代时选择系数较简单的方程(5)写解把两个未知数的值用大括号联立起来特别提醒:1.两个方程同一未知数的系数的绝对值相等或成倍数关系时,解方程组应考虑用加减消元法.2.如果同一未知数的系数的绝对值既不相等又不成倍数关系,我们应设法将一个未知数的系数的绝对值转化为相等关系.3.用加减法时,一般选择系数比较简单(同一未知数的系数的绝对值相等或成倍数关系)的未知数作为消元对象.【考点目录】【考点1】代入消元法解二元一次方程组;【考点2】加减消元法解二元一次方程组;【考点3】同解方程组;【考点4】整体思想解二元一次方程组;【考点5】求解二元一次方程组——错题复原问题;【考点6】求解二元一次方程组——参数问题;【考点7】构造二元一次方程组求解。
北师大版初中数学八年级(上)5-2 求解二元一次方程组(第2课时)(学案+练习)

2 求解二元一次方程组(第2课时)学习目标1. 会用加减消元法解二元一次方程组.(重点)2. 进一步理解二元一次方程组的“消元”思想,初步体会数学研究中“化未知为已知”的化归思想.(难点)自主学习学习任务一 探究加减法解二元一次方程组 3521,2511.x y x y ⎧+=⎪⎨-=-⎪⎩①② 发现方程①和②中的5y 和-5y 互为 ,将方程①和②的左右两边分别相加,然后根据等式的基本性质消去未知数 ,得到一个关于 的一元一次方程,从而实现化“二元”为“一元”的目的.解:①+②,得 , 解得 .把 代入①,解得 . 所以原方程组的解为 . 学习任务二 用加减法解二元一次方程组解二元一次方程组257,23 1.x y x y -=⎧⎨+=-⎩解:②-①,得 ,解得 .把 代入①,得 , 解得 .所以方程组的解为 .归纳:在方程组的两个方程中,若某个未知数的系数是相反数,则可直接把这两个方程的两边分别 ,消去这个未知数,若某个未知数的系数相等,可直接把这两个方程的两边分别 ,消去这个未知数,得到一个一元一次方程,从而求出它的解,这种解二元一次方程组的方法叫做加减消元法,简称加减法.合作探究用加减消元法解二元一次方程组的基本思路是什么?用加减消元法解二元一次方程组的主要步骤有哪些?例1解方程组2312, 3417.x yx y+=⎧⎨+=⎩例2用加减消元法解方程组:4,4333(4)4(2). x yx y⎧+=⎪⎨⎪-=+⎩当堂达标1.用加减法解方程组324,233,x yx y⎧-=⎪⎨+=⎪⎩①②下列解法正确的是()A.①×2-②×3,消去yB.①×3+②×2,消去yC.①×3+②×2,消去xD.①×3-②×2,消去x2.由方程组223,224,x y mx y m-=+⎧⎨+=+⎩可得x与y的关系式是()A.3x=7+3mB.5x-2y=10C.-3x+6y=2D.3x-6y=23.已知二元一次方程组23,24,m nm n-=⎧⎨-=⎩则m+n的值是.4.解下列方程组:(1)3,1;x yx y-=⎧⎨+=⎩(2)3415,2410;x yx y+=⎧⎨-=⎩(3)133,2223 3.x yx y⎧-=-⎪⎨⎪+=⎩课后提升1.对于非零的两个实数m,n,定义一种新运算,规定m*n=am-bn,若2*(-3)=8,5*3=-1,则(-3)*(-2)的值为.2.已知实数a,b满足方程组327,238,a ba b+=⎧⎨+=⎩则a2-b2的值是.反思感悟我的收获:我的易错点:参考答案当堂达标1.B2.D3.-14.解:(1)3,1.x yx y⎧-=⎪⎨+=⎪⎩①②①+②,得2x=4,解得x=2.把x=2代入①,得2-y=3,解得y=-1.所以原方程组的解是2,1. xy=⎧⎨=-⎩(2)3415, 2410. x yx y⎧+=⎪⎨-=⎪⎩①②①+②,得5x=25,解得x=5.把x=5代入②,得2×5-4 y=10,解得y=0.所以原方程组的解是5,0. xy=⎧⎨=⎩(3)133, 2223 3.x yx y⎧-=-⎪⎨⎪+=⎩①②由①,得x-3y=-6,③②+③,得3x=-3,解得x=-1.把x=-1代入③,得y=5 3 .所以原方程组的解是1,5.3 xy=-⎧⎪⎨=⎪⎩课后提升1.1 2.-3。
初二数学解二元一次方程练习题
初二数学解二元一次方程练习题解二元一次方程是初中数学中的重要内容。
通过练习题的形式,我们可以巩固和应用所学的知识,提高解题能力。
下面是一些初二数学解二元一次方程的练习题。
第一题:解方程组:2x - 3y = 45x + 4y = -7解答:首先,我们可以选择消元法解此方程组。
将第一个方程乘以5,第二个方程乘以2,得到:10x - 15y = 2010x + 8y = -14然后,我们减去两个方程,得到:-23y = 34解得y = -34/23将y的值代入第一个方程,得到:2x - 3(-34/23) = 42x + 102/23 = 42x = 4 - 102/23将整数和分数合并,得到:2x = 92/23化简得:x = 46/23所以,方程组的解为x = 46/23,y = -34/23。
第二题:解方程组:3x - 2y = 14x + 5y = 19解答:这道题我们可以选择代入法解题。
首先,我们将第一个方程化简,得到:y = (3x - 1)/2然后,我们将y的值代入第二个方程,得到:4x + 5((3x - 1)/2) = 194x + 15x - 5 = 19化简后的方程是:19x = 24解得x = 24/19将x的值代入第一个方程,得到:3(24/19) - 2y = 1化简得:72/19 - 2y = 1-2y = 1 - 72/19化简得:-2y = -53/19解得y = 53/38所以,方程组的解为x = 24/19,y = 53/38。
第三题:解方程组:7x - 4y = 83x + 2y = -10这道题我们可以使用消元法解题。
将第一个方程乘以3,第二个方程乘以7,得到:21x - 12y = 2421x + 14y = -70然后,我们减去两个方程,得到:-26y = -94解得y = 94/26将y的值代入第一个方程,得到:7x - 4(94/26) = 8化简得:7x - 376/26 = 87x = 8 + 376/26化简得:7x = 56/13解得x = 8/13所以,方程组的解为x = 8/13,y = 94/26。
二元一次方程组解法代入消元法
二元一次方程组解法代入消元法嘿,朋友!咱们来唠唠二元一次方程组的代入消元法。
就好比有两个超级神秘的小怪兽,一个叫x,一个叫y,它们藏在两个方程里。
比如说方程一是3x + 2y = 10,方程二是2x - y = 3。
这y就像个调皮的小跟班,在方程二里看着就比较好欺负。
那咱就从方程二开始下手,把y单独拎出来,就像从一群小伙伴里把那个最弱小的揪出来一样。
从2x - y = 3,咱能得到y = 2x - 3。
这就好像是把小跟班y的身份给彻底曝光了,它现在只能听咱们的话啦。
然后呢,咱们就把这个被驯服的y = 2x - 3代入到方程一里面,就像是把小跟班送进了另一个神秘基地一样。
方程一就变成了3x+2(2x - 3)=10。
这时候就像是把两个原本分开的小怪兽世界给打通了。
接着展开括号,3x + 4x - 6 = 10,这就像把小怪兽们的秘密武器都给亮出来了。
然后7x - 6 = 10,就好像小怪兽们要开始最后的决战啦。
把 - 6移到等号右边,7x = 10 + 6,这就像是小怪兽在给自己补充能量呢。
7x = 16,然后算出x = 16/7,这就像终于找到了小怪兽x的老巢。
再把x = 16/7代入y = 2x - 3里,这就像是拿着找到的宝藏钥匙去开另一个宝箱。
y = 2×(16/7)-3,这就像沿着小怪兽留下的痕迹去寻找另一个小怪兽y。
计算一下,y = 32/7 - 21/7 = 11/7。
就好像把另一个小怪兽也给收服了。
再比如说方程组是x + 3y = 8和4x - y = 6。
这里面的y在4x - y = 6里就像个刺头,不过咱还是能把它变成y = 4x - 6。
然后代入x + 3y = 8,就成了x + 3(4x - 6)=8,就像把刺头送到了一个新的包围圈。
展开括号,x+12x - 18 = 8,就像打开了刺头的秘密防线。
13x - 18 = 8,算出x = 26/13 = 2。
再把x = 2代入y = 4x - 6,得到y = 8 - 6 = 2。
代入消元法解二元一次方程组练习题
测试 消元(一)学习要求会用代入消元法解二元一次方程组.课堂学习检测一、填空题1.已知方程6x -3y =5,用含x 的式子表示y ,则y =______.2.若和是关于x ,y 的方程y =kx +b 的两个解,则k =______,b =______.3.在方程3x +5y =10中,若3x =6,则x =______,y =______.二、选择题4.方程组的解是( ). (A)无解 (B)无数解 (C) (D) 5.以方程组的解为坐标的点(x ,y )在平面直角坐标系中的位置是( ). (A)第一象限(B)第二象限 (C)第三象限 (D)第四象限 6.下列方程组中和方程组同解的是( ). (A) (B) (C) (D) 三、用代入消元法解下列方程7.8. ⎩⎨⎧-==1,1y x ⎩⎨⎧==3,2y x ⎩⎨⎧=++=143,5y x y x ⎩⎨⎧=-=.3,2y x ⎩⎨⎧-==.2,3y x ⎩⎨⎧-=+-=1,2x y x y ⎩⎨⎧=+-=732,43y x y x ⎩⎨⎧=+=.732,11y x x ⎩⎨⎧=+=.732,5y x y ⎩⎨⎧=+--=.7386,43y x y x ⎩⎨⎧-==.43,1y x x ⎩⎨⎧=+=+.53,1y x y x ⎩⎨⎧=+=+.643,02b a b a综合、运用、诊断一、填空题9.小明用36元买了两种邮票共40枚,其中一种面值1元,一种面值0.8元,则小明买了面值1元的邮票______张,面值0.8元的邮票______张.10.已知和都是方程ax -by =1的解,则a =______,b =______. 11.若|x -y -1|+(2x -3y +4)2=0,则x =______,y =______.二、选择题12.用代入消元法解方程组使得代入后化简比较容易的变形是( ). (A)由①得 (B)由①得 (C)由②得 (D)由②得y =2x -513.已知x =3t +1,y =2t -1,用含x 的式子表示y ,其结果是( ).(A) (B) (C) (D) 14.把x =1和x =-1分别代入式子x 2+bx +c 中,值分别为2和8,则b 、c 的值是( ).(A) (B) (C) (D) 三、用代入消元法解下列方程组15. 16.⎩⎨⎧-==.2,1y x ⎩⎨⎧==.0,2.y x ⎩⎨⎧=-=+②①52,243y x y x 342y x -=432x y -=25+=y x 31-=x y 21+=y x 352-=x y 312--=x y ⎩⎨⎧==4,3c b ⎩⎨⎧-==4,3c b ⎩⎨⎧-=-=4,3c b ⎩⎨⎧=-=4,3c b ⎩⎨⎧-=-=-.234,423x y y x ⎩⎨⎧==-.3:4:,52y x y x拓展、探究、思考17.如果关于x,y的方程组的解中,x与y互为相反数,求k的值.⎪⎩⎪⎨⎧-=-+=-3 21,734kyxkyx。
人教版初中数学消元-解二元一次方程组精选课时练习(含答案)2
y
1
x 2
26.
y
7 2
参考答案
答案第 1页,总 3页
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
x 9 27. 2
y 4
x 10
x 6
28.(1)
y
10
(2)
y
4
x 1
29.
y
1
x 2
x 3
30.(1)
y
2
,(2)
y
2
.
x 5
x 3
31.(1)是
y
B.①×(﹣3)+②×2,消去 x
C.①×2﹣②×3,消去 y
D.①×3﹣②×2,消去 x
2.关于 x,y
的方程组
a1x+b1y=c1 a2x+b2y=c2
的解是
x y
= =
4 1
,则关于
x,y
的方程组
a1 a2
x-1 x-1
+b1 +b2
-y -y
=c1 =c2
的解是( )
A.
x y
= =
3 1
B.
(1)反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“ ”.
(2)请选择一种你喜欢的方法,完成解答.
2x 3y 7
37.解方程组:
x
3
y
8
.
5x 3y n 38.已知关于 x,y 的二元一次方程组 3x 2 y 2n 1 的解适合方程 x+y=6,求 n 的
值.
试卷第 4页,总 6页
x
x
y
y
3.2
3.2
的解为(
)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二数学代入消元法解二元一次方程组--------3月23日作业
1、代入消元法的概念:将方程组中一个方程的某个未知数用含有另一个未知数的代数式表示出来,并代入方程中,从而一个未知数,化二元一次方程组为,这种解方程组的方法称为代入消元法,简称.
2、用代入法解方程组23328y x x y =-⎧⎨+=⎩
①②时,将方程①代入方程②中,所得的方程正确的是( ) A.3430x x +-= B. 3468x x +-= C. 3238x x +-= D. 3268x x +-=
3、从方程组45x m m y -==+⎧⎨⎩
中,求得x 与y 的关系式是( ) A .1x y +=- B .1x y += C .9x y += D. 9x y +=-
4、已知360x y +-=,用含x 的代数式表示y =,用含y 的代数式表示x =.
5、已知二元一次方程346,x y +=当,x y 互为相反数时,x =,y =;当,x y 相等时,x =,y =.
6、已知13a b a x y +-与2a b b x y -是同类项,则a =,b =.
7、已知x 的相反数是31y +,y 的相反数是21x -,则2()x y +的值为.
8、在代数式2x px q ++中,当x =-1时,它的值为5,当x =3时,它的值为3,则p =,q =.
9、用代入法解下列方程组:
(1) ⎩⎨⎧+==+②y x ①y x ;3,1423 (2)⎩⎨⎧=+=+②
y x ①y x .134,1632
10、先阅读,然后接方程组.材料:解方程组104()9x y x y y --=⎧⎨--=⎩①②
时,可由①得1x y -=③,然后再将③
代入②得4×1-y =5,∴y =-1,进而求得方程组的解为01x y =⎧⎨=-⎩
,这种方法称为“整体代入法”. 请用这样的方法解下列方程组.
2320235297x y x y y --=⎧⎪⎨-++=⎪⎩
①②。
