图像放大算法比较研究

合集下载

图像放大算法范文

图像放大算法范文图像放大算法是指将低分辨率图像放大到高分辨率的过程。

在图像处理中，图像放大是一个具有挑战性的问题，因为放大图像时往往会引入模糊、失真等问题。

然而，通过使用一些高级的算法和技术，可以获得更好的放大效果。

在实际应用中，图像放大主要有两种方式：插值和超分辨率。

插值是一种基本的图像放大技术，它利用邻近像素的信息对低分辨率图像进行放大。

最简单的插值算法是最近邻插值，在放大时将每个像素复制为一个矩阵区域。

这种算法易于实现，但会导致锯齿状的边缘。

另一种常用的插值算法是双线性插值，它使用邻近的四个像素的信息进行插值计算。

这种算法较第一种算法的效果更好，但对于边界和细节较为平滑的图像效果较差。

超分辨率是一种通过利用多个低分辨率输入图像来产生高分辨率图像的技术。

这种技术通常需要在训练期间学习一个映射函数，然后将其应用于输入图像。

近年来，基于深度学习的超分辨率算法取得了显著的成果。

其中最著名的算法是SRCNN（超分辨率卷积神经网络）和ESPCN（极速超分辨率）。

这些算法通过深度卷积神经网络学习输入图像与目标图像之间的映射，达到超分辨率的效果。

除了插值和超分辨率之外，还有一些其他的图像放大算法。

例如，自适应边缘增强（AEE）算法可以通过增强边缘信息来提高图像的质量。

另外，基于频域的算法，如小波变换，也常用于图像放大领域。

这些算法将图像从空域转换到频域，利用频域的特性对图像进行放大处理。

总结起来，图像放大算法是一个涉及到信号处理、图像处理和机器学习等多个领域知识的复杂问题。

插值和超分辨率是两种常用的图像放大方式，它们分别通过邻近像素的信息和多个输入图像的映射来实现图像放大。

此外，还有一些其他的算法，如自适应边缘增强和基于频域的算法，也可用于图像放大领域。

随着科技的发展，越来越多的新算法将会被提出，并不断改进图像放大的效果。

基于阶梯细化的图像放大算法研究解读

基于阶梯细化的图像放大算法研究
数字图像放大是重要的图像处理技术之一,在众多领域都有重要的应用。

数字图像放大就是将原始图像的分辨率提高,基本的方法是图像插值。

图像插值的算法很多,如经典的最近邻域插值、双线性插值等。

图像放大算法面临的两个主要问题是放大的图像会出现细节模糊化和边缘的锯齿失真。

本论文针对图像放大时边缘出现的锯齿失真,分析锯齿出现的原因,提出数字图像中的边缘是由一系列阶梯构成的,是不连续的;并认为边缘的这种不连续性在图像放大过程中也被放大,从而产生锯齿失真。

根据上述分析,本论文提出了基于阶梯细化的图像放大算法。

该算法是一种综合性的算法,即在图像的非边缘区域采用经典的双线性插值算法;同时根据Canny边缘检测的结果,进一步进行阶梯检测,滤除不会产生锯齿失真的竖直和水平边缘,在使用经典算法会产生明显锯齿失真的包含一系列阶梯的边缘区域,运用基于阶梯细化的插值算法。

该插值算法在放大图像的同时,抑制了边缘中的阶梯被放大,从而达到减少锯齿失真的目的。

最后的实验结果对比和分析表明,在阈值设置合适的前提下,该算法可以在一定程度上抑制边缘锯齿失真。

【关键词相关文档搜索】：通信与信息系统; 图像处理; 图像放大; 阶梯细化; 插值; 锯齿效应
【作者相关信息搜索】：兰州大学;通信与信息系统;万毅;侯国强;。

图像放大的两种编程算法的实现

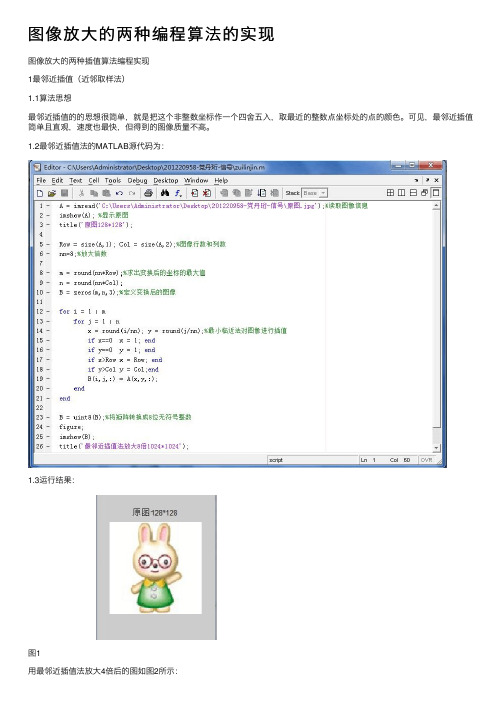
图像放⼤的两种编程算法的实现图像放⼤的两种插值算法编程实现1最邻近插值（近邻取样法）1.1算法思想最邻近插值的的思想很简单，就是把这个⾮整数坐标作⼀个四舍五⼊，取最近的整数点坐标处的点的颜⾊。

可见，最邻近插值简单且直观，速度也最快，但得到的图像质量不⾼。

1.2最邻近插值法的MATLAB源代码为：1.3运⾏结果：图1⽤最邻近插值法放⼤4倍后的图如图2所⽰：图22双线性内插值法2.1算法思想在双线性内插值法中，对于⼀个⽬的像素，设置坐标通过反向变换得到的浮点坐标为(i+u,j+v)，其中i、j均为⾮负整数，u、v为[0,1)区间的浮点数，则这个像素得值f(i+u,j+v)可由原图像中坐标为(i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定，即：f(i+u,j+v)=(1-u)(1-v)f(i,j)+(1-u)vf(i,j+1)+u(1-v)f(i+1,j)+uvf(i+1,j+1)其中f(i,j)表⽰源图像(i,j)处的的像素值，以此类推。

这就是双线性内插值法。

双线性内插值法计算量⼤，但缩放后图像质量⾼，不会出现像素值不连续的的情况。

由于双线性插值具有低通滤波器的性质，使⾼频分量受损，所以可能会使图像轮廓在⼀定程度上变得模糊。

在MATLAB中，可⽤其⾃带的函数imresize()来实现双线性内插值算法。

2.2程序代码双线性内插值算法的MATLAB源代码为：2.3运⾏结果程序运⾏后，原图如图3所⽰：图3双线性内插值法放⼤8倍后的图如图4所⽰：图43结论最近邻插值运算简单快速,能够保持插值图像边缘清晰,但边缘轮廓有显著的锯齿现象,图像背景产⽣马赛克,形成伪边缘,视觉效果差,重构误差较⼤与最邻近法相⽐,双线性内插法由于考虑了待采样点周围4个直接邻点对待采样点的影响,因此基本克服了前者灰度不连续的缺点,其计算量有所增⼤。

此⽅法仅考虑4个直接邻点灰度值的影响,⽽未考虑到各邻点间灰度值变化率的影响,因此具有低通滤波器的性质,使放⼤后图像的⾼频分量受到损失,图像的轮廓变得较模。

双线性插值图像放大算法优化及硬件实现

2、双线性插值硬件加速器设计
基于FPGA的双线性插值硬件加速器主要由输入模块、计算模块和输出模块三部分组成。其中，输入模块负责接收来自外部的图像数据；计算模块负责执行双线性插值算法；输出模块负责将计算结果输出到外部设备。
2、双线性插值硬件加速器设计
在计算模块中，我们采用了基于加权平均法和边缘保护法的双线性插值算法。具体来说，我们对四个相邻像素点进行加权平均，并根据目标像素点的位置关系分配不同的权重。同时，我们还会对目标像素点的周围像素点进行判断，如果存在边缘信息，则会保护这些信息不被丢失。
2、双线性插值硬件加速器设计
在实现过程中，我们采用了Verilog硬件描述语言来编写算法的硬件实现代码。在代码编写过程中，我们采用了流水线架构和并行计算技术，提高了算法的执行效率。我们还采用了一些优化技巧，如逻辑优化、时序优化等，提高了硬件加速器的性能和稳定性。
3、实验结果与分析
3、实验结果与分析
双线性插值图像放大算法优化及硬件实现
目录
01 一、双线性插值算法的优化
03 参考内容
02
二、双线性插值算法的硬件实现
内容摘要
随着图像处理技术的发展，图像放大已成为图像处理中一个重要的环节。在图像放大过程中，由于分辨率的降低和图像信息的损失，图像的质量往往会受到严重影响。为了提高图像的质量，可以采用插值算法对图像进行放大。其中，双线性插值算法是一种常用的方法，它通过对图像中相邻的四个像素点进行线性插值，得到放大后的像素值。
2、边缘保护法
2、边缘保护法
在双线性插值算法中，当目标像素点位于图像边缘时，其周围的四个相邻像素点可能会缺失。这时，如果直接进行线性插值，会导致放大后的图像边缘模糊甚至出现黑边。为了解决这个问题，我们引入了边缘保护法。具体来说，我们在计算目标像素点的值时，会根据其周围的像素点的位置关系，给它们分配不同的权重。这样就可以更好地保护图像的边缘信息，提高图像的质量。

图像放大缩小的原理和应用

图像放大缩小的原理和应用1. 原理图像放大缩小是数字图像处理中的一种基础操作，其原理是通过改变图像像素的尺寸来实现。

在图像放大时，通常采用插值算法来填充空白像素；而在图像缩小时，通常采用像素平均或取样的方式来减少像素。

1.1 图像放大原理图像放大的主要原理是通过插值算法来增加图像的像素数量，从而增大图像的尺寸。

插值算法可以根据原图像的像素值，在新的像素位置上生成合适的像素值。

常用的插值算法包括最近邻插值、双线性插值和双三次插值等。

最近邻插值是一种简单的插值算法，它通过找到离新像素位置最近的像素值来进行插值。

这种算法简单快速，但会导致图像边缘的锯齿效应。

双线性插值是一种更精确的插值算法，它考虑了新像素位置附近的像素值，并进行线性插值计算。

这种算法可以有效地减少锯齿效应，但对于像素边缘仍可能存在模糊问题。

双三次插值是一种更高级的插值算法，它在双线性插值的基础上添加了更多的像素信息，通过曲线拟合来生成更精确的像素值。

这种算法可以进一步减少锯齿效应和模糊问题，但计算复杂度也相应增加。

1.2 图像缩小原理图像缩小的主要原理是通过减少图像的像素数量来缩小图像的尺寸。

常用的缩小算法包括像素平均和取样算法。

像素平均算法是一种简单的缩小算法，它将原图像中的多个像素的 RGB 值取平均，生成新的像素值。

这种算法简单快速，但会导致图像细节丢失。

取样算法是一种更精确的缩小算法，它通过从原图像中选择几个有代表性的像素进行采样，并生成新的像素值。

这种算法可以保留更多的图像细节，但计算复杂度也相应增加。

2. 应用图像放大缩小在许多领域都有广泛的应用，下面列举了几个常见的应用场景：•数字摄影：在数字摄影中，图像放大可以用于增加图像的分辨率，从而提高图像的清晰度和细节呈现。

•医学影像：在医学影像领域，图像放大可以用于放大细胞、组织或病变区域，帮助医生进行更精确的诊断。

•图像处理：在图像处理领域，图像缩小可以用于生成缩略图，帮助用户快速浏览和索引大量图像；图像放大可以用于图像重建和增强，帮助改善图像质量。

基于偏微分的图像放大算法研究

（ｃｏｌｆｏｕｅ（０ｔａｅ，ｉｕｎＵｉｒｉ，ｈｎｄ６０５Ｃｉ）ＳｈｏｏＣｍｐｔｒｆｒ）ＳｃａｎｅｓｙＣｅｇｕ１６，ｈａＳｗｈｖｔ０ｎ
Ａｂｓｒｃ：ｎｔｏｓｈｅｒｓａｃｏｉａｅｚｏｍｉ，ｗｅａｌｚｈｄａｂｃｘｉｔｎｍｅｈｓｏｎｉａｅｔａｔＩｈｅｃｕｒｅｏｆｔｅｅｒｈｎｍｇｏｎｇｎａｙｅｔｅｒｗａｋｏｆｅｓｉｇｔｏｄｍｇｚｏｍｉｏｎｇ．ｋｎｄｖｎｔｇｅｏｆｔｅｉｔｂｌｄｇｎｆｒａｉｎｎｔｅｐｒｅｓｏｆｉａｇｏｏｉＴａｉｇａａａｐｒｄｃａｅｏｆｔｅｅｉｏｍｔｏｉｈｏｃｓｈｅｈｅｍｅｚｍｎｇ，ｈｉｒｉｌｒｐｅｔｓａｔｃｅｐｏｏｓｄａｉａｏｉｇｌｒｔｎｍｇｅｚｏｍｎａｇｏｉｈｍｓｄｎａｉｌｆｅｅｔａｑｕｔｏｎ．Ｔｈｅｌｒｔｂａｅｏｐｒａｄｉｒｎｉｌｅａｉｓｔａｇｏｉｈｍｆｒｔｏｎｃｅｇｅｅｅｔｎｉｓｃｄｕｔｄｄｔｃｉｇ，ｉａｅｍｇｓｏｈｉｔｅｐｏｒｙｏｏｅｈｅｅｅＵＳｈｅｉｅｐｌｎｅｉｔｒｏｌｔｏｎａｇｉｍｏｔｎｇｈｎｒｐｅｌｚｍｄｔｄｇｅｔｒｅｔｍｓｓｉｎｅｐａｉｌｏｒｔ．Ｂｙｄｌｉｔｓｉｅｈｍｅａｉｗｔｈｅｐｏｓｂｌｎｇｈ

基于模糊推理的图像放大算法

ＵｉｒｔｏｏｔａｄＴｌｏｍｎｃｔｎ，Ｎｎｉｇ１０３Ｃｉ）ｎｅｓｙｆｓｎｅｃｍｕｉｉｓａｊ００，ｈｎｖｉＰｓｅａｏｎ２ａ
Ａｂｓｒｃ：Ｉａｅｚｏｔｃｉｕｅｐａｓａｍｐｒａｔｒｌｎｍａｙｉａｅａｐｉａｉｎｓｓｅ．Ｓｎｅｆｚｙｔａｔｍｇｏｍｅｈｎｑｌｙｎｉｏｔｎｏｅｉｎｍｇｐｌｔｏｙｔｍｓｃｉｃｕｚｆａｕｅｉｎｆｔｅｍａｎｉｇｈｒｃｅｓｉｓａｎｖｌｉｇｏｍｔｏａｅｎｆｚｙｒａｏｉｇｉｅｔｒｓｏｅｏｈｉｍａｅｃａａｔｒｔ，ｏｅｍａｅｚｏｍｅｈｄｂｓｄｏｕｚｅｓｎｎｓｉｃ
ＩａｅＺｏｍｅｈｄＢａｅｏＦｕｚａｏｎｇｍｇｏＭｔｏｓｄｎｚｙＲｅｓｎｉ
ＧＮＺｎ－ａｇＱｉａＡｏｇｌｎ，Ｉ — ｉＬＨ
（ｉｇｕＰｏｉｃｅａｆｎｇｒｃｓｎＪｎｓｒｖｅＫｙＬｂｏｈａｅＰｏｅｓｇ＆ＩａｅＣｍｎｃｔｎＮｎｉａｎｉｍｇｏｍｕｉａｏ．ａｊｇｉｎ
ｊｃｎａｅｐｘｌａｅｃｎｉｅｅｓａｋｎｆｐｃｉｆｚｎｅｅｃｕｅａｄｔｅｆｚｙｒｌｓｒｉａｅｔｍｇｉｓｒｏｓｒｄａｉｄｏｅｉｃｕｚｉｆｎｅｒｌｎｈｚｅｅｎｉｅｄｓｆｙｒｓｕｕｍａ

基于水平集重构B样条的图像放大算法研究

ｗｒｐｉｚｄＢｓｄｏｅｌｖｌｓｔａｇｒｈ，ｔｅｉｇｓｓｏｈｄａｄｔｅｉｇｏｚｎａｕｖｓｗｅｅｒ－ｅｅｏｔｍｉ．ａｅｎｔｅｅｅｏｔｍｈｍａｅｗａｍｏｔｅｎｈｍａｅｈｒｏｔｌｃｒｅｒｅｅｈｌｉｉ
本文针对图像在放大过程中，易出现局部模糊不清容晰，产生锯齿状轮廓的图像，而传统的图像处理放大插值算
法方法难以有效解决该问题．了解决上述问题．出了一为提
其中（）＝卢（）非常有意义的是可以利用样条，
中图分类号：Ｐ９Ｔ３１文献标识码：Ｂ
ＩａｅＭａｎｆｃｔｎＵｓｎｖｌＳｔｍｇｇｉａｉｉｇＬｅｅ－ｅｉｏ
Ｒｅ０ｓｒｔ０ｎｄＢ — ｌｎｎｃｉｎｃｎｔｕｃｉｎａＳｐｉｅＦｕｔｏ
ｃｎｔｕｔｄｗｉｉｔｉｉｇｔｅｉｇｄｌｙｏｓｒｃｅｈｌｍａｎａｎｎｈｍａｅｆｅｉ．Ｆｎｌｅｉｔｉａｙ，ｔｅＢａｅｉｅｔｒｔｎｔｃｎｑｅｓｕｅｏｒｐｉｈｌｈｙｓａｒｓａｉｅｈｉｕｓｗａｓｄｔｅａｒｔｅｎｏｏ
第２卷第５９期
文章编号：０６９４（０２）５０６ — ４１０ — ３８２１０ — ２９０
计
算
机
仿
真
２２月０年５１

小波变换在图像缩放与放大中的插值算法优化与时域频域性能分析研究

小波变换在图像缩放与放大中的插值算法优化与时域频域性能分析研究图像缩放与放大是数字图像处理中常见的操作之一。

在传统的图像处理中，常用的插值算法包括最近邻插值、双线性插值和双三次插值。

然而，这些插值算法在处理图像时会产生一些问题，例如锯齿状边缘、模糊和失真等。

为了解决这些问题，研究者们引入了小波变换的思想，并提出了一些基于小波变换的插值算法。

小波变换是一种多尺度分析方法，它可以将信号分解成不同尺度的频率成分。

在图像处理中，小波变换可以将图像分解成不同频率的细节信息和低频信息。

通过对细节信息进行插值处理，可以实现图像的缩放与放大。

而小波变换的频域性能分析可以帮助我们评估不同插值算法的效果。

在小波变换的插值算法中，最常用的是基于小波插值的方法。

这种方法利用小波函数的性质，在图像的不同尺度上进行插值操作。

通过选择合适的小波函数和插值方法，可以实现高质量的图像缩放与放大。

例如，基于小波插值的方法可以消除锯齿状边缘，提高图像的清晰度和细节保留能力。

此外，小波变换的时域频域性能分析也是研究的重点之一。

时域分析可以帮助我们了解图像在时间上的变化规律，而频域分析则可以揭示图像在频率上的特征。

通过对小波变换的时域频域性能进行分析，可以评估不同插值算法在图像缩放与放大中的效果。

例如，我们可以通过时域分析来观察图像的边缘清晰度和细节保留能力，通过频域分析来观察图像的频率响应和频谱特征。

综上所述，小波变换在图像缩放与放大中的插值算法优化与时域频域性能分析是一个重要的研究方向。

通过优化插值算法，可以改善图像的质量和视觉效果。

通过时域频域性能分析，可以评估不同插值算法的优劣，并为图像处理提供参考。

未来，我们可以进一步研究小波变换的插值算法优化和性能分析方法，以提高图像的质量和处理效果。

图像放大算法设计毕业论文

图像放大算法设计毕业论文目录1绪论 (1)1.1课题背景 (1)1.2主要问题及研究意义 (1)1.3本课题的主要研究工作 (2)1.4本文的内容安排 (3)2图像放大技术 (4)2.1灰度图像的表示 (4)2.2数字图像的特点 (4)2.3什么是图像放大 (4)2.4最近邻插值 (5)2.5双线性插值 (6)2.6三次立方插值 (8)2.7本章小结 (9)3插值算法 (10)3.1峰值信噪比（PSNR） (10)3.2基于Ferguson曲面插值的图像放大方法 (11)3.2.1概述 (11)3.2.2 Ferguson双三次曲面 (11)3.2.3 Ferguson双三次曲面插值 (12)3.2.4 基于Ferguson曲面插值的算法描述 (12)3.3实验结果分析 (13)4 基于边缘信息的图像自适应插值算法 (16)4.1概述 (16)4.2 算法思想 (16)4.3 算法描述 (17)4.4 实验结果分析 (19)4.5 本章小结 (20)5 总结与展望 (21)5.1 总结 (21)5.2 展望 (21)致谢 (22)参考文献 (23)附录 (25)⏹1绪论⏹ 1.1课题背景现实生活中看到的、触摸到的都是具体的事物。

人们为了记录和表达这些信息，经常采用图像作为表现的方式。

随着数字时代的发展，需要将这些图像输入到计算机中，并在计算机中存储、处理，在网络中传输，从计算机中输出。

例如人们为了纪念生活中美好的瞬间拍摄的照片，或者从太空传回的记录大气和地面信息的卫星照片，为了广告宣传需要制作、打印长宽几十米的海报。

而目前的图像数字化输入设备扫描仪、数字相机等等都是通过采样图像上的微小区域，产生对应的像素点，从而形成一个点阵化的图像数据。

即对于固定的图像输入条件和固定的图像而言，可以获取的数据量是相对固定的。

可是，很多情况下，例如为了纪念生活中美好的瞬间需要将拍摄的照片放大后挂在墙上，为了观察细节需要将从太空传回的记录大气和地面信息的卫星照片放大，为了广告宣传需要将一张小小的胶片打印成长宽几十米的精致的海报，经常需要将图像进行放大。

图像放大算法

一、图像放大算法图像放大有许多算法，其关键在于对未知像素使用何种插值方式。

以下我们将具体分析几种常见的算法，然后从放大后的图像是否存在色彩失真，图像的细节是否得到较好的保存，放大过程所需时间是否分配合理等多方面来比较它们的优劣。

当把一个小图像放大的时候，比如放大400%，我们可以首先依据原来的相邻4个像素点的色彩值，按照放大倍数找到新的ABCD像素点的位置并进行对应的填充，但是它们之间存在的大量的像素点，比如p点的色彩值却是不可知的，需要进行估算。

图1-原始图像的相邻4个像素点分布图图2-图像放大4倍后已知像素分布图1、最临近点插值算法(Nearest Neighbor)最邻近点插值算法是最简单也是速度最快的一种算法，其做法是將放大后未知的像素点P，將其位置换算到原始影像上，与原始的邻近的4周像素点A,B,C,D做比较，令P点的像素值等于最靠近的邻近点像素值即可。

如上图中的P点，由于最接近D点，所以就直接取P=D。

这种方法会带来明显的失真。

在A,B中点处的像素值会突然出现一个跳跃，这就是出现马赛克和锯齿等明显走样的原因。

最临近插值法唯一的优点就是速度快。

2、双线性插值算法(Bilinear Interpolation)其做法是將放大后未知的像素点P，將其位置换算到原始影像上，计算的四個像素点A,B,C,D对P点的影响(越靠近P点取值越大，表明影响也越大)，其示意图如下。

图3-双线性插值算法示意图其具体的算法分三步：第一步插值计算出AB两点对P点的影响得到e点的值。

图4-线性插值算法求值示意图对线性插值的理解是这样的，对于AB两像素点之间的其它像素点的色彩值，认定为直线变化的，要求e点处的值，只需要找到对应位置直线上的点即可。

换句话说，A,B间任意一点的值只跟A,B有关。

第二步，插值计算出CD两点对P点的影响得到f点的值。

第三步，插值计算出ef两点对P点的影响值。

双线性插值算法由于插值的结果是连续的，所以视觉上会比最邻近点插值算法要好一些，不过运算速度稍微要慢一点，如果讲究速度，是一个不错的折衷。

图像放大方法概述

切尔（ｔｈｌ）插值算法．Ｍｉｅ＿等ｃ它们的目的是使插值的曲线显得更平滑．图像边缘的表现更加完美。
４．自适应祥条插值及其增强技
图５双线性插值算法４个邻近点影响未知点信息示意图
如放大４００％我们可以首先依据原上图中的Ｐ点由于最接近Ｄ点所
－。来的相邻４个像素点的色彩值如图１以就直接取ＰＤ，
按照放大倍数找到新的ＡＢＣＤ像素点
这放大方法概述
口中国新闻社影视部易瑁
一
、
图像放大算法
图像放大有许多算法，关键在其
估算。
Ｉ
．
越大）其示意图如图３，。
最临近点插值算法（ｅｒｓＮａｅｔ
其具体的算法分三步，一步插第
ｅｇｂｒ于对未知像素使用何种插值方式。以Ｎｉｈｏ）
Ｐ
，
第二步插值计算出ｃＤ两点对
Ｐ点的影响得到ｆ的值。点
其位置换算到原始影像上，算计
的四像素点ＡＢ，Ｄ对Ｐ点的影响Ｃ
（靠近Ｐ点取值越大，明影响也越表
第三步，插值计算出ｅ两点对Ｐｆ
的影像．过速度比较慢，如图６不。
ＦｎｌＣｔＰｏ等。ｉｕｒａ
为了得到更好的图像质量．以在
上的基础上．多新的算法不断涌许

数码相机中的图像放大算法浅谈

数码相机中的图像放大算法浅谈计算机专业990班张一一摘要: 全球高新技术的飞速发展，极大的促进了各项事业的进步与提高，计算机图形学已成为各领域迫切需要的技术，特别是数码相机进入千家万户，对数码相机的图片处理技术越来越高，对放大处理技术迫在眉睫。

关键词：数码相机灰度值插值Abstract: The rapid development of the high and new technology accelerates the enhancement of various puter graphics falls into the most urgent category needing developing.keyword: Digital cameraGray-scale Interpolation第1章绪论1.1 课题背景90年代崛起的数码相机，是现代通信、计算机产业、照相机产业高速发展的产物。

随着电信、计算机的普及和家庭化，数码相机的应用领域也日益广泛。

数码相机具有一些传统相机所无法比拟的优势：用传统相机拍摄的图像要进行数字化处理，须经过拍照、冲洗、扫描三个步骤，而用数码相机摄影则无需胶卷，无需暗室，无需扫描仪，拍摄的图像可直接输入到计算机中，用户可在计算机中对图像进行编辑、处理，在电脑或电视中显示，通过打印机输出或通过电子邮件传给别人，大大提高了工作效率。

1.2 本文工作本文主要是分析现在常用的数码变焦的算法，比较各种技术的优缺点，以找到最适合的图像缩放技术。

由于图像缩小一般不会太大损失图像质量，缩小后的图像失真不明显，所以以下的讨论重点放在图像放大上面。

第2章图像放大技术2.1 相关概念数码相机虽然沿用了传统拍摄中的用语，也由于成像原理的不同而有了一些特殊的专用名词，只有掌握了数字摄影中的一些新的相关新概念才能了解数码相机中的图像软件放大。

下面简单介绍一些最基本的常识：位（Bit）Bit是计算机处理中最小的数据单位，颜色经过数字化处理后转变为由一个个Bit组成的形态。

stable diffusion放大算法原理

stable diffusion放大算法原理【stable diffusion放大算法原理】导言：在数字图像处理领域，图像放大是一个关键的问题。

图像放大算法的目标是增加图像的尺寸，同时保持图像的细节和清晰度。

稳定扩散放大算法（stable diffusion enlargement algorithm）是一种常用的图像放大方法，具有较好的效果和广泛的应用。

本文将详细介绍stable diffusion放大算法的原理和步骤。

一、算法简介稳定扩散放大算法是一种无缝放大算法，通过对原始图像进行扩散处理，增加像素数目从而实现放大效果。

与传统的放大算法不同，stable diffusion放大算法可以更好地保留图像的细节信息和清晰度。

其核心思想是通过对每个像素进行扩散，使得扩散后的像素值与周围像素值的平均值接近，并且尽量减小图像的失真。

二、算法步骤1. 初始图像首先，选择一个待放大的图像作为初始图像。

该图像可以是任何分辨率的图像，且不限制于灰度图像或彩色图像。

2. 图像分割将初始图像分割成小块，每个小块大小为n×n。

分割后的小块数量为M×N，其中M和N分别为图像的行数和列数。

3. 边界处理对于分割后的每个小块，需要对其进行边界处理。

为了保证放大后的图像边缘的连续性和真实性，需要在每个小块的边界处进行插值处理。

4. 梯度计算在进行放大之前，需要计算每个小块的梯度信息。

传统的放大算法中，常常使用Sobel算子或拉普拉斯算子来计算图像的梯度值。

而在stable diffusion放大算法中，采用梯度修正的方法来计算梯度值，从而使得放大后的图像更加平滑。

5. 扩散过程在这一步骤中，通过对每个小块进行扩散处理，实现图像的放大效果。

扩散的具体方式为：将每个像素的值与其周围像素的平均值进行比较，如果差距较大，则将像素值向周围像素值的平均值靠近一定比例。

6. 图像拼接在完成每个小块的扩散后，将它们拼接在一起，形成放大后的图像。

如何在PS中实现照片无损放大？多种放大技法效果实测对比！

如何在PS中实现照⽚⽆损放⼤？多种放⼤技法效果实测对⽐！如何在PS中实现照⽚⽆损放⼤？多种放⼤技法效果实测对⽐！PS如何实现照⽚的⽆损放⼤，这⾥要说明的⼀点就是真正的丝毫⽆损是不可能的，这⾥的⽆损放⼤是指通过更好的算法来实现放⼤以后照⽚的细节与画质都在可⽤的，可接受的范围之内，所以这种⽆损放⼤是⼀种形象的说法。

今天紫枫就⽤PS做多种不同的照⽚放⼤操作实测对⽐，摆事实，讲道理，看看到底如何放⼤⼀张照⽚才是最好，最优的⽅法。

为了公平，公开，公正的对⽐四种照⽚放⼤的实测效果，都采⽤同⼀张照⽚，放⼤相同的倍数后来对⽐细节。

如图，要放⼤的⼀张照⽚，原尺⼨ 1366*768：第⼀种放⼤技法，PS直接放⼤照⽚。

这种放⼤⽅法是PS本⾝的放⼤算法，也是PS中最常⽤的放⼤⽅式，如图，选择图像⼤⼩：在原像素⼤⼩上添⼀个0，放⼤后像素为 13660*7680然后在百分之⼀百的⽐例下截图⼀个局部，以看到画⾯细节⽐较⽣硬，不⾃然感明显：第⼆种放⼤技法，智能对象放⼤照⽚。

第⼆种PS放⼤照⽚的⽅法我们使⽤智能对象，先打开照⽚，转换为智能对象：然后按 CTRL+T 进⼊变换状态，将长宽的百分⽐改为 1000%：回车确认以后，我们看到画⾯⽐较模糊，⽐第⼀种放⼤效果柔和⼀些：第三种放⼤技法，⽆损放⼤插件 AlienSkin BlowUp第三种放⼤我们使⽤⼀个PS⽆损放⼤插件 AlienSkin BlowUp，如图执⾏滤镜中的⽆损放⼤插件：在插件界⾯中输⼊放⼤后的尺⼨ 13660*7680：如图⽰，同样的局部细节效果，效果明显⽐第⼀种和第⼆种⽅法更好⼀些，⽐第⼀种更⾃然，⽐第⼆种更多细节：第四种放⼤技法，⽆损放⼤插件 PhotoZoom Pro 7第四种放⼤我们同样使⽤⼀个⽆损放⼤插件 PhotoZoom Pro 7，在插件中打开照⽚，界⾯如图⽰：输⼊同样的像素值完成照⽚放⼤：截图同样的部位看细节，这款插件因为是试⽤版，所以画⾯中有⽔印，这个插件放⼤以后照⽚⾊彩有明显变化，细节画质要好于 AlienSkin BlowUp，可惜没有破解版：最后，我们把四种放⼤的效果放在⼀张图上来对⽐观察⼀下：可以说术业有专攻，专业的⽆损放⼤插件效果要⽐PS本⾝的放⼤算法好。

图像插值放大方法的研究与应用

ｌ
訇地
图像插值放大方法的研究与应用
Ｔｈｅｒｅａｒｈａｎｄａｐｉａｔｏｎｏｅｄｉｍａｇｅｎｌｇｉｉｈｉｔｐｏｌｔｏｎｅｓｃｐｌｃｉｆｍｃａｌｉｅａｒｎｇｗｔｎｅｒａｉ
江风莲，曾志宏
ＪＡＮＧｅｇ１ｎＺＥＮＧｉｏｇｌＦｎ．ａ．ｉＺｈ－ｎｈ
０引言
图像放大是数字图像处理的一个基本内容，
即实现从低分辨率图像获得高分辨率图像的图像处理技术。它在图像显示、传输（信）通、图像分析、以及动画制作、电影合成等方面有着相当广泛的应用，特别是在医学影像的诊断过程中，现
有医疗设备对一些细小病变的的显示能力存在不足，为了协助医生进行诊断和治疗，通常需要合
适的图像插值放大算法将医学图像插值 “ 放大。
像素点的位置距离进行加权线性插值，即离原图像像素点越近的待插值像素点，原图像像素的加
收稿日期：２１ —１一５００１Ｏ基金项目：基于模糊逻辑的群控技术研究（Ａ０２８Ｊ８２）。
Ｉｌ．．．一
ＬＪ．．．．．
图１双线性插值算法原理示意图
作者简介：江凤莲（９０１７一），女，福建连城人，讲师，硕士，研究方向为数据库、图像处理。第３卷３第１期２１ — （）［８１０１１上１５

图像放大中的边缘细化算法研究

ＡｂｔａｔｓｒｃＪｇｉｓｄｓｏｔｎｏｅｅｇｓｍａｃｕｎｉｇｏｍｉｇＩｒｅｏｒｓａｎｓｃｉｔｒｉｎ，ｎｔｉｐｐｒａｍａｅｚｏｎａｇｅｉｔｒｉｎｔｄｅｙｏｃｒｉｍａｅｚｏｎ．ｎｏｄｒｔｅｔｉｕｈｄｓｏｔｏｈｒｏｉｓａｅｎｉｇｏｍｉｇｈ
ｖｒｃｌｄｅｈｃｉｏｐｏｕｅａｇｅｄｓｒｏ；ｕｉｄｅａｅｓｈｒｅｅｅｊｇｉｉｏｉｉｕｈｎｕｉｌｓｉｌ — ｅｉｇｓｗｉｗｌｎｔｒｄｃｇｉｉｏｔｎｂｔｎｅｇｒａｅｅｓｖｒｇｓｄｔｏｗｌｏｃｒｅｓｇｃａｓａａｇｔａｅｈｌｊｓｔｉｗａｅｓｒｎｌｔｗｎｃｌｏ
孔繁庭侯国强
（甘肃联合大学电子信息工程学院甘肃兰州７００）３００
摘
要
当图像放大时边缘会出现锯齿失真，了抑制这种失真，出了边缘阶梯细化的图像放大算法。该算法在图像的非边缘为提
区域采用经典的双线性插值算法；同时根据Ｃｎｙ缘检测的结果，ａｎ边进一步进行阶梯检测，除不会产生锯齿失真的竖直和水平边滤缘；而在使用经典算法会产生严重锯齿失真的边缘区域，用基于阶梯细化的插值算法；运该插值算法在放大图像的同时，抑制边缘中的阶梯被放大，而达到减少锯齿失真的目的。实验结果表明，从该算法比经典算法更能有效地抑制锯齿失真。
第２第４期７卷
２１００年４月
计算机应用与软件

图像的放大与缩小原理

图像的放大与缩小原理一、引言图像是我们生活中不可或缺的一部分，我们通过眼睛观察到的世界都是以图像的形式呈现在我们的大脑中。

然而，有时候我们需要对图像进行放大或缩小，以便更好地观察或处理。

本文将探讨图像放大与缩小的原理及其应用。

二、图像放大原理图像放大是指将原始图像的尺寸增加，使得图像中的细节更加清晰可见。

图像放大的原理主要有两种方法：插值和重采样。

1. 插值插值是一种通过已知数据点来估计未知数据点的方法。

在图像放大中，插值算法通过已知像素点的灰度值来计算新像素点的灰度值。

常见的插值算法有最近邻插值、双线性插值和双三次插值等。

- 最近邻插值：该方法简单地将新像素点的灰度值设置为距离最近的已知像素点的灰度值。

这种插值方法计算速度快，但会导致图像边缘出现锯齿状的伪影。

- 双线性插值：该方法通过对已知像素点的灰度值进行加权平均来计算新像素点的灰度值。

这种插值方法能够得到更平滑的图像，但在处理较大放大倍数时可能会导致图像模糊。

- 双三次插值：该方法在双线性插值的基础上进一步考虑了更多的像素点，通过更复杂的计算公式来估计新像素点的灰度值。

这种插值方法能够得到更加清晰的图像，但计算复杂度较高。

2. 重采样重采样是指在图像放大时改变像素点的数量和排列方式。

常见的重采样算法有最近邻重采样、双线性重采样和双三次重采样等。

- 最近邻重采样：该方法将新像素点的灰度值设置为距离最近的已知像素点的灰度值。

这种重采样方法计算速度快，但会导致图像边缘出现锯齿状的伪影。

- 双线性重采样：该方法通过对已知像素点的灰度值进行加权平均来计算新像素点的灰度值。

这种重采样方法能够得到更平滑的图像，但在处理较大放大倍数时可能会导致图像模糊。

- 双三次重采样：该方法在双线性重采样的基础上进一步考虑了更多的像素点，通过更复杂的计算公式来估计新像素点的灰度值。

这种重采样方法能够得到更加清晰的图像，但计算复杂度较高。

三、图像缩小原理图像缩小是指将原始图像的尺寸减小，以便在有限的显示空间内展示更多的图像信息。

图像放大的算法原理

图像放大的算法原理
图像放大是一种图像处理技术，它通过增加图像中每个像素的尺寸来将图像的大小放大。

图像放大的算法原理可以总结为以下几种常见方法：
1. 最邻近插值：最邻近插值算法将新像素的值设置为与原始图像中最近的像素的值相同。

这种方法简单快速，但可能会导致图像出现锯齿状边缘。

2. 双线性插值：双线性插值算法会根据原始图像中相邻的四个像素的值来计算新像素的值。

这种方法可以更平滑地放大图像，但可能会导致细节部分模糊。

3. 双三次插值：双三次插值算法在双线性插值的基础上进一步考虑了相邻像素的权重。

它通过使用更多的像素来计算新像素的值，可以更精确地恢复细节。

4. Lanczos插值：Lanczos插值算法通过使用Lanczos核函数进行插值计算，可以有效地抑制图像放大时的锐化伪影，并在放大时保持图像的细节。

这种方法计算复杂度较高，但可以得到较好的放大效果。

5. 深度学习方法：近年来，随着深度学习的发展，越来越多的基于神经网络的图像放大方法被提出。

这些方法通过训练神经网络来学习图像的放大映射关系，能够产生更加逼真的放大结果。

以上是几种常见的图像放大算法原理，不同的算法有不同的适用场景和对计算资
源的要求。

在实际应用中，可以根据具体的需求选择适合的算法来进行图像放大处理。

图像放大的改进算法

ｙ
原图像
放大后的图像
图２像素填充法
２２对双线性插值的改进．
性质２当１８＜ｔ＜２５，＜ｔ：２，５时ｔ，，）＜２５５。性质３当０＜ｔ＜１８０＜厂ｔ：，２时，（）＜ｔ，，。为了满足人的视觉系统习惯，使图像看上去既
如何改进双线性插值去掉或削弱虚边呢？
对文本图像（只有黑白）若（，的相邻四，Ｙ）点中，有一为Ｏ则放大图像中（，的值取为０，Ｙ），
则可取掉 “ 虚边” 对一般的灰度图像，。想办法使：（）１灰度值大的越大；２灰度值小的越小，（）则可削弱“ 虚影” 也就是要构造一个关于灰度值的函数，）使得 ” 满足下列性质：，）性质１当０ｔ２５，：，５时０ｔ２５，）５。由函数图像可看出，函数满足上述三个性质。其具体表达式为：
图２中每条直线的交点代表一个像素，来放本
大后的图像在（，像素的灰度值应为（，处，），Ｙ）的灰度值２５白）而按照双线性插值公式，在５（，其（Ｙ像素的灰度值则不为此值，，）这就是造成放大后图像有 “ 影 ”或 “ 边 ”的原因。影会使图像虚虚虚看上去不清晰，对文本图像而言，虚影则使文本看不清楚，响信息的正确理解。影这在带字幕的图像传输中，将造成很大的影响。
，
厂Ｏ０］（，）Ｙ＋［１１，）一ｆｏ０（，）一ｆ０１１（，）一，
０］ｙ＋（，））ｘｆｏ０