AP物理C力学讲义10 Simple harmonic motion
chap11-1-OS-2012

解:设两质点的谐振动方程分别为 2 x1 A cos ( t 10 )
T 2 x 2 A cos ( t 20 ) T
10
4 ,
A2
A1
20 10
X
20
, 0
3 4
质点1第一次经过平衡位置的时刻
t 4
T t1 8
简谐振动的速度和加速度
dx v A si n ( t 0 ) dt vm si n( t 0 )
速 度
v
A
d x a 2 2 A cos(t 0 ) dt am cos(t 0 ) 2 x
2
o
T 2
T
3T 2
如图为旋转矢量
作匀速转动矢量 A ,其端点M
A A t
O
0
M
M0 x
在x轴上的投影点 P的运动 是简谐振动。 左半圆各点的旋转矢量对应质点振动速度方向
t+
A x
与位移方向相反;右半圆各点的旋转矢量对应 质点振动速度方向与位移方向相同;
P
x A cos( t 0 )
x
o
2
取平衡位置 为坐标原点
mg l k
0
l0
kx,
2
d x dt 2
2
k x m
O
f
x
x
.
P
令
k g m l0
则
d x dt
2
2
x 0
2
由初始条件: A l ,
0 0
x l cos t
1 1 2 振动物体的动能为 Ek m m 2 l 2 sin2 t 2 2
AP物理1和AP物理2考试必备知识点

2014年5月,AP物理B考试完成了它的使命,就此退出历史舞台。
2015年,这门考试将被两门全新的考试所取代,分别为AP物理1和AP物理2。
虽然作为最后一次AP物理B考试,2014年5月的这次考题仍能给我们带来很多启发,并对之后的新考试、新题型给出非常重要的参考。
首先,本次考试的解答题部分题目数量较之前有所改变,在之前历年的考试中,AP物理B的考试一般包括6道大题,需要学生在90分钟的时间内完成,而在2014年的考试中,较少见的出了7道大题,时间仍是90分钟,这意味着两件事:1.每道题目内的小问数减少,同时题目的难度降低了;2.在解答题中考察的知识点范围更宽泛了。
在2015年即将到来的两门新考试中,在解答题的考察上会有比较明显的改变,我们来比较一下三门考试的解答题部分的异同:AP物理B:解答题共6道大题,时间90分钟,分值占50%。
对各道解答题的考试形式没有明确说明。
AP物理1:解答题共5道大题,时间90分钟,分值占50%。
明确将考察一道实验设计题,一道计算题,三道短问答题(其中一道需要学生进行辩证分析和叙述)。
AP物理2:解答题共4道大题,时间90分钟,分值占50%。
明确将考察一道实验设计题,一道计算题,两道短问答题(其中一道需要学生进行辩证分析和叙述)。
通过比较,我们可以发现,在2015年的两门新考试中,解答题部分的题目数减少了,对学生的辩证分析能力和叙述能力的要求进一步提高,解答题部分也将不再局限于对学生计算能力的考察,更将考察学生的文字叙述和书面表达能力。
其次,在考察内容上,本次考试7道大题分别考察了:单摆,流体力学,热学,静电力学,电磁感应,光电效应,光的折射这几大知识点,同时这些内容也是历年AP物理B考察的核心知识点,在每次考试中都是重点考察的对象,那么在2015年的新考试中,重点考察的内容会有什么变化呢?我们来比较一下三门考试的重点考察知识点:AP物理B:牛顿力学,流体力学,热学,电磁学,波动学和光学,现代物理。
大学物理chap. 15 for net

则A=A1+A2 , 两分振动相互加强
x1=A1cos( t+ 1) x2=A2cos( t+ 2)
x =A cos( t+ )
(2)若 2 1=(2k+1) 则A=|A1-A2|, 两分振动相互减弱 (k=0,1,2,…)
Answer:
(1) x = 0.12cos (t - /3) (m)
(2) v = - 0.12 sin (t - /3)= - 0.188 (m/s) a = - 0.12 2 cos (t - /3)= - 1.03 (m/s2) (3) t
5 / 6
0.83 ( s )
TB p302 example 12-3, 4, 5
Example
The bullet is embedded in the big block. (a). T=? A=? (b). How long it will take the whole system from the moment when the bullet stops in the big block to the highest position.
2
2. The Physical Pendulum (复摆) 2
d mgh 0 2 dt I
15-4 Superposition of Oscillations
A1 sin 1 A2 sin 2 A A12 A22 2 A1 A2 cos( 2 1 ) tg A1 cos 1 A2 cos 2
t
P
o
t x , v , a
第17章+振动

稳定时的振幅为: A = 求A 的极值得: pr = ω
2 0
f ( ω
2 0
p 2 ) 2+ 4β 2 p 2
A
2 β
2
β 0 β较小 β较大
O
当强迫力的 圆频率为pr 时 振幅最大,称 为位移共振。
ω0
p
§17 .6 同一直线上同频率的简谐振动的合成
1.分振动 : x1=A1cos(ω t+ϕ 1) x2=A2cos(ω t+ϕ 2) 2.合振动 : x = x1+ x2 x =A cos(ω t+ϕ ) 合振动是简谐振动, 其频率仍为ω
dx v= = −ωA sin(ω t + ϕ 0 ) dt
v ( t ) = ω A cos( ω t + ϕ 0 +
π
2
)
• 速度也是简谐振动
υ 比 x 超前 π/2
(2). 加速度 也是简谐振动,a 比 x 超前 π
d2x a= = −ω 2 A cos(ω t + ϕ 0 ) = ω 2 A cos(ω t + ϕ 0 + π ) d t2
2 A = A12 + A2 + 2 A1 A2 cos(ϕ 2 − ϕ1 )
A1 sin ϕ 1 + A2 sin ϕ 2 tg ϕ = A1 cosϕ 1 + A2 cosϕ 2
3.两种特殊情况 (1)若两分振动同相 ϕ 2−ϕ 1=±2kπ (k=0,1,2,…) 则A=A1+A2 , 两分振动相互加强 (2)若两分振动反相 ϕ 2−ϕ 1=±(2k+1)π 如 A1=A2 , 则 A=0 (k=0,1,2,…)
Physics 06 Simple Harmonic Motion (Lecture)

Physics (Lecture Notes) (by: Dr. Yu)Simple Harmonic Motion (SHM)Key Words:oscillatory motion: 振动Simple Harmonic Motion (SHM): 简谐运动Simple Harmonic Oscillation (SHO): 简谐振动amplitude: 振幅frequency: 频率period: 周期angular frequency: 角频率phase constant: 初相,相角,相差equilibrium position: 平衡点pendulum: 摆Simple Harmonic Motion (SHM), or Simple Harmonic Oscillation (SHO)For a spring problem:The Restoring Force: F kx =-k : Spring Constant (N/m)The Equation of Motion:ma kx =-2 =k a x x m ω⇒=--, where ω=The Solution for x (t):cos()x A t ωφ=+The Period: 2T πω= The Frequency: 12f T ωπ==sin()v A t ωωφ=-+2cos()a A t ωωφ=-+(Note that: 2=a x ω-)The Angular Frequency: 2f ωπ=The Total Energy: 221122E mv kx =+= constant 212kA =v ∴= or, v =±Pendulum:sin g g a L Lθθθ=-≅-2a θωθ=-, where ω=2 2T πω∴==Multiple Choice1. A mass on a spring undergoes SHM. It goes through 8 complete oscillations in 4.0 s. What is the period?a. 0.031 sb. 0.50 sc. 2.0 sd. 32 s2. An object in simple harmonic motion obeys the following position versus time equation:0.50sin 2y t π⎛⎫= ⎪⎝⎭, in meters. What is the amplitude of vibration? a. 0.25 m b. 0.50 m c. 0.75 m d.1.0 m3. Consider the question above. What is the maximum speed of the object?a. 0.79 m/sb. 1.25 m/sc. 1.65 m/sd. 2.33 m/s4. Consider the question above. What is the maximum acceleration of the object?a. 0.252/m sb. 0.50 2/m sc. 1.232/m sd. 2.462/m s5. A mass is attached to a vertical spring and bobs up and down between points A and B. Where is the mass located when its kinetic energy is a minimum?a. At either A or Bb. Midway between A and Bc. One-fourth of the way between A and Bd. None of the above6. Doubling only the amplitude of a vibrating mass-and-spring system produces what effect on the system's mechanical energy?a. Increases the energy by a factor of two.b. Increases the energy by a factor of three.c. Increases the energy by a factor of four.d. Produces no change.7. A mass m = 0.2 kg is attached to a spring. It oscillates on a horizontal frictionless surface at a frequency of (4/π) Hz when displaced a distance of 2.0 cm from equilibrium and released. What is the maximum velocity attained by the mass?a. 0.02 m/sb. 0.04 m/sc. 0.08 m/sd. 0.16 m/sAnswer: bbaca,cdWritten Problems1.The displacement of a particle at is given by the expression 4.0cos(3.0)=+, where x isx tππin meters and t is in seconds.a)Determine the frequency and period of the motion.b)Find the amplitude of the motion,c)Find the phase constant, andd)the displacement of the particle at 0.25=.t s2. A particle moving along the x axis in simple harmonic motion starts from its equilibriumposition, the origin, at 0t= and moves to the right. The amplitude of its motion is 2.00cm, and the frequency is 1.50Hz.a)Show that the displacement of the particle is given by 2.00sin(3.00)=cm.x tπb)Determine the maximum speed and the earliest time(0)t>at which the particle has this speed.c)Find the maximum acceleration, and the earliest time (0)t>at which the particle has this acceleration.d)Find the total distance traveled between 0=.t= and 1.00t s3. A 0.500-kg mass attached to a spring with a force constant of 8.00N/m vibrates in simpleharmonic motion with amplitude of 10.0 cm.a)Calculate the maximum value of its speed and acceleration.b)Find the speed and acceleration when the mass is 6.00 cm from the equilibrium position.c)Calculate the time it takes the mass to move from0x= cm.x= to8.004. A 7.00-kg mass is hung from the bottom end of a vertical spring fastened to an overheadbeam. The mass is set into vertical oscillations with a period of 2.60 s. Find the force constant of the spring.5.An automobile having a mass of 1000 kg is driven into a brick wall in a safety test. Thebumper behaves as a spring of constant 6⨯ and compresses 3.16 cm as the car is5.0010/N mbrought to rest. What was the speed of the car before impact, assuming that no energy is lost during impact with the wall?6. A simple pendulum has a mass of 0.250kg and a length of 1.00 m. It is displaced through anangle of15.0 and then released.a)What is the maximum speed?b)Find the maximum angular acceleration, andc)the maximum restoring force?7. A particle of mass m slides without friction inside a hemispherical bowl of radius R. Showthat, if it starts from rest with a small displacement from equilibrium, the particle moves in simple harmonic motion with an angular frequency equal to that of a simple pendulum oflength R, that is,ω=8. A simple pendulum with a length of 2.23 m and mass of 6.74 kg is given an initial speed of2.06 m/s at its equilibrium position. Assume that it undergoes simple harmonic motion anddetermine its (a) period, (b) total energy and (c) maximum angular displacement.9. A ball of mass m is connected to two rubber bands of length L, each under tension T, The ballis displaced by a small distance y perpendicular to the length of the rubber bands. Assuming that the tension does not change, show that (a) the restoring force is – (2T/L) y and (b) thesystem exhibits simple harmonic motion with an angular frequencyω=。
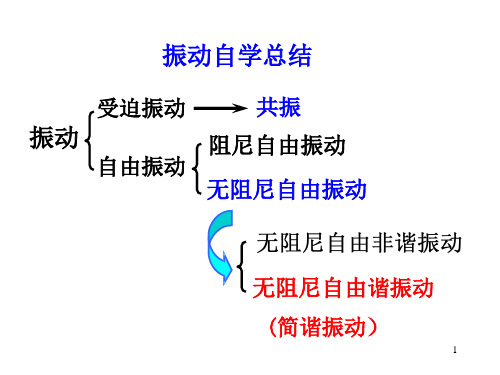
大学物理多媒体课件1振动自学总结
应用:测定未知频率
- A1
演示 激光演示李萨如图(KZ022)
16
y
x y
21 0 x
3 1
3 2
x = 0:y = 0
y
π 8
y
π 4
y
3π 8
y
π 2
17
三. 谐振分析
利用付里叶分解,可将任意振动分解成若干
SHM的叠加。
对周期性振动:T — 周期, = 2
x(t )
a0 2
[Ak
k 1
=P·/·4Q
=
Ⅱ、Ⅳ象限SHM
= -/4
y超前x—右旋
y落后x—左旋
(以为界,决定超前、落后)
15
② 1 m ,m, n 正整数 2 n
合成轨迹为稳定的闭合曲线 — 李萨如图
y A1
x y
x y
x达 到 最 大 的 次 数 y达 到 最 大 的 次 数
-A2 0
x A2
例如左图: x 3 y 2
t A
t=0
· t+
A
ox x
x = A cosBiblioteka t + )参考圆
(circle of reference)
3
0
v0< 0
x0 A/2 x
例如,已知 x0 A 2
v0 0
则由左图给出 π
v0> 0
3 8
[例] 已知:U 形管内液体质量为m,密度为 ,
管的截面积为S 。开始时,造成管两边液柱面 有一定的高度差,忽略管壁和液体间的摩擦。
6
4. SHM的表示法
x Acos( t )
①解析式
v d x Acos( t π )
大学物理教案英文版简谐振动Simple harmonic oscillation

+A +A
+ ωA − ωA
+ω2 A +ω2 A
φ=0
d 2 x( t ) a( t ) = dt 2 = − Aω 2 cos(ωt + φ )
x = + xm v = 0 a = −am x = 0 v = −v m a = 0 x = − xm v = 0 a = +am
§7.2 Simple harmonic oscillation
r A
ϕ
ω
r A1
ω
x
x 1 = A1 cos( ω t + ϕ 1 )
x 2 = A2 cos( ω t + ϕ 2 )
ϕ2
ϕ1
x = x1 + x 2
x2
x1
x
r r r A = A1 + A 2
= A cos( ω t + ϕ )
A=
2 A12 + A2 + 2 A1 A2 cos(ϕ 2 − ϕ 1 ) A1 sinϕ1 + A2 sinϕ 2 ϕ = arctg A1 cosϕ1 + A2 cosϕ 2
§7.4 simple harmonic motion and the uniform circular motion
ωA
A
x ( t ) = A cos(ωt + φ )
v ( t ) = − Aω sin(ωt + φ )
9
§7.4 simple harmonic motion and the uniform circular motion
1
§7.2 Simple harmonic oscillation
ap 物理c力学

ap 物理c力学AP物理C力学是高中物理学中的一门重要课程,主要研究物体的运动和力的相互作用。
力学是物理学的基础,对于我们理解自然界的运动规律和力的作用具有重要意义。
在AP物理C力学中,我们首先学习了质点的运动学,包括质点的位移、速度和加速度的概念。
通过运动学的学习,我们可以研究物体在空间中的运动方式以及运动的规律。
例如,我们可以通过运动学来描述一个自由落体物体的运动过程,计算它的落地时间和落地速度等。
在力学中,我们还学习了牛顿定律,这是力学研究的核心内容。
牛顿第一定律也称为惯性定律,它表明一个物体如果没有外力作用,将保持静止或匀速直线运动。
牛顿第二定律则给出了物体受到外力作用时的加速度与力的关系,即F=ma,其中F表示力,m表示物体的质量,a表示加速度。
牛顿第三定律则表明任何两个物体之间的相互作用力大小相等、方向相反。
通过学习牛顿定律,我们可以研究物体运动的原因和结果,解释各种力的作用和效果。
除了质点的运动学和牛顿定律,AP物理C力学还涉及到其他一些重要的内容。
例如,我们学习了机械能守恒定律,这是一个非常有用的定律,可以帮助我们计算物体在重力场中的机械能变化。
我们还学习了动量和冲量的概念,通过研究物体的动量和冲量,我们可以分析碰撞和爆炸等过程中物体的运动变化。
AP物理C力学还包括旋转运动和万有引力定律的学习。
旋转运动是物体绕固定轴线旋转的运动,通过学习旋转运动,我们可以研究物体的转动惯量、角动量和转动力矩等相关概念。
万有引力定律则是描述物体间引力相互作用的定律,它可以用来解释行星的运动、天体的引力等现象。
通过学习AP物理C力学,我们可以了解物体的运动规律和力的作用方式,掌握物理学中的基本概念和原理。
这不仅对于理解自然界的运动现象和力的作用具有重要意义,也为我们进一步学习和研究其他物理学分支提供了基础。
同时,AP物理C力学还培养了我们的逻辑思维能力和问题解决能力,帮助我们更好地理解和应用物理学知识。
