信号与系统课后习题与解答第七章
信号与系统课后习题与解答第七章
15- 分别绘出以下各序列的图形)()21()()1(n u n x n = )(2)()2(n u n x n =)()21()()3(n u n x n -= )()2()()4(n u n x n -=)1(2)()5(1-=-n u n x n )()21()()6(1n u n x n -=解)()1(n x 序列的图形如图5-1(a)所示。
)()2(n x 序列的图形如图5-1(b)所示。
)()3(n x 序列的图形如图5-1(c)所示。
)()4(n x 序列的图形如图5-1(d)所示。
)()5(n x 序列的图形如图5-1(e)所示。
(b)图5-1(a)(f)(e)(d)25- 分别绘出以下各序列的图形)()()1(n nu n x = )()()2(n nu n x --= )(2)()3(n u n x n -= )()21()()4(n u n x n --=)()21()()5(n u n x n --= )1()21()()6(1+=+n u n x n解) 序列的图形如图5-２(b)所示。
x()2(n 序列的图形如图5-２(c)所示。
x))3(n(x 序列的图形如图5-２(d)所示。
)4(n())5(n 序列的图形如图5-２(e)所示。
x()x 序列的图形如图5-２(f)所示。
())6(n(b)图5-2(c)(f)(e)(d)8-(a)35- 分别绘出以下各序列的图形)5sin()()1(πn n x =)510cos()()2(ππ-=n n x)5sin()65()()3(πn n x n =解)()1(n x 序列的图形如图5-３(a)所示。
)()2(n x 序列的图形如图5-３(b)所示。
)()3(n x 序列的图形如图5-３(c)所示。
图5-3(a)45- 判断以下各序列是否是周期性的，如果是周期性的，试确定其周期。
)873sin()()1(ππ-=n A n x)8()()2(π-=ne n x j解)1(因为3147322==πππw 是有理数，所以)(n x 是周期性的，且周期为14。
信号与系统 陈后金 第二版 课后习题答案(完整版)
（1） f (t) = 3sin 2t + 6 sinπ t
（2） f (t) = (a sin t) 2
（8）
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解：（1）因为 sin 2t 的周期为π ，而 sin πt 的周期为 2 。
显然，使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示，绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
（3） f (5 − 3t) （7） f ′(t) 解：（3）将 f (t) 表示成如下的数学表达式
（5） f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
（7）方法 1：几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变，所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理，在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号（方向向下，因为是负跳变），而在 0 < t < 2 的区间内有 f ′(t) = −0.5 （由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》（陈后金等编）作业参考解答
（2）显然，该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
《信号与系统》第七章 北京理工大学
罗斯判据
j
j
X ( s )e st ds
单边拉氏变换公式
X ( s) x(t )e st dt
0
u (t ) j x(t ) X ( s)e st ds 2j j
拉氏变换和傅氏变换的区别：
1) 分解为 e
j t
和 e 的和；
st
2) 傅氏是从 ，而拉氏是从 j j
e at sin 0t u (t )
F根据S域的微分性质
t n1 at 1 e u (t ) Re{s} a (n 1)! ( s a) n
2 ( s a ) 2 0
0
Re{ s} a
7.4常用函数的拉氏变换
2 单边左向信号的拉氏变换 A 指数信号
得
X ( s)
x(t )e st dt
拉普拉斯正变换
所以，
1 x(t ) 2j
j
j
X ( s)e st ds
拉普拉斯 反变换
拉普拉斯变换对
1 正变换公式
象函数
X ( s)
2 反变换公式
x(t )e st dt一对拉氏变换对原来自数1 x (t ) 2j
信号与系统第七章课后答案
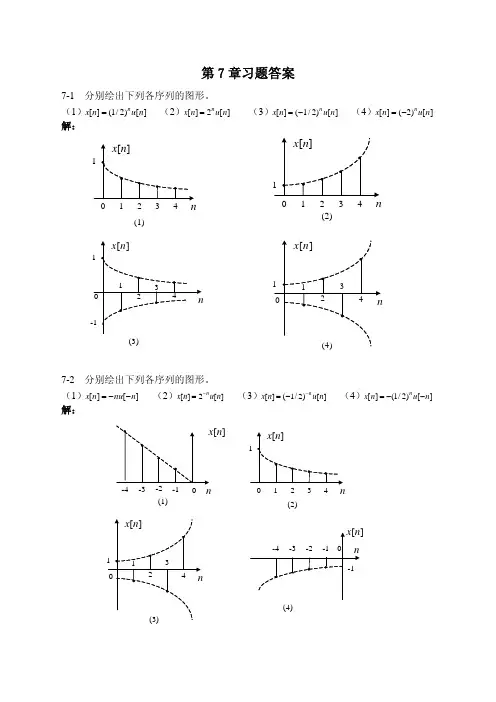
7-1 分别绘出下列各序列的图形。 （2）x[n] 2n u[n] （3）x[n] (1/ 2)n u[n] （4）x[n] (2) n u[ n] （1）x[n] (1/ 2)n u[n] 解：
x[ n ]
1
x[n]
1
0 1 2 (1) 3 4
n
0
1
2 3 (2)
x[n]
1
x[n]
-4
-3
-2 (1)
-1
0
n
0
1
2 (2)
3
4
n
x[n]
-4 1 0 1 2 3 4 -3 -2 -1 0
x[n] n
-1
n
(4)
(3)
7-3
分别绘出下列各序列的图形。 （2） x[n] cos
n 10 5
n （1） x[n] sin 5
1 z2 X (z) ( 1 1 2 z 1 )( 1 2 z 1 ) ( z 1 2 )( z 2 ) X (z) z 1 4 z ( z 1 2 )( z 2 ) 3( z 1 2 ) 3( z 2 )
X (z)
z 4z 3( z 1 2 ) 3 ( z 2 )
N
)
由于 x[n] 、 h[n] 均为因果序列，因此 y[n] 亦为因果序列，根据移位性质可求得
y [ n ] Z 1 [Y ( z )]
1 1 (1 a n 1 ) u [ n ] (1 a n 1 N ) u [ n N ] 1 a 1 a
7-24 计算下列序列的傅里叶变换。
(2)
信号与系统第七、八章课后习题
N k
当
2
2．线性时不变离散时间系统 ①线性 线性=叠加性+均匀性（齐次性）
c1 x1 (n) c2 x2 (n)
系统
c1 y1 (n) c2 y2 (n)
②时不变
x(n N )
系统
y (n N )
x ( n)
1 E
y ( n)
y ( n)
a
ay(n)
单位延时
1 T D z （ ）
已知激励初始状态y(-1)=0,y(-2)=1/2, fk=2ku(k),求系统 的零输入响应,零状态响应和全响应. 解: (1) 零输入响应 根据定义,零输入响应满足方程:
yx (k ) 3 yx (k 1) 2 yx (k 2) 0
其初始状态
1 yx (1) y (1) 0, yx 2 y 2 2
x(n)(n n0 ) x(n0 )(n n0 )
n
x(n)(n) x(0) (n) x(0)
n
n
x(n)(n n ) x(n ) (n n ) x(n )
0 0 n 0 0
x ( n)
k k 零状态响应
2 1 k k k (1) (2) (2) , k 0 3 3
离散时间系统的单位样值响应
(n)
零状态系统
h( n)
单位样值响应h(n)是系统在零状态时，由单位样值信 号作用之下产生的响应。因此，它是一个零状态响应。
同样，单位样值信号δ(n)仅在n=0时刻等于1，其它时 刻δ(n)=0，因此系统在n>0时的响应是零输入响应。
信号与系统7_梅森公式的证明及应用
梅森公式的推导
• 定理7 设Aij是行列式|A|中aij 余因式，则当 ij时，Aij= Pk△k 式中Pk是从节点i到j的第K条路的传输。△k 是不接触从i到j的第K条路的图行列式。他 是在图G中取掉Pk的所有节点和这些节点所 关联的支路后按（1-42）式算出的图行列 式。 表示所有可能的从节点i到j的路求和。
梅森公式注意事项
注意：
梅森公式只能求系统的总增益，即输出对输入的增益。而输出 对混合节点（中间变量）的增益就不能直接应用梅森公式。也 就是说对混合节点，不能简单地通过引出一条增益为一的支路， 而把非输入节点变成输入节点。对此问题有两种方法求其传递 函数：
一、把该混合节点的所有输入支路去掉，然后再用梅森公式。
•梅森公式的推导
定义下列矩阵
• 分支矩阵B
B是一个节点-支路关联矩阵。行对应于节点，列
对应于支路。
B=[bij]，bij={ 1，若支路j的起点是i }
0，
否则
因为每条支路只能有一个起点，故每列只能有一 个元素为1。
• 汇总矩阵S
S也是一个节点-支路关联矩阵。行对应于节点，
列对应于支路。
S=[sij]，sij={ 1，若支路j的起点是节点i }
二、分别用梅森公式求取输出节点及该节点对输入节点的传递 函数，然后把它们的结果相比，即可得到输出对该混合节点的 传递函数。
mk e
于是传递函数为
(s) C(s) 2
bde f (1 m dl) bg
R(s) R 1 (m dl ke h gkl) mh dlh mke
分析上式可以看到，传递函数的分子和分母取决于方 程组的系数行列式，而系数行列式又和信号流图的拓扑结 构有着密切的关系。从拓扑结构的观点，信号流图的主要 特点取决于回路的类型和数量。而信号流图所含回路的主 要类型有两种：单独的回路和互不接触回路。
信号与系统第七章课后习题答案
k 1
z
1
k
1 z 1 z
0 z
F( z )
k 1
f (k )z k
k
[(k 1) (k 2)]z k z2 z 1 z
k 1
z k z 1 z 1
例 7.1- 2 已知无限长因果序列f(k)=akε(k)。求f(k)
d d k f ( k ) ( z ) ( z ) F ( z ) z dz dz
d d d z k f ( k ) ( z ) z F ( z ) dz dz dz
|a|<|z|<|b|
Im[z]
Im[z] |a |
Im[z]
|a | o Re[z] o Re[z] o
|a|
Re[z] |b |
(a)
(b)
(c)
图 7.1-1 例7.1-2、例7.1-3、例7.1-4图
7.1.3 常用序列的双边Z变换
(1) f (k ) (k )。
F ( z)
k
例 7.2-3 已知
1 k 1 f (k ) 3 (k 1), 2
k
求f(k)的双边Z变换及其收敛域。 解 令f1(k)=3k+1ε(k+1)，则有
1 f ( k ) f1 ( k ) 2
z z2 由于 F1 ( z ) Z [ f1 (k )] z z3 z3
k
(k ) z k 1
（2） f1 (k ) (k m), f 2 (k ) (k m), m为正整数.
信号与线性系统分析(吴大正第四版)第七章习题答案
7.3 如图7-5的RC 带通滤波电路，求其电压比函数)()()(12s U s U s H 及其零、极点。
7.7 连续系统a 和b ，其系统函数)(s H 的零点、极点分布如图7-12所示，且已知当∞→s 时，1)(=∞H 。
（1）求出系统函数)(s H 的表达式。
（2）写出幅频响应)(ωj H 的表达式。
7.10 图7-17所示电路的输入阻抗函数)()()(11s I s U s Z =的零点在-2，极点在31j ±-，且21)0(=Z ，求R 、L 、C 的值。
7.14 如图7-27所示的离散系统，已知其系统函数的零点在2，极点在-0.6，求各系数a，b。
7.18 图7-29所示连续系统的系数如下，判断该系统是否稳定。
（1）3,210==a a ； （2）3,210-=-=a a ； （3）3,210-==a a 。
7.19 图7-30所示离散系统的系数如下，判断该系统是否稳定。
（1）1,2110-==a a ； （2）1,2110==a a ；（3）1,2110=-=a a 。
7.20 图7-31所示为反馈系统，已知44)(2++=s s ss G ，K 为常数。
为使系统稳定，试确定K 值的范围。
7.26 已知某离散系统的差分方程为)1()2()1(5.1)(-=---+k f k y k y k y（1） 若该系统为因果系统，求系统的单位序列响应h(k)。
（2） 若该系统为稳定系统，求系统的单位序列响应h(k)，并计算输入)()5.0()(k k f k ε-=时的零状态响应)(k y zs 。
7.28 求图7-36所示连续系统的系统函数)(sH。
7.30 画出图7-40所示的信号流图，求出其系统函数)(sH。
解(a)由s域系统框图可得系统的信号流图如图7-41(a)。
流图中有一个回路。
其增益为(b)由s 域系统框图可得系统的信号流图如图7-41(b)。
流图中有一个回路。
信号系统(第3版)习题解答
《信号与系统》（第3版）习题解析高等教育目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。
1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。
[提示：f ( 2t )表示将f ( t )波形压缩，f (2t)表示将f ( t )波形展宽。
](a) 2 f ( t - 2 ) (b) f ( 2t )(c) f ( 2t)(d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。
S RS LS C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T == )()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。
信号与系统第7章(陈后金)3
一、系统函数
2. H(z)与h[k]的关系
[k]
h[k] yzs [k] = [k]*h[k] h[k ]
Z { yzs [k ]} Z {h[k ]} H ( z) Z {h[k ]} Z { [k ]} 1
H ( z ) Z {h[k ]}
h[k ] Z [H ( z)]
H(z)
2.5 1.25 z 1 0.5 z 2 H ( z) 1 0.25 z 2
二、系统函数的零极点分布
系统函数可以表达为零极点增益形式，即
( z r1 )( z r2 )( z rm ) N ( z) H ( z) K D( z ) ( z z1 )( z z2 )( z zn )
-
-
-
W(z)
an-1 an
z域框图
二、离散系统的模拟框图
2. 级联型结构
将系统函数的N(z) 和D(z)分解为一阶或二阶实系
数因子形式，将它们组成一阶和二阶子系统，即
H(z) = H1(z) H2(z) ….. Hn(z)
画出每个子系统直接型模拟流图，然后将各 子系统级联。
X(z)
H1(z)
H2(z)
D(z)=0的根是H(z)的极点，在z平面用表示。 N(z)=0的根是H(z)的零点，在z平面用 表示。 例如
(2) 1 Im (z) j 0. 5j (3) 0. 5 0 0. 5j j Re (z) 0. 5 1
H (z)
z3(z 1 j)(z 1 j)
(z 0.5)(z 1)2(z 0.5 j0.5)(z 0.5 j0.5)
w[k ] a j w[k j ] x[k ]
信号与系统课后习题答案第7章
143
第7章 离散信号与系统的Z域分析 144
第7章 离散信号与系统的Z域分析
题图 7.7
145
第7章 离散信号与系统的Z域分析 146
第7章 离散信号与系统的Z域分析
题解图 7.31
147
第7章 离散信号与系统的Z域分析
(2) 由H(z)写出系统传输算子: 对应算子方程和差分方程为
148
7.25 已知一阶、二阶因果离散系统的系统函数分别如下， 求离散系统的差分方程。
111
第7章 离散信号与系统的Z域分析 112
第7章 离散信号与系统的Z域分析 113
第7章 离散信号与系统的Z域分析 114
第7章 离散信号与系统的Z域分析
7.26 已知离散系统如题图7.5所示。 (1) 画出系统的信号流图； (2) 用梅森公式求系统函数H(z)； (3) 写出系统的差分方程。
① 或者
② 容易验证式①、②表示同一序列。
57
第7章 离散信号与系统的Z域分析 58
第7章 离散信号与系统的Z域分析 59
第7章 离散信号与系统的Z域分析 60
第7章 离散信号与系统的Z域分析 61
第7章 离散信号与系统的Z域分析
也可以将Yzs(z)表示为
再取Z逆变换，得 ②
自然，式①、②为同一序列。
44
第7章 离散信号与系统的Z域分析 45
第7章 离散信号与系统的Z域分析 46
第7章 离散信号与系统的Z域分析
7.10 已知因果序列f(k)满足的方程如下，求f(k)。
47
第7章 离散信号与系统的Z域分析 48
第7章 离散信号与系统的Z域分析
(2) 已知K域方程为
49
信号与系统课后答案郑君里第7章
信号与系统课后答案：郑君里第7章简介本文是《信号与系统》课程的第7章课后答案，该章节由著名作者郑君里所撰写。
本章主要介绍了信号与系统的离散傅里叶变换（DFT）和离散时间傅里叶变换（DTFT）。
信号处理是一门研究如何用数学方法描述和处理各种信号的科学。
信号是信息的载体，而系统是对信号进行处理的载体。
离散傅里叶变换和离散时间傅里叶变换是信号与系统理论中最基本的工具之一，它们具有广泛的应用。
理解离散傅里叶变换和离散时间傅里叶变换的原理和性质对于理解信号与系统的基本原理和实际应用非常重要。
第7章课后题答案第1题根据定义，离散傅里叶变换（DFT）的计算公式如下：$$ X(k) = \\sum_{n=0}^{N-1} x(n) \\cdot e^{-j\\frac{2\\pi}{N} nk} $$其中，N表示信号的长度，N(N)表示输入信号的离散采样值，N(N)表示变换结果中的频谱系数。
根据公式，我们可以计算出给定信号的DFT变换。
第2题离散傅里叶变换的逆变换公式如下：$$ x(n) = \\frac{1}{N}\\sum_{k=0}^{N-1} X(k) \\cdot e^{j \\frac{2\\pi}{N} nk} $$逆变换可以将频域表示的信号转换回时域表示。
第3题离散时间傅里叶变换（DTFT）的计算公式如下：$$ X(e^{j\\omega}) = \\sum_{n=-\\infty}^{\\infty} x(n)\\cdot e^{-j\\omega n} $$DTFT是连续的频域表示，它不仅适用于周期信号，也适用于非周期信号。
第4题DTFT的逆变换公式如下：$$ x(n) = \\frac{1}{2\\pi} \\int_{-\\pi}^{\\pi}X(e^{j\\omega}) \\cdot e^{j\\omega n} d\\omega $$逆变换可以将频域表示的信号转换回时域表示。
第5题离散时间傅里叶变换的频谱无法在计算机中实现，因为DTFT变换结果是连续的函数。
信号与系统习题解答 (4)
(h) 由1 Re{s} 0, x(t)应为双边信号
x(t )
L -1 X
(s)
L
-1
s(s
s 1 1)( s
2)
L
-1
1/2
s
1/2 s2
1 2
u (t )
1 2
e 2t u (t )
7.11 已知因果系统的系统函数 入x(t)的零状态响应。
H
(s)
s2
s，1求系统对于下列输
（e） (f)
L {teatu(t)}sin
0 (t
)u(t)}
e e e e j0 j0t
j0 j0t
L{
2j
u(t)}
e e j0 j0t
e e j0 j0t
L{
u(t)} L {
u(t)}
2j
2j
e j0
1
e j0
1
s sin 0 0 cos0
X (s) (s 3) y(0) y`(0)
Y (s) s2 3s 2
s2 3s 2
Yx (s)
s2
X (s) 3s
2
s2
1 3s
2
2 s
1 s
2 s 1
s
1
2
yx (t) 1 2et e2t u(t)
1) 5s
6
L
-1
(s
(s 1) 2)(s
3)
L
-1
(
1 s 2)
(s
2
3)
e 2t u (t )
2e 3t u (t )
(f) 由0 Re{s} 1, x(t)应为双边信号
x(t )
信号与系统第7章 习题答案
提示：因为收敛域为 z
1 ，所以对应的是左边序列 4
1 az 1 1 , z 1 z a a
1 a 1 az 1 a z 1 a a 2 1 1 a2 X z 1 a 1 a a , 1 1 1 z a z a z a 1 z a 1 1 x n a n a u n a a 10 z 2 （5） X ( z ) , z 1 ( z 1)( z 1)
n
z 1
（7） 2 u ( n)
X z
n
2 n 2 un z n z
n 0
n
1 2 1 z
z , z2
z 2
（8） 2 u ( n)
n
X z
n
n
n 2 u n z n
9 n 10
（11） x( n) Ar cos( n0 ) u ( n)
(0 r 1)
cos0 n cos u n sin 0 n sin u n
y n cos0 n u n cos0 n cos sin 0 n sin u n
7.4 假设 x( n) 的 z 变换表示式如下，问 X ( z ) 可能有多少不同的收敛域，它们分别对应什么 序列？
z 1 （7） X ( z ) , z 6 (1 6 z 1 ) 2
解： （1） X ( z )
n
z 2 （8） X ( z ) , z 1 1 z 2
1 , z 0.5 1 0.5 z 1
奥本海姆版信号与系统课后答案
第七章7.6 解：见 8.17.8 解： (a) )]()([)21()(50πωδπωδπωk k j j X n k +--=∑= 信号截止频率 πω5=m采样频率 m s T ωπππω2102.022====对于正弦信号，会发生混叠 (b) ππω5==T c所以输出信号 )sin()21()(40t k t y k k π∑== 所以j e e t g tjk t jk k k 2)21()(40ππ-=-=∑ ∑-==44k t jk k e a π其中，⎪⎪⎩⎪⎪⎨⎧≤≤-=≤≤-=+-+14)21(0041)21(11k j k k j a k k k 7.10 解：(a) 错 信号时域为矩形波，频域为sinc 函数，无论怎么样都会混叠 (b) 符合采样定理，对(c) 符合采样定理，对7.15 解：要求 76N 2,76273ππππω>=⨯>即s 237max =<∴N N 取 7.16 解： 易见ππn n 2sin2满足性质1, 3对性质2，考虑时域乘积得频域卷积，易见2))2/sin((4][n n n x ππ=7.19 解：设x[n]经零值插入后得输出为z[n] (a) 531πω≤时， ⎪⎩⎪⎨⎧><=1101)(ωωωωωj e X ⎪⎪⎩⎪⎪⎨⎧>≤<=30531)(11ωωπωωωj e Z所以 ⎪⎪⎩⎪⎪⎨⎧><=3031)(11ωωωωωj e W因此可得，n n n w πω/)3(sin ][1=又由 ]5[][n w n y =可得 )5/()35(sin][1n n n y πω= (b) 531πω>时 ⎪⎪⎩⎪⎪⎨⎧>><=53031)(11πωωωωωj e Z)/()5(sin ][n nn w ππ=∴][51)5/()(sin ][n n n n y δππ== 7.21 解： 采样频率m s Tωππω2200002>== 即πω10000<m 时，可以恢复 (a) 可以(b) 不可以(c) 不能确定(d) 可以 (e) 不可以 (f) 可以 (g) 可以7.22 解：)(*)()(21t x t x t y = 则有πωωωω10000)()()(21>==j X j X j Y πω1000=∴m 因而 πωω20002=>m s故 s T s 3102-=<ωπ 7.23 解：见 8.27.24 解：见 8.37.29 解：见 8.107.31 解：见 8.157.35 解：见 8.247.38 解：见 8.97.41 解：见 8.197.45 解： 见 8.17。
郑君里《信号与系统》(第3版)课后习题详解(7-9章)【圣才出品】
，已知 y(-1)=0，y(-2)=0。 。
即
，解得
故全解为：
代入初始条件
，解得：
所以
y(n)
=
−
1 2
tan1 cos
nπ 2
+
1 2
sin
n
+
1 2
tan1
cos
n
u(n)
。
7-18 解差分方程
，已知 y(-1)=0
解得：
，故全解为：
代入初始条件 y(-1)=0，解得：
，
所以
。 。
7-15 解差分方程
，已知 y(0)=1。
解：由差分方程可得特征方程为 a+2=0，解得特征根 a=-2，故可设齐次解为
。
根据自由项形式设特解为
，将其代入原差分方程，则有
解得：
，故全解为：
。
代入初始条件 y(0)=1，解得：
，
所以
。
7-16 解差分方程
。 代入初始条件
，解得特征根 ，得
，解得
所以
。
（2）由特征方程
，解得特征根
。
代入初始条件
，得
，解得
所以
。
（3）由特征方程
，解得特征根
10 / 108
，故可设齐次解 ，故可设齐次解为： ，故可设齐次解为：
。 代入初始条件
所以
，得 ，解得
。
7-13 解差分方程
解：根据差分方程，可得特征方程为
4 / 108
所以 （3）当
时，有
，波形图如图 7-5（b）所示。
所以 所示。
，波形图如图 7-5（c）
信号与系统王明泉第七章习题解答
第7章离散时间系统的Z域分析7.1 学习要求（1）深刻理解z变换的定义、收敛域及基本性质，会根据z变换的定义和性质求解一些常用序列的z变换，能求解z反变换，深刻理解z变换与拉普拉斯变换得关系；（2）正确理解z变换的应用条件；（3）能用z域分析分析系统，求离散系统的零状态响应、零输入响应、完全响应、单位样值响应；（4）深刻理解系统的单位样值响应与系统函数H(z)之间的关系，并能用系统函数H(z)求解频率响应函数，能用系统函数的分析系统的稳定性、因果性。
7.2 本章重点（1）z变换（定义、收敛域、性质、反变换、应用）；（2）z域分析（求解分析系统）；（3）系统的频率响应函数。
7.3 本章的知识结构7.4 本章的内容摘要7.4.1 Z变换（1）定义∑∞-∞=-=n nzn x z X )()( 表示为：)()]([z X n x Z =。
（2）收敛域 1.有限长序列12(),()0,x n n n n x n n ≤≤⎧=⎨⎩其他 （1）当0,021>>n n 时，n 始终为正，收敛条件为0>z ； （2）当0,021<<n n 时，n 始终为负，收敛条件为∞<z ；（3）当0,021><n n 时，n 既取正值，又取负值，收敛条件为∞<<z 0。
2.右边序列11(),()0,x n n n x n n n ≥⎧=⎨<⎩ （1）当01>n 时，n 始终为正，由阿贝尔定理可知，其收敛域为1x R z >，1x R 为最小收敛半径；（2）当01<n 时，)(z X 分解为两项级数的和，第一项为有限长序列，其收敛域为∞<z ；第二项为z 的负幂次级数，由阿贝尔定理可知，其收敛域为1x R z >；取其交集得到该右边序列的收敛域为∞<<z R x 1。
3．左边序列2(),()0,x n n n x n n ≤⎧=⎨⎩其他（1）当02<n ，n 始终为负，收敛域为2x R z <，2x R 为最大收敛半径； （2）当02>n ，)(z X 可分解为两项级数的和，第一项为z 的正幂次级数，根据阿贝尔定理,其收敛域为2x R z <，2x R 为最大收敛半径；第二项为有限长序列，其收敛域为0>z ；取其交集，该左边序列的收敛域为20x R z <<。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
信号与系统课后习题与解答第七章) 序列的图形如图5-２(a)所示。
x()1(n 序列的图形如图5-２(b)所示。
x))2(n(x)3(n 序列的图形如图5-２(c)所示。
() 序列的图形如图5-２(d)所示。
x)4(n)(x 序列的图形如图5-２(e)所示。
()5(n)x 序列的图形如图5-２(f)所示。
())6(n(b)图5-2(c)n011234x (n )Λn1-1-2-34x (n )Λ2141811612(f)(e)n0123 x (n )Λn1123x (n )Λ(d)n123 x (n )Λ2-48-2141813-4(a)n011234 x (n )Λ234-11614-2-1-435- 分别绘出以下各序列的图形)5sin()()1(πn n x =)510cos()()2(ππ-=n n x)5sin()65()()3(πn n x n =解)()1(n x 序列的图形如图5-３(a)所示。
)()2(n x 序列的图形如图5-３(b)所示。
)()3(n x 序列的图形如图5-３(c)所示。
图5-3(a)n123 x (n )Λ456789n123 x (n )456789n0123 x (n )Λ4567891011121314151617181920ΛΛΛ10-6-5-4-3-2-145- 判断以下各序列是否是周期性的，如果是周期性的，试确定其周期。
)873sin()()1(ππ-=n A n x)8()()2(π-=ne n x j解)1(因为3147322==πππw 是有理数，所以)(n x 是周期性的，且周期为14。
)2(因为πππ168122==w为无理数，所以)(n x 是非周期性的。
55- 列出图45-所示系统的差分方程，已知边界条件0)1(=-y 。
分别求以下输入序列时的输出)(n y ，并绘出其图形（用逐次迭代方法求）。
图5-4∑E1)(n x 31)(n y)()()1(n n x δ= )()()2(n u n x = )5()()()3(--=n u n u n x解：由图45-可写出该系统的差分方程为)()1(31)(n x n y n y =--即)1(31)()(-+=n y n x n y)1(当)()(n n x δ=时，10311)1(31)0()0(=⨯+=-+=y y δ)()31()()31()1(31)()(...)31(31310)1(31)2()2(311310)0(31)1()1(2n u n y n y n n y y y y y n n==-+==⨯+=+==⨯+=+=所以δδδ 其图形如图)(55a -所示(b)图5-5(a)n011234y (n )Λn011234Λy (n )(c)011234Λy (n )567)2(当)()(n u n x =时，2)31(310311)1(31)0()0(0-==⨯+=-+=y u y 2)31(3341311)0(31)1()1(1-==⨯+=+=y u y 2)31(3134311)1(31)2()2(2-==⨯+=+=y u y …2)31(3)1(31)()(nn y n u n y -=-+= 所以 )(2)31(3)(n u n y n-=其图形如图)(55b -所示)3(当)5()()(--=n u n u n x 时，2)31(3)1(31)0()0(0-=-+=y u y 2)31(3)0(31)1()1(1-=+=y u y 2)31(3)1(31)2()2(2-=+=y u y 2)31(3)2(31)3()3(3-=+=y u y 2)31(3)3(31)4()4(4-=+=y u y 543121312131)4(310)5(=⨯=+=y y63121)5(310)6(=+=y yn n y 3121)(= )5(≥n所以 )5(3121)]5()(][)31(2123[)(-+---=n u n u n u n y n n其图形如图)(55c -所示65- 列出图65-所示系统的差分方程，已知边界条件0)1(=-y 并限定当0<n 时，全部0)(=n y ，若)()(n n x δ=，求)(n y 。
比较本题与55-题相应的结果。
图5-6∑E1)(n x 31)(n y解 由图65-可写出该系统的差分方程为)1()1(31)(-=--n x n y n y即)1()1(31)(-+-=n x n y n y若)()(n n x δ=，则有000)1()1(31)0(=+=-+-=δy y 110)0()0(31)1(=+=+=δy y310131)1()1(31)2(=+⨯=+=δy y2)31(03131)2()2(31)3(=+⨯=+=δy y32)31(0)31(31)3()3(31)4(=+⨯=+=δy y…1)31()1()1(31)(-=-+-=n n n y n y δ所以 )1()31()(1-=-n u n y n与题)1(55-比较，此题中的序列)(n y 的第一个非零值位于1=n ，而题)1(55-中的)(n y 的第一个非零值位于0=n 。
题)1(55-中的)(n y 向右移一个单位即可得到此题中的)(n y 。
75- 在题55-中，若限定当0>n 时，全部0)(=n y ，以0)1(=y 为边界条件，求当)()(n n x δ=时的响应)(n y ，这时，可以得到一个左边序列，试解释为什么会出现这种结果。
解 题55-中的差分方程为)1(31)()(-+=n y n x n y ① 若限定当0>n 时，全部0)(=n y ，则迭代时分别令,...2,1,0,1--=n 。
将①改写为)(3)(3)1(n x n y n y -=- 则有000)1(3)1(3)0(=-=-=δy y 330)0(3)0(3)1(-=-=-=-δy y 23)1(3)1(3)2(-=---=-δy y 33)2(3)2(3)3(-=---=-δy y…n n y --=3)(所以 )1(3)(---=-n u n y n)(n y 是个左边序列。
之所以得到一个左边序列，是因为限定了当0>n 时，0)(=n y ，即)(n y 的非零值只可能出现在0<n 的范围内。
85- 列出图75-所示系统的差分方程，指出其阶次。
图5-7∑E1)(n x 1b -)(n y 0b 0a 1a E1解 图75-所示系统的差分方程为 )1()()1()(1010-+=-+n x a n x a n y b n y b 此为一阶差分方程。
95- 列出图85-所示系统的差分方程，指出其阶次。
图5-8∑E 1)(n x )(n y E11b 2b 1a 0a E1解 图85-所示系统的差分方程为)1()()2()1()(1021-+=----n x a n x a n y b n y b n y此为二阶差分方程。
105- 已知描述系统的差分方程表示式为 ∑=-=70)()(r r r n x b n y试绘出此离散系统的方框图。
如果)()(,0)1(n n x y δ==-，试求)(n y ，指出此时)(n y 有何特点，这种特点与系统的结构有何关系。
解 此离散系统的方框图如图95-所示 若)()(n n x δ=，则∑=-=70)()(r r r n b n y δ即0)0(b y =，1)1(b y =，2)2(b y =，3)3(b y =4)4(b y =，5)5(b y =，6)6(b y =，7)7(b y =∑E1)(n x )(n y E1E1E1E 1E1E10b 1b 2b 3b 4b 5b 6b 7b而 当0<n 或7>n 时，0)(=n y此时)(n y 是有限长序列，且在非零值区间内的值为)7,...,0(=r b r ，即正好是各前向支路的增益。
)(n y 的这一特点确决于系统在结构上只有前向支路，没有反馈支路的特点。
115- 解差分方程)1( 1)0(,0)1(21)(==--y n y n y)2( 21)0(,0)1(2)(==--y n y n y)3( 1)1(,0)1(3)(==-+y n y n y)4( 1)0(,0)1(32)(==-+y n y n y 解 )1(特征方程为 021=-α求得特征根 21=α于是齐次解 n C n y )21()(•=因而 n n y )21()(=)2(特征方程为 02=-α 求得特征根 2=α 于是齐次解 n C n y 2)(•=将21)0(=y 代入上式，得21=C 因而 122)21()(-=•=n n n y)3(特征方程为 03=+α求得特征根 3-=α 于是齐次解 n C n y )3()(-•=将1)1(=y 代入上式，得31-=C因而 1)3()3(21)(--=-•-=n n n y)4(特征方程为 032=+α求得特征根 32-=α于是齐次解 n C n y )32()(-•=将1)0(=y 代入上式，得1=C因而 n n y )32()(-=125- 解差分方程)1( 1)2(,2)1(,0)2(2)1(3)(=-=-=-+-+y y n y n y n y )2( 1)1()0(,0)2()1(2)(=-==-+-+y y n y n y n y)3( 2)1(,1)0(,0)2()(===-+y y n y n y解 )1(特征方程为 0232=++αα 求得特征根 2,121-=-=αα 于是齐次解 n n C C n y )2()1()(21-+-= 将1)2(,2)1(=-=-y y 代入上式，得方程组⎪⎪⎩⎪⎪⎨⎧=+=--1412212121C C C C 解得 12,421-==C C 因而 n n n y )2(12)1(4)(---=)2(特征方程为 0122=++αα求得特征根 1,21-=α于是齐次解 n C n C n y )1)(()(21-+= 将1)2(,2)1(=-=-y y 代入上式，得方程组⎩⎨⎧=-⨯+-=1)1()(1212C C C 解得 1,221==C C因而 n n n y )1)(12()(-+=)3(特征方程为 012=+α求得特征根 j j -==21,αα于是齐次解 222121)()(ππn jn j n n eC eC j C j C n y -+=-+=)2sin()2cos(ππn n +=将2)1(,1)0(==y y 代入上式，得方程组⎩⎨⎧=-=+212121j C j C C C 解得 j C j C +=-=21,2121 因而 )()(21)(2222ππππn jn jn jn jeej een y ----+=)2sin()2cos(ππn n +=135- 解差分方程0)3(12)2(16)1(7)(=---+--n y n y n y n y5)3(,3)2(,1)1(-=-=-=y y y 解 特征方程为 01216723=-+-ααα 求得特征根 2,33,21==αα于是齐次解 n n C n C C n y 2)(3)(321•++•= 将5)3(,3)2(,1)1(-=-=-=y y y 代入上式，得方程组⎪⎩⎪⎨⎧-=++-=++-=⨯++5)3(8273)2(4912)(3321321321C C C C C C C C C 求得 1,1,1321-=-==C C C 因而 n n n n y 2)1(3)(+-=145- 解差分方程n n y n y +--=)1(5)(。