第七章 邻域运算-图像处理
数字图像处理要点简述详述

第一.二章.采样,量化,数字图像的表示 基本的数字图像处理系统系统的层次结构I 应用程序 I 开发工具 操作系统 设备驱动程序I硬件I图像处理的主要任务: 图像获取与数字化 图像增强 图像恢复 图像重建 图像变换 图像编码与压缩 图像分割 特点:(1) 处理精度高。
(2) 重现性能好。
(3) 灵活性髙1•图像的数字化包括两个主要步骤:离散和量化2. 在数字图像领域,将图像看成是许多大小相同、形状一致的像素组成3. 为便于数字存储和计算机处理可以通过数模转换(A/D)将连续图像变为数字图像。
4•数字化包括取样和量化两个过程:取样:对空间连续坐标(x,y)的离散化量化:幅值f(x,y)的离散化(使连续信号的幅度用有限级的数码表示的过程。
)5.数字化图像所需的主要硬件:♦采样孔、图像扫描机构、光传感器、量化器、输岀存储体6•取样和量化的结果是一个矩阵 7.其中矩阵中的每个元素代表一个邃塞8•存储一幅图像的数据量又空间分辨率和幅度分辨率决定 9•灵敏度、分辨率、信噪比是三大指标第三章,傅里叶变换,DCT变换,WHT•余弦型变换:•傅里叶变换(DFT)和余弦变换(DCT)O•方波型变换:•沃尔什•哈达玛变换(DWT)1•二维连续傅里叶正反变换:F(u,v)= I f f(x.y)eJ_oc J_ocf g y)= \f F(u, v)ej27r(nA+vv)dwdvJ —oo J —oo二维离散傅里叶变换:M — 1 N — I=乏疋 Fgg 宀SS)if=o v=O。
F(u, v)即为f (x, y)的频谱。
频谱的直流成分说明在频谱原点的傅里叶变换尸(0,0)等于图像的平均灰度级 卷积定理:/(x,y)*^(x, y)= ss /O, n)g(x 一 m, y~n)/?/=() n=02•二维离散余弦变换(DCT)一维离散余弦变换:EO)=%)岳gfg 芈严 其中 c®=怜 ""DCT 逆变换为F(u.v)=1~MN A =0 y=02 A r -1/(«)=咅 C(0) + \1三工 F (gsn(2n +1)« ~~2N3•—维沃尔什变换核g (W ):1 X_JL£(乂申)=丄口(一 1)®(”)為一】一心)<N i=o• 厂、Cn 7V--1 ^T-l码3》=卡吝 /G 〉耳(—1)635—一 3«JC> =牙中 O )n (—O务i二维:•正变换: 1 N —l. N —!■H —1护(“*) = —X X /X%」)口( — 1)4(5—373$一_W] N 宜 U • JO■逆变换二1 AT-l JV-l 片_]/(X.y )=丄 £ 乞 疗(心巧 口弟-i -心)JN 為 v=o ~。
邻域图像处理的图论算法在医学中的应用

邻域图像处理的图论算法在医学中的应用随着医疗技术的进步,医学图像处理成为当今医学领域的重要课题。
在医学图像处理中,邻域图像处理技术有着极为广泛的应用。
图论算法作为一种强大的工具,在邻域图像处理中发挥了重要作用。
1. 邻域图像处理及其应用邻域图像处理是一种基于空间邻域概念的图像处理技术,在该技术中,图像被视为由许多像素组成的点阵。
邻域图像处理的目的是通过把局部像素的特征与它们的周围像素进行比较,来降低噪音和增强图像的细节。
在医学图像处理中,邻域图像处理常常被用来帮助医生做出诊断。
邻域图像处理的应用非常广泛。
在医学影像处理中,有很多应用,如肺部结节检测、脑部疾病诊断等。
此外,邻域图像处理还被广泛应用于数字图像处理、计算机视觉、模式识别、信号处理等领域。
2. 图论算法在邻域图像处理中的应用图论算法是一种用于解决图论问题的数学方法。
与邻域图像处理相结合,可以解决很多医学图像处理中的问题。
例如,对于二维图像,邻域图像处理可用图论算法中的k邻域图来表示,其中每个像素或顶点与其相邻的顶点相连。
2.1 图像分割在图像分割中,将图片分割成几个部分,每个部分对应于不同的医学组织。
这是一项非常具有挑战性的任务,其实用在提取出关键区域需要处理成细胞核、血管和组织。
图论算法有助于处理这些问题。
例如,最小生成树算法(MST)就是一种基于邻域的图像分割方法。
在该方法中,图像被视为一个加权无向图,每个图像像素代表一个顶点,图像中相邻像素之间的距离在图的边上表示。
然后通过最小生成树的构建来自动分割医学图像,从而实现医学区域的分割。
2.2 图像的恢复和去噪图像的恢复和去噪在医学上也是一个十分重要的问题,因为医学图像通常有噪声干扰,而且很多医学图像的分辨率也很低。
在邻域图像处理中,图论算法也可以用来完成图像去噪和恢复。
具体的做法是通过对搜索图上的路径进行优化,以便减少相邻像素之间的噪声影响。
2.3 医学图像增强另一个医学用途是结合邻域图像处理技术和图论算法来增强医学图像。
邻域运算定义

2
2
4.9 3.5 4.2
1
1
1 2
26
2
4 3
2
5 7
1
1 6 4
4 4.5 5 5.7 6
3 1
3
1基本空间分析 3 4 GIS
32008-1176胡 嘉 骢BNUEP
地 理 信 息 系 统
基于栅格数据的叠置分析
成本距离的计算: 目标:最小累计成本路径 方法:循环迭代 最小累计成本计算示例: 源点格网矩阵 成本格网矩阵 连接格网矩阵 指派格网矩阵 输出格网矩阵
U
U
16
GIS基本空间分析
2008-11
胡 嘉 骢
BNUEP
地 理 信 息 系 统
基于栅格数据的叠置分析
二、栅格数据的空间变换——局部运算(点运算)
叠置分析
应用举例:通用土壤流失方程 A = R K L S C P ,其中,A:平均土壤流失量;R:降雨强度;K:土壤可蚀性;L:坡长 S:坡度;C:耕作因子;P:水土保持措施因素
12
GIS基本空间分析
2008-11
胡 嘉 骢
BNUEP
地 理 信 息 系 统
基于栅格数据的叠置分析
叠置分析
距离 0—500米 500—1000米 1000—1500米 >1500米
得分 0(不必建设) 1 2 3(必须建设)
人口密度 0 - 50 50 - 100 100 - 200 200 - 300
二、栅格数据的空间变换——邻域运算
叠置分析
邻域运算的运用——地形分析
21
GIS基本空间分析
2008-11
胡 嘉 骢
BNUEP
数字图像处理之邻域处理
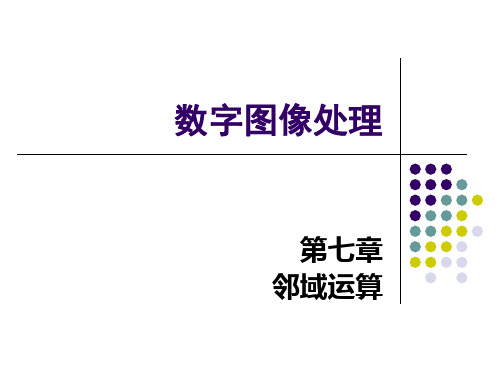
m 1 m 1
i0
j 0
m 1 m 1 T i , j f x i ,y j 2 2
演 示
100 96 87 86 92 95 101 106 121 133 99 102 98 103 87 99 111 121 97 95 94 103 102 100 89 87 85 78 79 67 72 75 74 73 86 84 88 92 97 90 102 100 98 90 91 88
使
f r
$进一步阅读:Gonzalez, p463.
4 边缘检测
4 边缘检测
梯度最大值及其方向
f x s in f y c o s 0
ta n
1
fy 或 fx fx fy
2 2
梯度最大值
4 边缘检测
2 2 2
G x, y e
e
r
2 2
2
2 平滑
设计离散高斯滤波器的方法:
设定σ2和n,确定高斯模板权值。如σ2 =2和 n=5:
[i,j] -2 -1 0 1 2 -2 0.105 0.287 0.135 0.287 0.105 -1 0.287 0.606 0.779 0.606 0.287 0 0.135 0.779 1 0.779 0.135 1 0.287 0.606 0.779 0.606 0.287 2 0.105 0.287 0.135 0.287 0.105
111 112
111 112
111 112
100 96 1 2 87 86 1 92 95
第七章-邻域运算-图像处理
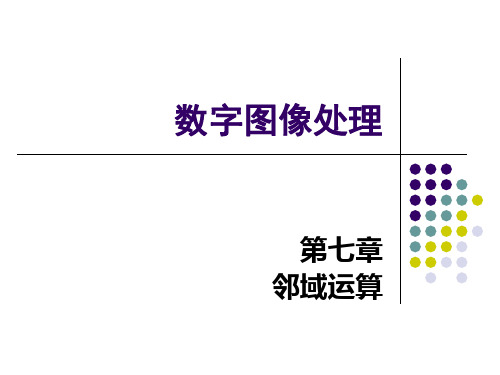
x
i
m 2
1
,
y
j
m 2
1
演示
100 101 98 97 100 79 96 106 103 95 89 67 87 121 87 94 87 72 86 133 99 103 85 75 92 99 111 102 78 74 95 102 121 111 112 73
86 102 84 100 88 98 92 90 97 91 90 88
100 101 98 97 1010 792 96 106 103 95 892 673 87 121 87 94 871 722 86 133 99 103 85 75 92 99 111 102 78 74 95 102 121 111 112 73
861 102 842 100 881 98 92 90 97 91 90 88
是消除或尽量减少噪声的影响,改善图像的质量。
假设
在假定加性噪声是随机独立分布的条件下,利用邻 域的平均或加权平均可以有效的抑制噪声干扰。
从信号分析的观点
图像平滑本质上低通滤波。将信号的低频部分通过, 而阻截高频的噪声信号。
问题
往往图像边缘也处于高频部分。
2 平滑
1)邻域平均(矩形邻域和圆形邻域)
T2, 2f x 1, y 1
1 引言
4)相关与卷积的物理含义
相关运算是将模板当权重矩阵作加权平均; 而卷积先沿纵轴翻转,再沿横轴翻转后再加
权平均。 如果模板是对称的,那么相关与卷积运算结
果完全相同。 邻域运算实际上就是卷积和相关运算,用信
号分析的观点就是滤波。
2 平滑
图像平滑的目的
12 4 6 4 2 21 2 3 2 1
图像处理 第七章 邻域运算

第七章 邻域运算目录1. 引言相关与卷积2. 平滑3. 中值滤波4. 边缘检测5.细化作业1.引言邻域运算是指当输出图象中每个象素是由对应的输入象素及其一个邻域内的象素共同决定时的图象运算,通常邻域是远比图象尺寸小的一规则形状,如正方形2x2、3x3、4x4或用来近似表示圆及椭圆等形状的多边形。
信号与系统分析中的基本运算相关与卷积,在实际的图象处理中都表现为邻域运算。
邻域运算与点运算一起形成了最基本、最重要的图象处理工具。
以围绕模板(filter mask, template )的相关与卷积运算为例,给定图象f(x,y)大小N×N,模板T(i, j)大小m ×m (m 为奇数),常用的相关运算定义为: 使模板中心T((m-1)/2,(m-1)/2)与f(x,y)对应,∑∑-=-=--+--+=•=101)21,21(),(),(),(m i m j m j y m i x f j i T y x f T y x g当m=3时,)1,1())2,2(),1()1,2(),1()0,2()1,()2,1(),()1,1()1,()0,1()1,1()2,0(),1()1,0()1,1()0,0(),(++++++++++-++-+-+--=y x f T y x f T y x f T y x f T y x f T y x f T y x f T y x f T y x f T y x g卷积运算定义为:∑∑-=-=-+--+-=•=101)21,21(),(),(),(m i m j m j y m i x f j i T y x f T y x g 当m=3时,)1,1())2,2(),1()1,2()1,1()0,2()1,()2,1(),()1,1()1,()0,1()1,1()2,0(),1()1,0()1,1()0,0(),(--+-++-+-++++-++++++=y x f T y x f T y x f T y x f T y x f T y x f T y x f T y x f T y x f T y x g可见,相关运算是将模板当权重矩阵作加权平均,而卷积与相关不同的只是在于需要将模板沿中心反叠(先沿纵轴翻转,再沿横轴翻转;即沿次对角线翻转)后再加权平均。
(完整版)数字图像处理:部分课后习题参考答案
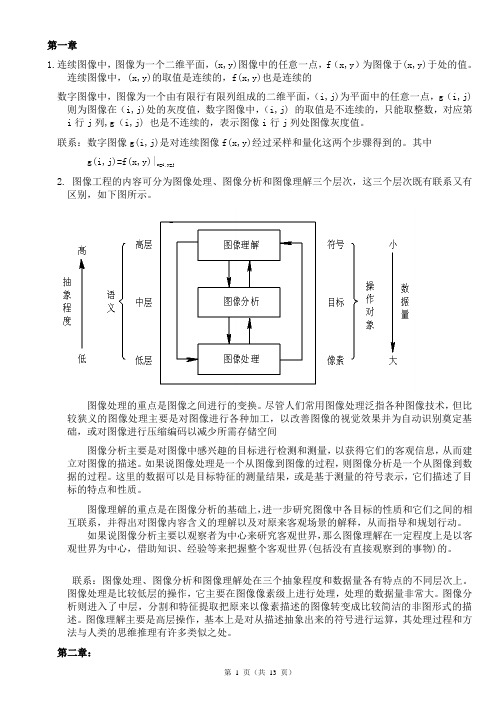
第一章1.连续图像中,图像为一个二维平面,(x,y)图像中的任意一点,f(x,y)为图像于(x,y)于处的值。
连续图像中,(x,y)的取值是连续的,f(x,y)也是连续的数字图像中,图像为一个由有限行有限列组成的二维平面,(i,j)为平面中的任意一点,g(i,j)则为图像在(i,j)处的灰度值,数字图像中,(i,j) 的取值是不连续的,只能取整数,对应第i行j列,g(i,j) 也是不连续的,表示图像i行j列处图像灰度值。
联系:数字图像g(i,j)是对连续图像f(x,y)经过采样和量化这两个步骤得到的。
其中g(i,j)=f(x,y)|x=i,y=j2. 图像工程的内容可分为图像处理、图像分析和图像理解三个层次,这三个层次既有联系又有区别,如下图所示。
图像处理的重点是图像之间进行的变换。
尽管人们常用图像处理泛指各种图像技术,但比较狭义的图像处理主要是对图像进行各种加工,以改善图像的视觉效果并为自动识别奠定基础,或对图像进行压缩编码以减少所需存储空间图像分析主要是对图像中感兴趣的目标进行检测和测量,以获得它们的客观信息,从而建立对图像的描述。
如果说图像处理是一个从图像到图像的过程,则图像分析是一个从图像到数据的过程。
这里的数据可以是目标特征的测量结果,或是基于测量的符号表示,它们描述了目标的特点和性质。
图像理解的重点是在图像分析的基础上,进一步研究图像中各目标的性质和它们之间的相互联系,并得出对图像内容含义的理解以及对原来客观场景的解释,从而指导和规划行动。
如果说图像分析主要以观察者为中心来研究客观世界,那么图像理解在一定程度上是以客观世界为中心,借助知识、经验等来把握整个客观世界(包括没有直接观察到的事物)的。
联系:图像处理、图像分析和图像理解处在三个抽象程度和数据量各有特点的不同层次上。
图像处理是比较低层的操作,它主要在图像像素级上进行处理,处理的数据量非常大。
图像分析则进入了中层,分割和特征提取把原来以像素描述的图像转变成比较简洁的非图形式的描述。
图像处理(四)

上次: 二、图像运算,三、图像变换1.图像的点运算(元素群运算)2.图像的代数运算3.图像的几何运算⇒上机实验一讲:4.图像的邻域(即点的邻域)操作输出图像中的每个像素值都是由输入图像中对应的像素及其某个邻域内的像素共同决定的,这种图像运算称为邻域运算。
通常邻域是指一个远远小于图像尺寸的形状规则的像素块,例如,5⨯的正方形(或其它形状)。
一幅图像所定义的所有邻3⨯、53域应该具有相同的大小。
邻域运算与点运算一起形成了最基本、最重要的图像处理方法。
邻域操作包括两种类型:滑动邻域操作和分离邻域操作。
邻域→点,称滑动邻域操作邻域→邻域,称分离邻域操作(1)滑动邻城操作sliding-neighborhood operation滑动邻域操作一次处理一个像素,输出图像的每一个像素的像素值都是通过对输入图像对应像素的某邻域内的像素值采用某种代数运算得到的。
滑动邻域操作,经常被用于图像的非线性滤波。
例如,一个使输出图像像素值等于输入图像对应像素的各个邻域像素值标准偏差的滑动邻域操作等。
非线性滤波器help nlfilterNLFILTER Perform general sliding-neighborhood operations.B = NLFILTER(A,[M N],FUN) applies the function FUN to each M-by-N sliding block of A. FUN is a function that accepts an M-by-N matrix as input and returns a scalar:C = FUN(X)C is the output value for the center pixel in the M-by-N block X. NLFILTER calls FUN for each pixel in A. NLFILTER zero pads the M-by-N block at the edges, if necessary.B = NLFILTER(A,[M N],FUN,P1,P2,...) passes the additional parameters P1,P2,..., to FUN.B = NLFILTER(A,'indexed',...) processes A as an indexed image, padding with ones if A is of class double and zeros if A is of class uint8.ExampleFUN can be a FUNCTION_HANDLE created using @. This example produces the same result as calling MEDFILT2 with a 3-by-3 neighborhood:B = nlfilter(A,[3 3],@myfun);where MYFUN is an M-file containing:function scalar = myfun(x)scalar = median(x(:));FUN can also be an inline object. The example above can be written as:fun = inline('median(x(:))');B = nlfilter(A,[3 3],fun);讲inline 函数有时为了描述某个数学函数的方便,可以用inline 函数来直接编写该函数,形式相当于已经介绍过的且经常使用的M 函数,但无需编写一个真正的M-文件它就可以描述出某种数学关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 引言
当m 3时
相关运算
fx,y T0,0f x1,y 1T0,1f x1,y
T0,2f x1,y 1T1,0f x,y 1
T1,1f x,yT1,2f x,y 1
T2,0f x1,yT2,1f x1,y
T2,2f x1,y 1
1 引言
卷积运算定义为:
fx,yT*fx,y
m i01m j01Ti,jfxim21,yjm21
权平均。 如果模板是对称的,那么相关与卷积运算结
果完全相同。 邻域运算实际上就是卷积和相关运算,用信
号分析的观点就是滤波。
2 平滑
图像平滑的目的
是消除或尽量减少噪声的影响,改善图像的质量。
假设
在假定加性噪声是随机独立分布的条件下,利用邻 域的平均或加权平均可以有效的抑制噪声干扰。
100 1011 928 971 100 79 96 1026 1033 952 89 67 87 1211 827 941 87 72 86 133 99 103 85 75 92 99 111 102 78 74 95 102 121 111 112 73
86 102 84 100 88 98 92 90 97 91 90 88
数字图像处理
第七章 邻域运算
CH7 邻域运算
一、引言 二、平滑 三、中值滤波 四、边缘检测 五、细化 上机实习
1 引言
1)邻域运算
定义 输出图像中每个像素是由对应的输入像素及其一个 邻域内的像素共同决定时的图像运算。
通常邻域是远比图像尺寸小的一规则形状。如下面 情况中,一个点的邻域定义为以该点为中心的一个 圆内部或边界上点的集合。
100 101 918 927 1010 79 96 106 1203 935 892 67 87 121 817 924 871 72 86 133 99 103 85 75 92 99 111 102 78 74 95 102 121 111 112 73
86 102 84 100 88 98 92 90 97 91 90 88
100 101 98 917 1020 791 96 106 103 925 839 672 87 121 87 914 827 721 86 133 99 103 85 75 92 99 111 102 78 74 95 102 121 111 112 73
86 102 84 100 88 98 92 90 97 91 90 88
当m 3时
fx,y T0,0f x1,y 1 T0,1f x 1,y T0,2f x1,y 1 T1,0f x,y 1 T1,1f x,y T1,2f x,y 1 T2,0f x1,y 1 T2,1f x 1,y T2,2f x1,y 1
1 引言
4)相关与卷积的物理含义
相关运算是将模板当权重矩阵作加权平均; 而卷积先沿纵轴翻转,再沿横轴翻转后再加
100 101 98 97 100 79 916 1026 1103 95 89 67 827 1231 827 94 87 72 816 1323 919 103 85 75 92 99 111 102 78 74 95 102 121 111 112 73
86 102 84 100 88 98 92 90 97 91 90 88
1 引言
3)模板(template,filter mask)的相关与 卷积运算
给定图像f(x,y)大小N*N,模板T(i,j)大小m*m (m为奇数)。
常用的相关运算定义为:使模板中心T((m1)/2,(m-1)/2) 与f(x,y)对应。
fx,yTfx,y
m i01m j01Ti,jfxim21,yjm21
100 101 98 97 100 791 96 106 103 95 89 672 87 121 87 94 87 721 86 133 99 103 85 75 92 99 111 102 78 74 95 102 121 111 112 73
826 1012 834 1020 828 981 92 90 97 91 90 88
100 101 98 97 1010 792 96 106 103 95 892 673 87 121 87 94 871 722 86 133 99 103 85 75 92 99 111 102 78 74 95 102 121 111 112 73
861 102 842 100 881 98 92 90 97 91 90 88
邻域运算与点运算一起构成最基本、最重 Nhomakorabea的图像处理方法。
1 引言
点+的邻域 点+的邻域
1 引言
举例
f x , y 1 5 f x , y 1 f x 1 , y f x , y f x 1 , y f x , y 1
进一步的表达
fx,y151fx,y11fx1,y 1fx,y1 15T1fx,y1T2fx1,y T5fx,y1 FT,f
12
1
23
2
12
1
1010 1021 918 97 100 79 926 1036 1203 95 89 67 817 1221 817 94 87 72 86 133 99 103 85 75 92 99 111 102 78 74 95 102 121 111 112 73
86 102 84 100 88 98 92 90 97 91 90 88
$进一步阅读:Gonzalez, p91.
1 引言
2)相关与卷积
信号与系统分析中基本运算相关与卷积,在实际图 像处理中都表现为邻域运算。
两个连续函数f(x)和g(x)的相关记作:
fx g x fa g x a d a
两个连续函数f(x)和g(x)的卷积定义为:
fx * g x fa g x a d a
演示
100 101 98 97 100 79 96 106 103 95 89 67 87 121 87 94 87 72 86 133 99 103 85 75 92 99 111 102 78 74 95 102 121 111 112 73
86 102 84 100 88 98 92 90 97 91 90 88
