变形截面容器内液体体积与液位高度关系
中考物理复习《浮力液面高度变化量计算方法与技巧》
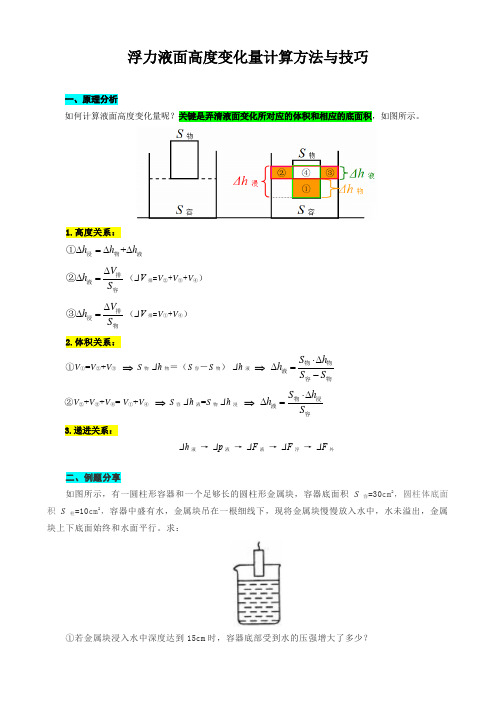
浮力液面高度变化量计算方法与技巧一、原理分析如何计算液面高度变化量呢?关键是弄清液面变化所对应的体积和相应的底面积,如图所示。
1.高度关系:+h h h ∆=∆∆浸物液①V h S ∆∆=排液容②(ΔV 排=V ②+V ③+V ④)V h S ∆∆=排浸物③(ΔV 排=V ①+V ④)2.体积关系:①V ①=V ②+V ③ ⇒ S 物·Δh 物=(S 容-S 物)·Δh 液 ⇒ S h h S S ⋅∆∆=-物物液物容②V ②+V ③+V ④= V ①+V ④ ⇒ S 容·Δh 液=S 物·Δh 浸 ⇒ S h h S ⋅∆∆=浸物液容3.递进关系:Δh 液 → Δp 液 → ΔF 液 → ΔF 浮 → ΔF 外二、例题分享如图所示,有一圆柱形容器和一个足够长的圆柱形金属块,容器底面积S 容=30cm 2,圆柱体底面积S柱=10cm 2,容器中盛有水,金属块吊在一根细线下,现将金属块慢慢放入水中,水未溢出,金属块上下底面始终和水面平行。
求:①若金属块浸入水中深度达到15cm 时,容器底部受到水的压强增大了多少?②若绳子从金属块底部刚好接触到水面时开始向下放下15cm时,容器底部受到水的压强增了多少?1.第1小问分析过程:要求水对容器底部增加的压强,也就是求水位增加的高度。
如何求水位增加的高度呢?思维过程如下:当圆柱体浸入水中15cm时,实际上是一个动态过程,圆柱体一边下降,水位一边上升,圆柱体下降的深度加上水位上升的高度刚好为15cm。
由此可见,如何将动态变化过程转化为静态过程才是解题关键。
多数同学可能有这样的思维过程:假设原来水位不变,我们把圆柱体浸入水中后排开的水用容器接到,然后将排开的水再倒回容器中。
这个时候有两种思考:(1)倒入圆柱体两边的空白处,这样水位上升的高度,Δh=V排/(S容-S柱)。
显然,圆柱体浸入水中的深度就是15cm+Δh,跟题意矛盾。
液面高度变化求法解析

Vol .5() No .3Mar .2021此i f教学参考习题研究液面高度变化求法解析石玉东(河北省献县商林中学河北沧州062250)文章编号:1〇〇2-218X (2021)03-0051-03 中图分类号:G 632.4 文献标识码:B摘要:对常见的液面高度变化问题进行分类,并对每类情况进行了详尽的解析;通过分析第1类物体上下移动型,总结出了求液面高度变化量的计算公式,并用此公式解决了第2和第3类问题;前3类都是物体浸入液体体积即V #变而液体总体积V 液总不变的问题,第4类是V *不变改变的问题,第5类是V *和V **都改变的问题。
关键词:液体;浮力;液面升降;体积浮力和液体压强是初中物理考查的重点和难点, 解答此类题目的关键在于正确求出液面高度的变化 量A A 。
那么,求解A A 有何规律可循呢?下面对相关问题分类进行说明。
_、物体上下移动型题目1物体放在柱形容器液体中,当物体在液体中向上、向下移动时,求液面高度的变化A A 。
解法1观察推导法观察物体浸人液体中的体积即^#变化时,液面 实际的升降情况,弄清的变化量A V#与容器中的哪部分体积相等,进而求出A /i 。
解法2假定分离法将物体在液面处分为上、下两部分,假定这两部 分在液面处分离,并使其中一部分上升或下降,弄清M 升'#,所以M j3容厶'V "排S 容。
原液面现液面图4图假定分离法:物体下移前,如图4所示,假定原液 面上部分不动,下部分沉底。
物体下移后,如图5所 示,假定现液面上部分不动,下部分沉底,设原液面上升的体积(图5中灰色部分)为A /^=f。
〇容排=A V ^ = S容A /i 升A V 升,比较图4和图5容 易看出AV 排=AV 升=S 容A/i 升,所以A/i 升=。
V#的变化量与容器中的哪部分体积相等,进而求出M 。
原液面现液面 AK ,,A /i #AK »J /j 飞八/ _ ——、H I—A"3-3- - _ ±2:•AK 轉,—:,TAK #图1图2图31.物体下移观察推导法:如图2所示,物体向下移动,V #变 2.物体上移观察推导法:如图7所示,物体向上移动,V 排变 小,液面下降。
变形截面容器内液体体积与液位高度关系

收稿日期:2002207228作者简介:李彩英(19442),女(汉族),山西武乡人,副教授,主要从事几何代数和高等数学的研究和教学。
文章编号:100027466(2003)0120021202变形截面容器内液体体积与液位高度关系李彩英,梁泰安,金 明(天津大学,天津 300072)摘要:介绍了10种变形截面容器以及各容器内存留液体体积与液位高度的函数关系,利用各种公式可快速准确计算出容器内存留液体的体积。
关 键 词:容器;液体;体积;液位高度中图分类号:T Q 05012 文献标识码:AThe functional relationship betw een the height and the volume of the rem ainingliquid in the containers with changeful cross sectionLI Cai 2ying ,LI ANG T ai 2an ,J I N M ing (T ianjin University ,T ianjin 300072,China )Abstract :T en kinds of containers with changeful cross sections were introduced 1The functional relationship between the heightand the v olume of the remaining liquid within these containers was als o presented 1The v olume of the remaining liquid in the con 2tainers can be calculated quickly and accurately by these formulae.K ey w ords :container ;liquid ;v olume ;liquid height符 号 说 明V ———存留液体体积,mm 3B ———矩形短边长度,mm h ———存留液体液位高度,mm D ———圆形直径,mmH ———容器高度,mma ———椭圆形半长轴长度,mm A ———正方形边长或矩形长边长度,mmb ———椭圆形半短轴长度,mm 通常见到的石油化工容器的结构大多数是以圆柱形筒体为主,所附设的各种封头形式虽然多种多样,但也都属于回转体。
各类储罐不同液位的体积计算

各类储罐不同液位的体积计算储罐是工业生产过程中常见的用于储存液体或气体的设备。
在工业生产中,准确计算储罐不同液位的体积非常重要,可以帮助企业进行生产计划、资产管理以及环境保护等方面的工作。
以下将介绍几种常见储罐不同液位的体积计算方法。
1.立式圆筒形储罐立式圆筒形储罐是储罐中最常用且最为简单的一种类型。
它的体积计算方法可以通过以下公式完成:V=π*h*(R^2-r^2)2.水平圆筒形储罐水平圆筒形储罐在储罐底部的中心线处有一个小孔,用于放出废液。
这种储罐的体积计算可以采用以下公式:V = L * (R^2 * arccos((R - h) / R) - (R - h) * (2 * R * h -h^2)^0.5)其中,V表示储罐在液位高度h处的体积,L是储罐的长度,R是储罐底部的半径。
当液位低于底部或高于储罐的长度时,对应的体积均为0。
3.球形储罐球形储罐通常用于大型液化气体的储存。
其体积计算方法可以通过以下公式完成:V = (pi / 6) * h * (3 * R^2 + h^2)其中,V表示储罐在高度h处的体积,pi是圆周率,R是储罐的半径。
当液位低于底部或高于储罐顶部时,对应的体积均为0。
4.圆锥形储罐圆锥形储罐通常用于粉体的存储。
它的体积计算方法可以通过以下公式完成:V=(1/3)*π*h*(R^2+R*r+r^2)其中,V表示储罐在高度h处的体积,π是圆周率,R和r分别为储罐顶部和底部的半径。
当液位低于底部或高于储罐顶部时,对应的体积均为0。
储罐不同液位的体积计算方法多种多样,需要根据实际储罐的形状和液位高度来选择合适的计算公式。
同时,在进行计算时也应注意单位的统一,以确保结果的准确性。
卧式容器液位与体积的关系

卧式容器液位与体积的关系The relations between volume and liquid heights in horizontal vessels江峡船舶柴油机厂 HYC摘 要:推导了卧式容器不同液位时的体积计算公式,利用计算机程序或EXCEL 可以方便的使用其结果。
关 键 词:卧式容器;体积;液位;计算;EXCEL设计和使用中常需知道容器内液体的液位与所占容积的关系,本文推导一般卧式容器液位与体积的关系,解决了卧式容器液位与体积的关系问题。
1.公式推导 1.1.圆柱筒体圆柱筒体液位与体积关系实为液位与圆面积关系见图1,圆方程为x 2+y 2=R 2,有:22dv l ds l x dy l dy =⋅=⋅⋅=⋅ 液位为h 时的体积为: ()2R hRV h dv l dy -+-==⋅⎰⎰2222()2(arcsin()2((arcsin )(2(arccos (R hRV h l dyh R l R R h R R h R l R R h R R hR R h lR ππ-+-=⋅-=⋅---=⋅+---=--⋅⎰1.2.椭圆柱筒体椭圆柱筒体液位与体积关系实为液位与椭圆面积关系见图2,椭圆方程为x 2/a 2+y 2/b 2=1,有:22dv l ds l x dy l dy =⋅=⋅⋅=⋅ 液位为h 时的体积为: ()2b hbV h dv l dy -+-==⋅⎰⎰222arccos )2b h b a l dy ba b b h l b b-+-=⋅-=⋅⎰1.3.标准椭圆封头(不含直边段)卧式椭圆封头液位与体积关系见图3。
液面为半椭圆,其面积S=πab/2;封头椭圆方程为4x 2 +y 2= R 2;轴垂面是圆,圆方程为z 2+y 2=R 2。
则有:a z==b x==22/2()/4s ab R yπππ===-液位为h时的体积为:22()()/4R h R hR RV h dv s dy R y dyπ-+-+--==⋅=-⋅⎰⎰⎰{}22233232233232()()41((())()()431(33)431()431()43R hRV h R y dyR R h R R h RR h R R h Rh h RRh hh R hπππππ-+-=-⋅⎧⎫=-+---⋅-+--⎨⎬⎩⎭⎧⎫=-⋅-+-++⎨⎬⎩⎭=-=-⎰2.公式应用2.1.卧式标准椭圆封头容器液位与体积关系根据1.1、1.3条公式得出卧式标准椭圆封头容器体积计算公式:)3(2)2)(arccos ()3(42)2)(arccos(222222hR h l R hR h R R h R R hR h l R hR h R R h R R V j -+⋅----=⋅-⋅+⋅----=ππ 2.2.卧式椭圆容器液位与体积关系卧式椭圆容器一般只有平封头或近似平封头,根据1.2条公式可计算其体积3.卧式椭圆封头容器体积计算公式在EXCEL 中的实际运用压力容器在设计和使用中不仅需要知道液位与体积关系,按《压力容器安全监察规程》还需要知道在不同温度下容器最大充液高度,在EXCEL 中使用本文公式非常方便,可避免复杂的计算,下面是我实际运用中的一个模式,见图4,只需输入公式和适当调整液位高度即可。
流体力学中的流体压力变化与高度关系

流体力学中的流体压力变化与高度关系流体力学是研究液体和气体的运动与力学性质的学科。
在研究流体力学过程中,流体压力的变化与高度之间的关系是一个重要的概念。
本文将介绍流体力学中的流体压力变化与高度之间的关系,并通过实例和公式进行说明。
一、流体压力的定义和基本概念流体压力指的是单位面积上受到的垂直力的大小。
一般来说,流体压力与流体所受外部力的大小和方向有关。
根据物理学的定义,流体压力可以通过以下公式计算:P = F / A其中,P表示流体的压力,F表示垂直于面积A的力的大小,A表示垂直于力F的面积。
二、流体压力的变化与高度之间的关系在自由液体(不受外界限制)中,流体压力会随着高度的增加而增加。
这是因为在重力作用下,液体的上层对下层施加了压力。
根据流体力学的基本原理,液体的压力增加与高度的关系可以通过下面的公式表示:ΔP = ρgh其中,ΔP表示液体压力的增加量,ρ表示液体的密度,g表示重力加速度,h表示液体的高度。
根据上述公式,可以看出液体的压力增加与液体密度、重力加速度以及液体高度有关。
当液体密度或液体高度增加时,液体压力也会相应增加。
而重力加速度是一个常数,对液体压力的影响相对较小。
三、实例分析以一个高度为10米的垂直液体柱为例,液体的密度为1000千克/立方米,现计算在该液体柱顶部和底部之间的压力差。
根据上述公式,可以计算出液体压力的增加量:ΔP = ρgh= 1000 * 9.8 * 10= 98,000 帕斯卡(Pa)通过计算可得,液体柱顶部和底部之间的压力差为98,000帕斯卡。
这意味着,在液体柱底部受到的压力比顶部大98,000帕斯卡。
四、结论在流体力学中,流体压力的变化与高度之间存在着明显的关系。
随着液体高度的增加,液体压力也会相应增加。
这一关系可以通过公式ΔP = ρgh来计算,其中ρ表示液体的密度,g表示重力加速度,h表示液体的高度。
需要注意的是,这个关系只适用于自由液体,并忽略了其他因素的影响。
液位的影响因素

液位的影响因素
液位的影响因素有以下几个:
1. 容器形状和尺寸:容器的形状和尺寸决定了液体填充的体积和液位的高度。
2. 液体的密度:液体的密度决定了在相同体积下液体的质量,从而影响液位的高度。
3. 引入和排出液体的速率:液体的引入和排出速率会改变液体的体积,进而影响液位的高度。
4. 外界环境因素:外部压力、温度和重力等因素也会对液体的液位产生影响。
5. 液体的粘度和表面张力:液体的粘度和表面张力也会对液位产生影响,例如高黏度液体会形成更高的液位。
总而言之,液位的影响因素包括容器形状和尺寸、液体的密度、引入和排出液体的速率、外界环境因素以及液体的粘度和表面张力。
力学专题 液面升降问题

液面升降问题考查要点液面升降问题是中考压轴题的考查热点,近三年(2014-2016年)的中考压轴题都是考查这方面的问题,以液体的压强和浮力为载体,考查学生对液体压强、浮力知识的综合运用能力。
解题思路利用量筒的原理1.基本思路:【例1】如图17-1所示,容器内分别装有水和盐水,在液面上浮着一块冰,问:(1)冰在水中熔化后,水面如何变化?(2)冰在盐水中熔化后,液面如何变化?(a)(b)图17-1【思路点拨】容器中的液面高度变化是由于容器中物体排开液体的体积与液体体积之和发生变化引起的。
根据,因容器内原来的水的体积不变,关键是比较两个体积,一个是冰熔化前,排开水的体积,一个是冰熔化成水后,水的体积。
求出这两个体积,再进行比较,就可得出结论。
【解】(1)如图(a)所示,冰在水中,熔化前处于漂浮状态。
===①冰熔化成水后,质量不变:=求得:==②比较①和②,=也就是冰熔化后体积变小了,恰好占据了原来冰熔化前在水中的体积。
所以,冰在水中熔化后液面不变(2)冰在盐水中:冰熔化前处于漂浮,如图(b),则===③冰熔化成水后,质量不变,推导与问题(1)相同。
=④比较③和④,因为<所以>也就是冰熔化后占据的体积要大于原来冰熔化前在盐水中的体积。
所以,冰在盐水中熔化后液面上升了。
【答案】(1)冰在水中熔化后液面不变。
(2)冰在盐水中熔化后液面上升。
【变式练习】冰放在密度小于冰的液体中,静止后处于什么状态,熔化后,液面又如何变化?【例2】如图17-2所示,底面积为的圆柱形容器内盛有适量的水,另一底面积为的圆柱体A有部分体积浸在水中,当圆柱体A相对于容器下降高度为h时(水没有溢出,圆柱体A也未全部没入水中),求:容器中液体高度的变化量?图17-2【思路点拨】解法一:画出情境图,如图17-3所示,找出体积之间的关系图17-3即:①Δh②②-①可得Δh因为所以ΔhhΔh=。
解法二:如图17-4,圆柱体下降h后,体积为的水被挤走,图17-4水被挤到原水面上圆柱体周围的区域,体积为Δh所以h解得Δh=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
收稿日期:2002207228
作者简介:李彩英(19442),女(汉族),山西武乡人,副教授,主要从事几何代数和高等数学的研究和教学。
文章编号:100027466(2003)0120021202
变形截面容器内液体体积与液位高度关系
李彩英,梁泰安,金 明
(天津大学,天津 300072)
摘要:介绍了10种变形截面容器以及各容器内存留液体体积与液位高度的函数关系,利用各种公式可快速准确计算出容器内存留液体的体积。
关 键 词:容器;液体;体积;液位高度中图分类号:T Q 05012 文献标识码:A
The functional relationship betw een the height and the volume of the rem aining
liquid in the containers with changeful cross section
LI Cai 2ying ,LI ANG T ai 2an ,J I N M ing (T ianjin University ,T ianjin 300072,China )
Abstract :T en kinds of containers with changeful cross sections were introduced 1The functional relationship between the height
and the v olume of the remaining liquid within these containers was als o presented 1The v olume of the remaining liquid in the con 2tainers can be calculated quickly and accurately by these formulae.
K ey w ords :container ;liquid ;v olume ;liquid height
符 号 说 明
V ———存留液体体积,mm 3B ———矩形短边长度,mm h ———存留液体液位高度,mm D ———圆形直径,mm
H ———容器高度,mm
a ———椭圆形半长轴长度,mm A ———正方形边长或矩形长边长度,mm
b ———椭圆形半短轴长度,mm
通常见到的石油化工容器的结构大多数是以圆柱形筒体为主,所附设的各种封头形式虽然多种多样,但也都属于回转体。
对于上述容器内存留液体体积与液位高度的函数关系,笔者已经有过一些研究和论述。
在化工容器和管道当中,还经常遇到一些变形截面容器,亦即容器的任一横截面形状都各不相同。
文中所涉及到的10种变形截面容器只是其中最常见的一部分,均为直立放置,它们的上下端面形状各不相同,1个端面为正方形或者矩形,而另1个端面为圆形或者椭圆形。
它们的共同之处在于,其外壁都是属于由4个斜平面以及4个斜锥曲面互相间隔,并且
相邻部分又互相吻合而共同组成的1个完整形体。
1 变形截面容器介绍
根据约定,把直立放置的变形截面容器上端面称为天,下端面称作地,把正方形、矩形简称作方和矩。
为了计算简便,文中所研究的变形截面容器的前后、左右均对称。
10种变形截面容器简称为天圆地方、天圆地矩、天椭圆地方、端面对称线对应平行的天椭圆地矩、端面对称线对应垂直的天椭圆地矩、天方地圆、天矩地圆、天方地椭圆、端面对称线对应平行的天矩地椭圆及端面对称线对应垂直的天矩地椭圆,其外形见图1。
第32卷 第1期2003年1月 石 油 化 工 设 备PETRO 2CHE MIC A L E QUIP ME NT V ol 132 N o 11 Jan 12003
图1 10种变形截面容器外形图
2 变形截面容器内存留液体体积计算公式
参照文献[1~3],利用数学微积分,并且经过复杂的分析以及运算,最终可以得到计算与图1a ~图1j 相对应的各种变形截面容器内存留液体体积的10个公式。
V =
112H
2πD 2h 3+4A (3H -2h )Dh 2
+43H 2-3Hh +h 2A 2h
(1)
V =
112H
2πD 2h 3+2(A +B )(3H -2h )Dh 2+43H 2-3Hh +h 2ABh (2)V =
1
3H
2
πabh 3+A (a +b )(3H -2h )h 2+
3H 2-3Hh +h 2A 2h (3)
V =
1
3H
2
πabh 3+(Ab +Ba )(3H -2h )h 2+
3H 2-3Hh +h 2ABh (4)
V =
1
3H
2
πabh 3+(Aa +Bb )(3H -2h )h 2+
3H 2-3Hh +h 2ABh
(5)
V =112H
24A 2h 3+4A (3H -2h )Dh 2
+π3H 2-3Hh +h 2D 2h
(6)
V =
112H
24ABh 3+2(A +B )(3H -2h )Dh 2+π3H 2-3Hh +h 2D 2h (7)V =
13H
2
A 2h 3+A (a +b )(3H -2h )h 2
+
π3H 2-3Hh +h 2abh (8)V =13H
2ABh 3+(Ab +Ba )(3H -2h )h 2
+π3H 2-3Hh +h 2abh (9)V =13H
2ABh 3+(Aa +Bb )(3H -2h )h 2
+π3H 2-3Hh +h 2abh (10)
3 结语
根据上述计算变形截面容器内存留液体体积的10个公式,分别输入已知的容器结构参数和存留液体液位高度数据,不仅可以顺利得到所需的容器内存留液体体积,还可以绘制出用于表示存留液体体积或质量的高度标尺。
经过多种场合反复计算验证,上述计算公式准确可靠。
参考文献:
[1] 樊映川.高等数学讲义[M].北京:人民教育出版社,1958.3412
3421
[2] 蔡高厅,叶宗泽.高等数学[M ].天津:天津大学出版社,
1994126622671
[3] 李彩英,梁泰安,周 伟,等.容器内存留液体体积与液位高度
函数关系[J ].石油化工设备,2001,30(6):252271
(张编)
欢迎赐稿 欢迎订阅
欢迎刊登广告
・22・ 石 油 化 工 设 备 2003年 第32卷。
