高中物理练习振动与波(习题含答案)
人教版高中物理选修一《波的形成》练习题(含解析)(3)

第三单元机械波第1课波的形成一、基础巩固1.关于机械振动和机械波,下列说法中正确的是()A.物体作机械振动时,一定产生机械波B.没有机械振动,也可能形成机械波C.有机械波,一定有质点作机械振动D.机械振动和机械波的产生无关【答案】C【解析】机械振动在介质中的传播称为机械波,所以有机械波必有机械振动,而有机械振动若没介质不会形成机械波,故C正确,ABD错误.2.下列关于横波、纵波的说法错误的是().A.凸凹相间的波叫横波,凸起的最高处叫波峰,凹下的最低处叫波谷B.质点振动方向和波的传播方向在同一直线上的波叫横波C.纵波的波形是疏密相间的,质点分布最密的部分叫密部,分布最疏的地方叫疏部D.质点的振动方向和波的传播方向在同一直线上的波叫纵波【答案】B【解析】物理学中把质点的振动方向与波的传播方向垂直的波称作横波,在横波中,凸起的最高处称为波峰,凹下的最低处称为波谷,故A正确;把质点的振动方向与波的传播方向在同一直线的波称作纵波,故B错误,D正确;质点在纵波传播时来回振动,其中质点分布最密集的地方称为密部,质点分布最稀疏的地方称为疏部,故C正确。
本题要求选错误的,故选B。
3.将一部手机调在接收信号就发出声响并且振动的状态,然后将这部手机放在密封的玻璃罩內,当我们抽掉玻璃罩内的空气后,再发出信号呼叫该手机,你可以看到().A.手机发出声音同时振动B.手机发出声音但是不振动C.手机没有发出声音也不振动D.手机没有发出声音但是在振动【答案】D【解析】声音是由物体的振动产生的,声音的传播需要介质,声音在真空中不能传播,所以抽调玻璃罩内的空气后,声音传播不出来,故能看到手机没有发出声音但是在振动,故D正确,ABC错误。
4.关于机械波的形成和传播,下列说法中正确的是().A.振动是波动的成因,波动是振动的传播B.一旦波源振动起来,介质中的各个质点也就同时开始振动C.波动过程是介质中质点由近及远移动的过程D.横波的传播需要介质,纵波的传播不一定需要介质【答案】A【解析】振动是的波的成因,波动是振动的传播,故A正确;机械波的形成可表述为离波源近的质点带动离波源远的质点,故离波源近的质点振动的早一些,故B错误;波动过程是介质中质点振动形式由近及远移动,而质点不随波迁移,故C错误;机械横波与纵波的传播,都需要介质,故D错误。
高中物理专题振动和波练习
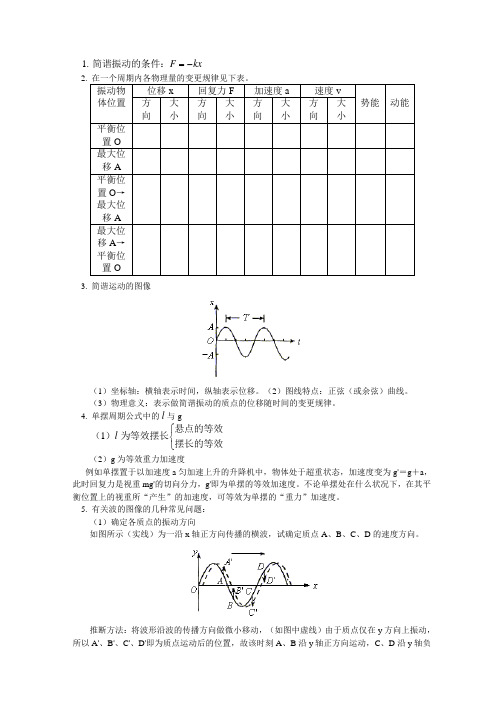
1. 简谐振动的条件:F kx =-3. 简谐运动的图像(1)坐标轴:横轴表示时间,纵轴表示位移。
(2)图线特点:正弦(或余弦)曲线。
(3)物理意义:表示做简谐振动的质点的位移随时间的变更规律。
4. 单摆周期公式中的l 与g ()为等效摆长悬点的等效摆长的等效1l ⎧⎨⎩(2)g 为等效重力加速度例如单摆置于以加速度a 匀加速上升的升降机中,物体处于超重状态,加速度变为g'=g +a ,此时回复力是视重mg'的切向分力,g'即为单摆的等效加速度。
不论单摆处在什么状况下,在其平衡位置上的视重所“产生”的加速度,可等效为单摆的“重力”加速度。
5. 有关波的图像的几种常见问题: (1)确定各质点的振动方向如图所示(实线)为一沿x 轴正方向传播的横波,试确定质点A 、B 、C 、D 的速度方向。
推断方法:将波形沿波的传播方向做微小移动,(如图中虚线)由于质点仅在y 方向上振动,所以A'、B'、C'、D'即为质点运动后的位置,故该时刻A 、B 沿y 轴正方向运动,C 、D 沿y 轴负方向运动。
从以上分析也可看出,波形方向相同的“斜坡”上速度方向相同。
(2)确定波的传播方向知道波的传播方向利用“微平移”的方法,可以很简洁地推断出各质点的振动方向。
反过来知道某一质点的运动方向,也可利用此法确定该波的传播方向。
另外还有一简便好用的推断方法,同学们也可以记住。
如图所示,若已知A 点速度方向向上,可假想在最靠近它的波谷内有一小球。
不难看出A 向上运动时,小球将向右滚动,此即该波的传播方向。
(3)已知波速v 和波形,画出再经△t 时间的波形图①平移法:先算出经时间波传播的距离=,再把波形沿波的传播方∆∆∆t x v t向平移即可。
因为波动图像的重复性,若知波长,则波形平移时波形不∆x n λλ 变,当时,可采取去整留零的方法,只需平移即可。
∆x n x n x x =+λλ②特殊点法:(若知周期T 则更简洁)在波形上找两个特殊点,如过平衡位置的点和与它相邻的波峰(谷)点,先确定这两点的振动方向,再看△t =nT +t ,由于经nT 波形不变,所以也实行去整nT 留零t 的方法,分别做出两特殊点经t 后的位置,然后按正弦规律画出新波形。
高考物理《机械振动和机械波》真题练习含答案

高考物理《机械振动和机械波》真题练习含答案1.[2023·新课标卷]船上的人和水下的潜水员都能听见轮船的鸣笛声.声波在空气中和在水中传播时的()A.波速和波长均不同B.频率和波速均不同C.波长和周期均不同D.周期和频率均不同答案:A解析:声波的周期和频率由振源决定,故声波在空气中和在水中传播的周期和频率均相同,但声波在空气和水中传播的波速不同,根据波速与波长关系v=λf可知,波长也不同,故A正确,B、C、D错误.故选A.2.[2024·浙江1月]如图1所示,质量相等的小球和点光源,分别用相同的弹簧竖直悬挂于同一水平杆上,间距为l,竖直悬挂的观测屏与小球水平间距为2l,小球和光源做小振幅运动时,在观测屏上可观测小球影子的运动.以竖直向上为正方向,小球和光源的振动图像如图2所示,则()A.t1时刻小球向上运动B.t2时刻光源的加速度向上C.t2时刻小球与影子相位差为πD.t3时刻影子的位移为5A答案:D解析:以竖直向上为正方向,根据图2可知,t1时刻,小球位于平衡位置,随后位移为负值,且位移增大,可知,t1时刻小球向下运动,A错误;t2时刻,光源的位移为正值,光源振动图像为正弦式,表明其做简谐运动,根据F回=-kx=ma可知,其加速度方向与位移方向相反,位移方向向上,则加速度方向向下,B错误;根据图2可知,小球与光源的振动步调总是相反,由于影子是光源发出的光被小球遮挡后,在屏上留下的阴影,可知,影子与小球的振动步调总是相同,即t2时刻小球与影子相位差为0,C错误;根据图2可知,t3时刻,光源位于最低点,小球位于最高点,根据光沿直线传播,光源能够在屏上留下影子的位置也处于最高点,影子位于正向最大位移处,根据几何关系有ll+2l =A+AA+x影子,解得x影子=5A,即t3时刻影子的位移为5A,D正确.3.[2024·吉林卷]某同学自制双缝干涉实验装置:在纸板上割出一条窄缝,于窄缝中央沿缝方向固定一根拉直的头发丝形成双缝,将该纸板与墙面平行放置,如图所示.用绿色激光照双缝,能够在墙面上观察到干涉条纹.下列做法可以使相邻两条亮条纹中央间距变小的是()A.换用更粗的头发丝B.换用红色激光照射双缝C.增大纸板与墙面的距离D.减小光源与纸板的距离答案:A解析:由于干涉条纹间距Δx=ldλ可知,换用更粗的头发丝,双缝间距d变大,则相邻两条亮条纹中央间距Δx变小,故A正确;换用红色激光照双缝,波长变长,则相邻两条亮条纹中央间距Δx变大,故B错误;增大纸板与墙面的距离l,则相邻两条亮条纹中央间距Δx 变大,故C错误;减小光源与纸板的距离,不会影响相邻两条亮条纹中央间距Δx,故D错误.故选A.4.[2024·浙江1月](多选)在如图所示的直角坐标系中,xOz平面为介质Ⅰ和Ⅱ的分界面(z轴垂直纸面向外).在介质Ⅰ中的P(0,4λ)处有一点波源,产生波长为λ、速度为v的波.波传到介质Ⅱ中,其速度为2v.图示时刻介质Ⅱ中仅有一个波峰,与x轴和y轴分别交于R 和S点,此时波源也恰好位于波峰.M为O、R连线的中点,入射波与反射波在O点相干加强,则()A .介质Ⅱ中波的频率为2v λB. S 点的坐标为(0,-2 λ)C .入射波与反射波在M 点相干减弱D. 折射角α的正弦值sin α=352 答案:BD解析:波从一种介质到另一种介质,频率不变,故介质Ⅱ中波的频率为f =v λ,A 错误;在介质Ⅱ中波长为λ′=2v f=2 λ,由于图示时刻介质Ⅱ中仅有一个波峰,与x 轴和y 轴分别交于R 和S 点,故S 点的坐标为(0,-2 λ),B 正确;由于S 为波峰,且波传到介质Ⅱ中,其速度为2 v .图示时刻介质Ⅱ中仅有一个波峰,与x 轴和y 轴分别交于R 和S 点,则R 也为波峰,故P 到R 比P 到O 多一个波峰,则PR =5λ,则OR =3λ,由于||MO -PM≠2n ·λ2 或(2n +1)λ2 (n =0,1,2,…),故M 点不是减弱点,C 错误;根据n =λ′λ=2 ,则n =sin αOR PR,解得sin α=352 ,D 正确. 5.[2021·天津卷]一列沿x 轴正方向传播的简谐横波,传播速度v =10 m/s ,t =0时位于坐标原点的质点从平衡位置沿y 轴正方向运动,下列图形中哪个是t =0.6 s 时的波形( )答案:B解析:由图中可以看出该波的波长为λ=4 m ,根据v =λT可知该列波的周期为T =0.4 s ,又因为t=0时位于坐标原点的质点从平衡位置沿y轴正方向运动,当t=0.6 s时经历了1.5 T,所以此时位于坐标原点的质点从平衡位置沿y轴负方向运动,结合图像可知B正确.6.[2023·湖南卷]如图(a),在均匀介质中有A、B、C和D四点,其中A、B、C三点位于同一直线上,AC=BC=4 m,DC=3 m,DC垂直AB.t=0时,位于A、B、C处的三个完全相同的横波波源同时开始振动,振动图像均如图(b)所示,振动方向与平面ABD垂直,已知波长为4 m.下列说法正确的是()A.这三列波的波速均为2 m/sB.t=2 s时,D处的质点开始振动C.t=4.5 s时,D处的质点向y轴负方向运动D.t=6 s时,D处的质点与平衡位置的距离是6 cm答案:C解析:由图(b)的振动图像可知,振动的周期为4 s,故三列波的波速为v=λT=4 m4 s=1m/s,A错误;由图(a)可知,D处距离波源C最近的距离为3 m,故开始振动后波源C处的横波传播到D处所需的时间为t C=DC v=3 m1 m/s=3 s故t=2 s时,D处的质点还未开始振动,B错误;由几何关系可知AD=BD=5 m,波源A、B产生的横波传播到D处所需的时间为t AB=ADv=5 m1 m/s=5 s故t=4.5 s时,仅波源C处的横波传播到D处,此时D处的质点振动时间为t1=t-t C =1.5 s由振动图像可知此时D处的质点向y轴负方向运动,C正确;t=6 s时,波源C处的横波传播到D处后振动时间为t2=t-t C=3 s由振动图像可知此时D处为波源C处传播横波的波谷;t=6 s时,波源A、B处的横波传播到D处后振动时间为t3=t-t AB=1 s由振动图像可知此时D处为波源A、B处传播横波的波峰.根据波的叠加原理可知此时D处质点的位移为y=2A-A=2 cm故t=6 s时,D处的质点与平衡位置的距离是2 cm,D错误.故选C.。
振动与波(习题)

第八讲振动与波课后练习1.如图所示为已知简谐运动的图像,试求出它的振动方程。
2.如图所示,在升降机的天花板上固定一摆长为l的单摆当升降机静止时,让摆球从θ角度处摆下,试分析:(1)当摆球摆到最高点时,升降机以加速度g下落,摆球相对于升降机如何运动?(2)当摆球摆到最低点时,升降机以加速度g下落,摆球相对于升降机如何运动?(3)若升降机以g加速度加速上升,则摆球相对于升降机又如何运动?3.如图,两段不可伸长细绳的一端分别系于两竖直杆上的A,B两点,另一端与质量为m的小球D相连。
已知A,B两点高度相差h,∠CAB=∠BAD=37°,∠ADB=90°,重力加速度为g。
现使小球发生微小摆动,则小球摆动的周期为( )A.π2π4.轻弹簧的劲度系数为k,一端固定在侧壁上,质量为m的物体与桌面间的摩擦力为f,以速度v0开始压缩弹簧,以后又被反向弹回并能脱离弹簧,设物体从压缩弹簧到速度为0所需时间为t1,再从速度为0到离开弹簧的时间为t2,求t1/t2的比值。
5.图 (a),(b)分别表示一列横波上相距3m的两个质点A和B的振动图像。
已知波长为3m<λ<12m,求:(1)波通过A,B两点经历的时间t。
(2)设P点距B点1/3m,且在AB的中间,则从t1=0开始,P点经过1s通过的路程是多少?6.如图所示,半径为45m的圆形广场,在中心O及周围一点A处,分别安装两λ=,不考虑传播中衰减及人的运动对台相同的扩音机,已知声波波长10m声音传播的影响。
现有一个人沿着广场周围行走,当他在B点时就听不到声音,然后他继续逆时针方向从B走到接近A的过程中,有几次听不到扩音机的声音?7.如图所示,一端固定在台上的弦线,用支柱支撑其R点和S点,另一端通过定滑轮吊一个1.6kg的重物,弹拨弦的RS部分,使其振动,则R、S点为波节,其间产生三个波腹的驻波,这时,如在弦的附近使频率为278Hz的音叉发音,则5s内可听到10次拍音,换用频率稍大的音叉,则拍音频率减小。
高三物理波的基础练习题及答案

高三物理波的基础练习题及答案【第一节】选择题1.下列选项中,哪个是机械振动最基本的要素?A. 能量B. 速度C. 频率D. 振幅答案:D2.下列选项中,属于横波的是:A. 音波B. 电磁波C. 地震波D. 水波答案:B3.一个机械波的频率为100Hz,周期为T,下列说法正确的是:A. T = 2sB. T = 10msC. T = 1000μsD. T = 0.01s答案:D4.波速为2m/s的波在5s内传播的距离为:A. 2mB. 10mC. 25mD. 12.5m答案:B5.两个波的频率分别为10Hz和20Hz,它们的周期之比为:A. 1:1B. 1:2C. 3:1D. 2:1答案:D【第二节】填空题1.波传播的基本特性是______。
答案:传播、传递2.一个波峰经过某固定点的时间称为波的______。
答案:周期3.波长是相邻两个______之间的距离。
答案:波峰(或波谷)4.频率是单位时间内波的_____。
答案:周期个数5.波速的单位是______。
答案:m/s6.一个波长为1m的横波,峰到波谷的距离为______。
答案:0.5m【第三节】解答题1.某波的波速为20m/s,频率为10Hz,求该波的波长和周期。
解答:波速(v)= 波长(λ) ×频率(f)20 = λ × 10λ = 2m周期(T)= 1 / 频率(f)T = 1 / 10 = 0.1s答案:波长:2m周期:0.1s2.已知某波的频率为100Hz,波长为0.02m,求该波的速度和周期。
解答:波速(v)= 波长(λ) ×频率(f)v = 0.02 × 100 = 2m/s周期(T)= 1 / 频率(f)T = 1 / 100 = 0.01s答案:速度:2m/s周期:0.01s【第四节】计算题1.一个波的频率为50Hz,速度为10m/s,求该波的波长和周期。
解答:由v = λ × f,可得λ = v / fλ = 10 / 50 = 0.2m周期(T)= 1 / 频率(f)T = 1 / 50 = 0.02s答案:波长:0.2m周期:0.02s2.波的频率为20Hz,周期为0.05s,求该波的波速和波长。
(文末附答案)2022届高中物理机械振动与机械波知识点汇总

(每日一练)(文末附答案)2022届高中物理机械振动与机械波知识点汇总单选题1、下列说法正确的是()A.洗衣机工作时机壳的振动频率等于其固有频率B.为了防止桥梁发生共振而坍塌,部队要齐步通过桥梁C.鼓手随音乐敲击鼓面时,鼓面的振动是自由振动D.较弱声音可震碎玻璃杯,是因为玻璃杯发生了共振s,振动2、如图所示,已知一列横波沿x轴传播,实线和虚线分别是t1时刻和t2时刻的图像,已知t2=t1+18周期为0.5s,则波的传播方向与传播距离是()A.沿x轴正方向,6 mB.沿x轴正方向,2 mC.沿x轴负方向,6 mD.沿x轴负方向,2 m3、一列沿x轴正方向传播的横波,其振幅为A,波长为λ,某一时刻的波形图如图所示,在该时刻某质点的坐标为(λ,0),经过四分之一周期后,该质点坐标为()A.(54λ,0)B.(λ,A)C.(λ,-A)D.(54λ,-A)4、某人有两部手机A和B,当用手机A(或B)拨打B(或A)的号码时,既能听到手机B(或A)的响声,又能看到B(或A)的显示屏上显示出A(或B)的号码。
现把手机A放到一个透明玻璃罩内,并抽成真空,再用手机B拨打手机A的号码,以下说法正确的是()A.既能听到A的响声,又能看到A的显示屏上显示出B的号码B.能听到A的响声,但不能看到A的显示屏上显示出B的号码C.不能听到A的响声,但能看到A的显示屏上显示出B的号码D.既不能听到A的响声,也不能看到A的显示屏上显示出号码5、一列简谐横波在均匀介质中沿x轴正方向传播,波源位于坐标原点,t=0时刻波源开始振动,在t=32T时刻的波形如图所示,此时,x=32λ处的质点刚开始振动。
振幅为A,波长为λ,质点振动周期为T,则下列说法正确的是()A.t=T时刻、x=λ处质点的振动方向沿y轴正方向B.波源处质点的振动方程为y=A sin(2πTt)C.经过一个周期T,质点通过的路程为λD.波源起振方向沿y轴负方向6、如图所示,S1、S2是两个振动完全相同的相干波源,其中实线表示波峰,虚线表示波谷。
振动和波动要点习题

振动和波一、选择题1.(3分,答D )已知一平面简谐波的表达式为cos()y A at bx =-(,a b 为正值常量),则 (A )波的频率为a (B )波的传播速度为/b a (C )波长为/b π (D )波的周期为2/a π2.(本题3分,答B )一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为[]3. (3分,答B )一质点在x 轴上作简谐振动,振幅A =4cm ,周期T =2s ,其平衡位置取作坐标原点,若t =0时刻质点第一次通过x =-2cm 处,且向x 轴负方向运动,则质点第二次通过x =-2cm 处的时刻为(A) 1s (B) (2/3)s (C)(4/3)s (D) 2s4. (3分,答D )一劲度系数为k 的轻弹簧,下端挂一质量为m 的物体,系统的振动周期为T 1.若将此弹簧截去一半的长度,下端挂一质量为m 21的物体,则系统振动周期T 2等于 (A) 2 T 1 (B) T 1(C)T 12/ (D) T 1 /2 (E) T 1 /45.(本题3分,答A )轴一简谐波沿Ox 轴正方向传播,t = 0 时刻的波形曲线如图所示,已知周期为 2 s ,则 P 点处质点的振动速度v 与时间t 的关系曲线为:6.(3分,答B )一平面简谐波在弹性媒质时,某一时刻媒质中某质元在负最大位移处,则它的能量是(A ) 动能为零 势能最大 (B )动能为零 势能为零 (C ) 动能最大 势能最大 (D )动能最大 势能为零v (m/s)O 1 t (s)ωA(C)· v (m/s)O1 t (s)ω A(A)·1 v (m/s)t (s)(D)O-ω A1 v (m/s) t (s)-ωA(B) O ··x o A x A 21 ω(A)A 21ω(B) A 21-(C) (D)o oo A 21-xxxAxAxAxω ω2O 1 y (m)x (m)t =0 A u图17.(3分,答D )沿相反方向传播的两列相干波,其波动方程为y 1=A cos2π (νt -x /λ)y 2=A cos2π (νt + x /λ) 叠加后形成的驻波中,波节的位置坐标为(A)x =±k λ.(B)x =±k λ/2 .(C)x =±(2k +1)λ/2 .(D)x =±(2k +1)λ/4 . 其中k = 0 , 1 , 2 , 3…….8.(3分,答D )如图所示,有一平面简谐波沿x 轴负方向传播,坐标原点O 的振动规律为y =A cos(ω t+φ0),则B 点的振动方程为 (A )y =A cos[ω t-(x/u )+φ0] (B )y =A cos ω[ t+(x/u )] (C )y =A cos{ω [t-(x/u ) ]+φ0} (D )y =A cos{ω[ t+(x/u ) ]+φ0}9.(3分,答D )一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中:(A )它的动能转换成势能. (B )它的势能转换成动能. (C )它从相邻的一段质元获得能量,其能量逐渐增大. (D )它把自己的能量传给相邻的一段质元,其能量逐渐减小. 10.(3分,答B )在波长为λ的驻波中,两个相邻波腹之间的距离为 (A )λ/4 (B )λ/2 (C )3λ/4 (D )λ11.(3分,答C )某时刻驻波波形曲线如图所示,则a 、b 两点振动的相位差是 (A )0 (B )/2π (C )π (D )5/4π12.(本题3分,答B)在驻波中,两个相邻波节间各质点的振动(A )振幅相同,相位相同 (B )振幅不同,相位相同 (C )振幅相同,相位不同 (D )振幅不同,相位不同 二、填空题1. (3分)已知一个简谐振动的振幅A=2cm, 角频率14s ωπ-=,以余弦函数表达式运动规律时的A -Ayxλ λ/2O ··a b · · · · · · · · ··x 2A A/2x 1初相12φπ=,试画出位移和时间的关系曲线(振动图线) 2.(4分)两个简谐振动方程分别为x 1=Acos(ω t ) ;x 2=Acos(ω t +π/3) 在同一坐标上画出两者的x-t 曲线.3. (3分)有两相同的弹簧,其劲度系数均为k .(1)把它们串联起来,下面挂一个质量为m 的重物,此系统作简谐振动的周期为;(2)把它们并联起来,下面挂一个质量为m 的重物,此系统作简谐振动的周期为.[答案:(1)22m k π,(2)22mkπ] 4.(4分)一弹簧振子系统具有1.0J 的振动能量,0.10m 的振幅和1.0m/s 的最大速率,则弹簧的劲度系数,振子的振动频率.[答案:2210N/m,1.6Hz ⨯]5.(3分)一平面机械波沿x =-1m 轴负方向传播,已知处质点的振动方程cos()y A t ωϕ=+,若波速为u ,求此波的波函数.[答案:cos{[(1)/]}y A t x u ωϕ=+++]6.(3分)一作简谐振动的振动系统,振子质量为2kg ,系统振动频率为1000Hz ,振幅为0.5cm ,则其振动能量为.(答案:29.9010J ⨯ )7.(3分)两个同方向同频率的简谐振动211310cos(),3x t ωπ-=⨯+221410cos()(SI)6x t ωπ-=⨯-,它们的合振幅是. (答案:2510m -⨯ )8.(3分)一平面简谐波沿Ox 轴正方向传播,波动表达式为cos[(/)/4]y A t x u ωπ=-+,则1x L =处质点的振动方程是;2x L =-处质点的振动和1x L =处质点的振动相位差为21φφ-=. (答案:1cos[(/)/4]y A t L u ωπ=-+,12()/L L u ω+)9.(5分)一余弦横波以速度u 沿x 轴正向传播,t 时刻波形曲线如图所示.试分别指出图中A ,B ,C 各质点在该时刻的运动方向.A 向下 ,B 向上 ,C 向上.10. (本题4分)一平面简谐波的表达式cos (/)cos(/)y A t x u A t x u ωωω=-=-其中/x u 表示,/x u ω表示,y 表示.[答案:波从坐标原点传至x 处所需时间(2分),x 处质点此原点处质点滞后的相位(1分),t 时刻x 处质点的振动位移(1分)]11. (本题3分)如图所示,两相干波源S 1和S 2相距为3λ/4,λ为波长,设两波在S 1 S 2连O Cyxu · · · A B线上传播,它们的振幅都是A ,并且不随距离变化,已知在该直线上S 1左侧各点的合成波强度为其中一个波强度的4倍,则两波源应满足的相位条件是__π/2_ 12. (3分)一驻波的表达式为y =2A cos(2πx/λ) cos(2πνt ),两个相邻波 腹之间的距离是.(答案:λ/2) 三、计算题1. (5分)一质点作简谐运动,其振动方程为110.24cos()()23x t SI ππ=+,试用旋转矢量法求出质点由初始状态运动到x =-0.12 m ,v <0的状态所经过的最短时间. 解:旋转矢量如图所示.图3分 由振动方程可得π21=ω,π=∆31φ1分667.0/=∆=∆ωφt s 1分2(本题10分)一质量m =0.25kg 的物体,在弹簧的力作用下沿x 轴运动,平衡位置在原点,弹簧的劲度系数k =25N/m.(1)求振动的周期T 和频率ω. (2)如果振幅A =15cm ,t =0时物体位于x =7.5cm 处,且物体沿x 轴反方向运动,求初速度v 0及初相φ.(3)写出振动的数值表达式. 解:(1)12/10k m s ωπ-== (2分)2/0.63T s πω== (1分)(2) A=15cm , 在t =0时,07.5cm x =,00v < 由2200(/)A x v ω=+得2200 1.3m/s v A x ω=--=- (2分)100(/)/3/3tg v x φωππ-=-=或400,/3x φπ>∴=(3分)(3)21510cos(10/3)(SI)x t π-=⨯+(2分)3.(10分)在一轻弹簧下端悬挂0100g m =砝码时,弹簧伸长8cm. 现在这根弹簧下端悬挂0250g m =物体,构成弹簧振子,将物体从平衡位置向下拉动4cm ,并给以向上的21cm/s 的初速度(令这时t=0).选x 轴向下,求振动方程的数值式.解:k = m 0g / ∆l 25.12N/m 08.08.91.0=⨯=N/mx (m) ωωπ/3π/3t = 0t0.12 0.24 -0.12 -0.24 OAAO xS 1S 211s 7s 25.025.12/--===m k ω(2分) 5cm )721(4/2222020=+=+=ωv x A cm (2分) 4/3)74/()21()/(tg 00=⨯--=-=ωφx v ,φ = 0.64 rad (3分))64.07cos(05.0+=t x (SI) (1分)4.(8分)在一竖直轻弹簧的下端悬挂一小球,弹簧被拉长0 1.2cm l =而平衡.再经拉动后,该小球在竖直方向作振幅为2cm A =的振动,试证此振动为简谐振动;选小球在正最大位移处开始计时,写出此振动的数值表达式.解:设小球的质量为m ,则弹簧的劲度系数(图参考上题)0/k mg l = 选平衡位置为原点,向下为正方向. 小球在x 处时,根据牛顿第二定律得202()d x mg k l x m dt -+=将k 代入整理后得 220d x g x dt l =-所以振动为简谐振动,其角频率为0/28.589.1(rad/s)g l ωπ===(5分)设振动表达式为 c o s ()x A t ωφ=+ 由题意:t=0时,200210m0x A v -==⨯=解得:0φ=2210cos(9.1)x t π-∴=⨯m (3分)5.(10分)在一轻弹簧下端悬挂m 0=100g 的砝码时,弹簧伸长8cm,现在这根弹簧下端悬挂m =250g 的物体, 构成弹簧振子. 将物体从平衡位置向下拉动4cm,并给以向上的21cm/s 的初速度(这时t =0) ,选x 轴向下,求振动方程的数值式. 解:物体受向下的重力和向上的弹性力.k=m 0g/∆l , x 0=4×10-2m, v 0=-21×10-2m/sω=()m l g m m k Δ0==7s -1A=22020ω/v x +=5×10-2m因A cos ϕ=4×10-2m, A sin ϕ=-v 0/ω=3×10-2m,有 ϕ=0.64rad 所以x=5×10-2cos(7t +0.64) (SI)6.(本题5分)一质量为0.2kg 的质点作简谐振动,其振动方程为10.6cos(5)(SI)2x t π=-求:(1)质点的初速度;(2)质点在正向最大位移一半处所受的力.解:(1)003.0sin(5)()0, 3.0m/s 2dx v t SI t v dt π==--==(2分) (2)2F ma m x ==-ω12x A =时, 1.5N F =-(无负号扣1分) (3分) 7.(5分)一平面简谐波沿x 轴正方向传播,波速为1m/s ,在x 轴上某质点的振动频率为1Hz ,振幅为0.01m. t = 0时该质点恰好在正最大位移处,若以该质点的平衡位置为x 轴的原点. 求此一维简谐波的表达式.解. 0.01cos[2()](m)y t x =-π8.(本题10分)某质点作简谐振动,周期为2s ,振幅为0.06m ,t =0时刻,质点恰好处在负最大位移处,求(1)该质点的振动方程.(2)此振动以波速u =2m/s 沿x 轴正方向传播时,形成的一维简谐波的波动表达式,(以该质点的平衡位置为坐标原点);(3)该波的波长. 解:(1)振动方程 00.06cos(2/2)0.06cos()(SI)y t t ππππ=+=+3分 (2)0.06cos[((/))0.06cos[(/2))(SI)y t x u t x ππππ=-+=-+ 4分(3)波长4m uT λ==9.(10分)一列平面简谐波在以波速5m/s u =,沿x 轴正向传播,原点O 处质点的振动曲线如图所示.1)求解并画出25cm x =处质元的振动曲线 2)求解并画出3s t =时的波形曲线 解:1)原点O 处质元的振动方程为211210cos(),(SI)22y t ππ-=⨯-(2分)波的表达式 (2分)211210cos((/5)),(SI)22y t x ππ-=⨯--x =25m 处质元的振动方程21210cos(3),(SI)2y t ππ-=⨯-振动曲线如右y-t 图 (2分)2)t=3s 时的波形曲线方程2210cos(/10),(SI)y x ππ-=⨯-(2分)波形曲线见右y-x 图 (2分)10.(10分)某质点作简谐振动,周期为2s ,振幅为0.6m ,t =0时刻,质点恰好处在负最大4O2 y(cm)t (s)2位移处,求(1)该质点的振动方程;(2)此振动以波速u =2m/s 沿x 轴正方向传播时,形成的一维简谐波的波动表达式,(以该质点的平衡位置为坐标原点);(3)该波的波长.解:(1) 振动方程)22cos(06.00π+π=ty )cos(06.0π+π=t (SI) (3分) (2) 波动表达式])/(cos[06.0π+-π=u x t y (4分)])21(cos[06.0π+-π=x t (SI)(3) 波长4==uT λm (3分)11.(5分)如图所示,一简谐波向x 轴正向传播,波速0500/,1,u m s x m P ==点的振动方程为10.03cos(500)(SI)2y t ππ=-. (1) 按图所示坐标系,写出相应的波的表达式; (2) 在图上画出t=0时刻的波形曲线.解:(1) 2m )250/500(/===νλu m 波的表达式 ]/2)1(21500cos[03.0),(λπ--π-π=x t t x y110.03cos[500(1)2/2]0.03cos(500)(SI)22t x t x =π-π--π=π+π-π(3分)(2) t = 0时刻的波形曲线x x x y π=π-π=sin 03.0)21cos(03.0)0,( (SI) (2分)12.(10分)图示一平面余弦波在t = 0 时刻与t = 2 s 时刻的波形图(波向左传播).已知波速为u ,波的周期大于2 s ,求(1) 坐标原点处介质质点的振动方程;(2) 该波的波动表达式. 解:(1) 比较t = 0 时刻波形图与t = 2 s 时刻波形图,可知此波向左传播.在t = 0时刻,O 处质点φcos 0A =,φωsin 00A -=<v ,故2πφ-= 又t = 2 s ,O 处质点位移为)24cos(2/ππ-=νA A 所以244πππ-=-ν,ν = 1/16 Hz 振动方程为)28/cos(0ππ-=t A y (SI)(2) 波速u = 20 /2 m/s = 10 m/s,波长λ = u /ν = 160 m 波动表达式]21)16016(2cos[π-+π=x t A y (SI) x (m)uP y (m)O-2-112-0.030.03x (m)O160A y (m)8020t =0t =2 s2A。
振动、波动练习题及答案

振动、波动练习题一.选择题1.一质点在X 轴上作简谐振动,振幅A=4cm。
周期T=2s。
其平衡位置取作坐标原点。
若t=0 时刻质点第一次通过x= -2cm 处,且向X 轴负方向运动,则质点第二次通过x= -2cm 处的时刻为()。
A 1sB 2sC 4sD 2s332.一圆频率为ω的简谐波沿X 轴的正方向传播,t=0 时刻的波形如图所示,则t=0 的波形t=0 时刻,X 轴上各点的振动速度υ与X轴上坐标的关系图应()3.图示一简谐波在 t=0 时刻的波形图,波速υ =200m/s ,则图中O 点的振动加速度的表达式为()2A a 0.4 2 cos( t ) 2 23B a 0.4 2 cos( t )22C a 0.4 2cos(2 t ) 4.频率为 100Hz ,传播速度为 300m/s 的平面简谐波,波线上两 点振动的相位差为 3 ,则这两点相距( )A 2mB 2.19mC 0.5mD 28.6m5.一平面简谐波在弹性媒质中传播,媒质质元从平衡位置运动到最大位置处的过程中, ( )。
A 它的动能转换成势能B它的势能转换成动C 它从相邻的一段质元获得能量其能量逐渐增大Da20.4 2 cos(2 t2)υ (m/s)Bυ (m/s)DX(m)D 它把自己的能量传给相邻的一段质元,其能量逐渐减小6.在下面几种说法中,正确的说法是:()。
A 波源不动时,波源的振动周期与波动的周期在数值上是不同的B 波源振动的速度与波速相同C 在波传播方向上的任一质点振动位相总是比波源的位相滞后D 在波传播方向上的任一质点振动位相总是比波源的位相超前7.一质点作简谐振动,周期为T,当它由平衡位置向X 轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的时间为()。
A TBTCTDT4 12 6 88.在波长为λ的驻波中两个相邻波节之间的距离为()。
A λB 3 λ/4C λ/2D λ /49.在同一媒质中两列相干的平面简谐波的强度之比I1I 4是,则两列波的振幅之比是:()A A1 4 BA1 2 CA1 16 DA11A2 A2 A2 A2 410.有二个弹簧振子系统,都在作振幅相同的简谐振动,二个轻质弹簧的劲度系数K 相同,但振子的质量不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.下列关于简谐振动和简谐波的说法,正确的是
A.媒质中质点振动的周期一定和相应的波的周期相等
B.媒质中质点振动的速度一定和相应的波的波速相等
C.波的传播方向一定和媒质中质点振动的方向一致
D.横波的波峰与波谷在振动方向上的距离一定是质点振幅的两倍
2.做简谐振动的单摆摆长不变,若摆球质量增加为原来的4倍,摆球经过平衡位置时速度减小为原来的1/2,则单摆振动的
A.频率、振幅都不变B.频率、振幅都改变
C.频率不变、振幅改变D.频率改变、振幅不变
3.家用洗衣机在正常脱水时较平稳,切断电源后,洗衣机的振动先是变得越来越剧烈,然后逐渐减弱。
对这一现象,下列说法正确的是
A.正常脱水时,洗衣机脱水缸的运转频率比洗衣机的固有频率大
B.正常脱水时,洗衣机脱水缸的运转频率比洗衣机的固有频率小
C.正常脱水时,洗衣机脱水缸的运转频率等于洗衣机的固有频率
D.当洗衣机的振动最剧烈时,脱水缸的运转频率恰好等于洗衣机的固有频率
4.两个振动情况完全一样的波源S1、S2相距6m,它们在空间产生的干涉图样如图所示,图中实线表示振动加强的区域,虚线表示振动减弱的区域,下列说法正确的是
A.两波源的振动频率一定相同
B.虚线一定是波谷与波谷相遇处
C.两列波的波长都为2m
D.两列波的波长都为1m
5.频率一定的声源在空气中向着静止的接收器匀速运动。
以u表示声源的速度,V表示声波的速度(u<V),v表示接收器接收到的频率。
若u增大,则
A.v增大,V增大 B. v增大,V不变
C. v不变,V增大
D. v减少,V不变
6.如图所示,沿x轴正方向传播的一列简谐横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是
A.图示时刻质点b的加速度将减小
B.从图示时刻开始,经过0.01s,质点a通过的路程为0.4m
C.若此波遇到另一列波并发生稳定干涉现象,则另一列波的频率为50Hz
D.若该波传播中遇到宽约4m的障碍物能发生明显的衍射现象
7.一列沿x轴正方向传播的简谐横波,周期为0.50s。
某一时刻,离开平衡位置的位移都相等的各质点依次为P1,P2,P3,……。
已知P1和P2之间的距离为20cm,P2和P3之间的距离为80cm,则P1的振动传到P2所需的时间为
A.0.50s
B.0.13s
C.0.10s
D.0.20s
8.弹性绳沿x轴放置,左端位于坐标原点,用手握住绳的左端,当t
=0时使其开始沿y轴做振幅为8cm的简谐振动,在t=0.25s时,绳
上形成如图所示的波形,则该波的波速为___________cm/s,t=
___________时,位于x=45cm的质点N恰好第一次沿y轴正向通过
平衡位置。
9.在t=0时刻,质点A开始做简谐运动,其振动图象如图乙所示。
质点A振
动的周期是s;t=8s时,质点A的运动沿y轴的方向(填“正”
或“负”);质点B在波动的传播方向上与A相距16m,已知波的传播速度为
2m/s,在t=9s时,质点B偏离平衡位置的位移是cm。
10. 同一音叉发出的声波同时在水和空气中传播,某时刻的波形曲线见图,则反映声波在水中传播的波形是 ;反映声波在空气中传播的
波形是
11.某质点做简谐运动,其位移随时间变化的关系式为t A x 4π
sin =,则质点
A.第1 s 末与第3 s 末的位移相同
B.第1 s 末与第3 s 末的速度相同
C.3 s 末至5 s 末的位移方向都相同
D.3 s 末至5 s 末的速度方向都相同
12.图中实线和虚线分别是x 轴上传播的一列简谐横波在t =0和t =0.03s
时刻的波形图,x =1.2m 处的质点在t =0.03s 时刻向y 轴正方向运动,则
A .该波的频率可能是125Hz
B .该波的波速可能是10m/s
C .t =0时,x =1.4m 处质点的加速度方向沿y 轴正方向
D 各质点在0.03s 内随波迁移0.9m
13.已知:一简谐横波在某一时刻的波形图如图所示,图中位于a 、b
两处的质元经过四分之一周期后分别运动到a′、b′处。
某人据此做
出如下判断:①可知波的周期,②可知波的传播速度,③可知波的
传播方向,④可知波的波长。
其中正确的是
A.①④
B.②④
C.③④
D.②③
14.一简谐机械波沿x 轴正方向传播,周期为T ,波长为λ。
若在x=0处
质点的振动图像如右图所示,则该波在t=T/2时刻的波形曲线为
15.如图所示为一简谐波在t=0时刻的波形图,介质中的质点P 做简谐运
动的表达式为y =A sin5πt ,求该波的速度,并画出t=0.3s 时的波形图(至少
画出一个波长)
16.一列简谐横波沿x 轴传播,周期为T ,t=0时刻的波形如图所示.此时平衡位置位于x=3 m 处的质点正在向上运动,若a 、b 两质点平衡位置的坐标分别为x a =2.5 m, x b =5.5 m,则
A.当a 质点处在波峰时,b 质点恰在波谷
B.t=T/4时,a 质点正在向y 轴负方向运动
C.t=3T/4时,b 质点正在向y 轴负方向运动
D.在某一时刻,a 、b 两质点的位移和速度可能相同
17.图示为一列沿x轴负方向传播的简谐横波,实线为t=0时刻的波形图,虚线为t=0.6 s时的波形图,波的周期T>0.6 s,则
A.波的周期为2.4 s
B.在t=0.9s时,P点沿y轴正方向运动
C.经过0.4s,P点经过的路程为4m
D.在t=0.5s时,Q点到达波峰位置
18.一列横波沿x轴正向传播,a,b,c,d为介质中的
沿波传播方向上四个质点的平衡位置。
某时刻的波形如图1
所示,此后,若经过3/4周期开始计时,则图2描述的是
A.a处质点的振动图像B.b处质点的振动图像
C.c处质点的振动图像D.d处质点的振动图像
19. 如右图,一列简谐横波沿x轴正方向传播,实线和虚线分别表示t1=0和t2=0.5s(T>0.5s)时的波形,能正确反映t3=7.5s时波形的是图
20.一列间谐横波沿直线由A向B传播,A、B相距0.45m,右图是A处质点
的振动图像。
当A处质点运动到波峰位置时,B处质点刚好到达平衡位置且
向y轴正方向运动,这列波的波速可能是
A.4.5/s B . 3.0m/s C . 1.5m/s D .0.7m/s
21.一列简谐横波在某一时刻的波形图如图1所示,图中P、Q两质点的横坐标分别为x=1.5m和x=4.5m。
P点的振动图像如图2所示。
在下列四幅图中,Q点的振动图像可能是
22.图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1 m处的质点,Q是平衡位置为x=4 m 处的质点,图乙为质点Q的振动图象,则
A.t=0.15s时,质点Q的加速度达到正向最大
B.t=0.15s时,质点P的运动方向沿y轴负方向
C.从t=0.10s到t=0.25s,该波沿x轴正方向传播了6 m
D.从t=0.10s到t=0.25s,质点P通过的路程为30 cm
23.有一种示波器可以同时显示两列波形。
对于这两列波,显示屏上横向每格代表的时间间隔相同。
利用此中示波器可以测量液体中的声速,实验装置的一部分如图1所示:管内盛满液体,音频信号发生器所产生的脉冲信号由置于液体内的发射器发出,被接受器所接受。
图2为示波器的显示屏。
屏上所显示的上、下两列波形分别为发射信号与接受信号。
若已知发射的脉冲信号频率为f=2000H Z,发射器与接收器的距离为s=1.30m,求管内液体中的声速。
(已知所测声速应在1300~1600m/s之间,结果保留两位有效数字。
)
24. 如图,一列沿x轴正方向传播的简谐横波,振幅为4cm,波速为2m/s,在波的传播方向上两质点A、B 的平衡位置相距0.8m(小于一个波长)。
当质点A在波谷位置时,质点B在x轴上方与x轴相距2cm的位置,则()
A.此波的波长可能为1.2m
B.此波的周期可能为1.2s
C.从此时刻起经过0.7s,B点可能在波谷位置
D.从此时刻起经过0.7s,B点可能在波峰位置
25、一列简谐横波在t=0时刻的波形如图中的实线所示,t=0.02s时刻的波形如图中虚线所示。
若该波的周期T大于0.02s,则该波的传播速度可能是
A.2m/s
B.3m/s
C.4m/s
D.5m/s。
