厦门大学大学物理第二学期期末习题集(振动与波习题)

合集下载

《大学物理》期末考试复习题(振动与波)

）
（A） 2 ；
答案：（D）
（B）
m1 m2
2
；
（C）
m2 m1
2
；
（D） 2
m2 . m1
一物体作简谐振动，振动方程为
x
A cos(t
1 4
) 。在
t = T/4（T
为周期）时刻，物体的
加速度为 ( )
(A)
2 2
A 2
；
(B)
2 2
A 2 ；
(C)
3 2
A 2
；
(D)
3 2
A 2
。
一弹簧振子，当把它水平放置时，它作简谐振动。若把它竖直放置或放在光滑斜面上，试判
一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的 1/4 时，其动能为振动总能量的
(A) 7/16 ； (B) 9/16 ； (C) 11/16 ； (D) 15/16 。 []
答案：（D）
第十章波动
10-1 机械波的几个概念
10-2 平面简谐波的波函数
如图所示，有一平面简谐波沿 x 轴负方向传播，
断下列情况正确的是
（A）竖直放置作简谐振动，在光滑斜面上不作简谐振动；
（B）竖直放置不作简谐振动，在光滑斜面上作简谐振动；
（C）两种情况都作简谐振动；
（D）两种情况都不作简谐振动。
[]
竖直放置放在光滑斜面上
答案：（C）
同一弹簧振子悬挂相同的质量，分别按如图（a）、（b）、（c）所示的三种方式放置，摩擦力都
(A) 曲线 3，1，2 分别表示 x，v，a 曲线； (B) 曲线 2，1，3 分别表示 x，v，a 曲线； (C) 曲线 1，2，3 分别表示 x，v，a 曲线； (D) 曲线 2，3，1 分别表示 x，v，a 曲线.

大学物理振动与波练习题与答案

大学物理振动与波练习题与答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第二章振动与波习题答案12、一放置在水平桌面上的弹簧振子，振幅2100.2-⨯=A 米，周期50.0=T 秒，当0=t 时 (1) 物体在正方向的端点；(2) 物体在负方向的端点；(3) 物体在平衡位置，向负方向运动； (4) 物体在平衡位置，向正方向运动。

求以上各种情况的谐振动方程。

【解】：π=π=ω45.02 )m ()t 4cos(02.0x ϕ+π=， )s /m ()2t 4cos(08.0v π+ϕ+ππ=(1) 01)cos(=ϕ=ϕ，， )m ()t 4cos(02.0x π=(2) π=ϕ-=ϕ，1)cos(， )m ()t 4cos(02.0x π+π=(3) 21)2cos(π=ϕ-=π+ϕ，， )m ()2t 4cos(02.0x π+π= (4) 21)2cos(π-=ϕ=π+ϕ，， )m ()2t 4cos(02.0x π-π=13、已知一个谐振动的振幅02.0=A 米，园频率πω4=弧度／秒，初相2/π=ϕ。

(1) 写出谐振动方程；(2) 以位移为纵坐标，时间为横坐标，画出谐振动曲线。

【解】：)m ()2t 4cos(02.0x π+π= ， )(212T 秒=ωπ=15、图中两条曲线表示两个谐振动(1) 它们哪些物理量相同，哪些物理量不同? (2) 写出它们的振动方程。

【解】：振幅相同，频率和初相不同。

虚线： )2t 21cos(03.0x 1π-π= 米实线： t cos 03.0x 2π= 米16、一个质点同时参与两个同方向、同频率的谐振动，它们的振动方程为t 3cos 4x 1= 厘米)32t 3cos(2x 2π+= 厘米试用旋转矢量法求出合振动方程。

【解】：)cm ()6t 3cos(32x π+=17、设某一时刻的横波波形曲线如图所示，波动以1米／秒的速度沿水平箭头方向传播。

大学物理习题集(下,含解答)

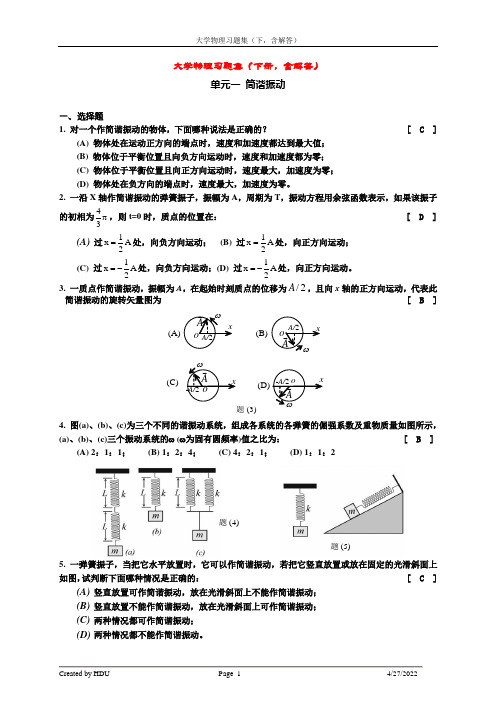
大学物理习题集（下册，含解答）单元一简谐振动一、选择题1. 对一个作简谐振动的物体，下面哪种说法是正确的？ [ C ](A) 物体处在运动正方向的端点时，速度和加速度都达到最大值； (B) 物体位于平衡位置且向负方向运动时，速度和加速度都为零； (C) 物体位于平衡位置且向正方向运动时，速度最大，加速度为零；(D) 物体处在负方向的端点时，速度最大，加速度为零。

2. 一沿X 轴作简谐振动的弹簧振子，振幅为A ，周期为T ，振动方程用余弦函数表示，如果该振子的初相为43π，则t=0时，质点的位置在： [ D ](A) 过1x A 2=处，向负方向运动； (B) 过1x A 2=处，向正方向运动；(C) 过1x A 2=-处，向负方向运动；(D) 过1x A 2=-处，向正方向运动。

3. 一质点作简谐振动，振幅为A ，在起始时刻质点的位移为/2A ，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为 [ B ]x o A x ω(A) A/2 ω (B) (C)(D)o ooxxxA x ω ωAxAxA/2 -A/2 -A/2 (3)题4. 图(a)、(b)、(c)为三个不同的谐振动系统，组成各系统的各弹簧的倔强系数及重物质量如图所示，(a)、(b)、(c)三个振动系统的ω (ω为固有圆频率)值之比为： [ B ](A) 2：1：1； (B) 1：2：4； (C) 4：2：1； (D) 1：1：25. 一弹簧振子，当把它水平放置时，它可以作简谐振动，若把它竖直放置或放在固定的光滑斜面上如图，试判断下面哪种情况是正确的： [ C ](A) 竖直放置可作简谐振动，放在光滑斜面上不能作简谐振动；(B) 竖直放置不能作简谐振动，放在光滑斜面上可作简谐振动； (C) 两种情况都可作简谐振动； (D) 两种情况都不能作简谐振动。

(4)题(5)题6. 一谐振子作振幅为A 的谐振动，它的动能与势能相等时，它的相位和坐标分别为： [ C ]2153(A),or ;A;(B),;A;3326623223(C),or ;A;(D),;A442332ππ±±π±±±π±ππ±±π±±±π±7. 一质点沿x 轴作简谐振动，振动方程为 10.04cos(2)3x t ππ=+（SI ），从t = 0时刻起，到质点位置在x = -0.02 m 处，且向x 轴正方向运动的最短时间间隔为 [ D ](A)s 81； (B) s 61； (C) s 41； (D) s 218. 图中所画的是两个简谐振动的振动曲线，这两个简谐振动叠加后合成的余弦振动的初相为[ C ]xtOx 1x 2(8)题(A) π23； (B) π； (C) π21 ； (D) 0二、填空题9. 一简谐振动用余弦函数表示，振动曲线如图所示，则此简谐振动的三个特征量为： A=10cm , /6rad /s =ωπ，/3=φπ10. 用40N 的力拉一轻弹簧，可使其伸长20 cm 。

C1(振动与波答案)

u
C1
解: 动力学表征式： F kx
运动学表征式： y A c os[ ( t
x
x
)]
u ：波沿传播方向传播距离落后的时间 u
x
u

：波沿传播方向传播距离落后的相位。
振动波动练习题（二）三、1
大学物理练习册振动波动
如图所示，以P点在平衡位置向正方向运动作为计时零点，已知圆频率为ω，振幅为A，简谐波以速度u向轴的正方向传播，试求：（1）P点的振动方程。（2）波动方程 u P · 解: t 0, x p 0, v p 0 p O
5 x B 5 m , B 点的振动方程： y B 5 c os t 20 x B 为原点的波动方程： y A 5 c os t 20 4 5
10m O A (a) 5m B -5 (b) O 0.5 1.5 t/s
2 3
C1
Ｂ
Ek 1 2
3 8
Ｃ
2
8 27
Ｄ
E k1
27 32
解：
kA
1 2
kx
2
4 9
kA
2
Ek2
3 8
kA
2
E k 2 / E k 1 27 : 32
答案：D
振动波动练习题（一）二、1
大学物理练习册振动波动
如图所示，有一条简谐振动曲线，请写出：振幅A ＝ _____cm，周期T＝_____s，圆频率ω＝______，初相位φo＝______，振动表达式x =_______cm，振动速度表达式υ＝_______ cm/s，振动加速度表达式a ＝___________cm/s2，t ＝3s的相位______。

大学物理振动与波练习题解

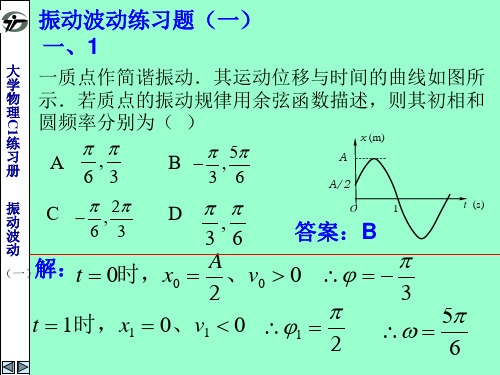
振动与波练习题2005一、填空题1.一物体作简谐振动，振动方程为x = A cos (ωt +π/ 4 )。

在t =T / 4 (T 为周期)时刻，物体的加速度为 .2.一质点沿x 轴作简谐振动，振动方程为x = 4×10－2 cos (2πt + π31) (SI) 。

从t = 0 时刻起，到质点位置在x = －2 cm 处，且向x 轴正方向运动的最短时间间隔为 0t =时，03πφ=；t 时刻，20x cm υ=->且43πφ所以＝。

433t ππωπ∆=-=由可得0.5()2t s ππωπ∆===3.已知两个简谐振动曲线如图1所示。

x 1的位相比x 2的位相为 B 。

(A) 落后π/2 （B ）超前π/2 (C) 落后π (D) 超前π4.一质点作简谐振动，周期为T 。

质点由平衡位置向X 轴正方向运动时，由平衡位置到二分之一最大位移这段路程所需要的时间为2222sin(/4)sin(/4)2cos(/4)cos(/4)/4112,222dx A t A t dt T d a A t A t dt T t T A a A πυωωπωπυπωωπωπυωω=-+=-+=-+=-+==＝＝代入得＝－解：由旋转矢量图可知6πϕ＝∆，所以1226TTt==∆=∆ππωϕ5.一平面简谐波，沿x轴负方向传播。

圆频率为ω，波速为u 。

设t＝T/4时刻的波形如图2所示，则该波的表达式为。

由t = 0的旋转矢量图可知：y0=－A，φπ=O点振动方程cos()y A tωπ=+波动方程：cos()xy A tuωπ⎡⎤=++⎢⎥⎣⎦6.当机械波在媒质中传播时，一媒质质元的最大变形量发生在位置处。

平衡位置处7.如图3所示两相干波源S1和S2相距λ/4，（λ为波长）S1的位相比S2的位相超前π/2,在S1，S2的连线上，S1外侧各点（例如P点）两波引起的两谐振动的位相差是.解：P点情况()21211222()2242r r S P S Pπππϕϕλλλπππλ---+=+=+=8.一质点作简谐振动。

大学物理习题及解答(振动与波、波动光学)

1．有一弹簧，当其下端挂一质量为m 的物体时，伸长量为9.8 ⨯10－2 m 。

假如使物体上下振动，且规定向下为正方向。

〔1〕t =0时，物体在平衡位置上方8.0 ⨯10－2 m处，由静止开始向下运动，求运动方程。

〔2〕t = 0时，物体在平衡位置并以0.60m/s 的速度向上运动，求运动方程。

题1分析：求运动方程，也就是要确定振动的三个特征物理量A 、ω，和ϕ。

其中振动的角频率是由弹簧振子系统的固有性质〔振子质量m 与弹簧劲度系数k 〕决定的，即m k /=ω，k 可根据物体受力平衡时弹簧的伸长来计算；振幅A 和初相ϕ需要根据初始条件确定。

解：物体受力平衡时，弹性力F 与重力P 的大小相等，即F = mg 。

而此时弹簧的伸长量m l 2108.9-⨯=∆。

如此弹簧的劲度系数l mg l F k ∆=∆=//。

系统作简谐运动的角频率为1s 10//-=∆==l g m k ω〔1〕设系统平衡时，物体所在处为坐标原点，向下为x 轴正向。

由初始条件t = 0时，m x 210100.8-⨯=，010=v 可得振幅m 100.8)/(2210102-⨯=+=ωv x A ；应用旋转矢量法可确定初相πϕ=1。

如此运动方程为])s 10cos[()m 100.8(121π+⨯=--t x〔2〕t = 0时，020=x ，120s m 6.0-⋅=v ，同理可得m 100.6)/(22202022-⨯=+=ωv x A ，2/2πϕ=；如此运动方程为]5.0)s 10cos[()m 100.6(122π+⨯=--t x2．某振动质点的x －t 曲线如下列图，试求：〔1〕运动方程；〔2〕点P 对应的相位；〔3〕到达点P 相应位置所需要的时间。

题2分析：由运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题。

此题就是要通过x －t 图线确定振动的三个特征量量A 、ω，和0ϕ，从而写出运动方程。

曲线最大幅值即为振幅A ；而ω、0ϕ通常可通过旋转矢量法或解析法解出，一般采用旋转矢量法比拟方便。

厦门大学大学物理B(下)期末复习

章节
物理图象
要点简谐振动定义： F kx （线性回复力）
d 2x 2 x 0 （运动方程） 2 dt
习题证明某振动为简谐振动，求振动圆频率习题：4-3、4-4
振动与波动
1 简谐振动
x A cos(t ) （振动式）
简谐振动能量： E Ek E p （弹簧振子）
波的强度： I I1 I 2 2 I1 I 2 cos 干涉相长条件： 2m m 0,1,2,... 干涉相消条件： ( 2m 1)
9 惠更斯原理，波的衍射、反射与折射
反射定律：i=i’ 折射定律：sini/sinr=u1/u2 半波反射和全波反射：发生条件由入射波和反射波干涉得到驻波；驻波的波节和波腹概念：光程、光程差相位差： 20 10 2 π

劈尖干涉：习题：12-5、12-6 （不规则劈尖的条纹移动）
劈
尖
干
涉
：
条纹间距： l 零级暗纹
2n
牛顿环：习题：12-7 （其它形式的环形条纹等厚干涉）
r2 牛顿环： 2nd ; d 2 2R

零级暗纹
牛顿环：
4 光的衍射现象
概念：菲涅尔衍射与夫琅和费衍射、衍射与干涉理解：透镜的作用以及透镜不引起附加的光程差
3 薄膜干涉
等倾干涉:
等倾干涉： 2d n2 n1 sin 2 i
2 2

2
（某些情况下不考虑半波损失）以下两类干涉都属于等厚干涉：
k 劈尖干涉： 2nd 2 ( 2k 1) 2
等倾干涉：习题：12-3、12-4 （增透膜和增反膜、肥皂膜）（波长变化引起光强消长）

振动和波动要点习题

振动和波一、选择题1.（3分,答D ）已知一平面简谐波的表达式为cos()y A at bx =-（,a b 为正值常量），则（A ）波的频率为a （B ）波的传播速度为/b a （C ）波长为/b π （D ）波的周期为2/a π2.（本题3分，答B ）一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为A 21，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为［］3. （3分,答B ）一质点在x 轴上作简谐振动，振幅A =4cm ，周期T =2s ，其平衡位置取作坐标原点，若t =0时刻质点第一次通过x =-2cm 处，且向x 轴负方向运动，则质点第二次通过x =-2cm 处的时刻为(A) 1s (B) (2/3)s (C)(4/3)s (D) 2s4. （3分,答D ）一劲度系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为T 1．若将此弹簧截去一半的长度，下端挂一质量为m 21的物体，则系统振动周期T 2等于 (A) 2 T 1 (B) T 1(C)T 12/ (D) T 1 /2 (E) T 1 /45.（本题3分，答A ）轴一简谐波沿Ox 轴正方向传播，t = 0 时刻的波形曲线如图所示，已知周期为 2 s ，则 P 点处质点的振动速度v 与时间t 的关系曲线为：6.（3分，答B ）一平面简谐波在弹性媒质时，某一时刻媒质中某质元在负最大位移处，则它的能量是（A ）动能为零势能最大（B ）动能为零势能为零（C ）动能最大势能最大（D ）动能最大势能为零v (m/s)O 1 t (s)ωA(C)· v (m/s)O1 t (s)ω A(A)·1 v (m/s)t (s)(D)O－ω A1 v (m/s) t (s)－ωA(B) O ··x o A x A 21 ω(A)A 21ω(B) A 21-(C) (D)o oo A 21-xxxAxAxAxω ω2O 1 y (m)x (m)t =0 A u图17.（3分，答D ）沿相反方向传播的两列相干波，其波动方程为y 1=A cos2π (νt －x /λ)y 2=A cos2π (νt + x /λ) 叠加后形成的驻波中,波节的位置坐标为(A)x =±k λ.(B)x =±k λ/2 .(C)x =±(2k +1)λ/2 .(D)x =±(2k +1)λ/4 . 其中k = 0 , 1 , 2 , 3…….8.（3分,答D ）如图所示，有一平面简谐波沿x 轴负方向传播，坐标原点O 的振动规律为y =A cos(ω t+φ0)，则B 点的振动方程为（A ）y =A cos[ω t-(x/u )+φ0] （B ）y =A cos ω[ t+(x/u )] （C ）y =A cos{ω [t-(x/u ) ]+φ0} （D ）y =A cos{ω[ t+(x/u ) ]+φ0}9.（3分,答D ）一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中：（A ）它的动能转换成势能. （B ）它的势能转换成动能. （C ）它从相邻的一段质元获得能量，其能量逐渐增大. （D ）它把自己的能量传给相邻的一段质元，其能量逐渐减小. 10.（3分，答B ）在波长为λ的驻波中，两个相邻波腹之间的距离为（A ）λ/4 （B ）λ/2 （C ）3λ/4 （D ）λ11.（3分,答C ）某时刻驻波波形曲线如图所示，则a 、b 两点振动的相位差是（A ）0 （B ）/2π （C ）π （D ）5/4π12.（本题3分，答B)在驻波中，两个相邻波节间各质点的振动（A ）振幅相同，相位相同（B ）振幅不同，相位相同（C ）振幅相同，相位不同（D ）振幅不同，相位不同二、填空题1. （3分）已知一个简谐振动的振幅A=2cm, 角频率14s ωπ-=，以余弦函数表达式运动规律时的A －Ayxλ λ/2O ··a b · · · · · · · · ··x 2A A/2x 1初相12φπ=，试画出位移和时间的关系曲线（振动图线） 2.（4分）两个简谐振动方程分别为x 1=Acos(ω t ) ；x 2=Acos(ω t +π/3) 在同一坐标上画出两者的x-t 曲线.3. (3分）有两相同的弹簧，其劲度系数均为k .（1）把它们串联起来，下面挂一个质量为m 的重物，此系统作简谐振动的周期为；（2）把它们并联起来，下面挂一个质量为m 的重物，此系统作简谐振动的周期为.[答案：（1）22m k π,（2）22mkπ] 4.(4分)一弹簧振子系统具有1.0J 的振动能量，0.10m 的振幅和1.0m/s 的最大速率，则弹簧的劲度系数，振子的振动频率.[答案：2210N/m,1.6Hz ⨯]5.（3分）一平面机械波沿x =-1m 轴负方向传播，已知处质点的振动方程cos()y A t ωϕ=+，若波速为u ，求此波的波函数.[答案：cos{[(1)/]}y A t x u ωϕ=+++]6.（3分）一作简谐振动的振动系统，振子质量为2kg ，系统振动频率为1000Hz ，振幅为0.5cm ，则其振动能量为.（答案：29.9010J ⨯ ）7.（3分）两个同方向同频率的简谐振动211310cos(),3x t ωπ-=⨯+221410cos()(SI)6x t ωπ-=⨯-，它们的合振幅是. （答案：2510m -⨯ ）8.（3分）一平面简谐波沿Ox 轴正方向传播，波动表达式为cos[(/)/4]y A t x u ωπ=-+，则1x L =处质点的振动方程是；2x L =-处质点的振动和1x L =处质点的振动相位差为21φφ-=. （答案：1cos[(/)/4]y A t L u ωπ=-+，12()/L L u ω+）9.（5分）一余弦横波以速度u 沿x 轴正向传播，t 时刻波形曲线如图所示.试分别指出图中A ，B ，C 各质点在该时刻的运动方向.A 向下，B 向上，C 向上.10. （本题4分）一平面简谐波的表达式cos (/)cos(/)y A t x u A t x u ωωω=-=-其中/x u 表示，/x u ω表示，y 表示.[答案：波从坐标原点传至x 处所需时间（2分），x 处质点此原点处质点滞后的相位（1分），t 时刻x 处质点的振动位移（1分）]11. （本题3分）如图所示，两相干波源S 1和S 2相距为3λ/4，λ为波长，设两波在S 1 S 2连O Cyxu · · · A B线上传播，它们的振幅都是A ，并且不随距离变化，已知在该直线上S 1左侧各点的合成波强度为其中一个波强度的4倍，则两波源应满足的相位条件是__π/2_ 12. （3分）一驻波的表达式为y =2A cos(2πx/λ) cos(2πνt )，两个相邻波腹之间的距离是.（答案：λ/2）三、计算题1. （5分）一质点作简谐运动，其振动方程为110.24cos()()23x t SI ππ=+，试用旋转矢量法求出质点由初始状态运动到x =-0.12 m ，v <0的状态所经过的最短时间．解：旋转矢量如图所示．图3分由振动方程可得π21=ω，π=∆31φ1分667.0/=∆=∆ωφt s 1分2（本题10分）一质量m =0.25kg 的物体，在弹簧的力作用下沿x 轴运动，平衡位置在原点，弹簧的劲度系数k =25N/m.（1）求振动的周期T 和频率ω. （2）如果振幅A =15cm ，t =0时物体位于x =7.5cm 处，且物体沿x 轴反方向运动，求初速度v 0及初相φ.（3）写出振动的数值表达式. 解：（1）12/10k m s ωπ-== (2分)2/0.63T s πω== (1分)(2) A=15cm ，在t =0时，07.5cm x =，00v < 由2200(/)A x v ω=+得2200 1.3m/s v A x ω=--=- (2分)100(/)/3/3tg v x φωππ-=-=或400,/3x φπ>∴=(3分)（3）21510cos(10/3)(SI)x t π-=⨯+(2分)3.（10分）在一轻弹簧下端悬挂0100g m =砝码时，弹簧伸长8cm. 现在这根弹簧下端悬挂0250g m =物体，构成弹簧振子，将物体从平衡位置向下拉动4cm ，并给以向上的21cm/s 的初速度（令这时t=0）.选x 轴向下，求振动方程的数值式.解：k = m 0g / ∆l 25.12N/m 08.08.91.0=⨯=N/mx (m) ωωπ/3π/3t = 0t0.12 0.24 -0.12 -0.24 OAAO xS 1S 211s 7s 25.025.12/--===m k ω(2分) 5cm )721(4/2222020=+=+=ωv x A cm (2分) 4/3)74/()21()/(tg 00=⨯--=-=ωφx v ，φ = 0.64 rad (3分))64.07cos(05.0+=t x (SI) (1分)4．（8分）在一竖直轻弹簧的下端悬挂一小球，弹簧被拉长0 1.2cm l =而平衡.再经拉动后，该小球在竖直方向作振幅为2cm A =的振动，试证此振动为简谐振动；选小球在正最大位移处开始计时，写出此振动的数值表达式.解：设小球的质量为m ，则弹簧的劲度系数（图参考上题）0/k mg l = 选平衡位置为原点，向下为正方向. 小球在x 处时，根据牛顿第二定律得202()d x mg k l x m dt -+=将k 代入整理后得 220d x g x dt l =-所以振动为简谐振动，其角频率为0/28.589.1(rad/s)g l ωπ===(5分)设振动表达式为 c o s ()x A t ωφ=+ 由题意：t=0时，200210m0x A v -==⨯=解得：0φ=2210cos(9.1)x t π-∴=⨯m (3分)5.(10分)在一轻弹簧下端悬挂m 0=100g 的砝码时,弹簧伸长8cm,现在这根弹簧下端悬挂m =250g 的物体, 构成弹簧振子. 将物体从平衡位置向下拉动4cm,并给以向上的21cm/s 的初速度(这时t =0) ，选x 轴向下，求振动方程的数值式. 解：物体受向下的重力和向上的弹性力.k=m 0g/∆l , x 0=4×10-2m, v 0=-21×10-2m/sω=()m l g m m k Δ0==7s -1A=22020ω/v x +=5×10-2m因A cos ϕ=4×10-2m, A sin ϕ=-v 0/ω=3×10-2m,有 ϕ=0.64rad 所以x=5×10-2cos(7t +0.64) (SI)6.（本题5分）一质量为0.2kg 的质点作简谐振动，其振动方程为10.6cos(5)(SI)2x t π=-求：（1）质点的初速度；（2）质点在正向最大位移一半处所受的力.解：（1）003.0sin(5)()0, 3.0m/s 2dx v t SI t v dt π==--==（2分）（2）2F ma m x ==-ω12x A =时， 1.5N F =-（无负号扣1分）（3分） 7.（5分）一平面简谐波沿x 轴正方向传播，波速为1m/s ，在x 轴上某质点的振动频率为1Hz ，振幅为0.01m. t = 0时该质点恰好在正最大位移处，若以该质点的平衡位置为x 轴的原点. 求此一维简谐波的表达式.解. 0.01cos[2()](m)y t x =-π8.（本题10分）某质点作简谐振动，周期为2s ，振幅为0.06m ，t =0时刻，质点恰好处在负最大位移处，求（1）该质点的振动方程.（2）此振动以波速u =2m/s 沿x 轴正方向传播时，形成的一维简谐波的波动表达式，（以该质点的平衡位置为坐标原点）；（3）该波的波长. 解：（1）振动方程 00.06cos(2/2)0.06cos()(SI)y t t ππππ=+=+3分（2）0.06cos[((/))0.06cos[(/2))(SI)y t x u t x ππππ=-+=-+ 4分（3）波长4m uT λ==9.（10分）一列平面简谐波在以波速5m/s u =，沿x 轴正向传播，原点O 处质点的振动曲线如图所示.1）求解并画出25cm x =处质元的振动曲线 2）求解并画出3s t =时的波形曲线解：1）原点O 处质元的振动方程为211210cos(),(SI)22y t ππ-=⨯-(2分)波的表达式 (2分)211210cos((/5)),(SI)22y t x ππ-=⨯--x =25m 处质元的振动方程21210cos(3),(SI)2y t ππ-=⨯-振动曲线如右y-t 图 (2分)2）t=3s 时的波形曲线方程2210cos(/10),(SI)y x ππ-=⨯-(2分)波形曲线见右y-x 图 (2分)10.（10分）某质点作简谐振动，周期为2s ，振幅为0.6m ，t =0时刻，质点恰好处在负最大4O2 y(cm)t (s)2位移处，求（1）该质点的振动方程；（2）此振动以波速u =2m/s 沿x 轴正方向传播时，形成的一维简谐波的波动表达式，（以该质点的平衡位置为坐标原点）；（3）该波的波长.解：(1) 振动方程)22cos(06.00π+π=ty )cos(06.0π+π=t (SI) (3分) (2) 波动表达式])/(cos[06.0π+-π=u x t y (4分)])21(cos[06.0π+-π=x t (SI)(3) 波长4==uT λm (3分)11.（5分）如图所示，一简谐波向x 轴正向传播，波速0500/,1,u m s x m P ==点的振动方程为10.03cos(500)(SI)2y t ππ=-. （1）按图所示坐标系，写出相应的波的表达式；（2）在图上画出t=0时刻的波形曲线.解：(1) 2m )250/500(/===νλu m 波的表达式 ]/2)1(21500cos[03.0),(λπ--π-π=x t t x y110.03cos[500(1)2/2]0.03cos(500)(SI)22t x t x =π-π--π=π+π-π(3分)(2) t = 0时刻的波形曲线x x x y π=π-π=sin 03.0)21cos(03.0)0,( (SI) (2分)12.（10分）图示一平面余弦波在t = 0 时刻与t = 2 s 时刻的波形图(波向左传播)．已知波速为u ，波的周期大于2 s ，求(1) 坐标原点处介质质点的振动方程；(2) 该波的波动表达式．解：(1) 比较t = 0 时刻波形图与t = 2 s 时刻波形图，可知此波向左传播．在t = 0时刻，O 处质点φcos 0A =，φωsin 00A -=<v ，故2πφ-= 又t = 2 s ，O 处质点位移为)24cos(2/ππ-=νA A 所以244πππ-=-ν，ν = 1/16 Hz 振动方程为)28/cos(0ππ-=t A y (SI)(2) 波速u = 20 /2 m/s = 10 m/s,波长λ = u /ν = 160 m 波动表达式]21)16016(2cos[π-+π=x t A y (SI) x (m)uP y (m)O-2-112-0.030.03x (m)O160A y (m)8020t =0t =2 s2A。

大学物理-波动光学习题(包括振动、波动、波的干涉、光的干涉、光的衍射、光的偏振)

第四篇光学第一章振动一、选择题1. 一质点作简谐振动, 其运动速度与时间的关系曲线如下图。

假设质点的振动规律用余弦函数描述，那么其初相应为：[ ] (A)6π (B) 65π (C) 65π- (D) 6π- (E) 32π-2. 如下图，一质量为m 的滑块，两边分别与劲度系数为k 1和k 2的轻弹簧联接，两弹簧的另外两端分别固定在墙上。

滑块m 可在光滑的水平面上滑动，O 点为系统平衡位置。

现将滑块m 向左移动x0，自静止释放，并从释放时开始计时。

取坐标如下图，那么其振动方程为：[ ] ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos(A)⎥⎦⎤⎢⎣⎡++=πt k k m k k x x )(cos (B)21210⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (C)⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (D) ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos (E)3. 一质点在x 轴上作简谐振动，振幅A = 4cm ，周期T = 2s, 其平衡位置取作坐标原点。

假设t = 0时刻质点第一次通过x = -2cm 处，且向x 轴负方向运动，那么质点第二次通过x = -2cm 处的时刻为：[ ](A) 1s ; (B)s 32; (C) s 34; (D) 2s 。

4. 一质点沿y 轴作简谐振动，其振动方程为)4/3cos(πω+=t A y 。

与其对应的振动曲线是: [ ]5. 一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的：[ ](A)167; (B) 169; (C) 1611; (D) 1613; (E) 1615。

(A)-(B)(C)(D)-06. 图中所画的是两个简谐振动的振动曲线，假设这两个简谐振动可叠加，那么合成的余弦振动的初相为： [ ] π21(A) π(B) π23(C) 0(D)二、填空题1. 一简谐振动的表达式为)3cos(ϕ+=t A x ，0=t 时的初位移为0.04m, s -1，那么振幅A = ，初相位 =2. 两个弹簧振子的的周期都是0.4s, 设开始时第一个振子从平衡位置向负方向运动，经过0.5s 后，第二个振子才从正方向的端点开始运动，那么这两振动的相位差为。

(完整版)大学物理振动习题含答案

一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。

若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ ［］2．3002：两个质点各自作简谐振动，它们的振幅相同、周期相同。

第一个质点的振动方程为x 1 = A cos(ωt + α)。

当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。

则第二个质点的振动方程为：(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x ［］3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，振动角频率为ω。

若把此弹簧分割成二等份，将物体m 挂在分割后的一根弹簧上，则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 ［］4．3396：一质点作简谐振动。

其运动速度与时间的曲线如图所示。

若质点的振动规律用余弦函数描述，则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 ［］5．3552：一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2。

将它们拿到月球上去，相应的周期分别为1T '和2T '。

则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >' ［］ 6．5178：一质点沿x 轴作简谐振动，振动方程为)312cos(1042π+π⨯=-t x (SI)。

大学物理-习题-简谐振动和波-学生版

大学物理-习题-简谐振动和波-学生版一．选择题《机械振动和机械波》模块习题 1. 对一个作简谐振动的物体，下面哪种说法是正确的？---------------------------------- 【C 】 (A) 物体处在运动正方向的端点时，速度和加速度都达到最大值； (B) 物体位于平衡位置且向负方向运动时，速度和加速度都为零； (C) 物体位于平衡位置且向正方向运动时，速度最大，加速度为零； (D) 物体处在负方向的端点时，速度最大，加速度为零。

2. 一个质点作简谐运动，振幅为 A，在起始时刻质点的位移为- A ，且向 x 轴正方向运动， 2 代表此简谐运动的旋转矢量为---------------------------------------------------------------------【B 】3. 一质点沿 x 轴作简谐振动，振动方程为x = 0.04 cos(2p t +1 p ) （SI），从 t = 0 时刻起， 3 到质点位置在 x = -0.02 m 处，且向 x 轴正方向运动的最短时间间隔为--------- 【D 】 1 1 1 1 (A) s ； (B) s ； (C) s ； (D) s 8 64 2 4 一弹簧振子，振动方程为x=0.1cos(πt-π/3)·m，若振子从 t=0 时刻的位置到达 x=-0.05m处，且向 X 轴负向运动，则所需的最短时间为------------------------【D 】（A）s/3；（B） 5s/3；（C） s/2；（D） 1s。

1 5. 频率为 100 Hz，传播速度为 300 m/s 的平面简谐波，波线上距离小于波长的两点振动的相位差为 p ，则此两点相距 --------------------------------------------------------------【C 】 3 (A) 2.86 m (B) 2.19 m (C) 0.5m (D) 0.25 m T 6. 一平面简谐波，沿 x 轴负方向传播，角频率为ω，波速为 u．设t = 时刻的波形如图（a） 4 所示，则该波的表达式为---------------------------------------------------------------------【】é æ x ö ùé æ x ö p ù （A）y = A cos êw ç t - u ÷ + p ú （B） y= A cos êw ç t - u ÷ + 2 ú ë è ø û ë è ø û é æx ö p ù é æ x ö ù （C）y = A cos êw ç t + u ÷ - 2ú （D）y = A cos êw ç t + u ÷ + p ú ë è ø û ë èø û 7. 在简谐波传播过程中，沿传播方向相距为l/2 ，（l为波长）的两点的振动速度必定：【A 】 (A) 大小相同，而方向相反； (B) 大小和方向均相同； (C) 大小不同，方向相同； (D) 大小不同，而方向相反。

振动与波习题

k （弹簧振子：） m
2
3、能量特征
1 E k mv 2 2 1 m 2 A2 sin 2 ( t 0 ) 2 1 2 2 kA sin ( t 0 ) 2
1 2 E p kx 2
1 2 kA cos 2 ( t 0 ) 2
1 2 E E k E p kA 2
振动一、谐振子 1、运动学特征： 2 x(t ) A cos( t ) A cos( t ) (1) T 2
A：振幅 T: 周期

T
：圆频率
( t ) : 相位，它是反映质点在t时刻振动
状态的物理量。

: 初相, t＝0 时刻的位相。
A、φ由初始条件决定。
5
t
O
t=5
4. 一质点作简谐振动，其振动方程为出质点由初始状态运动到 x=-0.12m, v<0的状
态所经过的最短时间。 t 解： t=0
1 1 x 0.24cos( t （SI）试用旋转矢量法求 ) 2 3

1 3
3 t 2 t ( s) 3
y A o
传播方向
P
X
例题2. 一平面简谐波以波速u=0.5m/s沿x轴负方向传播, t=2s时刻的波形如图所示, 求波动方程.
y(m) 0.5 o 1
u 2 x(m)
2x 解： ) 设波动方程为: y A cos( t l
由图可得:l=2m, A=0.5m
=2= 2u/ l= /2
2
1 1 1 2 x 2 3 10 sin(4t ) 3 10 cos(4t ) 6 6 2 2 2 3 10 cos(4t ) 3 1 x x x

N考核《大学物理学》机械振动与机械波部分练习题(解答)

《大学物理学》机械振动与机械波部分练习题（解答）一、选择题1．一弹簧振子，当把它水平放置时，它作简谐振动。

若把它竖直放置或放在光滑斜面上，试判断下列情况正确的是（ C ）（A ）竖直放置作简谐振动，在光滑斜面上不作简谐振动；（B ）竖直放置不作简谐振动，在光滑斜面上作简谐振动；（C ）两种情况都作简谐振动；（D ）两种情况都不作简谐振动。

2．两个简谐振动的振动曲线如图所示，则有（ A ）（A ）A 超前/2π；（B ）A 落后/2π；（C ）B 超前/2π；（D ）B 落后/2π。

3．一个质点作简谐振动，周期为T ，当质点由平衡位置向x 轴正方向运动时，由平衡位置到二分之一最大位移这段路程所需要的最短时间为：（ D ）（A ）/4T ；（B ）/6T ；（C ）/8T ；（D ）/12T 。

4．分振动方程分别为13cos(50)4x t ππ=+和234cos(50)4x t ππ=+（SI 制）则它们的合振动表达式为：（ C ）（A ）5cos(50)4x t ππ=+；（B ）5cos(50)x t π=；（C ）115cos(50)27x t tg ππ-=++；（D ）145cos(50)23x t tg ππ-=++。

5．两个质量相同的物体分别挂在两个不同的弹簧下端，弹簧的伸长分别为1l ∆和2l ∆，且1l ∆=22l ∆，两弹簧振子的周期之比T 1：T 2为（ B ）（A ）2；（B ）2；（C ）1/2；（D ）2/1。

6．一个平面简谐波沿x 轴负方向传播，波速ｕ=10m/s 。

x =0处，质点振动曲线如图所示，则该波的表式为（A ）)2202cos(2πππ++=x t y m ；-（B ）)2202cos(2πππ-+=x t y m ；（C ）)2202sin(2πππ++=x t y m ；（D ）)2202sin(2πππ-+=x t y m 。

大学物理题库-振动与波动

振动与波动题库一、选择题（每题3分）1、当质点以频率ν 作简谐振动时，它的动能的变化频率为（）（A ） 2v（B ）v （C ）v 2 （D ）v 42、一质点沿x 轴作简谐振动，振幅为cm 12，周期为s 2。

当0=t 时, 位移为cm 6，且向x 轴正方向运动。

则振动表达式为（） (A)）（3cos 12.0ππ-=t x （B ））（3cos 12.0ππ+=t x （C ））（32cos 12.0ππ-=t x （D ））（32cos 12.0ππ+=t x3、有一弹簧振子，总能量为E ，如果简谐振动的振幅增加为原来的两倍，重物的质量增加为原来的四倍，则它的总能量变为（）（A ）2E （B ）4E （C ）E /2 （D ）E /4 4、机械波的表达式为()()m π06.0π6cos 05.0x t y +=，则（）（Ａ）波长为100 ｍ（Ｂ）波速为10 ｍ·ｓ-1（Ｃ）周期为1/3 ｓ（Ｄ）波沿x 轴正方向传播 5、两分振动方程分别为x 1=3cos (50πt+π/4) ㎝和x 2=4cos (50πt+3π/4)㎝，则它们的合振动的振幅为（）(A) 1㎝（B ）3㎝（C ）5 ㎝（D ）7 ㎝6、一平面简谐波，波速为μ=5 cm/s ，设t= 3 s 时刻的波形如图所示，则x=0处的质点的振动方程为（）(A) y=2×10－2cos (πt/2－π/2) (m)(B) y=2×10－2cos (πt + π) (m)(C) y=2×10－2cos(πt/2+π/2) (m)(D) y=2×10－2cos (πt －3π/2) (m)7、一平面简谐波，沿X 轴负方向传播。

x=0处的质点的振动曲线如图所示，若波函数用余弦函数表示，则该波的初位相为（）（A ）0 （B ）π (C) π /2 (D) － π /28、有一单摆，摆长m 0.1=l ，小球质量g 100=m 。

厦门大学大学物理第二学期期末习题集(振动与波习题)

；（2）插入的偏振片只需要与两个偏振化方向正交的偏振片中的任一偏振片的偏振化方向平行时，都能达到该结果；（3）无论如何放置都无法使最后通过的光强为
I0
2
如图，介质I和III为空气(n1=1.00)，II 为玻璃 (n2=1.732)，玻璃的两表面相互平行。一束自然光由介质I中以i角入射。若使I，II交界面上的反射光为线偏振光，求
10. 用波长=500nm的单色光垂直照射在由两块玻璃板（一端刚好接触成为劈棱）构成的空气劈尖上。劈尖角 =210-4rad。现在劈尖内充满折射率为n=1.40的液体。求从劈棱数起第5个明条纹在
x x 充入液体前后移动的距离。（参考答案：
5 5
1.607(mm) 。 x5
d y 2 2 dt dt
2
a
o
b
1题图
x
上式是简谐振动的微分方程,它的通解为: y A cos(t 0 ) 所以木块的运动是简谐振动.
振动周期:
m a T 2 2 gS g
2
t 0 时， x b 0
v0 0
振幅: A
y0 b a
2 y0
2

(n1 )t
P
A A A 2AA 1 2 cos (n1 )t 2A 2A 1 cos 1 cos 2
2 1 2 2
d2
O
)t （2）若使O点处光强为零，有 (n1 (2m1 ) 2 (2m1 ) t (m 0,1 , )
在可见光范围内，取k=2和k=3，计算出波长分别为674nm和404nm。
在可见光范围内，取k=2，计算出波长分别为505nm。
9. 在空气中垂直入射的白光从肥皂膜上反射，在可见光谱中630nm 处有一干涉极大，而在525nm处有一干涉极小，在这极大与极小之间没有另外的极小。假定膜的厚度是均匀的，求这膜的厚度。肥皂水的折射率看作与水相同，为1.33。

大学物理振动与波练习题与标准答案

第二章振动与波习题答案12、一放置在水平桌面上的弹簧振子，振幅2100.2-⨯=A 米，周期50.0=T 秒，当0=t 时 (1) 物体在正方向的端点；(2) 物体在负方向的端点；(3) 物体在平衡位置，向负方向运动；(4) 物体在平衡位置，向正方向运动。

求以上各种情况的谐振动方程。

【解】：π=π=ω45.02)m ()t 4cos(02.0x ϕ+π=， )s /m ()2t 4cos(08.0v π+ϕ+ππ=(1) 01)cos(=ϕ=ϕ，， )m ()t 4cos(02.0x π=(2) π=ϕ-=ϕ，1)cos(， )m ()t 4cos(02.0x π+π= (3) 21)2cos(π=ϕ-=π+ϕ，， )m ()2t 4cos(02.0x π+π= (4) 21)2cos(π-=ϕ=π+ϕ，， )m ()2t 4cos(02.0x π-π=13、已知一个谐振动的振幅02.0=A 米，园频率πω4=弧度／秒，初相2/π=ϕ。

(1) 写出谐振动方程；(2) 以位移为纵坐标，时间为横坐标，画出谐振动曲线。

【解】：)m ()2t 4cos(02.0x π+π= ， )(212T 秒=ωπ=15、图中两条曲线表示两个谐振动(1) 它们哪些物理量相同，哪些物理量不同?(2) 写出它们的振动方程。

【解】：振幅相同，频率和初相不同。

【解】：)cm ()6t 3cos(32x π+=17、设某一时刻的横波波形曲线如图所示，波动以1米／秒的速度沿水平箭头方向传播。

(1) 试分别用箭头表明图中A 、B 、C 、D 、E 、F 、H 各质点在该时刻的运动方向；(2) 画出经过1秒后的波形曲线。

大学物理期末复习题---填空-计算题

第4章振动与波动填空题（1）一质点在X 轴上作简谐振动，振幅A ＝4cm ，周期T ＝2s ，其平衡位置取作坐标原点。

若t ＝0时质点第一次通过x ＝－2cm 处且向x 轴负方向运动，则质点第二次通过x ＝－2cm 处的时刻为__ __s 。

[答案：23s ]（2）一水平弹簧简谐振子的振动曲线如题4.2(2)图所示。

振子在位移为零，速度为－ωA 、加速度为零和弹性力为零的状态，对应于曲线上的____________点。

振子处在位移的绝对值为A 、速度为零、加速度为－ω2A 和弹性力为－KA 的状态，则对应曲线上的____________点。

习题4.2(2) 图[答案：b 、f ； a 、e]（3）一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点，已知周期为T ，振幅为A 。

（a ）若t=0时质点过x=0处且朝x 轴正方向运动，则振动方程为x=___________________。

（b ）若t=0时质点过x=A/2处且朝x 轴负方向运动，则振动方程为x=_________________。

[答案：cos(2//2)x A t T ππ=−； cos(2//3)x A t T ππ=+]（4）一横波的波动方程是))(4.0100(2sin 02.0SI x t y −=π，则振幅是____，波长是____，频率是____，波的传播速度是____。

[答案：0.02;2.5;100;250/m m Hz m s ]（5）产生机械波的条件是和。

[答案：波源；有连续的介质]（6）两列波叠加产生干涉现象必须满足的条件是，和。

[答案：频率相同，振动方向相同，在相遇点的位相差恒定。

]计算题振动4.3 质量为kg 10103−⨯的小球与轻弹簧组成的系统，按20.1cos(8)(SI)3x t ππ=+的规律作谐振动，求：(1)振动的周期、振幅和初位相及速度与加速度的最大值；(2)最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动能与势能相等? (3)s 52=t 与s 11=t 两个时刻的位相差；解：(1)设谐振动的标准方程为)cos(0φω+=t A x ，相比较则有：3/2,s 412,8,m 1.00πφωππω===∴==T A 又 πω8.0==A v m 1s m −⋅ 51.2=1s m −⋅2.632==A a m ω2s m −⋅(2) 0.63N m m F ma ==J 1016.32122−⨯==m mv E J 1058.1212−⨯===E E E k p当p k E E =时，有p E E 2=，即)21(212122kA kx ⋅= ∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=−=−=∆t t4.4 一质量为kg 10103−⨯的物体作谐振动，振幅为cm 24，周期为s 0.4，当0=t 时位移为cm 24+．求：(1)s 5.0=t 时，物体所在的位置及此时所受力的大小和方向； (2)由起始位置运动到cm 12=x 处所需的最短时间； (3)在cm 12=x 处物体的总能量．解：由题已知 s 0.4,m 10242=⨯=−T A∴ 1s rad 5.02−⋅==ππωT又，0=t 时，0,00=∴+=φA x 故振动方程为m )5.0cos(10242t x π−⨯=(1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=−t x πN102.417.0)2(10103232−−⨯−=⨯⨯⨯−=−=−=πωxm ma F方向指向坐标原点，即沿x 轴负向． (2)由题知，0=t 时，00=φ，t t =时 3,0,20πφ=<+=t v A x 故且 ∴ s 322/3==∆=ππωφt (3)由于谐振动中能量守恒，故在任一位置处或任一时刻的系统的总能量均为J101.7)24.0()2(10102121214223222−−⨯=⨯⨯⨯===πωA m kA E4.6 题4.6图为两个谐振动的t x −曲线，试分别写出其谐振动方程．习题4.6图解：由题4.6图(a)，∵0=t 时，s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ 即 1s rad 2−⋅==ππωT故 m )23cos(1.0ππ+=t x a 由题4.6图(b)∵0=t 时，35,0,2000πφ=∴>=v A x01=t 时，22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯= ∴ πω65=故 m t x b )3565cos(1.0ππ+=波动4.11 沿绳子传播的平面简谐波的波动方程为y =0.05cos(10x t ππ4−)，式中x ,y 以米计，t 以秒计．求：(1)绳子上各质点振动时的最大速度和最大加速度；(2)求x =0.2m 处质点在t =1s 时的位相，它是原点在哪一时刻的位相?这一位相所代表的运动状态在t =1.25s 时刻到达哪一点? 解: (1)将题给方程与标准式2cos()y A t x πωλ=−相比，得振幅05.0=A m ，圆频率10ωπ=，波长5.0=λm ，波速2.52u ωλυλπ===1s m −⋅．绳上各点的最大振速，最大加速度分别为ππω5.005.010max =⨯==A v 1s m −⋅222max 505.0)10(ππω=⨯==A a 2s m −⋅(2)2.0=x m 处的振动比原点落后的时间为08.05.22.0==u x s 故2.0=x m ,1=t s 时的位相就是原点(0=x )，在92.008.010=−=t s 时的位相，即 2.9=φπ．设这一位相所代表的运动状态在25.1=t s 时刻到达x 点，则825.0)0.125.1(5.22.0)(11=−+=−+=t t u x x m4.12 一列平面余弦波沿x 轴正向传播，波速为5m ·s -1，波长为2m ，原点处质点的振动曲线如题4.12图所示．(1)写出波动方程；(2)作出t =0时的波形图及距离波源0.5m 处质点的振动曲线．解: (1)由题4.14(a)图知，1.0=A m ，且0=t 时，0,000>=v y ，∴230πφ=，又5.225===λυuHz ，则ππυω52==习题4.12图(a)取 ])(cos[0φω+−=ux t A y ，则波动方程为30.1cos[5()]52x y t ππ=−+m(2) 0=t 时的波形如题4.12(b)图习题4.12图(b) 习题4.12图(c)将5.0=x m 代入波动方程，得该点处的振动方程为50.530.1cos[5]0.1cos(5)52y t t πππππ⨯=−+=+m 如题4.12(c)图所示．第7章静电场7.2 填空题（1）在静电场中，电势不变的区域，场强必定为。

振动与波习题练习

第4章振动与波动一、选择题1. 在下列所述的各种物体运动中, 可视为简谐振动的是[ ] (A) 将木块投入水中, 完全浸没并潜入一定深度, 然后释放(B) 将弹簧振子置于光滑斜面上, 让其振动(C) 从光滑的半圆弧槽的边缘释放一个小滑块(D) 拍皮球时球的运动. 2.一弹簧振子周期为T ．现将弹簧截去一半，仍挂上原来的物体, 则新的弹簧振子周期为[ ] (A) T (B) 2T(C) 1.4T (D) 0.7T3. 三只相同的弹簧(质量忽略不计)都一端固定, 另一端连接质量为m 的物体, 但放置情况不同．如图4-1-3所示，其中一个平放, 一个斜放, 另一个竖直放．如果让它们振动起来, 则三者的 [ ] (A) 周期和平衡位置都不相同(B) 周期和平衡位置都相同(C) 周期相同, 平衡位置不同(D) 周期不同, 平衡位置相同4. 如图4-1-4所示，升降机中有一个作谐振动的单摆, 当升降机静止时, 其振动周期为2 s ，当升降机以加速度上升时, 升降机中的观察者观察到其单摆的振动周期与原来的振动周期相比，将[ ] (A) 增大 (B) 不变(C) 减小 (D) 不能确定. 5. 两质点在同一方向上作同振幅、同频率的简谐振动．在振动过程中,每当它们经过振幅一半的地方时, 其运动方向都相反．则这两个振动的相位差为[ ] (A) π (B) π32 (C) π34 (D) π54 6 在简谐振动的速度和加速度表达式中，都有一个负号, 这是意味着[ ] (A) 速度和加速度总是负值(B) 速度的相位比位移的相位超前 π21, 加速度的相位与位移的相位相差π (C) 速度和加速度的方向总是相同(D) 速度和加速度的方向总是相反7一质点以周期T 作简谐振动, 则质点由平衡位置正向运动到最大位移一半处的最短时间为[ ] (A) 6T (B) 8T (C) 12T (D) T 127 8 一作简谐运动质点的振动方程为π)21π2cos(5+=t x , 它从计时开始, 在运动一个周期后[ ] (A) 相位为零 (B) 速度为零(C) 加速度为零 (D) 振动能量为零9 有一谐振子沿x 轴运动, 平衡位置在x = 0处, 周期为T , 振幅为A ，t = 0时刻振子过图4-1-3图4-1-42A x =处向x 轴正方向运动, 则其运动方程可表示为 [ ] (A) )21cos(t A x ω= (B) )cos(2t A x ω= (C) )3π2sin(--=T t A x π (D) )3π2cos(-=T t A x π 10. 当一质点作简谐振动时, 它的动能和势能随时间作周期变化．如果ν是质点振动的频率, 则其动能变化的频率为[ ] (A) ν4 (B) ν2 (C) ν (D) 2ν 11. 已知一简谐振动系统的振幅为A , 该简谐振动动能为其最大值一半的位置是[ ] (A) 12A (B) 22A (C) 32A (D) A 12. 一弹簧振子作简谐振动, 当其偏离平衡位置的位移大小为振幅的1/4时, 其动能为振动总能量的[ ] (A) 167 (B) 1615 (C) 169 (D) 1613 13 一轻质弹簧, 上端固定, 下端挂有质量为m 的重物, 其自由端振动的周期为T ．已知振子离开平衡位置为x 时其振动速度为v ，加速度为a ，且其动能与势能相等．试判断下列计算该振子劲度系数的表达式中哪个是错误的?[ ] (A) a mg k = (B) 22xm k v = (C) x ma k = (D) 22π4Tm k = 14. 设卫星绕地球作匀速圆周运动．若卫星中有一单摆, 下述哪个说法是对的?[ ] (A) 它仍作简谐振动, 周期比在地面时大(B) 它仍作简谐振动, 周期比在地面时小(C) 它不会再作简谐振动(D) 要视卫星运动速度决定其周期的大小15. 弹簧振子在光滑水平面上作谐振动时, 弹性力在半个周期内所做的功为[ ] (A) 2kA (B) 221kA (C) 241kA (D) 0 16 如果两个同方向同频率简谐振动的振动方程分别为π)433cos(73.11+=t x (cm)和 π)413cos(2+=t x (cm)，则它们的合振动方程为 [ ] (A) π)433cos(73.0+=t x (cm) (B) π)413cos(73.0+=t x (cm) (C) π)1273cos(2+=t x (cm) (D) π)1253cos(2+=t x (cm) 17. 两个同方向、同频率、等振幅的谐振动合成, 如果其合成振动的振幅仍不变, 则此二分振动的相位差为[ ] (A) 2π (B) 3π2 (C) 4π (D) π18. 关于振动和波, 下面几句叙述中正确的是[ ] (A) 有机械振动就一定有机械波(B) 机械波的频率与波源的振动频率相同(C) 机械波的波速与波源的振动速度相同(D) 机械波的波速与波源的振动速度总是不相等的19. 按照定义，振动状态在一个周期内传播的距离就是波长．下列计算波长的方法中错误的是[ ] (A) 用波速除以波的频率(B) 用振动状态传播过的距离除以这段距离内的波数(C) 测量相邻两个波峰的距离(D) 测量波线上相邻两个静止质点的距离20. 当x 为某一定值时, 波动方程)π(2cos λx T t A x -=所反映的物理意义是 [ ] (A) 表示出某时刻的波形 (B) 说明能量的传播(C) 表示出x 处质点的振动规律 (D) 表示出各质点振动状态的分布21. 已知一波源位于x = 5 m 处, 其振动方程为: )cos(ϕω+=t A y (m)．当这波源产生的平面简谐波以波速u 沿x 轴正向传播时, 其波动方程为[ ] (A) )(cos u x t A y -=ω (B) ])(cos[ϕω+-=ux t A y (C) ])5(cos[ϕω++-=u x t A y (D) ])5(cos[ϕω+--=u x t A y 22已知一列机械波的波速为u , 频率为ν, 沿着x 轴负方向传播．在x 轴的正坐标上有两个点x 1和x 2．如果x 1＜x 2 , 则x 1和x 2的相位差为[ ] (A) 0 (B) )(π221x x u -ν (C) π (D) )(π212x x u-ν 23. 一波源在XOY 坐标系中(3, 0)处, 其振动方程是)π120cos(t y =(cm)，其中 t 以s 计, 波速为50 m ?s -1 ．设介质无吸收, 则此波在x ＜3 cm 的区域内的波动方程为[ ] (A) )50π(120cos x t y +=(cm) (B) π]2.7)50π(120cos[-+=x t y (cm) (C) )50π(120cos x t y -=(cm) (D) π]2.1)50π(120cos[-+=x t y (cm) 24. 若一平面简谐波的波动方程为)cos(cx bt A y -=, 式中A 、b 、c 为正值恒量．则[ ] (A) 波速为c (B) 周期为b 1 (C) 波长为c π2 (4) 角频率为bπ2 25. 一平面简谐横波沿着Ox 轴传播．若在Ox 轴上的两点相距8λ（其中λ为波长）, 则在波的传播过程中, 这两点振动速度的[ ] (A) 方向总是相同 (B) 方向有时相同有时相反(C) 方向总是相反 (D) 大小总是不相等26. 当波动方程为)01.05.2π(cos 20x t y +=(cm) 的平面波传到x =100 cm 处时, 该处质点的振动速度为[ ] (A) )π5.2sin(50t )s cm (-1⋅ (B) )π5.2sin(50t -)s cm (-1⋅(C) )π5.2sin(π50t )s cm (-1⋅ (D) )π5.2sin(π50t -)s cm (-1⋅27. 一平面简谐波在弹性介质中传播, 在介质元从最大位移处回到平衡位置的过程中[ ] (A) 它的势能转换成动能(B) 它的动能转换成势能(C) 它从相邻的一段介质元中获得能量, 其能量逐渐增大(D) 它把自己的能量传给相邻的一介质元, 其能量逐渐减小28. 已知在某一介质中两列相干的平面简谐波的强度之比是421=I I ，则这两列波的振幅之比21A A 是 [ ] (A) 4 (B) 2 (C) 16 (D) 829. 有两列波在空间某点P 相遇, 某时刻观察到P 点的合振幅等于两列波的振幅之和, 由此可以判定这两列波[ ] (A) 是相干波 (B) 相干后能形成驻波(C) 是非相干波 (D) 以上三种情况都有可能30. 已知两相干波源所发出的波的相位差为?, 到达某相遇点P 的波程差为半波长的两倍, 则P 点的合成情况是[ ] (A) 始终加强(B) 始终减弱(C) 时而加强, 时而减弱, 呈周期性变化(D) 时而加强, 时而减弱, 没有一定的规律31. 在驻波中, 两个相邻波节间各质点的振动是[ ] (A) 振幅相同, 相位相同 (B) 振幅不同, 相位相同(C) 振幅相同, 相位不同 (D) 振幅不同, 相位不同32. 方程为)π100cos(01.01x t y -=m 和)π100cos(01.02x t y +=m 的两列波叠加后, 相邻两波节之间的距离为[ ] (A) 0.5 m (B) 1 m (C) ? m (D) 2? m33 1S 和2S 是波长均为λ的两个相干波的波源，相距λ43，1S 的相位比2S 超前2π．若两波单独传播时，在过1S 和2S 的直线上各点的强度相同，不随距离变化，且两波的强度都是0I ，则在1S 、2S 连线上1S 外侧和2S 外侧各点，合成波的强度分别是[ ] (A) 04I ，04I ; (B) 0，0;(C) 0，04I ; (D) 04I ，0．.二、填空题1. 一质点沿x 轴作简谐振动，平衡位置为x 轴原点，周期为T ，振幅为A ．(1) 若t = 0 时质点过x = 0处且向x 轴正方向运动，则振动方程为x = ．(2) 若t = 0时质点在2A x =处且向x 轴负方向运动，则质点方程为x = ．2. 一个作简谐振动的质点,其谐振动方程为π)23cos(π1052+⨯=-t x (SI)．它从计时开始到第一次通过负最大位移所用的时间为． 3. 一谐振动系统周期为0.6 s, 振子质量为200 g ．若振子经过平衡位置时速度为-1s cm 12⋅，则再经0.2 s 后该振子的动能为．4. 如图4-2-4，将一个质量为20 g 的硬币放在一个劲度系数为-1m N 40⋅的竖直放置的弹簧上, 然后向下压硬币使弹簧压缩1.0 cm,突然释放后, 这个硬币将飞离原来位置的高度为．5 如果两个同方向同频率简谐振动的振动方程分别为π)3110sin(31+=t x cm 和)π6110sin(42-=t x cm, 则它们的合振动振幅为．6. 已知由两个同方向同频率的简谐振动合成的振动，其振动的振幅为20 cm, 与第一个简谐振动的相位差为6π．若第一个简谐振动的振幅为cm 3.17cm 310=, 则第二个简谐振动的振幅为 cm ，两个简谐振动的相位差为． 7. 已知一平面简谐波的方程为: )π(2cos λνx t A y -=, 在ν1=t 时刻λ411=x 与 λ432=x 两点处介质质点的速度之比是． 8. 已知一入射波的波动方程为)4π4πcos(5x t y +=(SI), 在坐标原点x = 0处发生反射, 反射端为一自由端．则对于x = 0和x = 1 m 的两振动点来说, 它们的相位关系是相位差为．9. 已知一平面简谐波沿x 轴正向传播，振动周期T = 0.5 s ，波长? = 10 m , 振幅A = 0.1m ．当t = 0时波源振动的位移恰好为正的最大值．若波源处为原点，则沿波传播方向距离波源为2λ处的振动方程为．当2T t =时，4λ=x 处质点的振动速度为．10. 图4-2-10表示一平面简谐波在 t = 2 s 时刻的波形图，波的振幅为 0.2 m ，周期为4 s ．则图中P 点处质点的振动方程为．11.B 点引起的振动方程为t A y π2cos 11=．另一简谐波沿CP ()ππ2cos 22+=t A y ．P 点与B 点相距0.40 m ，与C 点相距u ＝0.20 m ?s -1．则两波在P 的相位差为．12. 如图4-2-12所示，一平面简谐波沿Ox 轴正方向传播，波长为λ，若1P 点处质点的振动方程为)π2cos(1ϕν+=t A y ，则2P 点处质点的振动方程为，与1P 点处质点振动状态相同的那些点的位置图4-2-4A 图4-2-11P B 1r 2r ...C x12是．13. 21S S 、为振动频率、振动方向均相同的两个点波源，振动方向垂直纸面，两者相距λ23为波长)(λ，如图4-2-27所示．已知1S 的初相位为π21． (1) 若使射线C S 2上各点由两列波引起的振动均干涉相消，则2S 的初相位应为_______________________．(2) 若使21S S 连线的中垂线M N 上各点由两列波引起的振动均干涉相消，则2S 的初相位应为________________________________________．第4章振动与波动2. B 5. D 6. C 7. C 10. B 11. B 14. C 16. C 18. D 20. D 21. B24. B 26. A 28. C 30. D 31. C 33. B 40. B 42. D 44. C 48. C 50. B53. B 54. C 55. B 57. C 59. C 60. B 66. B 68. B 71. B 74. C 75. D二、填空题 1. (1) ⎪⎭⎫ ⎝⎛-2ππ2cos Tt A ; 4. 1.5 s 7. J 106.34-⨯ 9. 1.25 cm 12. 5 cm 13. 10;2π 14. －1 16. 019. π)(SI)π4(cos 1.0-=t y , 1s m 26.1-⋅- 20. π)(SI)21π21cos(2.0-=t y P 21. 0 22. )π2π2cos(212ϕλν++-=L L t A y , ,2,1,01±±=+-k k L λ 27. ⋅⋅⋅±±=+,2,1,02ππ2k k , ⋅⋅⋅±±=+,2,1,02π3π2k k ∙∙∙M N1S 2S C 图4-2-13。

大学物理振动与波题库及答案

一、选择题：（每题3分）1、把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时．若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π． (B) π/2．(C) 0 ． (D) θ．［2、两个质点各自作简谐振动，它们的振幅相同、周期相同．第一个质点的振动方程为x 1 = A cos(ωt + α)．当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处．则第二个质点的振动方程为(A) )π21cos(2++=αωt A x ． (B) )π21cos(2-+=αωt A x ． (C) )π23cos(2-+=αωt A x ． (D) )cos(2π++=αωt A x ．［］3、一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2．将它们拿到月球上去，相应的周期分别为1T '和2T '．则有(A) 11T T >'且22T T >'． (B) 11T T <'且22T T <'．(C) 11T T ='且22T T ='． (D) 11T T ='且22T T >'．［］4、一弹簧振子，重物的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动．当重物通过平衡位置且向规定的正方向运动时，开始计时．则其振动方程为：(A) )21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x (C) )π21/(cos +=t k m A x (D) )21/cos(π-=t k m A x (E) t m /k A x cos = ［］5、一物体作简谐振动，振动方程为)41cos(π+=t A x ω．在 t = T /4（T 为周期）时刻，物体的加速度为(A) 2221ωA -． (B) 2221ωA ． (C) 2321ωA -． (D) 2321ωA ．［］6、一质点作简谐振动，振动方程为)cos(φω+=t A x ，当时间t = T /2（T 为周期）时，质点的速度为(A) φωsin A -． (B) φωsin A ．(C) φωcos A -． (D) φωcos A ．［］7、一质点作简谐振动，周期为T ．当它由平衡位置向x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为(A) T /12． (B) T /8．(C) T /6． (D) T /4．［］8、两个同周期简谐振动曲线如图所示．x 1的相位比x 2的相位 (A) 落后π/2． (B) 超前π/2． (C) 落后π ． (D) 超前π．［］9、一质点作简谐振动，已知振动频率为f ，则振动动能的变化频率是(A) 4f . (B) 2 f . (C) f .(D) 2/f . (E) f /4 ［］10、一弹簧振子作简谐振动，当位移为振幅的一半时，其动能为总能量的(A) 1/4. (B) 1/2. (C) 2/1. (D) 3/4. (E) 2/3. ［］11、一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的(A) 7/16. (B) 9/16. (C) 11/16.(D) 13/16. (E) 15/16. ［］12 一质点作简谐振动，已知振动周期为T ，则其振动动能变化的周期是(A) T /4． (B) 2/T ． (C) T ．(D) 2 T ． (E) 4T ．［］13、当质点以频率ν 作简谐振动时，它的动能的变化频率为(A) 4 ν． (B) 2 ν ． (C) ν． (D) ν21．［］14、图中所画的是两个简谐振动的振动曲线．若这两个简谐振动可叠加，则合成的余弦振动的初相为(A) π23． (B) π． (C) π21． (D) 0．［］15、若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则(A) 波速为C ． (B) 周期为1/B ．(C) 波长为 2π /C ． (D) 角频率为2π /B ．［］16、下列函数f (x , t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量．其中哪个函数表示沿x 轴负向传播的行波？(A) )cos(),(bt ax A t x f +=． (B) )cos(),(bt ax A t x f -=．(C) bt ax A t x f cos cos ),(⋅=． (D) bt ax A t x f sin sin ),(⋅=．［］17、频率为 100 Hz ，传播速度为300 m/s 的平面简谐波，波线上距离小于波长的两点振动的相位差为π31，则此两点相距(A) 2.86 m ． (B) 2.19 m ．A/ -A(C) 0.5 m ． (D) 0.25 m ．［］18、已知一平面简谐波的表达式为 )cos(bx at A y -=（a 、b 为正值常量），则(A) 波的频率为a ． (B) 波的传播速度为 b/a ．(C) 波长为 π / b ． (D) 波的周期为2π / a ．［］19、一平面简谐波的表达式为 )3cos(1.0π+π-π=x t y (SI) ，t = 0时的波形曲线如图所示，则(A) O 点的振幅为-0.1 m ．(B) 波长为3 m ． (C) a 、b 两点间相位差为π21 ． (D) 波速为9 m/s ．［］20、机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则 (A) 其振幅为3 m ． (B) 其周期为s 31．(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播．［］21、图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形．若波的表达式以余弦函数表示，则O 点处质点振动的初相为(A) 0．(B) π21． (C) π． (D) π23．［］22、一横波沿x 轴负方向传播，若t 时刻波形曲线如图所示，则在t + T /4时刻x 轴上的1、2、3三点的振动位移分别是 (A) A ，0，-A. (B) -A ，0，A. (C) 0，A ，0. (D) 0，-A ，0. ［］23一平面简谐波表达式为 )2(sin 05.0x t y -π-= (SI)，则该波的频率 ν (Hz)，波速u (m/s)及波线上各点振动的振幅 A (m)依次为(A) 21，21，－0.05． (B) 21，1，－0.05． (C) 21，21，0.05． (D) 2，2，0.05．［］24、在下面几种说法中，正确的说法是：(A) 波源不动时，波源的振动周期与波动的周期在数值上是不同的．(B) 波源振动的速度与波速相同．(C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于π计)．(D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前．(按差值不大于π计) ［］25、在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定x y O u(A) 大小相同，而方向相反． (B) 大小和方向均相同．(C) 大小不同，方向相同． (D) 大小不同，而方向相反．［］26、一平面简谐波沿x 轴负方向传播．已知 x = x 0处质点的振动方程为)cos(0φω+=t A y ．若波速为u ，则此波的表达式为(A) }]/)([cos{00φω+--=u x x t A y ． (B) }]/)([cos{00φω+--=u x x t A y ． (C) }]/)[(cos{00φω+--=u x x t A y ． (D) }]/)[(cos{00φω+-+=u x x t A y ．［］27、一平面简谐波，其振幅为A ，频率为ν ．波沿x 轴正方向传播．设t = t 0时刻波形如图所示．则x = 0处质点的振动方程为(A) ]21)(2cos[0π++π=t t A y ν． (B) ]21)(2cos[0π+-π=t t A y ν． (C) ]21)(2cos[0π--π=t t A y ν． (D) ])(2cos[0π+-π=t t A y ν．［］28、一平面简谐波的表达式为 )/(2cos λνx t A y -π=．在t = 1 /ν 时刻，x 1 = 3λ /4与x 2 = λ /4二点处质元速度之比是(A) -1． (B) 31． (C) 1． (D) 3 ［］29、在同一媒质中两列相干的平面简谐波的强度之比是I 1 / I 2 = 4，则两列波的振幅之比是(A) A 1 / A 2 = 16． (B) A 1 / A 2 = 4．(C) A 1 / A 2 = 2． (D) A 1 / A 2 = 1 /4．［］30、如图所示，两列波长为λ 的相干波在P 点相遇．波在S 1点振动的初相是φ 1，S 1到P 点的距离是r 1；波在S 2点的初相是φ 2，S 2到P 点的距离是r 2，以k 代表零或正、负整数，则P 点是干涉极大的条件为：(A) λk r r =-12． (B) π=-k 212φφ． (C) π=-π+-k r r 2/)(21212λφφ． (D) π=-π+-k r r 2/)(22112λφφ．［］31、沿着相反方向传播的两列相干波，其表达式为)/(2cos 1λνx t A y -π= 和 )/(2cos 2λνx t A y +π=．叠加后形成的驻波中，波节的位置坐标为 (A) λk x ±=． (B) λk x 21±=． (C) λ)12(21+±=k x ． (D) 4/)12(λ+±=k x ． x y t =t 0u O其中的k = 0，1，2，3, …．［］32、有两列沿相反方向传播的相干波，其表达式为)/(2cos 1λνx t A y -π= 和 )/(2cos 2λνx t A y +π=．叠加后形成驻波，其波腹位置的坐标为：(A) x =±k λ． (B) λ)12(21+±=k x ． (C) λk x 21±=． (D) 4/)12(λ+±=k x ．其中的k = 0，1，2，3, …． [ ]33某时刻驻波波形曲线如图所示，则a 、b 两点振动的相位差是(A) 0 (B) π21(C) π． (D) 5π/4．［］34、沿着相反方向传播的两列相干波，其表达式为)/(2cos 1λνx t A y -π= 和 )/(2cos 2λνx t A y +π=．在叠加后形成的驻波中，各处简谐振动的振幅是(A) A ． (B) 2A ．(C) )/2cos(2λx A π． (D) |)/2cos(2|λx A π．［］35、在波长为λ 的驻波中，两个相邻波腹之间的距离为(A) λ /4． (B) λ /2．(C) 3λ /4． (D) λ ．［］36、在波长为λ 的驻波中两个相邻波节之间的距离为(A) λ ． (B) 3λ /4．(C) λ /2． (D) λ /4．［］37在真空中沿着x 轴正方向传播的平面电磁波，其电场强度波的表达式是)/(2cos 0λνx t E E z -π=，则磁场强度波的表达式是：(A) )/(2cos /000λνμεx t E H y -π=． (B) )/(2cos /000λνμεx t E H z -π=．(C) )/(2cos /000λνμεx t E H y -π-=． (D) )/(2cos /000λνμεx t E H y +π-=．［］38、在真空中沿着z 轴负方向传播的平面电磁波，其磁场强度波的表达式为)/(cos 0c z t H H x +-=ω，则电场强度波的表达式为：(A) )/(cos /000c z t H E y +=ωεμ． (B) )/(cos /000c z t H E x +=ωεμ． (C) )/(cos /000c z t H E y +-=ωεμ．(D) )/(cos /000c z t H E y --=ωεμ．［］39、电磁波的电场强度E 、磁场强度 H 和传播速度 u 的关系是：(A) 三者互相垂直，而E 和H 位相相差π21． (B) 三者互相垂直，而且E 、H 、 u 构成右旋直角坐标系． (C) 三者中E 和H 是同方向的，但都与 u 垂直． (D) 三者中E 和H 可以是任意方向的，但都必须与 u 垂直．［］40、电磁波在自由空间传播时，电场强度E 和磁场强度H(A) 在垂直于传播方向的同一条直线上．(B) 朝互相垂直的两个方向传播．(C) 互相垂直，且都垂直于传播方向．(D) 有相位差π21．［］二、填空题：（每题4分）41、一弹簧振子作简谐振动，振幅为A ，周期为T ，其运动方程用余弦函数表示．若t = 0时，(1) 振子在负的最大位移处，则初相为______________________；(2) 振子在平衡位置向正方向运动，则初相为________________；(3) 振子在位移为A /2处，且向负方向运动，则初相为______．42、三个简谐振动方程分别为 )21cos(1π+=t A x ω，)67cos(2π+=t A x ω和)611cos(3π+=t A x ω画出它们的旋转矢量图，并在同一坐标上画出它们的振动曲线．43、一物体作余弦振动，振幅为15×10-2 m ，角频率为6π s -1，初相为0.5 π，则振动方程为x = ________________________(SI)．44、一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点．已知周期为T ，振幅为A ．(1) 若t = 0时质点过x = 0处且朝x 轴正方向运动，则振动方程为x =_____________________________．(2) 若t = 0时质点处于A x 21=处且向x 轴负方向运动，则振动方程为 x =_____________________________．45、一弹簧振子，弹簧的劲度系数为k ，重物的质量为m ，则此系统的固有振动周期为______________________．46、在两个相同的弹簧下各悬一物体，两物体的质量比为4∶1，则二者作简谐振动的周期之比为_______________________．47、一简谐振动的表达式为)3cos(φ+=t A x ，已知 t = 0时的初位移为0.04 m ，初速度为0.09 m/s ，则振幅A =_____________ ，初相φ =________________．48、一质点作简谐振动，速度最大值v m = 5 cm/s ，振幅A = 2 cm ．若令速度具有正最大值的那一时刻为t = 0，则振动表达式为_________________________．49、两个简谐振动曲线如图所示，则两个简谐振动的频率之比ν1∶ν2=__________________，加速度最大值之比a 1m ∶a 2m =__________________________，初始速率之比v 10∶v 20=____________________．50、有简谐振动方程为x = 1×10-2cos(π t +φ)(SI)，初相分别为φ1 = π/2，φ2 = π，φ3 = -π/2的三个振动．试在同一个坐标上画出上述三个振动曲线．51、一简谐振动曲线如图所示，则由图可确定在t = 2s时刻质点的位移为 ____________________，速度为 __________________．52、已知两个简谐振动的振动曲线如图所示．两简谐振动的最大速率之比为_________________．53、一水平弹簧简谐振子的振动曲线如图所示．当振子处在位移为零、速度为-ωA 、加速度为零和弹性力为零的状态时，应对应于曲线上的________点．当振子处在位移的绝对值为A 、速度为零、加速度为-ω2A 和弹性力为-kA 的状态时，应对应于曲线上的____________点．x (cm)t (s)O- x (cm)54、一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为A =_____________；ω =________________； φ =_______________．55、已知两个简谐振动曲线如图所示．x 1的相位比x 2 的相位超前_______．56、两个简谐振动方程分别为 t A x ωcos 1=，)31cos(2π+=t A x ω 在同一坐标上画出两者的x —t 曲线．xtO57、已知一简谐振动曲线如图所示，由图确定振子：(1) 在_____________s 时速度为零．(2) 在____________ s 时动能最大．(3) 在____________ s 时加速度取正的最大值．58、已知三个简谐振动曲线如图所示，则振动方程分别为：x 1 =______________________，x 2 = _____________________，x 3 =_______________________．59、图中用旋转矢量法表示了一个简谐振动．旋转矢量的长度为0.04 m ，旋转角速度ω = 4π rad/s ．此简谐振动以余弦函数表 x (cm)t (s)O 12示的振动方程为x =__________________________(SI)．60、一质点作简谐振动的角频率为ω 、振幅为A ．当t = 0时质点位于A x 21=处，且向x 正方向运动．试画出此振动的旋转矢量图．61、两个同方向的简谐振动曲线如图所示．合振动的振幅为_______________________________，合振动的振动方程为________________________________． 62、一平面简谐波．波速为6.0 m/s ，振动周期为0.1 s ，则波长为___________．在波的传播方向上，有两质点（其间距离小于波长）的振动相位差为5π /6，则此两质点相距___________．63、一个余弦横波以速度u 沿x 轴正向传播，t 时刻波形曲线如图所示．试分别指出图中A ，B ，C 各质点在该时刻的运动方向．A _____________；B _____________ ；C ______________ ． 64、一横波的表达式是 )30/01.0/(2sin 2x t y -π=其中x 和y 的单位是厘米、t 的单位是秒，此波的波长是_________cm ，波速是_____________m/s ．65、已知平面简谐波的表达式为 )cos(Cx Bt A y -=式中A 、B 、C 为正值常量，此波的波长是_________，波速是_____________．在波传播方向上相距为d 的两点的振动相位差是____________________．66、一声波在空气中的波长是0.25 m ，传播速度是340 m/s ，当它进入另一介质时，波长变成了0.37 m ，它在该介质中传播速度为______________．67、已知波源的振动周期为4.00×10-2 s ，波的传播速度为300 m/s ，波沿x 轴正方向传播，则位于x 1 = 10.0 m 和x 2 = 16.0 m 的两质点振动相位差为__________．68、一平面简谐波沿x 轴正方向传播，波速 u = 100 m/s ，t = 0时刻的波形曲线如图所示．可知波长λ = ____________；振幅A = __________；频率ν = ____________．69、频率为500 Hz 的波，其波速为350 m/s ，相位差为2π/3 的两点间距离为________________________．70、一平面简谐波沿x 轴正方向传播．已知x = 0处的振动方程为 )cos(0φω+=t y ，波速为u ．坐标为x 1和x 2的两点的振动初相位分别记为φ 1和φ 2，则相位差φ 1－φ 2 =_________________．·---y (m)71、已知一平面简谐波的波长λ = 1 m ，振幅A = 0.1 m ，周期T = 0.5 s ．选波的传播方向为x 轴正方向，并以振动初相为零的点为x 轴原点，则波动表达式为y = _____________________________________(SI)．72、一横波的表达式是)4.0100(2sin 02.0π-π=t y (SI)，则振幅是________，波长是_________，频率是__________，波的传播速度是______________．77、已知一平面简谐波的表达式为 )cos(bx at A -，（a 、b 均为正值常量），则波沿x 轴传播的速度为___________________．74、一简谐波的频率为 5×104 Hz ，波速为 1.5×103 m/s ．在传播路径上相距5×10-3 m 的两点之间的振动相位差为_______________．75、一简谐波沿BP 方向传播，它在B 点引起的振动方程为 t A y π=2cos 11．另一简谐波沿CP 方向传播，它在C 点引起的振动方程为)2cos(22π+π=t A y ．P 点与B 点相距0.40 m ，与C 点相距0.5 m （如图）．波速均为u = 0.20 m/s ．则两波在P 点的相位差为______________________．76、已知一平面简谐波的表达式为 )cos(Ex Dt A y -=，式中A 、D 、E 为正值常量，则在传播方向上相距为a 的两点的相位差为______________．77、在简谐波的一条射线上，相距0.2 m 两点的振动相位差为π /6．又知振动周期为0.4 s ，则波长为_________________，波速为________________．78、一声纳装置向海水中发出超声波，其波的表达式为)2201014.3cos(102.153x t y -⨯⨯=- (SI)则此波的频率ν = _________________ ，波长λ = __________________，海水中声速u = __________________．79、已知14℃时的空气中声速为340 m/s ．人可以听到频率为20 Hz 至20000 Hz 范围内的声波．可以引起听觉的声波在空气中波长的范围约为______________________________．80、一平面简谐波（机械波）沿x 轴正方向传播，波动表达式为)21cos(2.0x t y π-π= (SI)，则x = -3 m 处媒质质点的振动加速度a 的表达式为________________________________________．81、在同一媒质中两列频率相同的平面简谐波的强度之比I 1 / I 2 = 16，则这两列波的振幅之比是A 1 / A 2 = ____________________．82、两相干波源S 1和S 2的振动方程分别是)cos(1φω+=t A y 和)cos(2φω+=t A y . S 1距P 点3个波长，S 2距P 点 4.5个波长．设波传播过程中振幅不变，则两波同时传到P 点时的合振幅是________________．83、两相干波源S 1和S 2的振动方程分别是t A y ωcos 1=和)21cos(2π+=t A y ω．S 1距P 点3个波长，S 2距P 点21/4个波长．两波在P 点引起的两个振动的相位差是____________．84、两个相干点波源S 1和S 2，它们的振动方程分别是 )21cos(1π+=t A y ω和 )21cos(2π-=t A y ω．波从S 1传到P 点经过的路程等于2个波长，波从S 2传到P 点的路程等于7 / 2个波长．设两波波速相同，在传播过程中振幅不衰减，则两波传到P 点的振动的合振幅为__________________________．85、一弦上的驻波表达式为)90cos()cos(1.0t x y ππ=(SI)．形成该驻波的两个反向传播的行波的波长为________________，频率为__________________．86、一弦上的驻波表达式为 t x y 1500cos 15cos 100.22-⨯= (SI)．形成该驻波的两个反向传播的行波的波速为__________________．87、在弦线上有一驻波，其表达式为 )2cos()/2cos(2t x A y νλππ=, 两个相邻波节之间的距离是_______________．88、频率为ν = 5×107 Hz 的电磁波在真空中波长为_______________m ，在折射率为n = 1.5 的媒质中波长为______________m ．89、在电磁波传播的空间（或各向同性介质）中，任一点的E 和H 的方向及波传播方向之间的关系是：_________________________________________________________________________________________________________．90、在真空中沿着x 轴正方向传播的平面电磁波，其电场强度波的表达式为)/(2cos 600c x t E y -π=ν (SI)，则磁场强度波的表达式是______________________________________________________．(真空介电常量 ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m)91、在真空中沿着x 轴负方向传播的平面电磁波，其电场强度的波的表达式为)/(2cos 800c x t E y +π=ν (SI)，则磁场强度波的表达式是________________________________________________________．(真空介电常量 ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m)92、在真空中沿着z 轴正方向传播的平面电磁波的磁场强度波的表达式为])/(cos[00.2π+-=c z t H x ω (SI)，则它的电场强度波的表达式为____________________________________________________．（真空介电常量 ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m ）93、在真空中沿着负z 方向传播的平面电磁波的磁场强度为)/(2cos 50.1λνz t H x +π= (SI)，则它的电场强度为E y = ____________________．（真空介电常量ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m ）94真空中一简谐平面电磁波的电场强度振幅为 E m = 1.20×10-2 V/m 该电磁波的强度为_________________________．（真空介电常量 ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m ）95、在真空中沿着z 轴的正方向传播的平面电磁波，O 点处电场强度为)6/2cos(900π+π=t E x ν，则O 点处磁场强度为___________________________．（真空介电常量 ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m ）96、在地球上测得来自太阳的辐射的强度=S 1.4 kW/m 2．太阳到地球的距离约为1.50×1011 m ．由此估算，太阳每秒钟辐射的总能量为__________________．97、在真空中沿着z 轴负方向传播的平面电磁波，O 点处电场强度为)312cos(300π+π=t E x ν (SI)，则O 点处磁场强度为_____________________________________．在图上表示出电场强度，磁场强度和传播速度之间的相互关系．98、电磁波在真空中的传播速度是_________________(m/s)（写三位有效数字）．99、电磁波在媒质中传播速度的大小是由媒质的____________________决定的．100、电磁波的E 矢量与H 矢量的方向互相____________，相位__________．三、计算题：（每题10分）101、一质点按如下规律沿x 轴作简谐振动：)328cos(1.0π+π=t x (SI)．求此振动的周期、振幅、初相、速度最大值和加速度最大值．102、一质量为0.20 kg 的质点作简谐振动，其振动方程为)215cos(6.0π-=t x (SI)．求：(1) 质点的初速度；(2) 质点在正向最大位移一半处所受的力．z yxO103、有一轻弹簧，当下端挂一个质量m 1 = 10 g 的物体而平衡时，伸长量为 4.9 cm ．用这个弹簧和质量m 2 = 16 g 的物体组成一弹簧振子．取平衡位置为原点，向上为x 轴的正方向．将m 2从平衡位置向下拉 2 cm 后，给予向上的初速度v 0 = 5 cm/s 并开始计时，试求m 2的振动周期和振动的数值表达式．104、有一单摆，摆长为l = 100 cm ，开始观察时( t = 0 )，摆球正好过 x 0 = -6 cm 处，并以v 0 = 20 cm/s 的速度沿x 轴正向运动，若单摆运动近似看成简谐振动．试求(1) 振动频率； (2) 振幅和初相．105、质量m = 10 g 的小球与轻弹簧组成的振动系统，按)318cos(5.0π+π=t x 的规律作自由振动，式中t 以秒作单位，x 以厘米为单位，求(1) 振动的角频率、周期、振幅和初相；(2) 振动的速度、加速度的数值表达式；(3) 振动的能量E ；(4) 平均动能和平均势能．106、一质量m = 0.25 kg 的物体，在弹簧的力作用下沿x 轴运动，平衡位置在原点. 弹簧的劲度系数k = 25 N ·m -1．(1) 求振动的周期T 和角频率ω．(2) 如果振幅A =15 cm ，t = 0时物体位于x = 7.5 cm 处，且物体沿x 轴反向运动，求初速v 0及初相φ．(3) 写出振动的数值表达式．107、一质量为10 g 的物体作简谐振动，其振幅为2 cm ，频率为4 Hz ，t = 0时位移为－2 cm ，初速度为零．求(1) 振动表达式；(2) t = (1/4) s 时物体所受的作用力．108、两个物体作同方向、同频率、同振幅的简谐振动．在振动过程中，每当第一个物体经过位移为2/A 的位置向平衡位置运动时，第二个物体也经过此位置，但向远离平衡位置的方向运动．试利用旋转矢量法求它们的相位差．109、一物体质量为0.25 kg ，在弹性力作用下作简谐振动，弹簧的劲度系数k = 25 N ·m -1，如果起始振动时具有势能0.06 J 和动能0.02 J ，求(1) 振幅；(2) 动能恰等于势能时的位移；(3) 经过平衡位置时物体的速度．110、在一竖直轻弹簧下端悬挂质量m = 5 g 的小球，弹簧伸长∆l = 1 cm 而平衡．经推动后，该小球在竖直方向作振幅为A = 4 cm 的振动，求(1) 小球的振动周期； (2) 振动能量．111、一物体质量m = 2 kg ，受到的作用力为F = -8x (SI)．若该物体偏离坐标原点O 的最大位移为A = 0.10 m ，则物体动能的最大值为多少？112、一横波沿绳子传播，其波的表达式为)2100cos(05.0x t y π-π= (SI)(1) 求此波的振幅、波速、频率和波长．(2) 求绳子上各质点的最大振动速度和最大振动加速度．(3) 求x 1 = 0.2 m 处和x 2 = 0.7 m 处二质点振动的相位差．113、一振幅为 10 cm ，波长为200 cm 的简谐横波,沿着一条很长的水平的绷紧弦从左向右行进，波速为 100 cm/s ．取弦上一点为坐标原点，x 轴指向右方，在t = 0时原点处质点从平衡位置开始向位移负方向运动．求以SI 单位表示的波动表达式（用余弦函数）及弦上任一点的最大振动速度．114、一振幅为 10 cm ，波长为200 cm 的一维余弦波．沿x 轴正向传播，波速为 100 cm/s ，在t = 0时原点处质点在平衡位置向正位移方向运动．求(1) 原点处质点的振动方程．(2) 在x = 150 cm 处质点的振动方程．115、一简谐波沿x 轴负方向传播，波速为1 m/s ，在x 轴上某质点的振动频率为1 Hz 、振幅为0.01 m ．t = 0时该质点恰好在正向最大位移处．若以该质点的平衡位置为x 轴的原点．求此一维简谐波的表达式．116、已知一平面简谐波的表达式为 )37.0125cos(25.0x t y -= (SI)(1) 分别求x 1 = 10 m ，x 2 = 25 m 两点处质点的振动方程；(2) 求x 1，x 2两点间的振动相位差；(3) 求x 1点在t = 4 s 时的振动位移．117、一横波方程为 )(2cos x ut A y -π=λ，式中A = 0.01 m ，λ = 0.2 m ，u = 25 m/s ，求t = 0.1 s 时在x = 2 m 处质点振动的位移、速度、加速度．118、如图，一平面简谐波沿Ox 轴传播，波动表达式为])/(2cos[φλν+-π=x t A y (SI)，求 (1) P 处质点的振动方程； (2) 该质点的速度表达式与加速度表达式．119、一平面简谐波，频率为300 Hz ，波速为340 m/s ，在截面面积为3.00×10-2 m 2的管内空气中传播，若在10 s 内通过截面的能量为2.70×10-2 J ，求(1) 通过截面的平均能流；(2) 波的平均能流密度；(3) 波的平均能量密度．120、一驻波中相邻两波节的距离为d = 5.00 cm ，质元的振动频率为ν =1.00×103 Hz ，求形成该驻波的两个相干行波的传播速度u 和波长λ ．O P大学物理------振动与波参考答案一、选择题1 - 5 CBDBB 6 -10 BCBBD 11-15 EBBBC 16-20 ACDCB 21-25 DBCCA 26-30 ABACD 31-35 DCCDB 36-40 CCCBC二、填空题41.（1） π；（2）2/π-；（3）3/π； 42. 略； 43. 21510cos[6]2t ππ-⨯+； 44. （1）2cos[]2A t T ππ-， (2) 2cos[]3A t T πλ+；45. 2 46. 1:2； 47. m 05.0，π205.0- or 09.36-； 48. 25210cos[]22x t π-=⨯- ； 49. 1:2，1:4，1:2； 51. 0，s m /3； 52. 1:1； 53. e a f b ,,,；54. cm 10，s rad /6/π，3/π；55. 3/4π； 56. 略；57.（1）,...2,1,0,2/)12(=+n n ，（2）,...2,1,0,=n n ，（3）,...2,1,0,2/)14(=+n n ，； 58. t πcos 1.0，)2/cos(1.0ππ-t ，)cos(1.0ππ±t ； 59. ]24cos[04.0ππ-t ； 60. 略； 61. 21A A -， ]22cos[12ππ+-=t T A A x ； 62. m 6.0，m 25.0； 63. 向下，向上；64. cm 30，30； 65. c /2π，c B /，cd ； 66. s m /503；67. π；68. m 8.0，m 2.0，Hz 125；69. m 233.0；70. u x x /)(12-ω；71. ]24cos[1.0x t ππ-；72. cm 2，cm 5.2，Hz 100，51~2500；73. b a /； 74. 3/π； 75. 0；76. aE ； 77. m 4.2， s m /0.6；78. Hz 4100.5⨯，m 21086.2-⨯，s m /1043.13⨯； 79. m 2107.1~17-⨯； 80. )23cos(2.02x t πππ+-； 81. 4； 82. 0； 83. 0； 84. A 2； 85. m 2，Hz 45； 86. s m /100； 87. 2/λ； 88. m 6， m 4； 89. H E S ⨯= ； 90. )](2cos[59.1c x t H z -=πν； 91. )](2cos[12.2cx t H z +-=πν； 92. ])(cos[754πω+--=c z t E y ； 93. )](2cos[565λνπz t +； 94. 271091.1--⨯wm ；95. ]62cos[39.2ππν+=t H y ； 96. J 26100.4⨯；97. ]32cos[796.0ππν+-=t H y ；98. 81000.3⨯； 99. με,； 100. 垂直，相同，相同三、计算题101、解：周期 25.0/2=π=ωT s ，振幅 A = 0.1 m ，初相 φ = 2π/3，v max = ω A = 0.8π m/s ( = 2.5 m/s )，a max = ω 2A = 6.4π2 m/s 2 ( =63 m/s 2 )．102、解：(1) )25sin(0.3d d π--==t t x v (SI) t 0 = 0 , v 0 = 3.0 m/s ．(2) x m ma F 2ω-==A x 21= 时， F = -1.5 N ． 103、解：设弹簧的原长为l ，悬挂m 1后伸长∆l ，则 k ∆l = m 1g ，k = m 1g/ ∆l = 2 N/m取下m 1上m 2后， 2.11/2==m k ω rad/sω/2π=T =0.56 st = 0时， φcos m 10220A x =⨯-=-φωsin m/s 10520A -=⨯=-v解得 220201005.2m )/(-⨯=+=ωv x A m =-=-)/(tg 001x ωφv 180°+12.6°=3.36 rad也可取 φ = -2.92 rad振动表达式为 x = 2.05×10-2cos(11.2t -2.92) (SI)或 x = 2.05×10-2cos(11.2t +3.36) (SI)104、解：(1) 13.3/==l g ω rad/s ，5.0)2/(=π=ων Hz(2) t = 0 时，x 0 = -6 cm= A cos φ， v 0 = 20 cm/s= -A ω sin φ由上二式解得 A = 8.8 cm ，φ = 180°＋46.8°= 226.8°= 3.96 rad ，（或－2.33 rad ）105、解：(1) A = 0.5 cm ；ω = 8π s -1；T = 2π/ω = (1/4) s ；φ = π/3 (2) )318sin(1042π+π⨯π-==-t x v (SI))318cos(103222π+π⨯π-==-t x a (SI)(3) 2222121A m kA E E E P K ω==+==7.90×10-5 J(4) 平均动能 ⎰=TK t m T E 02d 21)/1(v⎰π+π⨯π-=-T t t m T 0222d )318(sin )104(21)/1(= 3.95×10-5 J = E 21同理 E E P 21== 3.95×10-5 J106、解： (1) 1s 10/-==m k ω， 63.0/2=π=ωT s(2) A = 15 cm ，在 t = 0时，x 0 = 7.5 cm ，v 0 < 0由 2020)/(ωv +=x A得 3.12020-=--=x A ωv m/sπ=-=-31)/(tg 001x ωφv 或 4π/3∵ x 0 > 0 ，∴ π=31φ(3) )3110cos(10152π+⨯=-t x (SI)107、解：(1) t = 0时，x 0 = -2 cm = -A , 故初相 φ = π ，ω = 2 πν = 8 π s -1)8cos(1022π+π⨯=-t x (SI)(2) t = (1/4) s 时，物体所受的作用力 126.02=-=x m F ω N 108、解：依题意画出旋转矢量图。

厦门大学大学物理第二学期期末习题集(振动与波习题)

《大学物理》期末考试复习题(振动与波)

大学物理振动与波练习题与答案

大学物理习题集(下,含解答)

C1(振动与波答案)

大学物理 振动与波练习题解

大学物理习题及解答(振动与波、波动光学)

厦门大学 大学物理B(下)期末复习

振动和波动要点习题

大学物理-波动光学习题(包括振动、波动、波的干涉、光的干涉、光的衍射、光的偏振)

(完整版)大学物理振动习题含答案

大学物理-习题-简谐振动和波-学生版

振动与波习题

N考核《大学物理学》机械振动与机械波部分练习题(解答)

大学物理题库-振动与波动

厦门大学大学物理第二学期期末习题集(振动与波习题)

大学物理振动与波练习题与标准答案

大学物理期末复习题---填空-计算题

振动与波习题练习

大学物理振动与波题库及答案

大学物理振动与波练习题解

厦门大学大学物理B(下)期末复习