大学物理振动习题含答案
大学物理振动练习题有答案
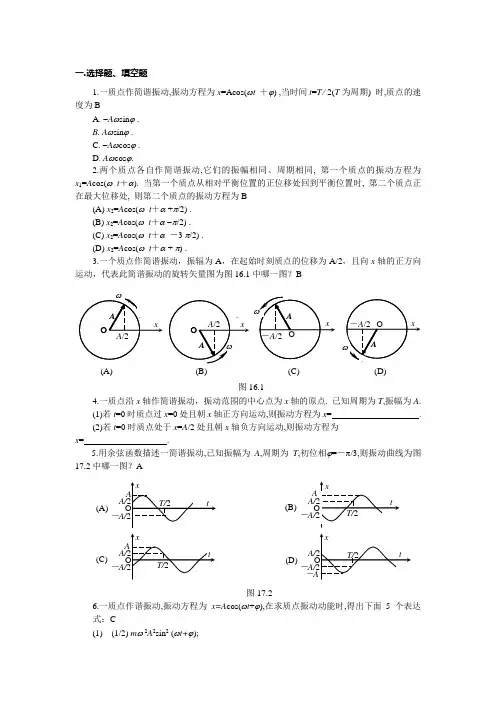
一.选择题、填空题1.一质点作简谐振动,振动方程为x =Acos(ωt ＋ϕ) ,当时间t =T / 2(T 为周期) 时,质点的速度为BA. -A ωsin ϕ .B. A ωsin ϕ .C. -A ωcos ϕ .D. A ωcos ϕ.2.两个质点各自作简谐振动,它们的振幅相同、周期相同, 第一个质点的振动方程为x 1=A cos(ω t ＋α). 当第一个质点从相对平衡位置的正位移处回到平衡位置时, 第二个质点正在最大位移处, 则第二个质点的振动方程为B(A) x 2=A cos(ω t ＋α +π/2) . (B) x 2=A cos(ω t ＋α -π/2) . (C) x 2=A cos(ω t ＋α －3 π/2) . (D) x 2=A cos(ω t ＋α + π) .3.一个质点作简谐振动，振辐为A ，在起始时刻质点的位移为A/2，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为图16.1中哪一图？B4.一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点. 已知周期为T ,振幅为A . (1)若t =0时质点过x =0处且朝x 轴正方向运动,则振动方程为x = . (2)若t =0时质点处于x =A /2处且朝x 轴负方向运动,则振动方程为x = .5.用余弦函数描述一简谐振动,已知振幅为A ,周期为T ,初位相ϕ=－π/3,则振动曲线为图17.2中哪一图？A6.一质点作谐振动,振动方程为x=A cos(ωt +ϕ),在求质点振动动能时,得出下面5个表达式：C(1) (1/2) m ω 2A 2sin 2 (ωt+ϕ); (2) (1/2) m ω2A 2cos 2 (ωt+ϕ);(A)图16.1(A) (C) (B) (D)图17.2(3) (1/2) kA2 sin (ωt+ϕ);(4) (1/2) kA2 cos 2 (ωt+ϕ);(5) (2π2/T2) mA2 sin2 (ωt+ϕ).其中m是质点的质量, k是弹簧的倔强系数,T是振动的周期,下面结论中正确的是(A) (1) ,(4) 是对的;(B) (2) ,(4) 是对的.(C) (1) ,(5) 是对的.(D) (3) ,(5) 是对的.(E) (2) ,(5) 是对的.7.一质点同时参与了两个同方向的简谐振动,它们的振动方程分别为x1=0.05cos(ω t+π/4) (SI)x2=0.05cos(ω t+19π/12) (SI)其合成运动的运动方程为x= .。
《振动力学》习题集(含问题详解)
《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面作微幅摆动，如图E1.1所示。
求系统的固有频率。
图E1.1解： 系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。
求系统的固有频率。
图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。
求系统的固有频率。
图E1.3解： 系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。
物理振动试题及答案解析
物理振动试题及答案解析1. 简谐运动的振动周期与哪些因素有关？答案：简谐运动的振动周期与振子的质量以及弹簧的劲度系数有关，与振幅无关。
2. 什么是阻尼振动？其振动周期与自由振动相比有何不同？答案：阻尼振动是指在振动过程中受到阻力作用的振动。
与自由振动相比，阻尼振动的振动周期会变长。
3. 简述单摆的周期公式。
答案：单摆的周期公式为 \( T = 2\pi \sqrt{\frac{L}{g}} \)，其中 \( T \) 是周期，\( L \) 是摆长，\( g \) 是重力加速度。
4. 什么是共振现象？请举例说明。
答案：共振现象是指当驱动力的频率接近或等于系统的固有频率时，系统振幅急剧增大的现象。
例如，当行人在桥上行走时，如果步频与桥的固有频率接近，可能会引起桥梁的共振，导致桥梁剧烈振动甚至断裂。
5. 请解释为什么在声波传播中，频率越高的声波传播距离越短？答案：频率越高的声波波长越短，波长越短的声波在传播过程中更容易受到空气分子的散射作用，因此传播距离较短。
6. 什么是多普勒效应？请用物理公式表达。
答案：多普勒效应是指当波源和观察者相对运动时，观察者接收到的波频率与波源发出的频率不同的现象。
多普勒效应的公式为 \( f'= \frac{f(u + v)}{u + v \cos \theta} \)，其中 \( f' \) 是观察者接收到的频率，\( f \) 是波源发出的频率，\( u \) 是波源的速度，\( v \) 是观察者的速度，\( \theta \) 是波源和观察者之间的夹角。
7. 请解释为什么在弹簧振子的振动过程中，振幅会逐渐减小？答案：在弹簧振子的振动过程中，振幅逐渐减小是因为存在阻力作用，如空气阻力或摩擦阻力，这些阻力会消耗振子的机械能，导致振幅减小。
8. 什么是机械波？请列举三种常见的机械波。
答案：机械波是指需要介质传播的波，其传播过程中介质的质点并不随波迁移，而是在平衡位置附近做振动。
大学物理 机械振动 试题(附答案)
w w w .z h i n a n ch e.com《大学物理》AI 作业No No..01机械振动一、选择题1.把单摆从平衡位置拉开，使摆线与竖直方向成一微小角度θ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相位为[C ](A)θ;(B)23;(C)0;(D)π21。
解：t =0时，摆角处于正最大处，角位移最大，速度为零，用余弦函数表示角位移，0=ϕ。
2.轻弹簧上端固定，下系一质量为1m 的物体，稳定后在1m 下边又系一质量为2m 的物体，于是弹簧又伸长了x ∆。
若将2m 移去，并令其振动，则振动周期为[B](A)gm x m T 122∆=π(B)gm x m T 212∆=π(C)gm xm T 2121∆=π(D)()gm m x m T 2122+∆=π解：设弹簧劲度系数为k ，由题意，x k g m ∆⋅=2，所以xgm k ∆=2。
弹簧振子由弹簧和1m 组成，振动周期为gm xm k m T 21122∆==ππ。
3.一劲度系数为k 的轻弹簧截成三等份，取出其中的两根，将它们并联在一起，下面挂一质量为m 的物体，如图所示。
则振动系统的频率为[B](A)m k π21(B)mk 621π(C)mk 321π(D)mk 321π解：每一等份弹簧的劲度系数k k 3=′，两等份再并联，等效劲度系数k k k 62=′=′′，所以振动频率mk m k 62121ππν=′′=4.一弹簧振子作简谐振动，总能量为1E ，如果简谐振动振幅增加为原来的两倍，重物的质量增加为原来的四倍，则它的总能量E 变为[D ](A)1E /4(B)1E /2(C)21E (D)41E 解：原来的弹簧振子的总能量212112112121A m kA E ω==，振动增加为122A A =，质量增加+w w w .z h i n a n ch e为124m m =，k 不变，角频率变为1122214ω===m k m k ，所以总能量变为()1212112121122222242142242121E A m A m A m E =⎟⎠⎞⎜⎝⎛=×⎟⎠⎞⎜⎝⎛××==ωωω5.一质点作简谐振动，周期为T 。
大学物理振动习题含答案
一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ ［ ］2．3002：两个质点各自作简谐振动，它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。
则第二个质点的振动方程为：(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x ［ ］3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，振动角频率为ω。
若把此弹簧分割成二等份，将物体m 挂在分割后的一根弹簧上，则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 ［ ］4．3396：一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述，则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 ［ ］5．3552：一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2。
将它们拿到月球上去，相应的周期分别为1T '和2T '。
则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >' ［ ］ 6．5178：一质点沿x 轴作简谐振动，振动方程为)312cos(1042π+π⨯=-t x (SI)。
大学物理振动习题含答案
一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ ［ ］2．3002：两个质点各自作简谐振动，它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。
则第二个质点的振动方程为：(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x ［ ］3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，振动角频率为ω。
若把此弹簧分割成二等份，将物体m 挂在分割后的一根弹簧上，则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 ［ ］4．3396：一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述，则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 ［ ］5．3552：一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2。
将它们拿到月球上去，相应的周期分别为1T '和2T '。
则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >' ［ ］ 6．5178：一质点沿x 轴作简谐振动，振动方程为)312cos(1042π+π⨯=-t x (SI)。
大学物理习题及解答(振动与波、波动光学)
1． 有一弹簧，当其下端挂一质量为m 的物体时，伸长量为9.8 ⨯10－2 m 。
假如使物体上下振动，且规定向下为正方向。
〔1〕t =0时，物体在平衡位置上方8.0 ⨯10－2 m处，由静止开始向下运动，求运动方程。
〔2〕t = 0时，物体在平衡位置并以0.60m/s 的速度向上运动，求运动方程。
题1分析：求运动方程，也就是要确定振动的三个特征物理量A 、ω，和ϕ。
其中振动的角频率是由弹簧振子系统的固有性质〔振子质量m 与弹簧劲度系数k 〕决定的，即m k /=ω，k 可根据物体受力平衡时弹簧的伸长来计算；振幅A 和初相ϕ需要根据初始条件确定。
解：物体受力平衡时，弹性力F 与重力P 的大小相等，即F = mg 。
而此时弹簧的伸长量m l 2108.9-⨯=∆。
如此弹簧的劲度系数l mg l F k ∆=∆=//。
系统作简谐运动的角频率为1s 10//-=∆==l g m k ω〔1〕设系统平衡时，物体所在处为坐标原点，向下为x 轴正向。
由初始条件t = 0时，m x 210100.8-⨯=，010=v 可得振幅m 100.8)/(2210102-⨯=+=ωv x A ；应用旋转矢量法可确定初相πϕ=1。
如此运动方程为])s 10cos[()m 100.8(121π+⨯=--t x〔2〕t = 0时，020=x ，120s m 6.0-⋅=v ，同理可得m 100.6)/(22202022-⨯=+=ωv x A ，2/2πϕ=；如此运动方程为]5.0)s 10cos[()m 100.6(122π+⨯=--t x2．某振动质点的x －t 曲线如下列图，试求：〔1〕运动方程；〔2〕点P 对应的相位；〔3〕到达点P 相应位置所需要的时间。
题2分析：由运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题。
此题就是要通过x －t 图线确定振动的三个特征量量A 、ω，和0ϕ，从而写出运动方程。
曲线最大幅值即为振幅A ；而ω、0ϕ通常可通过旋转矢量法或解析法解出，一般采用旋转矢量法比拟方便。
振动作业答案
《大学物理（下）》作业 No.1 机械振动（电气、计算机、詹班）班级 学号 姓名 成绩一 选择题1. 把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度，然后由静止放手任其振动，从放手时开始计时．若用余弦函数表示其运动方程，则该单摆振动的初相为 (A)． (B)/2． (C) 0 ． (D)．［ C ］[参考解答] 开始计时时，位移达到最大值。
2. 已知某简谐振动的振动曲线如图所示，位移的单位为厘米，时间单位为秒．则此简谐振动的振动方程为：(A) )3232cos(2π+π=t x ．(B) )3232cos(2π-π=t x ．(C) )3234cos(2π+π=t x ．(D) )3234cos(2π-π=t x ．(E) )4134cos(2π-π=t x ．［ C ］[参考解答] A=2 cm ，由旋转矢量法可得：3/20πϕ==t ，πϕ21==t ，s rad t /4314/3ππϕω==∆∆=，旋转矢量图： 3．一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的 （A ）7/16 （B ）9/16t (s)O-1 -212-2-1Ot=0t=1（C ）11/16 （D ）13/16 （E ）15/16[ E ][参考解答] 4/)cos(A t A x =+=ϕω，16/15)(sin ,4/1)cos(2=+=+ϕωϕωt t 即，1615)(sin max2max k k k E t E E =+=ϕω 4．图中所画的是两个简谐振动的振动曲线，若这两个简谐振动可叠加，则合成的余弦振动的初相位为：（A ）2π（B ）π（C ）23π（D ）0[ B ][参考解答] t=0时刻的旋转矢量图：二 填空题1.一竖直悬挂的弹簧振子，自然平衡时弹簧的伸长量为x 0，此振子自由振动的周期T = g x /20π．[参考解答] 受力分析如右图，以平衡位置为原点，向下为x轴正方向，有：22/22)/(dtXd m kX k mg x k mg kx dt xd m k mg x X =-=--=+-=-=令 对坐标X ，其运动为简谐运动， 其角频率满足：，mk =2ωg x T /2/20πωπ==πA/2-A A 合mg F kox2. 一质点作简谐振动，速度最大值v m = 5 cm/s ，振幅A = 2 cm ．若令速度具有正最大值的那一时刻为t = 0，则振动表达式为 )()2325cos(2cm t x π+=． [参考解答] s rad cm A A v m /5.2,2,=∴==ωωt =0时，质点通过平衡位置向正方向运动，初相为：230πϕ=3．一弹簧简谐振子的振动曲线如图所示，振子处在位移为零，速度为－ωA ，加速度为零和弹性力为零的状态，对应于曲线上的 b, f 点，振子处在位移的绝对值为A 、速度为零、加速度为－ω2A 和弹性力为－KA 的状态，则对应于曲线上的 a, e 点。
大学物理第九章振动学基础习题答案
第九章 振动学习题9-1 一小球与轻弹簧组成的振动系统，按(m) 3ππ8cos 05.0⎪⎭⎫ ⎝⎛+=t x ，的规律做自由振动，试求（1）振动的角频率、周期、振幅、初相、速度最大值和加速度最大值；（2）t=1s ，2s ，10s 等时刻的相位；（3）分别画出位移、速度和加速度随时间变化的关系曲线。
解：（1）ω=8πs -1，T=2π/ω=0.25s ，A=0.05m ，ϕ0=π/3，m A ω=v ，2m a A ω=（2）π=8π3t φ+ （3）略9-2 一远洋货轮质量为m ，浮在水面时其水平截面积为S 。
设在水面附近货轮的水平截面积近似相等，水的密度为ρ，且不计水的粘滞阻力。
（1）证明货轮在水中做振幅较小的竖直自由运动是谐振动；（2）求振动周期。
解：（1）船处于静止状态时gSh mg ρ=，船振动的一瞬间()F gS h y mg ρ=-++ 得F gSy ρ=-，令k gS ρ=，即F ky =-，货轮竖直自由运动是谐振动。
（2）ω==，2π2T ω==9-3 设地球是一个密度为ρ的均匀球体。
现假定沿直径凿通一条隧道，一质点在隧道内做无摩擦运动。
（1）证明此质点的运动是谐振动；（2）计算其振动周期。
解：以球心为原点建立坐标轴Ox 。
质点距球心x 时所受力为324433x mF G G mx x πρπρ=-=-令43k G m πρ=，则有F kx =-，即质点做谐振动。
（2）ω==2πT ω== 9-4 一放置在水平桌面上的弹簧振子，振幅A ＝2.0 ×10-2 m ，周期T s 。
当t ＝0时，（1）物体在正方向端点；（2）物体在平衡位置，向负方向运动；（3）物体在x ×10-2m 处，向负方向运动；（4）物体在x ＝-×10-2 m 处，向正方向运动。
求以上各种情况的振动方程。
解：ω=2π/T=4πs -1（1）ϕ0=0，0.02cos4(m)x t π=（2）ϕ0=π/2，0.02cos 4(m)2x t ππ⎛⎫=+ ⎪⎝⎭（3）ϕ0=π/3，0.02cos 4(m)3x t ππ⎛⎫=+ ⎪⎝⎭（4）ϕ0=4π/3，40.02cos 4(m)3x t ππ⎛⎫=+ ⎪⎝⎭9-5 有一弹簧，当其下端挂一质量为m 的物体时，伸长量为9.8 ×10-2 m 。
大学物理机械振动习题附答案要点
一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ ［ ］2．3002：两个质点各自作简谐振动，它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。
则第二个质点的振动方程为：(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x ［ ］3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，振动角频率为ω。
若把此弹簧分割成二等份，将物体m 挂在分割后的一根弹簧上，则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 ［ ］4．3396：一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述，则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 v 与a5．3552期分别为T 1和T 2。
将它们拿到月球上去，相应的周期分别为1T '和2T '。
则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >'［ ］ 6．5178：一质点沿x 轴作简谐振动，振动方程为)312cos(1042π+π⨯=-t x (SI)。
从t = 0时刻起，到质点位置在x = -2 cm 处，且向x 轴正方向运动的最短时间间隔为(A) s 81 (B) s 61 (C) s 41 (D) s 31 (E)［ ］7．5179：一弹簧振子，重物的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动。
振动 大学物理习题答案
，x
A12
A22
cos( t
tan 1
A1 ) A2
11-10 质量为 0.4kg 的质点同时参与相互垂直的两个谐振动：
x1
0.08 cos( 3
t
) 6
，
x2
0.06 cos( 3
t
) 3
求：（1）质点的轨迹方程；（2）质点在任一位置所受的力。
解：（1）设 x A1 cos( t 1 ) ， y A2 cos( t 2 ) ，消去 t 得
0.05sin 3
4 3
0.05 cos
0.06sin 4
0.06 cos
11.00 ， 84.8 1.48rad
4
4
（2）
3
1
2k
，3
2k
3 4
，k
0,1,2；
3
2
(2k
1)
，3
2k
5 4
，k
解：（1）由旋转矢量法知 ， 2 2 ， x 0.12 cos( t )
3
T2
3
（2） v d x 0.12 sin( t ) ， a d v 0.12 2 cos( t )
dt
3
dt
3
t 0.5s ， x 0.1039 m ， v 0.1885 m/s ， a 1.03m/s 2
dt2 m J / R2
（2）
k
，T 2 2 m J / R2
《振动力学》习题集(含答案)
《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。
求系统的固有频率。
图E1.1解： 系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。
求系统的固有频率。
图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。
求系统的固有频率。
图E1.3解： 系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。
物理振动试题及答案
物理振动试题及答案一、选择题（每题2分，共20分）1. 简谐振动的周期与振幅的关系是：A. 振幅越大，周期越长B. 振幅越大，周期越短C. 周期与振幅无关D. 振幅越大，周期越不稳定答案：C2. 阻尼振动的振幅会：A. 逐渐增大B. 逐渐减小C. 保持不变D. 先增大后减小答案：B3. 单摆的周期与摆长的关系是：A. 摆长越长，周期越长B. 摆长越长，周期越短C. 摆长与周期无关D. 摆长越长，周期先长后短答案：A4. 以下哪种振动是等幅振动：A. 阻尼振动B. 受迫振动C. 简谐振动D. 非线性振动答案：C5. 波的传播速度与介质的关系是：A. 介质越硬，波速越快B. 介质越软，波速越快C. 波速与介质无关D. 介质越软，波速越慢答案：A6. 波的干涉现象中，两列波的相位关系是：A. 总是相同的B. 总是相反的C. 总是相差180度D. 可以是任意的答案：A7. 波的衍射现象发生的条件是：A. 波长与障碍物尺寸相近B. 波长远大于障碍物尺寸C. 波长远小于障碍物尺寸D. 波速与障碍物无关答案：A8. 声波的频率与音调的关系是：A. 频率越高，音调越低B. 频率越高，音调越高C. 频率与音调无关D. 频率越低，音调越高答案：B9. 光的干涉现象中，两列光波的相位关系是：A. 总是相同的B. 总是相反的C. 总是相差180度D. 可以是任意的答案：A10. 光的衍射现象中，光波通过小孔后：A. 波长变长B. 波长变短C. 波长不变D. 波长变宽答案：C二、填空题（每题2分，共20分）1. 简谐振动的周期公式为 T = _______。
答案：2π√(L/g)2. 单摆的周期公式为 T = _______。
答案：2π√(L/g)3. 阻尼振动的振幅随时间的变化关系可以表示为 A(t) = A0 * e^(-γt)，其中γ是 _______。
答案：阻尼系数4. 波的干涉条件是两列波的频率 _______。
II2_振动和波+详细解答
振动1． 一倔强系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为1T ，若将此弹簧截去一半的长度,下端挂一质量为12m 的物体,则系统振动周期2T 等于 （A ）21T （B ）1T （C ）1T /2 （D ）1T /2 （E ）1T /4（C ）弹簧的弹性系数问题：一根弹簧，弹性系数为k ，把它截短以后，k 不是减小了，而是增大了。
为什么？因为我们知道胡克定律为：f kx =（力的大小），即 f k x=。
下面两根弹簧，本来材料、长度、弹性系数都是完全一样的，但是把其中的一根截短，加上相等的拉力f ，截短以后的弹簧伸长量要小于原来长度的弹簧的伸长量，弹性系数k 增大了。
f12T = 22k k =，下端挂一质量为12m的物体，则系统振动周期2T 为：2T 1112222T π⎛=== ⎝2． 图（下左）中三条曲线分别表示简谐振动中的位移x ，速度v 和加速度a ，下列说法中那一个是正确的？（A ）曲线3、1、2分别表示x 、v 、a 曲线。
（B ）曲线2、1、3分别表示x 、v 、a 曲线。
（C ）曲线1、3、2分别表示x 、v 、a 曲线。
（D ）曲线2、3、1分别表示x 、v 、a 曲线。
（E ）曲线1、2、3分别表示x 、v 、a 曲线。
（E ）位移x 与加速度a 的曲线时刻都是反相的，从图上看曲线1、3反相，曲线2是速度v 曲线；另外，速度比位移的位相超前2π，加速度比速度的位相超前2π，从图上看曲线3比2超前了2π，3是加速度曲线； 曲线2比1超前了2π，1是位移曲线。
3． 在t =0时，周期为T 、振幅为A 的单摆分别处于图（上右）(a)、(b)、(c)三种状态，若选单摆的平衡位置为x 轴的原点，x 轴正向指向右方，则单摆作小角度摆动的振动表达式分别为（1） ； （2） ； （3） 。
关键是写出初位相，用旋转矢量法最方便：0v (a)(b)t（a ）φ= -π/2（b ）φ= π/2（c ）φ= π所以： （1）Y=Acos (t T π2－2π) （2）Y=Acos (t T π2+2π) （3）Y=Acos (t Tπ2+π)4．一系统作谐振动，周期为T ，以余弦函数表达振动时，初位相为零，在0≤t ≤T /2范围内，系统在t = 、 时刻动能和势能相等。
《振动力学》习题集(含答案)
《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。
求系统的固有频率。
图E1.1解： 系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。
求系统的固有频率。
图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。
求系统的固有频率。
图E1.3解： 系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。
大学物理振动习题含答案
一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度 ,然后由静止放手任其振动,从放手时开始计时;若用余弦函数表示其运动方程,则该单摆振动的初相为A B /2 C 0 D2．3002：两个质点各自作简谐振动,它们的振幅相同、周期相同;第一个质点的振动方程为x 1 = A cos t + ;当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处;则第二个质点的振动方程为： A)π21cos(2++=αωt A x B )π21cos(2-+=αωt A x C)π23cos(2-+=αωt A x D )cos(2π++=αωt A x 3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面,振动角频率为;若把此弹簧分割成二等份,将物体m 挂在分割后的一根弹簧上,则振动角频率是 A 2 B ω2 C 2/ω D /24．3396：一质点作简谐振动;其运动速度与时间的曲线如图所示;若质点的振动规律用余弦函数描述,则其初相应为 A /6 B 5/6C -5/6D -/6E -2/35．3552：一个弹簧振子和一个单摆只考虑小幅度摆动,在地面上的固有振动周期分别为T 1和T 2;将它们拿到月球上去,相应的周期分别为1T '和2T ';则有A 11T T >'且22T T >'B 11T T <'且22T T <'C 11T T ='且22T T ='D 11T T ='且22T T >'6．5178：一质点沿x 轴作简谐振动,振动方程为)312cos(1042π+π⨯=-t x SI;从t = 0时刻起,到质点位置在x = -2 cm 处,且向x 轴正方向运动的最短时间间隔为 A s 81 B s 61 C s 41 D s 31 E s 217．5179：一弹簧振子,重物的质量为m ,弹簧的劲度系数为k ,该振子作振幅为A 的简谐振动;当重物通过平衡位置且向规定的正方向运动时,开始计时;则其振动方程为： A)21/(cos π+=t m k A x B )21/cos(π-=t m k A x C)π21/(cos +=t k m A x D )21/cos(π-=t k m A x E t m /k A x cos =v 213030图 8．5312：一质点在x 轴上作简谐振动,振辐A = 4 cm,周期T = 2 s,其平衡位置取作坐标原点;若t = 0时刻质点第一次通过x = -2 cm 处,且向x 轴负方向运动,则质点第二次通过x = -2 cm 处的时刻为A 1 sB 2/3 sC 4/3 sD 2 s9．5501：一物体作简谐振动,振动方程为)41cos(π+=t A x ω;在 t = T /4T 为周期时刻,物体的加速度为 A 2221ωA - B 2221ωA C 2321ωA - D 2321ωA10．5502：一质点作简谐振动,振动方程为)cos(φω+=t A x ,当时间t = T /2T 为周期时,质点的速度为A φωsin A -B φωsin AC φωcos A -φωcos A 11．3030x 1的相位比x 2的相位A 落后/2B 超前C 落后D 超前 12．3042：一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为,T A s B sC sD s 15．5186：已知某简谐振动的振动曲线如图所示,位移的单位为厘米,时间单位为秒;则此简谐振动的振动方程为： A)3232cos(2π+π=t x B )3232cos(2π-π=t x C )3234cos(2π+π=t x D )3234cos(2π-π=t x E)4134cos(2π-π=t x 16．3023：一弹簧振子,当把它水平放置时,它可以作简谐振动;若把它竖直放置或放在固定的光滑斜面上,A 竖直放置可作简谐振动,B 竖直放置不能作简谐振动,C 两种情况都可作简谐振动3270图 竖直放置放在光滑斜面上B x A CA/ -D 两种情况都不能作简谐振动17．3028：一弹簧振子作简谐振动,总能量为E 1,如果简谐振动振幅增加为原来的两倍,重物的质量增为原来的四倍,则它的总能量E 2变为A E 1/4B E 1/2C 2E 1D 4E 118．3393：当质点以频率作简谐振动时,它的动能的变化频率为A 4B 2CD ν2119;3560：弹簧振子在光滑水平面上作简谐振动时,弹性力在半个周期内所作的功为A kA 2B 221kAC 1/4kA 2D 020．5182：一弹簧振子作简谐振动,当位移为振幅的一半时,其动能为总能量的 A 1/4 B 1/2 C 2/1 D 3/4 E 2/3 21．5504：一物体作简谐振动,振动方程为)21cos(π+=t A x ω;则该物体在t = 0时刻的动能与t = T /8T 为振动周期时刻的动能之比为：A 1:4B 1:2C 1:1D 2:1E 4:1 22．5505：一质点作简谐振动,其振动方程为)cos(φω+=t A x ;在求质点的振动动能时,得出下面5个表达式： 1 )(sin 21222φωω+t A m 2)(cos 21222φωω+t A m3 )sin(212φω+t kA4 )(cos 2122φω+t kA5 )(sin 22222φω+πt mA T 其中m 是质点的质量,k 是弹簧的劲度系数,T 是振动的周期;这些表达式中A 1,4是对的B 2,4是对的C 1,5是对的D 3,5是对的E 2,5是对的 23．3008：一长度为l 、劲度系数为k 的均匀轻弹簧分割成长度分别为l 1和l 2的两部分,且l 1 = n l 2,n 为整数. 则相应的劲度系数k 1和k 2为 A 11+=n kn k , )1(2+=n k k B n n k k )1(1+=,12+=n k k C n n k k )1(1+=, )1(2+=n k k D 11+=n kn k , 12+=n k k 24．3562：图中所画的是两个简谐振动的振动曲线;若这两个简谐振动可叠加,则合成的余弦振动的初相为 A π23B πC π21D 0二、填空题：1．3009：一弹簧振子作简谐振动,振幅为A ,周期为T ,其运动方程用余弦函数表示;若0=t 时,1 振子在负的最大位移处,则初相为______________；2 振子在平衡位置向正方向运动,则初相为__________；3 振子在位移为A /2处,且向负方向运动,则初相为______;2．3390：一质点作简谐振动,速度最大值v m = 5 cm/s,振幅A = 2 cm;若令速度具有正最大值的那一时刻为t = 0,则振动表达式为_________________________;3．3557：一质点沿x 轴作简谐振动,振动范围的中心点为x 轴的原点;已知周期为T ,振幅为A ;1若t = 0时质点过x = 0处且朝x 轴正方向运动,则振动方程为 x =____________;2若t = 0时质点处于A x 21=处且向x 轴负方向运动,则振动方程为 x =_______________;4．3816：一质点沿x 轴以 x = 0 为平衡位置作简谐振动,频率为 Hz;t = 0时,x = 0.37 cm 而速度等于零,则振幅是___________,振动的数值表达式为_____________________;5．3817：一简谐振动的表达式为)3cos(φ+=t A x ,已知 t = 0时的初位移为0.04 m,初速度为0.09 m/s,则振幅A =_____________ ,初相 =________________;6．3818：两个弹簧振子的周期都是 s,设开始时第一个振子从平衡位置向负方向运动,经过 s 后,第二个振子才从正方向的端点开始运动,则这两振动的相位差为____________;7．3819：两质点沿水平x 轴线作相同频率和相同振幅的简谐振动,平衡位置都在坐标原点;它们总是沿相反方向经过同一个点,其位移x 的绝对值为振幅的一半,则它们之间的相位差为___________;8．3820：将质量为 0.2 kg 的物体,系于劲度系数k = 19 N/m 的竖直悬挂的弹簧的下端;假定在弹簧不变形的位置将物体由静止释放,然后物体作简谐振动,则振动频率为__________,振幅为____________;9．3033：一简谐振动用余弦函数表示,其振动曲线如图所示,则此简谐振动的三个特征量为A =_____________； =________________； =_______________;移为,;其振动曲线如图所示;根据此图,它的周期T =___________,用余弦函数描述时初相 =_________________;别为 3033图 3041 t 3046 3398图 -t (s) -3399图 356714．3567：图中用旋转矢量法表示了一个简谐振动;旋转矢量的长度为0.04 m,旋转角速度 = 4 rad/s;此简谐振动以余弦函数表示的振动方程为x=__________________________SI;15．3029：一物块悬挂在弹簧下方作简谐振动,当这物块的位移等于振幅的一半时,其动能是总能量的______________;设平衡位置处势能为零;当这物块在平衡位置时,弹簧的长度比原长长l ,这一振动系统的周期为________________________;16．3268一系统作简谐振动, 周期为T ,以余弦函数表达振动时,初相为零;在0≤t ≤T 21范围内,系统在t =________________时刻动能和势能相等;17．3561：质量为m 物体和一个轻弹簧组成弹簧振子,其固有振动周期为T. 当它作振幅为A 自由简谐振动时,其振动能量E = ____________;18．3821：一弹簧振子系统具有 J 的振动能量,0.10 m 的振幅和1.0 m/s 的最大速率,则弹簧的劲度系数为___________,振子的振动频率为_________;19．3401：两个同方向同频率的简谐振动,其振动表达式分别为：)215cos(10621π+⨯=-t x SI , )5cos(10222t x -π⨯=- SI它们的合振动的振辐为_____________,初相为____________;20．3839：两个同方向的简谐振动,周期相同,振幅分别为A 1 = 0.05 m 和A 2 = 0.07 m,它们合成为一个振幅为A = 0.09 m 的简谐振动;则这两个分振动的相位差___________rad;21．5314：一质点同时参与了两个同方向的简谐振动,它们的振动方程分别为)41cos(05.01π+=t x ω SI, )129cos(05.02π+=t x ω SI其合成运动的运动方程为x = __________________________;22．5315：两个同方向同频率的简谐振动,其合振动的振幅为20 cm,与第一个简谐振动的相位差为 –1 = /6;若第一个简谐振动的振幅为310cm = 17.3 cm,则第二个简谐振动的振幅为___________________ cm,第一、二两个简谐振动的相位差1 2为____________;三、计算题：1．3017：一质点沿x 轴作简谐振动,其角频率 = 10 rad/s;试分别写出以下两种初始状态下的振动方程：1 其初始位移x 0 = 7.5 cm,初始速度v 0 = 75.0 cm/s ；2 其初始位移x 0 =7.5 cm,初始速度v 0 =-75.0 cm/s;2．3018：一轻弹簧在60 N 的拉力下伸长30 cm;现把质量为4 kg 的物体悬挂在该弹簧的下端并使之静止,再把物体向下拉10 cm,然 后由静止释放并开始计时;求：1 物体的振动方程；2 物体在平衡位置上方5 cm 时弹簧对物体的拉力；3 物体从第一次越过平衡位置时刻起到它运动到上方5 cm 处所需要的最短时间;3．5191：一物体作简谐振动,其速度最大值v m = 3×10-2 m/s,其振幅A = 2×10-2 m;若t = 0时,物体位于平衡位置且向x 轴的负方向运动;求：1 振动周期T ；2 加速度的最大值a m ；3 振动方程的数值式;4．3391：在一竖直轻弹簧的下端悬挂一小球,弹簧被拉长l 0 = 1.2 cm 而平衡;再经拉动后,该小球在竖直方向作振幅为A = 2 cm 的振动,试证此振动为简谐振动；选小球在正最大位移处开始计时,写出此振动的数值表达式;5．3835在竖直悬挂的轻弹簧下端系一质量为 100 g 的物体,当物体处于平衡状态时,再对物体加一拉力使弹簧伸长,然后从静止状态将物体释放;已知物体在32 s 内完成48次振动,振幅为5 cm;1 上述的外加拉力是多大2 当物体在平衡位置以下1 cm 处时,此振动系统的动能和势能各是多少6．3836在一竖直轻弹簧下端悬挂质量m = 5 g 的小球,弹簧伸长l = 1 cm 而平衡;经推动后,该小球在竖直方向作振幅为A = 4 cm 的振动,求：1 小球的振动周期；2 振动能量;7．5506一物体质量m = 2 kg,受到的作用力为F = -8x SI;若该物体偏离坐标原点O 的最大位移为A = 0.10 m,则物体动能的最大值为多少8．5511 如图,有一水平弹簧振子,弹簧的劲度系数k = 24 N/m,重物的质量m = 6 kg,重物静止在平衡位置上;设以一水平恒力F = 10 N 向左作用于物体不计摩擦,使之由平衡位置向左运动了0.05 m 时撤去力F ;当重物运动到左方最远位置时开始计时,求物体的运动方程;1．3001：C ；2．3002：B ；3C ；5．3552：D ；6．5178：E ； 7．5179：B ；8．5312：B ；9．5501：B ；10．5502：B ；11．3030：B ；12．3042：B ；13．3254：D ；14．3270：B ；15．5186：C ；16．3023：C ；17．3028：D ；18．3393：B ；19．3560：D ；20．5182：D ；21．5504：D ；22．5505：C ；23．3008：C ；24．3562：B ；二、填空题：1．3009： ； - /2；2．3390：)212/5cos(1022π-⨯=-t x 3．3557： )212cos(π-πT t A ；)312cos(π+πT t A 4．3816： 0.37 cm ； )21cos(1037.02π±π⨯=-t x5．3817： 0.05 m ； 或°6．3818：7．3819： 32π±8．3820： Hz ； 0.103 m9．3033： 10 cm /6 rad/s ； /310．3041： 0； 3 cm/s11．3046： /4；)4/cos(1022π+π⨯=-t x SI 12．3398： s ； -2/355065511图13．3399： )cos(1063π+π⨯=-t x a SI ；)2121cos(1063π+π⨯=-t x b SI 14．3567：)214cos(04.0π-πt 15．3029： 3/4； g l /2∆π16．3268： T /8； 3T /817．3561： 222/2T mA π18．3821： 2×102 N/m ； Hz19．3401： 4×10-2 m ； π21 20．3839：21．5314： )1223cos(05.0π+t ω SI 或 )121cos(05.0π-t ω SI22．5315： 10； π-21 三、计算题：1．3017：解：振动方程：x = A cos t +1 t = 0时 x 0 =7.5 cm ＝A cos ；v 0 =75 cm/s=-A sin解上两个方程得：A =10.6 cm----------------1分； = -/4-------------------1分∴ x =×10-2cos10t -/4 SI------------1分2 t = 0时 x 0 =7.5 cm ＝A cos ； v 0 =-75 cm/s=-A sin解上两个方程得：A =10.6 cm, = /4-------------------1分∴ x =×10-2cos10t +/4 SI-------------1分2．3018：解： k = f/x =200 N/m , 07.7/≈=m k ω rad/s----------2分(1) 选平衡位置为原点,x 轴指向下方如图所示(2) t = 0时, x 0 = 10A cos,v 0 = 0 = -A sin解以上二式得： A = 10 cm, = 分 ∴ 振动方程x 2 物体在平衡位置上方5 cm 时,弹簧对物体的拉力：f = mg 而： a = -2x = 2.5 m/s 2∴ f =4 － N= N----------------------------------------------3分 3 设t 1时刻物体在平衡位置,此时x = 0,即： 0 = A cos t 1或cos t 1 = 0∵ 此时物体向上运动,v < 0；∴ t 1 = /2,t 1= /2 =s------------------------1分再设t 2时物体在平衡位置上方5 cm 处,此时x = -5,即：-5 = A cos t 1,cos t 1 =－1/2∵ 0, t 2 = 2/3, t 2=2 /3 = s-----------------------------2分t = t 1-t 2 = － s ＝ s-------------------------1分3．5191：解：1 v m = A ∴ = v m / A = s-1∴ T = 2/ s--------------------------------------------3分 2 a m = 2A = v m = ×10-2 m/s 2 ------------------------------2分 3 π=21φ , x = )215.1cos(π+t SI-----------3分 4．3391：解：设小球的质量为m ,则弹簧的劲度系数： 0/l mg k =选平衡位置为原点,向下为正方向．小球在x 处时,根据牛顿第二定律得：220d /d )(t x m x l k mg =+- 将 0/l mg k =,代入整理后得：0//d d 022=+l gx t x ∴ 此振动为简谐振动,其角频率为-------------------3分 π===1.958.28/0l g ω------------------------2分 设振动表达式为：)cos(φω+=t A x由题意：t = 0时,x 0 = A=2102-⨯m,v 0 = 0,解得： = 0--------------------------------------------------1分∴)1.9cos(1022t x π⨯=--------------------------2分 5．3835：解一：1 取平衡位置为原点,向下为x 正方向．设物体在平衡位置时弹簧的伸长量为l ,则有l k mg ∆=, 加拉力F 后弹簧又伸长x 0,则：0)(0=+-+∆x l k mg F解得： F = kx 0-------------------------------2分由题意,t = 0时v 0 = 0；x = x 0 则：02020)/(x x A =+=ωv ----------2分又由题给物体振动周期4832=T s,可得角频率 T π=2ω, 2ωm k =∴444.0)/4(22=π==A T m kA F N --------------------------------------------1分2 平衡位置以下 1cm 处：)()/2(2222x A T -π=v ---------------------------2分 221007.121-⨯==v m E KJ-----------------------------------------------2分2222)/4(2121x T m kx E p π== = ×10-4 J-------------------------1分解二：1 从静止释放,显然拉长量等于振幅A 5 cm,kA F =----------------2分2224νωπ==m m k , =Hz--------------------------------------------2分∴ F =N-------------------------------------------------------1分l 0 mg x kl 0k (l +x ) mg2 总能量：221011.12121-⨯===FA kA E J-------------------2分当x = 1 cm 时,x = A /5,E p 占总能量的1/25,E K 占24/25---------------2分∴ 21007.1)25/24(-⨯==E E K J,41044.425/-⨯==E E p J------------1分6．3836：解：1 )//(2/2/2l g m k m T ∆π=π=π=ω= s ------------------3分2 22)/(2121A l mg kA E ∆== = ×10-3 J ----------------------------------------2分7．5506：解：由物体受力F = -8x 可知物体作简谐振动,且和F = -kx 比较,知 k = 8 N/m,则：4/2==m k ωrad/s 2--------------------------------------------------2分 简谐振动动能最大值为：2221A m E Km ω== J----------------3分8．5511：解：设物体的运动方程为： )cos(φω+=t A x 恒外力所做的功即为弹簧振子的能量：F × = J---------------------------2分当物体运动到左方最远位置时,弹簧的最大弹性势能为 J,即：5.0212=kA J,∴ A = 0.204 m--------------------------------------------------------------------2分A 即振幅;4/2==m k ω rad/s 2 ⇒ = 2 rad/s---------------------------2分按题目所述时刻计时,初相为 = ------------------------------------------2分∴ 物体运动方程为： )2cos(204.0π+=t x SI----------------2分。
大学物理机械振动习题含答案
t （s ）v （m.s -1）12m v m vo1.3题图题图 第三章 机械振动一、选择题1．质点作简谐振动，距平衡位置2。
0cm 时，加速度a=4.0cm 2/s ,则该质点从一端运动到另一端的时间为（一端运动到另一端的时间为（ C ）A:1.2s B: 2.4s C:2.2s D:4.4s 解：解：s T t T xax a 2.2422,2222,22===\=====p pw pw w2．一个弹簧振子振幅为2210m -´,当0t =时振子在21.010m x -=´处，且向正方向运动，则振子的振动方程是：[ A ] A ：2210cos()m3x t p w -=´-；B ：2210cos()m 6x t pw -=´-；C ：2210cos()m 3xt pw -=´+ ；D ：2210cos()m 6x t pw -=´+；解：由旋转矢量可以得出振动的出现初相为：3p-3．用余弦函数描述一简谐振动，若其速度与时间（v —t ）关系曲线如图示，则振动的初相位为：[ A ] A ：6p ；B ：3p ；C ：2p ；D ：23p ；E ：56p解：振动速度为：max 0sin()v v t w j =-+0t =时，01sin2j =，所以06p j =或056p j = 由知1.3图，0t =时，速度的大小是在增加，由旋转矢量图知，旋转矢量在第一象限内，对应质点的运动是由正最大位移向平衡位置运动，速度是逐渐增加的，旋转矢量在第二象限内，对应质点的运动是由平衡位置向负最大位移运动，速度是逐渐减小的，所以只有06pj =是符合条件的。
符合条件的。
4．某人欲测钟摆摆长，将钟摆摆锤上移1毫米，测得此钟每分快0。
1秒，则此钟摆的摆长为（长为（ B ）A:15cm B:30cm C:45cm D:60cm 解：单摆周期解：单摆周期 ,2glT p=两侧分别对T ，和l 求导，有：求导，有：cm m m T dT dl l l dl T dT 3060)1.0(2121,21=-´-==\= 1.2题图题图xyoxy二、填空题1．有一放置在水平面上的弹簧振子。
《大学物理》振动练习题及答案解析
《大学物理》振动练习题及答案解析一、简答题1、如果把一弹簧振子和一单摆拿到月球上去,它们的振动周期将如何改变? 答案：弹簧振子的振动周期不变，单摆的振动周期变大。
2、完全弹性小球在硬地面上的跳动是不是简谐振动，为什么？答案：不是，因为小球在硬地面上跳动的运动学方程不能用简单的正弦或余弦函数表示，它是一种比较复杂的振动形式。
3、简述符合什么规律的运动是简谐运动答案：当质点离开平衡位置的位移`x`随时间`t`变化的规律，遵从余弦函数或正弦函数()ϕω+=t A x cos 时，该质点的运动便是简谐振动。
或：位移x 与加速度a 的关系为正比反向关系。
4、怎样判定一个振动是否简谐振动？写出简谐振动的运动学方程和动力学方程。
答案：物体在回复力作用下，在平衡位置附近，做周期性的线性往复振动，其动力学方程中加速度与位移成正比，且方向相反:x dtxd 222ω-=或：运动方程中位移与时间满足余弦周期关系:)cos(φω+=t A x 5、分别从运动学和动力学两个方面说明什么是简谐振动？答案：运动学方面：运动方程中位移与时间满足正弦或余弦函数关系)cos(φω+=t A x 动力学方面：物体在线性回复力作用下在平衡位置做周期性往复运动，其动力学方程满足 6、简谐运动的三要素是什么？ 答案： 振幅、周期、初相位。
7、弹簧振子所做的简谐振动的周期与什么物理量有关？答案： 仅与振动系统的本身物理性质：振子质量m 和弹簧弹性系数k 有关。
8、如果弹簧的质量不像轻弹簧那样可以忽略，那么该弹簧的周期与轻弹簧的周期相比，是否有变化，试定性说明之。
答案：该振子周期会变大，作用在物体上的力要小于单纯由弹簧形变而产生的力，因为单纯由形变而产生的弹力中有一部分是用于使弹簧产生加速度的，所以总体的效果相当于物体质量不变，但弹簧劲度系数减小，因此周期会变大。
9、伽利略曾提出和解决了这样一个问题：一根线挂在又高又暗的城堡中，看不见它的上端而只能看见其下端，那么如何测量此线的长度？答案：在线下端挂一质量远大于线的物体，拉开一小角度，让其自由振动，测出周期T ，便可依据单摆周期公式glT π2=计算摆长。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
大学物理振动习题含答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度 ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相为 (A) (B) /2 (C) 0 (D) ［ ］2．3002：两个质点各自作简谐振动，它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(t + )。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。
则第二个质点的振动方程为： (A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x ［ ］ 3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，振动角频率为。
若把此弹簧分割成二等份，将物体m 挂在分割后的一根弹簧上，则振动角频率是(A) 2 (B) ω2 (C) 2/ω (D) /2 ［ ］4．3396：一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述，则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 ［ ］5．3552：一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2。
将它们拿到月球上去，相应的周期分别为1T '和2T '。
则有 (A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >' ［ ］6．5178：一质点沿x 轴作简谐振动，振动方程为)312cos(1042π+π⨯=-t x (SI)。
从t = 0时刻起，到质点位置在x = -2 cm 处，且向x 轴正方向运动的最短时间间隔为(A) s 81 (B) s 61 (C) s 41 (D) s 31 (E) s 21 ［ ］7．5179：一弹簧振子，重物的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动。
当重物通过平衡位置且向规定的正方向运动时，开始计时。
则其振动方程为：(A))21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x (C))π21/(cos +=t k m A x (D) )21/cos(π-=t k m A x v (m/s) t (s) Omm v 21(E) t m /k A x cos = ［ ］8．5312：一质点在x 轴上作简谐振动，振辐A = 4 cm ，周期T = 2 s ，其平衡位置取作坐标原点。
若t = 0时刻质点第一次通过x = -2 cm 处，且向x 轴负方向运动，则质点第二次通过x = -2 cm 处的时刻为(A) 1 s (B) (2/3) s (C) (4/3) s (D) 2 s ［ ］9．5501：一物体作简谐振动，振动方程为)41cos(π+=t A x ω。
在 t = T /4（T 为周期）时刻，物体的加速度为 (A) 2221ωA - (B) 2221ωA (C) 2321ωA - (D) 2321ωA ［ ］10．5502：一质点作简谐振动，振动方程为)cos(φω+=t A x ，当时间t = T /2（T 为周期）时，质点的速度为(A) φωsin A - (B) φωsin A (C) φωcos A -φωcos A ］ 11．3030x 1的相位比x 2的相位(A) 落后π/2 (B) 超前π/2 (C) 落后π(D) 超前π ［ ］12．3042：一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为A 21，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为 ［ ］13．3254：一质点作简谐振动，周期为T 。
质点由平衡位置向x 轴正方向(A) T /4 (B) T /6 (C) T /8 (D) T 14．3270(A) 2.62 s (B) 2.40 s(C) 2.20 s (D) 2.00 s 15．5186：已知某简谐振动的振动曲线如图所示，位移的单位为厘米，时间单位为秒。
则此简谐振动的振动方程为：(A) )3232cos(2π+π=t x (B) )3232cos(2π-π=t x (C))3234cos(2π+π=t x (D) )3234cos(2π-π=t x3270图x (C)(E))4134cos(2π-π=t x ［ ］ 16．3023：一弹簧振子，当把它水平放置时，它可以作简谐振动。
若把它(A) (B) (C) 两种情况都可作简谐振动(D) 两种情况都不能作简谐振动 ［ ］ 17．3028：一弹簧振子作简谐振动，总能量为E 1，如果简谐振动振幅增加为原来的两倍，重物的质量增为原来的四倍，则它的总能量E 2变为(A) E 1/4 (B) E 1/2 (C) 2E 1 (D) 4 E 1 ［ ］18．3393：当质点以频率ν 作简谐振动时，它的动能的变化频率为(A) 4 ν (B) 2 ν (C) ν (D) ν21 ［ ］19。
3560：弹簧振子在光滑水平面上作简谐振动时，弹性力在半个周期内所作的功为(A) kA 2 (B) 221kA (C) (1/4)kA 2 (D) 0 ［ ］20．5182：一弹簧振子作简谐振动，当位移为振幅的一半时，其动能为总能量的(A) 1/4 (B) 1/2 (C) 2/1 (D) 3/4 (E) 2/3 ［ ］21．5504：一物体作简谐振动，振动方程为)21cos(π+=t A x ω。
则该物体在t = 0时刻的动能与t = T /8（T 为振动周期）时刻的动能之比为：(A) 1:4 (B) 1:2 (C) 1:1 (D) 2:1 (E) 4:1 ［ ］22．5505：一质点作简谐振动，其振动方程为)cos(φω+=t A x 。
在求质点的振动动能时，得出下面5个表达式： (1) )(sin 21222φωω+t A m (2))(cos 21222φωω+t A m(3) )sin(212φω+t kA (4) )(cos 2122φω+t kA (5) )(sin 22222φω+πt mA T其中m 是质点的质量，k 是弹簧的劲度系数，T 是振动的周期。
这些表达式中(A) (1)，(4)是对的 (B) (2)，(4)是对的 (C) (1)，(5)是对的(D) (3)，(5)是对的 (E) (2)，(5)是对的 ［ ］23．3008：一长度为l 、劲度系数为k 的均匀轻弹簧分割成长度分别为l 1和l 2的两部分，且l 1 = n l 2，n 为整数. 则相应的劲度系数k 1和k 2为(A) 11+=n kn k ， )1(2+=n k k (B) n n k k )1(1+=，12+=n k k 竖直放置 放在光滑斜面上A/ -A(C) n n k k )1(1+=， )1(2+=n k k (D)11+=n kn k ， 12+=n k k ［ ］ 24．3562：图中所画的是两个简谐振动的振动曲线。
若这两个简谐振动可叠加，则合成的余弦振动的初相为(A) π23 (B) π (C) π21 (D) 0 ［ ］二、填空题：1．3009：一弹簧振子作简谐振动，振幅为A ，周期为T ，其运动方程用余弦函数表示。
若0=t 时，(1) 振子在负的最大位移处，则初相为______________；(2) 振子在平衡位置向正方向运动，则初相为__________；(3) 振子在位移为A /2处，且向负方向运动，则初相为______。
2．3390：一质点作简谐振动，速度最大值v m = 5 cm/s ，振幅A = 2 cm 。
若令速度具有正最大值的那一时刻为t = 0，则振动表达式为_________________________。
3．3557：一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点。
已知周期为T ，振幅为A 。
(1)若t = 0时质点过x = 0处且朝x 轴正方向运动，则振动方程为 x =____________。
（2）若t = 0时质点处于A x 21=处且向x 轴负方向运动，则振动方程为 x =_______________。
4．3816：一质点沿x 轴以 x = 0 为平衡位置作简谐振动，频率为 0.25 Hz 。
t = 0时，x = -0.37 cm 而速度等于零，则振幅是___________，振动的数值表达式为_____________________。
5．3817：一简谐振动的表达式为)3cos(φ+=t A x ，已知 t = 0时的初位移为0.04 m ，初速度为0.09 m/s ，则振幅A =_____________ ，初相φ=________________。
6．3818：两个弹簧振子的周期都是0.4 s ，设开始时第一个振子从平衡位置向负方向运动，经过0.5 s 后，第二个振子才从正方向的端点开始运动，则这两振动的相位差为____________。
7．3819：两质点沿水平x 轴线作相同频率和相同振幅的简谐振动，平衡位置都在坐标原点。
它们总是沿相反方向经过同一个点，其位移x 的绝对值为振幅的一半，则它们之间的相位差为___________。
8．3820：将质量为 0.2 kg 的物体，系于劲度系数k = 19 N/m 的竖直悬挂的弹簧的下端。
假定在弹簧不变形的位置将物体由静止释放，然后物体作简谐振动，则振动频率为__________，振幅为____________。
9．3033：一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为A =_____________；ω =________________；φ=_______________。
t10．3041：一简谐振动曲线如图所示，则由图可确定在t = 2s 时刻质点的位移为____________，速度为__________________。
11．3046：一简谐振动的旋转矢量图如图所示，振幅矢量长2cm ，则该简谐振动的初相为__________。
振动方程为______________________________。
12．3398：一质点作简谐振动。
其振动曲线如图所示。
根据此图，它的周期T =___________，用余弦函数描述时初相 φ =_________________。