拔河的力学分析

合集下载

拔河中的力学浅析

拔河中的⼒学浅析拔河是我国群众喜闻乐见的团队竞技（娱乐）项⽬。

在我国，拔河起源于2000多年前春秋时期的楚国。

据《墨⼦·鲁问》记载，在楚越战争期间，由于越国位于楚国下游河流，战事失利时可顺流⽽退，鲁班为帮助楚国发明的“钩强”，在越国顺流⽽退时，“钩强”可以“钩”住逃跑的越国船只；并且在越国进攻猛烈时，还可以⽤来顶住来进攻的船只。

后来，为了训练这⼀战术形成⼀种称之为“牵钩”的游戏（训练⽅法）。

据唐朝封演（⽣卒年不详，今河北景县⼈）《封⽒闻见记》中说：“拔河，古谓之牵钩，襄汉风俗。

”说明，拔河这⼀名字⾄少在唐朝时就已经正式使⽤了。

世界上许多国家都有拔河运动，只是规则不尽相同。

1900-1920之间，拔河还是奥运会⽐赛项⽬，1920年奥运会上由于缺乏统⼀规则⽽发⽣激烈争吵，之后奥委会经表决将拔河从奥运竞赛项⽬中去除。

1960年，英国、瑞典拔河协会制定了国际拔河⽐赛规则，并成⽴了国际拔河联合会(Tug of War inInternationaI Federation，TWIF) 正式成⽴，1964年在巴尔⼲运动会上组织了⾸次国际拔河⽐赛，1965年开始举办欧洲锦标赛，1975年开始举办世界锦标赛。

此后欧洲锦标赛和世界锦标赛每年交替进⾏，让拔河重返奥运⼀直是该协会的重要⼯作之⼀。

拔河正式⽐赛⽤绳截⾯周长为10-12.5厘⽶，总长度不得少于33.5⽶。

绳上不许打结或其它任何有助于运动员握持的东西。

⽐赛时每队8⼈，按全队运动员的总体重分为480、520、560、600、640、680、720及720公⽄以上等8个级别进⾏⽐赛。

⽐赛种类有室内赛和室外赛、男⼦组与⼥⼦组、成年组与少年组等。

⽐赛时（请参见下图），只要将下图中红⾊标线拉过⾃⼰⼀⽅⽩线位置 (2m) 即获胜。

本⽂试图从⼒学⾓度分析⼀下拔河技巧中的⼒学技巧。

拔河实际就是在⽐较双⽅谁使的⼒更加有效（拉动对⽅）。

根据⽜顿第三定律，双⽅所受的⼒是始终相同的，所不同的是同样的⼒施加于双⽅产⽣出了不同的效果，这就体现出双⽅运动员使⼒的技巧性。

拔河的力学分析与技巧 (1)

拔河的力学分析与技巧精仪系机械06 郭瑶瑶 000608 摘要：本文简述了拔河中的力学特点，对拔河的方式、技巧、进行了深入的探讨与分析。

主要从摩擦力和重力矩两方面进行论述。

谈起拔河，可以算是我国一项古老的体育活动了。

比起别的体育活动，拔河可以说是运动场面最热烈的一个了。

而且它能体现出团队精神和力量，开展也很容易。

每年我校大一新生们都会举办一次拔河比赛，那场面的热烈，真可以说是喧呼动地，振惊远近了。

拔河的比赛规则很简单，就是两对人谁能把对方拉过边界，谁就能获胜。

中途不能摔倒。

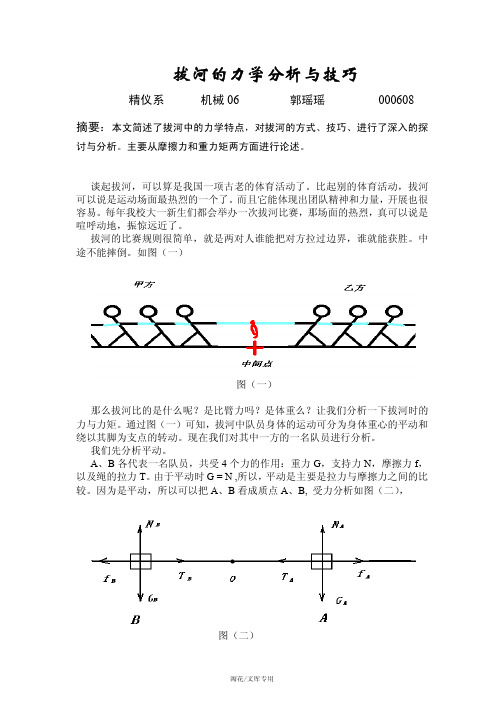
如图（一）图（一）那么拔河比的是什么呢？是比臂力吗？是体重么？让我们分析一下拔河时的力与力矩。

通过图（一）可知，拔河中队员身体的运动可分为身体重心的平动和绕以其脚为支点的转动。

现在我们对其中一方的一名队员进行分析。

我们先分析平动。

A、B各代表一名队员，共受4个力的作用：重力G，支持力N，摩擦力f，以及绳的拉力T。

由于平动时G = N ,所以，平动是主要是拉力与摩擦力之间的比较。

因为是平动，所以可以把A、B看成质点A、B, 受力分析如图（二），图（二）对绳子中点O来说，将取决于双方拉力T与摩擦力f的差F的大小。

其中，Fa = Ta – f a ; Fb = Tb – f b拉力是通过肌肉收缩而产生的力量，它与队员的身体素质有关，时拔河中起决定性作用的力学因素。

在双方拉力非常悬殊的情况下，肯定是拉力大的一方获胜。

可如果在拉力相当的情况下，若能增大摩擦力，就能削弱对方的拉力，一次来取得胜利。

而增大摩擦力，主要有两个因素，即由f = u N 可知，可以增加摩擦系数u ，即让队员穿上摩擦系数较大的鞋子。

还可以增大N，即让体重大的队员参加。

但摩擦力只是取胜的重要因素，若两方拉力悬殊太大，光靠增大摩擦力还是无法取胜。

此外，还要考虑拉力矩与重力矩的作用。

把拔河的人作为刚体来看，拔河的队员除了身体的平动以外，还存在以脚为支点的转动。

让我们以其中一名队员为例来分析。

拔过河的都知道，牛顿第三定律太扯了

拔过河的都知道，牛顿第三定律太扯了拔河比赛的力学探析内容提要：在教授牛顿第三定律时，一些老师会令同学做一个“对拉双秤”实验，让力气一大一小的两名同学相向而立，对拉钩在一起的两个弹簧秤。

由此宣称，秤上读数一致，牛顿第三定律得到实验验证。

本文认为，这种实验具有很大的迷惑性和欺骗性，实验结论更是错误的。

完整的实验及分析表明，牛顿第三定律的一个重要义项（作用力和反作用力大小相等）是不成立的。

笔者重新设计了实验，并给出实验真正支持的“角力定律”。

牛顿第三定律：“作用力和反作用力大小相等、方向相反、作用在同一条直线上。

”在讲解这条定律时，为了让学生容易理解、加深印象，一些老师会组织同学做一个对拉两个弹簧秤实验。

这个实验被众多人士认为是证明牛顿第三定律成立的经典实验。

实验一般由两名学生来做，其他同学围观。

做实验的两名同学通常一男一女，男生一看就是大力士，女生则看起来就弱不禁风。

大力士和“弱不禁风”离开一定距离，站在原地不动，各执一个弹簧秤，让两秤钩住，然后进行下列步骤：1，双方一齐拉动弹簧秤。

2，大力士主动拉弹簧秤，女生只是被动拉住弹簧秤。

3，女生主动拉弹簧秤，大力士只是被动拉住弹簧秤。

老师和其他同学全程围观，并得出结论。

这个实验很有观赏性，也很能调动学生的热情，但是，它有两大问题，一是该实验不完整，极具迷惑性和欺骗性；二是对弹簧秤上面产生的读数，其理解是错误的。

这些错误是致命的，它不仅误导了实验者自己，也误导了其他人，使人们误以为牛顿第三定律是个经得起实验验证的定律。

一、实验的致命伤：误将张力当拉力让大力士和女生站在原地不动对拉两个钩在一起的弹簧秤，无论是双方一齐拉动，还是一方主动一方被动拉，确实都会出现两个弹簧秤上的读数一致的情况，但是据此就得出结论，大力士作用于女生的拉力其大小等于女生作用于大力士的拉力，这是很荒谬的。

这个实验隐含的前提是，大力士手上的弹簧秤上面的读数表示的是大力士的拉力值，女生手上的弹簧秤上面的读数表示的是女生的拉力值。

对拔河比赛的力学分析

龙源期刊网对拔河比赛的力学分析作者：赵俊梅来源：《中学物理·初中》2012年第08期在拔河比赛中，假如甲队胜，甲队施的拉力一定比乙队的拉力大吗？答案是否定的.老师解释后学生往往还是似懂非懂.分析原因，是受力分析没掌握好，首先应选择研究对象，然后进行受力分析.1 以两个队伍为研究对象忽略绳子的质量，就好像两个人手拉手单人拔河一样，根据牛顿第三定律，作用力和反作用力大小相等，方向相反，无论哪一队胜，无论处在哪一阶段，甲队对乙队的拉力F2的大小始终等于乙队对甲队的拉力F1的大小.上面的解释学生能理解，但输赢的原因是什么呢？决定胜负的原因是各方与地面摩擦力的大小.这要以两队伍分别为研究对象，研究水平方向的受力情况，如图1所示.两队在比赛的相持阶段未分输赢时，双方可看作处于静止状态，都受平衡力，也就是甲方受到的地面给的静摩擦力F1等于F1，乙方受到的地面给的静摩擦力F2等于F2；因F1 与F2大小相等，这四个力大小都相等.在相持阶段随着拉力的增大，这四个力一起增大；当力达到并要超过乙方的最大静摩擦力，还没有达到甲方的最大静摩擦力时，乙方就开始滑动（因滑动摩擦力小于最大静摩擦力），此时这乙方的摩擦力F2小于F2了，乙方也就输了；（此时甲方受的摩擦力F1还等于此时的拉力F1.）可以说拔河比赛比的是本队与地面的最大静摩擦力的大小，哪一方与地面的最大静摩擦力小，哪一方输.2 以绳子为研究对象需考虑绳子的质量，绳子受重力.绳子静止时是相持阶段，绳子加速时决定胜负.绳子受重力和两方的拉力如图2所示.当绳子静止时，绳子受平衡力，只考虑水平方向，F1cosα=F2cosβ （α是F1与水平方向的夹角，β是F2与水平方向的夹角，此时F1与 F2不一定相等）.当绳子由静止开始运动时，就看F1cosα和F2cosβ哪个大，如果F1cosα>F2cosβ，绳子向甲方运动，甲方胜了，此时F1 不一定大于F2.也就是说胜利的一方拉力不一定大.两队比的是拉力在水平方向的分力的大小.事实上，实际问题因素还有很多，不可能完全分析清楚，例如双方用力的时机不同，往往影响胜负.绳子的重力与拉力比很小，是完全可以忽略的，常用第一种解释.。

不同拔河姿势的力学分析

不同拔河姿势的力学分析摘要：本文把人体简化为刚体进行力学分析和研究，通过比较不同姿势所能承受的拉力和力矩，对拔河比赛中不同情况采用不同身体姿势的效果进行了讨论，说明正确技术的运用是比赛胜负成败的关键。

为拔河比赛中如何采取正确的姿势提供理论依据。

关键词：拔河力学分析姿势一、引言拔河比赛是人数相等的双方对拉一根粗绳以比较力量的对抗性体育娱乐活动。

它可以锻炼身体，增强体质，更主要的是能增进人与人之间的感情，激发集体主义精神，让人们从中懂得“团结就是力量”的道理。

拔河容易开展以及运动场面的热烈、壮观而格外受到人们的欢迎，始终受到广大人民群众的喜爱,具有广泛的群众基础。

我校学员亦经常在节假日期间举行单位之间的拔河比赛。

然而，广大的爱好者对拔河技术却知之甚少，通常都会认为拔河比赛纯粹是比谁的力气大，没有什么技术可言。

这种观点无疑是错误的。

二、模型假设1．忽略绳子质量，由牛顿第三定律知绳子张力T处处相等；2．将人体简化为 3 刚体（重心以上为 a 段，重心以下至膝关节为 b 段，膝关节以下为 c段）的力学模型作为分析对象；3．不考虑手滑，即认为绳子与人固连在一起；4．不考虑参赛人员体重以及身高的差异；5. 忽略参赛人员的鞋底材料差异，即认为摩擦系数μ不因人而异。

三、不同姿势下的力学分析（一）高低重心姿势比赛时根据重心位置的高低可分为高重心姿势和低重心姿势。

当比赛双方采用的姿势不一样时，绳子必定与水平面形成一定夹角。

现对这两种姿势分析如下：参数设置：T—为绳子的最大拉力；N—地面的支持力；f—地面产生的摩擦力；μ—地面最大静摩擦系数；α—拉力与水平面所成的夹角（取逆时针为正）；β—重力与支撑点连线和地面所成的夹角；C—脚底支撑点。

首先比较双方姿势对抗拉力的效果。

当地面摩擦力未达到最大时，摩擦力 f 大小都为T cosα，双方产生的静摩擦力一样大，且都能保持平衡。

这时无须比较，而且在比赛中也无实际意义。

因此，重点应分析双方将被拉动处于临界状态时能对抗的最大拉力的大小。

试论拔河比赛中的力学原理

试论拔河比赛中的力学原理拔河比赛是一种体育运动，也是一种常见的物理现象，但它的原理却并不那么简单，其中许多问题概念性很强，必须注意分析。

现就拔河的力学原理讨论于下。

一、绳的力学质量为m的一根绳，它的两端分别受到沿绳向外的拉力f1和f2，设f1＞f2，则绳上各处的张力如何？为简化问题便于研究起见，可将绳均匀地分成质量相等的n段，且质量集中于各段的一点，如图1所示。

用整体法建立动力学方程与第2段，第2与第3段，…直至第（n-1）与第n段之间的张分别是：直至上述结果表明，n为正整数，t1＞t2＞……＞tn-1，当绳向f1方向作加速运动时，绳上各处的张力不等，前端的张力大，愈往后绳上张力愈小。

且绳的质量愈大、加速度愈大这个差别就愈明显。

当绳处于静止或匀速运动时，加速度a=0，则绳上各点的张力均相等。

当a≠0，而绳的质量在运动物的整体中可略去不计时，m≈0，f1-f2=ma≈0。

则亦有f1=t1=……=tn-1=f2，此时绳上各点的张力亦相等。

故当加速度a很小、绳的质量亦很小时，绳上各点的张力均相等，即f1=t1=……=tn-1=f2。

二、拔河比赛是连结体的力学拔河比赛的两队人和一根绳可看作是三个物体组成的连结体。

为便于研究，按通常情况设甲乙两队均由10人组成，总质量相等，m1=m2=m=700千克，绳的质量m=7千克（实际上中间那段质量还要小些）。

拔河比赛总是从静止开始的，故这个连结体不论向任何方向发生运动，总得在所受外力的合力不为零时才能发生。

设m1受外力f1，m2受外力f2，且f1＞f2，连结体就具有向左的加速度a（如图2所示）。

用隔离法建立它们的动力学方程：甲队： f1-t1=m1a ①绳：t1-t2=ma ②乙队： t2-f2=m2a ③用整体法建立的动力学方程f1-f2=（m1＋m2＋m）a ④联立①②③④式解得故t1-t2≈0。

当然，直接从②式的m<<m和a≈0，同样可得到t1≈t2的结果。

拔河比赛的胜负是由双方拉力的大小决定的吗

拔河比赛的胜负是由双方拉力的大小决定的吗拔河比赛的胜负是由双方拉力的大小决定的吗？决定拔河比赛胜负的力学观点是什么？现以甲、乙两队比赛时的受力情况作一解释，设绳子质量忽略不计，每队各受四个力的作用：绳对人的拉力、地面对人的摩擦力、人的重力和地面对人的弹力（如图所示）。

如果我们把甲、乙和绳子作为一个整体来研究，21F F 和是一对内力，而且是一对作用力与反作用力。

系统处于不管什么运动状态，它们总是大小相等，方向相反，相互作用在两个不同的物体上的。

故甲拉乙的力总是等于乙拉甲的力，不存在哪方对绳子的拉力更大的情况。

由此可知，甲、乙双方的拉力关系不是决定胜负的因素。

决定胜负的因素应该是作用在系统上的水平外力，即地面对甲、乙的静摩擦力21摩摩、F F 。

若甲、乙双方和地面间的摩擦系数相同，则最大静摩擦力的大小取决与它们对地面的压力。

这个压力在数值上等于它们的体重，如果21G G >,那么21摩摩F F >，其结果是甲胜乙，这也就是为什么大人总能胜过小孩的缘故。

由此看来，似乎只能是甲胜乙负，绝不可能是乙胜甲负，这种观点是否正确呢？事实上体重小的还是有可能胜过体重大的，那么决定胜负的主要因素是什么呢，是人的脚斜向前下方的对地的蹬力。

这个力的水平分力就是人对地面的静摩擦力，这个力越大，地面反过来作用与人的静摩擦力也就越大，那么该队就能取胜。

若人处于平衡状态，则外力的合力矩为零，若以脚着地点为支点（假设后脚与地面无作用力），应有：011=-b G a F ，如果b G a F 11>，人就要向前倾倒，为了防止倾倒，运动员的脚就会不由自主地向前移动而导致失败，这就是拔河比赛时，人为什么脚总是向斜前下方蹬地而身体向后倾的原因。

那么，当斜向下的蹬力的大小一定时，是不是其水平分量越大越好呢，改变蹬力的角度，尽量增大其水平分力，以增大地面的摩擦力，这种想法是有一定道理的，但人与地面的摩擦力有一个最大值，这个最大值与人与地面的正压力有关，水平分力增大，其正压力必然要减小，导致最大静摩擦力的减小。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

拔河的力学分析
拔河是我国古代的民间体育活动,历史悠久,深受广大民众的喜爱.那么拔河比的到底是什么呢?是力臂还是力矩.本篇论文就试从力学角度进行分析和探讨.
下面是双方队员拔河的情景.
我们可以把拔河的力学分析分成两个部分,第一:绳子的受力分析;第二,队员的受力分析.分析可知,拔河的队员的运动可分为身体重心的平动和绕以脚为轴的定点转动.
为了分析方便,我们把上图做一下简化.即把双方的人简化为简化为两个人,就是下图所示的情况来进行分析.
一.平动实质绳子拉力和与地面摩擦力的比较
上图的受力分析如下图所示
以A为研究对象,A共受四个力的作用: 重力G A, 支持力N A, 绳子对A的拉力T BA,摩擦力f A.在竖直方向上, 重力G A和支持力N A平衡,即G A = N A,所以平动时取决定做用的是绳子对A的拉力T BA和摩擦力f A的合力.令F xA= T BA- f A.
当T BA> f A.时, F xA>0,这时A就会受被拉动而产生水平的平动.当F xA<0,A就会拉
动B平动.当然当F xA=0,此时由A和B组成的系统就处于一种平衡状态,A和B谁也不能拉动对方.所以可以说摩擦力是决定谁能取胜因素.
摩擦力又是由谁决定的呢?由f =μN (1)和N=G (2),可得:
f=μG=μmg
所以真正得决定因素是人的质量,它决定了人所受的摩擦力的大小,所以一个大胖子和一个瘦瘦的小个子拔河,小个子是没有胜利的机会的.当然这里的模型忽略了人手的力量,如果大胖子的手上打滑,那他体重再大也没用.
二.以脚为轴的定轴状动.
拔河的人除了平动之外,还参与了一个以脚为轴的定轴转动.我们在看拔河比赛的时候都会看到拔河的人都在向后倾,如下图:
这是因为人的重力和绳子的拉力对人的脚都产生了一个力矩,这里是力矩平衡的问题.
即拉力矩M T与重力矩G T平衡问题.我们也可以像上次那样把问题简化一下,只研究一个人的受力情况.
为了保持人的身体平衡,人与地面就必须有一定的倾斜角度,此时脚底可以看成是定点,摩擦力为无穷大,所以不必考虑摩擦力的影响.
设人与地面间的夹角是θ,当θ≥90 °,即直立身体或身体向前倾的状态,此时重力矩不发挥作用或者起到相反的作用.这是人将进一步向前倾.因此拔河队员应采取后倾的姿势,即θ<90°的情况.
下面对θ<90°的情况作进一步的分析:设人的身高为H,倾角为θ,TBA与GA的作用点分别再人的肩部和重心处,大约相当于身高的0.8和0.6倍.TBA与GA距离支点e的距离分别为h和l,当拉力矩与重力矩平衡时有:
由图可知:h = 0.8 H sin θ , l = 0.6Hcos θ ,带入
上式得:
T BA 0.8 sin θ = G A 0.6cos θ
由上式可知,当T BA 大小一定时,力矩的大小只与G A 和θ有关,
所以下面将从这两个方面分别进行分析.
(1) 重力矩和倾斜角θ的关系
如左图正旋和余旋函数的变化规律,在0<θ<90°,sin θ为增
函数,而cos θ为减函数.在θ<45°时,有sin θ>cos θ.所以在这
个区间之内是有利于增大重力矩的.但是也并不是说θ越小越好,在人体全脚底接触地面接触地面时最有利于拔河,此时θ大约在30°左右.
另外,也可以得出θ与摩擦系数μ的关系为:
θ=arctan(k/μ)
由此可知μ越大, θ将越小.即在摩擦系数较大的情况下, θ可更小一些:而在摩擦系数较小时, θ会更大一些.即在地面较光滑时人的身体应站得直一些,而磨擦系数较大时,人可以将身体倾斜得更厉害一些.
(2) 重力矩与体重的关系
在T AB 和θ一定时,使G A 增大,则重力矩也可以增大.由此可见体重不仅可以增大摩
擦力,还可以增大重力矩的作用.
由以上的分析可知,在拔河中,最主要的因素是体重G A 和人与地面的倾角θ.而G A 是取
得胜利的很重要的决定性因素.同时要注意人的倾斜程度,并且倾斜程度应根据地面的摩擦系数μ决定.了解了以上的决定因素,相应的找合适的拔河队员,并注意适当的拔河方法,就会取得比赛的胜利.
H。