最新计算机中的数制和编码
计算机中的数制和编码

试比较下面二组数字: 3×102 和 3×1032 3.14 和 3.14159265
用科学计数法表示:N=2P×S
S 尾数(N的全部有效数字) P 阶码(指明小数点的位置) P和S均用二进制数表示,2为阶码的底
定点数:小数点位置固定不变, P=0 浮点数:小数点位置随P可变,P有一定的取值范围
+43=00101011 -43=10101011
真值 机器数
真值 机器数
机器数:带有数码化正负号的数 真值:机器数所代表的实际数值
3、有符号数的三种表示方法 原码表示方法
+43=00101011 -43=10101011
反码表示方法 (负数是原码求反)
+43=00101011 -43=11010100
二、不同进制数的相互转换
二进制数与八进制数、十六进制数之间的相互转换
方法简便
8=23
16=24
三位二进制数对应一位八进制数 四位二进制数对应一位十六进制数
二进制
八进制
以小数点为中心,整数部分从低位向高 位(即从右向左)每三位用一个八进制数来 表示,最后一组不足三位时,用 0 补齐;小 数部分从高位向低位(即从左向右)每三位 用一个八进制数来表示,最后不足三 位时, 用0补齐。
+1
……
……
……
126
+126
+126
127
+127
+127
128
-0
-127
129
-1
-126
……
……
254
-126
-1
计算机中的数制与编码

计算机中的数制与编码在计算机科学中,数制和编码是非常重要的概念。
数制是一种数学表示法,用于表示不同类型的数值。
而编码是将字符、符号或信息转化为特定形式的过程。
数制和编码在计算机中扮演着至关重要的角色,它们用于存储、传输和处理数字和数据。
数制(Number System)在计算机中,常见的数制有二进制、十进制、八进制和十六进制。
每种数制有其各自的特点和用途。
1. 二进制(Binary System):二进制是最常见和基础的数制,在计算机中广泛使用。
它只包含两个数字0和1,以2为基数。
计算机内部存储和处理的数据都是以二进制形式表示的。
每个二进制位称为一个bit(二进制位),每8位为一个字节(Byte)。
2. 十进制(Decimal System):十进制是我们日常生活中最常用的数制,以10为基数,包含0-9的数字。
在计算机中,通常使用十进制数制进行人机交互和显示。
3. 八进制(Octal System):八进制以8为基数,包含0-7的数字。
在计算机中,八进制表示法不太常用,但是在Unix操作系统中仍然使用八进制权限表示法。
4. 十六进制(Hexadecimal System):十六进制以16为基数,包含0-9的数字和A-F的字母。
在计算机中,十六进制数制常用于表示内存地址和字节编码。
十六进制数更加简洁和紧凑,便于人们阅读和理解。
编码(Coding)在计算机中,数据和字符需要以特定的方式进行编码,以便计算机可以正确存储和处理它们。
常见的编码方式包括ASCII码、Unicode、UTF-8和UTF-16等。
1.ASCII码:ASCII(American Standard Code for Information Interchange)是一种最早的字符编码标准,用于将字符映射为对应的数字编码。
ASCII码使用7位二进制数表示128个字符,包括英文字母、数字、标点符号和控制字符等。
2. Unicode:Unicode是一种字符编码标准,为世界上几乎所有的字符建立了唯一的数字表示。
计算机中的数值和编码

计算机中的数制和编码一、数制的概念:数制是用一组固定的数字和一套统一的规则来表示数目的科学方法。
按照进位方式计算的数制叫做进位数制。
例如:逢十进一即为十进制,逢二进一为二进制,逢八进一为八进制,逢十六进一为十六进制。
进位计数制有两个要素:基数和权值。
1、基数:它是指各种进位计数制中允许选用基本数码的个数。
例如:十进制的数码有0、1、2、3、4、5、6、7、8、9十个数码,所以十进制的基数为10;二进制的数码有0、1两个数码,所以二进制的基数为2;八进制的数码有0、1、2、3、4、5、6、7八个数码,所以八进制的基数为8;十六进制的数码有0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六个数码,所以十六进制的基数为16。
2、权值:每个数码所表示的数值等于该数码乘以一个与数码所在位置相关的常数,这个常数叫权值。
其大小是以基数为底,数码所在位置的序号为指数的整数次幂。
例如:十进制数356.4=3×100+5×10+6×1+0.4=3×102+5×101+6×100+4×10-1(3在百位上,所以3×100=3×102;5是在十位上,所以5×10=5×101;6是在个位上,所以6×1=6×100;0.4为小数,所以0.4=4×10-1)。
二、十进制(D ecimal notation)及其特点:1、两个特点:①、十个数码:0、1、2、3、4、5、6、7、8、9;②、进位方法:逢十进一,借一当十。
(满了10个就得进一位)2、基数:103、按权展开式:任意一个a位整数和b位小数的十进制数D可以表示为:D=D a-1×10a-1+D a-2×10a-2+…+D0×100+D-1×10-1+D-2×10-2+…+D-b×10-b4、十进制在书写中的三种表达方式:128或者128D或(128)10三、二进制(B inary notation)及其特点:1、两个特点:①、两个数码:0、1;②、进位方法:逢二进一,借一当二。
进制及编码

3. 计算机中的编码
BCD码
用二进制数为十进制数编码,每一位十进制数需要由 四位二进制数来表示。在计算机中较常用的是8421 BCD码(在以后的章节中简称BCD码)。 例如:(208)10=(0010 0000 1000)8421BCD (1001 0001 0111 0101) 8421BCD=(9175)10
16
3. 计算机中的编码
8421BCD码编码表 例:78D用8421BCD码表示为0111 1000
17
3. 计算机中的编码
ASCII码
记住的ASCII码:
0DH表示回车,0AH表示换行 目前,在微机、通信设备和仪器仪表中广泛采用的 30H~39H表示:‘0’~‘9’ 是美国标准信息交换码ASCII码。其中包括数字0~9、 41H表示‘A’ 英文26个大、小写字母、运算符、标点及其他的一些 61H表示‘a’ 控制符号。 例如:数字0的ASCII码为0110000B 或 30H 数字9的ASCII码为0111001B 或 39H 字母A的ASCII码为1000001B 或 41H ASCII码多用于微型计算机的输入/输出设备(如电 传打字机)及在数据传送过程中进行奇偶校验。
可以转换为移位与加法运算
除法运算(注意除数为2时的规律)
可以转换为移位与减法运算
21
乘除运算例
00001011×0100 =00101100B
00001011÷0100=00000010B
即:商=00000010B
余数=11B
22
2. 无符号数的表示范围:
0 ≤ X ≤ 2n-1 若运算结果超出这个范围,则产生溢出。 对无符号数:运算时,当最高位向更高位 有进位(或借位)时则产生 溢出。
计算机中的数制及其编码

一、计算机中的数制及其转换
2. 数制之间的转换
(4) 二、十六进制之间的转换
二进制十六进制: 以小数点为界,分别向左、向右四位一组分段,不足四位 补0(整部在前,小数部分在后),然后将每段换成对应的十 六进制数码。 十六进制二进制: 将每位十六进制数码换成对应的四位二进制数,然后去前 后无效的0。 例7 (10110101.10101011)2 =(1011 0101. 1010 1011)2 =(B5.AB)16 (56A.C4)16 =(0101 0110 1010. 1100 0100)2
一、计算机中的数制及其转换
2. 数制之间的转换
(2) 十进制数转换为非十进制数
例4 (123.45)10 =(? 2 123……..1 2 61…….1 2 30……0 2 15…...1 2 7…..1 2 3…..1 2 1….1 0 )2 低位
0
1
高位
除 到 商 为 0 时 停 止
1
1 0 0 1
一、计算机中的数制及其转换
2. 数制之间的转换
(1) 非十进制数转换为十进制数
例2:(345.67)8 = 3*82 + 4*81 + 5*80 + 6*8-1 + 7*8-2 = 192 + 32 + 5 + 0.75 + 0.109375 = (229.859375)10
例3: (2FA.D)16 = 2*162 + 15*161 + 10*160 + 13*16-1 = 512 + 240 + 10 + 0.8125 = (762.8125)10
+101.0001 1111.0001 10.1 ×100 000 000 +101 10100 101.0001 11001.0101 101 101 101
1-2计算机的数制与编码
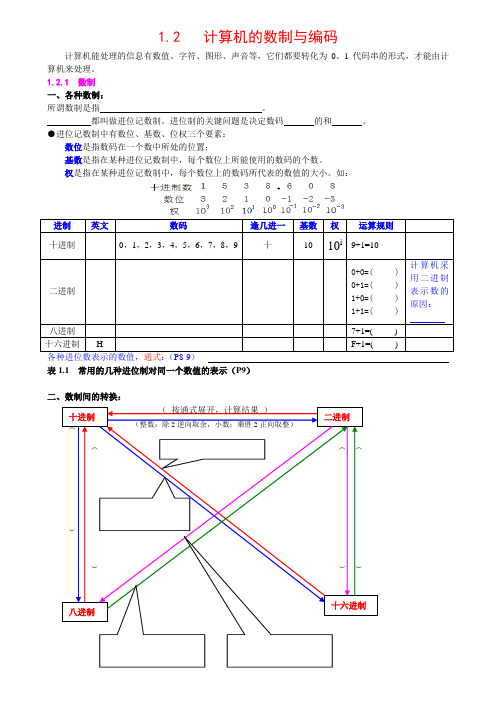
1.2 计算机的数制与编码计算机能处理的信息有数值、字符、图形、声音等,它们都要转化为0、1代码串的形式,才能由计算机来处理。
1.2.1 数制 一、各种数制:所谓数制是指 。
都叫做进位记数制。
进位制的关键问题是决定数码 的和 。
●进位记数制中有数位、基数、位权三个要素: 数位是指数码在一个数中所处的位置;基数是指在某种进位记数制中,每个数位上所能使用的数码的个数。
权是指在某种进位记数制中,每个数位上的数码所代表的数值的大小。
如:表1.1 常用的几种进位制对同一个数值的表示(P9)二、数制间的转换:例:(重点:十进制与二进制的互相转换)●各种进制转十进制●十进制转各种进制●二进制转八进制、八进制转二进制与二进制转十六进制、十六进制转二进制练习:P39:20、21、22、23、24、25、26、27、28、29(写在课本上)如何检查?(计算器!)1.2.2 ASCII码●通称为字符。
字符没有数值意义。
为了便于计算机的应用推广,这些字符必须用统一的规定编码方式来表示。
目前在国际上广泛采用“”表示、和作为使用的等。
●ASCII码的英文全称:,中文。
●ASCII码用位0、1代码串来编码一个符号,每个符号占的存储空间,字节最高位(左)为,作奇偶校验用。
(注:1字节= 位,一个字符的ASCII码占位,余下位用作)●ASCII码给出了个数码,个英文字母,个通用符号,个动作控制符的编码标准。
◆例:查表P308(1)字母“A”的ASCCII的二进制表示为:,十六进制表示为:,十进制表示为:(2)将字符“2”的ASCII码当成数值,转换为十进制数得到50,数字字符“5”的ASCII码转换为十进制数应得到●ASCII码的比较:(详见附录1:P308)空格(space)的ASCCII码是32‘0’~‘9’的ASCCII码是48~57‘A’~‘Z’的ASCCII码是65~90‘a’~‘z’的ASCCII码是97~1221.2.3 汉字编码1.国标码GB 2312-80《》1级汉字个,按顺序排列、2级汉字个,按排列,汉字有6763个,常用符号、字母、图形符号等682个,共计7445个。
计算机中的数制与编码

计算机中的数制与编码一、数制1、什么是进位计数制数制也称计数制,是指用一组固定的符号和统一的规则来表示数值的方法。
按进位的原则进行计数的方法,称为进位计数制。
比如,在十进位计数制中,是按照“逢十进一”的原则进行计数的。
常用进位计数制:a、十位制(Decimal notation);b、二进制(Binary notation);c、八进制(Octal notation);d、十六进制数(Hexdecimal notation)2、进位计数制的基数与位权"基数"和"位权"是进位计数制的两个要素。
(1)基数:所谓基数,就是进位计数制的每位数上可能有的数码的个数。
例如,十进制数每位上的数码,有"0"、"1"、"3",…,"9"十个数码,所以基数为10。
(2)位权:所谓位权,是指一个数值的每一位上的数字的权值的大小。
例如十进制数4567从低位到高位的位权分别为100、101、102、103。
因为:4567=4x103+5x 102+6x 101 +7x100(3)数的位权表示:任何一种数制的数都可以表示成按位权展开的多项式之和。
比如:十进制数的435.05可表示为:435.05=4x102+3x 101+5x100+0x10-1 +5x 10-2位权表示法的特点是:每一项=某位上的数字X基数的若干幂次;而幂次的大小由该数字所在的位置决定。
3、二进制数计算机中为何采用二进制:二进制运算简单、电路简单可靠、逻辑性强(1)定义:按“逢二进一”的原则进行计数,称为二进制数,即每位上计满2 时向高位进一。
(2)特点:每个数的数位上只能是0,1两个数字;二进制数中最大数字是1,最小数字是0;基数为2;比如:10011010与00101011是两个二进制数。
(3)二进制数的位权表示:(1101.101)2=1x23+1x 22+0x 21+1x 20+1x2-1 +0x 2-2+1x2-3(4)二进制数的运算规则1 加法运算① 0+0=0 ③ 1+1=10② 0+1=1+0=12 乘法运算① 0×0=0 ③ 1×1=1② 0×1=1×0=04、八进位制数(1)定义:按“逢八进一”的原则进行计数,称为八进制数,即每位上计满8时向高位进一。
计算机常用数制及编码

计算机常用数制及编码1.二进制数制:二进制是计算机中最基本的数制,只包含两个数字0和1、它是一种逢二进一的计数法,每位上的数值以2为底数的幂来表示。
例如,二进制数1101表示1*2^3+1*2^2+0*2^1+1*2^0=13、在计算机中,二进制数被广泛应用于存储和运算等操作。
2.八进制数制:八进制使用8个数字0-7来表示。
它是二进制数制的一种压缩表示方法,每3位二进制数可以表示为一位八进制数。
例如,二进制数1101可以表示为八进制数15、八进制数在计算机界并不常见,但在一些特定场景下仍然有一定的应用。
3.十进制数制:十进制是我们常用的数制,使用10个数字0-9来表示数值,每位上的数值以10为底数的幂来表示。
例如,十进制数123表示1*10^2+2*10^1+3*10^0=123、十进制数制通常用于人类的日常计算中,但在计算机中也会涉及到十进制的处理,例如在涉及到金额、日期和时间等数字的场景中。
4.十六进制数制:十六进制使用16个数字0-9和A-F来表示,其中A-F分别表示十进制数10-15、它是二进制数制的另一种压缩表示方法,每4位二进制数可以表示为一位十六进制数。
十六进制数常用于计算机领域,因为它们可以更紧凑地表示二进制数。
例如,二进制数1101可以表示为十六进制数D。
编码系统是为了实现计算机和人类之间的信息交流而发展的。
下面介绍几种常见的编码系统:1.ASCII码:ASCII(American Standard Code for Information Interchange)是最早和最广泛使用的字符编码系统之一、它使用7位二进制数(扩展ASCII使用8位二进制数)来表示128(或256)个字符,包括英文字母、数字、符号等。
ASCII码可以用于存储和表示文本文件中的字符。
2. Unicode编码:3.UTF-8编码:UTF-8(Unicode Transformation Format - 8-bit)是一种对Unicode进行可变长度编码的字符编码系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、不同进制数的相互转换
二进制数与八进制数、十六进制数之间的相互转换
方法简便
8=23
16=24
三位二进制数对应一位八进制数 四位二进制数对应一位十六进制数
二进制
八进制
以小数点为中心,整数部分从低位向高 位(即从右向左)每三位用一个八进制数来 表示,最后一组不足三位时,用 0 补齐;小 数部分从高位向低位(即从左向右)每三位 用一个八进制数来表示,最后不足三 位时, 用0补齐。
二进制、八进制、十六进制转换成十进制
-----------按权展开相加
例:(101.101)2=1×22+0×21+1×20+1×2-1+0×2-2+1×2-3=(5.625)10 (34.6)8=3×81+4×80+6×8-1=(28.75)10 (2AB.C)16=2×162+10 ×161+11 ×160+12 ×16-1 = 512 + 160 + 11 + 0.75 = (683.75)10
0110 0001B 61H ‘a’
0011 1001B 39H ‘9’
0110 0010B 62H ‘b’
…………
0110 0011B 63H ‘c’
00001000B 0AH
换行LF …………
00001011B 0DH 回车CR
0010 0000B 20H 空格SP
三、汉字的编码
西文字符的结构决定了它只要128个ASCII字符就 能够满足计算机进行信息处理的需要。而中文字符 有数万之众,为了适应计算机处理汉字信息的需要, 1981年我国颁布了“信息交换用汉字编码字符 集 ·基本集”(GB2312 - 80)供汉字信息在不同的 计算机系统之间交换信息使用 , 该标准称为 “ 国标 码”。
例如:
将(111001011010.10111001)2转换为十六进制数。 (1110 0101 1010 . 1011 1001)2 E 5 A. B 9 =(E5A.B9)16
常用不同进制数在书写时的表示方法
10011100B
B
二进制数
337Q
Q
八进制数
4B7DH
H
十六进制数
1339D 1339
常用的ASCII码(需要记住)
0011 0000B 30H ‘0’
0100 0001B 41H ‘A’
0011 0001B 31H ‘1’
0100 0010B 42H ‘B’
…………
0100 0011B 43H ‘C’
0011 0111B 37H ‘7’
…………
0011 1000B 38H ‘8’
D
十进制数
十进制数
§2.2 码制 字符的常用编码
一、BCD码(二—十进制数)
编码方式:用四位二进制数表示一位十进制数
0000
0
0001
1
0010
2
0011
3
0100
4
0101
5
0110
6
0111
7
1000
8
1001
9
1010 1011 1100 1101 1110 1111
丢弃不用
一、BCD码(二—十进制数)
进 入 夏 天 ,少 不了一 个热字 当头, 电扇空 调陆续 登场, 每逢此 时,总 会想起 那 一 把 蒲 扇 。蒲扇 ,是记 忆中的 农村, 夏季经 常用的 一件物 品。 记 忆 中 的故 乡 , 每 逢 进 入夏天 ,集市 上最常 见的便 是蒲扇 、凉席 ,不论 男女老 少,个 个手持 一 把 , 忽 闪 忽闪个 不停, 嘴里叨 叨着“ 怎么这 么热” ,于是 三五成 群,聚 在大树 下 , 或 站 着 ,或随 即坐在 石头上 ,手持 那把扇 子,边 唠嗑边 乘凉。 孩子们 却在周 围 跑 跑 跳 跳 ,热得 满头大 汗,不 时听到 “强子 ,别跑 了,快 来我给 你扇扇 ”。孩 子 们 才 不 听 这一套 ,跑个 没完, 直到累 气喘吁 吁,这 才一跑 一踮地 围过了 ,这时 母 亲总是 ,好似 生气的 样子, 边扇边 训,“ 你看热 的,跑 什么? ”此时 这把蒲 扇, 是 那 么 凉 快 ,那么 的温馨 幸福, 有母亲 的味道 ! 蒲 扇 是 中 国传 统工艺 品,在 我 国 已 有 三 千年多 年的历 史。取 材于棕 榈树, 制作简 单,方 便携带 ,且蒲 扇的表 面 光 滑 , 因 而,古 人常会 在上面 作画。 古有棕 扇、葵 扇、蒲 扇、蕉 扇诸名 ,实即 今 日 的 蒲 扇 ,江浙 称之为 芭蕉扇 。六七 十年代 ,人们 最常用 的就是 这种, 似圆非 圆 , 轻 巧 又 便宜的 蒲扇。 蒲 扇 流 传 至今, 我的记 忆中, 它跨越 了半个 世纪, 也 走 过 了 我 们的半 个人生 的轨迹 ,携带 着特有 的念想 ,一年 年,一 天天, 流向长
例如:
将(16.327)8转换为二进制数。 (16.327)8=(001 110 . 011 010 111)2 1 6.3 2 7 =(1110.011010111)2
二进制
十六进制
以小数点为中心,整数部分从低位向高位(即 从右向左)每四位用一个十六进制数来表示,最后 一组不足四位时,用 0 补齐;小数部分从高位向低 位( 即从左向右 )每四位用一个十六进制数来表 示,最后不足四 位时,用 0 补齐。
西文字符在计算机中的表示
10个数字:0~9 26个大写字母:A~Z 26个小写字母:a~z 32个可打印字符 34个不可打印字符
共128个字符
ASCII码的代码组成结构
b7 b6 b5 b4 b3 b2 b1 b0
0
最高位 高3位
低4位
bi=0或1 (i=0~6) 共有27=128种不同的表示。
微机中一个字节是8位,尽管ASCII码只用了低7 位,在计算机中一个ASCII字符仍用一个字节( 8bit ) 的空间来存放,最高位保持为“0”
组合式BCD码:一个字节(8位)为2位BCD码
(01101001)BCD = (69)10
非组合式BCD码(8)10
1、BCD码实际上是十进制数(不是二进制数)
2、BCD码转换成二进制数应按十进制数向二进制 数转换的办法进行
二、ASCII码(美国标准信息交换码)
长 的 时 间 隧 道,袅
计算机中的数制和编码
§2.1 数制 不同进制数的相互关系和转换
一、计数制
权
十进制数的计数方法
例:427=4×102+2×101+7×100
1、有十个符号:0、1、2、…、9
基 = 10
2、每个符号所代表的数与所处位置有关
3、遵从“逢十进一”的规则
二、不同进制数的相互转换
