高等数学自测题第13章自测题答案
八年级上册数学第十三章检测题(包含答案)

八年级上册数学第十三章测试卷知识要点一:轴对称1.观察下列图形,其中不是轴对称图形的是()A B C D2.下列图案中,是轴对称图形且有两条对称轴的是()A B C D3.下列说法错误的是()A.关于某条直线对称的两个三角形一定全等B.轴对称图形至少有一条对称轴C.全等三角形一定能关于某条直线对称D.角是关于它的平分线对称的图形4.如图,Rt△ABC中,∠ACB =90°,∠A =50°,将其折叠,使点A落在边CB上的A’处,折痕为CD,则∠A'DB等于()A.10°B.20°C.30°D.40°第4题第5题5.如图所示,若△ABC△A’B’C’沿着直线l对折后能够完全重合,我们说这两个图形关于这条直线对称,也就是说这两个三角形成_____,直线l叫作它们的_____,点B 和点B’叫作_____,AC=_____.∠A=_____.6.从轴对称的角度来看,下列各幅图中哪一个与众不同?请说明理由,(1)(2)(3)(4)(5)答:_____(填序号),其理由为:______________________________________________. 知识要点二:线段的垂直平分线的性质7.如图所示,CD是AB的垂直平分线,若AC=1.2cm,BD=2.3 cm,则四边形ACBD 的周长是()A.3.5cm B.7cm C.4.7cm D.4.6cm第7题第8题8.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为()A.6 B.5 C.4 D.39.如图所示,用两根钢索加固直立的电线杆,若要使钢索AB与AC的长度相等,需添加条件_____,理由是_____.第9题第10题10.如图所示,在Rt△ABC中,∠C=90°,沿着过点B的一条直线BE折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数等于_____.11.如图,△ABC中,D,E分别为AB,BC的中点,且FD⊥AB.若AC=10,BF=5,求证:FE⊥BC.知识要点三:画轴对称图形12.下列结论正确的是()A.如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形B.任何一个图形都具有对称轴,有的图形有不止一条对称轴C.如果△ABC≌△A₁B₁C₁,则△ABC和△A₁B₁C₁一定是轴对称图形D.如果△ABC和△A₁B₁C₁成轴对称,则△ABC≌△A₁B₁C₁.13.点P(a,b)是平面直角坐标系中的任意一点,则p(a,b)关于x轴的对称点P₁的坐标是_____,P(a,b)关于y轴的对称点P₂的坐标是_____14.如图所示,在平面直角坐标系内,线段AB垂直于y轴,垂足为B,且AB=2.如果将线段AB沿y轴翻折,点A落在点C处,那么点C的横坐标是_____.15.如图所示,在△ABC中,BC=AC,D是BC上一点,DF⊥AB,E为垂足,BF∥AC,试说明△BDF是轴对称图形,并指出它的对称轴.16.如图所示,写出点A,B,C关于y轴对称的点的坐标,并作与△ABC关于x轴对称的图形.知识要点四:等腰三角形17.如图所示,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB 于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF=CF,其中正确的有()A.①B.①②C.①②③D.①②③④18.如果等腰三角形的两个内角的比是2:5,那么底角的度数为_____.19.等腰三角形一腰上的高与底边的夹角为35°,则这个三角形的顶角为_____.20.如图所示,已知△ABC,CH⊥AB于H,点D在AC的延长线上,若∠BCD=3∠A.求证: AH =BC+BH.知识要点五:等边三角形21.若三角形三个内角的比为1:2:3,则它的最短边与最长边的比为()A.1:3 B.1:2 C.2:3 D.1:4 22.如图所示,△ABC是等边三角形,AD是∠BAC的平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD,其中正确的个数为()A.3个B.2个C.1个D.0个第22题图第23题图23.如图所示,在等边△ABC中,AB=3,∠ABC,∠ACB的平分线相交于O点,过O 作OE∥AB,OF∥AC,分别交BC于点E,F,则△OEF的周长为_____.24.如图所示,D为等边△ABC内任意一点,BP=AB,∠DBP=∠DBC,∠BPD=30°,试判断△ABD的形状,并说明理由.知识要点六:最短路径问题25.如图所示,直线l是一条河,P,Q两地相距8千米,P,Q两地到l的距离分别为2千米、5千米,欲在l的某点M修建一个水泵站,向P,Q两地供水.现有如下四种铺设管道方案,图中实线表示铺设的管道,则铺设的管道最短的是()26.如图所示,已知牧马营地在P处,每天牧马人要赶着马群先到河边饮水,再带到草地吃草,然后回到营地,请你替牧马人设计出最短的放牧路线.参考答案1.C 2.D 3.C 4.A5.轴对称图形对称轴对称点A'C’∠A’6.(5)因为它有无数条对称轴,其余图形均有两条对称轴7.B 8.B9.BD=DC 线段垂直平分线上的点到线段两个端点的距离相等10. 30°11.证明:∵D是AB中点,且FD上AB,∴FD是AB的垂直平分线.∴AF=BF.又∵AF=5 ,AC=AF+ CF=10.∴CF=5.∴BF=CF.∴F在线段BC的垂直平分线上,又∵E是BC中点,∴FE ⊥BC.12.D 13.(a,-b) (-a,6)14.-215.沿AB所在直线折叠,由DF⊥AB及∠FBE=∠A =∠ABC,知DE与用重合,BF与BD重合,所以点D与点F重合,△BDE与△BFE重合.所以△BDF是轴对称图形,直线AB是对称轴.16.A’(4,1)B’(1,-1)C’(3,2)图略17.C 18. 40°或75°19. 70°20.在AH上取一点E,作EH= BH,连接CE.∵CH⊥AB,∴CE=BC, ∠CBE=∠CEB.又∵∠BCD为△ACB的外角,∴∠BCD=∠A+∠ABC.又∵∠BCD=3∠A,∴∠ABC=2∠A,∴∠CEB=2∠A.又∵∠CEB为△ACE的外角,∴∠CEB= ∠A+∠ACE,∴∠A=∠ACE.∴.AE=CE,∴.AE=BC.∴AH=AE+HE=BC+BH.21.B 22.A 23.324. △ABD是等腰三角形,其中BD= AD.理由如下:连接CD.在△BDP与∠B DC中,BP=BC=AB,∠D BP=∠DBC,BD=BD.∴△BDP≌△BDC (SAS),∴∠BCD =∠BPD= 30°.故∠ACD= ∠ACB- ∠B CD=30°.∴∠BCD= ∠ACD.在△ACD与△BCD中,AC=BC,∠ACD=∠BCD,CD =CD,∴△ADC≌△BDC (SAS),∴BD =AD,∴△ABD是等腰三角形.25.B26.(1)作P关于河流的对称点P₁:(2)作P关于草地的对称点P₂:(3)连接P₁P₂,分别交河流和草地于A,B两点;(4)连接PA, PB.最短路径就是:P-A -B-P.。
(完整版)高等数学自测题第13章自测题1答案

第13章自测题1答案一、选择题(每小题4分)1、答:(A).2、答:(B).3、设C为分段光滑的任意闭曲线,ϕ(x)及ψ(y)为连续函数,则的值(A)与C有关(B)等于0(C)与ϕ(x)、ψ(x)形式有关(D)2π答( ) 答:(B)4、曲线积分的值(A)与曲线L及起点、终点均有关(B)仅与曲线L的起点、终点有关(C)与起点、终点无关(D)等于零答( ) 答:(B)二、填空题(每小题4分)1、L是xoy平面上具有质量的光滑曲线,其线密度为ρ(x,y),则L关于ox轴的转动惯量用曲线积分表示为___________. (ρ(x,y)为连续函数)。
答:2、设L是单连通域上任意简单闭曲线,a,b为常数,则 _______.答: 03、力构成力场,(y>0)若已知质点在此力场内运动时场力所做的功与路径无关,则m=________.答:14、设是某二元函数的全微分,则m=______.答:2三、解答题(每小题6分)1、求曲线ρ=a(1+cosθ)的长度(0≤θ≤2π, a>0).2、设曲线L 为摆线x =a (t -sin t ), y =a (1-cos t ) (0≤t ≤2π)的一拱,其线密度为1,求L 的形心坐标( ).3、求质点M (x ,y )受作用力沿路径L 所作的功W L 是从A (2,3)沿直线到B (1,1)的直线段. 解:L 的直线方程:12-=x y从2=x 到1=x⎰⋅=LsF w d ϖϖ⎰-++=AByx y x x y d )2(d )3(⎰-=12d )115(xx223-=4、质线L 为 其上任意点(x ,y )处的密度为 ,求此质线对于原点处的单位质点的引力 .5、设质线L 的方程为L 上任意点(x ,y )处的线密度为求质线L 的质量M 及质心坐标(ξ,η).解:L 的极坐标方程为 )cos 1(θ-=a r 0≤θ≤2πθθθd 2sin2d 'd 22a r r s =+=θθθμπ⎰⎰⎰-=+==2022d 2sin)cos 1(2d 1d asy x as M LLa 332=⎰⎰⎰-=-⋅⋅==ππθθθθθθθμξ2022022d 2sin )2sin 21(43d 2sin cos )cos 1(21d a a M Msx La 78-=由于L 关于OX 轴对称,221y x a+=μ关于y 是偶函数,故0=η∴ 质心:)0 , 78(a -6、计算 ,其中D 是由y =0和摆线x =a (t -sin t ), y =a (1-cos t ) 0≤t ≤2π 所围成的区域。
人教版 八年级数学上册第13章 13.1---13.3能力检测题含答案

人教版八年级数学上册第13章13.1---13.3能力检测题含答案13.1 轴对称一、选择题(本大题共10道小题)1. 在下列图形中是轴对称图形的是()2. 如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是()A.12 B.13 C.14 D.153. [2018·襄阳] 如图,在△ABC中,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,与BC,AC分别交于点D,E.若AE=3 cm,△ABD的周长为13 cm,则△ABC的周长为()A.16 cmB.19 cmC.22 cmD.25 cm4. 将一张长与宽的比为2∶1的长方形纸片按图①②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④中的纸片展开铺平,所得到的图案是()5. [2018·河北] 图是由“○”和“□”组成的轴对称图形,则该图形的对称轴是直线()A.l1B.l2C.l3D.l46. 如图,已知钝角三角形ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以点C为圆心,CA长为半径画弧①;步骤2:以点B为圆心,BA长为半径画弧②,交弧①于点D;步骤3:连接AD,交BC的延长线于点H.则下列叙述正确的是()A.BH垂直平分线段ADB.AC平分∠BADC.S△ABC=BC·AHD.AB=AD7. 对于△ABC,嘉淇用尺规进行如下操作:如图,(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点D;(2)作直线AD交BC边于点E.根据嘉淇的操作方法,可知线段AE是()A.△ABC的高线B.△ABC的中线C.边BC的垂直平分线D.△ABC的角平分线8. 如图,在△ABC中,点D在BC上,将点D分别以AB,AC为对称轴,画出对称点E,F,并连接AE,AF.根据图中标示的角度,∠EAF的度数为()A.113°B.124°C.129°D.134°9. 把一张长方形纸片按图2①②所示的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是图3中的()10. 如图,点P在直线l外,以点P为圆心,大于点P到直线l的距离为半径画弧,交直线l于点A,B;保持半径不变,分别以点A,B为圆心画弧,两弧相交于点Q,则PQ⊥l.上述尺规作图的依据是()A.一条直线与两平行线中的一条垂直,必然与另一条直线也垂直B.线段垂直平分线上的点与这条线段两个端点的距离相等,两点确定一条直线C.与线段两个端点距离相等的点在这条线段的垂直平分线上,两点确定一条直线D.角的内部到角的两边的距离相等的点在角的平分线上二、填空题(本大题共6道小题)11. 如图所示的4组图形中,左右两个图形成轴对称的是第________组(填序号).12. 如图所示图案是几种车的标志,在这几个图案中,轴对称图形有________个,其中只有一条对称轴的轴对称图形有________个,对称轴最多的轴对称图形有________条对称轴.13. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.14. 如图,点P在∠AOB内,M,N分别是点P关于OA,OB的对称点,连接MN交OA于点E,交OB于点F.若△PEF的周长是20 cm,则MN的长是________cm.15. 如图,DE是△ABC的边AC的垂直平分线,若BC=9,AD=4,则BD=________.16. 画图:试画出下列正多边形的所有对称轴,并完成表格.根据上表,猜想正n边形有条对称轴.三、解答题(本大题共4道小题)17. 把下列正多边形对称轴的条数填入表格中.图形正多边形的边数345678对称轴的条数________________________ 根据上表,请你就一个正n边形对称轴的条数做一个猜想,写出猜想的结果.(不用证明)18. 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若△ABC与△EBC的周长分别是26 cm和16 cm,求AC的长.19. 如图,在△ABC中,∠ACB=90°,BE平分∠ABC交AC于点E,DE垂直平分AB交AB于点D.求证:BE+DE=AC.20. 如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.人教版八年级数学13.1 轴对称培优训练-答案一、选择题(本大题共10道小题)1. 【答案】B2. 【答案】B[解析] ∵DE是△ABC的边AB的垂直平分线,∴AE=BE.∵AC =8,BC=5,∴△BEC的周长=BE+EC+BC=AE+EC+BC=AC+BC=13.3. 【答案】B[解析] 由作图可知,DE垂直平分线段AC,∴AD=CD,AE=EC=3 cm.∴AC=6 cm.∵AB+AD+BD=13 cm,∴AB+BD+CD=13 cm.∴△ABC的周长=AB+BD+CD+AC=13+6=19(cm).4. 【答案】A5. 【答案】C[解析] 沿着直线l3折叠,直线两旁的部分能够互相重合,因此该图形的对称轴是直线l3.6. 【答案】A[解析] 如图,连接CD,BD.∵CA=CD,BA=BD,∴点C,B都在线段AD的垂直平分线上.∴BH垂直平分线段AD.故选A.7. 【答案】A8. 【答案】D[解析] 连接AD.∵点D分别以AB,AC为对称轴,画出对称点E,F,∴∠EAB=∠BAD,∠FAC =∠CAD.∵∠B=62°,∠C=51°,∴∠BAC=∠BAD+∠CAD=67°.∴∠EAF=2∠BAC=134°.9. 【答案】C10. 【答案】C二、填空题(本大题共6道小题)11. 【答案】(3)(4)12. 【答案】32213. 【答案】(2,3)[解析] ∵△ABO是关于y轴对称的轴对称图形,∴点A(-2,3)与点B关于y轴对称.∴点B的坐标为(2,3).14. 【答案】2015. 【答案】516. 【答案】解:如图.故填3,4,5,6,n.三、解答题(本大题共4道小题)17. 【答案】解:345678猜想:一个正n边形有n条对称轴.18. 【答案】解:∵DE是AB的垂直平分线,∴AE=BE. ∵△EBC的周长是16 cm,∴BC+BE+EC=16 cm,即BC+AE+EC=AC+BC=16 cm.∵△ABC的周长是26 cm,∴AB+AC+BC=26 cm,∴AC=AB=10 cm.19. 【答案】证明:∵∠ACB=90°,∴AC⊥BC.又∵DE⊥AB,BE平分∠ABC,∴CE=DE.∵DE垂直平分AB,∴AE=BE.∵AC=AE+CE,∴BE+DE=AC.20. 【答案】证明:连接AC.∵点A在线段BC的垂直平分线MN上,∴AB=AC.∵AB=AD,∴AC=AD.∴点A在线段CD的垂直平分线上.13.2《画轴对称图形》1.将一张正方形纸片按如图所示的步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是 ( )A B C D2.点M(-3,2)关于x轴的对称点N的坐标是( )A.(3,2) B.(-3,2) C.(-3,-2) D.(3,-2)3. 在平面直角坐标系中,点关于轴的对称点在()A.第一象限B.第二象限C.第三象限D.第四象限4.若点A(4,3),点B(4,-3),则点A与点B的关系是( )A.关于x轴对称 B.关于直线x=-1对称C.关于y轴对称 D.关于直线y=-1对称5. 作已知点关于某直线的对称点的第一步是()A.过已知点作一条直线与已知直线相交B.过已知点作一条直线与已知直线垂直C.过已知点作一条直线与已知直线平行D.不确定6.小军同学在网格纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形,如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形的顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有 ( )A.3个B.4个 C.5个 D.无数个7. 点关于轴对称的点的坐标是________.8.将点A(-2,3)向下平移4个单位长度后得到点B,点B关于x轴对称的点C 的坐标为.9.若点A(2a+1.-3a+2)关于x轴对称的点在第四象限,则a的取值范围是 .10. 如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形________.三、解答题11.如图,给出了一个图案的一半,其中虚线l是这个图案的对称轴,请作出这个图形于l的轴对称图形,并说出这个图案的形状.12. 如图所示,已知,.试确定点坐标,使关于轴成轴对称图形,并连接,;作出关于轴的对称图形(不写作法),并写出,,的坐标.13.如图,△ABC 中,D 是BC 的中点,过D 点的直线GF交AC 于F ,交AC 的平行线BG 于G 点,DE ⊥DF ,交AB 于点E ,连结EG 、EF .(1)求证:BG =CF ;(2)请你判断BE +CF 与EF 的大小关系,并说明理由。
自测题(1-7章附参考答案)-高等数学上册.

第一章函数与极限一、选择题:1.函数的定义域是()(A; (B; (C;(D.2.函数的定义域是()(A;(B;(C;(D.3、函数是()(A偶函数; (B奇函数;(C非奇非偶函数;(D奇偶函数.4、函数的最小正周期是()(A2; (B; (C 4 ; (D .5、函数在定义域为()(A有上界无下界; (B有下界无上界;(C有界,且;(D有界,且.6、与等价的函数是()(A ; (B ; (C ; (D .7、当时,下列函数哪一个是其它三个的高阶无穷小()(A);(B);(C);(D).8、设则当()时有.(A; (B;(C; (D任意取 .9、设,则((A-1 ; (B1 ; (C0 ; (D不存在 .10、()(A1; (B-1;(C0; (D不存在.二、求下列函数的定义域:2、 .三、设(1)试确定的值使;(2)求的表达式 .四、求的反函数.五、求极限:1、;2、;3、;4、;5、当时,;6、 .六、设有函数试确定的值使在连续 .七、讨论函数的连续性,并判断其间断点的类型 .八、证明奇次多项式:至少存在一个实根 .第二章导数与微分一、选择题:1、函数在点的导数定义为()(A);(B);(C);(D);2、若函数在点处的导数,则曲线在点(处的法线()(A)与轴相平行;(B)与轴垂直;(C)与轴相垂直;(D)与轴即不平行也不垂直:3、若函数在点不连续,则在 ((A)必不可导;(B)必定可导;(C)不一定可导;(D)必无定义.4、如果=(),那么.(A ;(B ;(C ;(D .5、如果处处可导,那末()(A);(B);(C);(D).6、已知函数具有任意阶导数,且,则当为大于2的正整数时,的n阶导数是()(A);(B);(C);(D).7、若函数,对可导且,又的反函数存在且可导,则=()(A);(B);(C);(D).8、若函数为可微函数,则()(A)与无关;(B)为的线性函数;(C)当时为的高阶无穷小;(D)与为等价无穷小.9、设函数在点处可导,当自变量由增加到时,记为的增量,为的微分,等于()(A)-1;(B)0;(C)1;(D).10、设函数在点处可导,且,则等于().(A)0;(B)-1;(C)1;(D) .二、求下列函数的导数:1、;2、();3、;4、;5、设为的函数是由方程确定的;6、设,,求.三、证明,满足方程.四、已知其中有二阶连续导数,且,1、确定的值,使在点连续;2、求五、设求.六、计算的近似值 .七、一人走过一桥之速率为4公里/小时,同时一船在此人底下以8公里/小时之速率划过,此桥比船高200米,问3分钟后人与船相离之速率为多少?第三章微分中值定理一、选择题:1、一元函数微分学的三个中值定理的结论都有一个共同点,即()(A)它们都给出了ξ点的求法 .(B)它们都肯定了ξ点一定存在,且给出了求ξ的方法。
2023年人教版八年级数学上册第十三章综合测试卷及答案

2023年人教版八年级数学上册第十三章综合测试卷及答案一、单选题1.以下四大通讯运营商的企业图标中,是轴对称图形的是( )A .B .C .D .2.如图,已知AD 垂直平分线段BC ,25BAD Ð=°,那么C Ð的度数为()A .25°B .50°C .65°D .70°3.如图,DE ,DF 分别是线段AB ,BC 的垂直平分线,连接DA ,DC ,则( )A .∠A =∠CB .∠B =∠ADCC .DA =DCD .DE =DF4.如图,在ABC V 中,AB AC =,40A °Ð=,//CD AB ,则BCD Ð=( )A .40°B .50°C .60°D .70°5.如图,直线m n ∥,ABC V 是等边三角形,顶点B 在直线n 上,直线m 交AB 于点E ,交AC 于点F ,若1140Ð=°,则2Ð的度数是( )A .80°B .100°C .120°D .140°6.如图,在ABC V 中,AB AC =,30C Ð=°,AB AD ^,4AD cm =,则BC 的长为( ).A .8cmB .12cmC .15cmD .16cm7.如图,ABC V 中,若80BAC Ð=°,70ACB Ð=°,根据图中尺规作图的痕迹推断,以下结论错误的是( )A .40BAQ Ð=°B .12DE BD =C .AF AC =D .25EQF Ð=°8.在平面直角坐标系中,点A 的坐标为(-2,-3),点B 的坐标为(3,-3),下列说法不正确的是( )A .点A 在第三象限B .点B 在第二、四象限的角平分线上C .线段AB 平行于x 轴D .点A 与点B 关于y 轴对称9.如图,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚线BC 剪下△ABC ,展开即可得到一个五角星.若想得到一个正五角星(如图④,正五角星的5个角都是36°),则在图③中应沿什么角度剪,即∠ABC 的度数为( )A .144°B .126°C .120°D .108°10.如图,在ABC V 中,点D 为BC 边上一点,给出如下关系:①AD 平分BAC Ð;②AD BC ^于D ;③D 为BC 中点.甲说:如果①②同时成立,可证明AB AC =;乙说:如果②③同时成立,可证明AB AC =;丙说:如果①③同时成立,可证明AB AC =.则正确的说法是( )A .甲、乙正确,丙错误B .甲正确,乙、丙错误C .乙正确,甲、丙错误D .甲、乙、丙都正确11.如图,在平面直角坐标系中,点O 为坐标原点,点A 的坐标为(﹣5,12),它关于y 轴的对称点为B ,则△ABO 的周长为( )A .24B .34C .35D .3612.如图是A ,B ,C 三岛的平面图,C 岛在A 岛的北偏东35度方向,B 岛在A 岛的北偏东80度方向,C 岛在B 岛的北偏西55度方向,则A ,B ,C 三岛组成一个( )A .等腰直角三角形B .等腰三角形C .直角三角形D .等边三角形13.如图,在ABC V 中,根据尺规作图痕迹,下列说法不一定正确的是( )A .AF BF=B .12AE AC =C .90DBF DFB Ð+Ð=°D .BAF EBCÐ=Ð14.如图,C 为线段AB 上一动点(不与点A 、B 重合),在AB 同侧分别作正三角形ACD 和正三角形BCE ,AE 与BD 交于点F ,AE 与CD 交于点G ,BD 与CE 交于点H ,连接GH .以下五个结论:①AE =BD ;②GH ∥AB ;③AD =DH ;④GE =HB ;⑤∠AFD =60°,一定成立的是( )A .①②③④B .①②④⑤C .①②③⑤D .①③④⑤15.已知,在△ABC 中,AB AC =,如图,(1)分别以B ,C 为圆心,BC 长为半径作弧,两弧交于点D ;(2)作射线AD ,连接BD ,CD .根据以上作图过程及所作图形,下列结论中错误的是( )A .BAD CADÐ=ÐB .△BCD 是等边三角形C .AD 垂直平分BC D .ABDC S AD BC=g 16.如图,在Rt △ABC 中,∠CBA =90°,∠CAB 的角平分线AP 和∠MCB 的平分线CF 相交于点D ,AD 交CB 于点P ,CF 交AB 的延长线于点F ,过点D 作DE ⊥CF 交CB 的延长线于点G ,交AB 的延长线于点E ,连接CE 并延长交FG 于点H ,则下列结论:①∠CDA =45°;②AF ﹣CG =CA ;③DE =DC ;④CF =2CD +EG ;其中正确的有( )A .②③B .②④C .①②③④D .①③④17.如图所示,在四边形ABCD 中,2AD =,90A D Ð=Ð=°,60B Ð=°,2BC CD =,在AD 上找一点P ,使PC PB +的值最小;则PC PB +的最小值为( )A .4B .3C .5D .618.如图,在直角坐标系xOy 中,点P 的坐标为(4,3),PQ ⊥x 轴于Q ,M ,N 分别为OQ ,OP 上的动点,则QN +MN 的最小值为( )A .7225B .245C .125D .9625二、填空题19.如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A 滑行至B ,已知100m AB =,则这名滑雪运动员的高度下降了_______米.20.如图,在ABC V 中,已知∠C =90°,AB 的垂直平分线交BC ,AB 于点D ,E ,∠CAB =50°,那么∠CAD =___________.21.如图,等边三角形ABC 的边长为4,AD 是BC 边上的中线,F 是AD 边上的动点,E 是边AC 的中点.当△ECF 的周长取得最小值时,∠EFC 的度数为_____________.22.如图,在ABC V 中,AB AC =,30C Ð=°,AB AD ^,3cm =AD ,则BC 为____________cm .23.如图,在四边形ABCD 中,AB =AC ,DB 平分∠ADC ,∠BCD =150°.则∠ABD 的度数为 ___°.三、解答题24.如图,在△ABC 中,AB AC =,120BAC Ð=°,点D 、E 在BC 上,AD ⊥AC ,AE ⊥AB .求证:AED V 为等边三角形.25.如图,点D 是等边三角形ABC 的边BC 上一点,以AD 为边作等边△ADE ,连接CE .(1)求证:ABD ACE △≌△;(2)若∠BAD =20°,求∠AEC 的度数.26.如图,在ABC V 和ADE V 中,AB AC =,AD AE =,90BAC DAE Ð=Ð=°.(1)当点D 在AC 上时,如图①,线段BD ,CE 有怎样的数量关系和位置关系?请证明你的猜想;(2)将图①中的ADE V 绕点A 顺时针旋转()090a a °<<°,如图②,线段BD ,CE 有怎样的数量关系和位置关系?请说明理由.(3)拓展应用:已知等边ABC V 和等边ADE V 如图③所示,求线段BD 的延长线和线段CE 所夹锐角的度数.27.如图所示,D 是ABC V 边BC 的中点,E 是AD 上一点,满足AE BD DC ==,FA FE =.求ADC Ð的度数.28.如图,已知∠ABC=∠ADC=90°,BC=CD,CA=CE.(1)求证:∠ACB=∠ACD;(2)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P.①连接PE,交AM于点N,证明AM垂直平分PE;②点O是直线AE上的动点,当MO+PO的值最小时,证明点O与点E重合。
(word)职高数学基础模块上册13章测试题

集合测试题一选择题:给出四个结论:①{1,2,3,1}是由4个元素组成的集合②集合{1}表示仅由一个“1〞组成的集合③{2,4,6}与{6,4,2}是两个不同的集合④集合{大于3的无理数}是一个有限集其中正确的选项是();A.只有③④B.只有②③④C.只有①D.只有②以下对象能组成集合的是();A.最大的正数B. 最小的整数C.平方等于1的数D. 最接近1的数3.I={0,1,2,3,4},M={0,1,2,3},N={0,3,4},M (C I N)A.{2,4}B.{1,2}C{.0,1} D. 0,1,2,3}={a,b,c,d,e},M={a,b,d},N={b},那么(C I M) NA.{b}B.{a,d}C.{a,b,d}D.{b,c,e}={0,3},B={0,3,4},C={1,2,3}那么(B C)A();A.{0,1,2,3,4}B.C.{0,3}D .{0}6.设集合M={-2,0,2},N={0},那么();A.NB.N M C.NMD.MN7.设集合A(x,y)xy0,B(x,y)x且y0,那么正确的是() ;A.A BBB.A BC.A BD.AB8.设集合M x1x4,N x2x5,那么ABA.x1x5B.x2x4C.x2x4D.2,3 ,49.设集合Mxx4,N xx6,那么M N;B.x4x6C.D.x4x6以下命题中的真命题共有();x=2是x2x20的充分条件②x≠2是x2x20的必要条件③xy是x=y的必要条件④x=1且y=2是x1(y2)20的充要条件个个个个二填空题:本大题共6小题,每题4分,共24分.把答案填在题中横线上.1. 用列举法表示集合xZ 2 x4;3.{m,n}的真子集共3个,它们是;如果一个集合恰由5个元素组成,它的真子集中有两个分别是B={a,b,c},C={a,d,e},那么集合A= ;4 A (x,y)x y 3,B (x,y)3x y 1, 那么A B ;5.x24 0 是x+2=0的条件.三解答题:集合A=x0x 4,B x1 x 7,求A B,A B.2.全集I=R,集合A x1x3,求C I A.3.设全集I=3,4,3a2,M1,C IM3,a2a2,求值.?不等式?测试题一.填空题:(32%)1.设2x-3 <7,那么x <;5->0且+1≥0解集的区间表示为_________ ;x3.| |>1解集的区间表示为3________________;4.集合A=[2,4], 集合B=(-3,3],那么A∩B=,A ∪B= .不等式x2>2x的解集为____________;不等式2x2-3x-2<0的解集为________________.6.假设代数式x2x12有意义,那么x的取值集合是________________二.选择题:(20%)7. 设、、均为实数,且<,以下结论正确的选项是()。
冀教版八年级数学上册第十三章达标测试卷附答案 (2)
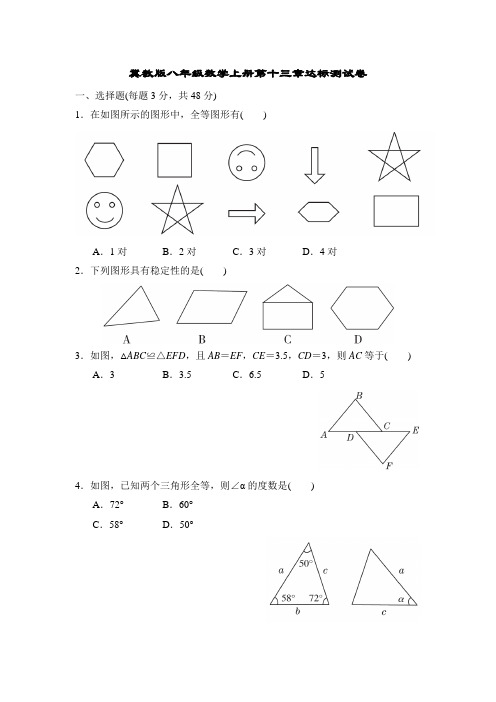
冀教版八年级数学上册第十三章达标测试卷一、选择题(每题3分,共48分)1.在如图所示的图形中,全等图形有()A.1对B.2对C.3对D.4对2.下列图形具有稳定性的是()3.如图,△ABC≌△EFD,且AB=EF,CE=3.5,CD=3,则AC等于() A.3 B.3.5 C.6.5 D.54.如图,已知两个三角形全等,则∠α的度数是()A.72°B.60°C.58°D.50°5.对于下列各组条件,不能判定△ABC≌△A′B′C′的一组是() A.∠A=∠A′,∠B=∠B′,AB=A′B′ B.∠A=∠A′,AB=A′B′,AC=A′C′C.∠A=∠A′,AB=A′B′,BC=B′C′ D.AB=A′B′,AC=A′C′,BC=B′C′6.下列定理中,没有逆定理的是()A.同旁内角互补,两直线平行B.直角三角形的两锐角互余C.互为相反数的两个数的绝对值相等D.同位角相等,两直线平行7.如图,如果△ABC≌△FED,那么下列结论错误的是()A.EC=BD B.EF∥AB C.DF=BD D.AC∥FD8.如图,B,D分别是位于线段AC两侧的点,连接AB,AD,CB,CD,则下列条件中,与AB=AD相结合无法判定△ABC≌△ADC的是()A.CB=CD B.∠BAC=∠DACC.∠BCA=∠DCA D.以上都无法判定9.如图,在四边形ABCD中,CB=CD,∠B=90°,∠ACD=∠ACB,∠BAD =70°,则∠BCD的度数为()A.145°B.130°C.110°D.70°10.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1,2,3,4的四块),聪明的小明经过仔细考虑认为只要带其中的两块碎片去玻璃店就可以让师傅配一块与以前一样的玻璃样板.你认为下列四个选项中考虑最全面的是()A.带其中的任意两块去都可以B.带1,2或2,3去就可以了C.带1,4或3,4去就可以了D.带1,4或2,4或3,4去均可11.如图,已知∠1=∠2,要使△ABC≌△ADE,还需条件() A.AB=AD,BC=DE B.BC=DE,AC=AEC.∠B=∠D,∠C=∠E D.AC=AE,AB=AD12.如图,是一个4×4的正方形网格,∠1+∠2+∠3+∠4+∠5+∠6+∠7等于()A.585°B.540°C.270°D.315°13.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于O,∠1=∠2,则图中的全等三角形有()A.1对B.2对C.3对D.4对14.根据下列条件利用尺规作图作△ABC,作出的△ABC不唯一的是() A.AB=7,AC=5,∠A=60°B.AC=5,∠A=60°∠C=80°C.AB=7,AC=5,∠B=40°D.AB=7,BC=6,AC=515.如图,已知∠1=∠2,AC=AD,添加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有()A.4个B.3个C.2个D.1个16.如图,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P从B向A运动,每秒走1米,Q从B向D运动,每秒走2米,P、Q 同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ 全等,则x的值为()A.4 B.6 C.4或9 D.6或9二、填空题(每题3分,共9分)17.如果两个三角形的两边及其中一边的对角对应相等,那么这两个三角形全等,其逆命题是________________________________________,这个逆命题是________命题.18.如图,△ABC的周长为32,AD⊥BC于点D,D是BC的中点,若△ACD的周长为24,那么AD的长为________.19.如图,CA⊥BE,且△ABC≌△ADE,则BC与DE的关系是____________.三、解答题(20题6分,26题12分,其余每题9分,共63分)20.如图,已知∠1=∠2,∠3=∠4,EC=AD.求证:AB=BE.21.如图,为了测量一幢楼的高AB,在旗杆CD与楼之间选定一点P.测得∠DPC +∠APB=90°,量得P到楼底的距离PB与旗杆的高度相等,等于8米,量得旗杆与楼之间的距离DB=33米,求楼高AB是多少米.22.如图,已知等边三角形ABC,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.求∠DFC的度数.23.如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线,一轮船离开码头,计划沿∠ADB的平分线航行,在航行途中的C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.24.如图,已知直角α,线段m,利用尺规作直角三角形ABC,使∠C=90°,AC =m,BC=2m.不写作法,但要保留作图痕迹.25.如图,已知正方形ABCD,从顶点A引两条射线分别交BC,CD于点E,F,且∠EAF=45°.求证:BE+DF=EF.26.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.(1)BF⊥CE,交CE于点F,交CD于点G(如图①),求证:AE=CG;(2)AH⊥CE,交CE的延长线于点H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.答案一、1.C点拨:本题是一道易错题,误认为图形的全等与图形的位置、方向等有关.2.A 3.C 4.D 5.C 6.C7.C8.C点拨:已知AB=AD,并且已知公共边AC,这两个条件与∠BCA=∠DCA 相结合,不符合全等的条件,所以选C.9.C点拨:由“SAS”可得△ACD≌△ACB,所以∠BAC=∠DAC=35°,所以∠BCA=∠DCA=55°,则∠BCD=∠BCA+∠DCA=55°+55°=110°.10.D11.D12.A13.D14.C点拨:由于“两边和其中一边的对角对应相等的两个三角形不一定全等”,所以所作的三角形不唯一.15.B点拨:由∠1=∠2可得∠BAC=∠EAD,则已知三角形的一个角及其邻边对应相等.若按SAS判定可增加①;按ASA判定可增加③;按AAS判定可增加④,所以选B.16.B二、17.如果两个三角形全等,那么这两个三角形的两边及其中一边的对角对应相等;真18.8点拨:根据“AD⊥BC于点D,D是BC的中点”可由SAS证得△ABD≌△ACD,则△ABC的周长=△ACD的周长的2倍-2AD,即32=24×2-2AD,解得AD=8.19.相等且垂直点拨:由△ABC≌△ADE可知BC=DE,∠C=∠E.如图,延长ED交BC于点F,因为∠B+∠C=90°,所以∠B+∠E=90°,在△BEF 中,由三角形内角和定理可求得∠BFE=90°,即BC⊥DE.三、20.证明:∵∠1=∠2,∴∠1+∠EBD =∠EBD +∠2,即∠ABD =∠EBC .在△ABD 和△EBC 中,⎩⎨⎧∠ABD =∠EBC ,∠3=∠4,AD =EC ,∴△ABD ≌△EBC (AAS).∴AB =BE .21.解:由题意知∠CDP =∠ABP =90°.∵∠DPC +∠APB =90°,∠DPC +∠DCP =90°,∴∠DCP =∠APB ,在△CPD 和△P AB 中,⎩⎨⎧∠CDP =∠PBA ,DC =BP ,∠DCP =∠BP A ,∴△CPD ≌△P AB (ASA),∴PD =AB ,∵DB =33米,PB =8米,∴AB =PD =DB -PB =33-8=25(米).答:楼高AB 是25米.22.解:∵△ABC 为等边三角形,∴AC =AB ,∠B =∠BAC =∠ACB =60°.在△AEC 和△BDA 中,∵⎩⎨⎧AC =BA ,∠EAC =∠B ,AE =BD ,∴△AEC ≌△BDA (SAS).∴∠ACE =∠BAD .∴∠DFC =∠F AC +∠ACE =∠F AC +∠BAD =∠BAC =60°.23.解:轮船航行没有偏离指定航线.理由如下:由题意知DA =DB ,AC =BC .在△ADC 和△BDC 中,⎩⎨⎧DA =DB ,AC =BC ,DC =DC ,∴△ADC ≌△BDC (SSS).∴∠ADC =∠BDC ,即DC 为∠ADB 的平分线.∴轮船航行没有偏离指定航线.24.解:作出的△ABC 如图所示.25.证明:延长CD 到点G ,使DG =BE ,连接AG .在正方形ABCD 中,AB =AD ,∠B =∠ADC =90°, ∴∠ADG =∠B . 在△ABE 和△ADG 中,⎩⎨⎧AB =AD ,∠B =∠ADG ,BE =DG ,∴△ABE ≌△ADG (SAS). ∴AE =AG ,∠BAE =∠DAG . ∵∠EAF =45°,∴∠GAF =∠DAG +∠DAF =∠BAE +∠DAF =∠BAD -∠EAF =90°-45°=45°.∴∠EAF =∠GAF .在△AEF 和△AGF 中,⎩⎨⎧AE =AG ,∠EAF =∠GAF ,AF =AF ,∴△AEF ≌△AGF (SAS). ∴EF =GF .∵GF =DG +DF =BE +DF , ∴BE +DF =EF .26.(1)证明:∵点D 是AB 中点,∴AD =BD .又∵AC =BC ,CD =CD , ∴△ACD ≌△BCD (SSS).∴∠ADC =∠BDC =90°,∠ACD =∠BCD =45°. ∴∠CAD =∠CBD =45°, ∴∠CAE =∠BCG . 又∵BF ⊥CE ,∴∠CBG +∠BCF =90°. 又∵∠ACE +∠BCF =90°, ∴∠ACE =∠CBG . 又∵AC =BC ,∴△AEC ≌△CGB (ASA), ∴AE =CG . (2)解:BE =CM .证明:∵CH ⊥HM ,易得CD ⊥ED ,∴∠CMA +∠MCH =90°,∠BEC +∠MCH =90°. ∴∠CMA =∠BEC .又∵AC =BC ,∠ACM =∠CBE =45°,∴△CAM ≌△BCE (AAS). ∴BE =CM .八年级数学上册期中达标测试卷一、选择题(1~10小题各3分,11~16小题各2分,共42分)1.4的算术平方根是()A.±2 B. 2 C.±2 D.2 2.下列分式的值不可能为0的是()A.4x-2B.x-2x+1C.4x-9x-2D.2x+1x3.如图,若△ABC≌△CDA,则下列结论错误的是()A.∠2=∠1 B.∠3=∠4C.∠B=∠D D.BC=DC(第3题)(第5题)4.小亮用天平称得一个鸡蛋的质量为50.47 g,用四舍五入法将50.47精确到0.1为()A.50 B.50.0C.50.4 D.50.55.如图,已知∠1=∠2,AC=AE,添加下列一个条件后仍无法确定△ABC≌△ADE的是()A.∠C=∠E B.BC=DEC.AB=AD D.∠B=∠D6.如图,点A,D,C,E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE =10,AC=7,则AD的长为()A.5.5 B.4 C.4.5 D.3(第6题)(第8题)7.化简x 2x -1+11-x的结果是( )A .x +1 B.1x +1C .x -1D.x x -18.如图,数轴上有A ,B ,C ,D 四点,根据图中各点的位置,所表示的数与5-11最接近的点是( ) A .AB .BC .CD .D9.某工厂新引进一批电子产品,甲工人比乙工人每小时多搬运30件电子产品,已知甲工人搬运300件电子产品所用的时间与乙工人搬运200件电子产品所用的时间相同.若设乙工人每小时搬运x 件电子产品,则可列方程为( ) A.300x =200x +30B.300x -30=200x C.300x +30=200x D.300x =200x -3010.如图,这是一个数值转换器,当输入的x 为-512时,输出的y 是( )(第10题)A .-32B.32C .-2D .211.如图,从①BC =EC ;②AC =DC ;③AB =DE ;④∠ACD =∠BCE 中任取三个为条件,余下一个为结论,则可以构成的正确说法的个数是( ) A .1B .2C .3D .4(第11题) (第12题)12.如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ ,已知PQ =5,NQ =9,则MH 的长为( ) A .3B .4C .5D .613.若△÷a 2-1a =1a -1,则“△”是( )A.a+1a B.aa-1C.aa+1D.a-1a14.以下命题的逆命题为真命题的是() A.对顶角相等B.同位角相等,两直线平行C.若a=b,则a2=b2D.若a>0,b>0,则a2+b2>015.x2+xx2-1÷x2x2-2x+1的值可以是下列选项中的()A.2 B.1 C.0 D.-1 16.定义:对任意实数x,[x]表示不超过x的最大整数,如[3.14]=3,[1]=1,[-1.2]=-2.对65进行如下运算:①[65]=8;②[8]=2;③[2]=1,这样对65运算3次后的结果就为1.像这样,一个正整数总可以经过若干次运算后使结果为1.要使255经过运算后的结果为1,则需要运算的次数是() A.3 B.4 C.5 D.6二、填空题(17小题3分,18,19小题每空2分,共11分)17.如图,要测量河两岸相对的两点A,B间的距离,先在AB的垂线BF上取两点C,D,使BC=CD,再作出BF的垂线DE,使点A,C,E在同一条直线上,可以证明△ABC≌△EDC,从而得到AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是____________.(第17题)18.已知:7.2≈2.683,则720≈______,0.000 72≈__________.19.一艘轮船在静水中的最大航速为30 km/h,它以最大航速沿江顺流航行120 km 所用的时间与以最大航速逆流航行60 km所用的时间相同,如果设江水的流速为x km/h,根据题意可列方程为________________,江水的流速为________km/h.三、解答题(20小题8分,21~23小题各9分,24,25小题各10分,26小题12分,共67分)20.解分式方程.(1)3x-2=2-xx-2;(2)21+2x-31-2x=64x2-1.21.已知(3x+2y-14)2+2x+3y-6=0.求:(1)x+y的平方根;(2)y-x的立方根.22.有这样一道题:“计算x2-2x+1x2-1÷x-1x2+x-x的值,其中x=2 020.”甲同学把“x=2 020”错抄成“x=2 021”,但他的计算结果也是正确的.你说说这是怎么回事?23.如图,AB∥CD,AB=CD,AD,BC相交于点O,BE∥CF,BE,CF分别交AD于点E,F.求证:(1)△ABO≌△DCO;(2)BE=CF.(第23题)24.观察下列算式:①2×4×6×8+16=(2×8)2+16=16+4=20;②4×6×8×10+16=(4×10)2+16=40+4=44;③6×8×10×12+16=(6×12)2+16=72+4=76;④8×10×12×14+16=(8×14)2+16=112+4=116;….(1)根据以上规律计算: 2 016×2 018×2 020×2 022+16;(2)请你猜想2n(2n+2)(2n+4)(2n+6)+16(n为正整数)的结果(用含n的式子表示).25.下面是学习分式方程的应用时,老师板书的问题和两名同学所列的方程.根据以上信息,解答下列问题:(1)冰冰同学所列方程中的x表示______________________________________,庆庆同学所列方程中的y表示_____________________________________;(2)从两个方程中任选一个,写出它的等量关系;(3)解(2)中你所选择的方程,并回答老师提出的问题.26.如图①,AB=7 cm,AC⊥AB,BD⊥AB,垂足分别为A,B,AC=5 cm.点P 在线段AB上以2 cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t s(当点P运动至点B时停止运动,同时点Q停止运动).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等?并判断此时线段PC和线段PQ的位置关系,请分别说明理由.(2)如图②,若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为x cm/s,其他条件不变,当点P,Q运动到某处时,有△ACP与△BPQ 全等,求出相应的x,t的值.(第26题)答案一、1.D 2.A 3.D 4.D 5.B6.D 【点拨】∵AB ∥EF ,∴∠A =∠E .又AB =EF ,∠B =∠F ,∴△ABC ≌△EFD (ASA).∴AC =DE =7.∴AD =AE -DE =10-7=3.7.A 8.D 9.C 10.A 11.B 12.B13.A 【点拨】∵△÷a 2-1a =1a -1, ∴△=1a -1·a 2-1a=a +1a . 14.B 15.D 16.A二、17.ASA 18.26.83;0.026 8319.12030+x =6030-x;10 【点拨】根据题意可得12030+x =6030-x,解得x =10, 经检验,x =10是原方程的解,所以江水的流速为10 km/h.三、20.解:(1)去分母,得3=2(x -2)-x .去括号,得3=2x -4-x .移项、合并同类项,得x =7.经检验,x =7是原方程的解.(2)去分母,得2(1-2x )-3(1+2x )=-6.去括号,得2-4x -3-6x =-6,移项、合并同类项,得-10x =-5.解得x =12.经检验,x =12是原方程的增根,∴原分式方程无解.21.解:∵(3x +2y -14)2+2x +3y -6=0,(3x +2y -14)2≥0,2x +3y -6≥0,∴3x +2y -14=0,2x +3y -6=0.解⎩⎨⎧3x +2y -14=0,2x +3y -6=0,得⎩⎨⎧x =6,y =-2.(1)x +y =6+(-2)=4,∴x +y 的平方根为±4=±2.(2)y -x =-8,∴y -x 的立方根为3-8=-2.22.解:∵x 2-2x +1x 2-1÷x -1x 2+x -x =(x -1)2(x +1)(x -1)·x (x +1)x -1-x =x -x =0, ∴该式的结果与x 的值无关,∴把x 的值抄错,计算的结果也是正确的.23.证明:(1)∵AB ∥CD ,∴∠A =∠D ,∠ABO =∠DCO .在△ABO 和△DCO 中,⎩⎨⎧∠A =∠D ,AB =CD ,∠ABO =∠DCO ,∴△ABO ≌△DCO (ASA).(2)∵△ABO ≌△DCO ,∴BO =CO .∵BE ∥CF ,∴∠OBE =∠OCF ,∠OEB =∠OFC .在△OBE 和△OCF 中,⎩⎨⎧∠OBE =∠OCF ,∠OEB =∠OFC ,OB =OC ,∴△OBE ≌△OCF (AAS),∴BE =CF .24.解:(1) 2 016×2 018×2 020×2 022+16 =(2 016×2 022)2+16=4 076 352+4=4 076 356. (2)2n (2n +2)(2n +4)(2n +6)+16=2n (2n +6)+4=4n 2+12n +4.25.解:(1)小红步行的速度;小红步行的时间(2)冰冰用的等量关系:小红乘公共汽车的时间+小红步行的时间=小红上学路上的时间.庆庆用的等量关系:公共汽车的速度=9×小红步行的速度.(上述等量关系,任选一个就可以)(3)选冰冰的方程:38-29x +2x =1,去分母,得36+18=9x ,解得x =6,经检验,x =6是原分式方程的解.答:小红步行的速度是6 km/h ;选庆庆的方程:38-21-y=9×2y , 去分母,得36y =18(1-y ),解得y =13,经检验,y =13是原分式方程的解, ∴小红步行的速度是2÷13=6(km/h).答:小红步行的速度是6 km/h.(对应(2)中所选方程解答问题即可)26.解:(1)△ACP ≌△BPQ ,PC ⊥PQ .理由如下:∵AC ⊥AB ,BD ⊥AB ,∴∠A =∠B =90°.由题意知AP =BQ =2 cm ,∵AB =7 cm ,∴BP =5 cm ,∴BP =AC .在△ACP 和△BPQ 中,∵⎩⎨⎧AP =BQ ,∠A =∠B ,AC =BP ,∴△ACP ≌△BPQ .∴∠C =∠BPQ .易知∠C +∠APC =90°,∴∠APC +∠BPQ =90°,∴∠CPQ =90°,∴PC ⊥PQ .(2)由题意可知AP =2t cm ,BP =(7-2t )cm ,BQ =xt cm. ①若△ACP ≌△BPQ ,则AC =BP ,AP =BQ ,∴5=7-2t ,2t =xt ,解得x =2,t =1;②若△ACP ≌△BQP ,则AC =BQ ,AP =BP ,∴5=xt ,2t =7-2t ,解得x =207,t =74.综上,当△ACP 与△BPQ 全等时,x =2,t =1或x =207,t =74.。
高等数学自测题第13章 自测题2答案

第13章 自测题2答案一、选择题(每小题4分) 1、设OM 是从O (0,0)到M (1,1)的直线段,则与曲线积分⎰+=OMyx s eI d 22不相等的积分是(A)⎰102d 2xex(B) ⎰12d 2yey(C )⎰2d re r(D )⎰1d 2rer2、设L 是圆周 x 2+y 2=a 2 (a >0)负向一周,则曲线积分答 ( ) 答: (A) 3、设C 为沿x 2+y 2=R 2逆时针方向一周,则用格林公式计算,答( )答:(D ) 4、曲线积分的值(A)与曲线L的形状有关(B)与曲线L的形状无关(C)等于零(D)等于2π答( )答:(A)二、填空题(每小题4分)1、设f(x)有连续导数,L是单连通域上任意简单闭曲线,且则f(x)=_______.答:x2+c2、设是由A(-2,3)沿y=x2-1到点M(1,0),再沿y=2(x-1)到B(2,2)的路径,则 ________.答:103、设力的模 , 的方向与相同,则在力的作用下,质点沿曲线L:正向绕行一周,力所做的功可用曲线积分表示为________________.答:⎰+++-L yxyxxy22dd4、若是某二元函数的全微分,则m=______.答:1三、解答题(每小题6分)1、求自x=1到x=e之间的一段曲线的弧长。
2、设心脏线L的极坐标方程为r=a(1-cosθ) (0≤θ≤2π),其线密度为常量μ,求L 的形心坐标( ).3、求质点M (x , y )受作用力 沿路径L 所作的功W . L 是3、3 . 求质点M (x , y )受作用力 沿路径L 所作的功W . L 是沿椭圆4x 2+y 2=4顺时针方程的一周。
4、求半径为R 的均匀半圆周L (线密度为δ=1)对于位于圆心的单位质量的质点的引力。
5、设质线L 的方程为 ,L 上的任意点(x ,y )处的线密度为 求质线L 的质心坐标(ξ,η).解:L 参数方程⎪⎩⎪⎨⎧==ty t x 44sincos 0≤t ≤2πtt t t t s d sincossin cos 4d 44+=对L 方程质线的线密度yx xy +=μ而言,变量x 与y 是对等的,故..ηξ=质线L 的质量⎰=Lsm d μ⎰⎰⎰=+⋅⋅+=+=2332444444d cos sin4d sincossin cos 4sincossincos d ππtt t tt t t t tt tt syx xy L31=⎰⎰===237d cos sin 12d 1πμηξtt t sy mL103=故质心坐标为⎪⎭⎫ ⎝⎛103 , 1036、利用曲线积分计算星形线⎪⎩⎪⎨⎧==θθ33sin cos a y a x 所围区域面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第13章 自测题2答案
一、选择题(每小题4分) 1、
设OM 是从O (0,0)到M (1,1)的直线段,则与曲线积分⎰+=OM
y x s e
I d 2
2不
相等的积分是
(A)⎰1
02d 2x
e x
(B) ⎰1
02d 2y
e y
(C)⎰2
d r
e r (D)
⎰
1
d 2r
e r
2、
设L 是圆周 x 2+y 2=a 2 (a >0)负向一周,则曲线积分
答 ( ) 答: (A) 3、
设C 为沿x 2+y 2=R 2逆时针方向一周,则用格林公式计算,
答( )
答:(D ) 4、
曲线积分的值
(A)与曲线L的形状有关(B)与曲线L的形状无关
(C)等于零(D)等于2π
答( )
答:(A)
二、填空题(每小题4分)
1、
设f(x)有连续导数,L是单连通域上任意简单闭曲线,且则
f(x)=_______.
答:x2+c
2、
设是由A(-2,3)沿y=x2-1到点M(1,0),再沿y=2(x-1)到B(2,2)的路径,则 ________.
答:10
3、
设力的模 , 的方向与相同,则在力的作用下,质点沿
曲线L:正向绕行一周,力所做的功可用曲线积分表示为
________________.
答:⎰+
+
+
-
L y
x
y
x
x
y
2
2
d
d
4、
若是某二元函数的全微分,则m=______.
答:1
三、解答题(每小题6分)
1、求自x=1到x=e之间的一段曲线的弧长。
2、设心脏线L的极坐标方程为r=a(1-cosθ) (0≤θ≤2π),其线密度为常量μ,求L 的形心坐标( ).。
