公交站点IC刷卡计数算法及其MATLAB实现
基于Matlab仿真的公交系统运行时间可靠性评价方法

城市交通UrbanTransportofChina2006年7月第4卷第4期Jul.2006Vol.4No.4摘要:从公交系统发车时间可靠性,途中运行时间可靠性及出行者出行时刻、等待时间、途中乘运时间、到达终点的时间调查入手,通过对出行过程的分析,建立出行者在运行时间可靠性水平不同的3条公交线路之间的出行时间分布模型。
利用此模型,对出行者在3条公交线路之间的换乘过程中,多种不同公共交通服务水平对出行者的影响进行仿真。
对公交系统运行时间可靠性问题进行了分析探讨,提出了一套基于Matlab仿真技术的公共交通系统运行时间可靠性分析和评价方法,并应用所建模型进行公交系统运行时间的可靠性评价。
Abstract:Basedontheinvestigationofdeparturetimereliabilityoftrans-portsystemandtraveltimereliabilityandpassengerstarttimeandwait-ingtimeandcarriedtimeandarrivalfinaldestinationtime,theanalysisbeganwithanassumedpersonaljourney,thisstudyhassetupamodewhichcontainstheinterchangejourneysviadifferentdistributingmodesofpublictransport.Applythemodetosimulatetheimpactsofdeparturetimereliabilityofpublictransportservicesonarrivallateness,whichcon-tainsthreesectionspublictransportsarecarefullyanalysisanddiscussed.Asimulationmethodforanalysisandevaluationofoperationtimerelia-bilityoftransportsystemonMatlabisintroduced.Furthermore,accordingtothesimulationmethodcarriesoutevaluationoperationtimereliabilityoftransportsystem.关键词:公交系统;运行时间;可靠性;延误;Matlab仿真;评价方法Keywords:publictransportationsystem;runningtime;reliability;late-ness;Matlabsimulation;evaluationmethod中图分类号:U491文献标识码:A我国城市道路交通是包括行人、非机动车和机动车辆在内的混合交通,交通流中存在很多随机因素。
公交站点IC刷卡计数算法及其Matlab实现

1 现 状 分 析
智 能交 通系 统 要求 大 量 的交 通 流 信 息 共 享 ,
公交 I c卡 收费 系统 可记 载有 关公 共交 通流 信息 ,
具 有数 量大 、 自动化 、 覆盖 广 、 作 简单 、 操 生成 的数
广州 市市 内约有 3 0条 公交 线路 、 0 0 62 0多辆公 交
收 稿 日期 : 0 0 0 — 3 2 1—21 修 回 日期 : 0 0 0 0 2 1 33
*江 西 省 创 新 资 金项 目( 准 号 : O C l ) 助 批 YC 9 O O 资 作 者 简 介 : 伟 雄 (9 3 , 授 . 究 方 向 : 通 管 理 与规 划 , 通运 输 系统 分 析 . — i 1 9 0 1 2 q .o 查 16 )教 研 交 交 E mal 15 8 4 @ q cr : n
以下 3种情 况 : 1 I ) C卡 系 统 可 以 自动 记 录 每 1 车 到 达 、 辆
查 样本 数量 和特征 的要 求 , 与人 工调查 方法 相 比 , I c卡信 息 不 易 受 人 为 因 素 的 影 响 , 据 准 确 真 数
实 , 到的客 流结 果 更 能 真 实 反 映城 市 公 交 运 营 得 情 况 和居 民公 交 出行 特 征 。I 卡 系 统不 仅 给 乘 C 客、 公交 公 司带来 了 巨大 的便 利 , 而且 其数 据库 系
统 记 录 了大 量交 通 流 信 息 , 为交 通 调 查 提供 了最 原始 、 最直 接 和具有 丰 富操作 性 的第一 手 资料l , 3 ]
因此研 究从 I c卡 系 统数 据库 中获 取 交 通 流信 息 的方法 具有 重 要 的意 义 。本 文 所 提 出 的算 法 , 目 的就是 实现 从 I c卡 系统 数 据 库 中获 取 交通 流 信
Matlab在智能交通系统中的应用与案例研究

Matlab在智能交通系统中的应用与案例研究智能交通系统近年来受到了广泛关注,它利用计算机与通信技术来优化交通流量、提高交通效率与安全性。
在智能交通系统的发展中,Matlab作为一个功能强大的数值计算与数据分析软件,发挥了重要作用。
本文将探讨Matlab在智能交通系统中的应用,并通过一些案例研究来展示其价值。
一、交通流量预测交通流量的预测对于交通系统的优化至关重要。
Matlab提供了丰富的预测建模工具,可以通过历史交通数据进行统计分析,建立合适的模型进行预测,并进行模型评估。
例如,可以利用神经网络工具箱在Matlab中构建交通流量预测模型,基于历史数据来预测未来特定路段的交通流量,以便在实际交通管理中做出相应的调整和决策。
二、交通信号优化交通信号的优化是提高交通效率的关键步骤。
Matlab可以利用优化算法来进行交通信号的优化,以最小化交通拥堵并提高通行效率。
例如,可以通过Matlab中的遗传算法来确定最佳的交通信号配时方案,以最大程度地减少车辆等待时间和停止次数,并提高整体交通流动性。
这种基于优化的交通信号控制方法可以显著改善交通系统的性能。
三、交通事故分析交通事故的分析对于交通安全的提升和事故预防至关重要。
Matlab可以利用统计分析和数据挖掘技术来分析交通事故相关数据,以发现事故发生的规律和原因,并进一步提出改进建议。
例如,可以通过Matlab中的聚类分析工具来识别事故发生的热点区域,并研究其影响因素。
这些分析结果可为交通管理部门制定相关政策和措施提供依据。
四、车辆轨迹分析通过对车辆轨迹的分析可以对车辆行为进行研究,为交通管理提供有效的数据支持。
Matlab提供了强大的图像处理和轨迹分析工具,可以处理车辆行驶轨迹数据,并通过数据挖掘技术进行行为分析。
例如,可以利用Matlab中的图像处理工具箱对交通摄像头的图像进行处理,提取出车辆的轨迹信息,并进一步分析车辆的速度、加速度等行为信息。
这些分析结果有助于交通管理部门了解交通状况并制定针对性的措施。
公交站点IC刷卡计数算法及其Matlab实现

公交站点IC刷卡计数算法及其Matlab实现查伟雄;刘金行【摘要】中国大部分城市的公交公司早期并未充分利用信息技术和数据库技术,因此其IC刷卡记录与车辆调度记录很难达到精确性、实时性和关联性的要求.为了最大限度利用这些海量的原始记录,文中针对实际情况,在允许一定误差的前提下,提出了公交站点IC刷卡计数算法,并结合实例使用数学软件Matlab实现此算法.【期刊名称】《交通信息与安全》【年(卷),期】2010(028)002【总页数】5页(P93-97)【关键词】智能交通;IC卡收费系统;公交站点;Matlab【作者】查伟雄;刘金行【作者单位】华东交通大学交通运输与经济研究所,南昌,330013;华东交通大学交通运输与经济研究所,南昌,330013【正文语种】中文【中图分类】U495引言我国许多大城市都开始使用公交IC卡,并且已经初具规模。
例如,青岛市2 600辆电汽车已经配备了IC卡收费系统,占公交车总数的80%,每天持卡乘车约90万人·次,占无人售票款收入的70%;天津市区已有2 500辆公交车可以使用公交IC卡乘车,约占市区公交车总量的80%,市区已有12万乘客持卡坐车,约占乘坐公交车总人数的26%;太原市持卡者占总客运人次的40%;广州市市内约有300条公交线路、6 200多辆公交车,95%以上的公交车辆已开通或安装了车载收费机[1]。
南昌市市内有2 345辆公交车,全部安装并开通了车载收费机。
可以说持卡乘车是公交发展的必然趋势,但与国外相比,国内对收费系统的利用还远远不够[1]。
公交乘客是公共交通客流组成的基本要素,公交IC卡数据库记录了每1个公交乘客任何1次刷卡的相关信息,从这些信息中挖掘出反映公交运营状况的数据是可行的[2]。
IC卡信息量所反映的居民公交出行的数量及分布完全达到调查样本数量和特征的要求,与人工调查方法相比,IC卡信息不易受人为因素的影响,数据准确真实,得到的客流结果更能真实反映城市公交运营情况和居民公交出行特征。
完整版数字图像处理车牌识别课程设计matlab实现附源代码

精品实验项目字符识别预处理的设计与实现专业:电子信息工程姓名:高勇学号:2010021204指导老师:郑蕊蕊1目录一、实验类型:设计性实验 (3)二、实验目的 (3)三、实验设备:扫描仪、安装有MATLAB软件的计算机 (3)四、实验内容及原理 (3)(1)字符图像的获取 (3)(2)字符图像预处理 (3)(3)字符图像分割 (3)(4)函数的作用 (4)五、实验步骤 (8)1.载入车牌图像: (8)2.将彩图转换为灰度图并绘制直方图: (9)3. 用roberts算子进行边缘检测: (10)4.图像实施腐蚀操作: (10)5.平滑图像 (11)6. 删除二值图像的小对象 (12)7.车牌定位 (12)8.字符分割与识别 (14)9.车牌识别: (20)六、思考题 (27)2:实验类型一、设计性实验实验目的二、1. 掌握图像的获取、预处理和分割的原理及MATLAB实现方法。
2. 掌握使用扫描仪和计算机获取数字图像的方法,理解扫描仪的原理。
3. 自学一种字符图像的分割算法并用MATLAB编程实现该算法。
:实验设备三、扫描仪、安装有MATLAB软件的计算机实验内容及原理四、)字符图像的获取1(用扫描仪获取图像是字符图像处理常用的数字化过程的方法之一。
以办公设备中常用的台式扫描仪为例,其主要性能指标有x、y方向的分辨率、色彩分辨率(色彩位数)、扫描幅面和接口方式等,这些指标都可以从扫描仪的说明手册中获得。
分辨率的单位是dpi(Dot PerInch),意思是每英寸的像素点数。
扫描仪工作时,首先由可移动带状光源将光线照在欲输入的图稿上,并沿y方向扫描稿件,产生表示图像特征的反射光或透射光。
照射到原稿上的光线经反射后穿过一个很窄的缝隙,形成沿x 方向的光带,经光学系统采集和过滤成RGB三色光带分别照射到RGB分量的CCD上,CCD将光信号转换为模拟电信号。
内部电路的A/D变换器将模拟电信号转变为数字电子信号输送给计算机。
公交线路的选择Matlab程序

clear,clc%从Excel中导入数据a=importdata('C:\Users\Wan Huajian\Desktop\第四组,第七题程序\第四组第七题数据.xls','Sheet1');gq_zd=a.data.Sheet1;gq_xl=a.rowheaders.Sheet1;%输入起点和终点的数据q=[3359 1557 971 8 148 87];z=[1828 481 485 73 485 3676];%%%第一问的程序%直达hc_0_SJ=zeros(1,length(q));hc_0_XL=zeros(1,length(q));hc_0_xl=zeros(11,length(q));for k=1:length(q)[i1,j1]=find(gq_zd==q(k));[i2,j2]=find(gq_zd==z(k));b=intersect(i1,i2);if ~isempty(b)v=zeros(1,length(b));for i=1:length(b)s=b(i);t=find(gq_zd(s,:)==q(k));u=find(gq_zd(s,:)==z(k));if t<uv(i)=(u-t)*3;endend[ii,jj,vv]=find(v);[aa,bb]=min(vv);hc_0_SJ(k)=aa;hc_0_XL(k)=b(jj(bb));endend%%%换乘一次q(7)=3676;z(7)=1189;A=cell(7,1);for k=1:length(q)[i1,j1]=find(gq_zd==q(k));[i2,j2]=find(gq_zd==z(k));B=cell(length(i1),length(i2));for xl_q=1:length(i1)for xl_z=1:length(i2)c=intersect(gq_zd(i1(xl_q),j1(xl_q):end),gq_zd(i2(xl_z),1:j2(xl_z)));B(xl_q,xl_z)={c};endendA(k)={B};endhc_1_SJ=zeros(1,6);hc_1_q_xl=zeros(5,6);hc_1_z_xl=zeros(5,6);hc_1_zz=zeros(120,6);for k=7[i1,j1]=find(gq_zd==q(k));[i2,j2]=find(gq_zd==z(k));sj=inf*ones(length(i1),length(i2));index=zeros(length(i1),length(i2));for xl_q=1:length(i1)for xl_z=1:length(i2)if ~isempty(A{k}{xl_q,xl_z})h=zeros(1,length(A{k}{xl_q,xl_z}));for i=1:length(A{k}{xl_q,xl_z})d=gq_zd(i1(xl_q),:);e=find(d==A{k}{xl_q,xl_z}(i));f=gq_zd(i2(xl_z),:);g=find(f==A{k}{xl_q,xl_z}(i));h(i)=(e-j1(xl_q))*3+(j2(xl_z)-g)*3;end[sj_ ind]=min(h(i));sj(xl_q,xl_z)=sj_;index(xl_q,xl_z)=A{k}{xl_q,xl_z}(ind);endendendhc_1_SJ(k)=min(min(sj));[qd_ zd_]=find(sj==min(min(sj)));hc_1_q_xl(1:length(qd_),k)=i1(qd_);hc_1_z_xl(1:length(zd_),k)=i2(zd_);hc_1_zz(1:length(qd_),k)=diag(index(qd_,zd_));end%换乘两次hc_2_SJ=zeros(1,6);hc_2_q_XL=zeros(1,6);hc_2_ql_XL=zeros(1,6);hc_2_z_XL=zeros(1,6);hc_2_q_ZZ=zeros(1,6);hc_2_z_ZZ=zeros(1,6);for k=1[i1,j1]=find(gq_zd==q(k));[i2,j2]=find(gq_zd==z(k));bb=inf*ones(length(i1),length(i2));dd=zeros(length(i1),length(i2));ee=zeros(length(i1),length(i2));ff=zeros(length(i1),length(i2));for xl_q=1:length(i1)for xl_z=1:length(i2)d=gq_zd(i1(xl_q),j1(xl_q):end);f=gq_zd(i2(xl_z),1:j2(xl_z));gq_zd_bj=gq_zd;gq_zd_bj([i1(xl_q);i2(xl_z)],:)=0;ql=zeros(1,size(gq_zd,1));aa=zeros(1,size(gq_zd,1));gg=zeros(1,size(gq_zd,1));hh=zeros(1,size(gq_zd,1));for ql_=1:size(gq_zd,1)s=intersect(d,gq_zd_bj(ql_,:));t=intersect(f,gq_zd_bj(ql_,:));ql(ql_)=(length(s)>=1)&(length(t)>=1);if ql(ql_)==1n_q=zeros(1,length(s));n_z=zeros(1,length(t));for i=1:length(s)m_q=find(d==s(i));n_q(i)=m_q;endfor j=1:length(t)m_z=find(f==t(j));n_z(j)=m_z;endN_Q=min(n_q);N_Z=max(n_z);ql_q=find(gq_zd_bj(ql_,:)==d(N_Q));ql_z=find(gq_zd_bj(ql_,:)==f(N_Z));if ql_q<ql_zaa(ql_)=N_Q*3+(ql_z-ql_q)*3+(j2(xl_z)-N_Z)*3;gg(ql_)=d(N_Q);hh(ql_)=f(N_Z);endendend[ii,jj,vv]=find(aa);[ss,tt]=min(vv);if ~isempty(ss)bb(xl_q,xl_z)=ss;dd(xl_q,xl_z)=jj(tt);ee(xl_q,xl_z)=gg(jj(tt));ff(xl_q,xl_z)=hh(jj(tt));endendendhc_2_SJ(k)=min(min(bb));[xx,yy]=find(bb==hc_2_SJ(k));hc_2_q_XL(k)=i1(xx(1));hc_2_z_XL(k)=i2(yy(1));hc_2_ql_XL(k)=dd(xx(1),yy(1));hc_2_q_ZZ(k)=ee(xx(1),yy(1));hc_2_z_ZZ(k)=ff(xx(1),yy(1));end%%%第二问的程序D=cell(39,1);D(1)={[0567 0042 0025]};D(2)={1487};D(3)={[0303 0302]};D(4)={0566};D(5)={[0436 0438 0437 0435]};D(6)={[0392 0394 0393 0391]};D(7)={[0386 0388 0387 0385]};D(8)={[3068 0617 0619 0618 0616]};D(9)={1279};D(10)={[2057 0721 0722 0720]};D(11)={[0070 2361 3721]};D(12)={[0609 0608]};D(13)={[2633 0399 0401 0400]};D(14)={[3321 2535 2464]};D(15)={[3329 2534]};D(16)={[3506 0167 0168]};D(17)={[0237 0239 0238 0236 0540]};D(19)={[0180 0181]};D(20)={[2079 2933 1919 1921 1920]};D(21)={[0465 0467 0466 0464]};D(22)={3457};D(23)={2512};D(24)={[0537 3580]};D(25)={[0526 0528 0527 0525]};D(26)={[3045 0605 0607]};D(27)={[0087 0088 0086]};D(28)={[0855 0856 0854 0857]};D(29)={[0631 0632 0630]};D(30)={[3874 1426 1427]};D(31)={[0211 0539 0541 0540]};D(32)={[0978 0497 0498]};D(18)={0668};D(33)={[1894 1896 1895]};D(34)={[1104 0576 0578 0577]};D(35)={[3010 0583 0582]};D(36)={[3676 0427 0061 0060]};D(37)={[1961 2817 0455 0456]};D(38)={[3262 0622]};D(39)={[1956 0289 0291]};T1=[01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23]; T2=[24 25 26 12 27 28 29 30 31 32 18 33 34 35 36 37 38 39 24];a1=T1(1:end-1);b1=T1(2:end);w1=2.5*ones(1,length(a1));a2=T2(1:end-1);b2=T2(2:end);w2=2.5*ones(1,length(a2));R=sparse([a1,a2],[b1,b2],[w1,w2]);R(39,39)=0;h=view(biograph(R,[],'ShowWeights','on'));gq_dt_gq_SJ=zeros(1,length(q));gq_dt_gq_q_XL=zeros(1,length(q));gq_dt_gq_z_XL=zeros(1,length(q));gq_dt_gq_q_ZZ=zeros(1,length(q));gq_dt_gq_z_ZZ=zeros(1,length(q));gq_dt_gq_path=cell(1,length(q));for k=1:6[i1,j1]=find(gq_zd==q(k));[i2,j2]=find(gq_zd==z(k));gq_dt_gq_sj=inf*ones(length(i1),length(i2));kk=zeros(length(i1),length(i2));ll=zeros(length(i1),length(i2));path_=cell(length(i1),length(i2));for xl_q=1:length(i1)for xl_z=1:length(i2)d=gq_zd(i1(xl_q),j1(xl_q):end);f=gq_zd(i2(xl_z),1:j2(xl_z));fj_q=zeros(1,length(d));fj_z=zeros(1,length(f));gq_q=zeros(1,length(d));gq_z=zeros(1,length(f));for i=1:length(d)for m=1:39if ~isempty(intersect(D{m},d(i)));fj_q(i)=m;gq_q(i)=d(i);endendendfor j=1:length(f)for n=1:39if ~isempty(intersect(D{n},f(j)));fj_z(j)=n;gq_z(j)=f(j);endendend[ii1,jj1,vv1]=find(fj_q);[ii2,jj2,vv2]=find(fj_z);gq_dt_gq_=zeros(length(vv1),length(vv2));oo=cell(length(vv1),length(vv2));for ii=1:length(vv1)for jj=1:length(vv2)[d,p]=graphshortestpath(R,vv1(ii),vv2(jj));gq_dt_gq_(ii,jj)=jj1(ii)*3+d+(j2(xl_z)-jj2(jj))*3;oo(ii,jj)={p};endendif ~isempty(gq_dt_gq_)gq_dt_gq_sj(xl_q,xl_z)=min(min(gq_dt_gq_));[mm,nn]=find(gq_dt_gq_==min(min(gq_dt_gq_)));path_(xl_q,xl_z)=oo(mm(1),nn(1));kk(xl_q,xl_z)=gq_q(jj1(mm(1)));ll(xl_q,xl_z)=gq_z(jj2(nn(1)));endendendgq_dt_gq_SJ(k)=min(min(gq_dt_gq_sj));[xx,yy]=find(gq_dt_gq_sj==gq_dt_gq_SJ(k));gq_dt_gq_q_XL(k)=i1(xx(1));gq_dt_gq_z_XL(k)=i2(yy(1));gq_dt_gq_q_ZZ(k)=kk(xx(1),yy(1));gq_dt_gq_z_ZZ(k)=ll(xx(1),yy(1));gq_dt_gq_path(k)=path_(xx(1),yy(1));end%%%第三问程序q(7)=3676;z(7)=1189;hc_0_SJ_3=zeros(1,length(q));hc_0_XL_3=zeros(1,length(q));hc_0_BX=zeros(1,length(q));for k=7[i1,j1]=find(gq_zd==q(k));[i2,j2]=find(gq_zd==z(k));hc_0_sj_3=inf*ones(length(i1),length(i2));hc_0_xl_3=zeros(length(i1),length(i2));hc_0_bx=zeros(length(i1),length(i2));for xl_q=1:length(i1)for xl_z=1:length(i2)d=gq_zd(i1(xl_q),j1(xl_q):j1(xl_q)+1);f=gq_zd(i2(xl_z),j2(xl_z));[i11,j11]=find(gq_zd==d(1));[i12,j12]=find(gq_zd==d(2));[i21,j21]=find(gq_zd==f(1));b1=intersect(i11,i21);b2=intersect(i12,i21);if ~isempty(b2)for i=1:length(b2)s=b2(i);t=find(gq_zd(s,:)==d(2));u=find(gq_zd(s,:)==f(1));if t<uv(i)=(u-t)*3;endend[ii,jj,vv]=find(v);[aa,bb]=min(vv);hc_0_sj_3(xl_q,xl_z)=aa(1);hc_0_xl_3(xl_q,xl_z)=b2(end);hc_0_bx(xl_q,xl_z)=d(2);endendend%乘车时间hc_0_SJ_3(k)=min(min(hc_0_sj_3));[xx,yy]=find(hc_0_sj_3==hc_0_SJ_3(k));hc_0_XL_3(k)=hc_0_xl_3(xx(1),yy(1));hc_0_BX(k)=hc_0_bx(xx(1),yy(1));end。
Matlab在智能交通与智能城市中的应用实践

Matlab在智能交通与智能城市中的应用实践智能交通与智能城市是当下深受关注的热门话题,而Matlab作为一种重要的计算软件,也在这个领域发挥着重要的作用。
本文将从智能交通和智能城市的角度出发,探讨Matlab在这两个领域中的应用实践。
一、智能交通中的应用实践智能交通的概念涵盖了交通信息管理、交通控制、交通管理和交通运营等方面。
而Matlab在智能交通领域的应用主要体现在数据处理和算法优化两个方面。
1.1 数据处理智能交通系统需要大量的数据进行分析和处理,以便优化交通流量、提高交通安全等。
而Matlab作为一种强大的数据处理工具,能够帮助开发人员快速高效地处理这些数据。
首先,Matlab可以对交通数据进行预处理。
例如,可以通过Matlab对原始交通数据进行噪声去除、异常值检测等操作,进一步提高数据的可靠性。
其次,Matlab可以利用其丰富的数据分析工具对交通数据进行深入的统计分析。
通过对交通数据的离散化、聚类分析等处理,可以获取到交通流量、车速等关键信息,为交通运营的决策提供有力支持。
1.2 算法优化在智能交通系统中,优化算法的设计和应用是至关重要的。
而Matlab拥有强大的数学计算和优化工具箱,可以帮助开发人员设计和应用各种优化算法。
以交通信号优化为例,Matlab可以根据交通流量、车辆速度等参数,利用优化算法对信号的灯周期进行优化。
通过最小化车辆的延误和排队长度,可以提高交通效率和减少拥堵。
此外,Matlab还可以应用在路径规划、交通仿真等方面。
通过设计合理的路径规划算法,可以帮助驾驶员选择最佳路线,并减少交通拥堵。
而通过交通仿真,可以模拟真实的交通场景,从而评估各种交通策略的效果。
二、智能城市中的应用实践智能城市是指利用信息技术手段对城市的各个方面进行综合优化和智能化管理的城市。
而Matlab在智能城市领域的应用主要涉及城市规划、能源管理和环境监测等方面。
2.1 城市规划在城市规划中,Matlab可以通过模型构建和仿真来评估不同城市规划方案的效果。
Matlab实现公交查询
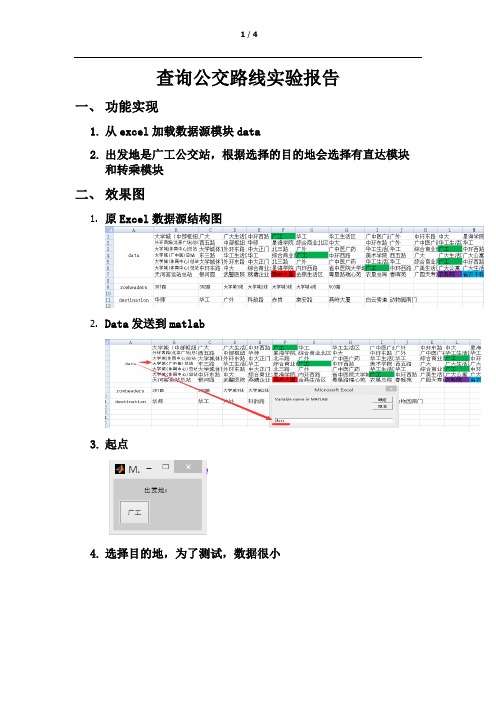
查询公交路线实验报告一、功能实现1.从excel加载数据源模块data2.出发地是广工公交站,根据选择的目的地会选择有直达模块和转乘模块二、效果图1.原Excel数据源结构图2.Data发送到matlab3.起点4.选择目的地,为了测试,数据很小5.选择目的为华工,可以直达线路的公交6.目的地为燕塘,需要换乘的公交线路指导三、源码1.从excel加载数据源模块%从Excel中导入数据 dataa=importdata('I:\复习\大四第一学期\matlab\实验\实验报告\buses.xls','Sheet1');2.输入起点和判断选择的目的地%输入的起点sta=menu('出发地:','广工');A=['广工']; 、rowheaders={'381路','382路','大学城1线','大学城2线','大学城3线','大学城4线','503路'};destination={'华师','华工','广外','科韵路','赤岗','棠安路','燕岭大厦','白云索道','动物园南门'};%判断输入的目的地des=menu('选择目的地:',destination{:});for i=1:9if des==iB=destination{i};endend3.直达模块, flag=1%data数据arr = cell(1); %arr = cell(1,7);i=0;v=0;flag=0;for k=1:7 %7个,角标超过了矩阵的维数for f=1:33 %33个if strcmp(data{k,f},B)%1.一次直达for j=1:33if strcmp(data{k,j},A)count='选择广工站!';i=i+1;h=rowheaders{1,k};arr{1,i}=sprintf('%s%s',h,'----------------->乘坐到',B,'下车');%使用= = = >加上矩阵尺寸必须同意。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
公交站点IC刷卡计数算法及其MATLAB实现查伟雄1,刘金行(1华东交通大学,南昌330013)摘要:中国大部分城市的公交公司早期并未成熟利用信息技术和数据库技术,因此其IC刷卡记录与车辆调度记录很难达到对精确性、实时性和关联性的要求。
为了最大限度利用这些海量的原始记录,本文针对实际情况,在允许一定误差的前提下,提出了公交站点IC刷卡计数算法,并能够结合实例使用数学软件MATLAB实现此算法。
关键词:智能交通,IC卡收费系统,公交站点,MATLAB中图分类号:U495 文献标识码:ABus Station IC Credit Cards Counting Algorithm andMatLab ImplementationZHA Wei-xiong, LIU Jin-hang(1.School of Eastchina Jiao Tong University,Nanchang 330013)Abstract: In early time,most of the city's public transport company in China is not mature use of information technology and database technology, so the IC credit cards records and vehicle scheduling records difficult to achieve on the accuracy, timeliness and relevance requirements. In order to maximize the use of these massive amounts of original records, this paper depending on the circumstances allowed under the premise of a certain error is proposed Bus Station IC credit card counting algorithm, and can combine instances of the use of mathematical software MATLAB realization of this algorithm.Key words: Intelligent Transportation System, IC card payment system, public transportation sites, MatLabCLC number: U495 Document code: A0 引言现在,我国许多大城市都开始使用公交IC卡,并且已经初具规模。
例如,青岛市2 600辆电汽车已经配备了IC卡收费系统,占公交车总数的80%,每天持卡乘车90万人次,占无人售票款收入的70%左右;天津市区已有2 500辆公交车可以使用公交IC卡乘车,占市区公交车总量的80%,市区已有12万乘客持卡坐车,占乘坐公交车总人数的26%;太原市持卡者占总客运人次的40%;广州市市内约有300条公交线路、6 200多辆公交车,95%以上的公交车辆已开通或安装了车载收费机[1]。
可以说持卡乘车是公交发展的必然趋势,但与国外相比,国内对收费系统的利用还远远不够[1]。
IC卡系统不仅给乘客、公交公司带来了具大的便利,而且其数据库系统记录了大量交通流信息,为交通调查提供了最原始、最直接和具有丰富操作性的第一手资料[2],因此研究从IC卡系统数据库中获取交通流信息的方法具有很重要的意义。
1 现实中IC卡系统现状现实中的IC卡系统存在以下三种情况:(1)IC卡系统与车辆调度系统共用一个时间钟,并且可以自动记录每一辆车到达、离作者简介:查伟雄,男,1963年生,教授开任一站点的时间,如使用了公交车GPS,便能够实现对任何装有终端的公交车进行实时监控[5],或者直接采集公交车行驶公里数,也可以实现对中间站点的记录[6]。
这类情况可以利用IC刷卡记录在数据库中自动匹配站点,即而准确无误差地将各站点任意时段的刷卡数统计出来。
这类情况无需设计算法,只需要在数据库系统中进行检索即可直接得到所需要的信息。
(2)IC卡系统与车辆调度系统共用一个时间钟,并且可以自动记录车辆从起点站发车时间和到达终点站时间,但不能够记录车辆到达、离开中间各站的时间[2]。
这类情况说明车辆调度系统仅仅停留在车辆发车与收车的调度上,并未实现对中间站的实时记录。
车辆调度系统不能够实时记录车辆到达、离开中间各站的时间,并不意味着IC卡系统的刷卡记录失去了作为交通流量调查原始资料的作用。
我们仍然可以按照公交车的运行规律设计算法,在一定误差范围内将刷卡记录匹配到各站点,戴霄、陈学武已经提出针对这种情况的相关算法。
(3)IC卡系统与车辆调度系统分别使用自己的时间钟,并且人工记录车辆从起点站发车时间和到达终点站时间,甚至仅仅人工记录车辆运行误差时间。
这类情况比起前者来说更为复杂,车辆发车时间、中间各站点间停留时间、收车时间均无准确记录,要把平均每天每条线路数万条刷卡记录准确匹配到线路各站点间,几乎不可能做到。
虽然这对于统计来说非常不利,但它却是存在于现实中最多的情况之一。
如果在允许一定误差的前提下,通过研究公交车运行规律,则可以设计算法将每一条刷卡记录匹配到线路各站点。
2 针对第三种情况的算法公交车的运行规律一般是:一、每辆车所跑线路、工作时间相对稳定。
二、每辆车每天从第一次发车开始,在以后的工作时间内一般属于循环作业,即:若线路形状为环形线路,则车辆沿环形线路持续作顺时针运动或逆时针运动;若线路形状为路段线路,则车辆重复作起点站——终点站——起点站运动。
跟据观察发现,车辆调度时为了尽可能提高经济效益,每辆车在完成一轮循环回到原始出发点时不会长时间停留,所停留时间与中间站点停留时间相差无几。
每辆车在一天当中不会轻易改变其所在线路号,在无故障的情况下,也不会停止车辆的循环作业。
在设计算法时,考虑到由于刷卡时间记录由IC系统自动记录,其时间精确到秒,而人工记录完全精确不到这一时间单位,甚至有较大误差。
按照人工记录形成的行车记录表来将刷卡记录划分至每一循环阶段的方法在程序对表格进行操作时是行不通的,因此本算法提出将所有刷卡记录和每辆车当天经过所有站点一起进行匹配的基本思想。
提出此思想的根据在于:许多公交公司在管理中为了加强管理力度,为每辆公交车从起始站到终点站人为规定了明确的行程时间,前车不许压点(故意放慢速度),后车不许提前(故意加快速度),对于公交车司机来说,每次的循环作业时间是相对固定的,这种现象可以证明本文算法的合理性。
本算法流程如下:图1. 算法流程图Fig1. Algorithm flow chart具体步骤如下:STEP1: 对IC刷卡源数据和行车记录表进行预处理,将IC卡源数据整理成至少具有以下三列信息的表格形式,命名为IC:表1. IC样表Tab1. IC Sample Table将行车记录表整理成至少具有以下二列信息的表格形式,命名为PLAN:表2. PLAN样表Tab2. PLAN Sample Table在形成表格的时候应该注意:为了方便MA TLAB计算,将刷卡时间的数值类型由时间型改为数值型,车号和卡号也都由文本型改为数值型,数值转换格式以EXCEL为标准。
其中IC表必须包含完整的全天刷卡记录,PLAN表中车号排列顺序必须符合当天的完整发车顺序。
由于行车记录表中起点站出发时间和终点站到达时间均不准确,因此无法对精确到秒的IC表进行关联操作,对本算法来说属于无效数据。
整个算法只利用行车记录表中的各线路发车次数和IC表中刷卡时间来确定全线路各站点刷卡数。
STEP2:确定各线路站点时距比例信息,即确定每条路线的公交车每次循环作业所经过的各站点间距离时所用的时间比例,可以采用人工调查方法,也可以根据距离来确定,本算法利用公式来确定比例,其中为第i站到第i+1站间距离,,Z为该线路的站点总数,由于将所有线路均抽象成环形线路,因此站间距离必然也有Z个。
第L条线路设数组,中的元素(i)=。
从数组的第二个元素起执行(i)=(i)+(i-1)计算,直至最后一个元素。
STEP3:按车号筛选出发生于每一辆车的刷卡记录,并将每一辆车的刷卡记录形成一个子过程。
(1)生成代表含有线路号信息的刷卡时间流水数据的初始空数组CARD(),生成代表含有线路站点数的初始空数组CARD1();(2)导入表IC,生成矩阵IC,导入表PLAN,生成矩阵PLAN,令n=1;(3)判断IC(n,2)是否为0,若为0,则转步骤(8),否则,令B= IC(n,2);(4)寻找PLAN(:,2)中所有与B相等的元素,记录个数为M;(5)从PLAN(:,2)中查出第一个与IC(n,2)相等的元素所在行数X,则令线路号L=PLAN(X,1),将L作为一个元素写入数组CARD,并将M作为一个元素写入CARD1;(6)将IC(:,2)所有与B相等的元素所在行的第一个元素同时写入CARD和CARD1,然后将IC(:,2)中所有与B相等的元素清零,将PLAN(:,2)中所有与B相等元素清零;(7)计算IC的行数ICL=size(IC,1);(8)n=n+1,若n>ICL,则结束,否则返回步骤(3);STEP4:按时间段筛选刷卡时间记录。
(1)设TIME=1;(2)生成与CARD同维的零数组CARD3。
对CARD的每一个元素执行判断R=(TIME-1)/24<CARD(1)<(TIME)/24,若R=1,则将此元素写入同样位置的CARD3;STEP5:为CARD和CARD1中的每个刷卡时间数据匹配站点。
(1)生成L个空矩阵,l=1……L,分别对应于L条线路;(2)令N=1;计算数组CARD的维数W=size(CARD(1,:));(3)由于EXCEL中转换为数值类型后的时间数值取值范围为[0,1],可以通过检测大于1的元素来寻找CARD和CARD1中非刷卡时间记录的元素位置。
查找CARD数组中第N个大于1的元素位置C,得到线路号,查找对应数组,计算数组元素个数Z,生成零矩阵A=zeros(1,Z);(4)查找CARD数组中第N+1个大于1的元素位置D,令H= ;(5)若CARD3(C+1)>0,则计算H1)+ CARD(C-1)+(CCARD3的余数MOD,在数组中查找大于MOD的第一个元素的位置z,z就是刷卡记录CARD3(C+1)在线路CARD(C)刷卡的站点位置,令A[1,z]= A[1,z]+1;(6)依次对CARD3(C+1)以后的元素执行步骤(5),直至CARD3(D-1);(7)N=N+1,重复步骤(3) (4) (5) (6)。
