一上.使每条线上的数都相等
小学五年级奥数第10讲 数阵(含答案分析)

第10讲数阵一、知识要点填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较常见的填数问题。
这里,和同学们讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二、精讲精练【例题1】把5、6、7、8、9五个数分别填入下图的五个方格里,如图a 使横行三个数的和与竖行三个数的和都是21。
练习1:1.把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2.把1—9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3.将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
【例题2】将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
练习2:1.把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2.把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
3.将1——8八个数填入下图方格里,使上面四格、下面四格、左四格、右四格、中间四格以及对角线四格内四个数的和都是18。
第1题第二题第三题【例题3】将1——6这六个数分别填入下图的圆中,使每条直线上三个圆内数的和相等、且最大。
练习3:1.将1——6六个数分别填入下图的○内,使每边上的三个○内数的和相等。
2.将1——9九个数分别填入下图○内,使每边上四个○内数的和都是17。
3.将1——8八个数分别填入下图的○内,使每条安上三个数的和相等。
第1题第二题第三题【例题4】将1——7分别填入下图的7个○内,使每条线段上三个○内数的和相等。
练习4:1.将1——9填入下图的○中,使横、竖行五个数相加的和都等于25。
一年级数学上册.使每条线上的数都相等

□3 +□8 =□5 +□6
大小搭配
○ 在 里分别填上3、4、5、6、7,使每条线上的三个数相加都得12。
方法一:先填2所在线上剩下的两个数。
用3、4、5、6、7这五个数填在○里
3
4
每个数字只能用一次
每条线上的三个数相加的和都是12
7
5
6
5
先填哪一条线上的数?
3
3
说一说找到的信息, 指一指哪三条线
8
4
7
6
5
7 5
8
6
4
根据已知数再找和
巩固练习:
○ 把1、2、3、4、5、7这六个数填在 里,使每条线上的四个
数相加的和等于15。
最小数1
像这样有公共加数的 情况下,我们先把共有加
3
1
2
15-1-7=7
数进行大小搭配,再把剩 上的和是否相等。
下2+6+4=12
12-2-4=6
12-3-4=5
验证: 左2+6+4=12 右4+5+3=12 下2+7+3=12
○ 在 里分别填上3、4、5、6、7,使每条线上的三个数相加都得12。
7
两个大数填在顶点可 以吗?
2
7+6>12
6
跟进练习:
○ 在 里分别填上4、5、6、7、8,使每条线上的三个数相加都得15。
4
34
25
7
5
最大数7
验证:1+7+3+4=15 1+7+2+5=15 每条线上的数和都是15。
小学数学思维拓展训练《数字迷藏》专题讲座之(9)(含参考答案)

第9讲数字迷藏(含参考答案和部分解题思路)一、解题技巧:1. 当数字和我们捉迷藏时,我们要仔细观察图形,确定图形中关键的位置应填几。
图形中关键的位置一般在三角形、长方形、正方形的顶点、图形中的中心和交叉的位置。
2. 将所填的数与所提供的数字联系起来考虑,一般要先计算所填数字的总和与提供的数字的和之间差多少,从而确定关键位置应填几。
二、新课教学1. 例1、在右图中分别填入1至9使两条直线上的五个数的和相等,和是多少呢?解题思路:在这9个数中选出一个数,填入中心的圆中,再把剩下的8个数两两搭配成和相等的四组,分别填入相对应的位置中。
如中心填5,那么4+6=10,3+7=10,2+8=10,1+9=10.或者中心填1,2+9=1,3+8=11,4+7=11,5+6=11.或者中心填3,1+5+7+8=21,2+4+6+9=21 (详见上图,答案3自己做)巩固练习。
(1) 将11、12、13、14、15、16、17这7个数分别填入下面的中,使每条线上的和都等于44。
解题思路:这是7个连续自然数,同样按照上面的道理,先确定中间数“17”,然后,将剩下的6个数两两搭配,组成三组和相等的数,再分别填入相应的位置中。
这7个数的和是98,三条线上各数字的和是44×3=132,中间的数多算了2次。
(132-98)÷2=17。
中间的17就是这样求得的。
(2) 在下图中填入2~10,使横行竖行中的五个数的和相同,和是多少呢?2107 5 6 3 948找出这9个连续自然数最中间的数“6”,把6填入最中间的位置,再把剩下的8个数两两搭配,组成和是12的4组数,再把各数填入相应的位置。
(3) 把1、4、7、10、13、16、19这7个数填入☆中,使每条直线上三个数的和相等。
解题思路:这是一组等差数列,先找出最中间的数“10”,将10填入最中间的星星中,再可按上面的方法,将各数填入相应的位置。
2. 例2、把9、12、15、18、21、27、33分别填入下图中的圆圈内,使每条直线上的三个数的和相等。
苏教版三年级奥数 第7讲 填数游戏专题

习题四、1、将数字2、3、4、5、6、7、8填入下图的小圆圈中,使每个三角形上的数字之和以及每条直线上的三个数字之和都相等。
2、将1∽8这8个数字分别填入下图的小圆圈内使横行、竖行、大圆环、小圆环上的四个数的和都相等。
8、将数字3∽11填在下图的方框中,使图中每一横行、竖行及对角线上的三个数的和都等于21。
9、把数字1∽7填在下图的小圆圈中,使每条直线上的三个数及大圆圈上的三个数的和均相等。
10、将数字0、1、3、4、5、6、7填入下图的方框中,使每行、每列上三个数的和均相等。
11、将数字1∽9填入下图的圆圈中,使中间小三角形三条边上的6个数之和与大三角形三条边上的6个数之和相等。
3、将1∽9这9个数字填入下面九个小三角形中,使大三角形每条边上的五个小三角形内的数字之和都相等。这个和最小是多少?
例题5、在右图各圆的空缺部分分别填上3、5、8、7,使每个圆中的四个数的和都等于21.
习题五、1、在下图中各圆的空缺部分分别填上1、2、4、6,使每个圆中的四个数的和都等于15。
2、在下图中各圆的空缺部分分别填上4、5、7、9,使每个圆中的四个数的和都等于27。
3、在下图中各圆的空缺部分分别填上6、8、10、11,使每个圆中的四个数的和都等于33。
提优部分
1、将数字1∽9填在下图中,使图中每一横行、竖行及对角线上的三个数的和都相等。
2、把2、4、6、7、8、10分别填入下图的空格中,使图中每一横行、竖行及对角线上三个数之和均为18.
9
5
3
3、将4、6、10、11、12填入下图的空格中,使图中每一横行、竖行及对角线上三个数之和均为24.
一上奥数(数阵、填数、填符号、搭配、路线、排队)

1.数阵图类型 发射型:封闭型2.突破方法:①找数字出现最多的线,用加减法去算②头中尾,填中间,大小大小手拉手3.数阵图歌数阵图,真有趣,每条线,和相等数越多,先找他,头中尾,中间填10.9.3.在图中空格里填上一个数,使得横行、竖行的三个数的和等于9.4.把4、5、7、8四个数填在四个空格里,使得横行、竖行三个数相加等于18.5.在圆圈里填上合适的数,使每条线上三个数的和都等于10.6.在正方形中填上合适的数,使横行、竖行、斜行上的三个数相加都等于18.7.把数字1、2、3、4、6、7、8、9分别填入下面八个圆圈中,使每条线上的三个数字的和等于15.8.把1、2、3、4、5这五个数填入图中的方格中,使横行、竖行三个数的和都相等.9.把1、2、3、4、5这五个数填入图中的方格中,使横行、竖行三个数的和都等于9.10.把1、2、3、4、5、6、7这七个数填入下面的圆中,使每条线上的三个数相加都相等.11.把1、2、3、4、5、6、7这七个数填入下面的圆中,使每条线上的三个数相加和都等于14.12.把2、3、4、5、6、7、8这七个数填入下面的圆中,使每条线上的三个数和都等于15.13.把4、6、9、11这四个数分别填入下图的圆圈中,使每条线上及大圆圈上的各数相加和都相等.14.把5、5、7、7、9、9分别填在下面的圆圈里,使每条边上都有5、7、9.8简单数阵知识点:11. (2)填数,使每条线上的三个数之和都得15.2.在圆圈里填上合适的数,使每条线上三个数的和都等于8.3.要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?4.在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.5.在下面的○里填上适当的数,使每条线上的三个数之和都是12.6.把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.7.把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.8.把3,4,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为 20.9.把4、6、9、11这四个数分别填入下图的圆圈中,使每条线上及大圆圈上的各数相加和都相等.10.在每个方格内,只能填1、2、3三个数字,使横行、竖行的三个数相加都相等,但每一横行、竖行的三个数字互不相同.54、634和8,5和7随便填1.相邻数加法和减法的特征: ①加法特征:大小、大小和相等,是横式变形的根本.②减法特征:相邻两数相减,差永远是1.(减法相等的依据)③根据等式是天平,可以左右加减同一个数(等式重要性质)2.重要方法:①找特殊:对于多个式子,有些式子的填法很多(不作为突破点),要学会寻找填法较少或者唯一的作为突破点;②分组法:几个连续数的“和”填式子,找中间数9横式填数知识点:3.不等式填数,先假设是等式,然后根据要求填写合适的数.4.当你不会做题的时候,往数学方法靠近,千万不可“胡猜乱想”:①学习方法第一位②多看看前面的笔记,帮助自己理解.(每个算式中,同一个数只能用一(1)()+()=()+()(2)()+()-()=()(3)()-()+()=()2.把1、2、3、4、5、6、7、8这8个数分别填入下面的方框里(每个数只能用一次),使等式成立.3.把4、5、6、7、9、13分别填入下面的中(每个数只能用一次),使等式成立.4.将0、1、2、3、7、8、9填入下面的方格内,使算式成立.5.把2、3、4、6、7、9分别填入下面6个圆圈中,使3个算式成立.6.在下面括号里填入适当的数.()-9>26+7 (2)()-12<10+207.把1~10这十个数填入横线中,使等式成立.(每个数只能用一次)8.智力擂台.(1)把0、1、2、3、4、5按要求填在方格里,每个数只能用一次.□-□=□-□=□-□如果是加法算式,又可以怎样填呢?□+□=□+□=□+□(2)数学谜语.像个蛋,不是蛋;说它圆,不太圆;说它没有它又有,十、百、千、万连成串.猜一数字.9.把1、2、3、6、7、8、9分别填入□中,使算式成立:10.用2、3、4、5、6、7、8、9这八个数编出下面两道加减混合算式(每个数只能用一次).11.在括号里填入合适的数,使不等式成立.15+3>() 27-()>26-7 9+()<()29四个数值编三道加减混合算式.(每个算式中每个数只能用一次)(1)()+()=()+()(2)()+()-()=()(3)()-()+()=()2.把0、1、2、3、7、8、9分别填入□中,使算式成立:3.把3、4、5、6、32、33、34、35这8个数填入下面的两个算式中,使等式成立.4.在5、6、7、8、9、10、11中选择6个数填入下面的算式,使等式成立.()+()=()+()=()+()()-()=()-()=()-()5.括号里最小能填几?()-4>7+2 26-()<9+146.用2、4、5、6、7和10组成加减两个算式(每个数字只能使用一次).()+()=()()-()=()7.从1——9这九个数中选出4个数进行组合,使他们相加的和是100.8.把1~10这十个数填入横线中,使等式成立.(每个数只能用一次)参考答案:课堂共同学习1.(1)3+6=4+5 (2)3+6-4=5 (3)5-3+4=6(答案不唯一:核心借助3+6=4+5)2.1+8-7=2,3+6-4=5(答案多多,核心借助大小大小和相等)3.①6+7=13,②9-5=44.8+9=20-3=17(突破点:中间第一个必然为2,最后一个首位必然是1)5.3+7=10,9-4=5,2+6=8(突破点:只有2+6=8)6.43,41(最小和最大填法)7.(突破点在最后一个)8.(1)5-4=3-2=1-0 (2)0+5=1+4=2+3 (3)0 9.8+9=23-6=1710.2+9-8=3, 7-5+4=6(答案多多)11.略课后自我提升:1.(1)26+29=27+28 (2)26+29-27=28 (3)28-26+27=292.8+9=20-3=173.3+35-4=34 5+33-6=324.5+11=6+10=7+9 6-5=8-7=10-95.14 、 46.5+2=7 10-4=67.32+68=1008.略1.填符号核心理念:看得数,变少了,找减号,变多了,找加号.2.对于相同数字填符号:如4 4 4 4 = 0(运用组合法靠近要求的结果)三种组合:①单个为4 ②4+4=8 ③4-4=03.对于相邻位置凑数字:①找靠近结果的数字组合 ②剩下的按照加减去推断 如:1 2 3 4 5 =33,优先考虑23结合.(选择填“>、<、=、+、或-”).10 15○9+6 18-7○1115○5=20 19○2○8=9 20○0=10○10 11○3○5=92.将1、2、3、4、5、6、7、8分成和相等的四组填入下面的方格中.3.将1、2、3、4、5、6、7、8分成和相等的两组组填入下面的方格中.4.在四个4中间填上“+、-”号,使算式成立.(写出三种不同的填法)4 4 4 4 = 010巧填符号知识点:4 4 4 4 = 04 4 4 4 = 05.在下面的方格中填入适当的数,使相邻三个数相加的和都是10.6.在数字之间添上“十”号,位置相邻的两个数字可以组成一个数.5 6 7 8 9 = 98.7.在下图五个2中间填上“+、-”号,使算式成立.(写出三种不同的填法)2 2 2 2 2 = 22 2 2 2 2 = 22 2 2 2 2 = 28.在方格里填上合适的数,使等式成立.(1)9=□+2+3(2)□=□-4-1(3)8-□=□+59.在下面的数字间填上“+、-”号,使算式成立.(位置相邻的数字可以组成一个数)1 2 3 4 5 = 51 2 3 4 5 = 241 2 3 4 5 = 610.在六个8之间填上加减号,使等式成立(提示位置相同的数字可以组成一个数)8 8 8 8 8 8=8811.在1、3、5、7、9之间填上“+或-”(位置相邻的数可以组成一个数),使等式成立.1 3 5 7 9 =7912.在合适的地方填写“+或-”,使等式成立.1 2 3 4 5 6=1-”,使等式成立.5 5 5 5 = 02.在合适的地方填写“+或-”,使等式成立.1 2 3 4 5 = 73.在所给的已知数之间,填上“+或-”使等式成立.(1)8 4 3 = 9 (2)5 6 3 = 8(3)7 2 1 = 8 (4)9 5 2 = 64.在下列各数之间填上“+或-”(相邻数可以组成一个数),使他们结果为10.2 2 2 1 1 1 = 105.在○中填入“+或-”,使等式成立.(1)8○9=19○2 (2)30○15=9○6(3)3○8=14○3 (4)20○20=17○176.在1、2、3、4、5之间填上“+”(位置相邻,可以组成一个数),使他们和等于33. 1 2 3 4 5 =337.在6个6之间填上“+或-”,使下面的等式成立. 6 6 6 6 6 6=0 6 6 6 6 6 6=12参考答案:课堂共同学习:(部分有答案)6.5+6+78+9=98.8.(1)4;(2)多种答案如:5、10;(3)多种答案如:0、3和1、2 11.13+57+9=79 12.1+2+3-4+5-6=1课后自我提升:(部分有答案) 2.1+2+3-4+5=7 4.22-2-11+1=10 6.1+23+4+5=331.组合问题: 按照从左往右的顺序先固定一个,然后交换后面的位置,或者和后面的每一个都结合.2.搭配问题:①标号码 ②画线条 ③数数量(加法思维)11搭配组合知识点:3. 简单的数码分类方法:①在个位:从1数到60,个位有6个2②在十位:从1数到60,十位只有20——29有10个24.培养学生严谨的顺序思维,做到不重复和不遗漏.有3顶不同颜色的草帽和3条不同颜色的彩带,你知道有几种不同的搭配方式吗?3.10个小朋友要分两伙做游戏,一共有几种不同的分法?4.某人数数,他从一开始,按照1、2、3、4…的顺序一直数到22,他一共数了几个1,几个2?5.小芳与3个小朋友见面,互相握手问好,一共要握几次手?6.中午学生食堂供应主食3种:米饭、馒头、面条,菜4种:青菜、鱼、牛肉、鸡肉.小红到食堂吃饭,主食和菜各挑选一份,她一共有几种不同的选法?7.用7、2、1三个数字可以组成多少个不同的三位数?8.老师有2件不同款式的上衣,有3条不同颜色的裤子,你知道老师能搭配出几种不同的穿着方式吗?9.星星面前有一盘花生米,他“1、2、3、4、5.....”一个一个的往下数,一直数到35.星星一共数了几个5,一共数了几个2?10.4个人下围棋,每两个人下一盘围棋,一共下了几盘围棋?11.明明有一个5分硬币,4个2分硬币,8个1分硬币,要组成8分,共有几种不同的搭配方法?12.从小力、小红、小新、小芳4人中挑选2位同学参加小记者选拔比赛,一共有几种不同的选法?3条不同款式的裤子.一件上衣搭配一条裤子,一共有多少种不同的搭配方法?2.小冉有3条不同款式的裙子,5双不同款式的靴子,某日她要去参加聚会,若穿裙子和靴子,则不同的穿着搭配方式的种数为() A.7 B.8 C.153.用9、0、5三个数字,可以组成多少个不同的三位数?4.课间时间到了,学校为同学们准备的点心有4种:饼干、面包、薯条、蛋挞;准备的饮料有3种:果汁、牛奶、酸奶.每位同学可以任意选择一种点心和一种饮料,请问有几种不同的选择方法?5.红、黄、绿三种颜色可以组成不同的信号方式,有几种不同的信号方式?6.甜甜学数数:1、2、3、4、…一个接一个地往下数,一直数到45,她一共数了()个含有数字5的自然数.7.用2,3,4三个数字可以组成多少个不同的三位数?写出并从小到大排列.8.从A、B、C、D四位同学中任选2人参加学校演讲比赛,一共有几种不同的可能性?并列举各种可能的结果.参考答案:课堂共同练习:1.4个2.9种3.5种4.13个1,6个25.6次6.12种7.6个8.6种9.4个5,14个210.6盘11.7种12.6种课后自我提升:1.6种2.C3.4个4.12种5.6种6.5个7.一共有6个;从小到大排列为:234<243<324<342<423<4328.一共有6种不同的可能性,分别是:AB ,AC ,AD ,BC ,BD ,CD .1.学习树状加法图:2.标号→画线→数数进行相加3.小猫要回家,它可以有几种不同的走法?4.从甲地到乙地有3条路,从乙地到丙地有4条路,那么从甲地经过乙地到丙地有几种走法?5.一只蜜蜂,从“1”爬到“6”处,有几种不同的走法?6.小蚂蚁从1走到5,不走重复路,有几种不同的走法?7.小明、小红、小强、小莉是好朋友,这天他们每两人互通了一次电话。
数阵

数阵数阵是由幻方演化出来的另一种数字图。
幻方一般均为正方形。
图中纵、横、对角线数字和相等。
数阵则不仅有正方形、长方形,还有三角形、圆、多边形、星形、花瓣形、十字形,甚至多种图形的组合。
变幻多姿,奇趣迷人。
一般按数字的组合形式,将其分为三类,即辐射型数阵、封闭型数阵、复合型数阵。
数阵的特点是:每一条直线段或由若干线段组成的封闭线上的数字和相等。
它的表达形式多为给出一定数量的数字,要求填入指定的图中,使其具备数阵的特点。
解数阵问题的一般思路是:1.求出条件中若干已知数字的和。
2.根据“和相等”,列出关系式,找出关键数——重复使用的数。
3.确定重复用数后,对照“和相等”的条件,用尝试的方法,求出其他各数。
有时,因数字存在不同的组合方法,答案往往不是唯一的。
一、辐射型数阵例1将1~5五个数字,分别填入下图的五个○中,使横、竖线上的三个数字和都是10。
解:已给出的五个数字和是:1+2+3+4+5=15题中要求横、竖每条线上数字和都是10,两条线合起来便是20了。
20-15=5,怎样才能增加5呢?因为中心的一个数是个重复使用数。
只有5连加两次才能使五个数字的和增加5,关键找到了,中心数必须填5。
确定了中心数后,按余下的1、2、3、4,分别填在横、竖线的两端,使每条线上数的和是10,便可以了。
通过尝试,可以填为:例2 将1~7七个数字,分别填入图中的各个○内,使每条线上的三个数和相等。
解:图中共有3条线,若每条线数字和相等,三条线的数字总和必为3的倍数。
设中心数为a,则a被重复使用了2次。
即,1+2+3+4+5+6+7+2a=28+2a28+2a应能被3整除。
(28+2a)÷3=28÷3+2a÷3其中28÷3=9…余1,所以2a÷3应余2。
由此,便可推得a只能是1、4、7三数。
当a=1时,28+2a=30 30÷3=10,其他两数的和是10-1=9,只要把余下的2、3、4、5、6、7,按和为9分成三组填入两端即可。
如何用1-100这100个数字组成一个九宫格使得每行、每列和对角线上的数字之和都相等

筛选结果:最终筛选出符合条件的 9个数字,填入九宫格中,完成题 目要求
九宫格的排列方式:1-9、1018、19-27、28-36、37-45、 46-54、55-63、64-72、73-99
数字的顺序:按照从小到大的顺 序排列,每行三个数字,共三行
对角线上的数字之和:每条对角 线上的数字之和都相等,等于45
棋类游戏:在五子棋、围棋等 棋类游戏中,九宫格常被用作 棋盘的格子
数学教育:用于教授数学基 础概念,如加法、减法等
音乐教育:用于教授音符和 音阶,将音乐理论可视化
心理学研究:用于研究人类 认知和注意力等心理现象
九宫格的变种:除了传统的九宫格,还有多种变种,如旋转九宫格、镜像九宫格 等。
九宫格的拓展:九宫格可以拓展到其他领域,如数学、计算机科学、艺术等。
确定对角线数字的方法:通过计算 和推理,确定九宫格对角线上的数 字。
举例说明:以1-9这9个数字为例, 通过计算可以确定对角线上的数字 为5。
添加标题
添加标题
添加标题
添加标题
对角线数字的特点:对角线上的数 字之和相等,且每行、每列的数字 之和也相等。
注意事项:在确定对角线数字时,需 要注意数字的排列顺序,以保证每行、 每列和对角线上的数字之和相等。
特殊情况:如果九宫格中有相同 的数字,则它们必须位于同一行 或同一列
数字的选择:1-100中选取9个数字,每个数字只出现一次
排列方式:采用旋转、对称等方式排列数字,使得每行、每列和对角线上的数字之和相 等
组合技巧:利用数字的特性,如奇偶性、大小关系等,进行组合,使得组合具有规律性 和美感
实例展示:展示一些成功的数字组合,并分析其特点
由1-100这100个数字组成
求加法算式中的未知加数·数学苏教版一上-特训班(含答案)
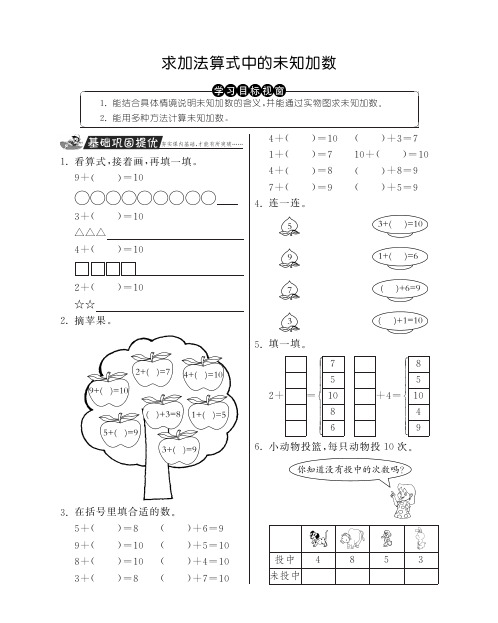
想一想 , 回答下面的问题 ㊂ 7.看一看 , = ( 条)
( ) 一共堆了 ( 1
( ) 从 上 面 第 2 层 起, 每一层都比上 4 8. 面一层多 ( ) 根木头 ㊂
( ) 最下面一层有 ( 3
( ) 最上面一层有 ( 2
) 层木头 ㊂
) 根木头 ㊂
) 根木头 ㊂
1 1.在
里填合适的数 ㊂ -5<8-6 -1
) ) 1 3.( 1 9 ( 2 2 3 3 4
=
( 只) +2 -3
3+4< 2+
4-0< 3+
>8-1
-6>7-5 <
跃过去, 你就是尖子生!
1 2.在
里 填 合 适 的 数, 使每条线上的 里的数 ㊂
数相加的和都等于 填一填 ㊂ 9.画一画 , ( ) 1 ( ) 2 әәәә ( ) 4 ʀʀʀ ( ) 3 ѲѲ
3+ 4+ 2+ 3+
=7 =8 =1 0 =9 填一填 ㊂ 1 3.想一想 , ( ) 1 从左 往 右 数 , 是 第 6 个 ; 从右 往左数 , 是 第 4 个 ㊂ 共有 ( ) 个㊂ 和
求加法算式中的未知加数
并能通过实物图求未知加数 ㊂ 1.能结合具体情境说明未知加数的含义 , 2.能用多种方法计算未知加数 ㊂
夯实课内基础, 才能有所突破
接着画 , 再填一填 ㊂ 1.看算式 , ) 9+ ( =1 0 3+ ( ) =1 0 ) =1 0 ) =1 0
4.连一连 ㊂
4+ ( 7+ (
1 0.看图列式计算 ㊂
一
( ) 想一想 , 括号里最大填几 ? 2 = ( 只) 6+ ( ( ) +3<7 ( ) <9 4+ (
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
1
2
15-1-7=7
数进行大小搭配,再把剩 下的数根据和相等进行两
7
10
两组合,最后验算每条线 上的和是否相等。
4
34
25
7
5
最大数7
验证: 1+7+3+4=15 1+7+2+5=15 每条线上的数和都是15。
7
5
6
5
2
6
42
7
3
最小的数是3和Biblioteka 12-2-3=7验证:左2+7+3=12 右3+5+4=12
下2+6+4=12
12-2-4=6
12-3-4=5
验证: 左2+6+4=12 右4+5+3=12 下2+7+3=12
○ 在 里分别填上3、4、5、6、7,使每条线上的三个数相加都得12。
7
两个大数填在顶点可 以吗?
4
每个数字只能用一次
每条线上的三个数相加的和都是12
7
5
6
5
先填哪一条线上的数?
2
6
42
7
3
12-2=10
10
73
10 64
12-43=5
○ 在 里分别填上3、4、5、6、7,使每条线上的三个数相加都得12。
方法二:先把小数分别填在顶点,再确定和哪个大数搭配。
3
4
知道两头的数,怎样
确定中间的数是几?
人教版一年级上册第94页思考题 宁波市奉化区尚田镇中心小学 毛燕
把3、5、6、8这4个数填在□里,每个数只能用一次。
□3 +□8 =□5 +□6
大小搭配
○ 在 里分别填上3、4、5、6、7,使每条线上的三个数相加都得12。
方法一:先填2所在线上剩下的两个数。
用3、4、5、6、7这五个数填在○里
3
2
7+6>12
6
跟进练习:
○ 在 里分别填上4、5、6、7、8,使每条线上的三个数相加都得15。
3
3
说一说找到的信息, 指一指哪三条线
8
4
7
6
5
7 5
8
6
4
根据已知数再找和
巩固练习:
○ 把1、2、3、4、5、7这六个数填在 里,使每条线上的四个
数相加的和等于15。
最小数1
像这样有公共加数的 情况下,我们先把共有加
