行车道板配筋计算
第七讲行车道板的计算资料

三、板的有效工作宽度 (一)单向板
1、受力分析:
设想:a mxmax mxdy M
则:
a M mx max
a——弯矩图形的换算宽度,定义为板的有效工作宽度,或 荷载有效分布宽度。 影响mxmax的因素:
1)支承条件:双向板、单向板、悬臂板 2)荷载长度:单个车轮、多个车轮作用 3)荷载到支承边的距离
拟定构件截面形式和细部尺寸计算最不利内力验算强度刚度稳定性判断尺寸是否合理修正计算过程内力计算截面配筋验算开始拟定尺寸是否通过计算结束截面计算混凝土结构原理预应力混凝土结构课程解决下部结构桥墩桥台一行车道板的类型1行车道板的作用1直接承受车辆轮压
第五章 简支梁桥的计算
§5-1 概述
桥梁设计顺序:
拟定构件截面形式和细部尺寸——计算最不利 内力——验算强度、刚度、稳定性——判断尺寸是 否合理,修正
(3)荷载靠近板支承处 ax a ' 2x
(二)悬臂板 1、受力分析:
a
M0 mx max
Pl0 0.465P
2.15l0
2l0
可见,悬臂板的a 接近于2倍的悬臂 长,故荷载可近 似地按45o角向悬 臂支承处分布。
2、《桥规》规定: (1)单个荷载: a a2 2H 2b' a1 2b'
b、当t/h≥1/4时:
跨中: 支点:
M中 0.7M 0
M 支 0.7M 0
2、支点剪力: 支点剪力Q支的计算公式:
Q支
gl0 2
(1
)(A1
y1
A2
y2 )
其中:矩形部分荷载合力A1Fra bibliotekp b1
行车道板的计算

行车道板的计算1、荷载分布宽度的计算根据《桥规》4.1.3条的规定1、1 平行于板的跨径方向的荷载分布宽度b=b1+2h=0.6+2×0.2=1m1、2 垂直于板的跨径方向的荷载分布宽度1)单个车轮在板的跨径中部时a=(a1+2h)+L/3=(0.2+2×0.2)+2/3=1.27m<2L/3=1.33m2)两个相同车轮在板的跨径中部时a=(a1+2h)+d+L/3=(0.2+2×0.2)+1.4+2/3=2.67m<2L/3+d=2.73m3)车轮在板的支承处时a=(a1+2h)+t=(0.2+2×0.2)+0.22=0.82m4)车轮在板的支承处时a=(a1+2h)+t+2x=(0.2+2×0.2)+0.22+2×x一、内力计算采用近似方法计算(参考《桥梁设计与计算邵旭东》),即先按相同跨径的简支板进行计算。
1、恒载内力(1)、每延米板上的恒载g混凝土桥面铺装 g1=0.2×2×24=9.6KN/mT梁翼缘板 g2=[0.3×0.16+(0.25+0.16)×0.6/0.2]×2×25=8.55 KN/m 每延米板宽恒载合计 g=g1+g2=18.15 KN/m(2)、恒载产生的内力弯矩Mg=1/8×g×Ll2=18.15×2×2/8=9.075KN.m剪力Qg=0.5×g×L=0.5×18.15×2=18.15KN2、活载产生的内力经过分析,汽车荷载作用在两翼板中间时为最不利位置根据《桥规》4.1.3条的规定2、1平行于板的跨径方向的荷载分布宽度b=b1+2h=0.6+2×0.2=1m2、2垂直于板的跨径方向的荷载分布宽度单个车轮在板的跨径中部时a=(a1+2h)+L/3=(0.2+2×0.2)+2/3=1.27m<2L/3=1.33mMop=(1+u) ×P/4a×(L-b/4)=1.3×140/4/1.33×(1-1/4)=25.7KNmQop=(1+u) ×P/4a=1.3*140*2/4/1.33=68KN3、最不利荷载组合:承载能力极限状态下的基本组合M1=1.2Mg+1.4Mop=1.2×9.075+1.4*25.75=46.94KNmQ1=1.2Qg+1.4Qop=1.2×18.15+1.4*68=116.98KN此T梁板厚取25cm,梁高为170cm,25/175<1/4,所以跨中弯矩修正系数为0.5。
行车道板的计算

得 每米板宽的支点最大弯矩:
M s M sP M sg
(a)
b b1 2h
a
a2
全跨满布条形荷载的有效分布宽度比局
Байду номын сангаас、板的有效工作宽度
(2)垂直于板的跨径方向的荷载分布宽度: 1)单个车轮在板的跨径中部:
l 2 a a1 2h 且 l 3 3
2)多个相同车轮在板的跨径中部,当
l 2 a a1 2h d l d 各单个车轮按上式计算的荷载分布 3 3
三、板的有效工作宽度
1. 单向板 荷载有效分布宽度特点:
d:相邻车
l
b
b2
两边固结板的有效工作宽度比简支板小
(30%~40%)
部分布荷载小
荷载愈靠近支承边,有效工作宽度愈小
《桥规》(D62)4.1.3 计算整体单向板时, 车轮在板上的分布宽度按下列规定采用: (1)平行于板的跨径方向的荷载分布宽度:
45
b2
行 车 方 向
h
o
h
b2
45
作用与砼桥面板顶面的矩形荷 载压力的边长为
沿纵向:a2 a1 2h 沿横向:b2 b1 2h
a2
a2
图 车辆荷载在桥面板上的分布
a1
o
二、车轮荷载在板上的分布
当车辆荷载作用于桥面板上的局部分布荷载为:
(对于车辆荷载,P取后轴轴载140kN)
(a)
y
l 截面弯矩图 2
dy
(
mx m xmax
a2
a
得:弯矩图形的换算宽度为:
M a m x max
a — —板的有效工作宽度, 或荷载有 效分布宽度,以此板承 受车轮荷载产 生的总弯矩,既满足弯 矩最大值的要 求,又方便计算。
桥梁8—行车道板计算
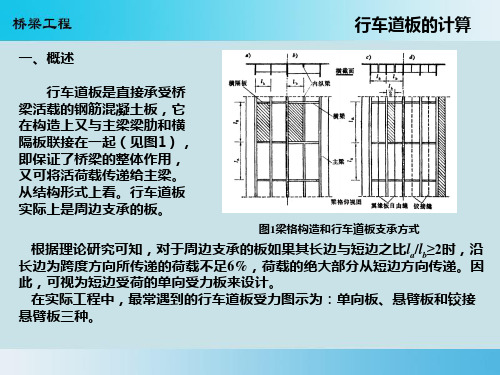
行车道板的计算一、概述行车道板是直接承受桥梁活载的钢筋混凝土板,它在构造上又与主梁梁肋和横隔板联接在一起(见图1),即保证了桥梁的整体作用,又可将活荷载传递给主梁。
从结构形式上看。
行车道板实际上是周边支承的板。
根据理论研究可知,对于周边支承的板如果其长边与短边之比l a /l b ≥2时,沿长边为跨度方向所传递的荷载不足6%,荷载的绝大部分从短边方向传递。
因此,可视为短边受荷的单向受力板来设计。
在实际工程中,最常遇到的行车道板受力图示为:单向板、悬臂板和铰接悬臂板三种。
图1梁格构造和行车道板支承方式二、板的有效工作宽度(一)单向板跨径为l 、宽度较大的行车道板的受力状态如图(2)。
当荷载以a 1×b 1的分布面积作用在板上时,板除了在计算跨径x方向产生挠曲变形w x 外,在沿垂直于计算跨径的y 方向同时发生挠曲变形w y (图2b )。
这说明在荷载作用下不仅直接承压的宽度为a 1的板条受力,其邻近其邻近的板也参与工作,共同图2 行车道板的受力状态承担车轮荷载所产生的弯矩,其沿y 方向的分布情况如图2a 中m x 所示。
可见,跨中弯矩m x 的实际图形是呈曲线形分布的。
假设,以a ×mx 的矩形来代替此曲线图形,即使得则:得到板的换算宽度为:Mdy m m a x x ==⨯⎰max maxx m M a =式中M ——车轮荷载沿跨径l 产生的总弯矩。
m xmam ——荷载中心处的最大单宽弯矩值,可按弹性板的理论计算。
上式中a 就是我们定义的板的有效工作宽度(或称有效分布宽度),以此板宽来承受车轮荷载产生的总弯矩,既满足了弯矩最大值的要求,计算起来也较方便。
为设计方便,《桥规》对于单向板的有效工作宽度偏安全地作了如下规定:(1)图3板桥的计算跨度为l,当一个集中车轮荷载作用在板中时,其折算为车轮荷载的有效分布宽度b为:a= a1+l / 3 (1)整体式简支板桥,当跨径l>3m时,车轮上两端轮子的有效分布宽度会出现重叠现象(图3),此时的有效分布宽度a为(见图4)a = a2+ 2H+d+l / 3 = a1+ d+l /3 (2)图3 板的有效分布宽度(2)当计算支点剪力时,以荷载位于支承处最为不利。
桥梁工程课程设计装配式钢筋混凝土简支T形梁桥设计行车道板内力计算

桥梁工程中,装配式钢筋混凝土简支T形梁桥的行车道板内力计算是一个重要的设计环节。
下面是一般的步骤和方法:
确定桥梁的几何参数:包括桥梁的跨径、梁的高度、梁的宽度等。
这些参数将对后续的内力计算和设计有重要影响。
荷载计算:根据设计标准和实际使用情况,确定桥梁所承受的荷载类型和荷载大小。
这些荷载包括静载荷和动载荷,如自重、活载、风荷载等。
梁的截面设计:根据荷载计算结果和梁的几何参数,进行梁的截面设计。
设计要满足强度、刚度和稳定性等方面的要求,通常使用混凝土弯曲构件的设计方法进行计算。
内力计算:根据梁的截面设计结果,进行内力计算。
这包括正截面和反截面的内力计算,以确定在不同工况下的梁的弯矩、剪力、轴力和反弯矩等。
钢筋配筋设计:根据内力计算结果,进行钢筋配筋设计。
配筋设计要满足混凝土和钢筋的受力要求,同时考虑施工的可行性和经济性。
校核和优化设计:对设计结果进行校核和优化,确保梁的结构安全可靠,并满足设计要求。
需要注意的是,上述步骤是一个简化的桥梁设计流程,实际设计中还需考虑很多其他因素,如桥墩的设计、桥面铺装、伸缩缝的设置等。
因此,在实际工程中,最好由专业的桥梁工程师进行详细的设计和计算,以确保桥梁的结构安全可靠。
行车道板的配筋计算

行车道板截面强度及配筋计算拟采用混凝土的强度等级为C50,受力钢筋采用HRB335,查《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTG D62—2004 (以下简称《公预规》)第25页表5.2.1可知混凝土强度等级为C50、钢筋种类为HRB335时相对极限受压区高度0.56b ξ=。
查《公预规》表3.1.4和表3.2.3-1得'22.4280280cd sd sd f MPaf MPa f MPa===查《公预规》第5.1.5条得0 1.0γ=拟采用単筋矩形截面形式。
假设38s a mm =,则有效受压区高度01253887h mm =-=,根据《公预规》第25页5.2.2公式5.2.2-1002d cd x M f bx h γ⎛⎫≤- ⎪⎝⎭ 31.025.4281022.41872x x ⎛⎫⨯⨯≤⨯⨯- ⎪⎝⎭ 求得15x mm =根据《公预规》第25页5.2.2公式5.2.2-2sd s cd f A f bx =222.41000151200280cd s sd f bx A mm f ⨯⨯===选用HRB335φ14间距100mm ,2153.9101539s A mm =⨯=,取保护层厚度为30mm ,014125(30)882h mm =-+= 配筋验算如下:根据《公预规》第25页5.2.2公式5.2.2-2sd s cd f A f bx =28015391922.41000sd s cd f A x mm f b ⨯===⨯ 02cd x f bx h ⎛⎫- ⎪⎝⎭ =61922.4100019881033.4102MPa -⎛⎫⨯⨯⨯-⨯= ⎪⎝⎭ >0d M γ=25.428MPa00.56884919b h mm x mm ξ=⨯=>=满足《公预规》25页5.2.2条要求。
板的配筋同时也满足《公预规》9.2条的构造要求。
斜截面验算:32030.50100.5010 1.0 1.8310008880.52041.446td f bh KN KNα--⨯=⨯⨯⨯⨯⨯=>即满足30200.5010d td V f bh γα-≤⨯,根据《公预规》5.2.10条,当满足此式时可以不进行斜截面抗剪承载力验算,只需按9.3.13条构造要求配置箍筋。
桥梁工程9(行车道板内力计算)

THANKS
感谢观看
弹性力学基础
弹性力学是研究弹性物体在外 力作用下的应力、应变和位移 的一门学科。
弹性力学的基本假设包括连续 性、均匀性、各向同性、小变 形等。
弹性力学的基本方程包括平衡 方程、几何方程、物理方程等, 用于描述物体的应力、应变和 位移之间的关系。
有限元方法
有限元方法是数值分析中的一种方法,用于求解偏微分方程和积分方程。
行车道板内力计算的重要性
行车道板内力计算是确保桥梁结 构安全性和耐久性的关键环节。
通过准确的内力计算,可以优化 行车道板的结构设计,降低材料 消耗和施工成本,提高桥梁的整
体性能和经济效益。
内力计算的结果还可以为桥梁的 监测和维护提供参考,有助于及 时发现和处理潜在的安全隐患。
02
行车道板内力计算的基本原理
在桥梁工程中,有限元方法常用于分析结构的应力、应变和位移等。
有限元方法的基本思想是将连续的物体离散成有限个小的单元,并对每 个单元进行受力分析,最后将所有单元的受力情况综合起来得到整个物 体的受力情况。
边界条件和载荷条件
01
边界条件是指在求解域的边界上所受的力或位移的限制条件。
02
载荷条件是指作用在结构上的外力,包括重力、风载荷、雪载
对未来研究的展望
研究方向
未来的研究可以针对行车道板内力的计算方法进行深入探讨,研究更加精确和可靠的数值模拟方法, 以提高内力计算的精度和可靠性。同时,可以结合新材料、新工艺和新结构形式的应用,研究相应的 内力计算方法和设计准则,以适应工程实践的发展需求。
跨学科合作
桥梁工程中的行车道板内力计算涉及到多个学科领域的知识,如结构力学、材料科学、数值计算等。 未来的研究可以加强跨学科的合作与交流,综合运用不同学科的理论和方法,共同推动桥梁工程领域 的发展和创新。
行车道板计算及配筋指导书

10 行车道板计算考虑到主梁翼缘板内配筋是连续的,故行车道板可按悬臂板(边梁)和两端固结的连续板(中梁)两种情况来计算。
10.1 悬臂板荷载效应计算由于横隔梁宽跨比大于2,故悬臂板可按单向板计算[6],悬臂长度为1.15m ,计算时取悬臂板宽度为1.0 m 。
10.1.1 永久作用(1)主梁架设完毕时桥面板可看成80cm 长的单向悬臂板,计算图式见图10-1 b 。
计算悬臂根部一期永久作用效应为: 弯矩:22g1111M =0.121250.70.081250.7232-⨯⨯⨯⨯-⨯⨯⨯⨯⨯0.898=-(kN·m)剪力:110.121250.70.081250.45 3.52g V =⨯⨯⨯+⨯⨯⨯⨯=(kN·m)(2)成桥后桥面现浇部分完成后,施工二期永久作用,此桥面板可看成跨径为0.9m 的悬臂单向板,计算图式如图10-1c 、d 所示。
图中:g 1=0.12×1×25=3.0(kN/m ),为现浇部分自重;P =1.5kN ,为防撞栏重力。
计算二期永久作用效应如下:弯矩:2 3.00.20(0.90.2/2) 1.5g M =-⨯⨯--⨯(0.9-0.10)=-1.643(kN·m)剪力:V g2=3.0×0.20+1.5=2.1(kN)(3)总永久作用效应综上所述,悬臂根部永久作用效应为: 弯矩:M g =-0.898-1.643=-2.541(kN·m) 剪力:V g =3.5+2.1=5.6(kN)a)c)g 1b)d)'1q r=3.5kN/m图10-1 悬臂版计算图式(尺寸单位:mm )10.1.2 可变作用在边梁悬臂版处,只作用有人群,计算图式为10-1d 弯矩:M r =213.50.652-⨯⨯=-0.74(kN·m)剪力:V r =3.5×0.65=2.275(kN)10.1.3 承载能力极限状态作用基本组合按《桥规》4.1.6条:M d =1.2M g +1.4×0.8×Mr=-(1.2×2.541+1.4×0.8×0.74)=-3.878(kN·m)V d =1.2Vg+1.4×0.8×Vr=1.2×5.6+1.4×0.8×2.275=9.268(kN)10.2 连续板荷载效应计算对于梁肋间的行车道板,在桥面现浇部分完成后,行车道板实质上是一个支承在一系列弹性支承上的多跨连续板,实际受力很复杂。
