机械原理matlab作业
matlab平面连杆结构分析(机械原理课程设计)

优化参数:连杆 长度、角度、质 量等
优化结果:得到 最优的连杆结构 设计
感谢观看
汇报人:
平面连杆结构的应用范围
机械工程:用于设计、分析和优化机械设 备
生物医学:用于设计、分析和优化假肢、 康复设备等
航空航天:用于设计、分析和优化飞机、 火箭等航天器
机器人技术:用于设计、分析和优化机器 人关节、机械臂等
汽车工业:用于设计、分析和优化汽车底 盘、悬挂系统等
建筑工程:用于设计、分析和优化建筑结 构、桥梁等
03
平面连杆结构的运动学分析
平面连杆结构的运动学方程
平面连杆结构的运动学方程是描述连杆系统运动状态的数学模型 运动学方程包括位移方程、速度方程和加速度方程 运动学方程的建立需要知道连杆系统的几何参数和运动参数 运动学方程的求解可以通过数值积分方法或解析方法进行
平面连杆结构的运动学特性
运动学方程:描述连杆结构的运动状态 运动学参数:包括位移、速度、加速度等 运动学约束:限制连杆结构的运动范围 运动学仿真:通过计算机模拟连杆结构的运动过程
平面连杆结构的形状优化
优化目标:提 高连杆结构的 稳定性和刚度
优化方法:有 限元分析、拓
扑优化等
优化参数:连 杆的长度、宽
度、厚度等
优化效果:提 高连杆结构的 承载能力和使
用寿命
平面连杆结构的拓扑优化
拓扑优化:通过改变材料的分布和形状, 约束条件:结构的刚度、强度、稳定
以实现最优的结构性能
性等性能要求
目标函数:最小化重量或体积,同时 满足给定的性能要求
优化方法:遗传算法、粒子群算法、 模拟退火算法等
设计变量:材料的分布和形状
应用领域:汽车、航空航天、机械制 造等
matlab机电系统仿真大作业
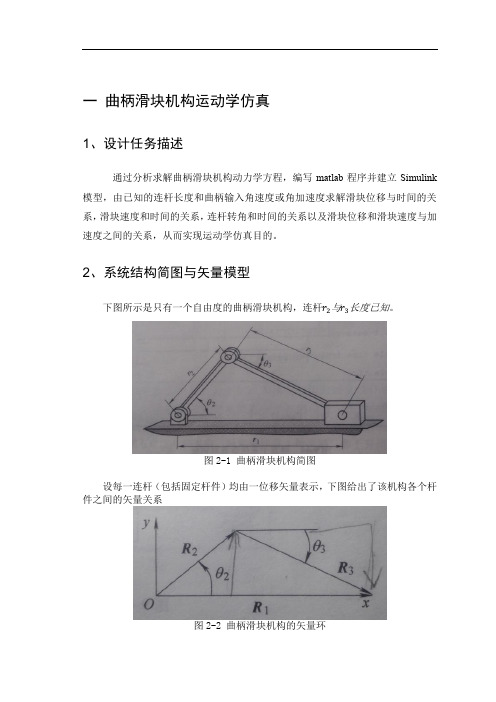
一曲柄滑块机构运动学仿真1、设计任务描述通过分析求解曲柄滑块机构动力学方程,编写matlab程序并建立Simulink 模型,由已知的连杆长度和曲柄输入角速度或角加速度求解滑块位移与时间的关系,滑块速度和时间的关系,连杆转角和时间的关系以及滑块位移和滑块速度与加速度之间的关系,从而实现运动学仿真目的。
2、系统结构简图与矢量模型下图所示是只有一个自由度的曲柄滑块机构,连杆r2与r3长度已知。
图2-1 曲柄滑块机构简图设每一连杆(包括固定杆件)均由一位移矢量表示,下图给出了该机构各个杆件之间的矢量关系图2-2 曲柄滑块机构的矢量环3.匀角速度输入时系统仿真3.1 系统动力学方程系统为匀角速度输入的时候,其输入为ω2=θ2,输出为ω3=θ3,θ3;v 1=r 1,r 1。
(1) 曲柄滑块机构闭环位移矢量方程为:R 2+R 3=R 1(2) 曲柄滑块机构的位置方程{r 2cos θ2+r 3cos θ3=r 1r 2sin θ2+r 3sin θ3=0(3) 曲柄滑块机构的运动学方程通过对位置方程进行求导,可得{−r 2ω2sin θ2−r 3ω3sin θ3=r 1r 2ω2cos θ2+r 3ω3cos θ3=0由于系统的输出是ω3与v 1,为了便于建立A*x=B 形式的矩阵,使x=[ω3v 1],将运动学方程两边进行整理,得到{v 1+r 3ω3sin θ3=−r 2ω2sin θ2−r 3ω3cos θ3=r 2ω2cos θ2将上述方程的v1与w3提取出来,即可建立运动学方程的矩阵形式(r 3sin θ31−r 3cos θ30)(ω3v 1)=(−r 2ω2sin θ2r 2ω2cos θ2) 3.2 M 函数编写与Simulink 仿真模型建立3.2.1 滑块速度与时间的变化情况以及滑块位移与时间的变化情况仿真的基本思路:已知输入w2与θ2,由运动学方程求出w3和v1,再通过积分,即可求出θ3与r1。
机械原理课程设计matlab程序及成果图

Wjr_main.m%1.输入已知数据clear;l2=0.1605;%AB的长度单位ml4=0.6914;%CD的长度单位ml5=0.2074;%DE的长度单位ml1=0.370;%AC的长度单位ml1p=0.6572;%CF的长度单位momg2=8.378;af2=0;hd=pi/180;du=180/pi;%2.调用子函数abc.m计算牛头刨机构位移,角速度,角加速度for n1=1:689;tt2(n1)=-0.4488+(n1-1)*hd;ll=[l2,l4,l5,l1,l1p];[tt,omg,af]=abc(tt2(n1),omg2,af2,ll);s4(n1)=tt(1);tt4(n1)=tt(2);tt5(n1)=tt(3);sE(n1)=tt(4);v34(n1)=omg(1);omg4(n1)=omg(2);omg5(n1)=omg(3);vE(n1)=omg(4);a3(n1)=af(1);af4(n1)=af(2);af5(n1)=af(3);aE(n1)=af(4);end%3.位移,角速度,角加速度figure(1);n1=1:689;t=(n1-1)*pi/180;subplot(2,2,1); %绘角位移及位移线图plot(t,tt4*du,'r-.');grid on;hold on;axis auto;[haxes,hline1,hine2]=plotyy(t,tt5*du,t,sE);grid on;hold on;xlabel('时间/份');axes(haxes(1));ylabel('角位移/\circ');axes(haxes(2));ylabel('位移/m');hold on;grid on;text(1.15,-0.65,'tt_4');text(3.4,0.27,'tt_5');text(2.25,-0.15,'s_E');subplot(2,2,2); %绘角速度及速度线图plot(t,omg4,'r-.');grid on;hold on;axis auto;[haxes,hline1,hline2]=plotyy(t,omg5,t,vE); grid on;hold on;xlabel('时间/份')axes(haxes(1));ylabel('角速度/rad\cdots^{-1}')axes(haxes(2));ylabel('速度/m\cdots^{-1}')hold on;grid on;text(3.1,0.35,'\omg_4')text(2.1,0.1,'\omg_5')text(5.5,0.45,'v_E')subplot(2,2,3); %绘角加速度和加速度图plot(t,af4,'r-.');grid on;hold on;axis auto;[haxes,hline1,hline2]=plotyy(t,af5,t,aE); grid on;hold on;xlabel('时间/份')axes(haxes(1));ylabel('角加速度/rad\cdots^{-2}')axes(haxes(2));ylabel('加速度/m\cdots^{-2}')hold on;text(1.5,0.3,'\af_4')text(3.5,0.51,'\af_5')text(1.5,-0.11,'a_E')wjr_abc.mfunction[tt,omg,af]=abc(tt2,omg2,af2,ll)l2=ll(1);l4=ll(2);l5=ll(3);l1=ll(4);l1p=ll(5);%1.计算角位移和线位移s4=sqrt((l2*cos(tt2))*(l2*cos(tt2))+(l1+l2*sin(tt2))*(l1+l2*sin(tt2))); tt4=acos((l2*cos(tt2))/s4);tt5=asin((l1p-l4*sin(tt4))/l5);sE=l4*cos(tt4)+l5*cos(tt5);tt(1)=s4;tt(2)=tt4;tt(3)=tt5;%2.计算角速度和线速度A=[cos(tt4),-s4*sin(tt4),0,0; %速度分析矩阵之从动件位置参数矩阵sin(tt4),s4*cos(tt4),0,0;0,-l4*sin(tt4),-l5*sin(tt5),-1;0,l4*cos(tt4),l5*cos(tt5),0];B=[-l2*sin(tt2); %原动件位置参数矩阵l2*cos(tt2);0;0];omg=A\(omg2*B);v34=omg(1);omg4=omg(2);omg5=omg(3);vE=omg(4);%计算角加速度和加速度A=[cos(tt4),-s4*sin(tt4),0,0; %速度分析矩阵之从动件位置参数sin(tt4),s4*cos(tt4),0,0;0,-l4*sin(tt4),-l5*sin(tt5),-1;0,l4*cos(tt4),l5*cos(tt5),0];At=[-omg4*sin(tt4),-v34*sin(tt4)-s4*omg4*cos(tt4),0,0;omg4*cos(tt4),v34*cos(tt4)-s4*omg4*sin(tt4),0,0;0,-l4*omg4*cos(tt4),-l5*omg5*cos(tt5),0;0,-l4*omg4*sin(tt4),-l5*omg5*sin(tt5),0];Bt=[-l2*omg2*cos(tt2);-l2*omg2*sin(tt2);0;0];af=A\(-At*omg+omg2*Bt);a34=af(1);af4=af(2);af5=af(3);aE=af(4);wjr_force.m%1.输入已知数据clear;l2=0.1605;%AB的长度单位ml4=0.6914;%CD的长度单位ml5=0.2074;%DE的长度单位ml1=0.370;%AC的长度单位ml1p=0.6572;%CF的长度单位momg2=8.378;%单位rad/shd=pi/180;du=180/pi;H=0.6;%行程单位msEmax=0.5046; sEmin=0.0954;%单位mJs4=0.9; Js5=0.015;%单位kgm^2g=9.8;%单位m/s^2m4=22; m5=3; m6=52;%kgG4=196; G5=29.4; G6=509.6;%单位NFc=1400;%2.机构运动分析% 位移及角位移for n1=1:689;tt2(n1)=-0.4488+(n1-1)*hd;s4(n1)=sqrt((l2*cos(tt2(n1)))*(l2*cos(tt2(n1)))+(l1+l2*sin(tt2(n1)))*(l1+l2 *sin(tt2(n1))));tt4(n1)=acos((l2*cos(tt2(n1)))/s4(n1));tt5(n1)=asin((l1p-l4*sin(tt4(n1)))/l5);sE(n1)=l4*cos(tt4(n1))+l5*cos(tt5(n1));end%2.计算角速度和线速度for n1=1:689;A=[cos(tt4(n1)),-s4(n1)*sin(tt4(n1)),0,0; %速度分析矩阵之从动件位置参数sin(tt4(n1)),s4(n1)*cos(tt4(n1)),0,0;0,-l4*sin(tt4(n1)),-l5*sin(tt5(n1)),-1;0,l4*cos(tt4(n1)),l5*cos(tt5(n1)),0];B=[-l2*sin(tt2(n1)); %原动件位置参数矩阵l2*cos(tt2(n1));0;0];omg=A\(omg2*B);v34(n1)=omg(1);omg4(n1)=omg(2);omg5(n1)=omg(3);vE(n1)=omg(4);%计算角加速度和加速度A=[cos(tt4(n1)),-s4(n1)*sin(tt4(n1)),0,0; %速度分析矩阵之从动件位置参数sin(tt4(n1)),s4(n1)*cos(tt4(n1)),0,0;0,-l4*sin(tt4(n1)),-l5*sin(tt5(n1)),-1;0,l4*cos(tt4(n1)),l5*cos(tt5(n1)),0];At=[-omg4(n1)*sin(tt4(n1)),-v34(n1)*sin(tt4(n1))-s4(n1)*omg4(n1)*cos(tt4(n1)),0,0;omg4(n1)*cos(tt4(n1)),v34(n1)*cos(tt4(n1))-s4(n1)*omg4(n1)*sin(tt4(n1 )),0,0;0,-l4*omg4(n1)*cos(tt4(n1)),-l5*omg5(n1)*cos(tt5(n1)),0;0,-l4*omg4(n1)*sin(tt4(n1)),-l5*omg5(n1)*sin(tt5(n1)),0];Bt=[-l2*omg2*cos(tt2(n1));-l2*omg2*sin(tt2(n1));0;0];af=A\(-At*omg+omg2*Bt);a34(n1)=af(1);af4(n1)=af(2);af5(n1)=af(3);aE(n1)=af(4);end%3.机构的力平衡计算for n1=1:689;%计算各铰链点坐标xa=0;ya=l1;xb(n1)=l2*cos(tt2(n1));yb(n1)=l1+l2*sin(tt2(n1));xc=0;yc=0;xd(n1)=l4*cos(tt4(n1));yd(n1)=l4*sin(tt4(n1));xe(n1)=sE(n1);ye=l1p;%计算各质心坐标xs4(n1)=(xc+xd(n1))/2;ys4(n1)=(yc+yd(n1))/2;xs5(n1)=(xd(n1)+xe(n1))/2;ys5(n1)=(yd(n1)+ye)/2;xs6=0.15;%各质心点加速度as4x(n1)=-l4*(af4(n1)*sin(tt4(n1))+omg4(n1)^2*cos(tt4(n1)))/2;as4y(n1)=l4*(af4(n1)*cos(tt4(n1))-omg4(n1)^2*sin(tt4(n1)))/2;adx=-l4*(af4(n1)*sin(tt4(n1))+omg4(n1)^2*cos(tt4(n1)));ady=l4*(af4(n1)*cos(tt4(n1))-omg4(n1)^2*sin(tt4(n1)));as5x(n1)=adx+l5*(af5(n1)*sin(tt5(n1))+omg5(n1)^2*cos(tt5(n1)))/2; as5y(n1)=ady+l5*(af5(n1)*cos(tt5(n1))-omg5(n1)^2*sin(tt5(n1)))/2; as6(n1)=aE(n1);%惯性力及惯性力矩F4x(n1)=-m4*as4x(n1);F4y(n1)=-m4*as4y(n1);F5x(n1)=-m5*as5x(n1);F5y(n1)=-m5*as5y(n1);F6(n1)=-m6*as6(n1);M4(n1)=-Js4*af4(n1);M5(n1)=-Js5*af5(n1);%未知力系数矩阵xya=zeros(15);xya(1,2)=-1;xya(1,4)=-1;xya(2,3)=-1;xya(2,5)=-1;xya(3,1)=1;xya(3,4)=yb(n1)-ya;xya(3,5)=xa-xb(n1);xya(4,4)=1;xya(4,6)=-1;xya(5,5)=1;xya(5,7)=-1;xya(6,6)=cos(tt4(n1));xya(6,7)=sin(tt4(n1));xya(7,6)=1; xya(7,8)=-1;xya(7,10)=-1;xya(8,7)=1;xya(8,9)=-1;xya(8,11)=-1;xya(9,6)=ys4(n1)-yb(n1);xya(9,7)=xb(n1)-xs4(n1);xya(9,8)=yc-ys4(n1); xya(9,9)=xs4(n1)-xc;xya(9,10)=yd(n1)-ys4(n1);xya(9,11)=xs4(n1)-xd(n1);xya(10,10)=1;xya(10,12)=-1;xya(11,11)=1;xya(11,13)=-1;xya(12,10)=ys5(n1)-yd(n1); xya(12,11)=xd(n1)-xs5(n1);xya(12,12)=ye-ys4(n1);xya(12,13)=xs5(n1)-xe(n1);xya(13,12)=1;xya(14,13)=1;xya(14,14)=-1;xya(15,13)=xs6;xya(15,15)=1;%已知力矩阵if vE(n1)<0&sE(n1)>=(sEmin+0.05*H)&sE(n1)<=(sEmax-0.05*H)D=[0;0;0;0;0;0;-F4x(n1);-F4y(n1)+G4;-M4(n1);-F5x(n1);-F4y(n1)+G5;-M5( n1);-Fc-F6(n1);G6;0;];elseD=[0;0;0;0;0;0;-F4x(n1);-F4y(n1)+G4;-M4(n1);-F5x(n1);-F4y(n1)+G5;-M5( n1);-F6(n1);G6;0;];end%未知力矩阵FR=inv(xya)*D;M2(n1)=FR(1);FR12x(n1)=FR(2);FR12y(n1)=FR(3);FR45x(n1)=FR(10);FR45y(n1)=FR(11);FR16(n1)=FR(14);M6(n1)=FR(15);end%4.输出力的分析图figure(2);n1=1:689;t=(n1-1)*2*pi/360;subplot(2,2,1); %绘平衡力矩图plot(t,M2);grid on;hold on;axis auto;title('平衡力矩M_2')xlabel('时间/份');ylabel('力矩/N\cdotm');hold on;grid on;text(3.8,880,'M_2');subplot(2,2,2); %绘A处x方向约束反力即FR12x plot(t,FR12x,'-');grid on;hold on;axis auto;title('转动副A处约束反力')xlabel('时间/份');ylabel('力/N');hold on;grid on;text(1.1,5000,'F_R_1_2_x')plot(t,FR12y,'r-.'); %绘A处y方向约束反力即FR12y grid on;hold on;text(1.1,-3000,'F_R_1_2_y')subplot(2,2,3); %绘移动副FR16plot(t,-FR16);grid on;hold on;axis auto;title('移动副6约束反力F_R_1_6')xlabel('时间/份')ylabel('力/N')grid on;hold on;text(1.5,3100,'F_R_1_6')subplot(2,2,4); %绘转动副D处约束反力plot(t,FR45x,'-');grid on;hold on;axis auto;title('转动副D处约束反力')xlabel('时间/份')ylabel('力/N')grid on;hold on;text(1.1,-900,'F_R_4_5_x')plot(t,FR45y,'r-.');grid on;hold on;text(1.1,-3700,'F_R_4_5_y')。
matlab机械原理运动解析

matlab机械原理运动解析MATLAB机械原理运动解析是指使用MATLAB软件进行机械系统的运动学和动力学分析的过程。
通过建立数学模型,运用MATLAB进行编程计算,可以实现对机械系统的运动规律、动态特性和性能进行评估和预测。
具体来说,MATLAB机械原理运动解析包括以下步骤:1.建立数学模型:根据机械系统的物理模型,建立相应的数学模型,包括运动学和动力学方程。
这些方程可以描述系统的位移、速度、加速度、力矩等物理量之间的关系。
2.编写MATLAB程序:根据建立的数学模型,使用MATLAB编程语言编写程序,进行数值计算和分析。
MATLAB提供了丰富的数值计算函数库和图形界面工具,方便用户进行数据处理和可视化。
3.数值求解:通过MATLAB的数值计算功能,求解数学模型中的方程,得到机械系统的运动学和动力学特性。
这包括求解位置、速度、加速度等物理量的时间历程,以及分析系统的稳定性和振动等动态行为。
4.结果分析和优化:根据计算结果,对机械系统的性能进行分析和评估。
如果需要改进系统的性能,可以对数学模型进行优化设计,并重新进行数值计算和验证。
至于具体的MATLAB机械原理运动解析示例,比如平面连杆机构的分析,可以通过封闭矢量多边形法求解位置方程,得到构件的位置、速度和加速度;或者采用解析法进行机构运动分析,通过建立数学模型并对其进行封闭矢量多边形法求解,得到构件的运动规律。
此外,还可以使用MATLAB对其他类型的机械系统进行运动学和动力学分析,例如齿轮传动系统、凸轮机构等。
总之,MATLAB机械原理运动解析是一种基于数学模型的计算机辅助分析方法,通过MATLAB编程实现机械系统的运动学和动力学分析,有助于优化机械系统的设计和性能。
机械原理matlab编程

机械原理(Matlab绘图)专业班级学号姓名:图一:导杆的角位移曲线和刨刀的位移曲线x1=linspace(0,2*pi,100);l1=100;l3=360;l4=200;l6=200;y=336;w1=2*pi;x3=atan((l6+l1*sin(x1))./(l1*cos(x1)));for i = 1 : 100;if x3(i)<0x3(i)=x3(i)+pi;endendS3=l1*cos(x1)./cos(x3);V23=(-1)*w1*l1*sin(x1-x3);w3=w1*l1*cos(x1-x3)./S3;a23=w3.^2.*S3-w1.^2*l1*cos(x1-x3);A3=(w1.^2.*l1.*sin(x3-x1)-2.*w3.*V23)./S3;x4= atan((y-l3*sin(x3))./l4);Se=l3*cos(x3)+l4*cos(x4);w4=(-1)*w3.*l3.*cos(x3)./(l4.*cos(x4));Ve=(-1)*w3.*l3.*sin(x3-x4)./cos(x4);A4=(x3.^2.*l3.*sin(w3)+x4.^2.*l4.*sin(x4)-A3.*l3.*cos(x3))./(l4.*cos(x4)); ae=(-1)*(A3.*l3.*sin(x3-x4)+w3.^2.*l3.*cos(x3-x4)-w4.^2.*l4)./cos(x4); plotyy(180*x1./pi,180*x3./pi,180*x1./pi,Se/1000);xlabel('x1/(°)'),ylabel('x3(°)');title('导杆的角位移曲线和刨刀的位移曲线');text(150,108,'x3');text(200,60,'Se');grid on;plotedit on;图二:导杆的角速度曲线和刨刀的速度曲线x1=linspace(0,2*pi,100);l1=100;l3=360;l4=200;l6=200;y=336;w1=2*pi;x3=atan((l6+l1*sin(x1))./(l1*cos(x1)));for i = 1 : 100;if x3(i)<0x3(i)=x3(i)+pi;endendS3=l1*cos(x1)./cos(x3);V23=(-1)*w1*l1*sin(x1-x3);w3=w1*l1*cos(x1-x3)./S3;a23=w3.^2.*S3-w1.^2*l1*cos(x1-x3);A3=(w1.^2.*l1.*sin(x3-x1)-2.*w3.*V23)./S3;x4= atan((y-l3*sin(x3))./l4);Se=l3*cos(x3)+l4*cos(x4);w4=(-1)*w3.*l3.*cos(x3)./(l4.*cos(x4));Ve=(-1)*w3.*l3.*sin(x3-x4)./cos(x4);A4=(x3.^2.*l3.*sin(w3)+x4.^2.*l4.*sin(x4)-A3.*l3.*cos(x3))./(l4.*cos(x4)); ae=(-1)*(A3.*l3.*sin(x3-x4)+w3.^2.*l3.*cos(x3-x4)-w4.^2.*l4)./cos(x4); plotyy(180*x1./pi,w3,180*x1./pi,Ve/1000);xlabel('x1/(°)'),ylabel('w3(rad/s)');title('导杆的角速度曲线和刨刀的速度曲线');grid on;text(100,-5,'Ve');text(100,1.8,'w3');axis([0 400 -7 4]);plotedit on;图三:导杆的角加速度曲线和刨刀的加速度曲线x1=linspace(0,2*pi,100);l1=100;l3=360;l4=200;l6=200;y=336;w1=2*pi;x3=atan((l6+l1*sin(x1))./(l1*cos(x1)));for i = 1 : 100;if x3(i)<0x3(i)=x3(i)+pi;endendS3=l1*cos(x1)./cos(x3);V23=(-1)*w1*l1*sin(x1-x3);w3=w1*l1*cos(x1-x3)./S3;a23=w3.^2.*S3-w1.^2*l1*cos(x1-x3);A3=(w1.^2.*l1.*sin(x3-x1)-2.*w3.*V23)./S3;x4= atan((y-l3*sin(x3))./l4);Se=l3*cos(x3)+l4*cos(x4);w4=(-1)*w3.*l3.*cos(x3)./(l4.*cos(x4));Ve=(-1)*w3.*l3.*sin(x3-x4)./cos(x4);A4=(x3.^2.*l3.*sin(w3)+x4.^2.*l4.*sin(x4)-A3.*l3.*cos(x3))./(l4.*cos(x4)); ae=(-1)*(A3.*l3.*sin(x3-x4)+w3.^2.*l3.*cos(x3-x4)-w4.^2.*l4)./cos(x4); plotyy(180*x1./pi,A3,180*x1./pi,ae/1000);xlabel('x1/(°)'),ylabel('A3(rad/s^2)'),grid;title('导杆的角加速度曲线和刨刀的加速度曲线');text(250,25,'ae');text(300,50,'A3');plotedit on;图四:凸轮从动件位移曲线h=20;F1=2*pi/3;F2=pi/2;i=1;for x=0:0.01:2*pi;if x>=0&x<=2*pi/3;S(i)=h*(1-cos(pi*x./F1))./2;elseif x>=2*pi/3&x<=pi;S(i)=h;elseif x>=pi&x<=5*pi/4;S(i)=h-2*h*(x-pi).^2./(F2.^2);elseif x>=5*pi/4 &x<=3*pi/2;S(i)= 2*h*(F2-x+pi).^2./(F2.^2); elseif x>=3*pi/2 &x<=2*pi;S(i)=0;endi=i+1;x=0:0.01:2*pi;plot(x,S);title('从动件位移曲线');axis([0 7 0 25]);xlabel('x/(rad)');ylabel('S/(mm)');grid on;图五:凸轮的理论轮廓曲线和实际轮廓曲线e=10;Rt=10;Rb=25;w=2*pi;F1=2*pi/3;F2=pi/2;i=1;for f=0:0.01:2*pi;if f>=0&f<=2*pi/3;S(i)=h*(1-cos(pi*f./F1))./2;elseif f>=2*pi/3&f<=pi;S(i)=h;elseif f>=pi&f<=5*pi/4;S(i)=h-2*h*(f-pi).^2./(F2.^2);elseif f>=5*pi/4 &f<=3*pi/2;S(i)= 2*h*(F2-f+pi).^2./(F2.^2);elseif f>=3*pi/2 &f<=2*pi;S(i)=0;endi=i+1;endf=0:0.01:2*pi;s0=sqrt((Rb.^2)-(e.^2));x =e*cos(f)+(s0+S).*sin(f);y =(s0+S).*cos(f)-e*sin(f);d1=e*(-1).*sin(f).*w+(s0+S).*cos(f).*w;d2=(s0+S).*sin(f).*(-1).*w-e*cos(f).*w;x1=x+Rt*d2./sqrt((d1.^2)+(d2.^2));y1=y-Rt*d1./sqrt((d1.^2)+(d2.^2));plot(x,y,'k-',x1,y1,'k-.');title('凸轮的理论轮廓曲线和实际轮廓曲线'); text(-10,-30,'实际轮廓曲线');text(-10,-40,'理论轮廓曲线');axis([-40 50 -55 40 ]);hold on;plot(0,0);text(0,-3,'O');。
机械原理大作业--牛头刨床仿真分析(matlab)全自动版本

牛头刨床机构运动分析一、设计小组人员构成二、设计任务1、机构结构分析2、机构运动分析建立数学模型,解析法进行运动分析;程序编写;上机调试程序;位移、速度和加速度运动曲线图与分析;三、设计参数四、设计分工五、 设计内容如右图,建立直角坐标系,并标出各杆矢量及方位角。
利用两个封闭图形ABCA 及CDEGC ,由此可得:l 6⃑⃑⃑ +l 3⃑⃑⃑ =s 3⃑⃑⃑ , l 3⃑⃑⃑ +l 4⃑⃑⃑ =l 6′⃑⃑⃑ +S E ⃑⃑⃑⃑投影方程式为:s 3 cos θ3=l 1 cos θ1 s 3sin θ3=l 6+l 1sin θ1 l 3cos θ3+l 4cos θ4−s E =0l 3sin θ3+l 4sin θ4=l 6′有以上各式即可求得s 3 、θ3 、θ4 四个运动那个变量,二滑块2的方位角θ2=θ3。
然后,分别将上式对时间去一次、二次导数,并写成矩阵形式,即得以下速度和加速度方程式:[cos θ3−s 3sin θ3sin θ3s 3cos θ30 00 00 −l 3sin θ30l 3cos θ3−l 4sin θ4−1l 4cos θ40] [s 3ω3ω4v E ]=ω1[−l 1sin θ1l 1cos θ100][cos θ3−s 3sin θ3sin θ3s 3cos θ30 00 00 −l 3sin θ30l 3cos θ3−l 4sin θ4−1l 4cos θ40] [s 3α3α4αE ] =- [−ω3sin θ3 −s 3sin θ3−s 3ω3sin θ3ω3cos θ3 s 3cos θ3−s 3ω3sin θ30 00 00 −l 3ω3cos θ30 −l 3ω3sin θ3−l 4ω4cos θ4 0−l 4ω4sin θ4 0] [s 3ω3ω4v E ]+ ω1[−l 1ω1cos θ1−l 1ω1sin θ100]而ω2=ω3 、α2=α3 。
机械原理matlab分析大作业3-28
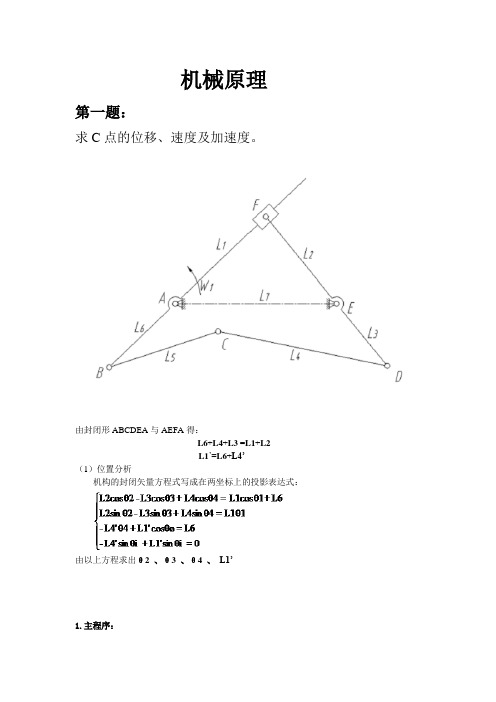
机械原理第一题:求C点的位移、速度及加速度。
由封闭形ABCDEA与AEFA得:L6+L4+L3 =L1+L2L1’=L6+L4’(1)位置分析机构的封闭矢量方程式写成在两坐标上的投影表达式:由以上方程求出θ2 、θ3 、θ4 、L1’1.主程序:%输入已知数据l2=60;l3=35;l4=75;l5=50;l6=40;l7=70;hd=pi/180;du=180/pi;omega1=10;alpha1=0;%调用子函数计算角位移,角速度及角加速度for n1=1:66 %曲柄转角范围theta1(n1)=(n1-1)*hd;ll=[l2,l3,l4,l5,l6,l7];[theta,omega,alpha]=six_bar(theta1(n1),omega1,ll);l1(n1)=theta(1);theta2(n1)=theta(2);theta4(n1)=theta(3);theta3(n1)=theta(4);v1(n1)=omega(1);omega2(n1)=omega(2);omega3(n1)=omega(3);omega4(n1)=omega(4);a1(n1)=alpha(1);alpha2(n1)=alpha(2);alpha3(n1)=alpha(3);alpha4(n1)=alpha(4);e nd%图像输出figure(1);n1=1:66;t=(n1-1)*2*pi/360;subplot(2,2,1);%滑块F线位移L1图像输出plot(theta1*du,l1,'k');title('L1线位移图');xlabel('角位移\theta_1/\circ')ylabel('线位移/mm')grid on;hold on;gtext('L1')pause(1);subplot(2,2,2);%theta2、theta3、theta4角位移图像输出plot(theta1*du,theta2*du,'g',theta1*du,theta3*du,'r',theta1*du,th eta4*du);title('\theta_2、\theta_3、\theta_4角位移图');xlabel('角位移\theta_1/\circ')ylabel('角位移/\circ')grid on;hold on;legend('\theta_2','\theta_3','\theta_4');pause(1);subplot(2,2,3);%滑块F的速度图像输出plot(theta1*du,v1,'k');title('滑块F的速度图');xlabel('角位移\theta_1/\circ')ylabel('速度/mm\cdots^{-1}')grid on;hold on;gtext('v1')pause(1);subplot(2,2,4);%滑块F的加速度图像输出plot(theta1*du,a1,'k');title('滑块F的加速度图');axis auto;xlabel('角位移\theta_1/\circ')ylabel('加速度/mm\cdots^{-2}')grid on;hold on;gtext('a1');pause(5);figure(2);subplot(1,2,1);%omega2、omega3和omega4角位移图像输出plot(theta1*du,omega2,'g',theta1*du,omega3,'r',theta1*du,omega4,' b');title('\omega_2、\omega_3、\omega_4角速度图');axis auto;grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('角速度/rad\cdots^{-1}')box on;legend('\omega_2','\omega_3','\omega_4');pause(1);subplot(1,2,2);%alpha2、alpha3和alpha4角加速度图像输出plot(theta1*du,alpha2,'g',theta1*du,alpha3,'r',theta1*du,alpha4,' b');title('\alpha_2、\alpha_3、\alpha_4角加速度图');axis auto;grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('角加速度/rad\cdots^{-2}')box on;legend('\alpha_2','\alpha_3','\alpha_4');pause(5);figure(3);xC=-l6*cos(theta1+pi)+l5*cos(theta3);yC=l6*sin(theta1+pi)+l5*sin(theta3);% rC=sqrt(xC.*xC+yC.yC)vCX=-omega1*l6*sin(theta1+pi)-omega3*l5.*sin(theta3);vCY=omega1*l6*cos(theta1+pi)+omega3*l5.*cos(theta3);% v3=sqrt(vCX.*vCX+vCY.*vCY);subplot(2,2,1);hold on;grid on;%C点x、y方向位移图像输出plot(theta1*du,xC,'r',theta1*du,yC);axis auto;hold on;grid on;title('C点位移图');xlabel('角位移\theta_1/\circ')ylabel('位移/mm')grid on;hold on;legend('xC','yC');pause(1);subplot(2,2,2);grid on;hold on;%C点x、y方向速度图像输出plot(theta1*du,vCX,'k',theta1*du,vCY);title('C点速度图');xlabel('角位移\theta_1/\circ')ylabel('速度/mm\cdots^{-1}')legend('vCX','vCY');pause(1);aCX=omega1*omega1*l6*cos(theta1)-omega3.*omega3.*l5.*cos(theta3)-alpha3.*l5.*sin(theta3);aCY=omega1*omega1*l6*sin(theta1)-omega3.*omega3.*l5.*sin(theta3)+ alpha3.*l5.*cos(theta3);%a3=sqrt(aCX.*aCX+aCY.*aCY);subplot(2,2,3);%C点x、y方向加速度图像输出plot(theta1*du,aCX,'r',theta1*du,aCY,'b');title('C点加速度图');grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('加速度/mm\cdots^{-2}')box on;legend('aCX','aCY');%主程序结束2.子程序:%子函数function[theta,omega,alpha]=six_bar(theta1,omega1,ll)l2=ll(1);l3=ll(2);l4=ll(3);l5=ll(4);l6=ll(5);l7=ll(6);%1.计算角位移和线位移l1=l7*cos(theta1)+sqrt((l7*cos(theta1))*(l7*cos(theta1))-l7*l7+l2 *l2);theta2=asin((l1*sin(theta1))/l2);A=2*l4*(l6*sin(theta1)-l3*sin(theta2).*sin(theta2));B=2*l4*(l6*cos(theta1)+l7-l3*cos(theta2));C=l4*l4-l5*l5+l6*l6+l7*l7+l3*l3-2*l3*l6*(cos(theta1)*cos(theta2)+ sin(theta1)*sin(theta1))-2*l7*l3*cos(theta2)+2*l6*l7*cos(theta1); theta4=2*atan((A+sqrt(A.*A+B.*B-C.*C))/(B-C));theta3=asin((l6*sin(theta1)+l4*sin(theta4)-l3*sin(theta2))/l5); theta(1)=l1;theta(2)=theta2;theta(3)=theta4;theta(4)=theta3;%2利用矩阵计算角速度和线速度D=[-l5*sin(theta3),l4*sin(theta4),-l3*sin(theta2+pi),0l5*cos(theta3),-l4*cos(theta4),-l3*cos(theta2+pi),00,0,l2*sin(theta2),cos(theta1)0,0,-l2*cos(theta2),sin(theta1)];E=[l6*sin(theta1+pi);-l6*cos(theta1+pi);l1*sin(theta1);-l1*cos(theta1)];omega=D\(omega1*E);v1=omega(4);omega2=omega(3);omega3=omega(1);omega4=omega(2);%3利用矩阵计算角加速度和加速度Dt=[-l5*omega3*cos(theta3),l4*omega4*cos(theta4),-l3*omega2*cos(t heta2),0-l5*omega3*sin(theta3),l4*omega4*sin(theta4),-l3*omega2*sin(theta 2),00,0,l2*omega2*cos(theta2),-omega1*sin(theta1)0,0,l2*omega2*sin(theta2),omega1*cos(theta1)];Et=[l6*omega1*cos(theta1);l6*omega1*sin(theta1);l1*omega1*cos(theta1)+v1*sin(theta1);l1*omega1*sin(theta1)-v1*cos(theta1)];alpha=D\(-Dt*omega+omega1*Et);a1=alpha(4);alpha2=alpha(3);alpha3=alpha(1);alpha4=alpha(2);%3子程序结束3.图像输出:%1.滑块F线位移L1图像输出%2.theta2、theta3、theta4角位移图像输出%3.滑块F的速度图像输出%4.滑块F的加速度图像输出%5.omega2、omega3和omega4角位移图像输出%6.alpha2、alpha3和alpha4角加速度图像输出%7.C点x、y方向位移图像输出%8.C点x、y方向速度图像输出%9.C点x、y方向加速度图像输出。
机械原理matlab作业

1.在图示的铰链四杆机构中,AB 为主动杆,以s rad /47.10=ω匀角速度逆时针旋转,各杆长度分别为mm l mm l mm l mm l 80,100,120,404321====,连杆点F 的位置是FE ⊥BC ,BE 长mm S 60=,EF 长mm T 10=,选取直角坐标系如图所示。
求当曲柄1与x 轴正向夹角为 360~01=ϕ时,连杆2和摇杆3所转过的角度2ϕ、3ϕ以及它们的角速度和角加速度2ω、3ω、2α、3α,并求出连杆点F 的各位置坐标、速度和加速度。
规定ϕ角从轴x 正向测量时,逆时针为正,反之为负。
y机械原理作业撰写要求机械原理电算分析是机械原理课程学习的重要环节,是检验学生综合素质与实践能力培养的手段。
1、作业内容顺序作业内容顺序一般为:题目、数学模型、程序设计、计算结果和附件M 文件。
2、作业格式要求作业格式要求见摸板,纸张大小一律使用A4复印纸。
3. 书写规定 3.1公式公式号按顺序编号,如(2)表示第2个公式。
公式应采用公式编辑器输入,选择默认格式,公式号右对齐,公式调整至基本居中。
3.2 插表每个表格均应有标题(由表序和表名组成),如第一个插表的序号为“表1”。
表格统一用三线表,表序与表名之间空一格,表名中不允许使用标点符号,表名后不加标点。
标题置于表上,要求用5号字(包括表中的内容)。
3.3 插图插图应与文字紧密配合,文图相符,内容正确。
图题置于图的下方,要求用5号字。
插图应采用AutoCAD 绘制,然后拷贝粘贴到Word 文档,以利于以后编辑。
3.4物理量的名称、符号和计量单位物理量的名称、符号和计量单位应统一按照机械原理教科书的规定书写,某一量的名称、符号和计量单位应与教科书的规定相一致。
4. 排版要求4.1正文字体要求、每部分标题左顶边、小三宋体加粗。
正文文字用宋体小四号汉字和四号“Times New Roman”英文字体,每自然段首行缩进2个字符。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.在图示的铰链四杆机构中,AB 为主动杆,以s rad /47.10=ω匀角速度逆时针旋
转,各杆长度分别为mm l mm l mm l mm l 80,100,120,404321====,连杆点F 的
位置是FE ⊥BC ,BE 长mm S 60=,EF 长mm T 10=,选取直角坐标系如图所示。
求当曲
柄1与
x 轴正向夹角为 360~01=ϕ时,连杆2和摇杆3所转过的角度2ϕ、3ϕ以及它们
的角速度和角加速度2ω、3ω、2α、3α,并求出连杆点F 的各位置坐标、速度和加速度。
规定
ϕ
角从轴
x 正向测量时,逆时针为正,反之为负。
y
机械原理作业撰写要求
机械原理电算分析是机械原理课程学习的重要环节,是检验学生综合素质与实践能力培养的手段。
1、作业内容顺序
作业内容顺序一般为:题目、数学模型、程序设计、计算结果和附件M 文件。
2、作业格式要求
作业格式要求见摸板,纸张大小一律使用A4复印纸。
3. 书写规定 3.1公式
公式号按顺序编号,如(2)表示第2个公式。
公式应采用公式编辑器输入,选择默认格式,公式号右对齐,公式调整至基本居中。
3.2 插表
每个表格均应有标题(由表序和表名组成),如第一个插表的序号为“表1”。
表格统一用三线表,表序与表名之间空一格,表名中不允许使用标点符号,表名后不加标点。
标题置于表上,要求用5号字(包括表中的内容)。
3.3 插图
插图应与文字紧密配合,文图相符,内容正确。
图题置于图的下方,要求用5号字。
插图应采用AutoCAD 绘制,然后拷贝粘贴到Word 文档,以利于以后编辑。
3.4物理量的名称、符号和计量单位
物理量的名称、符号和计量单位应统一按照机械原理教科书的规定书写,某一量的名称、符号和计量单位应与教科书的规定相一致。
4. 排版要求
4.1正文字体要求、
每部分标题左顶边、小三宋体加粗。
正文文字用宋体小四号汉字和四号“Times New Roman”英文字体,每自然段首行缩进2个字符。
4.2行间距要求
每章题目与每节题目之间的行距设置:每章题目后设1.5倍行距,段后0.5 行。
每节题目与小节题目之间的行距设置:每节题目后设1.5倍行距,段后0.5 行。
4.3正文章节序号编制
每部分编写为:1、2、…;
每部分以下层次依次为:以括号为序,如(1),(2)…。
5. 程序编写要求
程序的编写要加上必要的注视和说明以便于阅读。
程序中采用的字符变量和常量,用与机械原理教科书和作业中的字符相一致,如果是希腊字符,请参照附件。
作业格式要求摸板:
1 题目:铰链四杆机构的运动分析(小三号宋体加粗)
使用方法(首行缩进2字符,小4号宋体,1.5单倍行距)
图1所示的四杆机构为例,设己知各构件的尺寸及原动件1的方位角和等角速度,需对其位置、速度和加速度进行分析。
为了对机构进行运动分析.先如图建立直角坐标系,并将各构件表示为杆矢,为了求解方便将各杆矢用指数形式的复数表示。
图1 铰链四杆机构 (5号宋体)
插图应与文字紧密配合,文图相符,内容正确。
选图要力求精练。
图题置于图的下方,要求用5号字。
如果有两张照片,并排放置。
如果只有1照片,居中放置。
插图应采用AutoCAD 绘制,然后拷贝粘贴到Word 文档,以利于以后编辑。
2 数学模型(小三号宋体加粗)
(1) 速度分析
使用方法(首行缩进2字符,小4号宋体,1.5单倍行距)
(1)
其中,w 为转速,μ为摩擦系数,F 为轴肩对材料的压力。
公式号按顺序编号,如(2)表示第2个公式。
公式尽量采用公式编辑应用程序输入,选择默认格式,公式号右对齐,公式调整至基本居中。
(2) 加速度分析
使用方法(首行缩进2字符,小4号宋体,1.5单倍行距)
(2)
其中,w 为转速,μ为摩擦系数,F 为轴肩对材料的压力。
公式号按顺序编号,如(2)表示第2个公式。
公式尽量采用公式编辑应用程序输入,选择默认格式,公式号右对齐,公式调整至基本居中。
)
(45)
(02020i i i r r r r r r F w Q +++=
μπ)
(45)
(02020i i i r r r r r r F w Q +++=
μπ
3 程序设计(小三号宋体加粗)
使用方法(首行缩进2字符,小4号宋体,1.5单倍行距)
4 计算结果(小三号宋体加粗)
使用方法(首行缩进2字符,小4号宋体,1.5单倍行距)
表1 熔化焊参数(5号宋体居中)
编号
道次
电流 (A )
电压 (V ) 气体流量 (L/min )
焊接速度 (cm/min)
1
一道
191
22.9
12
40
二道 211 24 12 43 2
一道
191
22.9
12
40
二道 211 24 12 40 3
一道
191
22.9
12
40
二道
211
24
12
40
每个表格均应有标题(由表序和表名组成)。
表序一般顺序编排。
表格统一用三线表,表序与表名之间空一格,表名中不允许使用标点符号,表名后不加标点。
标题置于表上,要求用5号字(包括表中的内容)。
全表如铰链四杆机构的运动分析
1 题目:铰链四杆机构的运动分析(小三号宋体加粗)
使用方法(首行缩进2字符,小4号宋体,1.5单倍行距) 如图1所示,已知铰链四杆机构各构件的尺寸为: 6.1011=l mm ,
2542=l mm ,8.1773=l mm ,8.3044=l mm ,及原动件1以角速度2501=ωrad/s 逆时针转动,计算连杆2和摇杆3的角位移、角速度及角加速度,并绘制出运动线图。
图1 铰链四杆机构运动简图
插图应与文字紧密配合,文图相符,内容正确。
选图要力求精练。
图题置于图的下方,要求用5号字。
如果有两张照片,并排放置。
如果只有1照片,居中放置。
插图应采用AutoCAD 绘制,然后拷贝粘贴到Word 文档,以利于以
后编辑。
2 数学模型(小三号宋体加粗)
(1) 位置分析
使用方法(首行缩进2字符,小4号宋体,1.5单倍行距) 如图可写出机构各杆矢所构成的矢量封闭方程
4
321l l l l +=+ (1)
其复数形式表示为
3213421θθθi i i e l l e l e l +=+ (2)
将上式的实部和虚部分离,得
⎭
⎬⎫
=++=+3322113342211sin sin sin cos cos cos θθθθθθl l l l l l l (3) 联解上式即可求得二个未知方向角2θ和3θ。
(2)速度分析
将式(2)对时间t 求一次导数, 得速度关系
3
21332211θθθωωωi i i e l e l e l =+ (4)
将上式的实部和虚部分开,有
⎭
⎬⎫
=+=+333222111333222111sin sin sin cos cos cos θωθωθωθωθωθωl l l l l l (5) 联解上式即可求得二个角速度2ω、3ω。
若用矩阵形式来表示,则上式可写为
⎥⎦
⎤
⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢
⎣⎡--1111132332
2332
2cos sin cos cos sin sin θθωωωθθθθl l l l l l (6) (3)加速度分析
将式(2)对时间t 求二次导数,可得加速度关系
3
32212333322222211θθθθθωαωαωi i i i i e il e l e il e l e il +=++ (7)
将上式的实部和虚部分开,有
3
2333332222222121132
3333322222221211sin cos sin cos sin cos sin cos sin cos θωθαθωθαθωθωθαθωθαθωl l l l l l l l l l -=-+-+=++ (8)
联解上式即可求得二个角加速度2α、3α。
上式用矩阵得形式可表示为
⎥
⎦
⎤
⎢⎣⎡⎥⎦⎤⎢
⎣⎡--32332
2332
2cos cos sin sin ααθθθθl l l l
⎥⎦⎤⎢⎣⎡+⎥⎦
⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡---=111111132333222333222sin cos sin sin cos cos θωθωωωωθωθωθωθωl l l l l l (9)
公式号按顺序编号,如(2)表示第2个公式。
公式尽量采用公式编辑应用程序输入,选择默认格式,公式号右对齐,公式调整至基本居中。
3 程序设计(小三号宋体加粗)
使用方法(首行缩进2字符,小4号宋体,1.5单倍行距)
4 计算结果(小三号宋体加粗)
使用方法(首行缩进2字符,小4号宋体,1.5单倍行距) 图2为运算结果和四杆机构的运动线图
图2。
