工程力学习题课
工程力学教程第二版课后习题答案

工程力学教程第二版课后习题答案工程力学是一门应用力学原理研究工程结构和材料力学性能的学科。
作为工程学的基础课程之一,工程力学的学习对于培养工程师的分析和解决实际工程问题的能力至关重要。
而工程力学教程第二版是一本经典的教材,其中的课后习题是帮助学生巩固所学知识的重要辅助材料。
本文将为读者提供工程力学教程第二版课后习题的答案,帮助读者更好地理解和掌握工程力学的知识。
第一章:静力学1. 问题:一根长度为L,截面为矩形的梁,其宽度为b,高度为h。
梁的两端分别固定在支座上,中间有一个集中力P作用在梁上。
求梁在P作用下的最大弯矩和最大剪力。
答案:根据静力学原理,我们可以通过平衡力和力矩来求解该问题。
首先,根据平衡力的原理,梁在P作用下的最大剪力等于P。
其次,根据力矩的原理,梁在P作用下的最大弯矩等于P乘以梁的长度L的一半。
因此,最大弯矩为PL/2。
第二章:动力学1. 问题:一个质量为m的物体以速度v沿着水平方向运动,突然撞击到一个质量为M的静止物体上。
求撞击后两个物体的速度。
答案:根据动量守恒定律,撞击前后两个物体的总动量保持不变。
设撞击后质量为m的物体的速度为v1,质量为M的物体的速度为v2。
由动量守恒定律可得mv = mv1 + Mv2。
另外,根据能量守恒定律,撞击前后两个物体的总动能保持不变。
设撞击前质量为m的物体的动能为1/2mv^2,撞击后质量为m的物体的动能为1/2mv1^2,质量为M的物体的动能为0(静止)。
由能量守恒定律可得1/2mv^2 = 1/2mv1^2 + 0。
综上所述,可以解得v1 = (m - M)v / (m + M),v2 = 2m / (m + M)。
第三章:应力分析1. 问题:一个长方体的尺寸为a×b×c,其材料的杨氏模量为E,泊松比为v。
求该长方体在x、y、z方向上的应力分量。
答案:根据应力分析的原理,我们可以通过应力的定义和杨氏模量、泊松比的关系来求解该问题。
工程力学-26习题课

求:σr3
M0
A
M0
F
F
B
45°
A B
分析:A点应力状态
σ = E ε0 τ=?
与B点的τ相等!
Aσ τ
σ Bτ
σ45°
如何求B点的τ?
τ
BB
σ
利用广义胡克定律,
45°
σ-45°
[ ( )] ε −450
=
1 E
σ −450
−ν
0 + σ 450
σ −450
=
σ
2
+
σ
2
cos(−2 × 450 ) − τ
组合变形的形式很多,我们应着重掌 握其计算原理和方法,而不是简单记住教 材中现有公式。
p. 154 例9-5 —— 要点:找危险截面
7kN
0.75kNm
7kN
0.75kNm
T
(kNm) 0.75
z
7kN
y 0.75kNm
A B
T
(kNm)
1.4
My (kNm)
0.77
M(z kNm) 1.60
M (kNm)
第一步——选微元体(原则:各面应力已知或可求) (1)一般为直六面体; (2)各边长为无穷小;dx,dy,dz→0 (3)各面应力均匀分布; (4)平行两面对应应力数值相等。 注意:应力下角标含义
相关定义:主平面,主应力 应力状态分类: 单向应力状态 二向(平面)应力状态 三向(空间)应力状态
第二步——单元体局部平衡
M
FQmax= F
Mmax= F/4
注意: FQmax ,Mmax可能位于不同截面, 它们取极值时 F可能位于不同位置。
工程力学第01章习题

工程力学第01章习题课1.静力学公理公理1力的平行四边形法则作用在物体上同一点的两个力,可以合成为一个台力.合力的大小和方向由这两个力为边构成的平行四边形的对角线确定.即合力矢等于这两个力矢的几何和.公理2二力平衡条件作用在刚体上的两个力,使刚体保持平衡的必要和充分条件是:这两个力的大小相等,方向相反,且作用在同一直线上.公理3加减平衡力系原理在已知力系上加上或减去任意的平衡力系,并不改变原力系对刚体的作用.公理4作用和反作用定律作用力和反作用力总是同时存在,两力的大小相等,方向相反,沿着同一直线,分别作用在两个相互作用的物体上.公理5刚化原理变形体在某一力系作用下处于平衡,如将此变形体刚化为刚体,其平衡状态保持不变.推论l力的可传性作用于刚体A某点的力,可以沿着它的作用线移到刚体内任意一点,并不改变该力对刚体的作用.推论2三力平衡汇交定理作用于刚体上三个相互平衡的力,若其中两个力的作用线汇交于一点,则此三力必在同一平面内,且第三个力的作用线通过汇交点.2.约束和约束力约束:对非自由体的某些位移起限制作用的周围物体.结束力:约束对物体的作用力.约束的类型:(1)具有光滑接触面的约束:约束力作用在接触点处,方向沿接触面的公法线指向被约束的物体,如图1-1(a)所示.(2)软绳、链条或胶带等构成的约束软绳:约束力作用在接触点,方向沿着绳索背离物体,如图所示链条或胶带:约束力沿轮缘的切线方向,如图所示.(3)光滑镜链约束:方向不能确定,但其作用线必垂直于轴线并通过轴心,如图所示(4)其它约束a.滚动支座:约束性质与光滑接触面约束相同,其约束必垂直于支承面,且通过铰链中心,如图所示.b.球铰链:约束力方向不能确定,但通过接触点与球心,如图所示.c.正推轴承:限制轴的径向位移和轴向位移,如图所示.例题:如图的匀质球C重P,杆AB由固定铰链A固连于墙上,绳BF连接墙体和杆,且杆和绳不计重量,试画出球C和杆AB的受力图.解:球C受主动力P,以及D、E两处的光滑支承面对球的约束力,这三个力必交于球心C处,如图杆AB在E处受球对它的作用力,在B处受绳对它的拉力,在A处受镀链对它的作用力, F的方向由三力汇交可确定A例题:下面图中是否有错误?如何改正作业题“1-1画出下列各图中物体A ,ABC或构件AB,AC的受力图。
《工程力学》课后习题与答案全集

由 ,作出速度平行四边形,如图示:
即:
7.图示平行连杆机构中, mm, 。曲柄 以匀角速度 2rad/s绕 轴转动,通过连杆AB上的套筒C带动杆CD沿垂直于 的导轨运动。试示当 时杆CD的速度和加速度。
解:取CD杆上的点C为动点,AB杆为动系。对动点作速度分析和加速度分析,如图(a)、(b)所示。图中:
解:设该力系主矢为 ,其在两坐标轴上的投影分别为 、 。由合力投影定理有:
=-1.5kN
kN
kN
;
由合力矩定理可求出主矩:
合力大小为: kN,方向
位置: m cm,位于O点的右侧。
2.火箭沿与水平面成 角的方向作匀速直线运动,如图所示。火箭的推力 kN与运动方向成 角。如火箭重 kN,求空气动力 和它与飞行方向的交角 。
(d)由于不计杆重,杆AB在A、C两处受绳索作用的拉力 和 ,在B点受到支座反力 。 和 相交于O点,
根据三力平衡汇交定理,
可以判断 必沿通过
B、O两点的连线。
见图(d).
第二章力系的简化与平衡
思考题:1.√;2.×;3.×;4.×;5.√;6.×;7.×;8.×;9.√.
1.平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm,求此力系向O点简化的结果,并确定其合力位置。
则
(mm/s)
故 =100(mm/s)
又有: ,因
故:
即:
第四章刚体的平面运动
思考题
1.×;2.√; 3.√;4.√;5.×.
习题四
1.图示自行车的车速 m/s,此瞬时后轮角速度 rad/s,车轮接触点A打滑,试求点A的速度。
《工程力学(第2版)》课后习题及答案—理论力学篇

第一篇理论力学篇模块一刚体任务一刚体的受力分析(P11)一、简答题1.力的三要素是什么?两个力使刚体平衡的条件是什么?答:力的三要素,即力的大小、力的方向和力的作用点。
两个力使刚体处于平衡状态的必要和充分条件:两个力的大小相等,方向相反,作用在同一直线上。
2.二力平衡公理和作用与反作用公理都涉及二力等值、反向、共线,二者有什么区别?答:平衡力是作用在同一物体上,而作用力与反作用力是分别作用在两个不同的物体上。
3.为什么说二力平衡公理、加减平衡力系公理和力的可传性都只适用于刚体?答:因为非刚体在力的作用下会产生变形,改变力的传递方向。
例如,软绳受两个等值反向的拉力作用可以平衡,而受两个等值反向的压力作用就不能平衡。
4.什么是二力构件?分析二力构件受力时与构件的形状有无关系。
答:工程上将只受到两个力作用处于平衡状态的构件称为二力构件。
二力构件受力时与构件的形状没有关系,只与两力作用点有关,且必定沿两力作用点连线,等值,反向。
5.确定约束力方向的原则是什么?活动铰链支座约束有什么特点?答:约束力的方向与该约束阻碍的运动方向相反。
在不计摩擦的情况下,活动铰链支座只能限制构件沿支承面垂直方向的移动。
因此活动铰链支座的约束力方向必垂直于支承面,且通过铰链中心。
6.说明下列式子与文字的意义和区别:(1)12=F F ,(2)12F F =, (3)力1F 等效于力2F 。
答:若12=F F ,则一般只说明两个力大小相等,方向相反。
若12F F =,则一般只说明两个力大小相等,方向是否相同,难以判断。
若力1F 等效于力2F ,则两个力大小相等,方向和作用效果均相同。
7.如图1-20所示,已知作用于物体上的两个力F1与F2,满足大小相等、方向相反、作用线相同的条件,物体是否平衡?答:不平衡,平衡是指物体相对于惯性参考系保持静止或匀速直线运动的状态,而图中AC 杆与CB 杆会运动,两杆夹角会在力的作用下变大。
二、分析计算题1.试画出图1-21各图中物体A 或构件AB 的受力图(未画重力的物体重量不计,所有接触均为光滑接触)。
【工程力学 课后习题及答案全解】第12章杆类构件的静载强度设计习题解
12-7 T 形截面外伸梁,受力与 截面尺寸如图所示,其中 C 为截面形 心, I z = 2.136 × 107 mm4。梁的材料为 铸铁,其抗拉许用应力 [σ ]+ = 30MPa,
抗压许用应力 [σ ]− = 60MPa。试校核该
F—RA57 — FRB
习题 12-7 图
梁是否安全。
解:1. ∑ M B = 0 ,FRA = 37.5kN(↑)
Iz = 33760 cm4
σ max
=
M max W
=
252 1500
× ×
103 10 −6
= 168 MPa
4.5q
A C
4.5q
B D
3500 3500 3500
σ max −[σ ] = 3 ×100% = 1.8% < 5% ,工程上是允许的。
(b)
[σ ] 165
此时 C 截面翼缘和腹板交界点的应力:
正确答案是 C 。
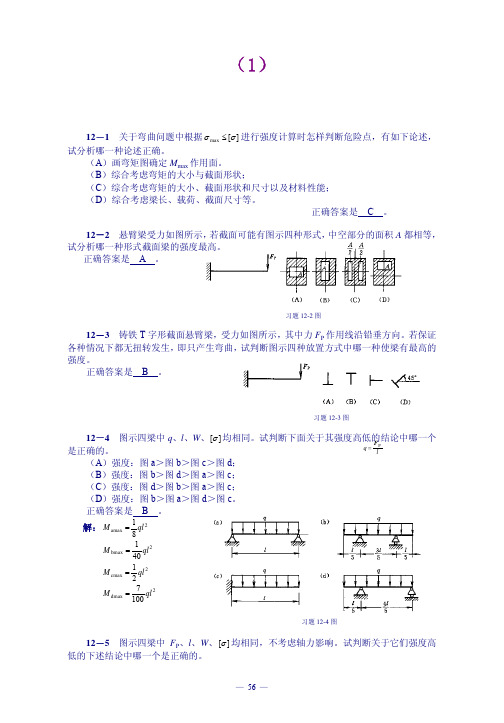
12-2 悬臂梁受力如图所示,若截面可能有图示四种形式,中空部分的面积 A 都相等, 试分析哪一种形式截面梁的强度最高。
正确答案是 A 。
习题 12-2 图
12-3 铸铁 T 字形截面悬臂梁,受力如图所示,其中力 FP 作用线沿铅垂方向。若保证 各种情况下都无扭转发生,即只产生弯曲,试判断图示四种放置方式中哪一种使梁有最高的 强度。
= 252 ×103 165 ×106
= 1.5273 ×10−3 m3
(1) 初选 No.45c 工字钢 W = 1570 cm3,Iz = 35280 cm4
C 截面上翼缘与腹板交界点上应力:
σ
=
MC Iz
(225 − 18) ×10−3
工程力学习题及答案

⼯程⼒学习题及答案⼯程⼒学复习题课程⼯程⼒学专业班级⼀、单项选择题(每⼩题2分,共20分)在每⼩题列出的四个选项中只有⼀个选项是符合题⽬要求的,请将正确选项前的字母填在题后的括号内。
1.三个刚⽚⽤三个铰两两相联,所得的体系( )A.⼀定为⼏何不变体系B.⼀定为⼏何瞬变体系C.⼀定为⼏何常变体系D.不能确定2.图⽰体系是( )A.⽆多余联系的⼏何不变体系B.有多余联系的⼏何不变体系C.瞬变体系D.常变体系3.图⽰三铰拱,已知三个铰的位置,左半跨受均布荷载,其合理拱轴的形状为( )A.全跨圆弧B.全跨抛物线C.AC段为园弧,CB段为直线D.AC段为抛物线,CB段为直线4.图⽰结构A端作⽤⼒偶m,则B端转⾓ B的值为( )A.mlEI6B.mlEI3C.mlEI2D.mlEI5.图⽰桁架C点⽔平位移的值为( ) A.PaEAB.12Pa EAC.14Pa EAD.06.图⽰刚架的超静定次数为A.1B.2C.3D.47.图⽰超静定则架,⽤⼒法计算时,不能选为基本体系的是图( )8.下列弯矩图中正确的是图( )9.图⽰结构中,BA杆B端的⼒矩分配系数等于( )10.图⽰结构截⾯K剪⼒影响线是图( )⼆、填空题(每⼩题2分,共16分)11.在具有⼀个⾃由度的体系上加上⼀个⼆元体(⼆杆结点)时,所得新体系的⾃由度为_____。
12.位移互等定理的表达式是________。
13.图⽰对称结构,截⾯K弯矩的绝对值为________。
14.图⽰结构,作⽤荷载P,不计轴向变形时,⽀座A的反⼒矩M A等于________。
15.已知图⽰连续梁(a)的弯矩图(b),则A端剪⼒等于________kN。
16.⽤⼒矩分配法计算图⽰连续梁时,算⾄放松结点C分配传递后,当前结点B的结点不平衡⼒矩(约束⼒矩)等于________kN.m17.⼒P在梁ABC上移动过程中,截⾯K中产⽣的变矩(绝对值)的最⼤值为________kN·m18.图中给出了截⾯K弯矩M K影响线的形状,该影响线在截⾯K下⾯的纵标等于________。
(完整版)工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Me2
Me3
Me1
n
Me4
B
C
A
D
Me2
Me3
Me1
n
Me4
B 解:计算外力偶矩
C A
D
Me
9549
P n
Me1 15900 N m
Me2 Me3 4780 N m
Me4 6379 N m
计算 CA 段内任横一截面 2-2 截
面上的扭矩 .假设 T 2为正值. 由平衡方程
Me2
Me3 2
求CD段内的轴力
R
A
40kN B
55kN 25kN
C
D
3
20kN E
FN3 25 20 0
FN3 25kN
20kN
FN3 5(kN) ()
求DE段内的轴力
R
40kN
55kN 25kN
20kN
4
FN4 20( kN ) ( )
FN4
20kN
40kN
55kN 25kN
20kN
A 600 10
(1) Ⅰ-Ⅰ、Ⅱ-Ⅱ、Ⅲ-Ⅲ截面的轴力并作轴力图
(2) 杆的最大正应力max
(3) B截面的位移及AD杆的变形
Ⅲ
Ⅱ
Ⅰ
DⅢ l3
F3
C
Ⅱ
l2
F1 F2
B
A Ⅰ
l1
Ⅲ
R
DⅢ l3
Ⅱ
F3
C
Ⅱ
l2
Ⅰ
F2
F1
B
A Ⅰ
l1
解:求支座反力 R = -50kN (1) Ⅰ-Ⅰ、Ⅱ-Ⅱ、Ⅲ-Ⅲ
FN1
F1
截面的轴力并作轴力图
在 AD 段内
B1 C
T3 Me4 6370 N m Me2 T1
注意:若假设扭矩为正值,则
扭矩的实际符号与计算符号相同. 作出扭矩图
从图可见,最大扭矩
在 CA段内.
Me1 3 Me4
A 3D Me4
T3
6370 N·m
+ _
Tmax 9560 N m
4780 N·m 9560 N·m
例题5 图示等直杆,已知直径d=40mm,a=400mm,材料的
B 300 C 500 50
+
FN1=10kN (拉力) FN2=50kN (拉力) FN3= - 5kN (压力) FN4=20kN (拉力)
5
FNmax 50( kN ) 发生在BC段内任一横截面上
例题5 图示为一变截面圆杆ABCD。已知F1=20kN, F2=35kN,F3=35kN。l1=l3=300mm,l2=400mm。 d1=12mm,d2=16mm,d3=24mm。试求:
ΔlAD ΔlAB ΔlBC ΔlCD -0.47 10-4mm
2、扭矩符号的规定 (Sign convention for torque)
Me
采用右手螺旋法则,当力偶矩矢的指
n Me
•
x
向背离截面时扭矩为正,反之为负.
3、扭矩图( Torque diagram)
Me
用平行于杆轴线的坐标 x 表示横
剪切弹性模量G=80GPa,DB=1°. 试求: (1) 画扭矩图;
(1) AD杆的最大切应力;
(2)求单位长度扭转角. 解:画扭矩图
M 2M
3M
Tmax= 3Me
DCB
A
计算外力偶矩M
DB= CB+ DC=1°
( Mea 2Mea ) 180 1
GIp GIp
π
aa
2M M
2a 3M +
例题12 作梁的内力图.
解 (1)支座反力为
RA
F1=2kN
F2=2kN RBm=10kN.m
A
C
D
4m
4m
4m
BE 3m
例题2 矩形截面铸铁梁的荷载和截面尺寸如图所示.铸铁的抗拉
许用应力为 [t] = 30MPa ,抗压许用应力为[c] =160MPa.,
h =50mm,b=25,校核梁的强度.
max = 176.8MPa
发生在AB段.
Ⅲ
R
DⅢ l3
Ⅱ
F3
C
Ⅱ
l2
Ⅰ
F2
F1
B
A Ⅰ
l1
(3) B截面的位移及AD杆的变形
Δl AB
FN1l1 EA1
2.53 10-4m
ΔlBC
FN2l2 EA2
1.42 10-4m
ΔlCD
FN 3 l3 EA3
1.58 10-4m
uB ΔlCD ΔlBC -0.3mm
FN2 =-15kN (-) FN3 =- 50kN (-)
Ⅲ
R
DⅢ l3
Ⅱ
F3
C
Ⅱ
l2
Ⅰ
F2
F1
B
ⅠA
l1
(2) 杆的最大正应力max
AB段:
AB
FN1 A1
176.8MPa
()
BC段:
BC
FN2 74.6MPa A2
()
DC段:
DC
FN 3 A3
110.5MPa
()
FN1 =20kN (+) FN2 =-15kN ( - ) FN3 =- 50kN ( - )
Me1
Mx 0
B C2 A
Me2 Me3 T2 0
Me2
T2 Me2 Me3 9560 N m
Me3 T2 x
结果为负号,说明T 2 应是负值扭矩 同理,在 BC 段内
BC
T1 Me2 4780 N m
Me2 T1 x
Me4 D
同理,在 BC 段内
Me2 1 Me3
T1 Me2 4780 N m
截面的位置;用垂直于杆轴线的
n T
•
x
坐标 T 表示横截面上的扭矩,正
的扭矩画在 x 轴上方,负的扭矩画在 x 轴下方. •
T
T
Me
x
•
+
_
x
例题1 一传动轴如图所示,其转速 n = 300 r/min ,主动轮A输 入的功率为P1 = 500 kW . 若不计轴承摩擦所耗的功率,三个从 动轮输出的功率分别为P2 = 150 kW 、P3 = 150 kW 及 P4 = 200 kW. 试做扭矩图.
R
40kN
55kN 25kN
20kN
A
B
C
D
E
求AB段内的轴力
R
A
40kN
B
1
55kN 25kN
C
D
20kN E
R
FN1
FN1 R 0
FN1 R 10( kN ) ( )
求BC段内的轴力 R
A
40kN
55kN 25kN
B
C
D
2
20kN E
R
40kN
FN2
FN2 R 40 0 FN2 R 40 50( kN ) ( )
F1 FN1 0
FN1 20kN ()
Ⅲ
R
DⅢ l3
Ⅱ
F3
C
Ⅱ
l2
R
FN3 FN2
Ⅰ
F2
F1
B
ⅠA
l1
F1 F2
FN3 R 0 FN3 50kN ()
F1 F2 FN2 0 FN2 15kN ()
Ⅲ
R
DⅢ l3
-
50
Ⅱ
F3
C
Ⅱ
l2
15
Ⅰ
F2
F1
B
ⅠA
l1
20
+
FN1 =20kN (+)
例题 1 一等直杆其受力情况如图所示, 作杆的轴力图.
40kN
55kN 25kN
20kN
A 600 B 300 C 500 D 400 E
解: 求支座反力
Fx 0 R 40 55 25 20 0 R 10kN
40kN
55kN 25kN
20kN
A 600
B
C 300
500
D 400 E
