《电路理论基础》(第三版 陈希有)习题答案第三章
《电路理论基础》(第三版_陈希有)习题答案第七章
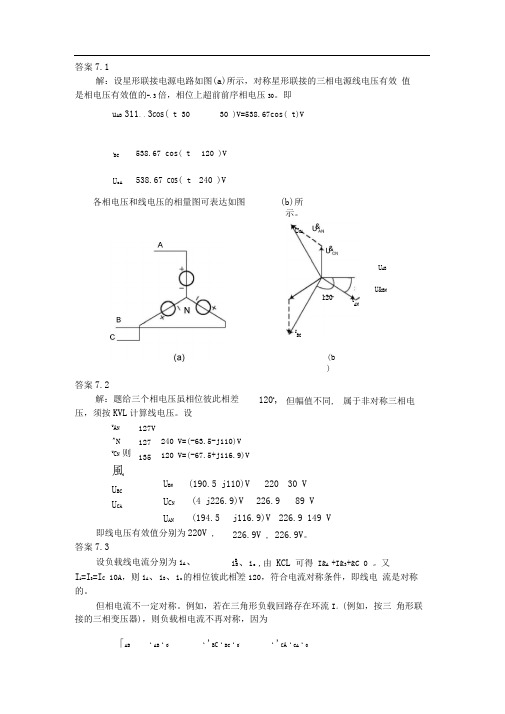
「AB1AB 1 0, 1'B C 1BC 1, 1'C A 1CA 1答案7.1解:设星形联接电源电路如图(a)所示,对称星形联接的三相电源线电压有效 值 是相电压有效值的-.3倍,相位上超前前序相电压30。
即 u AB 311、、3COS ( t 30 30 )V=538.67cos( t)V UBC538.67 cos( t 120 )V U cA538.67 COS ( t 240 )V各相电压和线电压的相量图可表达如图(b)所示。
U CAU AB120(b )UBCU&BNUAN答案7.2解:题给三个相电压虽相位彼此相差压,须按KVL 计算线电压。
设 U A N ^N UC N 则 風U BC U CA 120O, 但幅值不同, 属于非对称三相电127V127 135 240 V=(-63.5-j110)V 120 V=(-67.5+j116.9)VU B N (190.5 j110)V U C N U AN 220 30 V(4 j226.9)V 226.9 (194.5 89 V j116.9)V 226.9 149 V 226.9V , 226.9V 。
即线电压有效值分别为220V , 答案7.3 设负载线电流分别为i A 、I A =I B =I C 10A ,则i A 、i B 、i c 的相位彼此相差120,符合电流对称条件,即线电 流是对称的。
但相电流不一定对称。
例如,若在三角形负载回路存在环流I 。
(例如,按三 角形联接的三相变压器),则负载相电流不再对称,因为i B 、i c ,由 KCL 可得 I&A +I&3+&C 0 。
又B、不满足对称条件。
而该环流对线电流却无影响,因为每个线电流都是两个相电流之差(如图题7.3),即I A I 'AB I 'CA I AB I CA , I B I 'B C I 'A B I BC I AB , I C I ' CA I 'B C I CA I BC图题7.3如已知负载对称,则相电流也是对称的,每相电流为10八、3 5.77 A答案7.4负载各相阻抗化为星形联接为Z (8 j6)3 3由三角形联接得相电流与线电流关系得即负载相电流为47.6A 答案7.5解:电路联接关系如图(a)所示。
电路理论基础习题答案第三章

I4答案解:应用置换定理,将电阻 R 支路用I 0.5A 电流源代替,电路如图(b )所 示。
对电路列节点电压方程:(4-1 ) Um2IU n2 40.5A1 1 6VU n 1 (1)Un234.54.5I 0.5A解得U n11V则R Um 2I答案解:(a )本题考虑到电桥平衡,再利用叠加定理,计算非常简单(1)3V 电压源单独作用,如图(a-1)、(a-2)所示。
l i' 4答,o (a-2)3 4 8由分流公式得:I l(2) 1A 电流源单独作用,如图(a-3)所示1A3V 14 8考虑到电桥平衡,III 0,在由分流公式得:I ; 1A — 3A1 34(3) 叠加:I I ' I " 1AI i I i' I i"2R 1 I 12.007W(b )(1) 4V 电压源单独作用,如图(b-1)由图(b-1)可得,11' 3U 6AI I 2 I 1'5A(2) 2A 电流源单独作用,如图(b-2)所示(1/3)-1=1——O ------ ((a-3)U---------------- ---------------------' 2I4V(b-1)17/12A所示。
2 4V (2+2)2VU '' 2-22A=2V 2 2I I ' I " I ' kI s(1)将已知条件代入(1)式得0 I ' k 4A 1A I k 2A1A对节点②列KCL 方程得,I , 3U 2A I , 4A对节点③列KCL 方程得,nnnI I 2 3U 0解得I " 5A (3) 叠加in11 11 111nI I IR I 12 16A 4A= 10A 5A 5A= 10A100W答案解:禾U 用叠加定理,含源电阻网络中的电源分为一组,其作用为 |',如图 (b)所示。
《电路理论基础》(第三版陈希有)习题答案第十章

i答案10.1解:t ::: 0时,电容处于开路,故u C (0 _) = 10mA 2k 「- 20V 由换路定律得:u C (0 .) +(0”20V换路后一瞬间,两电阻为串联,总电压为 u C (0 )。
所以再由节点①的KCL 方程得:i C (0 ) =10mA -i 1(0 .)二(10-5)mA =5mA答案10.2解:t :::0时电容处于开路,电感处于短路,3门电阻与61电阻相并联,所以45V6i(0J3A ,L(0Ji(0」= 2A(5+8 + 6 3)0 6+36+3u C (0J =8 i(0J = 24V 由换路定律得:U C (0 ) 7C (0J =24V ,匚(0.) “L (0_)=2A由KVL 得开关电压:u(0 ) --U c (0 ) 8 匚(0 .)=(-24 8 2)V 8V答案10.3解:t ::: 0时电容处于开路,i =0 ,受控源源电压4i =0 ,所以U C (0 J =U C (0」=U 1(0」61.5V = 0.6V(9 6尸等效电阻i i (0 )=%(0 .) (2 2)k 」=5mA(b)所示。
R 段「4i (6 3)i容i时间常数二 R C 二 0 ・1st 0后电路为零输入响应,故电容电压为:u C (t)二 u C (0 ,)e~ =0.6e A0°V6“电阻电压为:“⑴工―6门 i 6门 ^C-dUc ^0.72e 10t V (t 0)dt答案10.43解:t :::0时电感处于短路,故L(0J= 39A=3A ,由换路定律得:6 + 3i L (0^i L (0J=3A求等效电阻的电路如图(b)所示。
等效电阻R 「6 •色卫=8」,时间常数.二L/R =0.5s6+3t 0后电路为零输入响应,故电感电流为i L (t) =i L (0 .)e^^ =3e 2t A (t _o ) 电感电压._2tu ,(t)二 L 匕二-24e V (t .0)dt31电阻电流为U 36C 汽L +U 1小2八i 3 2e A33「3「31电阻消耗的能量为:W3°= f 30i ;dt = f12/dt =12[-0.25ed=3W答案10.5解:由换路定律得i L (0.) “L (0」=0,达到稳态时电感处于短路,故LG) =20/4=5A求等效电阻的电路如图(b)所示。
电路理论基础(哈尔滨工业大学陈希有第3版)3

u U = f2( I )
+ N1 I S=I
U = f1 (I ) i O I
置换定理的证明
U -
(c) 置换定理图示
说明: (1)置换定理要求置换后的电路有惟一解; 置换定理要求置换后的电路有惟一解; 置换定理要求置换后的电路有惟一解 (2)除被置换部分发生变化外,其余部分在置换前后必须保持完全相同; 除被置换部分发生变化外, 除被置换部分发生变化外 (3)若电路中某两点间电压为零,则可将量值为零的电压源接于该两点间, 若电路中某两点间电压为零,则可将量值为零的电压源接于该两点间, 若电路中某两点间电压为零 相当于将该两点短路;若电路中某支路电流为零, 相当于将该两点短路;若电路中某支路电流为零,则可将量值为零的电流 源串接于该支路,相当于将该支路断开。 源串接于该支路,相当于将该支路断开。
第3章 电路定理
提要 本章介绍电路理论中的几个常用定理。首先介绍置换定理; 本章介绍电路理论中的几个常用定理。首先介绍置换定理;然 后介绍齐性定理和叠加定理;它们是体现线性电路特点的重要定理, 后介绍齐性定理和叠加定理;它们是体现线性电路特点的重要定理,是 线性方程的齐次性和可加性在电路中的体现;其次介绍戴维南定理和诺 线性方程的齐次性和可加性在电路中的体现; 顿定理,它们是化简线性一端口电路的有效方法; 顿定理,它们是化简线性一端口电路的有效方法;最后介绍与基尔霍夫 定律同样适用的特勒根定理,并以此证明互易定理。 定律同样适用的特勒根定理,并以此证明互易定理。
0.5' I I' 2Ω U 'S 1 1Ω US2 IS (b) 1Ω + U' −
0.5" I I" 2Ω 1Ω + 1Ω (c) U" −
电路理论基础孙立山陈希有主编第3章习题答案详解
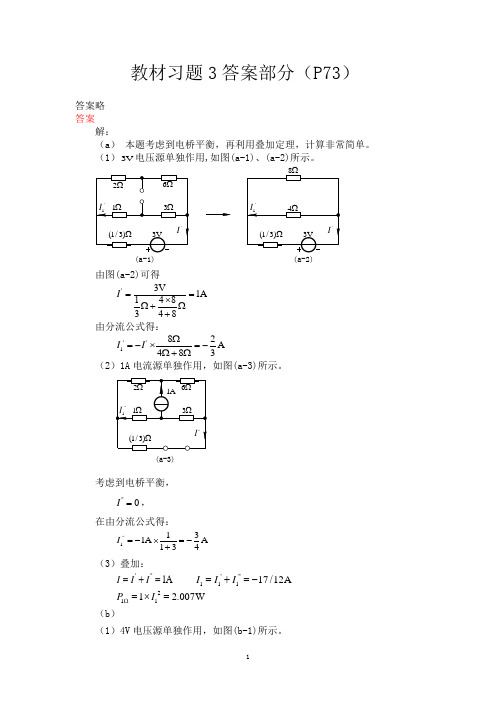
教材习题3答案部分(P73)答案略 答案解:(a ) 本题考虑到电桥平衡,再利用叠加定理,计算非常简单。
(1)3V 电压源单独作用,如图(a-1)、(a-2)所示。
(a-1)(a-2)由图(a-2)可得'3V1A 148348I ==⨯Ω+Ω+由分流公式得:''182A 483I I Ω=-⨯=-Ω+Ω(2)1A 电流源单独作用,如图(a-3)所示。
(a-3)考虑到电桥平衡,"0I =,在由分流公式得:"1131A A 134I =-⨯=-+ (3)叠加:'"1A I I I =+= '"11117/12A I I I =+=-2111 2.007W P I Ω=⨯=(b )(1)4V 电压源单独作用,如图(b-1)所示。
'I '由图(b-1)可得,'24V2V (2+2)U Ω⨯==Ω'136A I U =-=- ''21'5A I I I =+=-(2)2A 电流源单独作用,如图(b-2)所示。
(b-2)''222A=2V 22U ⨯=Ω⨯+ "''2311A 2I I =⨯= 对节点②列KCL 方程得,"""1132A 4A I U I +==对节点③列KCL 方程得,"""230I I U ++=解得"5A I =(3) 叠加'"1116A 4A=10A I I I =+=---'"5A 5A=10A I I I =+=---2111100W P I Ω=⨯Ω=答案略答案略答案解 :利用叠加定理,含源电阻网络中的电源分为一组,其作用为'I ,如图(b)所示。
S I 为一组,其单独作用的结果I '' 与S I 成比例,即:"S I kI =,如图(c)所示。
电路理论基础习题答案

电路理论基础习题答案第一章1-1. (a)、(b)吸收10W ;(c)、(d)发出10W. 1-2. –1A; –10V; –1A; – 4mW.1-3. –0.5A; –6V; –15e –t V; 1.75cos2t A; 3Ω; 1.8cos 22t W.1-4. u =104 i ; u = -104 i ; u =2000i ; u = -104 i ; 1-5.1-6. 0.1A. 1-7.1-8. 2F; 4C; 0; 4J. 1-9. 9.6V,0.192W, 1.152mJ; 16V , 0, 3.2mJ.1-10. 1– e -106t A , t >0 取s .1-11. 3H, 6(1– t )2 J; 3mH, 6(1–1000 t ) 2 mJ;1-12. 0.4F, 0 .1-13. 供12W; 吸40W;吸2W; (2V)供26W, (5A)吸10W. 1-14. –40V , –1mA; –50V, –1mA; 50V , 1mA. 1-15. 0.5A,1W; 2A,4W; –1A, –2W; 1A,2W. 1-16. 10V ,50W;50V ,250W;–3V ,–15W;2V ,10W. 1-17. (a)2V;R 耗4/3W;U S : –2/3W, I S : 2W; (b) –3V; R 耗3W; U S : –2W, I S :5W; (c)2V ,–3V; R 耗4W;3W;U S :2W, I S :5W; 1-18. 24V , 发72W; 3A, 吸15W;24V 电压源; 3A ↓电流源或5/3Ω电阻. 1-19. 0,U S /R L ,U S ;U S /R 1 ,U S /R 1 , –U S R f /R 1 . 1-20. 6A, 4A, 2A, 1A, 4A; 8V, –10V , 18V . 1-21. K 打开:(a)0, 0, 0; (b)10V , 0, 10V; (c)10V,10V ,0; K 闭合: (a)10V ,4V ,6V; (b)4V ,4V ,0; (c)4V,0,4V; 1-22. 2V; 7V; 3.25V; 2V. 1-23. 10Ω.1-24. 14V .1-25. –2.333V , 1.333A; 0.4V , 0.8A.1-26. 12V , 2A, –48W; –6V , 3A, –54W . ※第二章2-1. 2.5Ω; 1.6R ; 8/3Ω; 0.5R ; 4Ω; 1.448Ω; . R /8; 1.5Ω; 1.269Ω; 40Ω; 14Ω. 2-2. 11.11Ω; 8Ω; 12.5Ω. 2-3. 1.618Ω.2-4. 400V;363.6V;I A =.5A, 电流表及滑线电阻损坏. 2-6. 5k Ω. 2-7. 0.75Ω.2-8. 10/3A,1.2Ω;–5V ,3Ω; 8V ,4Ω; 0.5A,30/11Ω. 2-9. 1A,2Ω; 5V,2Ω; 2A; 2A; 2A,6Ω. 2-10. –75mA; –0.5A.2-11. 6Ω; 7.5Ω; 0; 2.1Ω. 2-12. 4Ω; 1.5Ω; 2k Ω. 2-13. 5.333A; 4.286A. 2-14. (a) –1 A ↓; (b) –2 A ↓, 吸20W. 2-16. 3A. 2-17. 7.33V . 2-18. 86.76W. 2-19. 1V , 4W. 2-20. 64W.2-21. 15A, 11A, 17A. 2-23. 7V , 3A; 8V ,1A. 2-24. 4V , 2.5V, 2V. 2-26. 60V . 2-27. 4.5V. 2-28. –18V .2-29. 原构成无解的矛盾方程组; (改后)4V ,10V . 2-30. 3.33 k , 50 k . 2-31. R 3 (R 1 +R 2 ) i S /R 1 .2-32. 可证明 I L =-u S /R 3 . 2-33. –2 ; 4 .2-34. (u S1 + u S2 + u S3 )/3 . ※第三章3-1. –1+9=8V; 6+9=15V; sin t +0.2 e – t V. 3-2. 155V . 3-3. 190mA.i A0 s 1 12 3 1-e -t t 0 t ms i mA 410 0 t ms p mW 4 100 2 25i , A 0.4 .75 t 0 .25 1.25 ms -0.4 (d) u , V 80 0 10-20 t , ms(f ) u , V 1000 10 t , ms (e)p (W) 100 1 2 t (s) -103-4. 1.8倍.3-5. 左供52W, 右供78W. 3-6. 1; 1A; 0.75A.3-7. 3A; 1.33mA; 1.5mA; 2/3A; 2A. 3-8. 20V , –75.38V.3-9. –1A; 2A; –17.3mA. 3-10. 5V , 20; –2V, 4. 3-12. 4.6. 3-13. 2V; 0.5A. 3-14. 10V , 5k .3-15. 4/3, 75W; 4/3, 4.69W. 3-16. 1, 2.25W. 3-18. 50. 3-19. 0.2A. 3-20. 1A. 3-21. 1.6V . 3-22. 4A; –2A.3-23. 23.6V; 5A,10V . 3-24. 52V . ※第四章4-1. 141.1V , 100V , 50Hz, 0.02s,0o , –120o ; 120 o.4-2. 7.07/0 o A, 1/–45 o A, 18.75/–40.9 oA. 4-3. 3mU , 7.75mA .4-4. 10/53.13o A, 10/126.87o A, 10/–126.87oA,10/–53.13oA ;各瞬时表达式略。
《电路理论基础》(第三版 陈希有)习题答案第四章

答案4.1解:将非线性电阻左侧电路用戴维南定理进行等效化简,如图(b)所示。
1(b)列KVL 方程11V I U Ω⨯+= (1) 将非线性电阻特性2(1S )I U =⨯代入方程(1),得210U U +-= 解得0.618V U '=, 1.618V U ''=-(舍去) 2(1S )0.382A I U '=⨯=答案4.2解:将非线性电阻之外的电路等效化简,得图(b)所示电路。
1Ω(b)列KVL 方程1180I U Ω⨯+-= (1) 将I I U 22+=代入方程(1),得23180I I +-=解得:3A, 6A I I '''==-22()215V ()224VU I I U I I '''=+=''''''=+=答案4.3解:由非线性电阻的电压电流关系特性1I =2I = 得211100U I = ,222400U I = (1) 对回路列KVL 方程125V U U += (2) 将式(1)代入式(2)22121004005I I +=由非线性电阻串联可知 12I I =即215005I =解得10.1A I '= ,10.1A I ''=-(舍去) 即10.1A I =2111001V U I ==答案4.4解:对节点①、②列节点电压方程,其中非线性电阻电流设为未知量:121221112()n n s G G U G U GU I I +-=-- (1)21232S 2()n n G U G G U I I -++=+ (2)为消去12I I 、,须列补充方程11111222212S2()()(3)()()(4)n n n I f U f U I f U f U U U ==⎧⎨==--⎩将式(3)代入式(1)、(2),整理后得1212211212S11S121232212S2S ()()()()()n n n n n n n n n G G U G U f U f U U U G U G U G G U f U U U I +-++--=⎧⎨-++---=⎩答案4.5解:设回路电流方向如图所示。
《电路理论基础》(第三版--陈希有)习题答案第十章Word版

答案10.1解:0<t 时,电容处于开路,故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得:V 20)0()0(==-+C C u u换路后一瞬间,两电阻为串联,总电压为)0(+C u 。
所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得:m A 5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解:0<t 时电容处于开路,电感处于短路,Ω3电阻与Ω6电阻相并联,所以A 3)363685(V45)0(=Ω+⨯++=-i ,A 2)0(366)0(=⨯+=--i i L V 24)0(8)0(=⨯=--i u C 由换路定律得:V 24)0()0(==-+C C u u ,A 2)0()0(==-+L L i i 由KVL 得开关电压:V 8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u答案10.3解:0<t 时电容处于开路,0=i ,受控源源电压04=i ,所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C0>t 时,求等效电阻的电路如图(b)所示。
等效电阻Ω=++-==5)36(4i ii i i u R时间常数s 1.0i ==C R τ0>t 后电路为零输入响应,故电容电压为:V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为:V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4解:0<t 时电感处于短路,故A 3A 9363)0(=⨯+=-L i ,由换路定律得: A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=+⨯+=836366i R ,时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应,故电感电流为A e 3e )0()(2/t t L L i t i --+==τ)0(≥t电感电压V e 24d d )(21t L tiL t u --==)0(>tΩ3电阻电流为 A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为:W 3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解:由换路定律得0)0()0(==-+L L i i ,达到稳态时电感处于短路,故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答案3.1解:应用置换定理,将电阻R 支路用0.5A I =电流源代替,电路如图(b)所示。
I2对电路列节点电压方程:1212(1)0.5A 44n n I U U +Ω⨯-=-ΩΩ12116V(1)3 4.5 4.5n n U U -+Ω++⨯=ΩΩΩ0.5A I =解得11V n U =则12n UR I==Ω答案3.2解:(a ) 本题考虑到电桥平衡,再利用叠加定理,计算非常简单。
(1)3V 电压源单独作用,如图(a-1)、(a-2)所示。
(a-1)(a-2)由图(a-2)可得'3V1A 148348I ==⨯Ω+Ω+由分流公式得:''182A 483I I Ω=-⨯=-Ω+Ω(2)1A 电流源单独作用,如图(a-3)所示。
(a-3)考虑到电桥平衡,"0I =,在由分流公式得:"1131A A 134I =-⨯=-+(3)叠加:'"1A I I I =+= '"11117/12A I I I =+=-2111 2.007W P I Ω=⨯=(b )(1)4V 电压源单独作用,如图(b-1)所示。
'2I '(b-1)由图(b-1)可得,'24V2V (2+2)U Ω⨯==Ω'136A I U =-=-''21'5A I I I =+=-(2)2A 电流源单独作用,如图(b-2)所示。
(b-2)''222A=2V 22U ⨯=Ω⨯+ "''2311A 2I I =⨯=对节点②列KCL 方程得,"""1132A 4A I U I +==对节点③列KCL 方程得,"""230I I U ++=解得"5A I =(3) 叠加'"1116A 4A=10A I I I =+=---'"5A 5A=10A I I I =+=---2111100W P I Ω=⨯Ω=答案3.3解 :利用叠加定理,含源电阻网络中的电源分为一组,其作用为'I ,如图(b)所示。
S I为一组,其单独作用的结果I '' 与S I 成比例,即:"S I kI =,如图(c)所示。
II kI (a)(b)(c)+'"'S I I I I kI =+=+ (1)将已知条件代入(1)式得''04A1A 2AI k I k ⎧=+⨯⎪⎨-=+⨯⎪⎩联立解得:'2A I =,12k =即:S 12A+2I I =-⨯将1A I =代入,解得S 6A I =答案3.4解:(1)125V U U ==时,电路对称,12n n U U =,可化简成图 (b)所示。
1U 2U (b)Ω41U 2U (a)对电路列节点电压方程,得1211(11)S 1.511n U U U ++⨯=+ΩΩ1 3.75V n U =o 11 2.5V (10.5)n U U Ω=⨯=+Ω(2)当123V U U =-=时,0.5Ω上电流为零,图(a)电路可化简成图(c)所示。
Ω41U 1U -(c)由分压公式得12114//4[()]3V 1(4//4)1U U U ΩΩ=--=Ω+ΩΩ+Ω解得o 12/2 1.5V U U ==(3)当18V U =,22V U =时,可看作1(53)V U =+,2(53)V U =-,即可视(a)、(b)电路所加激励之和。
应用叠加定理,o oo 2.5V 1.5V 4V U U U '''=+=+= 注释:差模或共模电压作用于对称电路时,可以采用简便计算方法;将一般电压分解成差模分量与共模分量代数和,再应用叠加定理也可简化计算。
答案3.5解:根据叠加定理,将图(a)等效成图 (b)与图 (c)的叠加。
I (b)2(c)由已知条件得S11S128W14V 2AI P U I '=== 28V U '= 112V U ''=22254W18V 3AS I S P U I ''=== 所以12S S I I 、共同作用时11126V U U U '''=+= 22226V U U U '''=+= 每个电源的输出功率分别为S1S1152W I P I U == S2S2278W I P I U ==答案3.6解:应用戴维南定理或诺顿定理(1) 图(a)电路求开路电压和等效电阻,分别如图(a-1)和图(a-2)所示。
OC 3A 5(5V)10V U =⨯Ω+-=OCU +-i(a-1)(a-2)(a-3)图(b )电路等效过程如下:(b-1)OC(b-2)(b-3)OC 10A 540V 90V U =⨯Ω+= i 5R =Ω图(c )电路等效过程如下:OC U +-(c-1)5ΩiR (c-3)(c-2)OC 1A 510V 15V U =⨯Ω+= i 5R =Ω图(d )电路等效过程如下:OCiR (d-1)(d-2)(d-3)OC 10A 550V 100V U =⨯Ω+= i 5R =Ω图(e )电路等效过程如下:(e-1)iR (e-2)(e-3)图(f )电路等效过程如下:OCU +-iR (f-1)(f-2)(f-3)图(g )电路等效过程如下:1(g-1)1(g-2)i(g-3)图(h )电路等效过程如下:(h-3)(h-2)(h-1)OC U +-如果电路的等效内阻为非零的确定值,则电路既存在戴维南等效电路,又存在诺顿等效电路;如果电路的等效内阻为零,则只能等效成戴维南电路;如果电路的等效内阻为无穷大,则只能等效成诺顿电路。
答案3.7abab(a-1)(b-1)'解:(a)(1)求开路电压OC U 开路时,对节点①由KCL ,20I I -+=,0I =开路电压OC 8V-10=8V U I =Ω(2)求等效电阻求i R 时8V 独立电压源置零,外加电压U ',如图(a-1)所示 。
由 KVL 得'10U I =-Ω对节点①由KCL 得,'2I I I I =-=''1010i U I R I I-Ω===-Ω(b)(1)求开路电压对节点①列KCL 方程211A I I =- (1)对回路1l 列KVL 方程得OC 1112108U I I I =-Ω+Ω=Ω (2)对回路2l :12101020V I I Ω-Ω= (3)将式(1)代入式(3),与式(2)联立,解得1 1.5A I = OC 12V U =(2)求等效电阻求i R 时将独立源置零,外加激励电流I 求ab 端口响应电压f U ,如图(b-1)所示。
由图(b-1)可知,112I I = (1)对回路1l 列KVL 方程'112108U I I I =-Ω+Ω=Ω (2)将式(1)代入式(2),得4i UR I==Ω答案3.8解:将含源电阻网络化为戴维南等效电路,如图 (b)所示。
由此图求得:U +-U +-(b)OCi ()U U R R R=⨯+ (1) 将10R =Ω时,15V U =;20R =Ω,20V U =代入式(1),得OC i OC i 15V ()101020V ()2020U R U R ⎧=⨯Ω⎪+Ω⎪⎨⎪=⨯Ω⎪+Ω⎩联立解得:10i R =Ω 30V oc U =(1) 式可表示为30V()10U R R=⨯Ω+当30R =Ω时30V3022.5V (1030)U =⨯Ω=+Ω注释:一端口外接电路发生变化时,宜采用戴维南或诺顿定理进行分析。
答案3.9首先将开关右侧电路化简为戴维南等效电路,如图(b)所示,其开路电压为3V ,等效电阻为10ΩR 10Ω(b)开关断开时=13V U 得:OC i 13V 13V 3V1A 10U R --==Ω开关短接时=3.9A I 得:OC i 3V3.9A 10U I R =+=Ω联立求解得:OC 18V U = ,i 5R =Ω答案3.10解:将含源电阻网络等效为戴维南电路。
如图(b )所示。
负载电阻R 消耗的功率可表示为bU +-2OC i ()R U P R R R=⨯+ (1) 将已知条件分别代入(1)式,得2OC i2OC i ()1022.5W 10()2020W 20U R U R ⎧⨯Ω=⎪+Ω⎪⎨⎪⨯Ω=⎪+Ω⎩ 联立解得i 10R =Ω OC 30V U =当30R =Ω时22OC i 30V ()303016.9W 30(1030)R U P R ⎛⎫=⨯Ω=⨯Ω≈ ⎪+Ω+Ω⎝⎭答案3.11解:将图(a )电路化简如图(b )所示。
S I6(b)-+UOC62(62)S iI U U R Ω-=⨯Ω+Ω+代入两个已知条件:2A S I =时,0U =: OC 62A 12V U =Ω⨯=S 0I =时,2V U =-: OC i i 2V(8)8V+1A 2U R R -=-Ω+⨯=⨯Ω解得:OC 12V U = i 4R =Ω答案3.12解:(1)根据叠加定理和齐性定理,将电流I 写成一般表达式S I I I KI I '''''=+=+ (1)式中,SI KI '=是电流源单独作用时产生的电流;I ''是N 内独立电源作用产生的电流。
由已知条件得1.2mA 0K I ''=⨯+1.4mA 10mA K I ''=⨯+解得0.02K =, 1.2mA I ''= 代入式(1)得S 0.02 1.2mA I I =+所以当S 15mA I =时0.0215mA 1.2mA 1.5mA I =⨯+=(2)将22'左边等效成戴维南电路。
如图(b )所示U +-R Rb由(1)的计算结果得OC o ()(50100) 1.5mA 225mV U R R I =+=+Ω⨯=当R 改为Ω200时,OC o 225mV0.9mA (50200)U I R R ===++Ω答案3.13解:将开关S 左侧的电路化为最简等效电路。
3S (a)(b)6iR(c)ocU A由题意得(1)求开路电压OC U由图(a )可知,开路电压为3Ω电阻两端电压,即OC 35A=15V U =Ω⨯(2)求等效电阻i R将独立电压源置零,对3个2Ω电阻联接做星-三角变换。
电路如图 (b)所示。
