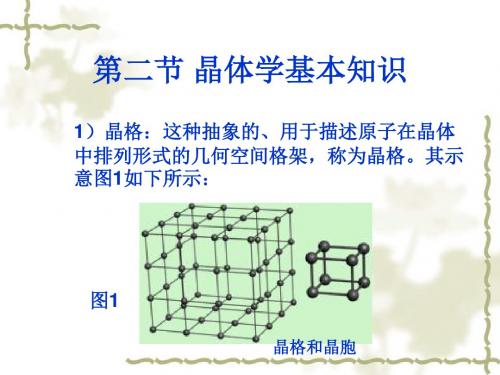
2 晶体学基本知识
图2-24 单斜晶系中的晶轴
38
图2-25 单斜晶系中的坐标系,其中y轴是二次旋转轴
39
正交晶系
晶轴。正交晶系的特点是具有三个互相垂直的二 次旋转轴，或有二个互相垂直的对称面。在222 点群和mmm点群中，分别选这三个二次旋转轴为 a、b、c轴；在mm2点群中则选唯一的一个二次 旋转轴为c轴，选两个对称面的法线方向为a轴 和b轴，晶格常数大小为：c<a<b，晶轴之间夹 角为===90。 坐标轴（x、y、z）。因为正交晶系的晶轴互相垂 直，分别选晶轴a、b、c为坐标轴x、y、z。正 交晶系的实例如图1-26所示。
的点群； 晶体中一共有32个这样的点群；
32
晶轴和直角坐标轴
33
晶轴和直角坐标轴的选择
晶面符号和晶棱符号的确定取决于晶 轴的选择，晶轴选择方式不同，晶面符号 和晶棱符号也不一样。 其次，在讨论晶体的弹性性质、介电 性质和压电性质时，采用直角坐标系是比 较方便的。由于晶轴之间夹角不一定等于 90，所以选定晶轴之后，有时还要另选直 角坐标系。选择不同的直角坐标系，所得 到的数学表达式也不一样。 为了避免混乱，必须对晶轴的选择和 直角坐标系的选择作共同的规定。
中 级 晶 族
三 角
3
有 1 个 3 次轴（3 次旋转倒反轴） 32 3m
3m
6
6
六 六 角 有 1 个 6 次轴（6 次旋转倒反轴） 6/m 622 6mm
6 m2
6/mmm 高 级 晶 族 有 几 个 高 次 轴 23 m3 有 4 个 3 次轴 432
立 方
43m
m3m
小结 summary
对称元素和对称操作
42
图2-27 四方晶系的晶轴
43
三角晶系和六角晶系
晶轴。三角晶系和六角晶系的特点是具有一 个三次旋转轴或六次旋转轴。通常都是选三 次轴或六次轴为c轴，选二次轴或对称面的 法线为a、b轴。晶格常数大小为：a=bc， 晶轴之间夹角为==90,=120。 坐标轴（x、y、z）。通常选z轴平行于c轴， x轴与a轴一致，y轴垂直于ac平面。三角晶 系和六角晶系的实例如图2-28和图2-29所示 。
40
图2-26 酒石酸钾钠（KNT）在非铁电相时属于
222点群，其中a、b、c轴都是二次旋转轴
41
四方晶系
晶轴。四方晶系的特点是具有一个四次旋转 轴或四次旋转倒反轴。通常都是选四次轴 为c轴，选一个二次轴为a轴，如果无二次 轴，则选最小晶胞中的两个等长轴之一为a 轴。晶格常数大小为：a=bc，晶轴之间夹 角为===90。 坐标轴（x、y、z）。因为四方晶系的晶轴互 相垂直，分别选晶轴a、b、c为坐标轴x、y 、z。四方晶系的实例如图1-27所示。
晶体的三十二个点群 对称性和点群对于压电铁电体非常重要！ 只有晶体才会有压电铁电性，不存在非晶
压电铁电体。但是有非晶半导体和非晶磁 性材料。
31
晶体中的点群
由于无限大周期性的限制，晶体中的对称 操作只能有：1，2，3，4，6，， 1 m, 4 ；
由这些对称操作所构成的集合就是晶体中
44
图2-28
-石英晶体属于32点群，c轴为三次轴
，a、b、d轴为二次旋转轴
45
图2-29 碘酸锂晶体属于6点群，c轴为6次旋转轴
46
立方晶系
晶轴。立方晶系的特点是具有四个三次旋转 轴（包括旋转倒反轴），同时不是有三个 相互垂直的四次旋转轴（包括旋转倒反轴 ），就是有三个相互垂直的二次旋转轴， 分别选择这些四次或二次轴为a、b、c轴。 晶格常数大小为：a=b=c，晶轴之间夹角为 ===90。 坐标轴（x、y、z）。通常选择晶轴a、b、c 为坐标轴x、y、z。
34
三斜晶系
晶轴。三斜晶系除了一次旋转轴或一次旋转倒反轴 外，无其它对称元素。因此只能选择三个不在同 一平面上的晶棱方向作为晶轴。晶轴的安排是c 轴为直立，b轴为左右并向右倾，a轴为前后方向 并向前倾。晶格常数的大小为b>a>c，晶轴间的 夹角为，并有>90，>90。 坐标轴（x、y、z）。目前都选择z轴与晶轴c重合 ；x轴在晶轴a和c组成的平面内，并指向+a方向 ；y轴垂直于ac平面，并指向+b方向，如图1-23 所示。
35
图2-23 三斜晶系中的晶轴与坐标系
36
单斜晶系
晶轴。单斜晶系的特点是具有一个二次旋转 轴或二次旋转倒反轴。选二次轴为b轴，并 在与b轴垂直的平面上选择相交的晶棱方向 作为c轴和a轴。晶格常数大小为：abc， a>c，晶轴之间夹角为==90，>90。单 斜晶系的实例如图1-24所示。 坐标轴（x、y、z）。目前选择y轴与b轴重合 ；z轴与c轴重合，x轴垂直于bc平面，如图 2-25所示。
1
2
低 级 晶 系
单 斜
只有 1 个方向上具有 2 次轴（或 2 次旋转倒反轴）
2m
2 /m
222 mm2 mmm 4
正 交
在 3 个相互垂直的方向上有 2 次轴 （或 2 次旋转倒反轴）
4
四 方 4/m 有 1 个 4 次轴（4 次旋转倒反轴） 422 4mm
4 2m
只 有 1 个 高 次 轴 4/mmm 3
12
图2-15
13
对称面（镜面）mirror
为一假想平面，相应的对称操作为对此平 面的反映。对称面将图形分为镜像反映的 两个相等的部分。图2-16表示通过对称面 m把M反映到M’。对称面在图形上常用双线 或粗线表示，国际符号为“m”。
14
图2-16 m
15
旋转轴（对称轴）roTaTion
为一假想直线，相应的对称操作为对此轴线 的旋转。一个晶体如绕此轴旋转360/n后， 能够复原，则称此晶体具有n次旋转轴或简 称n次轴。由于晶体结构的周期性（即晶体 的平移对称性）给晶体的转动对称性带来了 严格的限制，即n只能等于1、2、3、4、6， 或者说晶体只可能具有1、2、3、4、6次旋 转轴，不可能具有5次或高于6次的旋转轴。
对称类型 国际符号 1 熊夫利斯符号 C1 Ci C2 Cs C2h D2 C2v D2h C4 S4 C4h D4 C4v D2d D4h C3 C3i D3 C3v D3d C6 C6i C6h D6 C6v D3d D6h T Th O Td Oh 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
9
对称性和对称操作
10
晶体中可能的对称操作
11
对称中心 inversion
为一假想的定点，相应的对称操作为对此 定点的反演（或倒反）。图2-15表示通过 对称中心c把M点反演到M’点。如果把对称 中心作为坐标原点，那么对称中心的作用 将使点M(x,y,z)反演到点M’(-x,-y,-z)。 或者作通过对称中心的任意直线，在此直 线上，距对称中心等距离的两端，一定可 以找到相对应的点M和M’。对称中心的国际 符号是“1”。
数，压电常数等 研究方便：立方晶体11= 22= 33，其它 ij=0 计算方便
8
对称操作和对称元素
能使对称图形复原的动作称为对称操作
，例如，前面提到的对称轴的旋转，对 称面的反映，此外，对称中心点的反演 （或倒反）等，都是对称操作。 进行对称操作时，还必须依赖于一定的 几何元素，如对称中心、对称面、对称 轴等，这些几何元素又称为对称元素
6
晶体的对称性是由其内部格子结构所决 定的。它不仅与晶体的结构有密切关系 ，而且也于晶体的力学、电学、光学以 及压电铁电性质等有密切关系。 可以说，晶体的对称性是晶体分类的基 础，也是研究晶体其它性质的基础。 这里先主要介绍的对称性，不包括平移 对称性在内，所以是宏观对称性
7
晶体结构本身具有对称性，x-射线衍射 晶体的物理性质与对称性有关，介电常
第二章 晶体结构及其弹性性质
• 2-1 晶体结构和基本概念
• 2-2 晶体的弹性性质 • 2-3 弹性常数与对称性
晶系和布喇菲格子
通常描写晶胞的六个 物理量是三个基矢的 长度和基矢之间的夹 角，如图所示 a，b，c，，，通 常又称为晶格常数， 可以由x射线确定 根据a，b，c，， ，的不同，晶格可 分为七大晶系和十四 种布喇菲格子
28
32 poinT groups
人们经过长期研究的结果，发现这八种对 称元素共有32种组合方式，即32种点群。 这32种点群对应于晶体的32种宏观对称类 型，就是说自然界千千万万种晶体，可以 归纳为32种宏观对称类型。
29
晶 族
晶 系 三 斜
对称特点 只有 1 次轴（或 1 次旋转倒反轴） 无 高 次 轴 HexagonalFra bibliotek simple
Trigonal: simple Cubic: simple(sc), body-cenTered(bcc), facecenTered(fcc)
4
对称性和点群 symmeTry and poinT groups
了解对称性和对称操作，认识晶体的
三十二个点群 To undersTand The symmeTry and 32 poinT groups in crysTals
2
2
3
27
1 2 3 4 6 1 m 4
知道了晶体的八个基本的宏观对称元素后， 下一个问题就是：在晶体中，究竟有哪些对 称元素和对称操作可以同时存在？它们的组 合方式有多少种？在数学上，把对称元素（ 或对称操作）的集合叫做“对称群”。因为 上述对称元素中，不包括平移对称性，进行 对称操作时总是有一点保持不动，所以只包 括上述对称元素的集合叫做“点群”。
16
17
旋转轴符号
结晶学基础
然两两反向平行而且相等。用它可以作为判 断晶体有无对称中心的依据。
4、旋转反伸轴（Lin）
旋转反伸轴是一根假想的直线，当晶体围 绕此直线旋转一定角度后，再对此直线上 的一个点进行反伸，才能使晶体上的相等 部分重复。 相应的对称操作是围绕一根直线的旋转和 对此直线上一个点反伸的复合操作。
只有晶体才能称为真正的固体。
5、准晶体
1985年在电子显微镜研究中，发现了一种新 的物态，其内部结构的具体形式虽然仍在探 索之中，但从其对称性可见，其质点的排列 应是长程有序，但不体现周期重复，不存在 格子构造，人们把它称为准晶体。
二、晶体的基本性质
一切晶体所共有的，并且是由晶体的格子构造所决定的性 质，称为晶体的基本性质。
晶体中对称轴举例
横截面形状
晶体对称定律：在晶体中不可能存在五次 及高于六次的对称轴。因为不符合空间格 子规律，其对应的网孔不能毫无间隙地布 满整个平面。
在一个晶体中，除L1外，可以无、也可有
一或多种对称轴，而每一种对称轴也可有一 或多个。
表示方法为3L4、4L3、6L2等。 对称轴在晶体中可能出露的位置： ⑴通过晶面的中心； ⑵通过晶棱的中点；
⑵行列：结点在直线上的排列即构成行列。
行列中相邻结点间的距离称为该行列的结点间距。 同一行列或彼此平行的行列上结点间距相等； 不同方向的行列，其结点间距一般不等。
行
列
⑶ 面网：结点在平面上的分布构成面网。 面网上单位面积内结点的数目称为网面密 度。 互相平行的面网，网面密度相同；不平行 的面网，网面密度一般不等。 相互平行的相邻两面网之间的垂直距离称 为面网间距。
第二节 晶体学基本
4）晶面和晶向
①晶面：晶格中由一系列原子组成的平面称 为晶面。
晶面用晶面指数来表示： 现以图3立方晶格中晶面A为例,说明确定晶面
指数的方法.
a.以晶胞的三条棱边为空间坐标轴 OX、OY、OZ，坐标轴的原点O应选 在待定晶面以外，以免截距为零。
b.晶胞棱边长a、b、c分别为OX、 OY、OZ轴上的度量单位，求出待定 晶面在三个坐标轴上的截距。A晶面 在三个坐标轴上的截距分别为∞、1、 1。
图2
晶胞的棱边长度a、b、 c和棱边夹角α、β、γ 称为晶格常数。度量单 位均为Å（1Å=10-10m） 和度。当棱边长度 a=b=c,棱边夹角 α=β=γ=90°时，这种 晶胞称为简单立方晶胞。 由简单立方晶胞组成的 晶格称为简单立方晶格。 在简单立方晶格中，晶 格常数常用边长a、b、 c来表示。
倒易点阵的本质
图4 立方晶格中的三种重要晶面 a)（110）面； b)（100）面 c)（111）面
②晶向：在晶体中，通过两个以上原子中心的直线构成一 个原子列，各种原子列的位向称为晶向。
晶向用晶面指数来表示：
晶向指数：现以图3立方体晶格中晶向OE 为例，说明晶向指数的确定方法。 a.在晶格中设空间坐标轴OX、OY、OZ， 坐标轴的原点O应在所求晶向的直线上。
三斜 Triclinic
abc ===90°
多晶体结构
如果一块晶体内部的晶格位向（即原子排列的方向） 完全一致，称这块晶体为单晶体。实际使用的金属 材料，目前只有采用特殊的方法才能得到单晶体。 实际使用的金属材料，哪怕是在很小体积中也包含 有许多外型不规则的小晶体，每个小晶体内部的晶 格位向都是一致的，而各小晶体之间位向却不相同， 如图所示。
图 单晶体与多晶体示意图 a)单晶体 b)多晶体
晶体学及其应用
晶体学及其应用晶体学是一门研究晶体结构及性质的学科，它的应用范围广泛，可以涉及到材料科学、化学、物理、生物学等多个领域。
本文将介绍晶体学的基本概念、方法、发展历程和广泛应用的几个领域。
一、晶体学的基本概念晶体学是研究晶体内部原子结构的学科，晶体则是具有等距的、有序排列的原子结构的物质。
晶体的基本结构单元是晶胞，由空间对称性相同的晶体结构单元周期性重复组成。
晶体学的主要研究内容包括晶体结构的测定、分析和解释，以及晶体的生长、合成和性质研究等方面。
二、晶体学的方法晶体学研究晶体结构的方法主要包括X射线衍射、中子衍射、电子衍射、红外线光谱、拉曼光谱等。
其中，X射线衍射是最常用的方法，它可用于测定晶体结构中原子的位置、晶体中原子间的距离和晶胞参数等信息。
中子衍射则是用来研究晶体内部的原子核结构。
而其他方法则可以从晶体的光学、热学、电学等性质中获取晶体结构的信息。
三、晶体学的发展历程晶体学的发展可以追溯到17世纪，当时科学家们已经开始关注晶体的结构和形成机制。
然而，在19世纪初，晶体学才正式形成为独立的学科，并逐渐发展成现代实验科学。
到20世纪初，X 射线衍射成为了测定晶体结构的基本方法，也是晶体学的重大里程碑。
此后，晶体学的发展得到迅速推进，新的方法和技术也不断涌现。
当代晶体学已经成为一门多学科交叉的综合学科，对于新材料、新技术的研究和开发起着重要的作用。
四、晶体学的应用晶体学的应用领域广泛，可以涉及到材料科学、化学、物理、生物学等多个领域。
其中，以下几个领域是晶体学应用的主要方向。
1.材料科学。
晶体学是合成新材料、改良材料的重要基础。
例如，通过晶体学的知识，可以合成出在不同方向上具有不同性能的块状材料或纤维材料。
还可以利用晶体学的技术，将材料表面形成一层具有晶体结构的薄膜，使材料的性能得到提高。
2.医学。
晶体学对于研究蛋白质的结构和功能有重要意义，这对于开发新型药物和治疗疾病具有重大意义。
例如，晶体学的技术可以应用于治疗癫痫、阿尔兹海默症等疾病的药物研发。
晶体学基础知识点及思维导图
HOMEWORKS知识点晶体结构Crystal structure 点阵结构Lattice晶胞Unit cells晶系Crystal systems布拉菲格子The Bravais lattices点群point group空间群space group关系Relationships/思维导图Mind mapping具体中文解释粒子抽象成点，形成了点阵结构，而这些点连接起来就形成了晶格，可以说点阵和晶格具有同一性，但区别于点阵具有唯一性，晶格不具有。
同样我们需要区别“lattice ”的意义 它在这应该准确的代表点阵结构而不是单单的点阵，点阵结构是具体的客观存在的而点阵是人为抽象出来的，相比于点阵对应的点阵点，点阵结构对应的就是结构基元。
晶胞堆砌成了点阵结构，晶胞又具有晶胞参数和晶胞内容两方面，也就是说可以这么表示晶胞=点阵格子+结构基元。
根据晶胞的晶胞参数我们可以把晶体的结构从宏观上分为七个方面，也就是七大晶系.七大晶系结合晶胞类型产生了14种Bravais晶格点群表示的是晶体中所包含所有点对称操作的（旋转、反应、反演）的集合。
（晶体的宏观性质不变)。
点群描述了分子结构和晶体的宏观对称性（后来老师讲点群只是对于结构基元里的原子的对称排布，我个人后来查阅思考了一下，这是局限的，点群所描述的对称性正是可以描述宏观的晶格以及肉眼可见的晶体的对称性，所以它才被引为宏观对称性。
）微观对称元素：点阵、滑移面、旋转轴（无数阶次）而晶体的宏观对称元素和微观对称元素在内的全部对称元素的一种组合就构成晶体的一种微观对称类型也就是空间群，它反应的是内部微观结构的对称性（结构基元内部原子）或者是微观的晶胞堆积方式的不同。
晶体的宏观对称性就是晶体微观对称性的宏观表现。
晶系与对称的关系：七种晶系从宏观的对称操作来看，有旋转、反射、反演，这些构成的是32种点群。
而晶系必须符合平移操作（晶体对称定律的要求），结合平移我们限定了它有14种Bravais 格子。
晶体学基础必学知识点
晶体学基础必学知识点1. 晶体的定义：晶体是由原子、离子或分子以有序排列形成的固态物质。
2. 结晶学：研究晶体的结构、性质以及晶体的生长过程。
3. 晶体的晶格：晶体具有规则的周期性排列结构，可以用晶格来描述。
4. 晶胞：晶体中最小的重复单元，可以通过平移来产生整个晶体结构。
5. 晶体的晶系：根据晶胞的对称性，晶体可以分为七个晶系，分别为三斜晶系、单斜晶系、正交晶系、四方晶系、六方晶系、菱方晶系和立方晶系。
6. 晶体的晶面和晶向：晶体表面上的平面称为晶面，晶体内部的线段称为晶向。
7. 晶体的点阵和晶格常数：晶胞中的基本单位称为点阵，晶体的晶格常数是指晶格中基本单位的尺寸参数。
8. 布拉格方程：描述X射线或中子衍射中晶体衍射角度与晶格参数之间的关系。
9. 动态散射理论：描述X射线或中子与晶体中原子、离子或分子相互作用的过程。
10. 逆格子：描述晶格的倒数空间，逆格子与晶格的结构存在对偶关系。
11. 晶体缺陷：晶体中的缺陷包括点缺陷、线缺陷和面缺陷，晶体缺陷对晶体的性质和行为有重要影响。
12. 晶体生长：研究晶体从溶液或气体中的形成过程，包括核化、生长和晶面的形态演化等。
13. 晶体的结构表征方法：包括X射线衍射、中子衍射、电子衍射、扫描电子显微镜和透射电子显微镜等。
14. 晶体结构的解析和精修：通过衍射数据和晶体学软件对晶体的结构进行解析和精修，得到晶体的准确原子位置和结构参数。
15. 晶体的物理和化学性质：晶体的结构对其性质有重要影响，包括光学性质、电学性质、磁学性质和力学性质等。
16. 晶体学的应用：晶体学在材料科学、化学、生物学、地质学和矿物学等领域有广泛的应用，如材料合成、催化剂设计、药物研发和矿石勘探等。
晶体光学必备知识点
晶体光学必备知识点关键信息项1、晶体的定义与分类晶体的概念：＿___________________________晶体的分类方式：＿___________________________常见晶体类型：＿___________________________2、晶体的光学性质折射率：＿___________________________双折射现象：＿___________________________光轴：＿___________________________3、晶体的偏振特性偏振光的产生与类型：＿___________________________晶体对偏振光的作用：＿___________________________ 4、晶体的颜色与吸收晶体颜色的成因：＿___________________________吸收光谱：＿___________________________5、晶体的光学观测方法显微镜观测：＿___________________________偏光显微镜的使用：＿___________________________11 晶体的定义与分类晶体是由原子、离子或分子在空间按一定规律周期性地重复排列构成的固体物质。
其具有规则的几何外形、固定的熔点和各向异性等特征。
111 晶体的分类方式多种多样，常见的有以下几种：按化学成分分类，可分为无机晶体和有机晶体。
无机晶体如石英、氯化钠等，有机晶体如尿素、蔗糖等。
按晶体结构分类，可分为七大晶系，分别是立方晶系、四方晶系、正交晶系、单斜晶系、三斜晶系、六方晶系和菱方晶系。
按功能分类，可分为光学晶体、电学晶体、磁学晶体等。
112 常见的晶体类型包括：离子晶体，由正负离子通过离子键结合而成，具有较高的熔点和硬度，如氯化钠。
原子晶体，由原子通过共价键结合而成，具有很高的熔点和硬度，如金刚石。
分子晶体，由分子通过分子间作用力结合而成，熔点和硬度通常较低，如干冰。
晶体学复习
晶体学复习1 结晶学基础1.1概述1.2 第一章：晶体和非晶质体1.2.1 概念（格子、举例）晶体：具有格子构造的固体非晶质体：不具有格子构造的物质晶体的现代定义是：晶体是内部质点在三维空间成周期性重复排列的固体；或者说，晶体是具有格子构造的固体。
相应地，内部质点在三维空间成周期性重复排列的固体，便称为结晶质晶体的分布极为广泛，不只局限于矿物的范畴。
本质：在一切晶体中，组成它们的质点（原子、离子、离子团、分子等）在空间都是按格子构造的规律来分布的。
例如，石墨、石英、玻璃。
结论：一定化学成分的矿物，大部分都具有由原子规则排列的内部结构。
1.2.2 基本性质（6个）①最小内能：②稳定性：③对称性：④异向性：⑤均一性：⑥自限性：1.2.3 晶体的对称要素组合及规律(9个要素)对称指：物体相同部分的有规律重复.晶体的对称性也是相对的，而不对称则是绝对的。
晶体宏观对称要素：①对称中心（C）:假想的一个点，相应的操作是对于这个点的反伸。
其作用相当于一个照相机.结论：晶体如具有对称中心，晶体上的所有晶面，必定全都成对地呈反向平行的关系。
其对称中心必定位于几何中心。
符号为“C”标志：晶体上的所有晶面都两两平行，同形等大，方向相反。
②对称面：为一假想的面，对称操作为对此平面的反映。
方法：P 2P 3P…… 9PP与面、棱有着的关系：（1）对称面垂直并平分晶体上的晶面晶棱；（2）垂直晶面并平分它的两个晶棱的夹角；（3）包含晶棱③对称轴（L n）：为一假想的直线。
对称操作为绕此直线的旋转，可使晶体上的相同部分重复出现。
使相同部分重复出现的最小旋转角，称为基转角（α），旋转一周中，相同部分重复出现的次数，称为轴次（ n ）。
α、 n 之间的关系为：n = 360o/ α对称定律：晶体外形上可能出现的对称轴的轴次，不是任意的，只能是1 2 3 4 6 。
高次对称轴：轴次高于2的对称轴称（3、4、6）对称轴在晶体中可能出露的位置是：（1）两个相对晶面的连线；（2）两个相对晶棱中点的连线；（3）相对的两个角顶的连线（4）一个角顶与之相对的晶面之间的连线④旋转反身轴（L i n）旋转反伸轴是一假想直线和其上一点所构成的一种复合对称要素。
晶体学基础知识
不同晶面族的晶面间距也不相同。
面心立方和密堆六方的原子堆垛
原子的密排面的形式：在平面上每个原子与六个原子相切。
hcp中为(0001)面，
按 –ABABAB-方式堆垛。
Fcc中为{111}面，
按 –ABCABCABC-方式 堆垛。
平行六面体的三个棱长a、b、c和及其夹角α 、 β 、γ ，可决定平行六面体尺寸和形状，这六 个量亦称为点阵常数。
晶系
晶系——按点阵常数的特征对晶体的分类，可分为7大 晶系。
晶向与晶面指数
晶向——空间点阵中阵点列的方向。空间中任两阵点
的连线的方向，代表了晶体中原子列的方向。 晶向指数——表示晶向方位符号。
晶向与晶面指数
晶面：空间中不在一直线任三个阵点的构成的平面，
代表了晶体中原子列的方向。 晶面指数：表示晶面方位的符号。
立方系典型晶面
晶向与晶面指数
晶面指数与晶向指数关系：（hkl）⊥［hkl］
c
(111) [111]
c (110)
b a
a
b [110]
晶面间距
晶面间距：指相邻两个平行晶面之间的距离。 晶面间的距离越大，晶面上的原子排列越密集。 同一晶面族的原子排列方式相同，它们的晶面间的间
晶体学基础知识
晶格与晶胞
晶格
为了表达空间原子排列的几何规律，把粒子(原子或分 子)在空间的平衡位置作为阵点，人为地将阵点用一系 列相互平行的直线连接起来形成的空间格架称为晶格。
Байду номын сангаас 晶格与晶胞
晶胞——构成晶格的最基本单元，在三维空间 重复堆砌可构成整个空间点阵，通常为小的平 行六面体。
晶格与晶胞
1.晶体学基础
原子可在 顶角、线 、面、内 部。
晶胞参数：
平行六面体的三根棱长a、b、c及其夹角α、β、γ是表示它本 身的形状、大小的一组参数，称为点阵参数（晶胞参数）
依照晶胞参数之间的关系，所有晶体的空间点阵可以划分为7个晶系：
晶 系 立方晶系 四方晶系 a=b=c a=b≠c 格子常数特点 α=β=γ=90° α=β=γ=90°
晶面族指数：用晶面族中 某个最简便的晶面指数填 在大括号{ }内作为该晶面
族的指数。
晶面间距
一般是晶面指数数值越小，其面间距较大，并且其阵点密度较大
a
b
(100)
(110) (210) (4-10) (130)
晶面间距的计算
一组平行晶面的晶面间距dhkl与晶面指数和晶格常数a、b、c有下列关系：
（2）晶胞
ClNa+
空间格子+基元
●晶胞：是指晶体结构中的平行六面体单位，其形状大小与对应的 空间格子中的平行六面体一致。 ●晶胞：是描述晶体结构的基本组成单位。 ●晶胞：能够反映整个晶体结构特征的最小结构单元。
周期性、对称 性
晶胞的选取不是唯一的！
晶胞的选取原则： 1）充分表示出晶体的对称性 2）三条棱边尽量相等 3）夹角尽量为直角 4）单元体积尽可能小
晶体结构=空间点阵+结构基元
实际晶体——质点体积忽略——空间点阵——阵点连线——晶格（空间格子）
等同点： 各阵点的周围 环境完全相同， 周围阵点排布 及取向完全相 同。 A位臵
B位臵
空间格子有下列几种要素存在：
面网
平行六面体
晶面：可将晶体点阵在任意方向上分解 为相互平行的节点平面。 晶面族：对称性高的晶体中，不平行的 两组以上的晶面，它们的原子排列状况 是相同的，这些晶面构成一个晶面族。 晶向：也可将晶体点阵在任意方向上分 解为相互平行的节点直线组，质点等距 离的分布在直线上。 晶向族：晶体中原子排列周期相同的所 有晶向为一个晶向族。
晶体知识点总结
晶体知识点总结晶体是指在一定条件下，原子或分子按照一定的规律排列组合而成的具有一定几何形状和对称性的固体。
晶体学是研究晶体结构和性质的学科。
晶体学的发展为科学家们研究固体的结构和性质提供了重要的工具和方法。
本文将对晶体学的基本概念、晶体的结构和性质、晶体的生长和应用等方面进行总结。
一、晶体学的基本概念1. 晶体的定义和分类晶体是由一定数量的原子或分子根据一定的对称性和有序规律排列组合而成的固体。
晶体根据其对称性可以分为立方晶系、四方晶系、正交晶系、单斜晶系、三斜晶系和六角晶系六类。
根据其结构可以分为金属晶体、离子晶体、共价晶体和分子晶体等。
2. 晶体的对称性晶体的对称性是指晶体在不同的方向上具有相同的结构特征或具有对称性，可以分为旋转对称性和平移对称性。
旋转对称性是指晶体绕某个轴旋转一定角度后，其结构特征不发生变化。
平移对称性是指晶体在一定方向上进行平移后，其结构特征保持不变。
晶体的对称性是晶体学研究的重要内容之一。
3. 晶体的晶格晶体的晶格是指晶体中原子或分子排列的周期性和规律性。
晶体的晶格可以分为原子晶格和离子晶格。
原子晶格是指晶体中原子的排列规律，原子之间的距离和方向是有规律的。
离子晶格是指晶体中离子的排列规律。
晶格的性质直接影响着晶体的物理性质和化学性质。
4. 晶体的晶体结构晶体结构是指晶体中原子或分子排列的空间结构特征。
根据晶体结构的不同，晶体可以分为简单周期晶体和复杂周期晶体。
简单周期晶体是指晶体结构具有简单重复周期的特征，例如金属晶体。
复杂周期晶体是指晶体中存在复杂的周期结构，例如离子晶体和分子晶体。
二、晶体的结构和性质1. 基本结构单元晶体的基本结构单元是晶体中最小的重复单元，晶格中的原子或分子就是以基本结构单元为基础进行排列组合的。
不同类型的晶体具有不同的基本结构单元。
例如，金属晶体的基本结构单元是原子，而离子晶体的基本结构单元是离子。
2. 晶体的晶体形貌晶体的晶体形貌是指晶体在外形上的特征。