转盘轴承力矩载荷下的变形计算
轴承的计算公式.
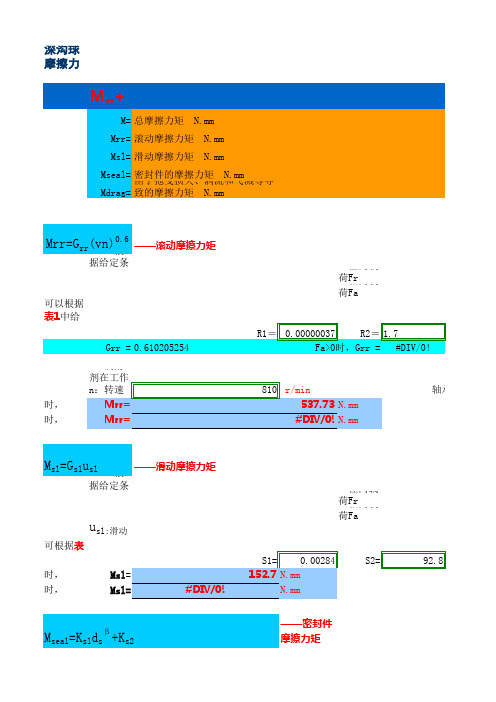
M=Mrr+Msl+Mseal+Mdrag
M= 总摩擦力矩 N.mm Mrr= 滚动摩擦力矩 N.mm Msl= 滑动摩擦力矩 N.mm Mseal= 密封件的摩擦力矩 N.mm Mdrag= 由于拖曳损失、涡流和飞溅等导致的摩擦力矩 N.mm
轴向载荷Fa
usl:滑动摩擦系数,当润滑条件良好,可取以下值:0.05(矿物油);0.04(合成油);0.1(以传动液润滑)
Gsl的值可根据表1中给出的公式计算,几何常数S则可从表2中找到
当Fa=0时, Msl=
S1= 0.00284
S2=
152.7 N.mm
92.8
当Fa>0时, Msl=
#DIV/0!
N.mm
Mseal=Ksldsβ +Ks2
——密封件摩擦力矩
Ksl:根据轴承类型而定的常数,查表3
ds:轴承肩部直径,
需轴承厂商提供:
β :根据轴承和密封圈类型而定的指数,表3可查:
Ks2:根据轴承和密封圈类型而定的常数,表3可查:
Mseal=
853.93 N.mm
0.028 98.3
Mdrag=Vm Kball dm5 n2
v:润滑剂在工作温度的运动粘度,对于脂润滑,则为基础油的粘度
n:转速
810 r/min
当Fa=0时, Mrr=
537.73 N.mm
当Fa>0时, Mrr=
#DIV/0! N.mm
轴承额定动载荷
Msl=Gslusl
——滑动摩擦力矩
Байду номын сангаас
Gsl:根据给定条件计算该变量:轴承平均直径 dm=0.5(D+d)
滚动轴承当量动载荷的计算

17
0.
47
0.
强烈冲击
1.8~3.0
破碎机、轧钢机等
45
1.
正装:两轴承窄边相对,也称“面对面”安装。
求轴承的内部轴向力Fs1和Fs2 。பைடு நூலகம்
28
0.
56 0.
计算轴向载荷时,要综合考虑内部轴向力和外加轴向载荷的作用。
滚滚动动轴轴承承当当量量动动载载荷荷的的计计算算
(2)径向载荷系数X、轴向载荷系数Y
e是Fa对当量动载荷影
响程度的参数。
查表时,先按Fa/C0的值 查得对应的e,再根据 Fa/Fr>e或Fa/Fr≤e来确定 X、Y值。
轴承类 型
Fa/C0
判别值 e
0.014
0.028
深沟球
0.056 0.084
轴承(6 0.11
类)
0.17 0.28
0.42
0.56
0.19 0.22 0.26 0.28 0.30 0.34 0.38 0.42 0.44
滚动轴承当量动载荷的计算
二、滚动轴承当量动载荷的计算
1.当量动载荷的计算公式
P=KP(XFr+YFa)
KP ──载荷系数,查表; Fr ──轴承所承受的径向载荷,N; Fa ──轴承所承受的轴向载荷,N; X、Y──径向载荷系数、轴向载荷系数,查表。
47
0.
滚动轴承当量动载荷的计算 滚动轴承的当量动载荷是由轴承实际所受载荷转换得到的与基本额定动载荷的确定条件及性质相同的假想载荷,用“P”表示。
2.如何查取径向载荷系数X 、轴向载荷系数Y ? 3.如何计算当量动载荷P ?
为使内部轴向力得到平衡,轴承要成对使用。
KP ──载荷系数,查表;
轴承的摩擦系数及摩擦力矩计算04.03

轴承的摩擦系数
为便于与滑动轴承比较,滚动轴承的摩擦力矩可按轴承内径由下式计算:M=uPd/2
这里,
M:摩擦力矩,
u:摩擦系数,表1
P:轴承负荷,N
d:轴承公称内径,mm
摩擦系数u受轴承型式、轴承负荷、转速、润滑方式等的影响较大,一般条件下稳定旋转时的摩擦系数参考值如表1所示。
对于滑动轴承,一般u=,有时也达。
各类轴承的摩擦系数u
轴承型式摩擦系数u
深沟球轴承
角接触球轴承
调心球轴承
圆柱滚子轴承
满装型滚针轴承
带保持架滚针轴承
圆锥滚子轴承
调心滚子轴承
推力球轴承
推力调心滚子轴承由轴承摩擦引起的轴承功率损失可用以下计算公式得出
NR = 1,05 x 10-4 Mn
其中
NR = 功率损失,W
M = 轴承的总摩擦力矩,Nmm
n = 转速,r/min
电机扭矩公式:T=9550*P/n
T:电机转矩
P:电机功率KW
n:转速r/min。
转盘轴承载荷能力计算小程序

30 输入 1000 输入 sin45 89.504046
轴向载荷 径向载荷 倾覆力矩
2847.5712 2847.5712
355.9464
三排滚子组合 转盘轴承的载 荷 主推力滚珠直 径 滚珠长度 回转中心 滚珠个数
50 输入
49.5 输入 3150 输入 164.93358
副推力滚珠直 径 滚珠长度 回转中心 滚珠个数
40 输入
40 输入 3125 输入 204.5307292
主推力轴向载 荷
主径向载荷
400454.61 KN 88173.492 KN
副推力轴 向载荷 副径向载 荷
321031.4325 KN 70685.82 KN
主倾覆力矩
157679 KN.m
总轴向载荷 总径向载荷 总倾覆力矩
721486.04 KN 158859.31 KN 283081.91 KN.m
18 输入 3000 输入 436.3322
球珠组合转盘 轴承的载荷
滚珠直径 滚珠长度 回转中心 滚珠个数
50 49.5 4500 241.66092
轴向载荷 径向载荷 倾覆力矩
483926 KN 21356.784 KN 53231825402.9033 KN.m
径向滚子 直径 滚珠长度 回转中心 滚珠个数
18 输入
转盘 轴承 承载 能力 载荷 计算
承载能力的载 荷计算 四点接触球转 盘轴承载荷 钢球直径 回转中心 接触角 钢球数量
25 输入 1000 输入 sin45 107.40485
轴向载荷 径向载荷 倾覆力矩
2372.976 KN 2372.976 KN
296.622 KN.m
**黄色为必须 输入数值
转盘轴承承载能力计算方法的研究

sin α ϕm = cos α ϕm =
A × sin α 0 + δ a + Ri × θ × cos ϕ S mϕ A × cos α 0 + δ r × cos ϕ S mϕ
辅推力滚道钢球的接触角 α ϕs 变为:
α ϕs = cos α ϕs =
A × sin α 0 − δ a − Ri × θ × cos ϕ S sϕ A × cos α 0 + δ r × cos ϕ S sϕ
n ⎡ ⎤ ⎛ ⎞ D ⎢ ⎥ ε 2 M = M 1 + M 2 = Pmax × sin α × Z × × ⎢ J M (ε 1 ) + ⎜ J M (ε 2 )⎥ ⎟ ⎜ ⎟ 2 ⎢ ⎥ ⎝ ε1 ⎠ ⎣ ⎦ D = Pmax 1 × sin α × Z × × J M (ε 1 , ε 2 ) 2
ϕ = ±ϕ 0
P (ϕ ) ×
ϕ = ±ϕ 0
∫
0
n ⎤ ⎤ ⎡ 1 ( ) − − 1 1 cos ϕ ⎥ cos ϕdϕ ⎥ ⎢ ⎥ ⎦ ⎣ 2ε 1 ⎦
同理,辅推力滚道一侧的合力矩 M2 为:
M 2 = Pmax 2 × sin α × Z ×
D × J M (ε 2 ) 2
M1 与 M2 的合力矩应与外加的倾覆力矩 M 相平衡:
动体上的最大载荷 Pmax,根据 Hertz 接触理论可以求出滚动体的最大接触应力。 对于球轴承,最大接触应力 σ max =
858 n a × nb
3
(∑ ρ )
2
× Pmax
max
对于滚子轴承,最大接触应力 σ max = 190.6 ×
∑ρ×P
l
转化成接触应力 转盘轴承的静安全系数 f s 是指其额定静载荷与当量静载荷的比值。
转盘轴承承载能力及额定寿命的计算方法

摘要 :以 Hertz弹性接触理论和 Lundberg - Palmgren的疲劳寿命理论为基础 ,结合转盘轴承特殊的结构形式和 受载条件 ,导出了接触强度校核及寿命估算的理论公式以及动 、静承载能力曲线的绘制方法 ,并绘制了动 、静承 载能力曲线 ,为转盘轴承的设计和选型提供了可靠的理论依据 。 关键词 :滚动轴承 ;转盘轴承 ;承载 ;接触强度 ;寿命 中图分类号 : TH133. 33 文献标志码 : B 文章编号 : 1000 - 3762 (2008) 02 - 0007 - 03
S
L10
式中 : S为失效概率 ;点接触 e = 10 /9,线接触 e =
9 /8; LS 为失效概率为 S 时的寿命 ; L10 为失效概率 为 0. 1时的寿命 。
下列各式中下标 i, e分别表示内 、外圈 ;下标 b
表示整个轴承 ;下标 1, 2分别代表主 、辅推力滚道 。
δ Q <m
= Knm
1. 5 <m
(1)
辅推力沟道上钢球的载荷
δ Q < s
= Kns
1. 5 <s
(2)
内圈发生位移后 , 不同角位置 < 处钢球的接
触角 α<m ,α<s也会发生改变 , 主推力沟道钢球的接
触角 α<m变为
sinα<m
= A sinα0
+δa + R iθcos<
Sm <
co sα<m
2f - 1
( 1 ±γ) 1 /3
Dw Dpw
0. 3
·
F (Dw ) Z - 1 /3
对于滚子轴承
QC =B
( 1 γ) 29 /27 ( 1 ±γ) 1 /4
转盘轴承力矩载荷下的变形计算

转盘轴承力矩载荷下的变形计算摘要:通过分析四点接触转盘轴承受倾覆力矩时的套圈位移与接触变形、轴承接触角变化的关系,得出转盘轴承倾覆力矩载荷下套圈倾角变形计算公式,为转盘轴承力矩载荷下变形提供了精确的计算方法。
最后用所得的力矩计算公式进行实例计算,并做出力矩-变形曲线。
关键词:四点接触;转盘轴承;力矩载荷;变形计算转盘轴承主要用在起重、建筑工程等大型机械设备中,国内也对其进行了较多的研究。
转盘轴承主要承受的是轴向力和倾覆力矩,而在很多情况下,倾覆力矩是轴承的主要载荷。
在力矩作用下,轴承的转角变形将很大的影响着整个机械的刚度和工作精度等性能。
所以有必要对转盘轴承力矩载荷承载-变形关系进行分析。
以往的转盘轴承在力矩作用下变形计算公式复杂,且计算过程中有时难以收敛。
这里对四点接触转盘轴承承载时变形的几何关系进行分析,得到轴承转角位移与接触变形的关系计算式。
在此基础上,推导出转盘轴承的倾覆力矩与变形计算式。
一、转盘轴承的受力变形四点接触转盘轴承受倾覆力矩时,轴承内、外套圈产生相对倾角,设外圈保持固定不动。
忽略倾角引起的径向位移,则受力后的处在位置角i处滚珠(0≤<)由于转角而引起的轴向位移为:ai= cosi (1)式中:Dw——滚珠中心圆直径(mm)。
转盘轴承的套圈位移和滚珠接触变形如图1所示。
在外沟道曲率中心Oe建立坐标系,变形前的内沟道中心为Oi,坐标分别为(x,y)。
变形后的内沟道中心Oii,坐标分别为(xi,yi)。
A和Ai分别是变形前后的沟道中心距。
则变形前内外沟道中心距:A=re+ri-Dw(2)式中:ri、re——内、外沟道曲率半径(mm);Dw——滚珠直径(mm)。
变形前内沟道曲率中心Oi的坐标(x,y):y=Acos(3)式中:——初始接触角x=Asin (4)转盘轴承受矩载荷引起内外套圈位移后,位置角i处内、外圈沟道曲率中心距为:Ai=re+ri-(Dw-i)(5)式中:i——内外套圈和滚珠接触变形总量(mm)。
回转转盘轴承承载计算实例详解

回转转盘轴承承载计算实例详解假设我们需要设计一个能够承受1000吨荷载的回转转盘,直径为10米。
我们将使用滚子转盘轴承来支撑和传递荷载。
下面是计算的详细步骤:第一步:确定所使用的轴承类型和参数根据设计要求,我们选择了滚子转盘轴承。
根据轴承的类型和尺寸,我们可以得到一些必要的参数,如滚子直径、滚子数量、接触角、滚子材料等信息。
第二步:计算滚子的等效负荷根据滚子的材料和几何参数,我们可以得到滚子的基本动态载荷额定值C。
然后,根据荷载特性,在垂直和水平方向上计算滚子的等效负荷。
对于水平方向上的荷载,我们需要考虑滚子对称排列的情况。
第三步:计算滚子转盘的等效负荷滚子转盘的等效负荷可以通过将滚子的等效负荷乘以滚子数量得到。
在纵向和横向方向上都要进行计算,以考虑荷载的不同作用方向。
第四步:根据滚子转盘的等效负荷计算负载接触应力根据滚子转盘的等效负荷和轴承的几何参数,可以计算滚子转盘的接触应力。
第五步:根据滚子转盘的接触应力判断轮廓变形情况根据滚子转盘的接触应力和材料弹性参数,可以计算出轮廓变形。
如果轮廓变形过大,会影响到传递荷载的能力和轴承的寿命。
第六步:根据回转转盘的尺寸和材料回转转盘的自身重量对轴承的承载能力也会造成一定的影响。
根据回转转盘的尺寸和材料密度,可以计算出其自身重量。
第七步:根据合成荷载计算轴承的等效动态负荷根据回转转盘的荷载和自身重量,可以计算出合成荷载。
根据荷载特性和标准系数,可以将合成荷载转化为等效动态负荷。
第八步:检查轴承的额定动态负荷是否满足要求根据轴承的额定动态负荷额定值和计算得到的等效动态负荷,可以判断轴承是否能够满足设计要求。
如果额定动态负荷大于等效动态负荷,则说明轴承能够满足要求。
总结:通过以上的步骤,我们可以根据回转转盘的设计要求和参数,计算出所使用的滚子转盘轴承的承载能力和使用寿命。
同时,我们还可以对轴承的安全性能进行评估和优化,以提高回转转盘的使用寿命和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
转盘轴承力矩载荷下的变形计算
摘要:通过分析四点接触转盘轴承受倾覆力矩时的套圈位移与接触变形、轴承接触角变化的关系,得出转盘轴承倾覆力矩载荷下套圈倾角变形计算公式,为转盘轴承力矩载荷下变形提供了精确的计算方法。
最后用所得的力矩计算公式进行实例计算,并做出力矩-变形曲线。
关键词:四点接触;转盘轴承;力矩载荷;变形计算
转盘轴承主要用在起重、建筑工程等大型机械设备中,国内也对其进行了较多的研究。
转盘轴承主要承受的是轴向力和倾覆力矩,而在很多情况下,倾覆力矩是轴承的主要载荷。
在力矩作用下,轴承的转角变形将很大的影响着整个机械的刚度和工作精度等性能。
所以有必要对转盘轴承力矩载荷承载-变形关系进行分析。
以往的转盘轴承在力矩作用下变形计算公式复杂,且计算过程中有时难以收敛。
这里对四点接触转盘轴承承载时变形的几何关系进行分析,得到轴承转角位移与接触变形的关系计算式。
在此基础上,推导出转盘轴承的倾覆力矩与变形计算式。
一、转盘轴承的受力变形
四点接触转盘轴承受倾覆力矩时,轴承内、外套圈产生相对倾角,设外圈保持固定不动。
忽略倾角引起的径向位移,则受力后的处在位置角i处滚珠(0≤<)由于转角而引起的轴向位移为:
ai= cosi (1)
式中:Dw——滚珠中心圆直径(mm)。
转盘轴承的套圈位移和滚珠接触变形如图1所示。
在外沟道曲率中心Oe建立坐标系,变形前的内沟道中心为Oi,坐标分别为(x,y)。
变形后的内沟道中心Oii,坐标分别为(xi,yi)。
A和Ai分别是变形前后的沟道中心距。
则变形前内外沟道中心距:
A=re+ri-Dw(2)
式中:ri、re——内、外沟道曲率半径(mm);
Dw——滚珠直径(mm)。
变形前内沟道曲率中心Oi的坐标(x,y):
y=Acos(3)
式中:——初始接触角
x=Asin (4)
转盘轴承受矩载荷引起内外套圈位移后,位置角i处内、外圈沟道曲率中心距为:
Ai=re+ri-(Dw-i)(5)
式中:i——内外套圈和滚珠接触变形总量(mm)。
套圈移动后内沟道曲率中心Oii坐标(xi,yi):
yi=Aicosi (6)
xi=Aisini(7)
式中:i ——套圈位移后,位置角i处的接触角。
即有Ai=(8)
轴承位移前后内沟道曲率中心的坐标关系:
xi=x+ai(9)
yi=y(10)
由式(3)、式(6)、式(8)、式(9)和式(10)可以得到转盘轴承受力位移后的接触角:
cosi =(11)
将式(8)、式(9)和式(10)代入式(5)中得出转盘轴承位移ai和滚珠接触弹性变形i关系式:
i=Dw -(re+ri-)(12)
二、转盘轴承倾覆力矩的计算
四点接触转盘轴承某滚珠上的接触受力由点接触的受力变形关系计算公式 : Qi=Ki i3/2 (13)
式中:Qi——滚珠和套圈接触受力(N);
i——滚子与内外套圈接触处的总的弹性变形量(mm);
Ki——系数。
对于滚珠与内外套圈接触的系数:
Ki=1/(2.97×10-4[(∑ii)1/3+(∑ie)1/3])3/2
式中,、是滚珠与内、外圈点接触相关的系数,可根据文献[7]计算内、外沟道主曲率函数F(ii)、F(ie)进行查表得到。
内、外沟道主曲率和∑ii (ie)=×(2+-),参数i=,fi、fe分别为内、外沟道沟曲率半径系数。
主曲率和以内圈接触“±”取“-”,以外圈接触计算“±”取“+”。
在转盘轴承承受倾覆力矩时,内外圈产生相对倾角,使每个滚子的受力大小各不相同。
由图2可知,每个滚珠上由接触受力产生的力矩
将式(13)带入上式,得到:
Mi=Kii3/2sinicosi(15)
根据四点接触转盘轴承在力矩载荷下,外载荷与内部滚子负荷平衡的条件,轴承受到总力矩
M=Mi=Kii3/2sinicosi(16)
式中,sini由式(11)得sini=(1-()2)1/2。
将式(1)、(12)、(13)带入式(16)中,得
M=Ki(Dw-(re+ri-((x+cosi)2+y2)1/2))3/2 •(1-)1/2cosi(17)
上式可知,倾覆力矩M是倾角的非线性函数,可经过计算机非线性数值计算方法反复进行迭代求解。
三、实例分析
某四点接触转盘轴承,结构参数:Dw=40,Dw=1900,初始接触角a=50°,滚珠数Z=120,内、外沟曲率半径系数fi(e)==0.53。
试分析其倾覆力矩M与倾角的关系曲线。
该轴承初始中心距由式(1)得:
A=re+ri-Dw =2.4mm
初始内沟道曲率中心Oi的坐标(x,y)由式(2)、式(3)得:
y=Acos=2.4cos50°1.54269mm
x=Acos=2.4sin50°1.83851mm
滚珠受力过程中接触角增加使系数Ki略有增加。
经过计算表明,系数Ki在接触角为80°比接触角为50°大0.4%。
因此,简便起见,系数Ki按初始接触角50°计算。
具体计算结果如下:
ri===0.01353237
∑ii=0.0535160889
∑ie=0.053506931
F(ii)=0.894230362
查表并插值计算得=0.689077493
(ie)=0.891485912
查表并插值计算得=0.692919723
则Ki=1/(2.97×10-4[(∑ii)1/3+(∑ie)1/3])3/2
≈570954
将已知相关数据带入式(17)进行计算,得:
M=570954(Dw-(re+ri-((x+cosi)2+y2)1/2))3/2 •(1-)1/2cosi
用MATLAB对上式进行牛顿法非线性数值计算。
经过程序运算后,倾覆力矩M与轴承倾角变形的关系曲线如图3所示:
四、结语
四点接触转盘轴承力矩载荷下倾角变形对机械的工作性能有很大的影响。
通过
对转盘轴承承载时变形的几何关系进行分析,推导出转盘轴承的倾覆力矩与变形关
系计算式。
并进行了实例计算,绘制出力矩-变形曲线。
整个计算过程简便,为四点接触转盘轴承力矩载荷下变形分析提供了理论依据。
这将有助于四点接触转盘轴承
的设计、使用以及刚度、振动的分析。
参考文献
[1]徐立民,陈卓.回转支承[M].合肥:安徽科学技术出版社,1988.
[2]杜睿,吴志军.单排球式回转支承的承载能力分析[J].机械设计与制造,2006,(9).
[3]苏立樾,苏健.转盘轴承静载荷承载曲线的创建[J].轴承,2004,(6).
[4]汪洪,陈原.转盘轴承承载能力及额定寿命的计算方法[J].轴承,2008,(2).
[5]郑兰疆,李彦,赵武,等.大型回转轴承的承载性能分析[J].机械设计与研
究,2008,(4).
[6]Harris T A.Rolling Bearing Analysis(Third Edition)[M].New York: John Wilcy and Sons.Inc.,1991.
[7]万长森.滚动轴承的分析方法[M].北京:机械工业出版社,1987.
[8]常巍,谢光军,黄朝峰.MATLABR2007基础与提高[M].北京:电子工业出版社,2007.。
