浙江省历年高考立体几何大题总汇题目及答案

合集下载

2010-2014五年高考(浙江卷)文科数学立体几何

2010-2014五年高考（浙江卷）文科数学立体几何1．（2010浙江文8）若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（A）3523cm3（B）3203cm3（C）2243cm3（D）1603cm32．（2011浙江文7）几何体的三视图如图所示，则这个几何体的直观图可以是3．（2012浙江文3）已知某三棱锥的三视图（单位：cm）如图所示，则该三棱锥的体积是（A）1 cm3（B）2 cm3（C）3 cm3（D）6 cm34．（2013浙江文5）已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（A）108cm3（B）100 cm3（C）92cm3（D）84cm35．(2014浙江文3)某几何体的三视图(单位：cm)如图所示，则该几何体的体积是( )．（A ）72 cm 3 （B ）90 cm 3（C ）108 cm 3 （D ）138cm 36．（2011浙江文4）若直线l 不平行于平面a ，且l a ∉，则(A) a 内存在直线与异面 (B) a 内不存在与l 平行的直线(C) a 内存在唯一的直线与l 平行 (D) a 内的直线与l 都相交7．（2012浙江文5）设l 是直线，,αβ是两个不同的平面(A)若//,//l l αβ，则//αβ (B)若//,l l αβ⊥，则αβ⊥(C)若,l αβα⊥⊥，则l β⊥(D)若,//l αβα⊥，则l β⊥ 8．（2013浙江文4）设m 、n 是两条不同的直线，α、β是两个不同的平面，(A)若m ∥α，n ∥α,则m ∥n (B)若m ∥α，m ∥β,则α∥β(C)若m ∥n ，m ⊥α,则n ⊥α (D)若m ∥α，α⊥β,则m ⊥β9．(2014浙江文6)设m ，n 是两条不同的直线，α，β是两个不同的平面．( )．(A)若m ⊥n ，n ∥α，则m ⊥α (B)若m ∥β，β⊥α，则m ⊥α(C)若m ⊥β，n ⊥β，n ⊥α，则m ⊥α (D)若m ⊥n ，n ⊥β，β⊥α，则m ⊥α10．（2010浙江文20）如图，在平行四边形ABCD 中，AB=2BC ，∠ABC=120°。

近五年浙江数学高考立体几何考题

近五年##数学高考立体几何考题[2018年]3．某几何体的三视图如图所示〔单位：cm〕,则该几何体的体积〔单位：cm3〕是A．2B．4C．6D．8⊄⊂6．已知平面α,直线m,n满足mα,nα,则"m∥n〞是"m∥α〞的A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件8．已知四棱锥S−ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点〔不含端点〕,设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S−AB−C的平面角为θ3,则A．θ1≤θ2≤θ3B．θ3≤θ2≤θ1C．θ1≤θ3≤θ2D．θ2≤θ3≤θ119．〔本题满分15分〕如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2．〔Ⅰ〕证明：AB1⊥平面A1B1C1；〔Ⅱ〕求直线AC1与平面ABB1所成的角的正弦值．[2017]3．某几何体的三视图如图所示〔单位：cm〕,则该几何体的体积〔单位：cm2〕是〔〕A．+1B．+3C．+1D．+39．〔5分〕如图,已知正四面体D﹣ABC〔所有棱长均相等的三棱锥〕,P、Q、R 分别为AB、BC、CA上的点,AP=PB,==2,分别记二面角D﹣PR﹣Q,D﹣PQ ﹣R,D﹣QR﹣P的平面角为α、β、γ,则〔〕A．γ＜α＜βB．α＜γ＜β C．α＜β＜γD．β＜γ＜α19．〔15分〕如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点．〔Ⅰ〕证明：CE∥平面PAB；〔Ⅱ〕求直线CE与平面PBC所成角的正弦值．[2016]文科2．已知互相垂直的平面α,β交于直线l,若直线m,n满足m∥α,n⊥β,则〔〕A ．m ∥lB ．m ∥nC ．n ⊥lD ．m ⊥n9．某几何体的三视图如图所示〔单位：cm 〕,则该几何体的表面积是cm 2,体积是cm 3．14．如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=,∠ADC=90°,沿直线AC 将△ACD 翻折成△ACD ′,直线AC 与BD ′所成角的余弦的最大值是．18．如图,在三棱台ABC ﹣DEF 中,平面BCFE ⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3．〔Ⅰ〕求证：BF ⊥平面ACFD ；〔Ⅱ〕求直线BD 与平面ACFD 所成角的余弦值．[2016]理科2．已知互相垂直的平面α,β交于直线l,若直线m,n 满足m ∥α,n ⊥β,则〔〕A ．m ∥lB ．m ∥nC ．n ⊥lD ．m ⊥n11．某几何体的三视图如图所示〔单位：cm 〕,则该几何体的表面积是cm 2,体积是cm 3．14．如图,在△ABC 中,AB=BC=2,∠ABC=120°．若平面ABC 外的点P 和线段AC 上的点D,满足PD=DA,PB=BA,则四面体PBCD 的体积的最大值是．17．如图,在三棱台ABC ﹣DEF 中,已知平面BCFE ⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,〔Ⅰ〕求证：BF ⊥平面ACFD ；〔Ⅱ〕求二面角B ﹣AD ﹣F 的余弦值．[2015]文科2、某几何体的三视图如图所示〔单位：cm 〕,则该几何体的体积是A.8 cm 3B.12 cm 3C.323cm 3D.403cm 34、设α,β是两个不同的平面,l ,m 是两条不同的直线,且l ⊂α,m ⊂β.A.若l ⊥β,则α⊥βB. 若α⊥β,则l ⊥mC. 若l ∥β,则α∥βD. 若α∥β,则l ∥m7、如图,斜线段AB 与平面α所成的角为60°,B 为斜足,平面上的动点P 满足∠PAB=30°,则点P 的轨迹是A.直线B.抛物线C.椭圆D.双曲线的一支18、〔本题满分15分〕如图,在三棱柱ABC －A 1B 1C 1中,∠BAC=90°,AB=AC=2,A 1A=4,A 1在底面ABC 的射影为BC 的中点,D 是B 1C 1的中点.〔Ⅰ〕证明：A 1D ⊥平面A 1BC ；〔Ⅱ〕求直线A 1B 和平面BB 1C 1C 所成的角的正弦值.[2015]理科2、某几何体的三视图如图所示〔单位：cm 〕,则该几何体的体积是A.8 cm 3B.12 cm 3C.323cm 3D.403cm 38．如图,已知△ABC,D 是AB 的中点,沿直线CD 将△ACD 折成△A ′CD,所成二面角A ′﹣CD ﹣B 的平面角为α,则〔〕A ． ∠A ′DB ≤α B ． ∠A ′DB ≥αC ． ∠A ′CB ≤αD ．∠A ′CB ≥α 13．如图,三棱锥A ﹣BCD 中,AB=AC=BD=CD=3,AD=BC=2,点M,N 分别是AD,BC 的中点,则异面直线AN,CM 所成的角的余弦值是．17．〔15分〕〔2015•##〕如图,在三棱柱ABC ﹣A 1B 1C 1中,∠BAC=90°,AB=AC=2,A 1A=4,A 1在底面ABC 的射影为BC 的中点,D 是B 1C 1的中点．〔1〕证明：A 1D ⊥平面A 1BC ；〔2〕求二面角A 1﹣BD ﹣B 1的平面角的余弦值．[2014]文科3. 某几何体的三视图〔单位：cm 〕如图所示,则该几何体的体积是〔〕A. 372cmB. 390cmC. 3108cmD. 3138cm6.设m 、n 是两条不同的直线,α、β是两个不同的平面,则〔〕A.若n m ⊥,α//n ,则α⊥mB.若β//m ,αβ⊥,则α⊥mC.若β⊥m ,β⊥n ,α⊥n ,则α⊥mD.若n m ⊥,β⊥n ,αβ⊥,则α⊥m20、如图,在四棱锥BCDE A -中,平面ABC ⊥平面BCDE ；90CDE BED ∠=∠=︒,2AB CD ==,1DE BE ==,AC =〔1〕证明：AC ⊥平面BCDE ；〔2〕求直线AE 与平面ABC 所成的角的正切值.[2014]理科〔3〕某几何体的三视图〔单位：cm 〕如图所示,则此几何体的表面积是A. 902cmB. 1292cmC. 1322cmD. 1382cm20. 如图,在四棱锥BCDE A -中,平面⊥ABC 平面======∠=∠AC BE DE CD AB BED CDE BCDE ,1,2,90,02.（1）证明：⊥DE 平面ACD ;（2）求二面角E AD B --的大小DEB C。

浙江省历年高考立体几何大题总汇(题目与答案)

1.（本题满分15 分）如图，平面PAC ⊥平面ABC ，ABC 是以AC 为斜边的等腰直角三角形。

E,F ,O分别为PA, PB, PC 的中点，AC 16, PA PC 10 。

（I ）设 C 是OC 的中点，证明：PC // 平面BOE ；（II ）证明：在ABO 内存在一点M ，使FM ⊥平面BOE ，并求点M 到OA , OB 的距离。

zyx2.如图，在棱长为 1 的正方体ABCD －A1B1C1D1 中，P 是侧棱CC1 上的一点，CP=m ，（Ⅰ）试确定m，使得直线AP 与平面BDB 1D1 所成角的正切值为 3 2 ；（Ⅱ）在线段A1C1 上是否存在一个定点Q，使得对任意的m，D1Q 在平面APD 1 上的射影垂直于AP，并证明你的结论。

3. 如图甲，△ABC 是边长为 6 的等边三角形，E，D 分别为AB 、AC 靠近B、C 的三等分点，点G 为BC 边的中点．线段AG 交线段ED 于F 点，将△AED 沿ED 翻折，使平面AED ⊥平面BCDE ，连接AB 、AC 、AG 形成如图乙所示的几何体。

（I）求证BC⊥平面AFG ；（II）求二面角B－AE －D 的余弦值．.4 在如图所示的几何体中，EA 平面ABC，DB 平面ABC，AC BC ，AC BC BD 2AE ，M是AB的中点．（1）求证：CM EM ；D（2）求CM与平面CDE所成的角ECAMB4.如图，矩形ABCD 和梯形BEFC 所在平面互相垂直，BE ∥CF ，BCF CEF ，AD 3，E F 2．90D（Ⅰ）求证：AE ∥平面DCF ；AC （Ⅱ）当AB 的长为何值时，二面角 A EF C 的大小为60 ？BF E（第18 题）25.如图，在矩形ABCD 中，点E，F 分别在线段AB ，AD 上，AE=EB=AF= FD 4.沿直3线EF 将AEF 翻折成A' EF , 使平面A' EF 平面BEF.（I）求二面角A' FD C 的余弦值；（II ）点M ，N 分别在线段FD，BC 上，若沿直线MN 将四边形MNCD 向上翻折，使 C与A' 重合，求线段FM 的长.6.如图，在三棱锥P-ABC 中，AB ＝AC，D 为BC 的中点，PO⊥平面ABC ，垂足O 落在线段AD 上，已知BC＝8，PO＝4，AO＝3，OD＝2（Ⅰ）证明：AP⊥BC；（Ⅱ）在线段AP 上是否存在点M ，使得二面角A-MC-B 为直二面角？若存在，求出AM 的长；若不存在，请说明理由。

(浙江版)高考数学分项汇编专题10立体几何(含解析)理

第十章立体几何一．基础题组1. 【2014年.浙江卷.理3】某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是 A. 902cm B. 1292cm C. 1322cm D. 1382cm【答案】：Ｄ2. 【2013年.浙江卷.理12】若某几何体的三视图(单位：cm)如图所示，则此几何体的体积等于__________cm 3.【答案】：243. 【2012年.浙江卷.理10】已知矩形ABCD，AB＝1，BC ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中，( )A．存在某个位置，使得直线AC与直线BD垂直B．存在某个位置，使得直线AB与直线CD垂直C．存在某个位置，使得直线AD与直线BC垂直D．对任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直【答案】B4. 【2012年.浙江卷.理11】已知某三棱锥的三视图(单位：cm)如图所示，则该三棱锥的体积等于__________ cm3．【答案】15. 【2011年.浙江卷.理3】若某几何体的三视图如图所示，则这个几何体的直观图可以是【答案】 D【解析】：A，B与正视图不符，C与俯视图不符，故选D6. 【2011年.浙江卷.理4】下列命题中错误的是（A ）如果平面αβ⊥平面，那么平面α内一定存在直线平行于平面β （B ）如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β （C ）如果平面αγ⊥平面，平面βγ⊥平面，=l αβ⋂，那么l γ⊥平面（D ）如果平面αβ⊥平面，那么平面α内所有直线都垂直于平面β 【答案】 D7. 【2009年.浙江卷.理5】在三棱柱111ABC A B C -中，各棱长相等，侧掕垂直于底面，点D 是侧面11BB C C 的中心，则AD 与平面11BB C C 所成角的大小是 ( )A ．30B ．45C ．60D ．90【答案】：C8. 【2009年.浙江卷.理12】若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是3cm ．【答案】：189. 【2008年.浙江卷.理14】如图，已知球O 点面上四点A 、B 、C 、D ，DA ⊥平面ABC ，AB ⊥BC ，DA=AB=BC=3，则球O 点体积等于【答案】9π210. 【2007年.浙江卷.理6】若P 是两条异面直线,l m 外的任意一点，则（A ）过点P 有且仅有一条直线与,l m 都平行（B ）过点P 有且仅有一条直线与,l m 都垂直（C ）过点P 有且仅有一条直线与,l m 都相交（D ）过点P 有且仅有一条直线与,l m 都异面【答案】B选项D 不正确，因为过点P 与,l m 都异面的直线有数条. 故选B.11. 【2005年.浙江卷.理6】设α、β 为两个不同的平面，l 、m 为两条不同的直线，且l ⊂α，m ⊂β，有如下的两个命题：①若α∥β，则l ∥m ；②若l ⊥m ，则α⊥β．那么(A) ①是真命题，②是假命题 (B) ①是假命题，②是真命题 (C) ①②都是真命题 (D) ①②都是假命题【答案】D12. 【2005年.浙江卷.理12】设M 、N 是直角梯形ABCD 两腰的中点，DE ⊥AB 于E (如图)．现将△ADE 沿DE 折起，使二面角A －DE －B 为45°，此时点A 在平面BCDE 内的射影恰为点B ，则M 、N 的连线与AE 所成角的大小等于_________．【答案】90° 【解析】：13. 【2015高考浙江，理2】某几何体的三视图如图所示（单位：cm ），则该几何体的体积是（） A.38cm B. 312cm C.3323cm D. 3403cm【答案】C.14. 【2015高考浙江，理13】如图，三棱锥A BCD -中，3,2AB AC BD CD AD BC ======，点,M N 分别是,AD BC 的中点，则异面直线AN ，CM 所成的角的余弦值是．【答案】87.15. 【2015高考浙江，理17】如图，在三棱柱111ABC A B C --中，90BAC ∠=，2AB AC ==，14A A =，1A 在底面ABC 的射影为BC 的中点，D 为11B C 的中点.（1）证明：1A D ⊥平面1A B C ；（2）求二面角1A -BD-1B 的平面角的余弦值.【答案】（1）详见解析；（2）18-.【考点定位】1.线面垂直的判定与性质；2.二面角的求解16.二．能力题组1. 【2013年.浙江卷.理10】在空间中，过点A作平面π的垂线，垂足为B，记B＝fπ(A)．设α，β是两个不同的平面，对空间任意一点P，Q1＝fβ[fα(P)]，Q2＝fα[fβ(P)]，恒有PQ1＝PQ2，则( )．A．平面α与平面β垂直B．平面α与平面β所成的(锐)二面角为45°C．平面α与平面β平行D．平面α与平面β所成的(锐)二面角为60°【答案】：A∴点Q1与Q2重合于同一点由此可得，四边形PP1Q1P2为矩形，且∠P1Q1P2是二面角α-l-β的平面角∵∠P1Q1P2是直角，∴平面α与平面β垂直，故选A2. 【2009年.浙江卷.理17】如图，在长方形ABCD 中，2AB =，1BC =，E 为DC 的中点，F 为线段EC （端点除外）上一动点．现将AFD ∆沿AF 折起，使平面ABD ⊥平面ABC ．在平面ABD 内过点D 作DK AB ⊥，K 为垂足．设AK t =，则t 的取值范围是．【答案】：1,12⎛⎫⎪⎝⎭3. 【2007年.浙江卷.理16】已知点O 在二面角AB αβ--的棱上，点P 在α内，且45POB ∠=︒.若对于β内异于O 的任意一点Q ，都有45POQ ∠≥︒，则二面角AB αβ--的取值范围是_____________. 【答案】,2ππ⎡⎤⎢⎥⎣⎦【解析】4. 【2006年.浙江卷.理14】正四面体ABCD的棱长为1，棱AB∥平面α，则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是.【答案】1] 42【解析】5. 【2015高考浙江，理8】如图，已知ABC ∆，D 是AB 的中点，沿直线CD 将ACD ∆折成A CD '∆，所成二面角A CD B '--的平面角为α，则（）A. A DB α'∠≤B. A DB α'∠≥C. A CB α'∠≤D. A CB α'∠≤【答案】B.在Rt A BP '∆中，2222222(2cos )4cos A P A B BP t t θθ''=-=-=-，三．拔高题组1. 【2014年.浙江卷.理20】（本题满分15分）如图，在四棱锥BCDE A -中，平面⊥ABC 平面======∠=∠AC BE DE CD AB BED CDE BCDE ,1,2,90,02.（1）证明：⊥DE 平面ACD ; （2）求二面角E AD B --的大小4681012141618EA【答案】（Ⅰ）详见解析；（Ⅱ）二面角E AD B --的大小是6π．【解析】试题分析：（Ⅰ）求证：⊥DE 平面ACD ，证明线面垂直，先证线线垂直，即证线和平面内两条相交直线垂直，由已知可得DE DC ⊥，只需证明AC DE ⊥，或AD DE ⊥，由已知平面⊥ABC 平面BCDE ，只在Rt AED 中，1DE =，AD =，得AE =R t A B D中，BD =2AB =，AD =，得3BF =23AF AD =，从而23GF =，在,ABE ABG中，利用余弦定理分别可得2cos ,143BAE BG ∠==，在BFG中，222cos 22GF BF BG BFG BF GF +-∠==⋅，所以6BFG π∠=，即二面角E AD B --的大小是6π．方法二：以D 为原点，分别以射线,DE DC 为,x y 轴的正半轴，建立空间直角坐标系D xyz -如图所示，由题意可知各点坐标如下：()()()(()0,0,0,1,0,0,0,2,0,,1,1,0D E C A B ，设平面ADE 的法向量为()111,,m x y z =，平面ABD 的法向量为()222,,n x y z =，可算得(0,2,AD =-，()(1,1,0,1,2,DB AE ==-，由00m AD m AE ⎧⋅=⎪⎨⋅=⎪⎩得，1111102020y x y ⎧-=⎪⎨-=⎪⎩，可取(0,1,m =，由00n AD n BD ⎧⋅=⎪⎨⋅=⎪⎩得，22220200y x y ⎧--=⎪⎨+=⎪⎩，可取(1,1,2n =，于是3cos ,2m n m n m n ⋅〈〉==，由题意可知，所求二面角是锐角，故二面角E AD B --的大小是6π． 4681012141618试题点评：本题主要考查空间点，线，面位置关系，二面角等基础知识，空间向量的应用，同时考查空间想象能力，与推理论证，运算求解能力．2. 【2013年.浙江卷.理20】(本题满分15分)如图，在四面体A －BCD 中，AD ⊥平面BCD ，BC ⊥CD ，AD ＝2，BD ＝.M 是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且AQ ＝3QC ．(1)证明：PQ ∥平面BCD ；(2)若二面角C －BM －D 的大小为60°，求∠BDC 的大小．【答案】在Rt△BDM中，23BG DMHGBMθ⋅==.在Rt△CHG中，tan∠CHG＝3cossin CGHGθθ==所以tan θ从而θ＝60°.即∠BDC＝60°.方法二：(1)证明：如图，取BD的中点O，以O为原点，OD，OP所在射线为y，z轴的正半轴，建立空间直角坐标系Oxyz.由题意知A (0，2)，B (0，0)，D (0，0)．设点C 的坐标为(x 0，y 0,0)．因为3AQ QC =，所以Q 00331,,4442x y ⎛⎫+⎪ ⎪⎝⎭. 因为M 为AD 的中点，故M (0，1)．又P 为BM 的中点，故P 10,0,2⎛⎫ ⎪⎝⎭，所以PQ＝0033,,0444x y ⎛⎫+ ⎪ ⎪⎝⎭. 又平面BCD 的一个法向量为u ＝(0,0,1)，故PQ ·u ＝0. 又PQ ⊄平面BCD ，所以PQ ∥平面BCD ．(2)解：设m ＝(x ，y ，z )为平面BMC 的一个法向量．由CM ＝(－x 00y ,1)，BM ＝(0,1)，知000,0.x x y y z z ⎧-+)+=⎪⎨+=⎪⎩ 取y ＝－1，得m＝001,y x ⎛- ⎝. 又平面BDM 的一个法向量为n ＝(1,0,0)，于是|cos 〈m ，n 〉|＝||1||||2⋅==m n m n，即200y x ⎛= ⎝⎭① 又BC ⊥CD ，所以CB ·CD ＝0，故(－x 0，0y ,0)·(－x 00y ,0)＝0，即x 02＋y 02＝2.②联立①，②，解得000,x y =⎧⎪⎨=⎪⎩(舍去)或00,22x y ⎧=±⎪⎪⎨⎪=⎪⎩ 所以tan ∠BDC=.又∠BDC 是锐角，所以∠BDC ＝60°.3. 【2012年.浙江卷.理20】如图，在四棱锥P －ABCD 中，底面是边长为∠BAD ＝120°，且PA ⊥平面ABCD，PA =M ，N 分别为PB ，PD 的中点．(1)证明：MN ∥平面ABCD ；(2)过点A 作AQ ⊥PC ，垂足为点Q ，求二面角A －MN －Q 的平面角的余弦值．【答案】（1）详见解析；（2.【解析】A(，0,0)，B (0，－3,0)，C，0,0)，D (0,3,0)，P(，0,)，M(2-，32-)，N(32)，Q，0)．设m ＝(x，y ，z )为平面AMN的法向量．由33(22AM =-，33(22AN =，，知30230.2x y x y -+=+=，取z ＝－1，得m ＝(0，－1)．设n ＝(x ，y ，z )为平面QMN 的法向量．由3(2QM =-，3(2QN =，知30,230.623x y z x y z ⎧-+=⎪⎪⎨⎪-++=⎪⎩取z ＝5，得n ＝(，0,5)．于是cos 〈m ，n〉＝||||⋅=⋅m n m n ．所以二面角A MN Q 的平面角的余弦值为33．方法二：在菱形ABCD 中，∠BAD=120°，得AC=AB=BC=CD=DA ，BD=AB ．又因为PA ⊥平面ABCD ，所以PA ⊥AB ，PA ⊥AC ，PA ⊥AD ．所以PB =PC =PD ．所以△PBC ≌△PDC ．而M ，N 分别是PB ，PD 的中点，所以MQ =NQ ，且AM =12PB =12PD =AN ．取线段MN 的中点E ，连结AE ，EQ ，则AE ⊥MN ，QE ⊥MN ，所以∠AEQ 为二面角A －MN －Q 的平面角．由AB =PA = 故在△AMN 中，AM =AN =3，MN =12BD =3，得2AE =．在直角△PAC 中，AQ ⊥PC，得AQ =QC =2，PQ =4，在△PBC 中，2225cos 26PB PC BC BPC PB PC +-∠==⋅，得MQ ==在等腰△MQN 中，MQ =NQMN =3，得2QE ==．在△AEQ中，2AE =，2QE =，AQ =222cos 2AE QE AQ AEQ AE QE +-∠==⋅．所以二面角A －MN －Q 的平面角的余弦值为33． 4. 【2011年.浙江卷.理20】（本题满分15分）如图，在三棱锥P ABC -中，AB AC =，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上，已知BC=8，PO=4，AO=3，OD=2（Ⅰ）证明：AP ⊥BC ；（Ⅱ）在线段AP 上是否存在点M ，使得二面角A-MC-β为直二面角？若存在，求出AM 的长；若不存在，请说明理由。

浙江省《立体几何》高考真题汇编

2014--2018浙江省《立体几何》高考真题汇编2014年浙江理（3）某几何体的三视图（单位：cm）如图所示，则此几何体的表面积是A. 902cm D. 1382cmcm C. 1322cm B. 12922014年浙江理 17、如图，某人在垂直于水平地面ABC的墙面前的点A 处进行射击训练.已知点A到墙面的距离为AB，某目标点P沿墙面上的射击线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小.若15BCM∠=︒,则tanθ的最大值是=，30AB m=，25AC m(仰角θ为直线AP与平面ABC所成角)2014年浙江理 20.（本题满分15分）如图，在四棱锥A BCDE-中，平面ABC?平面BCDE ,AC=.==,190AB CD∠=∠=︒，2CDE BEDDE BE==,2(Ⅰ)证明：DE?平面ACD;(Ⅱ)求二面角B AD E--的大小.2014年浙江文 2. 设四边形ABCD的两条对角线为AC、BD，则“四边形ABCD为菱形”是“BDAC⊥”的（）A. 充分不必要条件B. 必要不成分条件C. 充要条件D. 既不充分也不必要条件2014年浙江文 3. 某几何体的三视图（单位：cm）若图所示，则该几何体的体积是（）A. 372cmB. 390cmC. 3108cmD. 3138cm2014年浙江文 10.如图，某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练，已知点A 刀枪面对而距离为AB ，某目标点P 沿墙面上的射线CM 移动，此人为了准确瞄准目标点P ，需计算由点A 观察点P 的仰角θ的大小（仰角θ为直线AP 与平面ABC 所成的角），若m AB 15=，m AC 25=，ο30=∠BCM ，则θtan 的最大值是（） A. 530 B. 1030 C.934 D. 9352014年浙江文6. 设m 、n 是两条不同的直线，α、β是两个不同的平面，则（）A.若n m ⊥，α//n ，则α⊥mB.若β//m ，αβ⊥，则α⊥mC.若β⊥m ，β⊥n ，α⊥n ，则α⊥mD.若n m ⊥，β⊥n ，αβ⊥，则α⊥m2014年浙江文 20、（本小题满分15分）如图，在四棱锥BCDE A -中，平面ABC ⊥平面BCDE ；90CDE BED ∠=∠=︒，2AB CD ==，1DE BE ==，2AC =. （1）证明：AC ⊥平面BCDE ；（2）求直线AE 与平面ABC 所成的角的正切值.2015年浙江理 2．（5分）（2015?浙江）某几何体的三视图如图所示（单位：cm ），则该几何体的体积是（）A ． 8cm 3B ． 12cm 3C ．D ．2015年浙江理 8．（5分）（2015?浙江）如图，已知△ABC，D 是AB 的中点，沿直线CD 将△ACD 折成△A′CD，所成二面角A′﹣CD ﹣B 的平面角为α，则（）A ． ∠A′DB≤αB ． ∠A′DB≥αC ． ∠A′CB≤αD ． ∠A′CB≥α2015年浙江理 13．（4分）（2015?浙江）如图，三棱锥A ﹣BCD 中，AB=AC=BD=CD=3，AD=BC=2，点M ，N 分别是AD ，BC 的中点，则异面直线AN ，CM 所成的角的余弦值是．2015年浙江理 17．（15分）（2015?浙江）如图，在三棱柱ABC ﹣A 1B 1C 1中，∠BAC=90°，AB=AC=2，A 1A=4，A 1在底面ABC 的射影为BC 的中点，D是B 1C 1的中点．（1）证明：A 1D⊥平面A 1BC ；（2）求二面角A 1﹣BD ﹣B 1的平面角的余弦值．2015年浙江文 2．（5分）与2015年浙江理的第2题相同2015年浙江文 7、如图，斜线段与平面所成的角为，为斜足，平面上的动点满足，则点的轨迹是（）A ．直线B ．抛物线B ．C ．椭圆D ．双曲线的一支AB α60o B αP 30∠PAB =o P2015年浙江文 4、设，是两个不同的平面，，是两条不同的直线，且，（）A ．若，则B ．若，则C ．若，则D ．若，则2015年浙江文 18. （本题满分15分）如图，在三棱柱ABC ﹣A 1B 1C 1中，∠BAC=90°，AB=AC=2，A 1A=4，A 1在底面ABC 的射影为BC 的中点，D 是B 1C 1的中点．(1)证明: ；(2)求直线和平面所成的角的正弦值.αβl m l α⊂m β⊂l β⊥αβ⊥αβ⊥l m ⊥//l β//αβ//αβ//l m 11D A BC A ⊥平面1A B 11B C B C2016浙江文 2. 已知互相垂直的平面交于直线l .若直线m ，n 满足m ∥α，n ⊥β，则（）∥l ∥n ⊥l ⊥n2016浙江文 9. 某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是______cm 2,体积是______cm 3.2016浙江文 14．如图，已知平面四边形ABCD ，AB =BC =3，CD =1，AD=，∠ADC =90°．沿直线AC 将△ACD 翻折成△ACD'，直线AC 与BD'所成角的余弦的最大值是______．αβ，52016浙江文 18. （本题满分15分）如图，在三棱台ABC-DEF中，平面BCFE⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3.（I）求证：BF ⊥平面ACFD；（II）求直线BD与平面ACFD所成角的余弦值.2016浙江理 2．（5分）已知互相垂直的平面α，β交于直线l，若直线m，n满足m∥α，n⊥β，则（）A．m∥l B．m∥n C．n⊥l D．m⊥n2016浙江理 11．（6分）某几何体的三视图如图所示（单位：cm），则该几何体的表面积是______cm2，体积是______cm3．2016浙江理 14．（4分）如图，在△ABC中，AB=BC=2，∠ABC=120°．若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=BA，则四面体PBCD 的体积的最大值是______．2016浙江理 17．（15分）如图，在三棱台ABC﹣DEF中，已知平面BCFE ⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3，（Ⅰ）求证：BF⊥平面ACFD；（Ⅱ）求二面角B﹣AD﹣F的余弦值．2017年浙江3．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）A．+1B．+3 C．+1 D．+3π2π23π23π22017年浙江 9．如图，已知正四面体D–ABC（所有棱长均相等的三棱锥），P，Q，R分别为AB，BC，CA上的点，AP=PB，，分别记二面角D–PR–Q，D–PQ–R，D–QR–P的平面角为α，β，γ，则（）A．γ<α<βB．α<γ<βC．α<β<γD．β<γ<α2017年浙江 19．（本题满分15分）如图，已知四棱锥P–ABCD，△PAD 是以AD为斜边的等腰直角三角形，，CD⊥AD，PC=AD=2DC=2CB，E 为PD的中点．（Ⅰ）证明：平面PAB；（Ⅱ）求直线CE与平面PBC 所成角的正弦值．2BQ CRQC RA==//BC AD//CE2018年浙江省 3．某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是（）A ．2B ．4C ．6D ．82018年浙江省 8．已知四棱锥S ?ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为θ1，SE 与平面ABCD 所成的角为θ2，二面角S ?AB ?C 的平面角为θ3，则（）A ．θ1≤θ2≤θ3B ．θ3≤θ2≤θ1C ．θ1≤θ3≤θ2D ．θ2≤θ3≤θ12018年浙江省 19．（本题满分15分）如图，已知多面体ABCA 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC =120°，A 1A =4，C 1C =1，AB =BC =B 1B =2．（Ⅰ）证明：AB 1⊥平面A 1B 1C 1；（Ⅱ）求直线AC 1与平面ABB 1所成的角的正弦值．俯视图正视图。

专题15：立体几何高考真题浙江卷赏析(原卷版)

专题15：立体几何高考真题浙江卷赏析（原卷版）题型一：三视图1．2019年浙江省高考数学试卷祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同，则积不容易”称为祖暅原理，利用该原理可以得到柱体体积公式V Sh =柱体，其中S 是柱体的底面积，h 是柱体的高，若某柱体的三视图如图所示，则该柱体的体积是（）A ．158B ．162C ．182D ．322．2017年全国普通高等学校招生统一考试数学（浙江卷）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是A ．+12πB ．+32πC ．3+12πD ．3+32π 3．2014年全国普通高等学校招生统一考试文科数学（浙江卷）某几何体的三视图如图所示（单位：cm ），则该几何体的体积是（）A ．83cmB ．123cmC ．3233cm D ．4033cm4．2014年全国普通高等学校招生统一考试文科数学（浙江卷）某几何体的三视图（单位：cm ）如图所示，则该几何体的体积是（）A ．B ．C ．D ．5．2014年全国普通高等学校招生统一考试理科数学（浙江卷）某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是A ．90B ．129C ．132D ．138题型二：点线面的基本关系6．2011年浙江省普通高等学校招生统一考试文科数学若直线l 不平行于平面a ，且l a ⊄，则 A ．a 内的所有直线与l 异面 B ．a 内不存在与l 平行的直线 C ．a 内存在唯一的直线与l 平行 D ．a 内的直线与l 都相交7．（2013•浙江）设m 、n 是两条不同的直线，α、β是两个不同的平面，（） A ．若m ∥α，n ∥α，则m ∥n B ．若m ∥α，m ∥β，则α∥β C ．若m ∥n ，m ⊥α，则n ⊥α D ．若m ∥α，α⊥β，则m ⊥β8．2014年全国普通高等学校招生统一考试文科数学（浙江卷）设、是两条不同的直线，、是两个不同的平面，则（）A ．若，，则B ．若，，则C ．若，，，则D ．若，，，则9．2015年全国普通高等学校招生统一考试文科数学（浙江卷）设α，β是两个不同的平面，l ，m 是两条不同的直线，且l α⊂，m β⊂（） A ．若l β⊥，则αβ⊥ B ．若αβ⊥，则l m ⊥ C ．若//l β，则//αβD ．若//αβ，则//l m10．2016年全国普通高等学校招生统一考试文科数学（浙江卷）已知互相垂直的平面αβ，交于直线l.若直线m ，n 满足m ∥α，n ⊥β，则 A ．m ∥lB ．m ∥nC ．n ⊥lD ．m ⊥n题型三：夹角问题11．浙江省2019年普通高等学校招生全国统一考试数学试题已知三棱锥P ABC -中，ABC ∆为正三角形，PA PB PC >>，且P 在底面ABC 内的射影在ABC ∆的内部（不包括边界），二面角PAB C ，二面角P BC A --，二面角P AC B --的大小分别为α，β，γ，则（） A ．αβγ>>B ．γαβ>>C ．αγβ<<D ．αβγ<<12．2015年全国普通高等学校招生统一考试理科数学（浙江卷）如图，已知ABC ∆，D 是AB 的中点，沿直线CD 将ACD ∆折成A CD ∆'，所成二面角A CD B '--的平面角为α，则（）A ．A DB α∠'≤ B ．A DB α∠'≥C ．A CB α∠'≤D ．A CB α∠'≤13．2017年全国普通高等学校招生统一考试数学（浙江卷）如图，已知正四面体D –ABC （所有棱长均相等的三棱锥），P ，Q ，R 分别为AB ，BC ，CA 上的点，AP=PB ，2BQ CRQC RA==，分别记二面角D –PR –Q ，D –PQ –R ，D –QR –P 的平面角为α,β,γ，则A ．γ<α<βB ．α<γ<βC ．α<β<γD ．β<γ<α【答案】B14．2018年全国普通高等学校招生统一考试数学（浙江卷）已知四棱锥S ABCD -的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为1θ，SE 与平面ABCD 所成的角为2θ，二面角S AB C --的平面角为3θ，则（） A ．123θθθ≤≤ B ．321θθθ≤≤ C ．132θθθ≤≤ D ．231θθθ≤≤15．2020年浙江省高考数学试卷如图，三棱台ABC—DEF中，平面ACFD⊥平面ABC，∠ACB=∠ACD=45°，DC =2BC．（I）证明：EF⊥DB；（II）求DF与面DBC所成角的正弦值．。

2004—2019浙江高考真题《立体几何》汇编

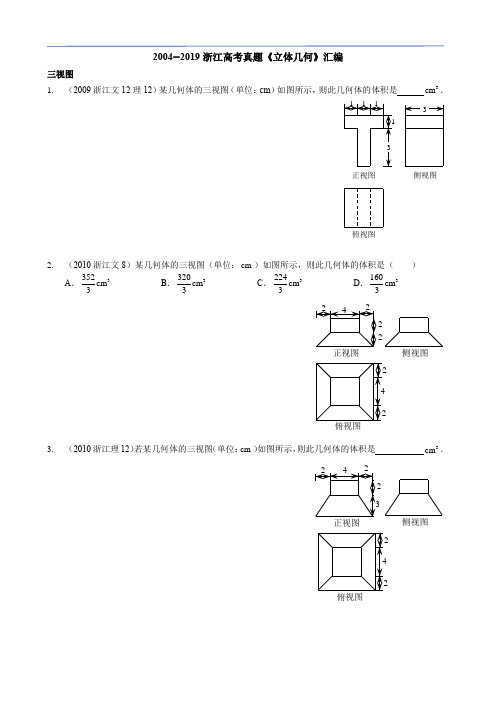
2004−2019浙江高考真题《立体几何》汇编三视图1. （2009浙江文12理12）某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．2. （2010浙江文8）某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是（）A ．3352cm 3B ．3320cm 3C ．3224cm 3D ．3160cm 33. （2010浙江理12）若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．侧视图俯视图正视图侧视图俯视图侧视图俯视图4. （2011浙江文7）某几何体的三视图如图所示，则这个几何体的直观图可以是（）5. （2011浙江理3）某几何体的三视图如图所示，则这个几何体的直观图可以是（）6. （2012浙江文3）已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积是（）A ．13cmB ．23cmC ．33cmD ．63cmDC BA侧视图俯视图正视图DCB A 侧视图俯视图正视图侧视图俯视图正视图7. （2012浙江理11）已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积等于 3cm ．8. （2013浙江文5）已知某几何体的三视图（单位：cm ）如图所示，则该几何体的体积是（）A ．1083cmB ．1003cmC ．923cmD ．843cm9. （2013浙江理12）若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积等于 3cm ．侧视图俯视图正视图俯视图侧视图正视图侧视图正视图3410. （2014浙江文3）某几何体的三视图（单位：cm ）如图所示，则该几何体的体积是（）A ．723cmB ．903cmC ．1083cmD ．1383cm11. （2014浙江理3）某几何体的三视图（单位：cm ）如图所示，则该几何体的表面积是（）A ．902cmB ．1292cmC ．1322cmD ．1382cm12. （2015浙江文2理2）某几何体的三视图如图所示（单位：cm ），则该几何体的体积是（）A ．83cmB ．123cmC ．3233cmD ．403cm俯视图侧视图正视图俯视图侧视图正视图侧视图正视图13. （2016浙江理11）某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是 2cm ，体积是 3cm ．14. （2016浙江文9）某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是 2cm ，体积是 3cm ．15. （2017浙江3）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是（）A ．12π+B ．32π+C ．312π+D ．332π+俯视图正视图316. （2018浙江3）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是（）A ．2B ．4C ．6D ．817. （2019浙江4）祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V Sh 柱体，其中S 是柱体的底面积，h 是柱体的高．若某柱体的三视图如图所示（单位：cm ），则该柱体的体积（单位：3cm ）是（） A ．158B ．162C ．182D ．324俯视图正视图俯视图侧视图正视图点、直线、平面位置关系18. （2005浙江文7理6）设α，β为两个不同的平面，l ，m 为两条不同的直线，且l α⊂，m β⊂．有如下两个命题：①若αβ∥，则l m ∥；②若l m ⊥，则αβ⊥．那么（） A ．①是真命题，②是假命题 B ．①是假命题，②是真命题C ．①②都是真命题D ．①②都是假命题19. （2007浙江文7理6）若P 是两条异面直线l ，m 外的任意一点，则（）A ．过点P 有且仅有一条直线与l ，m 都平行B ．过点P 有且仅有一条直线与l ，m 都垂直C ．过点P 有且仅有一条直线与l ，m 都相交D ．过点P 有且仅有一条直线与l ，m 都异面20. （2008浙江文9）对两条不相交的空间直线a 与b ，必存在平面α，使得（）A ．a α⊂，b α⊂B ．a α⊂，b α∥C ．a α⊥，b α⊥D ．a α⊂，b α⊥21. （2009浙江文4）设α，β是两个不同的平面，l 是一条直线，以下命题正确的是（）A ．若l α⊥，αβ⊥，则l β⊂B ．若l α∥，αβ∥，则l β⊂C ．若l α⊥，αβ∥，则l β⊥D ．若l α⊥，αβ⊥，则l β⊥22. （2010浙江理6）设l ，m 是两条不同的直线，α是一个平面，则下列命题正确的是（）A ．若l m ⊥，m α⊂，则l α⊥B ．若l α⊥，l m ∥，则m α⊥C ．若l α∥，m α⊂，则l m ∥D ．若l α∥，m α∥，则l m ∥23. （2011浙江文4）若直线l 不平行于平面α，且l α⊄，则（）A ．α内的所有直线与l 异面B ．α内不存在与l 平行的直线C ．α内存在唯一的直线与l 平行D ．α内的直线与l 都想交24. （2011浙江理4）下列命题中错误的是（）A ．如果αβ平面⊥平面，那么平面α内一定存在直线平行于平面βB ．如果αβ平面不垂直于平面，那么平面α内一定不存在直线垂直于平面βC ．如果αγ平面⊥平面，βγ平面⊥平面，l αβ=，那么l γ⊥平面D ．如果αβ平面⊥平面，那么平面α内所有直线都垂直于平面β25. （2012浙江文5）设直线l 是直线，α，β是两个不同的平面．（）A ．若l α∥，l β∥，则αβ∥B ．若l α∥，l β⊥，则αβ⊥C ．若αβ⊥，l α⊥，则l β⊥D ．若αβ⊥，l α∥，则l β⊥26. （2013浙江文4）设m ，n 是两条不同的直线，α，β是两个不同的平面．（）A ．若m α∥，n α∥，则m n ∥B ．若m α∥，m β∥，则αβ∥C ．若m n ∥，m α⊥，则n α⊥D ．若m α∥，αβ⊥，则m β⊥27. （2014浙江文6）设m ，n 是两条不同的直线，α，β是两个不同的平面．（）A ．若m n ⊥，n α∥，则m α⊥B ．若m β∥，βα⊥，则m α⊥C ．若m β⊥，n β⊥，n α⊥，则m α⊥D ．若m n ⊥，n β⊥，βα⊥，则m α⊥28. （2015浙江文4）设α，β是两个不同的平面，l ，m 是两条不同的直线，且l α⊂，m β⊂．（）A ．若l β⊥，则αβ⊥B ．若αβ⊥，则l m ⊥C ．若l β∥，则αβ∥D ．若αβ∥，则l m ∥29. （2016浙江文2理2）已知互相垂直的平面α，β交于直线l ，若直线m ，n 满足m α∥，n β⊥，则（） A ．m l ∥ B ．m n ∥C ．n l ⊥D ．m n ⊥30. （2018浙江6）已知平面α，直线m ，n 满足m α⊄，n α⊂，则“m n ∥”是“m α∥”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件小题31. （2004浙江文15）已知α平面⊥β平面，l αβ=，P 是空间一点，且P 到平行α，β的距离分别是1，2，则点P 到l 的距离为．32. （2004浙江理16）已知平面α和平面β相交于直线l ，P 是空间一点，P A ⊥α，垂足为A ，PB ⊥β，垂足为B ，且1PA =，2PB =，若点A 在β内的射影与点B 在α内的射影重合，则点P 到l 的距离为．33. （2004浙江文10理10）如图，在正三棱柱111ABC A B C -中，已知1AB =，D 在棱1BB 上，且1BD =，若AD 与平面11AA C C 所成的角为α，则sin α=（） ABCDDB 1A 1C 1CBA34. （2005浙江文12理12）设M ，N 是直角梯形ABCD 两腰的中点，DE ⊥AB 于E （如图）．现将△ADE沿DE 折起，使二面角A DE B --为45°，此时点A 在平面BCDE 内的射影为点B ，则M ，N 的连线与AE 所成角的大小等于．35. （2006浙江文8）如图，正三棱柱111ABC A B C -的各棱长都为2，E ，F 分别是AB ，11A C 的中点，则EF 的长是（） A ．2BCD36. （2006浙江理9）如图，O 是半径为1的球的球心，点A ，B ，C 在球面上，OA ，OB ，OC 两两垂直，E ，F 分别是大圆弧AB 与AC 的中点，则点E ，F 在该球面上的球面距离是（） A ．4π B ．3π C ．2π D．4B 1C 1A 1FE CBA37. （2006浙江文14）如图，正四面体ABCD 的棱长为1，平面α过棱AB ，且CD α∥，则正四面体上的所有点在平面α内的射影构成的图形面积是．38. （2006浙江理14）正四面体ABCD 的棱长为1，棱AB ∥平面α，则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是．39. （2007浙江文17理16）已知点O 在二面角AB αβ--的棱上，点P 在α内，且45POB ∠=︒．若对于β内异于O 的任意一点Q ，都有45POQ ∠≥︒，则二面角AB αβ--的大小是．40. （2008浙江文15理14）如图，已知球O 的面上四点A ，B ，C ，D ，DA ⊥平面ABC ，AB ⊥BC ，DA AB BC ===O 的体积等于．BDACαBDACαDBCA41. （2008浙江理10）如图，AB 是平面α的斜线段．．．，A 为斜足．若点P 在平面α内运动，使得△ABP 的面积为定值，则动点P 的轨迹是（） A ．圆B ．椭圆C ．一条直线D ．两条平行直线42. （2009浙江理5）在三棱柱111ABC A B C -中，各棱长相等，侧棱垂直于底面，点D 是侧面11BB C C 的中心，则AD 与平面11BB C C 所成角的大小是（） A ．30° B ．45°C ．60°D ．90°43. （2009浙江理17）如图，在长方形ABCD 中，2AB =，1BC =，E 为DC 的中点，F 为线段EC （端点除外）上一动点，现将AFD △沿AF 折起，使平面ABD ⊥平面ABC ，在平面ABD 内过点D 作DK AB ⊥，K 为垂足，设AK t =，则t 的取值范围是．PABαKFDCBA44. （2012浙江理10）已知矩形ABCD ，1AB =，BC ．将△ABD 沿矩形的对角线BD 所在的直线进行翻折，在翻折过程中，（）A ．存在某个位置，使得直线AC 与直线BD 垂直B ．存在某个位置，使得直线AB 与直线CD 垂直C ．存在某个位置，使得直线AD 与直线BC 垂直D ．对于任意位置，三对直线“AC 与BD ”，“AB 与CD ”，“AD 与BC ”均不垂直45. （2013浙江理10）在空间中，过点A 作平面π的垂线，垂足为B ，记()B f A π=．设α，β是两个不同的平面，对空间任意一点P ，()1Q f f P βα=⎡⎤⎣⎦，()2Q f f P αβ⎡⎤=⎣⎦，恒有12PQ PQ =，则（） A ．α平面与β平面垂直 B ．α平面与β平面所成的（锐）二面角为45° C ．α平面与β平面平行 D ．α平面与β平面所成的（锐）二面角为60°46. （2014浙江文10理17）如图，某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练．已知点A 到墙面的距离为AB ，某目标点P 沿墙面上的射线CM 移动，此人为了准确瞄准目标点P ，需计算由点A 观察点P 的仰角θ的大小．若15m AB =，25m AC =，30BCM ∠=︒，则tan θ的最大值是．（仰角θ为直线AP 与平面ABC 所成角）PMCB A47. （2015浙江文7）如图，斜线段AB 与平面α所成的角为60︒，B 为斜足，平面α上的动点P 满足30PAB ∠=︒，则点P 的轨迹是（）A ．直线B ．抛物线C ．椭圆D ．双曲线的一支48. （2015浙江理8）如图，已知ABC △，D 是AB 的中点，沿直线CD 将ACD △翻折成A CD '△，所成（） A ．A DB α'∠≤B ．A DB α'∠≥C ．A CB α'∠≤D ．A CB α'∠≥49. （2015浙江理13）如图，在三棱锥A BCD -中，3AB AC BD CD ====，2AD BC ==，点M ，N 分别为AD ，BC 的中点，则异面直线AN ，CM 所成的角的余弦值是．αPBAA'DCBAMNDCBA50. （2016浙江文14）如图，已知平面四边形ABCD ，3AB BC ==，1CD =，AD =90ADC ∠=︒．沿直线AC 将△ACD 翻折成△ACD'，直线AC 与BD'所成角的余弦的最大值是．51. （2016浙江理14）如图，在△ABC 中，2AB BC ==，120ABC ∠=︒．若平面ABC 外的点P 和线段AC 上的点D ，满足PD DA =，PB BA =，则四面体PBCD 的体积的最大值是．52. （2017浙江9）如图，已知正四面体D ABC -（所有棱长均相等的三棱锥），P ，Q ，R 分别为AB ，BC ，CA 上的点，AP PB =，2BQ CRQC RA==，分别记二面角D PR Q --，D PQ R --，D QR P --的平面角为α，β，γ，则（） A ．γαβ<<B ．αγβ<<C ．αβγ<<D ．βγα<<D'DC APDCBARCQBP A D53. （2018浙江8）已知四棱锥S ABCD -的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为1θ，SE 与平面ABCD 所成的角为2θ，二面角S AB C --的平面角为3θ，则（） A ．123θθθ≤≤ B ．321θθθ≤≤ C ．132θθθ≤≤ D ．231θθθ≤≤54. （2019浙江8）设三棱锥V ABC -的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点）．记直线PB 与直线AC 所成的角为α，直线PB 与平面ABC 所成的角为β，二面角P AC B --的平面角为γ，则（） A ．,βγαγ<< B ．,βαβγ<< C ．,βαγα<< D ．,αβγβ<<大题55. （2004浙江文19）如图，已知正方形ABCD 和矩形ACEF所在的平面互相垂直，AB =1AF =，M 是线段EF 的中点．（1）求证：AM ∥平面BDE ；（2）求证：AM ⊥平面BDF ；（3）求二面角A DF B --的大小．M FEDCBA56. （2004浙江理19）如图，已知正方形ABCD 和矩形ACEF所在的平面互相垂直，AB =1AF =，M 是线段EF 的中点．（1）求证：AM ∥平面BDE ；（2）求二面角A DF B --的大小；（3）试在线段AC 上确定一点P ，使得PF 与BC 所成的角是60︒．57. （2005浙江文18）如图，在三棱锥P ABC -中，AB BC ⊥，12AB BC PA ==，点O ，D 分别是AC ，PC 的中点，OP ⊥底面ABC ．（1）求证：OD ∥平面PAB ；（2）求直线OD 与平面PBC 所成角的大小．58. （2005浙江理18）如图，在三棱锥P ABC -中，AB BC ⊥，AB BC kPA ==，点O ，D 分别是AC ，PC 的中点，OP ⊥底面ABC ．（1）求证：OD ∥平面PAB ；（2）当12k =，求直线PA 与平面PBC 所成角的大小；（3）当k 取何值时，O 在平面PBC 内的射影恰好为PBC △的重心？MFEDCBA59. （2006浙江文17）如图，在四棱锥P ABCD -中，底面为直角梯形，AD BC ∥，90BAD ∠=︒，PA ⊥底面ABCD ，且2PA AD AB BC ===，M ，N 分别为PC ，PB 的中点．（1）求证：PB DM ⊥；（2）求BD 与平面ADMN 所成角．60. （2006浙江理17）如图，在四棱锥P ABCD -中，底面为直角梯形，AD BC ∥，90BAD ∠=︒，PA ⊥底面ABCD ，且2PA AD AB BC ===，M ，N 分别为PC ，PB 的中点．（1）求证：PB DM ⊥；（2）求CD 与平面ADMN 所成的角．61. （2007浙江理19）在如图所示的几何体中，EA ⊥平面ABC ，DB ⊥平面ABC ，AC ⊥BC ，且2AC BC BD AE ===，M 是AB 的中点．（1）求证：CM EM ⊥；（2）求CM 与平面CDE 所成的角．62. （2007浙江文20）在如图所示的几何体中，EA ⊥平面ABC ，DB ⊥平面ABC ，AC BC ⊥，且2AC BC BD AE ===，M 是AB 的中点．（1）求证：CM EM ⊥；（2）求DE 与平面EMC 所成角的正切值．63. （2008浙江文20理18）如图，矩形ABCD 和梯形BEFC 所在平面互相垂直，BE ∥CF ，90BCF CEF ∠=∠=︒，AD ，2EF =．（1）求证：AE DCF ∥平面；（2）当AB 的长为何值时，二面角A EF C --的大小为60°？64. （2009浙江文19）如图，DC ⊥平面ABC ，EB DC ∥，22AC BC EB DC ====，120ACB ∠=︒，P ，Q 分别为AE ，AB 的中点．（1）证明：PQ ACD ∥平面；（2）若AD 与平面ABE 所成角的正弦值．FEDCBA QPCDEBA65. （2009浙江理20）如图，平面PAC ⊥平面ABC ，ABC △是以AC 为斜边的等腰直角三角形，E ，F ，O 分别为P A ，PB ，AC 的中点，16AC =，10PA PC ==．（1）设G 是OC 的中点，证明：FG ∥平面BOE ；（2）证明：在ABO △内存在一点M ，使FM ⊥平面BOE ，并求点M 到OA ，OB 的距离．66. （2010浙江文20）如图，在平行四边形ABCD 中，2AB BC =，120ABC ∠=︒，E 为线段AB 的中点，将ADE △沿直线DE 翻折成A DE '△，使平面A DE '⊥平面BCD ，F 为线段A C '的中点．（1）求证：BF ∥平面A DE '；（2）设M 为线段DE 的中点，求直线FM 与平面A DE '所成角的余弦值．67. （2010浙江理20）如图，在矩形ABCD 中，点E ，F 分别在线段AB ，AD 上，243AE EB AF FD ====，沿直线EF 将AEF △翻折成A EF '△，使平面A EF '⊥平面BEF ．（1）求二面角A FD C '--的余弦值；（2）点M ，N 分别在线段FD ，BC 上，若沿直线MN 将四边形MNCD 向上翻折，使C 与A '中和，求线段FM 的长．GF EPOCBAA'MFED CBANM A'F EDCB A68. （2011浙江文20）如图，在三棱锥P ABC -中，AB AC =，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上．（1）证明：AP BC ⊥；（2）已知8BC =，4PO =，3AO =，2OD =，求二面角B AP C --的大小．69. （2011浙江理20）如图，在三棱锥P ABC -中，AB AC =，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上．已知8BC =，4PO =，3AO =，2OD =．（1）证明：AP BC ⊥；（2）在线段AP 上是否存在点M ，使得二面角A MC B --为直二面角？若存在，求出AM 的长；若不存在，请说明理由．70. （2012浙江文20）如图，在侧棱垂直底面的四棱柱1111ABCD A B C D -中，AD ⊥AB，AB =2AD =，4BC =，12AA =，E 是1DD 的中点，F 是平面11B C E 与直线1AA 的交点．（1）证明：（i ）11EF A D ∥；（ii ）111BA B C EF ⊥平面；（2）求1BC 与11B C EF 平面所成角的正弦值．OPDCBAOPDCBAD 1C 1B 1A 1EF B D CA71. （2012浙江理20）如图，在四棱锥P ABCD -中，底面是边长为的菱形，120BAD ∠=︒，且PA ABCD ⊥平面，PA =，M ，N 分别为PB ，PD 的中点．（1）证明：MN ∥平面ABCD ；（2）过点A 作AQ PC ⊥，垂足为点Q ，求二面角A MN Q --的平面角的余弦值．72. （2013浙江文20）如图，在四棱锥P ABCD -中，P A ⊥平面ABCD ，2AB BC ==，AD CD ==PA 120ABC ∠=︒．G 为线段PC 上的点．（1）证明：BD ⊥平面P AC ；（2）若G 为PC 的中点，求DG 与平面APC 所成的角的正切值；（3）若G 满足PC ⊥平面BGD ，求PGGC的值．73. （2013浙江理20）如图，在四面体A BCD -中，AD ⊥平面BCD ，BC CD ⊥，2AD =，BD =．M是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且3AQ QC =．（1）证明：PQ BCD ∥平面；（2）若二面角C BM D --的大小为60°，求BDC ∠的大小．QMNDABPGDB APQPMDBA74. （2014浙江文20）如图，在四棱锥A BCDE -中，平面ABC ⊥平面BCDE ，90CDE BED ∠=∠=︒，2AB CD ==，1DE BE ==，AC =（1）证明：AC BCDE ⊥平面；（2）求直线AE 与平面ABC 所成角的正切值．75. （2014浙江理20）如图，在四棱锥A BCDE -中，平面ABC ⊥平面BCDE ，90CDE BED ∠=∠=︒，2AB CD ==，1DE BE ==，AC（1）证明：DE ACD ⊥平面；（2）求二面角B AD E --的大小．76. （2015浙江文18）如图，在三棱柱111ABC A B C -中，90BAC ∠=︒，2AB AC ==，14AA =，1A 在底面ABC 的射影为BC 的中点，D 为11B C 的中点．（1）证明：11A D A BC ⊥平面；（2）求直线1A B 和平面11BB C C 所成的角的正弦值．BED CABED CAC 1B 1A 1DC BA77. （2015浙江理17）如图，在三棱柱111ABC A B C -中，90BAC ∠=︒，2AB AC ==，14AA =，1A 在底面ABC 的射影为BC 的中点，D 为11B C 的中点．（1）证明：11A D A BC ⊥平面；（2）求二面角11A BD B --的平面角的余弦值．78. （2016浙江文18）如图，三棱台ABC DEF -中，平面BCFE ⊥平面ABC ，90ACB ∠=︒，1BE EF FC ===，2BC =，3AC =．（1）求证：BF ⊥平面ACFD ；（2）求直线BD 与平面ACFD 所成角的余弦值．79. （2016浙江理17）如图，在三棱台ABC DEF -中，平面BCFE ⊥平面ABC ，90ACB ∠=︒，1BE EF FC ===，2BC =，3AC =．（1）求证：BF ⊥平面ACFD ；（2）求二面角B AD F --的平面角的余弦值．C 1B 1A 1DC BA80. （2017浙江19）如图，已知四棱锥P −ABCD ，△P AD 是以AD 为斜边的等腰直角三角形，BC ∥AD ，CD ⊥AD ，22PC AD DC CB ===，E 为PD 的中点．（1）证明：CE ∥平面P AB ；（2）求直线CE 与平面PBC 所成角的正弦值．81. （2018浙江19）如图，已知多面体111ABCA B C ，1A A ，1B B ，1C C 均垂直于平面ABC ，120ABC ∠=︒，14A A =，11C C =，12AB BC B B ===．（1）证明：1111AB A B C ⊥平面；（2）求直线1AC 与平面1ABB 所成的角的正弦值．82. （2019浙江19）如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ，90ABC ∠=︒，30BAC ∠=︒，11A A AC AC ==，E ，F 分别是AC ，11A B 的中点．（1）证明：EF BC ⊥；（2）求直线EF 与平面1A BC 所成角的余弦值．ED CBAPC 1B 1A 1CBAC 1B 1A 1FECBA。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

AC?ABCPACABC为斜边的等腰直角三是以1.（本题满分15分）如图，平面，⊥平面10PC?16,PA?PA,PB,PCAC?E,F,O的中点，角形。

分别为BOE//OCCPC设是平面的中点，证明：；（I）.s.5.u.c.o.m w.w.w.OBABOMFMBOEMOA?的距内存在一点，使到（II）证明：在⊥平面,，并求点离。

zy－CD中，P是侧棱CC上的一点，，ABCD2.如图，在棱长为1的正方体CP=mAB1111123所成角的正切值为D（Ⅰ）试确定m，使得直线AP与平面BDB；11上的射影Q在平面APDmC上是否存在一个定点Q，使得对任意的，D（Ⅱ）在线段A1111垂直于AP，并证明你的结论。

的三等分CAC靠近B、分别为ABC是边长为6的等边三角形，E，DAB、如图甲，△3.使平面沿ED翻折，交线段AGED于F点，将△AED为点，点GBC边的中点．线段形成如图乙所示的几何体。

ACAB、、AGBCDEAED⊥平面，连接⊥平面AFG；I （）求证BC D的余弦值．－－）求二面角（IIBAE.BC?AC??DBEA，平面ABC，ABC，所4在如图示的几何体中，平面AE2BC?BD?AC?的中点．M 是AB，EM?CM D；（1）求证：所成的角CM与平面CDE（2）求ECAMBCF∥ABCDBEFCBE，，面互相垂图，矩形和梯形直所在平5. 如3?AD2?EF90??BCF??CEF，，． D∥AEDCF A 平面（Ⅰ）求证：；C60C?A?EFAB？的长为何值时，二面角的大小为（Ⅱ）当BFE题）（第182.?FD4沿直AD，上，AE=EB=AF=FABCD6. 如图，在矩形中，点E，分别在线段AB3??EFA'AEF,'AEF?BEF. 使平面翻折成将线EF平面CA'?FD?）求二面角的余弦值；I （C 向上翻折，使将四边形BC上，若沿直线MNMNCD，分别在线段，）点（IIMNFD'A.与FM重合，求线段的长7. 如图，在三棱锥P-ABC中，AB＝AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上，已知BC＝8，PO＝4，AO＝3，OD＝2（Ⅰ）证明：AP⊥BC；（Ⅱ）在线段AP上是否存在点M，使得二面角A-MC-B为直二面角？若存在，求出AM的长；若不存在，请说明理由。

32中，底面是边长为P-ABCD的菱形，8. 如图，在四棱锥62的中点。

分别为PB,PDM, ，ABCDBAD=120∠°，且PA⊥平面，NPA= ABCD；1（）证明：MN∥平面A-MN-Q的平面角的余弦值。

QAQ作⊥PC，垂足为点，求二面角A2（）过点BCD??BCDADA平面如图，在四面体中，，9.22BD?BM2PMADBC?CDAD?是，，是的中点，的中．ACQC3AQ?Q上，且．点，点在线段BCD//PQ；（Ⅰ）证明：平面BDC?60?D?C?BM的大小为，求（Ⅱ）若二面角的大小．o60??BAD?DE BCABCDEF/ADABCD/，，中，已知平面如图，在五面体10. ，E1?DE2?EFAB?，．EF/BC/ （；1）求证：DEFB?的体积．2）求三棱锥（FDCBA（第16题图）o90??BCA1CA?CB?2AAC?BABC?A 中，已知．，，11. 如图，在直三棱柱1111CCBBA 与（1）求异面直线夹角的余弦值；1B11 1C?B?AB （2）求二面角平面角的余弦值．A 11C BA（第22题图）1BCNABCD60?BCAD?ABC?BC//AD是，中，，，1412(本小题分)在等腰梯形290ABABCD??DABC，得到梯形的中点．将梯形（如图）绕旋转．?C??ABCAC（1）求证：；平面??/NC/DAD平面2）求证：；（?CNA?C?的余弦值．3）求二面角（?D D AC NB，BCAD//为直角梯形，P-ABCD中，底面ABCD分）13. （本题满分14如图，在四棱锥上是棱PCADQ为的中点，M，平面∠ADC=90°PAD⊥底面ABCD，P13==BC．AD=1，CD=2P的点，A=PD，2；⊥平面）求证：平面PQBPAD（I M --，，设30°PM=tMC为）若二面角（II MBQC t的值试确定DQCABBCD?．41°， , 如图，直角梯形中，BC = CD = AB//CD= 90ABCDCD FDABABCD,EC：= 2CE=FD.,AD = BD且有丄底面丄底面2B I( 求证：AD F :)丄N ,上一点在平面上的射影恰好是的中点试求二面角(II )若线段BF BDFECM.的余弦值B-MF-Cx y轴，、OP所在直线为OC）如图，连结OP，以O为坐标原点，分别以OB、1.证明：（I z xyz?轴，建立空间直角坐标系O轴，，k.s.5.u.c.o.m w.w.w.????4,0,3C(0,8,0),FA(0,?8,0),OB0,0,0(8,0,0),,4,3),P(0,0,6),E(0,?由题意得，，则??,G0,4,04,3)?OE?(0,OB?(8,0,0),z，因此平面BOE的法向因0n?FG?FG3??4,4,FG?(4)?(0,3,n不在得，又直线，量为BOEBOEFG//内，因此有平面平面y??,0x,y3)(x?4,y,?FM?，因为II（）设点M的坐标为，则00009x?x??4,y n//FM?FM，即点，所以有，因此有平面BOE0049??AOB?04,?,xoy的内部区域满足不等式组的坐标为M中，，在平面直角坐标系??4??0x???0y?MABO?，使的坐标满足上述不等式组，所以在内存在一点，经检验，点M??8?x?y?94,M?FMOBBOEOA．的坐标得点平面，由点M到，的距离为4s.5.u.c.o.m w.w.w.,BD?O连AC,设AC（１）2. 解法１：.，连OG与面BDD B交于点GAP11,OGBDDB面APC?B因为PC//面BDD,面1111m1?PC?OGPCOG//故。

所以。

22BAO?面BDDAO?DB,AO?BB,所以. 又111所成的角。

B即为AP与面BDD?AGO故11212?mRt2?AOG中，tanAGO?3.，即△在m321?m2BDDB所成的角的正切值为３AP与平面时，直线。

故当113APDQ?AC Q. ，使得（Ⅱ）依题意，要在上找一点111OAC Q点。

的中点可推测即为所求的111.ACCAAADQ?面.DO?ACDO?因为，所以1111111111APA.DO?AP?面ACC又。

,故1111垂直。

ADPAP上的射影与DO在平面从而111（１）建立如图所示的空间直角坐标系，则解法二：C(0,1,0), ，ｍ)A(1,0,0),B(1,1,0),P(0,1,(0,0,1). (1,1,1),DD(0,0,0),B11(0,0,1),BB?BD?(?1,?1,0),所以1,0).,1AC?(?1mAP?(?1,1,),DD为平面BB00,?BD?AC?BB?知ACAC. 的一个法向量又由111?AP B面BDD与所成的角为，设11?2|AP?|AC???cos(???sin)则2|AP|?|AC|2m?2?22321??m. ，解得依题意有：32m?2?222)(31?1?m2所成的角的正切值为３与平面BDDB AP故当时，直线。

113xCA Q，设此点的横坐标为上存在这样的点，（２）若在11,0)?x(Qx,1?x,1),DQ?(x,1。

则1。

等价于依题意，对任意的m要使D1Q在平面APD1上的射影垂直于AP1?Dx)?0?xQ1?0?x?(1?Q?AP?AP?D12CA Q.即的中点时，满足题设的要求为11BCAC的三等分点，点G为，ABC是等边三角形，E，D分别为AB在图甲中，由△3. (Ⅰ) ．…2分DE，DE⊥GF，//BC边的中点，易知DE⊥AF…………………………… ．FFG=，所以DE⊥平面AFG在图乙中，因为DE⊥AF，DE⊥GF，AF 4．，所以BC⊥平面AFG…分又DE//BC………………………………………………… ，DE⊥AEDBCDE，平面GF平面BCDE=DE，DE ⊥AF，(Ⅱ) 因为平面AED⊥平面，FG两两垂直．所以FA，FD z,x,y轴，建立如图所示所在的直线为F为坐标原点，分别以FG，FD，A以点F),),23B(3,?30A(0,0)E0?F?2xyz,(0,，所以．则的空间直角坐标系，，,13,BE3,?23)?(AB?,?(3?分．60)，……………………………………)zn?(x,y,设平面ABE．的一个法向量为??03z?23x?3y?0AB??n??，即，则???0y?3x???0?n?BE??1?x1?z?3y?)(n?1,3,?1．取，，则分，则8………………………………)m?(1,00,的一个法向量，为平面ADE显然5nm??cos?m,n??．所以10分………………………………………………5|?||n|m5DAEB?D??B?AE?．12的余弦值为分为钝角，所以二面角二面角………54.方法一：的中点，，）（1证明：因为AC=BCM是AB所以CM⊥AB． CM⊥EM．ABC，所以又EA ⊥平面，连结，垂足是HCDE作）解：过点（2MMH⊥平面CM是直线，∠FCMMD、MF，连结F于点ED并延长交CH．和平面CDE所成的角．因为MH⊥平面CDE，所以MH⊥ED，又因为CM⊥平面EDM，所以CM ⊥ED，则ED⊥平面CMF，因此ED⊥MF．aa，AC＝设EA＝2，BD＝BC＝2a，M在直角梯形ABDE中，AB＝是2AB的中点，6a3 aa＝，MD，EM，＝＝所以DE3 是直角三角形，其中∠EMD＝90°得△EMD MD?EM a2?＝所以MF．DE MF，所以∠FCM=45°，=1在Rt△CMF中，tan∠FCM=MC 45°．CDE所成的角是故CM与平面方法二：轴，yx轴和如图，以点C为坐标原点，以CA，CB分别作为，C-xyz过点C作与平面ABC垂直的直线为z轴，建立直角坐标系，则设EA=a，0，a），aB （0，2，0），C（2 a）A（2a，0，0，. 0），a，a（0，2 a，2 a）， A（A CMEM0），a，-a），a=（，a）证明：因为（ 1，=（-a，CMEM=0 所以，·CMEM?.故yx n=（1，，垂直，）与平面CDE（2）解：设向量o0CDnnCE??，，则CDnCEn··=0.=0即，C CD E=(0,2a,2a),, （因为2a,0,a）=z=-2，=2 所以y，00，）即 n=（1，2，-2nCM2CMn?cos,???，2nM. °与平面CMCDE所称的角是45 直线方法一：5.CF?EGEDGCFG于，连结（Ⅰ）证明：过点作，交DA CG B FHEBCGE可得四边形为矩形，ABCD又为矩形，ADEG ADGE∥所以为平行四边形，，从而四边形DG∥AE．故?DGDCF?DCFAE平面平面，，因为∥AEDCF平面所以．EFBH?AHBFEH交，连结（Ⅱ）解：过点的延长线于作．BCBEFCAB?ABCD?，，得平面由平面BEFC?AB平面，EFAH?从而．C?EF??AHBA为二面角所以的平面角．3?AD?EG2EF?1EFG△FG?Rt60??CFE，所以．，中，因为在，4CF?CE?EF，又因为，所以z3BE?CG?从而．DA 33C?BEH?BEsin?BH于是．2BxFAHB?AB?BHtan，因为yE960C??EFAAB．所以当的大小为为时，二面角2xz CFCB，CDCy轴，建立和轴，分别作为方法二：如图，以点轴和为坐标原点，以xyzC?空间直角坐标系．c，CF?AB?a，BE?b设，，(0，，cF(00，C0)0)0)b，B(3，0，0)EA(3，(3，0，)a，，，则．，0)b，BE?(0，)(CB?3，0，0)AE?(0，b，?a，（Ⅰ）证明：，，0??0CBBECBCE BE??AECBCB，，从而所以，，ABE?CB平面所以．DCFCB?因为平面，∥ABEDCF所以平面平面．∥AEDCF故．平面0)b，(3，，?cb，0)?CE3EF?(?（Ⅱ）解：因为，，0?EFCE2?EF||所以，，从而，0)?bb?3?(c????2，2?)b?c(?3??4?，b?3c解得．0)，F(0，40)E(3，3，所以，．AEF)(1，y，zn?与平面设垂直，0??0nEFnAE，则，33)，，3n?(1解得．aBEFC?BA)，0，aBA?(0，又因为平面，1a33|BAn|????|cos?n，BA|所以，2|||n|BA2274a?a9?a．得到2960C?EF?AAB时，二面角的大小为所以当．为2方法一：6.?HA（Ⅰ）解：取线段EF的中点H，连结??F?AAE的中点，因为是EF及H?EFH?A所以????EF?AAH.EFA平面平面又因为平面BEF，及??AH所以。