浙江高考数学压轴题:立体几何选择题学生版
2005-2017年浙江高考文科数学历年真题之立体几何大题(学生版)

2005-2017年浙江高考文科数学历年真题之立体几何大题(学生版)1、(2005年)如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=12P A,点O、D分别是AC、PC的中点,OP⊥底面ABC.(Ⅰ)求证OD∥平面PAB(Ⅱ) 求直线OD与平面PBC所成角的大小;2、(2006年)如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.(Ⅰ)求证:PB⊥DM;(Ⅱ)求BD与平面ADMN所成的角。
3、(2007年)在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC BC ⊥,且2A C B C B D A E ===,M 是AB 的中点.(I )求证:CM EM ⊥;(II )求DE 与平面EMC 所成的角的正切值.4、(2008年)如图,矩形ABCD 和梯形BEFC 所在平面互相垂直,BE//CF ,∠BCF=∠CEF=︒90,AD=3,EF=2。
(Ⅰ)求证:AE//平面DCF ;(Ⅱ)当AB 的长为何值时,二面角A-EF-C 的大小为︒60?EDCMAB5、(2009年)如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.(Ⅰ)证明:PQ∥平面ACD;(Ⅱ)求AD与平面ABE所成角的正弦值.6、(2010年)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°。
E为线段AB的中点,将△ADE 沿直线DE翻折成△A’DE,使平面A’DE⊥平面BCD,F为线段A’C的中点。
(Ⅰ)求证:BF∥平面A’DE;(Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。
7、(2011年)如图,在三棱锥P ABC -中,AB AC =,D 为BC 的中点,PO ⊥平面ABC ,垂足O 落在线段AD 上.(Ⅰ)证明:AP ⊥BC ;(Ⅱ)已知8BC =,4PO =,3AO =,2OD =.求二面角B AP C --的大小.8、(2012年)如图,在侧棱锥垂直底面的四棱锥1111ABCD A B C D -中,,A D B C//AD11,2,4,2,AB AB AD BC AA E DD ⊥===是的中点,F 是平面11B C E 与直线1AA 的交点。
高考数学高考数学压轴题立体几何多选题分类精编及答案
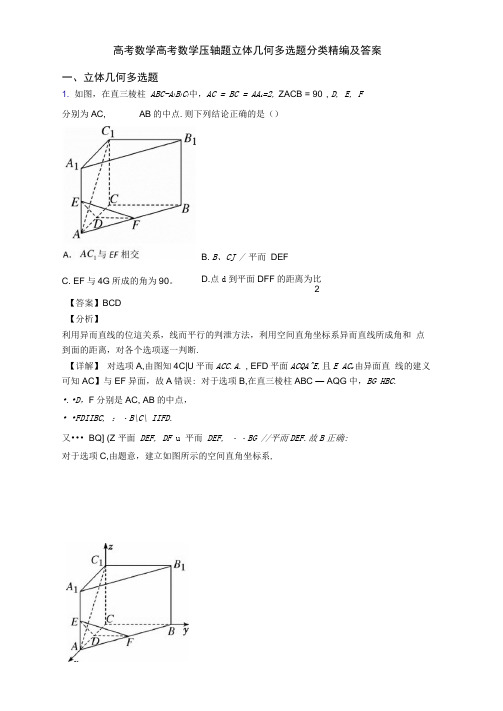
高考数学高考数学压轴题立体几何多选题分类精编及答案一、立体几何多选题1. 如图,在直三棱柱ABC-A}B}C}中,AC = BC = AA i=2, ZACB = 90°, D, E, F分别为AC, AB的中点.则下列结论正确的是()B. B、CJ /平而DEFD.点d到平面DFF的距离为比C. EF与4G所成的角为90。
2【答案】BCD【分析】利用异而直线的位這关系,线而平行的判泄方法,利用空间直角坐标系异而直线所成角和点到面的距离,对各个选项逐一判断.【详解】对选项A,由图知4C|U平而ACC.A. , EFD平面ACQA^E,且E AC r由异面直线的建义可知AC】与EF异面,故A错误: 对于选项B,在直三棱柱ABC — AQG中,BG HBC.•.•D,F分别是AC, AB的中点,• •FDIIBC, :・B\C\ IIFD.又••• BQ] (Z 平面DEF, DF u 平而DEF, ・・BG //平而DEF.故B正确:对于选项C,由题意,建立如图所示的空间直角坐标系,则C(0,0, 0), A(2,0t 0), 5(0,2, 0),人(2,0, 2),坊(0,2, 2), C 】(0,0, 2),D(l,o, 0), E(2,0, 1), F(1,1, 0)..\EF = (-1,1, T), AC ;=(—2,0, 2).•.•EFAC ; = 2+0—2 = 0, :.EF 丄 AC ;, 丄 A©.•.•EF 与AC ;所成的角为90。
,故c 正确:对于选项D,设向量匝= (x,y, Z)是平而DEF 的一个法向疑.・••万E = (ho ・ 1) , DF = (0,l, 0),取 X = 1 ♦则 z=—1 ‘ ・••帀=(h 0, —1),设点耳到平而DEF 的距离为d ・二点d 到平而DEF 的距离为空,故D 正确.2故选:BCD【点睛】本题主要考查异而直线的位置关系,线而平行的判定,异而直线所成角以及点到而的距 离,还考查思维能力及综合分析能力,属难题.2. 已知球O 为正方体ABCD-AgD 、的内切球,平而A {C }B 截球O 的而积为24兀, 下列命题中正确的有()A. 异而直线AC 与所成的角为60。
第5讲 立体几何选择压轴题(解析版)

第5讲 立体几何选择压轴题一、单选题1.(浙江超级全能生3月联考)如图,已知在中,为线段上一点,沿将翻转至,若点在平面内的射影恰好落在线段上,则二面角的正切的最大值为( )AB .1C D【答案】C【分析】过作交BC 于E ,连接EH ,结合已知条件有二面角的平面角为,而,设且,则,即可求,,应用函数与方程思想,构造且在上有解求参数m 的范围,即可得二面角正切的最大值.【解析】过作交BC 于E ,连接EH ,∵在平面内的射影恰好落在线段上,即面,∴且,,即面,面,则,ABC 90,1,2,BAC AB BC D ∠=︒==BC AD ABD △AB D 'B 'ADC H AC B DC A '--B 'B E BC '⊥B DC A '--B EH '∠tan B H B EH m EH ''∠==AH x =01x <<HC x =B H '2HC EH =()g x 01x <<B DC A '--B 'B E BC '⊥B 'ADC H AC B H '⊥ABC B H BC '⊥B E BC '⊥B E B H B '''=BC ⊥B HE 'EH ⊂B HE 'BC EH ⊥∴二面角的平面角为,在中,,若令,则,又, ∴,且, 故,则,即方程在上有解时,m 的最大值即为所求,而开口向上且,即,对称轴. ∴当时,,显然成立; 当时,当对称轴在上,恒成立;当对称轴在上,,即; ∴综上,有,即,故二面角. 故选C . 【点睛】关键点点睛:利用三垂线定理找到二面角的平面角,进而根据线段关系、勾股定理求,,由,结合函数与方程的思想求参数m 范围,进而确定最大值. 2.(浙江宁波模拟)设三棱锥的底面是正三角形,侧棱长均相等,是棱上的点(不含端点),记直线与直线所成角为,直线与平面所成角为,二面角的平面角为,则A .B .C .D .【答案】B【分析】本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各B DC A '--B EH '∠Rt B HE 'tan B H B EH EH ''∠=AH x =HC x =1AB AB '==B H '=22HC x EH ==01x <<tan B EH m '∠==2222()(4)340g x m x x m =+-+-=01x <<()g x 21680m ∆=-≥202m <≤21x m=+22m =(0,1)3x =202m <<1(0,)22(1)(40f m =->1[,232(0)340f m =->243m >2423m <≤[(33m ∈-⋃B DC A '--B H 'EH tan B H B EH m EH''∠==V ABC -P VA PB AC αPB ABC βP AC B --γ,βγαγ<<,βαβγ<<,βαγα<<,αβγβ<<种角的计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图形特征,则可事倍功半.【解析】方法1:如图为中点,在底面的投影为,则在底面投影在线段上,过作垂直,易得,过作交于,过作,交于,则,则,即,,即,综上所述,答案为B .方法2:由最小角定理,记的平面角为(显然)由最大角定理,故选B .方法3:(特殊位置)取为正四面体,为中点,易得,故选B . 【点睛】常规解法下易出现的错误有,不能正确作图得出各种角.未能想到利用“特殊位置法”,寻求简便解法.3.(湖南长沙市·长沙一中高三月考)在三棱锥中,,二面角的余弦值为,当三棱锥的体积的最大值为时,其外接球的表面积为 A .B .C .D .【答案】B G AC V ABC O P D AO D DE AE //PE VG P //PF AC VG F D //DH AC BG H ,,BPF PBD PED α=∠β=∠γ=∠cos cos PF EG DH BD PB PB PB PBα===<=βαβ>tan tan PD PD ED BDγ=>=βy >ββα<V AB C --γ'γ'=γβ<γ'=γV ABC -PVA cos sin sin α=⇒α=β=γ=A BCD -60BAC BDC ∠=∠=︒A BC D --13-A BCD-45π6π7π8π【分析】根据两个射影,结合球的图形,可知二面角的平面角为;根据题意可知当,时,三棱锥的体积最大.根据体积的最大值可求得BC 的长,结合图形即可求得球的半径,进而求得表面积.【解析】如图,设球心在平面内的射影为,在平面内的射影为,则二面角的平面角为,点在截面圆上运动,点在截面圆上运动,由图知,当,时,三棱锥的体积最大,此时与是等边三角形, 设,则,,, ,解得, ,,设,则,解得∴,球的半径,所求外接球的表面积为,故选B .【点睛】本题考查了三棱锥外接球的综合应用,根据空间几何关系求得球的半径,进而求得表面积,对空间想象能力要求较高,属于难题.4.(天一大联考(理))在棱长为的正四面体中,点为所在平面内一动点,且满足,则的最大值为( ) A .B .C .D .【答案】B A BC D --AMD ∠AB AC =BD CD =A BCD -O ABC 1O BCD 2O A BC D--AMD ∠A 1O D 2OAB AC =BD CD =A BCD -ABC ∆BDC ∆BC a =AM DM ==2BCD S ∆=sin()h AM AMD π=-∠=313124A BCD DBC V S h a -∆=⋅==a =32DM =21DO =212O M =2AMD θ∠=21cos 22cos 13θθ=-=-tan θ=22tan 2OO O M θ==O R ==246S R ππ==2ABCD P ABC 433PA PB +=PD 3332【分析】由题意可知,点在所在平面内的轨迹为椭圆,且该椭圆的焦点为、,长轴长为,然后以线段的中点为坐标原点,直线所在直线为轴,以所在直线为轴建立空间直角坐标系,求出椭圆的方程,利用二次函数的基本性质可求得的最大值.【解析】如图所示,在平面内,,所以点在平面内的轨迹为椭圆,取的中点为点,连接,以直线为轴,直线为建立如下图所示的空间直角坐标系,则椭圆的半焦距,长半轴, 所以,椭圆方程为. 点在底面的投影设为点,则点为的中心,, 故点正好为椭圆短轴的一个端点,,则, 因为,故只需计算的最大值.设,则,则,当时,取最大值,即,因此可得,P ABC A B 3AB O AB x CO yPDABC 432PA PB +=>P ABC AB O CO AB x OC y O xyz -1c=a =3b ==()2233104x y z +==D E EABC11333OE OC ===E 23CE OC ==DE ==222PD DE EP =+EP(),,0P xy 0,3E ⎛⎫ ⎪ ⎪⎝⎭22222241543333EP x y y y y y y ⎛=+-=-++=--+ ⎝⎭,933y ⎡=-∈-⎢⎣⎦2EP 22max 516393939EP ⎛⎛=-⨯--⨯-+= ⎝⎭⎝⎭2241640999PD ≤+=故的最大值为.故选B . 【点睛】关键点点睛:本题考查线段长度最值的求解,根据椭圆的定义得知点的轨迹是椭圆,并结合二次函数的基本性质求解的最大值是解题的关键,在求解时也要注意椭圆有界性的应用.5.(四川成都市·高三二模(理))已知四面体,,分别为棱,的中点,为棱上异于,的动点.有下列结论:①线段的长度为1;②若点为线段上的动点,则无论点与如何运动,直线与直线都是异面直线;③的余弦值的取值范围为; ④.其中正确结论的个数为( )A .1B .2C .3 D.4 【答案】B【分析】将正四面体放在正方体中观察,对于①,可根据分别为正方体前后两个面的中心可得出结论; 对于②,取为的中点,取为的中点,此时与相交;对于③,计算可得由逼近思想可作出判断;对于④,空间问题平面化的技巧,将三角形与放在同一平面上,可计算出. 【解析】PD 3P EP ABCD M N AD BC F AB A B MN G MN F G FG CD MFN ∠⎡⎢⎣⎭FMN 1,M N F AB G MN FG CD cos MBN ∠=>ABC ABD 2NFFM在棱长为四面体,显然,分别为正方体前后两个面的中心,故线段的长度为正方体棱长,故 ①对; 对于②:如图,取为的中点,取为的中点,取为的中点,则由正方体的性质易知,该三点在一条直线上,故此时与相交于,故②错;对于③,,,又有,1ABCD ,MN MN 1F ABG MN I CD FG CD I 22BC BN ==BM ===1MN =故,故点无限接近点时,会无限接近,故的余弦值的取值范围不为,③错误; 对于④,如图将等边三角形与铺平,放在同一平面上,故有,当且仅当为中点时取最小值,故在正方体中,故,故④对,故选B .【点睛】把空间中的最短路线问题利用展开图转化为平面上两点间距离最短的问题,从而使问题得到解决,这是求空间中最短路线的一种常用方法6.(内蒙古呼和浩特市·高三一模(理))四面体的四个顶点都在球O 上且,O 的表面积为( )A .B .C .D .【答案】B【分析】作出图形,根据题中的数据证明平面平面,并找出球心的位置,列出等式求出外接球的半径,结合球的表面积公式可得出结果.【解析】131cos MBN +-∠==>F B cos MFN ∠3MFN ∠⎡⎢⎣⎭ABC ABD ''''2N FFM M N F AB 2NFFM FMN 1ABCD 4AB AC BC BD CD =====AD =70π380π330π40πABC ⊥BCD取的中点,连接,设和的外心分别为,分别过点作平面和平面的垂线交于点,则点为外接球球心.由题意可知,和都是边长为4的等边三角形.为的中点,,且,平面,平面,平面平面, 易得,, 平面,平面∥AM ,同理可得∥DM ,则四边形为菱形, ,菱形为正方形,平面,平面,所以外接圆半径为, 因此,四面体的外接球的表面积为,故选B 【点睛】这个题目考查了外接球表面积的计算,找出球心位置,并计算外接球的半径是解答的关键,考查推理能力与计算能力.7.(山东日照市·高三一模)已知直三棱柱的侧棱长为,,.过、的中点、作平面与平面垂直,则所得截面周长为( )A .BC .D .【答案】C【分析】确定平面与各棱的交点位置,计算出截面各边边长,由此可得出所得截面周长.【解析】BC M AM DM 、ABC BCD△F E 、FE 、ABC BCD O O ABC BCD △M BC AM BC ∴⊥AM DM ==222,M A AD A DM D =+=∴AM DM ∴⊥,D C M B M ⋂=AM ∴⊥BCD AM ⊂ABC ∴ABC ⊥BCD 13ME MF AM ===23BE DM ==AM ⊥BCDO E ⊥BCD OE ∴OF OEMF AM DM ⊥OEMF OE ⊥BCD BE ⊂BCD OE BE ∴⊥OB ==ABCD 2804OB 3ππ⨯=111ABC A B C -2AB BC ⊥2AB BC ==AB 1BB E F α11AAC C +α如下图所示,取的中点,连接,取的,连接,取的中点,连接、,,为的中点,则,平面,平面,,,平面,、分别为、的中点,则且,平面, 平面,所以,平面平面,所以,平面即为平面,设平面交于点,在直棱柱中,且,所以,四边形为平行四边形,且, 、分别为、的中点,且, 所以,四边形为平行四边形,且, 且,且,所以,四边形为平行四边形, ,平面,平面,平面, 设平面平面,平面,所以,,,,所以,四边形为平行四边形,可得, 所以,为的中点, AC J BJ AJ D DE 11A C K KJ 1BK AB BC =J AC BJ AC ⊥1AA ⊥ABC BJ ⊂ABC 1BJ AA ∴⊥1AC AA A ⋂=BJ ∴⊥11AAC C D E AJ AB //DE BJ 12DE BJ =DE ∴⊥11AAC C DE ⊂DEF DEF ⊥11AAC C αDEF α11B C I 111ABC A B C -11//AA CC 11AA CC =11AAC C 11//AC AC ∴11AC A C =J K AC 11A C 1//AJ A K ∴1AJ A K =1AA KJ 1//KJ AA ∴1KJ AA =11//BB AA 11BB AA =1//KJ BB ∴1KJ BB =1BB KJ //DE BJ DE ⊄1BB KJ BJ ⊂1BB KJ //DE ∴1BB KJ α1BB KJ FG =DE ⊂α//DE FG //FG BJ ∴//BF GJ BFGJ 11122GJ BF BB KJ ===G KJ延长交于点,,所以,,,又,所以,,,为的中点, 因为平面平面,平面平面,平面平面,,,,,,为的中点, ,,则, 为的中点,,同理, 因为直棱柱的棱长为,为的中点,, 由勾股定理可得,且,平面,平面,平面,,、分别为、的中点,则,, 由勾股定理可得,同理因此,截面的周长为. 故选C .【点睛】思路点睛:本题考查直棱柱截面多边形周长的计算,在画几何体的截面,关键是画截面与几何体各面的交线,此交线只需两个公共点即可确定,作图时充分利用几何体本身提供的面面平行等条件,可以更快地确定交线的位置.8.(山东滨州市·高三一模)如图,斜线段与平面所成的角为,为斜足.平面上的动点满足,则点的轨迹为( ) DG 11A C H //DJ KH DJG HKG ∠=∠JDG KHG ∠=∠JG KG =DJG HKG ≅△△11122HK DJ AJ KC ∴===H ∴1KC //ABC 111A B C αABC DE =α111A B C IH =//DE IH ∴//DE BJ 1//BJ B K //DE IH 1//IH B K ∴I ∴11B C AB BC ⊥2AB BC ==AC ==J AC 12BJ AC ∴==12DE BJ ==IH =111ABC A B C -2F 1BB 1112BF BB ∴==EF ==IF =1//KJ BB 12KJ BB ==1BB ⊥ABC KJ ∴⊥ABC AC ⊂ABC KJ AC ∴⊥G D KJ AJ 112GJ KJ ==122DJ AJ ==DG ==GH =222DE IH EF IF DH ++++=++=AB απ4B αP π6PAB ∠=PA .圆B .椭圆C .双曲线的一部分D .抛物线的一部分【答案】B 【分析】首先建立空间直角坐标系,设,则点的轨迹是椭圆. 【解析】建立如图所示的空间直角坐标系,设所以点的轨迹是椭圆. 故选B .【点晴】方法点睛:本题考查空间向量、轨迹及其方程,涉及方程思想、数形结合思想和转化化归思想,考查空间想象能力逻辑思维能力、等价转化能力、运算求解能力,综合性较强,属于较难题型.9.(山东淄博市·高三一模)四棱锥中,侧面为等边三角形,底面为矩形,,(0,1,0),(0,0,1),(,,0)(0,1,1),(,,1)B A P x y AB AP x y ⇒=-=-22cos ,62(2)112AB AP x y ⇒<>=⇒+-=P (0,1,0),(0,0,1),(,,0)(0,1,1),(,,1)B A P x y AB AP x y ⇒=-=-22cos ,62(2)11AB AP x y ⇒<>=⇒+-=P S ABCD -SBC ABCD 2BC =,点是棱的中点,顶点在底面的射影为,则下列结论正确的是( )A .棱上存在点使得面B .当落在上时,的取值范围是C .当落在上时,四棱锥的体积最大值是2D .存在的值使得点到面【答案】A 【分析】对于A:取BC 的中点E ,连结DE ,取SC 中点P ,连结PE 、PD .利用面PDE ∥面BFS ,可以证明面; 对于B :利用S 与H 重合,图形不能构成四棱锥,判断B 错误;对于C :求出体积的最大值为1.故C 错误;对于D :先判断当的最大时,点B 到面的距离d 最大;然后求出,判断D 错误. 【解析】对于A :取BC 的中点E ,连结DE ,取SC 中点P ,连结PE 、PD . ∵PE 为△BCS 的中位线,∴ PE ∥BS又面BFS ,面BFS ,∴PE ∥面BFS ;在矩形ABCD 中,E 、F 分别为BC 、AD 的中点,∴DE ∥BF , 又面BFS ,面BFS ,∴DE 面BFS ; 又,∴面PDE ∥面BFS ,∴面.故A 正确;对于B :∵为等边三角形,,∴AB a F AD S ABCD H SC P //PD BSF H AD a (H AD S ABCD -a B SFC //PD BSF a =S ABCD V -S ABCD V -SFC 3d <BS ⊆PE ⊄BF ⊆DE ⊄DEPE E =//PD BSF SBC 2BC =SE =当S 与H 重合,图形不能构成四棱锥,与已知条件相悖,故B 错误;对于C :在Rt △SHE 中,当且仅当时,的最大值为1.故C 错误; 对于D :由选项C 的推导可知:当的最大时,点B 到面的距离d 最大.此时 ∴ ∴.故D 错误. 故选A 【点睛】(1)证明线面平行,用线面平行的判定定理,在面内找一条直线与已知直线平行; (2)等体积法是求三棱锥高的常用方法.10.(湖北武汉市·高三月考)已知三棱锥的各个顶点都在球的表面上,底面,,,,是线段上一点,且.过点作球的截面,若所得截面圆面积的最大值与最小值之差为,则球的表面积为( ) A . B .C .D .【答案】B 【分析】将三棱锥补成长方体,设,计算出球的半径为,计算出截面圆半径的最大值和最小值,根据已知条件可求得的值,可求得球的半径,进而可求得球的表面积. 【解析】平面,,将三棱锥补成长方体,如下图所示:a =SH =1213S ABCD V a-=⨯=≤232a =S ABCD V -S ABCD V -SFC 1122S BFC S ABCD V V --==SFCF ===1122224SFC S SF CF =⨯=⨯=△1325V d S ===<P ABC -O PA ⊥ABC AB AC ⊥6AB =8AC =D AB 2AD DB =D O 25πO 128π132π144π156πP ABC -PQMN ABEC -2PA x =O R =x O O PA ⊥ABC AB AC ⊥P ABC -PQMN ABEC -设,连接、、,可知点为的中点,因为四边形为矩形,,则为的中点,所以,且,设,且,,所以,球的半径为, 在中,,,,, 在中,,, 由余弦定理可得平面,平面,平面,则,,, 设过点的球的截面圆的半径为,设球心到截面圆的距离为,设与截面圆所在平面所成的角为,则.当时,即截面圆过球心时,取最小值,此时取最大值,即;当时,即与截面圆所在平面垂直时,取最大值,即,此时,取最小值,即.由题意可得,,解得所以,,AE BC F=OF DF OD O PE ABEC AE BC F =F AE //OF PA 12OF PA =2PA x =10AE ==PE ∴==O 12R PE ==Rt ABE △2ABE π∠=6AB =10AE =3cos 5AB BAE AE ∠==ADF 243AD AB ==5AF =DF ==PA ⊥ABCD OF ∴⊥ABCD DF ⊂ABCD OF DF ⊥12OF PA x ==OD ∴==D O r O d OD θsin d OD θ==0θ=O d r max r R ==2πθ=OD d max d OD ==r min r ==()()()222max min 1725r r x πππ⎡⎤-=+=⎣⎦0xx =R =因此,球的表面积为. 故选B . 【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径;③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.11.(安徽蚌埠市·高三二模(理))已知直四棱柱,其底面是平行四边形,外接球体积为,若,则其外接球被平面截得图形面积的最小值为( ) A . B .C .D .【答案】A 【分析】由条件可得为矩形,进而可得平面,所以,则四边形为正方形,所以直四棱柱为正四棱柱,设,由余弦定理可得的值,求出的值,由正弦定理可得的外接圆的半径为,由均值不等式可得的最小值,从而得出答案. 【解析】由直四棱柱内接于球,则四点在球面上, 所以四边形为球的一截面圆的内接四边形,所以对角互补. 又四边形是平行四边形,所以为矩形.在直四棱柱中,平面,所以 又,,所以平面,所以所以四边形为正方形,所以直四棱柱为正四棱柱.O 24132S R ππ==1111ABCD A B C D -ABCD 36π1AC BD ⊥11AB D 8π24310π8110π6πABCD BD ⊥1ACC BD AC ⊥ABCD 1111ABCD A B C D -1,AB AD a CC b ===11cos AD B ∠11sin AD B ∠11ABD 2r =r1111ABCD A B C D -,,,A B C D ABCD ABCD ABCD 1111ABCD A B C D -1CC ⊥ABCD 1CC BD ⊥1AC BD ⊥111AC CC C =BD ⊥1ACC BD AC ⊥ABCD 1111ABCD A B C D -由外接球体积为,则球的半径为,由为该外接球的直径,则设,则,则在中,由余弦定理可得所以设的外接圆的半径为,由正弦定理可得所以,即时取得等号,即的最小值为其外接球被平面截得图形面积的最小值为:故选A【点睛】关键点睛:本题考查几何体的外接球的截面面积问题,解答本题的关键是先由线面垂直关系得出直四棱柱为正四棱柱,然后由余弦定理和正弦定理得出的外接圆的半径,由均值不等式求出最小值,属于难题.34363Rππ=3R=1AC16AC=1,ABAD a CC b===2221236AC a b=+=22362b a=-11AB D11AB AD====11B D=2222111111111cos2AD B D ABAD BAD B D+-∠===⋅11sin AD B∠===11AB D r2111362sinaABrAD B-===∠22r⎫===≥==a=r11AB D28S rππ==1111ABCD A B C D-11AB D2r=12.(浙江省宁海中学高三月考)如图,在中,,,点E 为线段AB 上一点,将绕DE 翻折.若在翻折过程中存在某个位置,使得,记为的最小值,则( )A .B .C .D .【答案】C 【分析】易知,A 在以AD 为母线的圆锥上的一部分(弧AF ),与所成的最大角为,只需. 【解析】如图,与所成的最大角为,只需即可. 即, 即,即.故选C . 【点睛】本题考查几何中的翻折问题,考查学生的空间想象能力、转化与化归能力,是一道难题.ABC ∆36A ∠=AD DB BC ==ADE ∆AE CD ⊥θADE∠(15,20]θ∈(20,25]θ∈(25,30]θ∈(30,35]θ∈AE CD FGA ∠90FGA ∠≥AE CD FGA ∠90FGA ∠≥90(54)(90)AFG FAG ADE ADE ≥∠+∠=-∠+-∠27ADE ∠≥27(25,30]θ=∈13.(天津河西区·高三一模)将长、宽分别为和的长方形沿对角线折成直二面角,得到四面体,则四面体的外接球的表面积为( ) A . B .C .D .【答案】A 【分析】取的中点,说明为四面体的外接球的球心,求出球的半径,利用球体的表面积公式可求得结果. 【解析】取的中点,连接、,如下图所示:由题意,因为,为的中点,所以,, 所以,为四面体的外接球的球心,且球的半径为,因此,四面体的外接球的表面积为. 故选A . 【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径;③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.43ABCD AC A BCD -A BCD -25π50π5π10πAC O O A BCD -O AC OBOD 5AC ==90ABC ADC ∠=∠=O AC 1522OB OD AC OA OC =====O A BCD -O 52R =A BCD -2425R ππ=14.(江西八校4月联考(理))已知三棱锥的外接球的表面积为,,,,,则三棱锥的体积为( )A .8 BC .D .16【答案】A 【分析】求出球的半径得是球直径,中点是球心,取中点,则平面,求得后可得到底面的距离,从而可求得棱锥的高.【解析】设球半径为,则,,而,所以是球的直径,球心是中点,,所以中点是直角外心,所以平面,又平面,所以,,,, 是中点,所以. 故选A .【点睛】关键点点睛:本题考查求棱锥体积,关键是求得棱锥的高,由于已知外接球的表面积,求得 半径后确定就是球的直径,从而利用球的截面圆性质,易得平面的垂线,再由体积公式计算.15.(山西临汾市·高三一模(理))在棱长为2的正方体中,平面,则以平面P ABC-64π2AB=AC =AB AC ⊥8PA =P ABC -3PA PA O BC E OE ⊥ABC OE P R 2464R ππ=4R =8PA =PA O PA AB AC ⊥BC E ABCOE ⊥ABC AE ⊂ABC OE AE ⊥4BC ==122AE BC ==OE ===O AP 11122228332P ABC O ABC ABC V V S OE --==⨯⋅=⨯⨯⨯⨯=△PA ABC 1111ABCD A B C D -1B D α⊥截正方体所得的截面面积最大时的截面为底面,以为顶点的锥体的外接球的表面积为( )A .B .C .D .【答案】B【分析】由正方体的对称性,可知当截面为正六边形时,截面面积最大,再分当球心在棱锥内部时和当球心在棱锥外部时,建立方程求得外接球的半径可得选项. 【解析】如图,由正方体的对称性,可知当截面为正六边形, 设交截面于,则为的中点,所以设正六棱锥外接球的球心为,外接球半径为,当球心在棱锥内部时,有,解得,外接球面积为; 若球心在棱锥外部时,有,解得.∴以为顶点的锥体的外接球的表面积为.故选B . 【点睛】方法点睛:求解几何体外接球半径的思路是依据球的截面的性质:利用球的半径、截面圆的半径及球心到截面的距离三者的关系求解,其中确定球心的位置是关键.16.(浙江省宁海中学高三月考)如图,矩形中,,点在,上,满足,,将沿向上翻折至,使得在平面上的射影落在的重心处,设二面角的大小为,直线,与平面所成角分别为,,则( )α1B 12π253π203π6πEFGHKI EFGHKI 1B D EFGHKI M M 1B D 1112B M B D ==O R )222R R =+R =22543ππ⨯=(222R R =+-R =<1B 253πR r d 222R r d =+ABCD 236AB AD ==(),1,2i i E F i =CD AD 112E F =1221//E F E F 11DE F ∆11E F 11D E F ∆'D 'ABCD 22DE F ∆G D AB C '--αD A 'D C 'ABCD βγA .B .C .D .【答案】A 【分析】作的中垂线,根据几何关系得知点落在左边,故可得,则问题可解. 【解析】作的中垂线,中点为,取中点,故在上, 作交于,连接,如图所示:因为,,,可知点在左边, 则,由图可知,故 易知 ,由于 所以,则故选A 【点睛】关键点点睛:本题的关键在于根据几何图形关系判断.17.(河南高三一模(理))如图,在棱长为1正方体中,为棱的中点,动点αβγ>>γαβ>>αγβ>>βαγ>>AC ML G ML GN GA GC <<AC ML AC O 22E F H G DH GN AB ⊥AB N ,GAGC 112E F =1221//E F E F 3,2AB AD ==G ML GA GC <GA GN >GN GA GC <<tan ,tan ,tan D G D G D GGN GA GCαβγ'''===GN GA GC <<tan tan tan αβγ>>αβγ>>GN GA GC <<1111ABCD A B C D -M AB P在侧面及其边界上运动,总有,则动点的轨迹的长度为( )A .BC .D【答案】A 【分析】分别取、的中点、,连,利用线面垂直的判定定理和性质可证动点的轨迹是线段,求出的长度即可得解. 【解析】如图:分别取、的中点、,连,,,因为为的中点,为的中点,为正方形,所以, 又平面,所以,而,所以平面,所以,同理可得,又,所以平面, 因为平面,所以,因为动点在侧面及其边界上运动,所以动点的轨迹是线段,而,所以动点的11BCC B 1AP D M ⊥P 2π16BC 1BB E F EF P EF EF BC 1BB E F ,,AE AF EF 1,A M DM 1A F M AB E BC ABCD DM AE ⊥1D D ⊥ABCD 1D D AE ⊥1DMD D D =AE ⊥1D DM 1D M AE ⊥1D M AF ⊥AE AF A ⋂=1D M ⊥AEF AP ⊂AEF 1AP D M ⊥P 11BCC B P EF 2EF =P轨迹的长度为.故选A . 【点睛】关键点点睛:作出并证明动点的轨迹是本题解题关键,分别取、的中点、,连,则线段即为动点的轨迹,利用线面垂直的判定定理和性质即可得证.18.(江苏徐州市·高三二模)“帷幄”是古代打仗必备的帐篷,又称“幄帐”.如图是一种幄帐示意图,帐顶采用“五脊四坡式”,四条斜脊的长度相等,一条正脊平行于底面.若各斜坡面与底面所成二面角的正切值均为,底面矩形的长与宽之比为,则正脊与斜脊长度的比值为( )A .B .C .D .1【答案】B 【分析】取幄帐顶部,如图几何体,作平面,垂足为,则到边的距离相等,作于,于,得是二面角的平面角,是二面角的平面角,因此有,设,用表示出,即可得比值.【解析】取幄帐顶部,如图几何体,作平面,垂足为,则到边的距离相等,由平面,平面,得,同理. 作于,于, 因为,平面,所以平面,而平面,所以,所以是二面角的平面角,同理是二面角的平面角,,由已知,2P BC 1BB E F EF EF P 125:33589910ABCD EF -FO ⊥ABCD O O ,AB CD FM AB ⊥M FN BC ⊥N FNO ∠F BC O --FMO ∠F AB O --1tan tan 2FNO FMO ∠=∠=5,3AB a BC a ==a ,EF FB ABCD EF -FO ⊥ABCD O O ,AB CD FO ⊥ABCD BC ⊂ABCD FO BC ⊥FO OB ⊥FM AB ⊥M FN BC ⊥N FOFN F =,FO FN ⊂FON BC ⊥FON ON ⊂FON BC ON ⊥FNO ∠F BC O --FMO ∠F AB O --OM AB ⊥1tan tan 2FNO FMO ∠=∠=由,设,则,所以, 由得,,则, 由上知是正方形,,, 所以.故选B .【点睛】关键点点睛:本题考查由二面角计算线段长,考查学生的空间想象能力.解题是作出各斜坡面与底面所成二面角的平面角,利用它们的正切值均为,并设出底面矩形边长后,用底面矩形边长表示出正脊与斜脊的长度,从而得比值.19.(浙江名校协作体联考)在矩形中,,,E 、F 分别为边、上的点,且,现将沿直线折成,使得点在平面上的射影在四边形内(不含边界),设二面角的大小为,直线与平面所成的角为,直线与直线所成角为,则( )A .B .C .D .【答案】D:5:3AB BC =5,3AB a BC a ==32MO a =313tan 224FO MO FMO a a =⋅∠=⨯=1tan 2FO FNO ON ∠==32ON a =35222EF a a a =-⨯=OMBN 2OB a ==94FB a ===28994EF a FB a ==12ABCD AB =3AD =AD BC 2AE BF ==ABE △BE 1A BE 1A BCDE CDEF 1A BE C --θ1A B BCDE α1A E BCββαθ<<βθα<<αβθ<<αθβ<<【分析】根据题意作出相应的二面角,线面角,线线角,结合点在平面上的射影求解. 【解析】过A 作的垂线,分别交,,于M ,G ,N ,如图,显然.因为,所以直线与所成角即为.当在平面上的射影为G 时,平面,此时.于是当在平面上的射影在线段上时,,所以. 由于,,进而得,.因为是在平面上的射影,所以由线面角最小性知,即.再由二面角的最大性知.故选D .【点睛】关键点点睛:根据二面角平面角、线面角、异面直线所成的的角的定义,分别在图形中作出或找到是解题的关键,再根据位置分析角的变化范围即可比较大小.20.(河南高考适应性考试(理))棱长为的正方体密闭容器内有一个半径为的小球,小球可在正方体容器内任意运动,则其不能到达的空间的体积为( ) A . B . C . D . 【答案】A【分析】由题可得小球在八个角不能到达的空间相当于边长为2的正方体中间挖掉一个半径为1的球的剩余部分,小球在12条边活动不到的空间相当于高为2,底面积为4的正四棱柱中间挖掉底面积为,高为2的圆柱剩下的部分,且有3个,由此可计算出体积.【解析】由题可得小球在八个角不能到达的空间相当于边长为2的正方体中间挖掉一个半径为1的球的剩余部分,其体积为,小球在12条边活动不到的空间相当于高为2,底面积为4的正四棱柱中间挖掉底面积为,高为2的圆柱剩下的部分,且有3个,则其体积为,1A BCDE BE EB EFDC A MN θ'∠=//BC AD A E 'AD βA 'BCDE AE ⊥A EF '2πβ=A 'BCDE GN 2A ED π'∠<A ED β'=∠EA EA '=MA MA '=2EAA β'∠=2MAA θ'∠=AM AA 'ABCD 22EAA MAA βθ''∠=>∠=βθ>θα>,,βθα4122323π-4812π-4283π-13203π-π334421833ππ-⨯=-π()4223246ππ⨯-⨯=-则小球不能到达的空间的体积为.故选A . 【点睛】本题考查几何体体积的计算,解题的关键是得出小球在运动中不能到达的空间的结构特点. 21.(辽宁高三一模(理))球面上两点之间的最短连线的长度,就是经过这两个点的大圆在这两点间的一段劣弧的长度(大圆就是经过球心的平面截球面所得的圆),我们把这个弧长叫做两点的球面距离.已知正的项点都在半径为的球面上,球心到,则、两点间的球面距离为( ) A . B .C .D .【答案】C【分析】设球心为点,计算出,利用扇形弧长公式可求得结果.【解析】设球心为点,平面截球所得截面圆的半径为, 由正弦定理可得,,又,所以,为等边三角形,则,因此,、两点间的球面距离为.故选C . 【点睛】思路点睛:求球面距离,关键就是要求出球面上两点与球心所形成的角,结合扇形的弧长公式求解,同时在计算球的截面圆半径时,利用公式(其中为截面圆的半径,为球的半径,为球心到截面的距离)来计算.22.(湖北武汉市·高三月考)某圆锥母线长为2面面积的最大值为( )A .2B CD .1【答案】A【分析】如图截面为,P 为MN 的中点,设,,进而可得面积最大值. 【解析】()4228+2463233πππ⎛⎫--=- ⎪⎝⎭ABC 2ABC A B π2π23π34πO AOB ∠O ABC O r ==3sin AB ACB =∠233AB π∴==2OA OB ==AOB 3AOB π∠=A B 2233ππ⨯=22d R r -=r R d SMN (0=<≤OP x x =SMNS。
浙江高考试题分类汇编立体几何

浙江高考试题分类汇编立体几何The following text is amended on 12 November 2020.浙江高考试题分类汇编-立体几何一.选择题1.(2018 浙江 3)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 2)是( )A. 2B. 4C. 6D. 82.(2018 浙江 6).已知平面a ,直线m ,n 满足,m n αα⊄⊂,则“m ∥n ”是“m α”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件3、(2018 浙江 8)已知道四棱锥S-ABCD 的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ ,SE 与平面ABCD 所成的角为2θ,二面角S-AB-C 的平面角为3θ,则A. 123θθθ≤≤B. 321θθθ≤≤C. 132θθθ≤≤D. 231θθθ≤≤4.(2017 浙江 3)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是( )A .+1B .+3C .+1D .+35.(2017 浙江 9)如图,已知正四面体D﹣ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,==2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则()A.γ<α<βB.α<γ<βC.α<β<γD.β<γ<α6.(2015 浙江 2)某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A.8cm3B.12cm3C.D.7.(2015 浙江理 8)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′﹣CD﹣B的平面角为α,则()A.∠A′DB≤αB.∠A′DB≥αC.∠A′CB≤αD.∠A′CB≥α8.(2014 浙江理3)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是()A.90cm2B.129cm2C.132cm2D.138cm29.(2014浙江理3)某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.72cm3B.90cm3C.108cm3D.138cm3二.填空题1.(2016 浙江理11)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是cm2,体积是cm3.2.(2016 浙江理14)如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是.3.(2016 浙江文 9)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是cm2,体积是cm3.4.(2016 浙江文14)如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=,∠ADC=90°,沿直线AC将△ACD翻折成△ACD′,直线AC与BD′所成角的余弦的最大值是.5.(2015 浙江理 14)如图,三棱锥A﹣BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是.三.解答题1.(2018 浙江 19)如图,已知多面体ABC-A1B1C1,A1A、B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2。
压轴题05 立体几何压轴题(原卷版)--2023年高考数学压轴题专项训练(全国通用-文)

压轴题05立体几何压轴题题型/考向一:点、线、面间的位置关系和空间几何体的体积、表面积题型/考向二:外接球、内切球等相关问题题型/考向三:平面关系、垂直关系、体积、表面积等综合问题一、空间几何体的体积、表面积热点一空间几何体的侧面积、表面积柱体、锥体、台体和球的表面积公式:(1)若圆柱的底面半径为r,母线长为l,则S侧=2πrl,S表=2πr(r+l).(2)若圆锥的底面半径为r,母线长为l,则S侧=πrl,S表=πr(r+l).(3)若圆台的上、下底面半径分别为r′,r,则S侧=π(r+r′)l,S表=π(r2+r′2+r′l +rl).(4)若球的半径为R,则它的表面积S=4πR2.热点二空间几何体的体积柱体、锥体、台体和球的体积公式:(1)V柱体=Sh(S为底面面积,h为高);Sh(S为底面面积,h为高);(2)V锥体=13(S上+S下+S上S下)h(S上、S下分别为上、下底面面积,h为高);(3)V台体=13(4)V球=4πR3.3二、外接球、内切球问题类型一外接球问题考向1墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决,外接球的直径等于长方体的体对角线长.长方体同一顶点的三条棱长分别为a,b,c,外接球半径为R.则(2R)2=a2+b2+c2,即2R=a2+b2+c2.常见的有以下三种类型:考向2对棱相等模型对棱相等模型是三棱锥的三组对棱长分别相等模型,用构造法(构造长方体)解决,外接球的直径等于长方体的体对角线长,如图所示,(2R )2=a 2+b 2+c 2(长方体的长、宽高分别为a ,b ,c ),即R 2=18(x 2+y 2+z 2),如图.考向3汉堡模型汉堡模型是直三棱柱、圆柱的外接球模型,模型如下,由对称性可知,球心O 的位置是△ABC 的外心O 1与△A 1B 1C 1的外心O 2的连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=h 2,所以R 2=r 2+h 24.考向4垂面模型垂面模型是有一条侧棱垂直底面的棱锥模型,可补为直棱柱内接于球;如图所示,由对称性可知球心O 的位置是△CBD 的外心O 1与△AB 2D 2的外心O 2连线的中点,算出小圆O1的半径CO1=r,OO1=h2,则R=r2+h24.类型二内切球问题内切球问题的解法(以三棱锥为例)第一步:先求出四个表面的面积和整个锥体的体积;第二步:设内切球的半径为r,建立等式V P-ABC=V O-ABC+V O-P AB+V O-P AC+V O-PBC⇒V P-ABC=13S△ABC·r+13S△P AB·r+13S△P AC·r+13S PBC·r=13(S△ABC+S△P AB+S△P AC+S△PBC)r;第三步:解出r=3V P-ABCS△ABC+S△P AB+S△P AC+S△PBC.类型三球的截面问题解决球的截面问题抓住以下几个方面:(1)球心到截面圆的距离;(2)截面圆的半径;(3)直角三角形(球心到截面圆的距离、截面圆的半径、球的半径构成的直角三角形).三、平行关系和垂直关系的证明、二面角等热点一空间线、面位置关系的判定判断空间线、面位置关系的常用方法(1)根据空间线面平行、垂直的判定定理和性质定理逐项判断,解决问题.(2)利用直线的方向向量、平面的法向量判断.(3)必要时可以借助空间几何模型,如从长方体、四面体等模型中观察线、面的位置关系,并结合有关定理进行判断.热点二几何法证明平行、垂直1.直线、平面平行的判定及其性质(1)线面平行的判定定理:a⊄α,b⊂α,a∥b⇒a∥α.(2)线面平行的性质定理:a∥α,a⊂β,α∩β=b⇒a∥b.(3)面面平行的判定定理:a⊂β,b⊂β,a∩b=P,a∥α,b∥α⇒α∥β.(4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b⇒a∥b.2.直线、平面垂直的判定及其性质(1)线面垂直的判定定理:m⊂α,n⊂α,m∩n=P,l⊥m,l⊥n⇒l⊥α.(2)线面垂直的性质定理:a⊥α,b⊥α⇒a∥b.(3)面面垂直的判定定理:a⊂β,a⊥α⇒α⊥β.(4)面○热○点○题○型一点、线、面间的位置关系和空间几何体的体积、表面积一、单选题1.设l ,m 是两条不同的直线,α,β,γ是三个不同的平面,下列说法正确的是()A .若//l α,//m α,则//l mB .若//l α,//l β,则//αβC .若l α⊥,m α⊥,则//l mD .若αγ⊥,βγ⊥,则//αβ2.将半径为6的半圆卷成一个无底圆锥(钢接处不重合),则该无底圆锥的体积为()A .273πB .27πC .3πD .9π3.在正方体1111ABCD A B C D -中,直线m 、n 分别在平面ABCD 和11ABB A ,且m n ⊥,则下列命题中正确的是()A .若m 垂直于AB ,则n 垂直于AB B .若m 垂直于AB ,则n 不垂直于ABC .若m 不垂直于AB ,则n 垂直于ABD .若m 不垂直于AB ,则n 不垂直于AB4.如图是一款多功能粉碎机的实物图,它的进物仓可看作正四棱台,已知该四棱台的上底面边长为40cm ,下底面边长为10cm ,侧棱长为30cm ,则该款粉碎机进物仓的容积为()A .32cmB .386003cmC .3105002cmD .33cm5.已知在春分或秋分时节,太阳直射赤道附近.若赤道附近某地在此季节的日出时间为早上6点,日落时间为晚上18点,该地有一个底面半径为4m 的圆锥形的建筑物,且该建筑物在一天中恰好有四个小时在地面上没有影子,则该建筑物的体积为()A .643πB .π3C .16π3D .π36.攒尖是古代中国建筑中屋顶的一种结构形式,依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑.如故宫中和殿的屋顶为四角攒尖顶,它的主要部分的轮廓可近似看作一个正四棱锥,设正四棱锥的侧面等腰三角形的顶角为60°,则该正四棱锥的侧面积与底面积的比为()A .4B 3C D 7.在三棱锥A BCD -中,4AB AC BD CD BC =====,平面α经过AC 的中点E ,并且与BC 垂直,则α截此三棱锥所得的截面面积的最大值为()A B .34C 2D .328.已知圆台的母线长为4,上底面圆和下底面圆半径的比为1:3,其侧面展开图所在扇形的圆心角为π2,则圆台的高为()A .BC .4D .二、多选题9.已知平面α,β,直线l ,m ,则下列命题正确的是()A .若αβ⊥,,,m l m l αβα⋂=⊥⊂,则l β⊥B .若l αβα⊂∥,,m β⊂,则//l mC .若m α⊂,则“l α⊥”是“l m ⊥”的充分不必要条件D .若m α⊂,l α⊄,则“l α∥”是“l m ”的必要不充分条件10.下列说法正确的是()A .若直线a 不平行于平面α,a α⊄,则α内不存在与a 平行的直线B .若一个平面α内两条不平行的直线都平行于另一个平面β,则αβ∥C .设l ,m ,n 为直线,m ,n 在平面α内,则“l α⊥”是“l m ⊥且l n ⊥”的充要条件D .若平面α⊥平面1α,平面β⊥平面1β,则平面α与平面β所成的二面角和平面1α与平面1β所成的二面角相等或互补三、解答题11.已知直棱柱1111ABCD A B C D -的底面ABCD 为菱形,且2AB AD BD ===,1AA =,点E 为11B D 的中点.(1)证明://AE 平面1BDC ;(2)求三棱锥1E BDC -的体积.12.如图,在三棱柱111ABC A B C -中,ABC 为边长为2的正三角形,D 为BC 的中点,12AA =,且160CCB ∠= ,平面11BB C C ⊥平面ABC .(1)证明:1C D AB ⊥;(2)求三棱锥111B AA C -的体积.○热○点○题○型二外接球、内切球等相关问题一、单选题1.已知ABC 是边长为3的等边三角形,其顶点都在球O 的球面上,若球O 的体积为323π,则球心O 到平面ABC 的距离为()AB .32C .1D .22.已知三棱锥-P ABC 的底面ABC 是边长为1的正三角形,侧棱,,PA PB PC 两两垂直,若此三棱锥的四个顶点都在同一个球面上,则该球的表面积是()A .3πB .πC .3π4D .3π23.一个圆锥的底面圆和顶点都恰好在一个球面上,且这个球的半径为5,则这个圆锥的体积的最大值时,圆锥的底面半径为()A .103B .2C .3D 4.已知圆锥的侧面积为2π,母线与底面所成角的余弦值为12,则该圆锥的内切球的体积为()A .4π3B C D 5.如图,几何体Ω为一个圆柱和圆锥的组合体,圆锥的底面和圆柱的一个底面重合,圆锥的顶点为A ,圆柱的上、下底面的圆心分别为B 、C ,若该几何体Ω存在外接球(即圆锥的顶点与底面圆周在球面上,且圆柱的底面圆周也在球面上).已知24BC AB ==,则该组合体的体积等于()A .56πB .70π3C .48πD .64π6.已知矩形ABCD 的顶点都在球心为O 的球面上,3AB =,BC =,且四棱锥O ABCD-的体积为,则球O 的表面积为()A .76πB .112πCD 7.水平桌面上放置了4个半径为2的小球,4个小球的球心构成正方形,且相邻的两个小球相切.若用一个半球形的容器罩住四个小球,则半球形容器内壁的半径的最小值为()A .4B .2C .2D .68.已知三棱锥-P ABC 的四个顶点均在球O 的球面上,2PA BC ==,PB AC ==PC AB =Q 为球O 的球面上一动点,则点Q 到平面PAB 的最大距离为()A 2211B C 2211D 二、填空题9.在三棱锥-P ABC 中,PA ⊥平面ABC ,14AB AC PA AB AC ⊥=+=,,,当三棱锥的体积最大时,三棱锥-P ABC 外接球的体积为______.10.如图,在直三棱柱111ABC A B C -中,1AA AB BC ==.设D 为1AC 的中点,三棱锥D ABC -的体积为94,平面1A BC ⊥平面11ABB A ,则三棱柱111ABC A B C -外接球的表面积为______.11.如图,直三棱柱111ABC A B C -的六个顶点都在半径为1的半球面上,AB AC =,侧面11BCC B 是半球底面圆的内接正方形,则直三棱柱111ABC A B C -的体积为___________.12.如图所示的由4个直角三角形组成的各边长均相等的六边形是某棱锥的侧面展开图,若该六边形的面积为12,则该棱锥的内切球半径为___.○热○点○题○型三平面关系、垂直关系、体积、表面积等综合问题1.已知直棱柱1111ABCD A B C D -的底面ABCD 为菱形,且2AB AD BD ===,1AA =,点E 为11B D 的中点.(1)证明://AE 平面1BDC ;(2)求三棱锥1E BDC -的体积.2.如图,在四棱锥P ABCD -中,PAD 是等边三角形,底面ABCD 是棱长为2的菱形,平面PAD ⊥平面ABCD ,O 是AD 的中点,π3DAB ∠=.(1)证明:OB ⊥平面PAD ;(2)求点O 到平面PAB 的距离.3.如图,在三棱柱111ABC A B C -中,ABC 为边长为2的正三角形,D 为BC 的中点,12AA =,且160CCB ∠= ,平面11BB C C ⊥平面ABC .(1)证明:1C D AB ⊥;(2)求三棱锥111B AAC -的体积.4.如图1,在直角梯形ABCD 中,90ADC ∠=︒,AB CD ,122AD CD AB ===,E 为AC 的中点,将ACD 沿AC 折起,使折起后的平面ACD 与平面ABC 垂直,如图2.在图2所示的几何体D ABC -中:(1)求证:BC ⊥平面ACD ;(2)点F 在棱CD 上,且满足AD EF ,求几何体F BCE -的体积.5.在如图所示的几何体中,四边形ABCD 为菱形,60BCD ∠=︒,4AB =,EF CD ∥,2EF =,4CF =,点F 在平面ABCD 内的射影恰为BC 的中点G .(1)求证:平面ACE 平面BED;(2)求该几何体的体积.。
浙江省普通高校招生学考科目考试2021年高考数学高考数学压轴题 立体几何多选题分类精编附答案

对于D选项,过 点做 的平行线交 于 ,交 于 ,连接 ,则过 , , 的平面截正方体所得截面即为平行四边形 ,易知当 位于点 时,平行四边形 边 最小,且为 ,此时截面平行四边形 的面积最小,为四边形 的面积,且面积为 ,故D选项正确;
【答案】CD
【分析】
利用反证法可得A、B错误,取 为 的中点,取 的中点为 ,连接 ,可证明 平面 ,当平面 平面 时,四棱锥 体积最大值,利用公式可求得此时体积为 .
【详解】
如图(1),取 的中点为 ,连接 ,
则 , ,故 ,
故 即 .
若 ,因为 ,故 ,而 ,
故 平面 ,因为 平面 ,故 ,矛盾,故A错.
【详解】
如图所示,作AM⊥DE,交DE于M,延长AM交BC于N,连接A'M,A'N.
则A'M⊥DE,MN⊥DE, ,
∵ ∩MN=M,∴CD⊥平面A'MN,
又∵CD⊂平面ABDC,∴平面A'MN⊥平面ABDC,
在平面A'MN中作A'H⊥MN,则A'H⊥平面BCED,
∵二面角A'-DE-B为60°,∴∠A'EF=60°,
对于C,若 , ,则 ,即 ,即 ,故C正确;
对于D,
,又 , ,故D错误.
故选:BC
【点睛】
关键点睛:本题考查向量的运算,用已知向量表示某一向量的三个关键点:
(1)用已知向量来表示某一向量,一定要结合形,以图形为指导是解题的关键.
(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量.
浙江省高考数学压轴试卷
高考数学压轴试卷题号一二三总分得分一、选择题(本大题共11小题,共44.0分)1.已知全集U={1,2,3,4,5,6},集合A={1,3,5},B={1,2},则A∩(∁U B)()A. ∅B. {5}C. {3}D. {3,5}2.已知双曲线(a>0)的离心率为,则a的值为()A. B. C. D.3.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”.已知某“堑堵”的三视图如图所示,俯视图中间的实线平分矩形的面积,则该“堑堵”的表面积为()A. 4+2B. 2C. 4+4D. 6+44.若复数z满足:1+(1+2z)i=0(i是虚数单位),则复数z的虚部是()A. B. C. D.5.函数y=2x2-e|x|在[-2,2]的图象大致为()A. B.C. D.6.已知平面α与两条不重合的直线a,b,则“a⊥α,且b⊥α”是“a∥b”的()A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件7.(1-x)4(1+x)5的展开式中x3的系数为()A. 4B. -4C. 6D. -68.4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动.为了查.根据调查结果知道,从该校学生中任意抽取1名学生恰为读书迷的概率是.现在从该校大量学生中,用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中的“读书迷”的人数为X.若每次抽取的结果是相互独立的,则期望E(X)和方差D(X)分别是()A. ,B. ,C. ,D. ,9.已知A,B,C是球O球面上的三点,且,D为该球面上的动点,球心O到平面ABC的距离为球半径的一半,则三棱锥D-ABC体积的最大值为()A. B. C. D.10.设S n为等差数列{a n}的前n项和,若a7=5,S5=-55,则nS n的最小值为()A. B. C. D.11.某校毕业典礼由6个节目组成,考虑整体效果,对节目演出顺序有如下要求:节目甲必须排在前三位,且节目丙、丁必须排在一起,则该校毕业典礼节目演出顺序的编排方案共有()A. 120种B. 156种C. 188种D. 240种二、填空题(本大题共6小题,共32.0分)12.《九章算术》第七章“盈不足”中第一题:“今有共买物,人出八,盈三钱;人出七,不足四,问人数物价各几何?”借用我们现在的说法可以表述为:有几个人合买一件物品,每人出8元,则付完钱后还多3元;若每人出7元,则还差4元才够付款.问他们的人数和物品价格?答:一共有______人;所合买的物品价格为______元.13.已知x,y满足条件则2x+y的最大值是______,原点到点P(x,y)的距离的最小值是______14.在△ABC中,若b=2,A=120°,三角形的面积,则c=________;三角形外接圆的半径为________.15.已知向量、满足||=1,||=2,则|+|+|-|的最小值是______,最大值是______.16.已知实数f(x)=,若关于x的方程f2(x)+f(x)+t=0有三个不同的实根,则t的取值范围为______.17.已知直线y=-x+1与椭圆+=1(a>b>0)相交于A,B两点,且OA⊥OB(O为坐标原点),若椭圆的离心率e∈[,],则a的最大值为______.三、解答题(本大题共5小题,共60.0分)18.设函数f(x)=sin(ωx-)+sin(ωx-),其中0<ω<3,已知f()=0.(Ⅰ)求ω;(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在[-,]上的最小值.19.已知等差数列{a n}的前n项和为S n,若.(1)求首项a1与m的值;(2)若数列{b n}满足,求数列{(a n+6)•b n}的前n项和.20.如图,已知四棱锥P-ABCD,底面ABCD为菱形,AB=2,∠BAD=120°,PA⊥平面ABCD,M,N分别是BC,PC的中点.(1)证明:AM⊥平面PAD;(2)若H为PD上的动点,MH与平面PAD所成最大角的正切值为,求二面角M-AN-C的余弦值.21.已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点P(4,m)到焦点的距离为5.(1)求该抛物线C的方程;(2)已知抛物线上一点M(t,4),过点M作抛物线的两条弦MD和ME,且MD⊥ME,判断直线DE是否过定点?并说明理由.22.已知函数.若函数是单调递减函数,求实数a的取值范围;若函数在区间上既有极大值又有极小值,求实数a的取值范围.答案和解析1.【答案】D【解析】解:∵U={1,2,3,4,5,6},B={1,2},∴∁U B═{3,4,5,6},又集合A={1,3,5},∴A∩∁U B={3,5},故选:D.先由补集的定义求出∁U B,再利用交集的定义求A∩∁U B.本题考查交、并补集的混合运算,解题的关键是熟练掌握交集与补集的定义,计算出所求的集合.2.【答案】B【解析】解:双曲线,可得c=1,双曲线的离心率为:,∴,解得a=.故选:B.直接利用双曲线求出半焦距,利用离心率求出a即可.本题考查双曲线的离心率的求法,双曲线的简单性质的应用.3.【答案】D【解析】解:根据题意和三视图知几何体是一个放倒的直三棱柱ABC-A′B′C′,底面是一个直角三角形,两条直角边分别是、斜边是2,且侧棱与底面垂直,侧棱长是2,∴几何体的表面积S=2×+2×2+2×=6+4,故选:D.根据题意和三视图知几何体是一个放倒的直三棱柱,由三视图求出几何元素的长度,由面积公式求出几何体的表面积.本题考查三视图求几何体的表面积,由三视图正确复原几何体是解题的关键,考查空间想象能力.4.【答案】B【解析】解:由1+(1+2z)i=0,得z=,∴复数z的虚部是,故选:B.把已知等式变形,再由复数代数形式的乘除运算化简得答案.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.5.【答案】D【解析】【分析】本题考查的知识点是函数的图象,属于基础题.根据已知函数的解析式,分析函数的奇偶性,最大值及单调性,利用排除法,可得答案.【解答】解:∵,∴,故函数为偶函数,当时,,故排除A,B;当时,,则有解为x0,当时,时,故函数在[0,2]不是单调的,故排除C,故选D.6.【答案】A【解析】解:a⊥α,且b⊥α⇒a∥b,反之不成立.可能a,b分别于α,β斜交.∴“a⊥α,且b⊥α”是“a∥b”的充分不必要条件.故选:A.a⊥α,且b⊥α⇒a∥b,反之不成立.可能a,b分别于α,β斜交.本题考查了空间线面位置关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.7.【答案】B【解析】解:(1-x)4(1+x)5=(1-4x+6x2-4x3+x3)(1+5x+10x2+10x3+5x4+x5),故展开式中x3的系数为10-40+30-4=-4,故选:B.把(1-x)4和(1+x)5按照二项式定理展开,可得展开式中x3的系数.本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.8.【答案】B【解析】解:由题意,从该校学生中任意抽取1名学生恰为读书迷的概率.从该校大量学生中,用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中的“读书迷”的人数为X.若每次抽取的结果是相互独立的,所以.X0123p均值,方差.从该校学生中任意抽取1名学生恰为读书迷的概率.说明每次抽取的结果是相互独立的,推出.得到分布列,然后求解期望即可.本题考查独立重复实验的概率的分布列以及期望的求法,考查转化思想以及计算能力.9.【答案】D【解析】解:如图,在△ABC中,∵AB=AC=3,BC=3,∴由余弦定理可得cos A==-,则A=120°,∴sin A=.设△ABC外接圆的半径为r,则,得r=3.设球的半径为R,则,解得R=2.∵×3×3×=,∴三棱锥D-ABC体积的最大值为=,故选:D.由题意画出图形,求出三角形ABC外接圆的半径,设出球的半径,利用直角三角形中的勾股定理求得球的半径,则三棱锥D-ABC体积的最大值可求.本题主要考查空间几何体的体积等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想等,是中档题.10.【答案】A【解析】解:由题意可得,解可得a1=-19,d=4,∴S n=-19n=2n2-21n,∴nS n=2n3-21n2,设f(x)=2x3-21x2,f′(x)=6x(x-7),当0<x<7时,f′(x)<0;函数是减函数;当x>7时,f′(x)>0,函数是增函数;所以n=7时,nS n取得最小值:-343.故选:A.分别利用等差数列的通项公式及求和公式表示已知条件,然后求出得a1,d,在代入求和公式即可求解.本题主要考查了等差数列的通项公式及求和公式的简单应用,属于基础试题.11.【答案】A【解析】【分析】本题考查排列、组合的应用,注意题目限制条件比较多,需要优先分析受到限制的元素,是简单题.根据题意,由于节目甲必须排在前三位,对甲的位置分三种情况讨论,依次分析乙丙的加法原理计算可得答案.【解答】解:根据题意,由于节目甲必须排在前三位,分3种情况讨论:①甲排在第一位,节目丙、丁必须排在一起,则丙丁相邻的位置有4个,考虑两者的顺序,有2种情况,将剩下的3个节目全排列,安排在其他三个位置,有=6种安排方法,则此时有4×2×6=48种编排方法;②甲排在第二位,节目丙、丁必须排在一起,则丙丁相邻的位置有3个,考虑两者的顺序,有2种情况,将剩下的3个节目全排列,安排在其他三个位置,有=6种安排方法,则此时有3×2×6=36种编排方法;③甲排在第三位,节目丙、丁必须排在一起,则乙丙相邻的位置有3个,考虑两者的顺序,有2种情况,将剩下的3个节目全排列,安排在其他三个位置,有=6种安排方法,则此时有3×2×6=36种编排方法;则符合题意要求的编排方法有36+36+48=120种;故选:A.12.【答案】7 ;53【解析】解:设人数为x,物品价格为y,则,解得x=7,y=53.故答案为:7,53.列方程组求解.本题考查了方程的应用,属于基础题.13.【答案】6【解析】解:作出x,y满足条件的可行域如图:目标函数z=2x+y在的交点A(2,2)处取最大值为z=2×2+1×2=6.原点到点P(x,y)的距离的最小值是:|OB|=.故答案为:6;;画出约束条件表示的可行域,判断目标函数z=2x+y的位置,求出最大值.利用可行域转化求解距离即可.本题考查简单的线性规划的应用,正确画出可行域,判断目标函数经过的位置是解题的关键.14.【答案】2;2【解析】【分析】本题主要考查正弦定理的应用,三角形的面积公式,属于基础题.由条件求得c =2=b,可得B的值,再由正弦定理求得三角形外接圆的半径R的值.【解答】解:△ABC中,∵b=2,A=120°,三角形的面积S==bc•sin A=c•,∴c=2=b,故B=(180°-A)=30°.再由正弦定理可得=2R==4,∴三角形外接圆的半径R=2.故答案为2;2.15.【答案】4【解析】解:记∠AOB=α,则0≤α≤π,如图,由余弦定理可得:|+|=,|-|=,令x=,y=,则x2+y2=10(x、y≥1),其图象为一段圆弧MN,如图,令z=x+y,则y=-x+z,则直线y=-x+z过M、N时z最小为z min=1+3=3+1=4,当直线y=-x+z与圆弧MN相切时z最大,由平面几何知识易知z max即为原点到切线的距离的倍,也就是圆弧MN所在圆的半径的倍,所以z max=×=.综上所述,|+|+|-|的最小值是4,最大值是.故答案为:4、.通过记∠AOB=α(0≤α≤π),利用余弦定理可可知|+|=、|-|=,进而换元,转化为线性规划问题,计算即得结论.本题考查函数的最值及其几何意义,考查数形结合能力,考查运算求解能力,涉及余弦定理、线性规划等基础知识,注意解题方法的积累,属于中档题.16.【答案】(-∞,-2]【解析】解:原问题等价于f2(x)+f(x)=-t有三个不同的实根,即y=-t与y=f2(x)+f(x)有三个不同的交点,当x≥0时,y=f2(x)+f(x)=e2x+e x为增函数,在x=0处取得最小值为2,与y=-t只有一个交点.当x<0时,y=f2(x)+f(x)=lg2(-x)+lg(-x),根据复合函数的单调性,其在(-∞,所以,要有三个不同交点,则需-t≥2,解得t≤-2.原问题等价于f2(x)+f(x)=-t有三个不同的实根,即y=-t与y=f2(x)+f(x)有三个不同的交点,然后分x≥0和x<0两种情况代入解析式可得.本题考查了函数与方程的综合运用,属难题.17.【答案】【解析】解:设A(x1,y1)、B(x2,y2),由,消去y,可得(a2+b2)x2-2a2x+a2(1-b2)=0,∴则x1+x2=,x1x2=,由△=(-2a2)2-4a2(a2+b2)(1-b2)>0,整理得a2+b2>1.∴y1y2=(-x1+1)(-x2+1)=x1x2-(x1+x2)+1.∵OA⊥OB(其中O为坐标原点),可得•=0∴x1x2+y1y2=0,即x1x2+(-x1+1)(-x2+1)=0,化简得2x1x2-(x1+x2)+1=0.∴2•-+1=0.整理得a2+b2-2a2b2=0.∵b2=a2-c2=a2-a2e2,∴代入上式,化简得2a2=1+,∴a2=(1+).∵e∈[,],平方得≤e2≤,∴≤1-e2≤,可得≤≤4,因此≤2a2=1+≤5,≤a2≤,可得a2的最大值为,满足条件a2+b2>1,∴当椭圆的离心率e=时,a的最大值为.故答案为:.将直线方程代入椭圆方程,由韦达定理,向量数量积的坐标运算,求得2a2=1+,由离心率的取值范围,即可求得a的最大值.本题考查椭圆的标准方程,直线与椭圆的位置关系,韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.18.【答案】解:(Ⅰ)函数f(x)=sin(ωx-)+sin(ωx-)=sinωx cos-cosωx sin-sin(-ωx)=sinωx-cosωx=sin(ωx-),又f()=sin(ω-)=0,∴ω-=kπ,k∈Z,解得ω=6k+2,又0<ω<3,∴ω=2;(Ⅱ)由(Ⅰ)知,f(x)=sin(2x-),将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得到函数y=sin (x-)的图象;再将得到的图象向左平移个单位,得到y=sin(x+-)的图象,∴函数y=g(x)=sin(x-);当x∈[-,]时,x-∈[-,],∴sin(x-)∈[-,1],∴当x=-时,g(x)取得最小值是-×=-.【解析】本题考查了三角恒等变换与正弦型函数在闭区间上的最值问题,是中档题.(Ⅰ)利用三角恒等变换化函数f(x)为正弦型函数,根据f()=0求出ω的值;(Ⅱ)写出f(x)解析式,利用平移法则写出g(x)的解析式,求出x∈[-,]时g(x)的最小值.19.【答案】解:(1)由已知得a m=S m-S m-1=4,且a m+1+a m+2=S m+2-S m=14,设数列{a n}的公差为d,则有2a m+3d=14,∴d=2由S m=0,得,即a1=1-m,∴a m=a1+(m-1)×2=m-1=4∴m=5,a1=-4(2)由(1)知a1=-4,d=2,∴a n=2n-6∴n-3=log2b n,得.∴.设数列{(a n+6)b n}的前n项和为T n∴①②①-②得==∴【解析】(1)利用a m=S m-S m-1,转化求出数列的公差,然后利用已知条件求解m.(2)化简数列的通项公式,利用错位相减法求和求解即可.本题考查数列的递推关系式的应用,数列求和,考查转化思想以及计算能力.20.【答案】(1)证明:由四边形ABCD为菱形,∠BAD=120°,可得∠ABC=60°,△ABC 为正三角形.因为M为BC的中点,所以AM⊥BC.…(2分)又BC∥AD,因此AM⊥AD.因为PA⊥平面ABCD,AM⊂平面ABCD,所以PA⊥AM.而PA∩AD=A,所以AM⊥平面PAD.…(4分)(2)解:AB=2,H为PD上任意一点,连接AH,MH.由(1)知:AM⊥平面PAD,则∠MHA为MH与平面PAD所成的角.在Rt△MAH中,AM=,∴当AH最短时,∠MHA最大,即当AH⊥PD时,∠MHA最大.此时,tan∠MHA==又AD=2,∴∠ADH=45°,∴PA=2.由(1)知AM,AD,AP两两垂直,以A为坐标原点如图建立空间直角坐标系,则A(0,0,0),P(0,0,2),D(0,2,0),,,,则,,,设AC的中点为E,则,故就是面PAC的法向量,.设平面MAN的法向量为n=(x,y,1),二面角M-AN-C的平面角为θ..,∴二面角M-AN-C的余弦值为.…(12分)【解析】(1)利用菱形与等边三角形的性质可得:AM⊥BC,于是AM⊥AD.利用线面垂直的性质可得PA⊥AM.再利用线面垂直的判定与性质定理即可得出;(2)连接AH,MH.由(1)知:AM⊥平面PAD,可得:∠MHA为EH与平面PAD所成的角.在Rt△EAH中,AM=,可知:当AH最短时,∠MHA最大,即当AH⊥PD时,∠MHA最大.利用直角三角形边角关系可得PA=2.由(1)知AM,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系.求出法向量,利用向量夹角求解即可.本题考查了直线与平面垂直的判定.在题中出现了探究性问题,在解题过程中“空间问题平面化的思路”,是立体几何常用的数学思想,属于中档题.21.【答案】解:(1)由题意设抛物线方程为y2=2px,其准线方程为,∵P(4,m)到焦点的距离等于A到其准线的距离,∴,∴p=2.∴抛物线C的方程为y2=4x.(2)由(1)可得点M(4,4),可得直线DE的斜率不为0,设直线DE的方程为:x=my+t,联立,得y2-4my-4t=0,则△=16m2+16t>0①.设D(x1,y1),E(x2,y2),则y1+y2=4m,y1y2=-4t.∵•=(x1-4,y1-4)•(x2-4,y2-4),=x1x2-4(x1+x2)+16+y1y2-4(y1+y2)+16,=,=,=t2-16m2-12t+32-16m=0即t2-12t+32=16m2+16m,得:(t-6)2=4(2m+1)2,∴t-6=±2(2m+1),即t=4m+8或t=-4m+4,代入①式检验均满足△>0,∴直线DE的方程为:x=my+4m+8=m(y+4)+8或x=m(y-4)+4.∴直线过定点(8,-4)(定点(4,4)不满足题意,故舍去).【解析】(1)求出抛物线的焦点坐标,结合题意列关于p的等式求p,则抛物线方程可求;(2)由(1)求出M的坐标,设出直线DE的方程x=my+t,联立直线方程和抛物线方程,化为关于y的一元二次方程后D,E两点纵坐标的和与积,利用⊥得到t与m的关系,进一步得到DE方程,由直线系方程可得直线DE所过定点.本题考查抛物线的简单性质,考查了直线与圆锥曲线位置关系的应用,训练了平面向量在求解圆锥曲线问题中的应用,属中档题.22.【答案】解:(1),∵函数f(x)是单调递减函数,∴f'(x)≤0对(0,+∞)恒成立,∴-2x2+ax-1≤0对(0,+∞)恒成立,即对(0,+∞)恒成立,∵(当且仅当2x=,即x=时取等号),∴;(2)∵函数f(x)在(0,3)上既有极大值又有极小值.∴在(0,3)上有两个相异实根,即2x2-ax+1=0在(0,3)上有两个相异实根,,则,得,即.【解析】本题考查函数的导数的应用,函数的单调性以及函数的极值的求法,考查转化思想以及计算能力.(1)求出导函数,通过f'(x)≤0对(0,+∞)恒成立,分离变量推出a,利用基本不等式求解函数的最小值,得到a的范围.(2)通过函数f(x)在(0,3)上既有极大值又有极小值,则说明导函数有由两个零点,列出不等式组求解即可.。
浙江省普通高校招生学考科目考试立体几何多选题试题含答案
浙江省普通高校招生学考科目考试立体几何多选题试题含答案一、立体几何多选题1.如图①,矩形ABCD 的边2BC =,设AB x =,0x >,三角形BCM 为等边三角形,沿BC 将三角形BCM 折起,构成四棱锥M ABCD -如图②,则下列说法正确的有( )A .若T 为BC 中点,则在线段MC 上存在点P ,使得//PD 平面MATB .当)3,2x ∈时,则在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCDC .若使点M 在平面ABCD 内的射影落在线段AD 上,则此时该四棱锥的体积最大值为1 D .若1x =,且当点M 在平面ABCD 内的射影点H 落在线段AD 上时,三棱锥M HAB -6322++【答案】BCD 【分析】对于A ,延长AT 与DC 的延长线交于点N ,此时,DP 与MN 必有交点; 对于B ,取AD 的中点H ,表示出2223MH MT HT x --,验证当)3,2x ∈时,无解即可; 对于C ,利用体积公式21233V x x =⨯⨯-,借助基本不等式求最值即可; 对于D ,要求外接球半径与内切球半径,找外接圆的圆心,又内接圆半径为2323r =++【详解】对于A ,如图,延长AT 与DC 的延长线交于点N ,则面ATM ⋂面()MDC N MN =.此时,DP 与MN 必有交点,则DP 与面ATM 相交,故A 错误; 对于B ,取AD 的中点H ,连接MH ,则MH AD ⊥.若面MAD ⊥面ABCD ,则有2223MH MT HT x =-=- 当)3,2x ∈时,无解,所以在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCD故B 正确;对于C ,由题可知,此时面MAD ⊥面ABCD ,由B 可知,(3x ∈,所以()22222221223232331333232x x V x x x x ⎛⎫+-⎛⎫=⨯⨯-=-≤== ⎪ ⎪⎝⎭⎝⎭当且仅当223x x =-,即6x =时等号成立.故C 正确; 对于D ,由题可知,此时面MAD ⊥面ABCD ,且2MH =因为AHB ,MHB 都是直角三角形,所以M ABH -底面外接圆的圆心是中点,所以1R =,由等体积法,可求得内接圆半径为2323r =++,故61322R r ++=,故D 正确.故选:BCD . 【点睛】本题从多个角度深度考查了立体几何的相关内容,注意辅助线的作法,以及求内接圆半径的公式、基本不等式、构造函数等核心思想.2.如图,正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2,则下列说法正确的是( )A .异面直线1AB 与1AD 所成的角是3πB .1BD ⊥平面11AC DC .平面1ACB 截正四面体11A BDC -3D .正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD【分析】选项A ,利用正方体的结构特征找到异面直线所成的角;选项B ,根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证;选项C ,由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一;选项D ,分别求出正方体的体对角线长和正四面体11A BDC -的高,然后判断数量关系即可得解. 【详解】A :正方体1111ABCD ABCD -中,易知11//AD BC ,异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角,即11A BC ∠,11A BC 为等边三角形,113A BC π∠=,正确;B :连接11B D ,1B B ⊥平面1111DC B A ,11A C ⊂平面1111D C B A ,即111AC B B ⊥,又1111AC B D ⊥,1111B B B D B ⋂=,有11A C ⊥平面11BDD B ,1BD ⊂平面11BDD B ,所以111BD AC ⊥,同理可证:11BD A D ⊥,1111AC A D A ⋂=,所以1BD ⊥平面11AC D ,正确;C :易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=,错误;D :易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -22222262213⎛⎫--⨯ ⎪⎝⎭,故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23,正确. 故选:ABD. 【点睛】关键点点睛:利用正方体的性质,找异面直线所成角的平面角求其大小,根据线面垂直的判定证明1BD ⊥平面11AC D ,由正四面体的性质,结合几何图形确定截面的面积,并求高,即可判断C 、D 的正误.3.在三棱柱111ABC A B C -中,ABC ∆是边长为343( )A .直线1A C 与直线1BB 之间距离的最大值为3B .若1A 在底面ABC 上的投影恰为ABC ∆的中心,则直线1AA 与底面所成角为60︒ C .若三棱柱的侧棱垂直于底面,则异面直线AB 与1A C 所成的角为30D .若三棱柱的侧棱垂直于底面,则其外接球表面积为64π 【答案】AD 【分析】建立空间直角坐标系,用向量法求解. 【详解】如图示,以A 为原点,AC 为y 轴正方向,Ax 为x 轴正方向,过A 点垂直于面ABC 的向上方向为z 轴正方向建系,则()()()0,0,0,3,0,0,23,0,A B C 设()()()100010001000,,,3,3,,,23,,A x y z B x y z C x y z ++所以()()()1000100011,23,,,,,3,3,0,AC x y z BB x y z A B =---== 对于A:设n 为直线1A C 与直线1BB 的公垂线的方向向量,则有:11·0·0AC n BB n ⎧=⎪⎨=⎪⎩,即()()0000002300x x y y zz x x y y zz ⎧-+-=⎪⎨++=⎪⎩解得:()00,0n z x =- 设直线1A C 与直线1BB 之间距离为d ,则22011222200009||||z A B nd d x z n x z ===++ 22009x d ≥∴≤,即3d ≤,故A 正确;对于B :若1A 在底面ABC 上的投影恰为ABC ∆的中心,则(13,211A 底面法向量()(10,0,1,1,3,211m AA ==,设直线 1AA 与底面所成角为θ,则:121133sin |cos ,|143AA n θ===⨯,故B 错误; 对于C : 三棱柱的侧棱垂直于底面时,则(((1110,0,43,3,43,0,23,43,A B C则()()13,3,0,0,23,43,AB AC ==- 设异面直线AB 与1A C 所成的角为θ,则11165cos |cos ,|||10||||23215AB AC AB AC AB AC θ====⨯,故C 错误;对于D :若三棱柱的侧棱垂直于底面时,外接球的球心O 为上下底面中心DD 1连线的中点,所以外接球的半径()222324R =+=,所以2464S R ππ==.故D 正确故选:AD 【点睛】向量法解决立体几何问题的关键: (1)建立合适的坐标系; (2)把要用到的向量正确表示; (3)利用向量法证明或计算.4.如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点E ,F ,且2EF =.则下列结论正确的是( )A .三棱锥A BEF -的体积为定值B .当E 向1D 运动时,二面角A EF B --逐渐变小C .EF 在平面11ABB A 内的射影长为12D .当E 与1D 重合时,异面直线AE 与BF 所成的角为π4【答案】AC 【分析】对选项分别作图,研究计算可得. 【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形,1112212224BEF S EF BB ∆∴=⋅=⨯⨯=连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以,AO 是点A 到平面11BDD B 的距离,即22AO =11221334212A BEF BEF V S AO -∆∴=⨯=⨯⨯=A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ,连接11,AD AB , 由正方体性质知11AD AB =,M 是11B D 中点,AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角,在直角三角形1AA M 中,12tan 2MAA ∠=为定值. 选项C:如图,作1111,,,FH A B EG A B ET EG ⊥⊥⊥ 在直角三角形EFT 中,221cos 45222FT EF =⨯=⨯= 12HG FT ∴==选项D:当E 与1D 重合时,F 与M 重合,连接AC 与BD 交于点R ,连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角, 在三角形1AD R 中,22111132,2AD D R MB BB M B ===+=2AR = 由余弦定理得13cos AD R ∠= 故选:AC 【点睛】本题考查空间几何体性质问题.求解思路:关键是弄清(1)点的变化,点与点的重合及点的位置变化;(2)线的变化,应注意其位置关系的变化;(3)长度、角度等几何度量的变化.求空间几何体体积的思路:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法;若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.5.如图所示,在长方体1111ABCD A B C D -中,11,2,AB BC AA P ===是1A B 上的一动点,则下列选项正确的是( )A .DP 35B .DP 5C .1AP PC +6D .1AP PC +的最小值为1705【答案】AD 【分析】DP 的最小值,即求1DA B △底边1A B 上的高即可;旋转11A BC 所在平面到平面11ABB A ,1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值,即求1DA B △底边1A B 上的高,易知115,2A B A D BD ===,所以1A B 边上的高为355h =111,AC BC ,得11A BC ,以1A B 所在直线为轴,将11A BC 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',则AC '即为所求的最小值,易知11122,2,cos 10AA AC AAC ''==∠=-, 所以217042222()10AC '=+-⨯⨯⨯-= 故选:AD. 【点睛】本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否, (1)点的变化,点与点的重合及点的位置变化;(2)线的变化,翻折、旋转前后应注意其位置关系的变化;(3)长度、角度等几何度量的变化.6.如图,已知矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE ∆沿直线DE 翻折成1A DE ∆,若M 为线段1A C 的中点,则ADE ∆在翻折过程中,下列说法正确的是( )A .线段BM 的长是定值B .存在某个位置,使1DE AC ⊥C .点M 的运动轨迹是一个圆D .存在某个位置,使MB ⊥平面1A DE【答案】AC【分析】取CD 中点F ,连接BF ,MF ,根据面面平行的判定定理可得平面//BMF 平面1A DE ,由面面平行的性质定理可知//BM 平面1A DE ,可判断D ;在BFM ∆中,利用余弦定理可求得BM a =为定值,可判断A 和C ;假设1DE A C ⊥,由线面垂直的判定定理可得DE ⊥平面1A CE ,由线面垂直的性质定理可知1DE A E ⊥,与11DA A E ⊥矛盾,可判断B .【详解】解:取CD 的中点F ,连接BF ,MF ,∵M ,F 分别为1A C 、CD 中点,∴1MF A D ∥,∵1A D ⊂平面1A DE ,MF ⊄平面1A DE ,∴MF 平面1A DE ,∵DF BE ∥且DF BE =,∴四边形BEDF 为平行四边形,∴BF DE ,∵DE ⊂平面1A DE ,BF ⊄平面1A DE ,∴BF ∥平面1A DE ,又BF MF F =,BF 、MF ⊂平面BMF ,∴平面//BMF 平面1A DE ,∵BM ⊂平面BMF ,∴BM ∥平面1A DE ,即D 错误,设22AB AD a ==, 则112MF A D a ==,2BF DE a ==,145A DE MFB ︒∠=∠=, ∴222cos45BM MF BF MF BF a ︒=+-⋅⋅=,即BM 为定值,所以A 正确,∴点M 的轨迹是以B 为圆心,a 为半径的圆,即C 正确,∵2DE CE a ==,2CD AB a ==, ∴222DE CE CD +=, ∴DE CE ⊥,设1DE A C ⊥,∵1A C 、CE ⊂平面1A CE ,1AC CE C =, ∴DE ⊥平面1A CE ,∵1A E ⊂平面1A CE ,∴1DE A E ⊥,与11DA A E ⊥矛盾,所以假设不成立,即B 错误.故选:AC .【点睛】本题考查立体几何中的翻折问题,涉及到线段长度的求解、直线与平面位置关系的判定、点的轨迹的求解、反证法的应用等知识点,考查学生的空间立体感和推理论证能力.7.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,点P 在线段B 1C 上运动,则( )A .直线BD 1⊥平面A 1C 1DB .三棱锥P ﹣A 1C 1D 的体积为定值C .异面直线AP 与A 1D 所成角的取值范用是[45°,90°]D .直线C 1P 与平面A 1C 1D 6 【答案】ABD【分析】在A 中,推导出A 1C 1⊥BD 1,DC 1⊥BD 1,从而直线BD 1⊥平面A 1C 1D ;在B 中,由B 1C ∥平面 A 1C 1D ,得到P 到平面A 1C 1D 的距离为定值,再由△A 1C 1D 的面积是定值,从而三棱锥P ﹣A 1C 1D 的体积为定值;在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°];在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,利用向量法能求出直线C 1P 与平面A 1C 1D所成角的正弦值的最大值为3. 【详解】解:在A 中,∵A 1C 1⊥B 1D 1,A 1C 1⊥BB 1,B 1D 1∩BB 1=B 1,∴A 1C 1⊥平面BB 1D 1,∴A 1C 1⊥BD 1,同理,DC 1⊥BD 1,∵A 1C 1∩DC 1=C 1,∴直线BD 1⊥平面A 1C 1D ,故A 正确;在B 中,∵A 1D ∥B 1C ,A 1D ⊂平面A 1C 1D ,B 1C ⊄平面A 1C 1D ,∴B 1C ∥平面 A 1C 1D ,∵点P 在线段B 1C 上运动,∴P 到平面A 1C 1D 的距离为定值,又△A 1C 1D 的面积是定值,∴三棱锥P ﹣A 1C 1D 的体积为定值,故B 正确;在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°],故C 错误;在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系, 设正方体ABCD ﹣A 1B 1C 1D 1中棱长为1,P (a ,1,a ),则D (0,0,0),A 1(1,0,1),C 1(0,1,1),1DA =(1,0,1),1DC =(0,1,1),1C P =(a ,0,a ﹣1),设平面A 1C 1D 的法向量(),,n x y z =, 则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取x =1,得1,1,1n ,∴直线C 1P 与平面A 1C 1D 所成角的正弦值为: 11||||||C P n CP n ⋅⋅=∴当a =12时,直线C 1P 与平面A 1C 1D ,故D 正确. 故选:ABD .【点睛】求直线与平面所成的角的一般步骤:(1)、①找直线与平面所成的角,即通过找直线在平面上的射影来完成;②计算,要把直线与平面所成的角转化到一个三角形中求解;(2)、用空间向量坐标公式求解.8.如图,已知P 为棱长为1的正方体对角线1BD 上的一点,且()()10,1BP BD λλ=,下面结论中正确结论的有( )A .11A D C P ⊥;B .当1A P PD +取最小值时,23λ=; C .若()0,1λ∈,则7,312APC ππ⎛⎫∠∈ ⎪⎝⎭; D .若P 为1BD 的中点,四棱锥11P AA D D -的外接球表面积为94π. 【答案】ABD【分析】 以D 为坐标原点建立如图空间直角坐标系,利用向量关系可判断ABC ;根据几何体外接球关系建立方程求出球半径即可判断D.【详解】以D 为坐标原点建立如图空间直角坐标系,则()1,1,0B ,()10,0,1D ,设(),,P x y z ,()()10,1BP BD λλ=,1BP BD λ∴=,即()()1,1,1,1,1x y z λ--=--,则可解得()1,1,P λλλ--,对A ,()()()111,0,1,0,0,0,0,1,1A D C ,()11,0,1A D ∴=--,()11,,1C P λλλ=---,则()()()()11110110A D C P λλλ⋅=-⨯-+⨯-+-⨯-=,则11A D C P ⊥,故A 正确;对B ,()()()()()2222221111111A P PD λλλλλλ+=--+-+--+-+222223422333λλλ⎛⎫=-+=-+ ⎪⎝⎭ 则当23λ=时,1A P PD +取最小值,故B 正确; 对C ,()()1,0,0,0,1,0A C ,(),1,PA λλλ∴=--,()1,,PC λλλ=--,则222321cos 1321321PA PC APC PA PC λλλλλλ⋅-∠===--+-+⋅, 01λ<<,则2232123λλ≤-+<,则2111123212λλ-≤-<-+, 即11cos 22APC -≤∠<,则2,33APC ππ⎛⎤∠∈ ⎥⎝⎦,故C 错误; 对于D ,当P 为1BD 中点时,四棱锥11P AA D D -为正四棱锥,设平面11AA D D 的中心为O ,四棱锥11P AA D D -的外接球半径为R ,所以222122R R ⎛⎫-+= ⎪⎝⎭⎝⎭,解得34R =, 故四棱锥11P AA D D -的外接球表面积为94π,所以D 正确. 故选:ABD.【点睛】关键点睛:本题考查空间相关量的计算,解题的关键是建立空间直角坐标系,利用向量建立关系进行计算.。
2004—2019浙江高考真题《立体几何》汇编
2004−2019浙江高考真题《立体几何》汇编三视图1. (2009浙江文12理12)某几何体的三视图(单位:cm )如图所示,则此几何体的体积是 3cm .2. (2010浙江文8)某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( )A .3352cm 3B .3320cm 3C .3224cm 3D .3160cm 33. (2010浙江理12)若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是 3cm .侧视图俯视图正视图侧视图俯视图侧视图俯视图4. (2011浙江文7)某几何体的三视图如图所示,则这个几何体的直观图可以是( )5. (2011浙江理3)某几何体的三视图如图所示,则这个几何体的直观图可以是( )6. (2012浙江文3)已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是( )A .13cmB .23cmC .33cmD .63cmDC BA侧视图俯视图正视图DCB A 侧视图俯视图正视图侧视图俯视图正视图7. (2012浙江理11)已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积等于 3cm .8. (2013浙江文5)已知某几何体的三视图(单位:cm )如图所示,则该几何体的体积是( )A .1083cmB .1003cmC .923cmD .843cm9. (2013浙江理12)若某几何体的三视图(单位:cm )如图所示,则此几何体的体积等于 3cm .侧视图俯视图正视图俯视图侧视图正视图侧视图正视图3410. (2014浙江文3)某几何体的三视图(单位:cm )如图所示,则该几何体的体积是( )A .723cmB .903cmC .1083cmD .1383cm11. (2014浙江理3)某几何体的三视图(单位:cm )如图所示,则该几何体的表面积是( )A .902cmB .1292cmC .1322cmD .1382cm12. (2015浙江文2理2)某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )A .83cmB .123cmC .3233cmD .403cm俯视图侧视图正视图俯视图侧视图正视图侧视图正视图13. (2016浙江理11)某几何体的三视图如图所示(单位:cm ),则该几何体的表面积是 2cm ,体积是 3cm .14. (2016浙江文9)某几何体的三视图如图所示(单位:cm ),则该几何体的表面积是 2cm ,体积是 3cm .15. (2017浙江3)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是()A .12π+B .32π+C .312π+D .332π+俯视图正视图316. (2018浙江3)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A .2B .4C .6D .817. (2019浙江4)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V Sh 柱体,其中S 是柱体的底面积,h 是柱体的高.若某柱体的三视图如图所示(单位:cm ),则该柱体的体积(单位:3cm )是( ) A .158B .162C .182D .324俯视图正视图俯视图侧视图正视图点、直线、平面位置关系18. (2005浙江文7理6)设α,β为两个不同的平面,l ,m 为两条不同的直线,且l α⊂,m β⊂.有如下两个命题:①若αβ∥,则l m ∥;②若l m ⊥,则αβ⊥.那么( ) A .①是真命题,②是假命题 B .①是假命题,②是真命题C .①②都是真命题D .①②都是假命题19. (2007浙江文7理6)若P 是两条异面直线l ,m 外的任意一点,则( )A .过点P 有且仅有一条直线与l ,m 都平行B .过点P 有且仅有一条直线与l ,m 都垂直C .过点P 有且仅有一条直线与l ,m 都相交D .过点P 有且仅有一条直线与l ,m 都异面20. (2008浙江文9)对两条不相交的空间直线a 与b ,必存在平面α,使得( )A .a α⊂,b α⊂B .a α⊂,b α∥C .a α⊥,b α⊥D .a α⊂,b α⊥21. (2009浙江文4)设α,β是两个不同的平面,l 是一条直线,以下命题正确的是( )A .若l α⊥,αβ⊥,则l β⊂B .若l α∥,αβ∥,则l β⊂C .若l α⊥,αβ∥,则l β⊥D .若l α⊥,αβ⊥,则l β⊥22. (2010浙江理6)设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是( )A .若l m ⊥,m α⊂,则l α⊥B .若l α⊥,l m ∥,则m α⊥C .若l α∥,m α⊂,则l m ∥D .若l α∥,m α∥,则l m ∥23. (2011浙江文4)若直线l 不平行于平面α,且l α⊄,则( )A .α内的所有直线与l 异面B .α内不存在与l 平行的直线C .α内存在唯一的直线与l 平行D .α内的直线与l 都想交24. (2011浙江理4)下列命题中错误的是( )A .如果αβ平面⊥平面,那么平面α内一定存在直线平行于平面βB .如果αβ平面不垂直于平面,那么平面α内一定不存在直线垂直于平面βC .如果αγ平面⊥平面,βγ平面⊥平面,l αβ=,那么l γ⊥平面D .如果αβ平面⊥平面,那么平面α内所有直线都垂直于平面β25. (2012浙江文5)设直线l 是直线,α,β是两个不同的平面.( )A .若l α∥,l β∥,则αβ∥B .若l α∥,l β⊥,则αβ⊥C .若αβ⊥,l α⊥,则l β⊥D .若αβ⊥,l α∥,则l β⊥26. (2013浙江文4)设m ,n 是两条不同的直线,α,β是两个不同的平面.( )A .若m α∥,n α∥,则m n ∥B .若m α∥,m β∥,则αβ∥C .若m n ∥,m α⊥,则n α⊥D .若m α∥,αβ⊥,则m β⊥27. (2014浙江文6)设m ,n 是两条不同的直线,α,β是两个不同的平面.( )A .若m n ⊥,n α∥,则m α⊥B .若m β∥,βα⊥,则m α⊥C .若m β⊥,n β⊥,n α⊥,则m α⊥D .若m n ⊥,n β⊥,βα⊥,则m α⊥28. (2015浙江文4)设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂.( )A .若l β⊥,则αβ⊥B .若αβ⊥,则l m ⊥C .若l β∥,则αβ∥D .若αβ∥,则l m ∥29. (2016浙江文2理2)已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m α∥,n β⊥,则( ) A .m l ∥ B .m n ∥C .n l ⊥D .m n ⊥30. (2018浙江6)已知平面α,直线m ,n 满足m α⊄,n α⊂,则“m n ∥”是“m α∥”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件小题31. (2004浙江文15)已知α平面⊥β平面,l αβ=,P 是空间一点,且P 到平行α,β的距离分别是1,2,则点P 到l 的距离为 .32. (2004浙江理16)已知平面α和平面β相交于直线l ,P 是空间一点,P A ⊥α,垂足为A ,PB ⊥β,垂足为B ,且1PA =,2PB =,若点A 在β内的射影与点B 在α内的射影重合,则点P 到l 的距离为 .33. (2004浙江文10理10)如图,在正三棱柱111ABC A B C -中,已知1AB =,D 在棱1BB 上,且1BD =,若AD 与平面11AA C C 所成的角为α,则sin α=( ) ABCDDB 1A 1C 1CBA34. (2005浙江文12理12)设M ,N 是直角梯形ABCD 两腰的中点,DE ⊥AB 于E (如图).现将△ADE沿DE 折起,使二面角A DE B --为45°,此时点A 在平面BCDE 内的射影为点B ,则M ,N 的连线与AE 所成角的大小等于 .35. (2006浙江文8)如图,正三棱柱111ABC A B C -的各棱长都为2,E ,F 分别是AB ,11A C 的中点,则EF 的长是( ) A .2BCD36. (2006浙江理9)如图,O 是半径为1的球的球心,点A ,B ,C 在球面上,OA ,OB ,OC 两两垂直,E ,F 分别是大圆弧AB 与AC 的中点,则点E ,F 在该球面上的球面距离是( ) A .4π B .3π C .2π D.4B 1C 1A 1FE CBA37. (2006浙江文14)如图,正四面体ABCD 的棱长为1,平面α过棱AB ,且CD α∥,则正四面体上的所有点在平面α内的射影构成的图形面积是 .38. (2006浙江理14)正四面体ABCD 的棱长为1,棱AB ∥平面α,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是 .39. (2007浙江文17理16)已知点O 在二面角AB αβ--的棱上,点P 在α内,且45POB ∠=︒.若对于β内异于O 的任意一点Q ,都有45POQ ∠≥︒,则二面角AB αβ--的大小是 .40. (2008浙江文15理14)如图,已知球O 的面上四点A ,B ,C ,D ,DA ⊥平面ABC ,AB ⊥BC ,DA AB BC ===O 的体积等于 .BDACαBDACαDBCA41. (2008浙江理10)如图,AB 是平面α的斜线段...,A 为斜足.若点P 在平面α内运动,使得△ABP 的面积为定值,则动点P 的轨迹是( ) A .圆B .椭圆C .一条直线D .两条平行直线42. (2009浙江理5)在三棱柱111ABC A B C -中,各棱长相等,侧棱垂直于底面,点D 是侧面11BB C C 的中心,则AD 与平面11BB C C 所成角的大小是( ) A .30° B .45°C .60°D .90°43. (2009浙江理17)如图,在长方形ABCD 中,2AB =,1BC =,E 为DC 的中点,F 为线段EC (端点除外)上一动点,现将AFD △沿AF 折起,使平面ABD ⊥平面ABC ,在平面ABD 内过点D 作DK AB ⊥,K 为垂足,设AK t =,则t 的取值范围是 .PABαKFDCBA44. (2012浙江理10)已知矩形ABCD ,1AB =,BC .将△ABD 沿矩形的对角线BD 所在的直线进行翻折,在翻折过程中,( )A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对于任意位置,三对直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直45. (2013浙江理10)在空间中,过点A 作平面π的垂线,垂足为B ,记()B f A π=.设α,β是两个不同的平面,对空间任意一点P ,()1Q f f P βα=⎡⎤⎣⎦,()2Q f f P αβ⎡⎤=⎣⎦,恒有12PQ PQ =,则( ) A .α平面与β平面垂直 B .α平面与β平面所成的(锐)二面角为45° C .α平面与β平面平行 D .α平面与β平面所成的(锐)二面角为60°46. (2014浙江文10理17)如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练.已知点A 到墙面的距离为AB ,某目标点P 沿墙面上的射线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小.若15m AB =,25m AC =,30BCM ∠=︒,则tan θ的最大值是 .(仰角θ为直线AP 与平面ABC 所成角)PMCB A47. (2015浙江文7)如图,斜线段AB 与平面α所成的角为60︒,B 为斜足,平面α上的动点P 满足30PAB ∠=︒,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支48. (2015浙江理8)如图,已知ABC △,D 是AB 的中点,沿直线CD 将ACD △翻折成A CD '△,所成( ) A .A DB α'∠≤B .A DB α'∠≥C .A CB α'∠≤D .A CB α'∠≥49. (2015浙江理13)如图,在三棱锥A BCD -中,3AB AC BD CD ====,2AD BC ==,点M ,N 分别为AD ,BC 的中点,则异面直线AN ,CM 所成的角的余弦值是 .αPBAA'DCBAMNDCBA50. (2016浙江文14)如图,已知平面四边形ABCD ,3AB BC ==,1CD =,AD =90ADC ∠=︒.沿直线AC 将△ACD 翻折成△ACD',直线AC 与BD'所成角的余弦的最大值是 .51. (2016浙江理14)如图,在△ABC 中,2AB BC ==,120ABC ∠=︒.若平面ABC 外的点P 和线段AC 上的点D ,满足PD DA =,PB BA =,则四面体PBCD 的体积的最大值是 .52. (2017浙江9)如图,已知正四面体D ABC -(所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP PB =,2BQ CRQC RA==,分别记二面角D PR Q --,D PQ R --,D QR P --的平面角 为α,β,γ,则( ) A .γαβ<<B .αγβ<<C .αβγ<<D .βγα<<D'DC APDCBARCQBP A D53. (2018浙江8)已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S AB C --的平面角为3θ,则( ) A .123θθθ≤≤ B .321θθθ≤≤ C .132θθθ≤≤ D .231θθθ≤≤54. (2019浙江8)设三棱锥V ABC -的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点).记直线PB 与直线AC 所成的角为α,直线PB 与平面ABC 所成的角为β,二面角P AC B --的平面角为γ,则( ) A .,βγαγ<< B .,βαβγ<< C .,βαγα<< D .,αβγβ<<大题55. (2004浙江文19)如图,已知正方形ABCD 和矩形ACEF所在的平面互相垂直,AB =1AF =,M 是线段EF 的中点. (1)求证:AM ∥平面BDE ; (2)求证:AM ⊥平面BDF ; (3)求二面角A DF B --的大小.M FEDCBA56. (2004浙江理19)如图,已知正方形ABCD 和矩形ACEF所在的平面互相垂直,AB =1AF =,M 是线段EF 的中点. (1)求证:AM ∥平面BDE ; (2)求二面角A DF B --的大小;(3)试在线段AC 上确定一点P ,使得PF 与BC 所成的角是60︒.57. (2005浙江文18)如图,在三棱锥P ABC -中,AB BC ⊥,12AB BC PA ==,点O ,D 分别是AC ,PC 的中点,OP ⊥底面ABC .(1)求证:OD ∥平面PAB ;(2)求直线OD 与平面PBC 所成角的大小.58. (2005浙江理18)如图,在三棱锥P ABC -中,AB BC ⊥,AB BC kPA ==,点O ,D 分别是AC ,PC 的中点,OP ⊥底面ABC . (1)求证:OD ∥平面PAB ;(2)当12k =,求直线PA 与平面PBC 所成角的大小;(3)当k 取何值时,O 在平面PBC 内的射影恰好为PBC △的重心?MFEDCBA59. (2006浙江文17)如图,在四棱锥P ABCD -中,底面为直角梯形,AD BC ∥,90BAD ∠=︒,PA ⊥底面ABCD ,且2PA AD AB BC ===,M ,N 分别为PC ,PB 的中点. (1)求证:PB DM ⊥;(2)求BD 与平面ADMN 所成角.60. (2006浙江理17)如图,在四棱锥P ABCD -中,底面为直角梯形,AD BC ∥,90BAD ∠=︒,PA ⊥底面ABCD ,且2PA AD AB BC ===,M ,N 分别为PC ,PB 的中点. (1)求证:PB DM ⊥;(2)求CD 与平面ADMN 所成的角.61. (2007浙江理19)在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC ⊥BC ,且2AC BC BD AE ===,M 是AB 的中点.(1)求证:CM EM ⊥;(2)求CM 与平面CDE 所成的角.62. (2007浙江文20)在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC BC ⊥,且2AC BC BD AE ===,M 是AB 的中点.(1)求证:CM EM ⊥;(2)求DE 与平面EMC 所成角的正切值.63. (2008浙江文20理18)如图,矩形ABCD 和梯形BEFC 所在平面互相垂直,BE ∥CF ,90BCF CEF ∠=∠=︒,AD ,2EF =.(1)求证:AE DCF ∥平面;(2)当AB 的长为何值时,二面角A EF C --的大小为60°?64. (2009浙江文19)如图,DC ⊥平面ABC ,EB DC ∥,22AC BC EB DC ====,120ACB ∠=︒,P ,Q 分别为AE ,AB 的中点. (1)证明:PQ ACD ∥平面;(2)若AD 与平面ABE 所成角的正弦值.FEDCBA QPCDEBA65. (2009浙江理20)如图,平面PAC ⊥平面ABC ,ABC △是以AC 为斜边的等腰直角三角形,E ,F ,O 分别为P A ,PB ,AC 的中点,16AC =,10PA PC ==. (1)设G 是OC 的中点,证明:FG ∥平面BOE ;(2)证明:在ABO △内存在一点M ,使FM ⊥平面BOE ,并求点M 到OA ,OB 的距离.66. (2010浙江文20)如图,在平行四边形ABCD 中,2AB BC =,120ABC ∠=︒,E 为线段AB 的中点,将ADE △沿直线DE 翻折成A DE '△,使平面A DE '⊥平面BCD ,F 为线段A C '的中点. (1)求证:BF ∥平面A DE ';(2)设M 为线段DE 的中点,求直线FM 与平面A DE '所成角的余弦值.67. (2010浙江理20)如图,在矩形ABCD 中,点E ,F 分别在线段AB ,AD 上,243AE EB AF FD ====, 沿直线EF 将AEF △翻折成A EF '△,使平面A EF '⊥平面BEF . (1)求二面角A FD C '--的余弦值;(2)点M ,N 分别在线段FD ,BC 上,若沿直线MN 将四边形MNCD 向上翻折,使C 与A '中和,求线段FM 的长.GF EPOCBAA'MFED CBANM A'F EDCB A68. (2011浙江文20)如图,在三棱锥P ABC -中,AB AC =,D 为BC 的中点,PO ⊥平面ABC ,垂足O 落在线段AD 上. (1)证明:AP BC ⊥;(2)已知8BC =,4PO =,3AO =,2OD =,求二面角B AP C --的大小.69. (2011浙江理20)如图,在三棱锥P ABC -中,AB AC =,D 为BC 的中点,PO ⊥平面ABC ,垂足O 落在线段AD 上.已知8BC =,4PO =,3AO =,2OD =. (1)证明:AP BC ⊥;(2)在线段AP 上是否存在点M ,使得二面角A MC B --为直二面角?若存在,求出AM 的长;若不存在,请说明理由.70. (2012浙江文20)如图,在侧棱垂直底面的四棱柱1111ABCD A B C D -中,AD ⊥AB,AB =2AD =,4BC =,12AA =,E 是1DD 的中点,F 是平面11B C E 与直线1AA 的交点.(1)证明:(i )11EF A D ∥;(ii )111BA B C EF ⊥平面;(2)求1BC 与11B C EF 平面所成角的正弦值.OPDCBAOPDCBAD 1C 1B 1A 1EF B D CA71. (2012浙江理20)如图,在四棱锥P ABCD -中,底面是边长为的菱形,120BAD ∠=︒,且PA ABCD ⊥平面,PA =,M ,N 分别为PB ,PD 的中点.(1)证明:MN ∥平面ABCD ;(2)过点A 作AQ PC ⊥,垂足为点Q ,求二面角A MN Q --的平面角的余弦值.72. (2013浙江文20)如图,在四棱锥P ABCD -中,P A ⊥平面ABCD ,2AB BC ==,AD CD ==PA 120ABC ∠=︒.G 为线段PC 上的点. (1)证明:BD ⊥平面P AC ;(2)若G 为PC 的中点,求DG 与平面APC 所成的角的正切值;(3)若G 满足PC ⊥平面BGD ,求PGGC的值.73. (2013浙江理20)如图,在四面体A BCD -中,AD ⊥平面BCD ,BC CD ⊥,2AD =,BD =.M是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且3AQ QC =. (1)证明:PQ BCD ∥平面;(2)若二面角C BM D --的大小为60°,求BDC ∠的大小.QMNDABPGDB APQPMDBA74. (2014浙江文20)如图,在四棱锥A BCDE -中,平面ABC ⊥平面BCDE ,90CDE BED ∠=∠=︒,2AB CD ==,1DE BE ==,AC =(1)证明:AC BCDE ⊥平面;(2)求直线AE 与平面ABC 所成角的正切值.75. (2014浙江理20)如图,在四棱锥A BCDE -中,平面ABC ⊥平面BCDE ,90CDE BED ∠=∠=︒,2AB CD ==,1DE BE ==,AC(1)证明:DE ACD ⊥平面; (2)求二面角B AD E --的大小.76. (2015浙江文18)如图,在三棱柱111ABC A B C -中,90BAC ∠=︒,2AB AC ==,14AA =,1A 在底面ABC 的射影为BC 的中点,D 为11B C 的中点. (1)证明:11A D A BC ⊥平面;(2)求直线1A B 和平面11BB C C 所成的角的正弦值.BED CABED CAC 1B 1A 1DC BA77. (2015浙江理17)如图,在三棱柱111ABC A B C -中,90BAC ∠=︒,2AB AC ==,14AA =,1A 在底面ABC 的射影为BC 的中点,D 为11B C 的中点. (1)证明:11A D A BC ⊥平面;(2)求二面角11A BD B --的平面角的余弦值.78. (2016浙江文18)如图,三棱台ABC DEF -中,平面BCFE ⊥平面ABC ,90ACB ∠=︒,1BE EF FC ===,2BC =,3AC =.(1)求证:BF ⊥平面ACFD ;(2)求直线BD 与平面ACFD 所成角的余弦值.79. (2016浙江理17)如图,在三棱台ABC DEF -中,平面BCFE ⊥平面ABC ,90ACB ∠=︒,1BE EF FC ===,2BC =,3AC =.(1)求证:BF ⊥平面ACFD ;(2)求二面角B AD F --的平面角的余弦值.C 1B 1A 1DC BA80. (2017浙江19)如图,已知四棱锥P −ABCD ,△P AD 是以AD 为斜边的等腰直角三角形,BC ∥AD ,CD ⊥AD ,22PC AD DC CB ===,E 为PD 的中点. (1)证明:CE ∥平面P AB ;(2)求直线CE 与平面PBC 所成角的正弦值.81. (2018浙江19)如图,已知多面体111ABCA B C ,1A A ,1B B ,1C C 均垂直于平面ABC ,120ABC ∠=︒,14A A =,11C C =,12AB BC B B ===. (1)证明:1111AB A B C ⊥平面;(2)求直线1AC 与平面1ABB 所成的角的正弦值.82. (2019浙江19)如图,已知三棱柱111ABC A B C -,平面11A ACC ⊥平面ABC ,90ABC ∠=︒,30BAC ∠=︒,11A A AC AC ==,E ,F 分别是AC ,11A B 的中点. (1)证明:EF BC ⊥;(2)求直线EF 与平面1A BC 所成角的余弦值.ED CBAPC 1B 1A 1CBAC 1B 1A 1FECBA。
2013届浙江高考数学押题之立体几何
、选择题2013届浙江高考数学押题之立体几何1 .如图所示,在正方体ABCD A1 B1C1 D1中,E为DD1上一点,且DE 1DD1, F是侧面CDD1C1上的动点,且B1F //平面3A1 BE ,则B1F与平面CDD1C1所成角的正切值构成的集合是(3 3 t-C . {m | m —..;2}2 2 【答案】C2 一仁13}52 —{m | 13 m52}EDCA1B1D12 .棱长为2的正方体ABCD AB1G D1在空间直角坐标系中移动,但保持点A . B分别在x轴、y轴上移动,则点G到原点O的最远距离为(【答案】D3 .某三棱锥的三视图如图所示则该三棱锥的体积为(A . 1 B.【答案】A,已知该三视图中正视图和俯视图均为边长为 )32的正三角形,侧视图为如图所示的直角三角形4.设m、n是两条不同的直线,其中正确的命题是是两个不同的平面,n ,mB . // , m,n //m nC . ,m,n //m nD .7m, n m nB【答案】5 .某四棱锥的底面为正方形,其三视图如图所示,则该四棱锥的体积等于(C. 3A . 1【答案】6.设l, m是两条不同的直线,( )A.若l C.若l// 【答案】m, mm5答案:B,则I,则I//7 .设m,n是不同的直线,侧视图) 个平面,则下列命题正确的是B.若l , l // m,则mD.若l// , m//是不同的平面,下列命题中正确的是A.若m〃,n ,m n,则B.若m〃,nC.若m〃,n ,m/ /n,则,m n,则//D.若m〃,n , m//n,则/ /【答案】C8 .某三棱锥的三视图如图所示,该三棱锥的体积是()A.8B. 4C. 2D.43 3【答案】B9.如图,正四面体ABCD的顶点C在平面内,且直线BC与平面所成的角为45°,顶点B在平面上的射影为点0.当顶点A与点0的距离最大时,直线CD与平面所成角的正弦值等于()6 3 2 221 6 2 5 2 2B. ----------C. -----------D. ----------------12 5 4 12【答案】A10 .已知某几何体的三视图如图所示,则该几何体的体积是()14 .某几何体的三视图如图所示,根据图中标出的数据,则这个几何体的体积为 _________________ .【答案】(8)363 3 1 9,因此其几何体的体积为1815 .正方体ABCD A3GU的棱长为2, MN是它的内切球的一条弦(把球面上任意两点之间的连线段称为球的弦UlLU ULUT方体表面上的动点,当弦MN最长时,PM gPN的取值范围是8 3A .-------3【答案】A、填空题16 33D . 16 313 . 一个空间几何体的三视图如图所示,则该几何体的表面积为________________________【答案】50(13)时7區),P为正_____________________________________________________________【答案】0 ,16.如图,斜边长为4的直角ABC, B=90o, A 60o且A在平面上, B , C在平面的同侧,M为BC的中点•若ABC ,则M至序面的距离的取值范围是ABC在平面上的射影是以A为直角顶点的三角形三、解答题17 •如图,在梯形ABCD 中,AB//CD,AB AD , AD 4•点上的射影为点0 ,且PA PD 2 3,二面角P AD B(I)求直线0A与平面PAB所成角的大小;(n )若AB BP 8,求三棱锥P ABD的体积•P在平面ABCD为45°•【答案】解:(I)方法1: •/ PA PD, ••• P点在平面ABCD上的射影0在线段AD的中垂线上设AD的中点为E,连接EP,EO, • EO AD, EP A , • PEO为二面角P AD B的平面角,• PEO 45°在等腰△ PAD中,•/AD4, • EA ED 2,又PA PD 2 3,• PE 2 2 .在Rt △ PEO 中,得OP OE 2以O为原点,分别以平行于AD , AB的直线为x轴、y轴建立空间直角坐标系,则——urnP(0,0,2), A(2, 2,0),所以OA (2, 2,0), PA (2,2 ,2 ) uuu LT•/ AB// y轴,故可取一个AB的平行向量m 0,1,0 .设平面PAB的法向量是n (x, y, z),uuu rPA n0,2x2y 2z 0,则ir r即m n0,y0,取n(1,0,1)•直线AO与平面PAB所成角满足sin(2, 2,0) (1,0,1)<8 &所以直线OA与平面PAB所成角为300方法2:过O点作OHA B ,垂足为H ,连接PH过O作OKP H ,垂足为K ,连接AK .Q PO平面ABCD,• PO AB.QOH AB, • AB平面POH .又OK平面POH ,• ABO K ,又OKP H , •• OK 平面PAB••• OAK就是OA与平面PAB所成角•/ PA PD , • P点在平面ABCD上的射影0在线段AD的中垂线上,设AD的中点为E ,连接EP, EO,• EO AD, EP A , • PEO为二面角P AD B 的平面角,• PEO 45°. 在等腰△ PAD 中,•/ AD 4, • EA ED 2,又PA PD 2 3,[来源:Z+xx+] • PE 2 2 .在Rt △ PEO 中,得OP OE 2, • OA 2 2.又OH AE 2, PO 2,在Rt △ POH 中,可得OK 2OK 1 o•- sin OAK ——一,••• OAK 30OA 2所以直线OA与平面PAB所成角为30o(n)设AB x,则PB 8 x,连接OB.在Rt△ POB 中,PB2 PO2 OB2,又由(I )得OE AE , OE AE ,• OAE:45°,•• OAB45°在厶OAB中,OB2 AO2AB22AO ABc°s OAB8 x24x,又PB2(8 x)2,• 4 (8 2 x4x) (8x)2,得13得x —,即AB 1333•三棱锥P ABD的体积V P ABD 1SABDOP 1 1134 —522 —3 3 23918.如图:在直三棱柱ABC ABQ中,AB AC 1 , BAC 90°.(I )若异面直线AB与B i C i所成的角为60°,求棱柱的高h ;r(n )设D是BB i的中点,DC i与平面A BC i所成的角为【答案】解法1:( I )由三棱柱ABC A1B1C1是直三棱柱可知,AA即为高,如图1,因为BC//B1C1,所以ABC是异面直线AB与B1C1所成的角或其补角连接AQ,因为AB AC,所以AB AC <1 AA2 .在Rt △ ABC 中,由AB AC 1, BAC 90°,可得BC 2,当棱柱的高h变化时,求sin的最大值.又异面直线 AB 与BG 所成的角为60°,所以 ABC 60°,即厶ABC 为正三角形 于是 A 1B B 1C 1 J 2 .在Rt △ A AB 中,由/ AA 2 AB 罷,得AA 1,即棱柱的高为1(n )设AA h(h 0),如图1,过点D 在平面ABBA 内作DF AB 于F ,则 由 AG 平面 BAA , B ,, DF 平面 BAA B i ,得 AG DF .而AGIAB A,所以DF 平面ABC-故 DGF 就是DC 1与平面ABG 所成的角,即 DC 1F 在 Rt △ DFB 中,由 BD h ,得 DF —. h2' 2V h ^l 在 Rt △ DB 1C 1 中,由 B 1D, B 1C 1 2,得 DC 12hDF 2 h 2 1 hDC1 1h 2 8 h 4 9h 2 82因为h'十殳+932蟲+ 4当且仅当卅=2为h r故当h ■鹿时’的最大值—^―解法2-建立如图E 所示的空间直角坐标系如"设開=鬥3丸),则育 印』耳Q 』』), qcoim 如』血, 君之71®, 4^=(0,1,0), 4®-(1.0,-/2).二分uiur uuur (I )因为异面直 线AB 与BG 所成的角60°,所以cos60°UUUr 1 AUUur 1 IB 1C 1I |AB|即=4 21,得1 h 2 2,解得h 12a 2 12h ULUU h(n )由 D 是 BB 1 的中点,得 D(1,0,2),于是 DC 1 ( 1,1,2).uur设平面A 1BC 1的法向量为n (x,y,z),于是由n AB,n在 Rt △ DFC 1 中,sin即"崛时,等号成立,令 f (h)h h 4 9h 28uuuurAG ,可得图:A-C1【答案】(I )连结QM 因为点Q , M , N 分别是线段PB , AB , BC 的中点所以QM PA 且MN/ AC 从而QM 平面PAC 且MN/平面PAC又因为MN P QMM 所以平面 QMN 平面PAC 而QK 平面QMN 来源:] 所以Q!/平面PAC (n )方法1:过M 作MHL AK 于 H 连QH 则/ QHMP 为二面角Q AK M 的平面解得x 2 ,所以MK 的长度为2方法2:以B 为原点,以BC BA 所在直线为x 轴y 轴建空间直角坐标系 则 A (0,8,0), M (0,4,0), N4,0,0),P (0,8,8), Q 0,4,4),UULT n AB UU ULT n AG 0, x hz 0, y 0,0,可取 n (h, 0,1),于是sinI cos uuurDC 1, n |.因为 所以 f(h)故当h期时,Sin的最大值字 19 .如图,在三棱锥P ABC 中,直线PA平面ABC ,且 ABC 90 ,又点Q , M , N 分别是线段PB , AB , BC 的中点,且点K 是线段MN 上的动点• (I )证明:直线QK//平面PAC ;(n )若 PA AB BC =8,且二面角 QAK M 的平面角的余弦值为——,试求MK 的长度•9角,设 MK x ,且 PA PB PC 8则 MH2$‘2x x 24 2x 16,又QM 4,且cos QHM3,所以tan9QHMQM MH令 f(h)48时,等号成立•1而 |cosh 21 2 2 1h 4 9h 2 8uuur ——设 K (a , b ,o ),则 a +b =4, AQ =(0,-4,4), AK (a, 4a,0)记n (x, y, z)为平面AQK 的一个法向量,则则 n (a 4,a,a),LT又平面AKM 的一个法向量 m (0,0,1),设二面角Q AK M 的平面角为所以所以MK 的长度为 2(0,1).现将ABC 沿DE 折成直二面角A DE B . 1 时,面ADC 面ABE ; 2【答案】n AQ n Azky z ax (4 a) y4 a ,20.如图,ABC 中,B 90o , AB 2, BC 1,D 、E 两点分别在线段 AB, AC 上,满足:⑵ 当 (0,1)时,二面角E AC D 的大小能否等于 ?若能,求出 的值;若不能,请说明理由4则 |cos|=|mn||m|| n|a (a 4)2 2a 23,解得a 1,9AD AE AB AC(1)求证:当杯恳“ 一“=半・阳J所以当只■丄射\二面和疋-』C-D 的大小第于兰4 4如图,已知长方形 ABCD 中,AB 2,AD 1 , M 为DC 的中 点•将 ADM 沿AM 折起,使得平面 ADM 平面ABCM .(1) 求证:AD BM(2) 点E 是线段DB 上的一动点,当二面角E AM【答案】取AM 的中点O,AB 的中点B,则ON,OA,OD两两垂直,以O 为原点建立空间直角坐标系 ,如图.根据已知条件,得2A (2 ,0,0),B(J2,0),M(,0,0),D(0,0,派⑴杯涪^务=山址"眈"亚丄阳,二页施A-BE"平面对^AM - ?/. AD 丄面反工\又V BE C 血ECQ 二JSD 丄BEI _r 41 】 ” BO BC只当在尹'叫宁应飞减"叫T 而 人 Z£5D = ZDt B,/. RE 丄 DC :、駐 丄面片DC, O£ C 血梱E 昇.面心£丄面ADC ID 如橱豐秉,瞩期①工圧孟八 口近■匝儿1,0) 仅 0川.仍,AE - (0.4-'/SAX cf 占 W% -忑/ - LO) 设3a AEC 法向佩® = (■* …冷)* M%-/(£ = 01 _ , fc丫严茫1・取“L -d 】j ”)沙 八松LZ液面^£HTZERMfl 3Wn, - DJ - 0I 叫-J DCM•溢X —d 畤(1t^)=>"分)C7旳D 大小为时,试确定点E 的位置.2 2c 2),BM (0, 2,0), 2则x : y : z 0:(1) :2 ,,取n2(0,1,2)*由于二面角 E AM D大小为贝V cos —3| cos n1, n? |I n1n2 I11,由于2[0,1],|n1 ||n2 |(1)2 4 2故解得 2 33.故当E位于线段DB间,且DE2 3DB3时,二面角E AM D大小为__ 3(1)由于AD ( J则AD BM 0,故AD BM .(2)设存在满足条件的点则("‘ZE, 2)则点E的坐标为(亠22 2,222 ).2(其中[0,1])易得平面ADM的法向量可以取n i(0,1,0), 设平面AME的法向量为n2(x,y,z),则AM2,0,0),AE (222 )则―n2AE x(n222AM22)2xy( 2)(2Z(2DE,并设DE DB,7?(-y2(22, 2,23。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江高考数学压轴题:立体几何选择题1.已知在矩形ABCD 中,2AB =,4=AD ,E ,F 分别在边AD ,BC 上,且1AE =,3BF =,如图所示,沿EF 将四边形AEFB 翻折成A EFB '',则在翻折过程中,二面角B CD E '--的大小为θ,则tan θ的最大值为( )A B C D 2.在正三棱柱111ABC A B C -中,11AB AA ==,点P 满足1BP BC BB λμ=+,其中][0,1,0,1λμ⎡⎤∈∈⎣⎦,则( ) A .当1λ=时,△1AB P 的周长为定值B .当1μ=时,三棱锥1P A BC -的体积不是定值C .当12λ=时,有且仅有一个点P ,使得AP BP ⊥D .当12μ=时,有且仅有一个点P ,使得1A B ⊥平面1AB P3.已知三棱锥P ABC -三条侧棱,,PA PB PC 两两互相垂直,且2PA PB PC ===,,M N 分别为该三棱锥的内切球和外接球上的动点,则,M N 两点间距离的最小值为( )A .2+B 1C .2D 2-4.已知△ABC 在平面β内,不重合的两点P ,Q 在平面β同侧,在点M 从P 运动到Q 的过程中,记四面体M -ABC 的体积为V ,点A 到平面MBC 的距离为d ,则可能的情况是( )A .V 保持不变,d 先变大后变小B .V 保持不变,d 先变小后变大C .V 先变大后变小,d 不断变大D .V 先变小后变大,d 不断变小5.在三棱锥S ABC -中,,,SA SB SC 两两垂直且相等,若空间中动一点P 满足SP x SA y SB z SC →→→→=++,其中0,1,1x y z ≥≥≥且125x y z ++≤.记SP 与平面ABC 所成的角为θ,则sin θ的最大值为( )A .13BC .1D6.如图,在长方体1111ABCD A B C D -中,3AB =,5AD =,14AA =,点F 是1AA 的中点,点E 为棱BC 上的动点,则平面1C EF 与平面11ABB A 所成的锐二面角正切的最小值是( )A .513 BC D .135 7.如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练,已知点A 到墙面的距离为AB ,某目标点P 沿墙面上的射线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小,若15,25,30AB cm AC cm BCM ==∠=︒,则tan θ的最大值是( ).(仰角θ为直线AP 与平面ABC 所成的角)A B C D 8.已知棱长为2的正方体1111ABCD A B C D -,点A 在空间直角坐标系O xyz -的x 轴上移动,点C 在平面yOz 上移动,则1OC OB ⋅的最大值是( )A .2B .1C .4+D .69.如图,在三棱锥P ABC -中,5AB AC PB PC ====,4PA =,6BC =,点M 在平面PBC 内,且AM =,设异面直线AM 与BC 所成的角为α,则cos α的最大值为( )A B C .25 D 10.正三棱锥A BCD -中G 为BC 的中点,H 为BG 上的任意上点,设AH 与CD 所成的角的大小为1θ,AH 与平面BCD 所成的角的大小为2θ,二面角A BC D --的大小为3θ,则( )A .213θθθ≤≤B .123θθθ≤≤C .231θθθ≤<D .312θθθ≤≤11.已知三棱锥P ABC -,其中PA ⊥平面ABC ,2PA =,2AB AC ==,2BAC π∠=.已知点Q 为棱PA (不含端点)上的动点,若光线从点Q 出发,依次经过平面PBC 与平面ABC 反射后重新回到点Q ,则光线经过路径长度的取值范围为( )A .(1+B .)4C .4⎫⎪⎭D .( 12.如图,平面OAB ⊥平面α,OA α⊂,OA AB =,120OAB ∠=︒.平面α内一点P 满足PA PB ⊥,记直线OP 与平面OAB 所成角为θ,则tan θ的最大值是( )A B .15 C D .1313.如图,四边形ABCD 中90A CBD ∠=∠=︒,30CDB ∠=︒,AB AC =,沿直线BC 将ABC 折成A BC ',使点A '在平面BCD 上的射影在BCD △内(不含边界),记二面角A BC D '--的平面角大小为α,直线A B '、A D '与平面BCD 所成角分别为β、γ,则( )A .αβγ>>B .βαγ>>C .αγβ>>D .γβα>>14.已知直角梯形ABCD 满足://, AD BC CD DA ⊥,且△ABC 为正三角形.将△ADC 沿着直线AC 翻折至△AD C ',且AD BD CD '''<<,二面角 , , D AB C D BC A D AC B '''------的平面角大小分别为,,αβγ,直线, , D A D B D C '''与平面ABC 所成角分别是123,,θθθ,则( )A .123,θθθαγβ>>>>B .123,θθθαβγ<<>>C .123,θθθαβγ>><<D .123,θθθαβγ<<<<15.已知菱形ABCD ,60DAB ∠=︒,E 为边AB 上的点(不包括A B ,),将ABD △沿对角线BD 翻折,在翻折过程中,记直线BD 与CE 所成角的最小值为α,最大值为β( )A .αβ,均与E 位置有关B .α与E 位置有关,β与E 位置无关C .α与E 位置无关,β与E 位置有关D .αβ,均与E 位置无关16.如图,已知锐二面角l αβ--的大小为1θ,A α∈,B β∈,M l ∈,N l ∈,AM l ⊥,BN l ⊥,C ,D 为AB ,MN 的中点,若AM MN BN >>,记AN ,CD 与半平面β所成角分别为2θ,3θ,则( )A .122θθ<,132θθ<B .122θθ<,132θθ>C .122θθ>,132θθ<D .122θθ>,132θθ>17.已知正四面体P ABC -,Q 为ABC 内的一点,记PQ 与平面PAB PAC PBC 、、所成的角分别为,,αβγ,则下列不等式恒成立的个数为( )①222sin sin sin 2αβγ++≥ ②222cos os 2cos c αβγ++≥③222tan an 1tan t αβγ++≤ ④2221111tan an tan t αβγ++≤ A .0 B .1 C .2 D .318.如图,矩形ABCD 中,已知2AB =,4BC =,E 为AD 的中点. 将ABE △沿着BE 向上翻折至A BE ',记锐二面角A BE C '--的平面角为α,A B '与平面BCDE 所成的角为β,则下列结论不可能成立的是( )A .sin αβ=B αcos β=C .α2β<D .πα4β-> 19.如图,在大小为1θ的锐二面角l αβ--中,A α∈,B β∈,M 、N l ∈,AM l ⊥,BN l ⊥,C 、D 分别为AB 、MN 的中点.记直线AN 与半平面β的夹角为2θ,直线CD 与半平面β的夹角为3θ.若AM MN BN >>,则( )A .122θθ<,132θθ<B .122θθ<,132θθ>C .122θθ>,132θθ<D .122θθ>,132θθ>20.在三棱锥D ABC -中,222AD AB AC BC ===,点A 在面BCD 上的投影G 是BCD △的垂心,二面角G AB C --的平面角记为α,二面角G BC A --的平面角记为β,二面角G CD A --的平面角记为γ,则( )A .αβγ>>B .αγβ>>C .βγα>>D .γβα>>21.如图,在三棱锥A BCD -中,AB BC ⊥,BC CD ⊥,E ,F 分别为BC ,AD 的中点,记平面ABC 与平面BCD 所成的角为1θ,直线AC ,EF 与平面BCD 所成的角分别为2θ,3θ,若AB BC CD >>,则( )A .12θθ>, 132θθ<B .12θθ>,132θθ>C .12θθ<,132θθ<D .12θθ<,132θθ>22.如图,在等边三角形ABC 中,,D E 分别是线段,AB AC 上异于端点的动点,且BD CE =,现将三角形ADE 沿直线DE 折起,使平面ADE ⊥平面BCED ,当D 从B 滑动到A 的过程中,则下列选项中错误的是( )A .ADB ∠的大小不会发生变化B .二面角A BDC --的平面角的大小不会发生变化 C .BD 与平面ABC 所成的角变大 D .AB 与DE 所成的角先变小后变大23.已知底面ABCD 为正方形的四棱锥P ABCD -,P 点的射影在正方形ABCD 内,且P 到BC 的距离等于PD 的长,记二面角P AB C 的平面角为α,二面角P CD A --的平面角为β,二面角P AD C --平面角为γ,则下列结论可能成立的是( )A .αβγ==B .αγβ=<C .αβγ=<D .αβγ>=24.如图,长方形ABCD 中,AB =1AD =,点E 在线段AB (端点除外)上,现将ADE 沿DE 折起为A DE '.设ADE α∠=,二面角A DE C '--的大小为β,若π2αβ+=,则四棱锥A BCDE '-体积的最大值为( )A .14B .23CD 25.如图,ABC 是等腰直角三角形,AB AC =,点D 是AB 上靠近A 的三等分点,点E 是AC 上靠近C 的三等分点,沿直线DE 将ADE 翻折成A DE ',所成二面角A DE B '--的平面角为α,则( )A .A DB A EC α∠≥∠'≥' B .A EC A DB α∠≥∠'≥'C .A DB A EC α≥∠'∠≥'D .A EC A DB α≥∠'∠≥' 26.如图,三棱锥A BCD -的底面BCD 在平面α内,所有棱均相等,E 是棱AC 的中点,若三棱锥A BCD -绕棱CD 旋转,设直线BE 与平面α所成的角为θ,则cos θ的取值范围为( )A .⎤⎥⎣⎦B .5,16⎡⎤⎢⎥⎣⎦C .⎡⎢⎣⎦D .⎡⎢⎣⎦ 27.如图,在矩形ABCD 中,AD AB <,将ACD △沿AC 翻折至ACD '△,设直线AD '与直线BC 所成角为α,直线BD '与平面ACD '所成角为β,二面角A CD B '--的平面角为γ,当γ为锐角时( )A .αβγ>>B .γβα>>C .γαβ>>D .αγβ>> 28.如图,在长方形ABCD 中,AD CD <,现将ACD △沿AC 折至1ACD △,使得二面角1A CD B --为锐二面角,设直线1AD 与直线BC 所成角的大小为α,直线1BD 与平面ABC 所成角的大小为β,二面角1A CD B --的大小为γ,则,,αβγ的大小关系是( )A .αβγ>>B .αγβ>>C .γαβ>>D .不能确定29.如图,在四棱锥P ABCD -中,APB BPC CPD DPA ∠=∠=∠=∠,平面ADP ⊥平面DCP ,若APC α∠=,BPD β∠=,AP 与平面DCP 所成的角为γ,则以下结论正确的是( )A .γβα<<B .βαγ<<C .βγα<<D .γαβ<<30.在长方体1111ABCD A B C D -中,1AB =,1BC CC ==E ,F ,G 分别为AD ,AB ,11C D 上的点,AE ED =,AF FB =,11(4)DG GC λλ=≥,分别记二面角1G EF D --,G EF C --,G FB C --的平面角为α,β,γ,则( ) A .αβγ>>B .βγα>>C .γβα>>D .与λ有关31.如图,在菱形ABCD 中,60BAD ∠=︒,线段AD ,BD 的中点分别为E ,F ,现将ABD △沿对角线BD 翻折,则异面直线BE 与CF 所成的角的取值范围是A .,63ππ⎛⎫ ⎪⎝⎭B .,62ππ⎛⎤ ⎥⎝⎦C .,32ππ⎛⎤ ⎥⎝⎦D .2,33ππ⎛⎫ ⎪⎝⎭ 32.三棱锥P ABC -中,AB BC ⊥,D 是棱AB 上的动点,点P 在平面的射影在ABC 内部,PD 与BC 所成的角为α,PD 与面ABC 所成的角为β,二面角P AB C 为λ,则( )A .βαλ≤≤B .βλα≤≤C .λβα≤≤D .λαβ≤≤33.记{},min ,,a a b a b b a b ≤⎧=⎨>⎩,已知矩形ABCD 中,2AB AD =,E 是边AB 的中点,将ADE 沿DE 翻折至A DE '(A '不在平面BCD 内),记二面角A BC D '--为α,二面角A CD E '--为β,二面角A DE C '--为γ,二面角A BE D '--为θ,则{}min ,,,αβγθ=( )A .αB .βC .γD .θ 34.在四面体ABCD 中,BCD ∆为等边三角形,2ADB π∠=,二面角B AD C --的大小为α,则α的取值范围是()A .0,6π⎛⎤ ⎥⎝⎦B .0,4π⎛⎤⎥⎝⎦ C .0,3π⎛⎤ ⎥⎝⎦ D .0,2π⎛⎤⎥⎝⎦。
