立体几何证明题练习
立体几何
1．（2014•山东）如图，四棱锥P﹣ABCD中，AP⊥平面PCD，AD⊥BC，AB=BC=AD，E，F分别为线段AD，
PC的中点．
（⊥）求证：AP⊥平面BEF；
（⊥）求证：BE⊥平面PAC．
2．（2014•四川）在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形
（⊥）若AC⊥BC，证明：直线BC⊥平面ACC1A1；
（⊥）设D、E分别是线段BC、CC1的中点，在线段AB上是否存在一点M，使直线DE⊥平面A1MC？请证明你的结论．
3．（2014•江苏）如图，在三棱锥P﹣ABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6，BC=8，DF=5．求证：
（1）直线PA⊥平面DEF；
（2）平面BDE⊥平面ABC．
4．（2014•黄山一模）如图，PA垂直于矩形ABCD所在的平面，AD=PA=2，CD=2，E、F分别是AB、PD的中点．
（1）求证：AF⊥平面PCE；
（2）求证：平面PCE⊥平面PCD；
（3）求四面体PEFC的体积．
5．（2014•南海区模拟）如图，四棱锥P﹣ABCD的底面是直角梯形，AB⊥CD，AB⊥AD，⊥PAB和⊥PAD是两个边长为2的正三角形，DC=4，O为BD的中点，E为PA的中点．
（⊥）求证：PO⊥平面ABCD；
（⊥）求证：OE⊥平面PDC；
（⊥）求直线CB与平面PDC所成角的正弦值．
6．（2013•天津）如图，三棱柱ABC﹣A1B1C1中，侧棱A1A⊥底面ABC，且各棱长均相等．D，E，F分别为棱AB，BC，A1C1的中点．
（⊥）证明：EF⊥平面A1CD；
（⊥）证明：平面A1CD⊥平面A1ABB1；
（⊥）求直线BC与平面A1CD所成角的正弦值．
7．（2013•浙江）如图，在四棱锥P﹣ABCD中，PA⊥面ABCD，AB=BC=2，AD=CD=，PA=，
⊥ABC=120°，G为线段PC上的点．
（⊥）证明：BD⊥平面PAC；
（⊥）若G是PC的中点，求DG与PAC所成的角的正切值；
（⊥）若G满足PC⊥面BGD，求的值．
8．（2013•湖南）如图．在直棱柱ABC﹣A1B1C1中，⊥BAC=90°，AB=AC=，AA1=3，D是BC的中点，点E在棱BB1上运动．
（1）证明：AD⊥C1E；
（2）当异面直线AC，C1E 所成的角为60°时，求三棱锥C1﹣A1B1E的体积．
9．（2011•天津）如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，⊥ADC=45°，AD=AC=1，O为AC中点，PO⊥平面ABCD，PO=2，M为PD中点．
（⊥）证明：PB⊥平面ACM；
（⊥）证明：AD⊥平面PAC；
（⊥）求直线AM与平面ABCD所成角的正切值．
10．（2011•北京）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，⊥BAD=60°．（⊥）求证：BD⊥平面PAC；
（⊥）若PA=AB，求PB与AC所成角的余弦值；
（⊥）当平面PBC与平面PDC垂直时，求PA的长．
11．（2010•深圳模拟）如图，在四棱锥S﹣ABCD中，底面ABCD为正方形，侧棱SD⊥底面ABCD，E、F分别AB、SC的中点
（1）求证：EF⊥平面SAD
（2）设SD=2CD，求二面角A﹣EF﹣D的大小．
12．（2010•重庆）如图，三棱锥P﹣ABC中，PC⊥平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD⊥平面PAB．
（1）求证：AB⊥平面PCB；
（2）求二面角C﹣PA﹣B的大小的余弦值．。
立体几何证明题专项练习
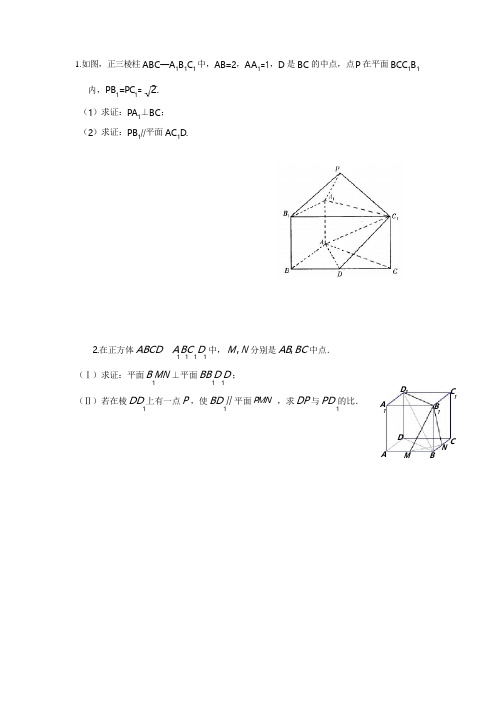
1.如图，正三棱柱ABC—A1B1C1中，AB=2，AA1=1，D是BC的中点，点P在平面BCC1B1内，PB1=PC1= 2.（1）求证：PA1⊥BC；（2）求证：PB1//平面AC1D.2.在正方体ABCD A BC D中，M,N分别是AB,BC中点．1111（Ⅰ）求证：平面B MN⊥平面BB D D；111（Ⅱ）若在棱DD上有一点P，使BD//平面PMN，求DP与PD的比．111A1D1C1B1D CA M BN3.在直三棱柱ABC-A B C中，AB=AC=AA=3a，B C=2a，D是BC的中点，F是1F B1111C C上一点，且CF=2a．1（1）求证：B F⊥平面ADF；1（2）求三棱锥D-AB F的体积；1（3）试在AA上找一点E，使得BE//平面ADF．1C1A1CDA B4.如图，在四棱锥P-ABCD中，侧面P AD是正三角形，且与底面ABCD垂直，底面ABCD是边长为2的菱形，∠BAD=60︒，N是PB 中点，过A、N、D三点的平面交PC于M．(1)求证：DP//平面ANC P（2）求证：M是PC中点；M（3）求证：平面PBC⊥平面ADMN D CNABEF DC5.已知直角梯形 ABCD 中, AB // CD , AB ⊥ BC , AB = 1, BC = 2, C D = 1 + 3, 过 A 作AE ⊥ CD ,垂足为 E , G 、F 分别 为AD 、CE 的中点,现将 ∆ADE 沿 AE 折叠,使得 DE ⊥ EC .(Ⅰ) 求证： BC ⊥ 面CDE ；(5 分)(Ⅱ) 求证： FG // 面BCD ；(5 分)（Ⅲ）在线段 AE 上找一点 R ,使得面 BDR ⊥ 面 DCB ,并说明理由. (5 分)D·G ·ABGAEFBC6.已知等腰梯形 PDCB 中（如图 1），PB=3，DC=1，PB=BC =2 ，A 为 PB 边上一点，且 P A=1△，将 P AD 沿 AD 折起，使面 P AD ⊥面 ABCD （如图 2）.（1）证明：平面 P AD ⊥PCD ；（2）试在棱 PB 上确定一点 M ，使截面 AMC把几何体分成的两部分VPDCMA: VMACB= 2 :1；（3）在 M 满足（2）的情况下，判断直线 PD是否平行面 AMC.7.如图，直三棱柱 ABC -A 1B 1C 1 中，∠ACB =90°，M ，N 分别为 A 1B ，B 1C 1 的中点．（1）求证 BC ∥平面 MNB 1；（2）求证平面 A 1CB ⊥平面 ACC 1A 1．A 1C 1NB 1MCAB8、如图，在四棱锥 P －ABCD 中，PD ⊥平面 ABCD ，四边形 ABCD 是菱形，AC ＝6，BD ＝8，E 是 PB 上任意一点，△AEC 面积的最小值是 3．（Ⅰ）求证：AC ⊥DE ；（Ⅱ）求四棱锥 P －ABCD 的体积．PEDFA BC9.如图所示,在直四棱柱 ABCD - A B C D 中,DB=BC, DB ⊥ AC ,点 M 是棱 BB 上一点.1 1 1 11（1）求证： B D // 面 A BD ； 1 11（2）求证： MD ⊥ AC ；（3）试确定点 M 的位置,使得平面 DMC ⊥ 平面 CC D D .111D 1 C 1A 1B 1DAMBC10.如图，已知矩形ABCD中，AB=10，BC=6，沿矩形的对角线BD把∆ABD折起，使A移到A1点，且A1在平面BCD上的射影O恰好在CD上。
最新立体几何证明题整理
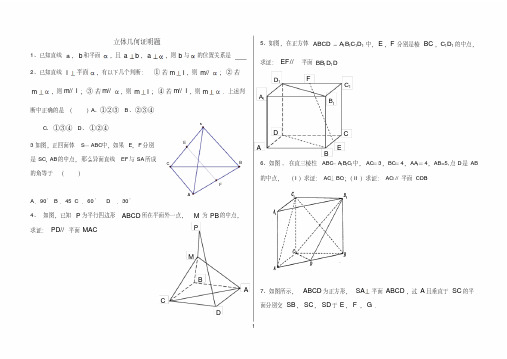
立体几何证明题1、已知直线a ，b 和平面，且a b ，a ，则b 与的位置关系是2、已知直线l平面，有以下几个判断：①若m l ，则m//；②若m，则m l //；③若m//，则ml ；④若m l //，则m．上述判断中正确的是（）A 、①②③ B 、②③④C 、①③④D 、①②④3如图，正四面体S －ABC 中，如果E ，F 分别是SC ，AB 的中点，那么异面直线EF 与SA 所成的角等于（）A ．90°B ．45C ．60°D ．30°4、如图，已知P 为平行四边形ABCD 所在平面外一点，M 为PB 的中点，求证：PD//平面MAC5、如图，在正方体1111ABCDA B C D 中，E ，F 分别是棱BC ，11C D 的中点，求证：EF//平面11BB D D6、如图, 在直三棱柱ABC －A 1B 1C 1中，AC ＝3，BC ＝4，AA 1＝4，AB=5,点D 是AB 的中点，（I ）求证：AC ⊥BC 1；（II ）求证：AC 1//平面CDB 17、如图所示，ABCD 为正方形，SA 平面ABCD ，过A 且垂直于SC 的平面分别交SB ，SC ，SD 于E ，F ，G ．CDABM P1A 1B 1D 1C FEABC D FECBAs求证：AE SB AG SD，8、如图，直角ABC△所在平面外一点S，且SA SB SC，点D为斜边AC的中点．（１）求证：SD平面ABC；（２）若AB BC，求证：BD面SAC9、在四棱锥P-ABCD中，∠DAB=∠ABC=90°，PA⊥底面ABCD；AB=BC=1，AD=2求证：平面PCD⊥平面PAC。
10、如图，在五面体ABCDEF中，点O是矩形ABCD的对角线的交点，面CDE是等边三角形，棱EF∥12BC（I）证明FO∥平面CDE；（II）设3BC CD，证明EO平面CDF11、已知正方体1111ABCD A B C D，O是底ABCD对角线的交点.求证：（１）OC1//面11AB D；（2 ）1AC面11AB D．SA BCFEDGASCBDD1ODBAC1B1A1CAB CDEFO12、如图，棱柱111ABC A B C 的侧面11BCC B 是菱形，11B C A B（Ⅰ）证明：平面1AB C平面11A BC ；（Ⅱ）设D 是11A C 上PABC 的点，且1//A B 平面1B CD ，求11:A D DC 的值.13、图，在三棱锥中，AB AC ，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上．（Ⅰ）证明：AP ⊥BC ；（Ⅱ）已知8BC ，4PO ，3AO ，2OD ．求二面角B APC 的大小．14、如图，正方形ABCD 和四边形ACEF 所在的平面互相垂直，CE ⊥AC,EF ∥AC,AB=2，CE=EF=1（Ⅰ）求证：AF ∥平面BDE （Ⅱ）求证：CF ⊥平面BDE15、如图1，在直角梯形CD 中，D//C ，D2，C 1，D2，是D 的中点，是C 与的交点．将沿折起到1的位置，如图2．（I ）证明：CD平面1C ；（II ）若平面1平面CD ，求平面1C 与平面1CD 夹角的余弦值．16、如图，直三棱柱ABC—A1B1C1 中，AC ＝BC ＝1，∠ACB ＝90°，AA1 ＝2，D 是A1B1 中点．（1）求证C1D ⊥平面A1B ；（2）当点 F 在BB1 上什么位置时，会使得AB1 ⊥平面C1DF ？并证明你的结论．17、如图，在正三棱柱ABC—A1B1C1中，AB＝AA1，D是CC1的中点，F是A1B的中点，⑴求证：DF∥平面ABC；⑵求证：AF⊥BD。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)
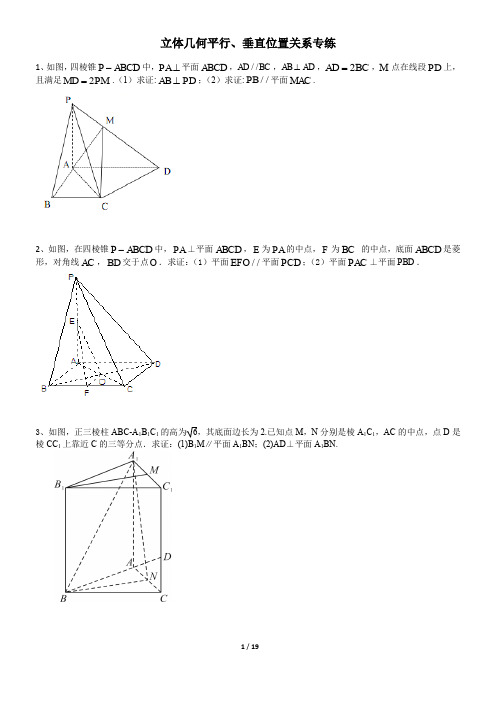
立体几何平行、垂直位置关系专练1、如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .2、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．3、如图，正三棱柱ABC-A 1B 1C 1的高为6，其底面边长为2.已知点M ，N 分别是棱A 1C 1，AC 的中点，点D 是棱CC 1上靠近C 的三等分点．求证：(1)B 1M ∥平面A 1BN ；(2)AD ⊥平面A 1BN.4、如图，等边三角形ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．(1)证明：CM⊥DE；(2)在边AC上找一点N，使CD∥平面BEN.5、如图，矩形ABCD所在平面与三角形ABE所在平面互相垂直，AE＝AB，M，N，H分别为DE，AB，BE 的中点．求证：(1)MN∥平面BEC；(2)AH⊥CE.6、如图，在三棱台ABCDEF中，CF⊥平面DEF，AB⊥BC.(1)设平面ACE∩平面DEF＝a，求证：DF∥a；(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在请确定点G的位置；若不存在，请说明理由．7、在三棱锥S ABC -中，平面SAB ⊥平面SBC ，AB BC ⊥，AS AB =，过A 作AF SB ⊥，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．（1）求证：平面EFG ∥平面ABC ．（2）求证：BC SA ⊥．8、如图，在直三棱柱111ABC A B C -中，AB BC ⊥，点D 为棱1C C 的中点，1AC 与1A D 交于点E ，1BC 与1B D 交于点F ，连结EF .求证：（1）//AB EF ；（2）平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．点，平面PAB ⊥底面ABCD ，90PAB ∠= ．求证：（1）//PB 平面AEC ；（2）平面PAC ⊥平面ABCD ．11、2.（2020·江苏省镇江高三二模）如图，三棱锥P ABC -中，点D ，E 分别为AB ，BC 的中点，且平面PDE ⊥平面ABC ．()1求证：//AC 平面PDE ；()2若2PD AC ==，PE =PBC ⊥平面ABC .12、（2020·江苏省建湖高级中学高三月考）如图，在四面体ABCD 中，,90AD BD ABC =∠= ，点,E F 分别为棱,AB AC 上的点，点G 为棱AD 的中点，且平面//EFG 平面BCD ．（1）求证：12EF BC =；（2）求证：平面EFD ⊥平面ABC ．点，PA ⊥平面ABCD .（1）求证：//PB 平面AEC ；（2）若四边形ABCD 是矩形且PA AD =，求证：AE ⊥平面PCD .14、（2020·江苏省高三二模）如图，在三棱柱111ABC A B C -中，侧面11ABB A ⊥底面ABC ，AB AC ⊥，E ，F 分别是棱AB ，BC 的中点.求证：（1）11AC ∥平面1B EF ；（2）1AC B E ⊥.15、（2020·江苏省连云港高三）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E 、F 分别为AD 、PB 的中点.（Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：//EF 平面PCD .16、（2020·江苏省苏州高三）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A1B 1∥平面DEC 1；（2）BE ⊥C 1E ．17、（2020·江苏省通州高三）如图，在三棱柱111ABC A B C -中，侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ；（2）求证:1C F ∥平面ABE ；18、（2020·江苏省高三三模）如图，三棱柱111ABC A B C -中，1BC B C =，O 为四边形11ACC A 对角线交点，F 为棱1BB 的中点，且AF ⊥平面11BCC B .（1）证明：//OF 平面ABC ；（2）证明：四边形11ACC A 为矩形.参考答案1．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .【解析】（1）∵四棱锥P ABCD -中，PA ⊥平面ABCD ，AB 平面ABCD ， ∴AB PA ⊥，又AB AD ⊥，,PA AD ⊂平面PAD ，PA AD A ⋂=， ∴AB ⊥面PAD .PD ⊂面PAD ，∴AB PD ⊥. （2）连结BD AC O ⋂=，连结MO ， ∵//AD BC ，2AD BC =，2DO BO ∴=,∵在PBD ∆中，2DM MP =，2DO BO =∴//PB MO ， 又PB ⊄面MAC ，MO ⊂面MAC ，∴//PB 面MAC .2．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ． 【详解】（1）因为在ΔPAC 中，E 为PA 的中点，O 为AC 的中点， 所以//EO PC又EO ⊄平面PCD ，PC ⊂平面PCD ， 所以//EO 平面PCD同理可证，//FO 平面PCD ，又EO FO O = ，EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD ．（2）因为PA ⊥平面ABCD ，BD ⊂平面ABCD ， 所以PA BD ⊥因为底面ABCD 是菱形，所以AC BD ⊥，又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
高中数学立体几何证明题汇总
高中数学立体几何证明题汇总立体几何常考证明题1.已知四边形ABCD是空间四边形，E,F,G,H分别是边AB,BC,CD,DA的中点。
1）证明EFGH是平行四边形。
2）已知BD=23，AC=2，EG=2，求异面直线AC、BD所成的角和EG、BD所成的角。
2.如图，已知空间四边形ABCD中，BC=AC,AD=BD，E 是AB的中点。
1）证明AB垂直于平面CDE。
2）证明平面CDE垂直于平面ABC。
3.如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点。
证明A1C平行于平面BDE。
4.已知三角形ABC中∠ACB=90，SA垂直于面ABC，AD垂直于SC。
证明AD垂直于面SBC。
5.已知正方体ABCD-A1B1C1D1，O是底面ABCD对角线的交点。
1）证明C1O平行于面AB1D1.2）证明AC1垂直于面AB1D1.6.正方体ABCD-A1B1C1D1中。
1）证明AC垂直于平面B1D1D。
2）证明BD1垂直于平面ACB1.7.正方体ABCD-A1B1C1D1中。
1）证明平面A1BD平行于平面B1DC。
2）已知E、F分别是AA1、CC1的中点，证明平面EB1D1平行于平面FBD。
8.四面体ABCD中，AC=BD，E、F分别为AD、BC的中点，且EF=AC/2，∠XXX。
证明BD垂直于平面ACD。
9.如图P是△ABC所在平面外一点，PA=PB，CB垂直于平面PAB，M是PC的中点，N是AB上的点，AN=3NB。
1）证明XXX垂直于AB。
2）当∠APB=90，AB=2BC=4时，求MN的长度。
10.如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是AB、AD、C1D1的中点。
证明平面D1EF平行于平面BDG。
11.如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点。
1）证明A1C平行于平面BDE。
2）证明平面A1AC垂直于平面BDE。
12、已知矩形ABCD，PA垂直于平面ABCD，AB=2，PA=AD=4，E为BC的中点。
立体几何证明题精选
立体几何证明题精选1.在多面体中，矩形ABB1A1和ACC1A1，AC垂直于BC。
证明BC垂直于平面ACC1A1，同时在线XXX上存在一点M，使得DE与平面A1MC平行。
2.在三棱锥P-ABC中，D，E，F分别是棱PC，AC，AB 的中点。
已知PA垂直于AC，PA=6，BC=8，DF=5.证明PA 平行于平面DEF，同时平面BDE垂直于平面ABC。
3.在四棱锥P-ABCD中，AP垂直于平面PCD，AD平行于BC，AB和BC分别为线段AD和PC的中点。
证明AP平行于平面BEF，同时BE垂直于平面PAC。
4.在四棱锥P-ABCD中，底面ABCD是平行四边形，BA=BD=BC=1，AD=2，PA=PD=√5，E和F分别是棱AD和PC的中点。
证明EF平行于平面PAB，同时平面PBC垂直于平面ABCD。
5.在三棱柱ABC-A1B1C1中，侧棱垂直于底面，AB垂直于BC，AA1=AC=2，BC=1，E和F分别是A1C1和BC的中点。
证明平面ABE垂直于平面B1BCC1，C1F平行于平面ABE，同时求三棱锥E-ABC的体积。
6.在四棱锥P-ABCD中，底面ABCD为矩形，PA垂直于平面ABCD，E为PD的中点。
证明PB平行于平面AEC，同时若AP=1，AD=3，则三棱锥P-ABD的体积为2/3，求A到平面PBC的距离。
7.在四棱锥中，平面ACD和平面ABD的交线为直线L，平面ABC和平面ACD的交线为直线M，平面ABC和平面ABD的交线为直线N，P为直线L上一点，Q为直线M上一点，R为直线N上一点，且PQR平行于平面ABCD，证明PR 平行于直线BD，同时求四面体PQRD的体积。
8.在长方体ABCD-A1B1C1D1中，底面A1B1C1D1为正方形，O为BD的中点，E为棱AA1上任意一点。
证明BD垂直于EC1，同时若AB=2，AE=2，OE垂直于EC1，则AA1的长度为2√2.。
立体几何专题
立体几何专题1. (北京文) (18) (本小题 14 分)如图，在四棱锥 P-ABCD 中，底面 ABCD 为矩形， 平面 PAD⊥平面 ABCD ， PA⊥ PD ， PA=PD ， E ， F 分别为 AD ， PB 的中点.( Ⅰ ) 求证： PE ⊥BC ； (Ⅱ)求证：平面 PAB ⊥平面 PCD ； (Ⅲ) 求证： EF∥平面 PCD.2. (北京理) (16) (本小题 14 分)如图， 在三棱柱 ABC- A 1B 1C 1 中， CC 1 」平面 ABC ， D ， E ， F ， G 分别为 AA 1，AC ， A 1C 1，BB 1 的中点， AB=BC= 5， AC= AA 1 =2．( Ⅰ ) 求证： AC⊥平面 BEF ； ( Ⅱ ) 求二面角B-CD-C 1 的余弦值； (Ⅲ) 证明： 直线 FG 与平面 BCD 相交．3. (江苏) (15) (本小题满分 14 分)在平行六面体ABCD 一 A B C D 中，AA = AB, AB 」B C ．求证： (1) AB∥平面A B C； (2) 平面ABB A 」平面A BC．4. (浙江) (19) (本题满分 15 分)如图，已知多面体 ABCA1B1C1，A1A， B1B， C1C均垂直于平面 ABC，∠ABC=120°， A1A=4， C1C=1， AB=BC=B1B=2．(Ⅰ)证明：AB1 ⊥平面A1B1C1；(Ⅱ)求直线 AC1 与平面 ABB1 所成的角的正弦值．1 1 1 1 1 1 1 1 1 1 1 1 1第 2 页共 10 页5. (天津文) (17)(本小题满分 13 分)如图，在四面体 ABCD 中，△ABC 是等边三角形，平面 ABC⊥平面 ABD，点 M 为棱AB 的中点， AB=2， AD= 2 3 ，∠BAD=90°．( Ⅰ )求证：AD⊥BC；( Ⅱ ) 求异面直线 BC 与 MD 所成角的余弦值；(Ⅲ)求直线 CD 与平面 ABD 所成角的正弦值．6. (天津理) (17)(本小题满分 13 分)如图，AD∥BC 且 AD=2BC，AD 」CD , EG∥AD且 EG=AD，CD∥FG 且 CD=2FG，DG 」平面ABCD， DA=DC=DG=2.(I)若 M 为 CF 的中点， N 为 EG 的中点，求证：MN∥平面CDE；(II)求二面角E BC F 的正弦值；(III)若点 P 在线段 DG 上，且直线 BP 与平面 ADGE 所成的角为60°，求线段 DP 的长.7. (全国卷一文)(18)(12 分)如图， 在平行四边形 ABCM 中， AB = AC = 3， ∠ACM = 90， 以 AC 为折痕 将△ ACM 折起，使点 M 到达点 D 的位置，且 AB⊥DA． (1)证明：平面 ACD ⊥平面 ABC ；(2) Q 为线段 AD 上一点， P 在线段 BC 上， 且 BP = DQ = DA ， 求三棱锥3Q ABP 的体积．8. (全国卷一理)(18)(12 分)如图， 四边形 ABCD 为正方形， E, F 分别为 AD, BC 的中点， 以 DF 为折 痕把 △DFC 折起，使点 C 到达点 P 的位置，且 PF 」BF . (1)证明：平面 PEF 」平面 ABFD ； (2)求 DP 与平面 ABFD 所成角的正弦值 .29. (全国卷二文)( 19) (12 分)如图，在三棱锥P ABC 中，AB = BC = 2 2，PA = PB = PC = AC = 4，O为AC 的中点．(1)证明：PO 」平面ABC；(2)若点M 在棱 BC 上，且MC = 2MB，求点C 到平面POM 的距离．10. (全国卷二理)(20)(12分)如图，在三棱锥P ABC 中，AB = BC = 2 2，PA = PB = PC = AC = 4，O 为AC 的中点．(1)证明：PO 」平面ABC；(2) 若点M 在棱BC 上，且二面角M PA C 为30，求PC 与平面 PAM 所成角的正弦值．POA CMB11. (全国卷三文)(19)(12分)如图，矩形ABCD所在平面与半圆弧 CD 所在平面垂直，M 是CD 上异于C， D 的点．(1)证明：平面AMD⊥平面BMC；(2)在线段AM 上是否存在点 P ，使得MC∥平面PBD ？说明理由．12. (全国卷三理)(19)(12分)如图，边长为 2 的正方形ABCD所在的平面与半圆弧CD 所在平面垂直，M 是CD 上异于C， D 的点．(1)证明：平面 AMD⊥平面BMC；(2) 当三棱锥M ABC 体积最大时，求面 MAB 与面MCD所成二面角的正弦值．13． (12 分)如图，四棱锥 P-ABCD 中，侧面 PAD 为等比三角形且垂直于底面 ABCD，1AB = BC = AD, 三BAD = 三ABC = 90o , E 是 PD 的中点.2(1) 证明：直线CE/ / 平面 PAB(2) 点 M 在棱 PC 上，且直线 BM 与底面 ABCD 所成锐角为45o ，求二面角 M-AB-D 的余弦值14． (12 分)如图，在四棱锥 P-ABCD 中， AB//CD，且三BAP = 三CDP = 90(1)证明：平面 PAB⊥平面PAD；(2)若 PA=PD=AB=DC, 三APD = 90 ,求二面角 A-PB-C 的余弦值.15. (12 分)如图，四面体 ABCD 中，△ABC 是正三角形，△ACD 是直角三角形，∠ABD= ∠CBD，AB=BD．(1) 证明：平面ACD⊥平面 ABC；(2) 过 AC 的平面交 BD 于点 E，若平面 AEC 把四面体 ABCD 分成体积相等的两部分，求二面角 D –AE –C 的余弦值．16．如图，在四棱锥 P-ABCD 中，底面 ABCD 为正方形，平面PAD⊥平面 ABCD，点 M在线段 PB 上， PD//平面 MAC， PA=PD= 6， AB=4．(I)求证： M 为 PB 的中点；(II)求二面角 B-PD-A 的大小；(III)求直线 MC 与平面 BDP 所成角的正弦值．17．如图，在三棱锥 P-ABC 中，PA⊥底面 ABC，三BAC = 90o .点 D， E， N 分别为棱PA， PC， BC 的中点， M 是线段 AD 的中点， PA=AC=4， AB=2.(Ⅰ)求证： MN∥平面BDE；(Ⅱ)求二面角 C-EM-N 的正弦值；7(Ⅲ) 已知点 H 在棱 PA 上，且直线 NH 与直线 BE 所成角的余弦值为，求线段 AH21的长.18.如图，几何体是圆柱的一部分，它是由矩形为旋转轴旋转得到的，是的中点.(Ⅰ)设是(Ⅱ)当上的一点，且，求的大小；，，求二面角的大小.(及其内部) 以边所在直线19． (本题满分 15 分)如图，已知四棱 P–ABCD，△PAD 是以 AD 为斜边的等腰直角三角形，BC∥AD，D⊥AD， PC=AD=2DC=2CB， E 为 PD 的中点.(Ⅰ)证明：CE∥平面PAB；(Ⅱ)求直线CE 与平面PBC 所成角的正弦值.。
高中立体几何证明题
高中立体几何证明题一、线面平行的证明题1已知正方体ABCD - A_{1}B_{1}C_{1}D_{1}，E，F分别是AB，BC的中点，求证：EF∥平面A_{1}C_{1}D。
解析1. 连接AC。
- 在 ABC中，因为E，F分别是AB，BC的中点，所以EF∥ AC。
2. 正方体ABCD - A_{1}B_{1}C_{1}D_{1}中：- AC∥ A_{1}C_{1}。
- 由EF∥ AC和AC∥ A_{1}C_{1}可得EF∥ A_{1}C_{1}。
- 又A_{1}C_{1}⊂平面A_{1}C_{1}D，EFnot⊂平面A_{1}C_{1}D。
- 根据线面平行的判定定理，所以EF∥平面A_{1}C_{1}D。
题2在三棱柱ABC - A_{1}B_{1}C_{1}中，D是AB的中点，求证：AC_{1}∥平面CDB_{1}。
解析1. 连接BC_{1}，交B_{1}C于点E。
- 在三棱柱ABC - A_{1}B_{1}C_{1}中，E为BC_{1}的中点。
2. 因为D是AB的中点：- 所以在 ABC_{1}中，DE∥ AC_{1}。
- 又DE⊂平面CDB_{1}，AC_{1}not⊂平面CDB_{1}。
- 根据线面平行的判定定理，可得AC_{1}∥平面CDB_{1}。
二、线面垂直的证明题3在四棱锥P - ABCD中，底面ABCD是正方形，PA = PB = PC = PD，求证：PA⊥平面ABCD。
解析1. 连接AC，BD交于点O，连接PO。
- 因为底面ABCD是正方形，所以O为AC，BD中点。
- 又PA = PC，PB = PD，根据等腰三角形三线合一的性质：- 可得PO⊥ AC，PO⊥ BD。
- 而AC∩ BD = O，AC⊂平面ABCD，BD⊂平面ABCD。
- 根据直线与平面垂直的判定定理，所以PO⊥平面ABCD。
- 又PA = PB = PC = PD，AO = BO = CO = DO，所以 PAO≅ PBO≅ PCO ≅ PDO。
立体几何证明及答案
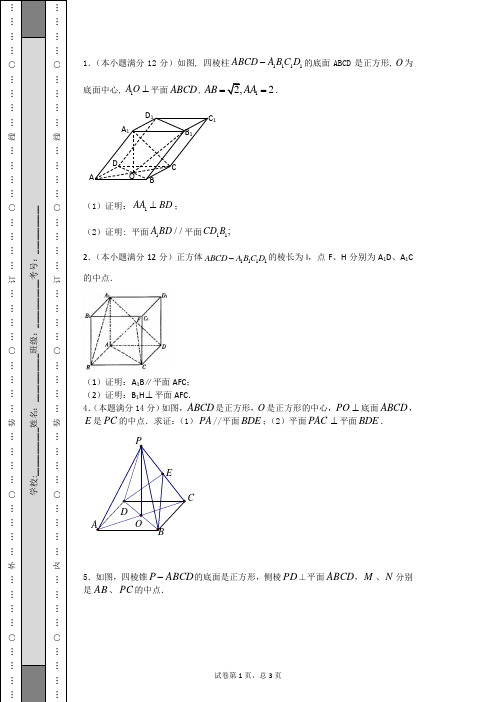
○…………外…………○…………装…………○…………订…………○…………线…………○………… 学校:___________姓名：___________班级：___________考号：___________ ○…………内…………○…………装…………○…………订…………○…………线…………○………… 1．（本小题满分12分）如图, 四棱柱1111ABCD A B C D -的底面ABCD 是正方形, O 为底面中心,1 AO ⊥平面ABCD ,12,2AB AA ==． （1）证明：1AA BD ⊥； （2）证明: 平面1//A BD 平面11;CD B 2．（本小题满分12分）正方体1111D C B A ABCD -的棱长为l ，点F 、H 分别为A 1D 、A 1C 的中点． （1）证明：A 1B ∥平面AFC ； （2）证明：B 1H ⊥平面AFC ． 4．（本题满分14分）如图，ABCD 是正方形，O 是正方形的中心，PO ⊥底面ABCD ，E 是PC 的中点．求证：（1）PA //平面BDE ；（2）平面PAC ⊥平面BDE ． 5．如图，四棱锥ABCD P -的底面是正方形，侧棱PD ⊥平面ABCD ，M 、N 分别是AB 、PC 的中点． A B CD A 1 B 1 C 1 D 1 O PE D A B C O○…………外…………○…………装…………○…………订…………○…………线…………○………… ※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※○…………内…………○…………装…………○…………订…………○…………线…………○………… （1）求证：//MN 平面PAD ；（2）求证：PCD PBC ⊥平面平面.6．如图，在四面体ABCD 中，CB CD AD BD =⊥，，点E F ，分别是AB BD ，的中点．求证：（1）直线//EF 面ACD ；（2）平面EFC ⊥面BCD ．7．如图，在直三棱柱111ABC A B C -中，1AA AC =，且11BC AC ⊥．（1）求证：平面1ABC ⊥平面11A ACC ；（2）若,D E 分别为是11A C 和1BB 的中点，求证：DE ‖平面1ABC ．8．如图，在直三棱柱ABC-A 1B 1C 1中，A 1B 1＝A 1C 1，D ，E 分别是棱BC ，CC 1上的点（点D 不同于点C ），且AD ⊥DE ，F 为B 1C 1的中点．求证：P M D C B A N○…………外…………○…………装…………○…………订…………○…………线…………○………… 学校:___________姓名：___________班级：___________考号：___________ ○…………内…………○…………装…………○…………订…………○…………线…………○………… （1）平面ADE ⊥平面BCC 1B 1； （2）直线A 1F ∥平面ADE ．参考答案1．（1）详见解析;（2）详见解析；（3）3．【解析】试题分析：（1）由题意BD ⊥AC ，因为A 1O ⊥平面ABCD 可知A 1O ⊥BD ，可证BD ⊥面A 1AC 即可证明结论；（2）由于A 1B 1∥AB ，AB ∥CD ，可得A 1B 1∥CD ，又A 1B 1=CD ，可得四边形A 1B 1CD 是平行四边形所以A 1D ∥B 1C ， 同理可证A 1B ∥CD 1，利用面面平行判定定理即可证明结结论； （3） 由于A 1O ⊥面ABCD 故A 1O 是三棱柱A 1B 1D 1-ABD 的高．又在RT △A 1OA 中，AA 1=2，AO = 1 ，可得A 1O=3,根据柱体体积公式即可求出三棱柱ABD-A 1B 1D 1的体积．试题解析：（1）证明：∵底面ABCD 是正方形 ∴BD ⊥AC又∵A 1O ⊥平面ABCD BD ⊂面ABCD ∴A 1O ⊥BD又∵A 1O∩AC=O A 1O ⊂面A 1AC ，AC ⊂面A 1AC∴BD ⊥面A 1AC AA 1⊂面A 1AC∴AA 1⊥BD 4分（2）∵A 1B 1∥AB AB ∥CD ∴A 1B 1∥CD 又A 1B 1=CD ∴四边形A 1B 1CD 是平行四边形 ∴A 1D ∥B 1C 同理A 1B ∥CD 1∵A 1B ⊂平面A 1BD, A 1D ⊂平面A 1BD, CD 1⊂平面CD 1B 1, B 1C ⊂平面CD 1B且A 1B∩ A 1D=A 1 CD 1∩B 1C=C∴平面A 1BD // 平面CD 1B 1 8分（3） ∵A 1O ⊥面ABCD ∴A 1O 是三棱柱A 1B 1D 1-ABD 的高．在正方形AB CD 中,AO = 1 ．在RT △A 1OA 中，AA 1=2，AO = 1 ∴A 1O=3 ∴21(2)1 (332)ABD V S AO ===三棱柱 所以, 三棱柱ABD-A 1B 1D 1的体积为3． 12分．考点：1．线面垂直的判定；2．面面平行的判定；3．柱体的体积公式．2．（1）见解析；（2）见解析.【解析】试题分析：（1）利用中点，结合三角形的中位线性质，只需取AC 中点E ，证A 1B ∥EF 即可；（2）注意到B 1H 即B 1D ，只需证B 1D 与AF 、AC 均垂直即可.试题解析：（1）连BD 交AC 于点E ，则E 为BD 的中点，连EF ，又F 为A 1D 的中点，所以EF ∥A 1B ， 3分又⊂EF 平面AFC ，⊄B A 1平面AFC ，由线面平行的判断定理可得A 1B ∥平面AFC 5分（2）连B 1C ，在正方体中A 1B 1CD 为长方形，∵H 为A 1C 的中点 ，∴H 也是B 1D 的中点，∴只要证⊥D B 1平面ACF 即可 6分由正方体性质得BD AC ⊥，B B AC 1⊥，∴⊥AC 平面B 1BD ，∴D B AC 1⊥ 9分又F 为A 1D 的中点，∴D A AF 1⊥，又11B A AF ⊥，∴⊥AF 平面A 1B 1D ，∴D B AF 1⊥，又AF 、AC 为平面ACF 内的相交直线， 11分∴⊥D B 1平面ACF.即⊥H B 1平面ACF. 12分考点：空间几何体，线面关系3． 见解析.【解析】试题分析：（1）证明线面平行，要找线线平行，在平面1AB D 内找一直线与1AC 平行即可.连1A B 交1AB于O,连OD ,则OD||1AC 即证.（2）依题意可得AD ⊥平面11BCC B ,故AD ⊥1BC .在矩形11BCC B 中，由条件可证111BDB BB C ∆∆,从而得11BC DB ⊥,故可得1BC ⊥平面1AB D . 试题解析：（1）连接11,A B AB O OD ⋂=连接1111//,,AC OD OD AB D AC AB D ⊂⊄面面 11//AC AB D 面 6分（漏线不在面内扣2分）（2）设D 为BC 中点，∴AD ⊥BC ，正三棱柱中，11BB ABC AD ABC AD BB ⊥⊂∴⊥面，面，,1111,BC BB B BC BB BCC B =⊂，平面111111,,AD BCC B BC BCC B AD BC ∴⊥⊂∴⊥平面平面 9分设11B D BC F =111DBB BB C 直角和直角中，1111111222BB BD DBB BB C BB B C ===∴，111,90,90BDF C BB CBB FBD BDF FBD ∴∠=∠∠+∠=∴∠+∠=又11BC B D ∴⊥ 13分又1111,,,BC AD AD B D D AD B D AB D ⊥=⊂平面11BC AB D ∴⊥平面 16分考点：线面平行，线面垂直的判定与性质4．见解析【解析】试题分析：（1）连接OE ，OE||PA ，由直线与平面平行的判定定理，可证得PA||平面BDE ；（2）由PO ⊥底面ABCD ，可得PO ⊥BD ；底面为正方形，可得BD ⊥AC ，由直线和平面垂直的判定定理，可得BD ⊥平面PAC ，由面面垂直的判定定理，可证得平面PAC ⊥平面BDE ． 试题解析：（1）连结OE Q O 是正方形的中心O AC \是的中点又Q E 是PC 的中点 \OE 是PCA V 的中位线 \ OE||PA又Q OE Ì 平面BDE,PA Ë 平面BDE \PA||平面BDE;（2）Q PO ⊥底面ABCD ，BD Ì平面ABCD \PO ⊥BD又Q BD ⊥AC AC PO O ?\BD ⊥平面PAC又Q BD Ì 平面BDE \平面PAC ⊥平面BDE ．考点：平面与平面垂直的判定；直线与平面平行的判定．5．（1）证明见解析；（2）证明见解析【解析】试题分析：（1）证明线面平行常用方法：一是利用线面平行的判定定理，二是利用面面平行的性质定理，三是利用面面平行的性质，注意把证明的条件写齐全；(2)要证平面与平面垂直，需要证明直线与平面垂直，证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法（若两条平行线中的一条垂直于这个平面，则另一条也垂直于这个平面.解题时，注意线线、线面与面面关系的相互转化.试题解析：解：（1)取PD 的中点F ，连接FN AF ,点N 是PC 的中点DC FN //∴，且DC FN 21= 又 四边形ABCD 是正方形，且点M 是AB 的中点DC AM //∴，且DC AM 21=AM FN //∴，且AM FN =∴四边形FNMA 是平行四边形，FA MN //∴又⊄MN 平面PAD ，⊂FA 平面PAD//MN ∴平面PAD⊥PD 平面ABCD ，且⊂BC 平面ABCDBC PD ⊥∴四边形ABCD 是正方形，CD BC ⊥∴又D CD PD =⊥∴BC 平面PCD又⊂BC 平面PBC∴平面PCD ⊥平面PBC . 考点：1、直线与平面平行的判定；2、平面与平面垂直的判定.6．（1）见解析 （2）见解析【解析】试题分析：（1）利用线面平行的判断定理证明线面平行，首先说明线线平行，然后再说明线面平行.（2）证明面面垂直的方法是利用线面垂直的判定定理首先说明线面垂直，然后再说明平面经过这条直线即可证明面面垂直解题时，注意线线、线面与面面关系的相互转化. 试题解析：（1）∵E F ，分别是AB BD ，的中点．∴EF 是ABD ∆的中位线，∴AD EF //，∵//EF ⊄面ACD ，AD ⊂面ACD ，∴直线//EF 面ACD ；（2）∵BD AD ⊥，AD EF //，∴BD EF ⊥，∵CD CB =，F 是BD 的中点，∴BD CF ⊥又F CF EF =⋂, ∴BD ⊥面EFC ，∵BD ⊂面BCD ，∴面EFC ⊥面BCD考点：平面与平面垂直的判定；直线与平面平行的判定．7．（1）见解析；（2）见解析【解析】试题分析：（1）由已知易知11A ACC 为正方形，可证A 1C ⊥平面ABC 1 ，因此平面ABC 1⊥平面11A ACC ；（2）方法一：取1A A 中点F ，连EF ，FD ，易知平面EFD ∥平面1ABC ，所以ED ∥平面1ABC ；方法二：A 1C 交AC 1于G 点连BG ，易证四边形BEDG 为平行四边形，可证DE ∥平面ABC 1．试题解析：（1）证明：在直三棱柱111ABC A B C -中，有1A A ⊥平ABC ．AC ABC ⊂面 ∴1A A AC ⊥， 又1A A AC =，∴11A ACC 为正方形，∴11A C AC ⊥ ．又BC 1⊥A 1C ，且111AC BC C = ∴A 1C ⊥平面ABC 1 ，而1AC ⊂面11A ACC 则平面ABC 1⊥平面11A ACC（2）方法一：取1A A 中点F ，连EF ，FD ，EF AB ，DF ∥1AC即平面EFD ∥平面1ABC ， 则有ED ∥平面1ABC方法二：A 1C 交AC 1于G 点连BG ， BE DG ，则有DE ∥BG ，即DE ∥平面ABC 1．考点：面面垂直的判定定理与线面平行的判定定理8．（1）见试题解析；（2）见试题解析。
高中数学立体几何证明题练习卷
高中数学立体几何证明题练习卷立体几何作为高中数学的重要组成部分，其中的证明题对于同学们的空间想象能力、逻辑推理能力以及数学语言的运用能力都有着较高的要求。
为了帮助同学们更好地掌握这部分知识，提高解题能力，特编制此练习卷。
一、选择题1、已知直线\（a\），＼（b\）和平面\（＼alpha\），若\（a\perp b\），＼（a\perp\alpha\），则（）A ＼（b\parallel\alpha\）B ＼（b\subset\alpha\）C ＼（b\perp\alpha\）D ＼（b\）与\（＼alpha\）相交或\（b\subset\alpha\）2、设\（＼alpha\），＼（＼beta\）是两个不同的平面，＼（l\），＼（m\）是两条不同的直线，且\（l\subset\alpha\），＼（m\subset\beta\），则下列命题中正确的是（）A 若\（l\parallel\beta\），则\（＼alpha\parallel\beta\）B 若\（＼alpha\perp\beta\），则\（l\perp m\）C 若\（l\perp m\），则\（＼alpha\perp\beta\）D 若\（＼alpha\parallel\beta\），则\（l\parallel m\）3、在正方体\（ABCD A_{1}B_{1}C_{1}D_{1}＼）中，＼（E\）为\（A_{1}C_{1}＼）的中点，则异面直线\（AE\）与\（CD_{1}＼）所成角的余弦值为（）A ＼（＼dfrac{＼sqrt{2}｝｛6}＼）B ＼（＼dfrac{＼sqrt{3}｝｛6}＼）C ＼（＼dfrac{＼sqrt{6}｝｛6}＼）D ＼（＼dfrac{＼sqrt{10}｝｛6}＼）二、填空题1、已知正三棱柱\（ABC A_{1}B_{1}C_{1}＼）的各棱长都为\（2\），＼（E\），＼（F\）分别是\（AB\），＼（A_{1}C_{1}＼）的中点，则\（EF\）的长为________。
2024届新高考数学大题精选30题--立体几何含答案
大题立体几何1(2024·黑龙江·二模)如图，已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2，M是BC的中点，N是AB1的中点，P是B1C1的中点．(1)证明：MN⎳平面A1CP；(2)求点P到直线MN 的距离．2(2024·安徽合肥·二模)如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠BAD=60°,M是侧棱PC的中点，侧面PAD为正三角形，侧面PAD⊥底面ABCD．(1)求三棱锥M-ABC的体积；(2)求AM与平面PBC所成角的正弦值．2024届新高考数学大题精选30题--立体几何3(2023·福建福州·模拟预测)如图，在三棱柱ABC-A1B1C1中，平面AA1C1C⊥平面ABC,AB= AC=BC=AA1=2，A1B=6．(1)设D为AC中点，证明：AC⊥平面A1DB；(2)求平面A1AB1与平面ACC1A1夹角的余弦值．4(2024·山西晋中·三模)如图，在六面体ABCDE中，BC=BD=6，EC⊥ED，且EC=ED= 2，AB平行于平面CDE，AE平行于平面BCD，AE⊥CD.(1)证明：平面ABE⊥平面CDE；(2)若点A到直线CD的距离为22，F为棱AE的中点，求平面BDF与平面BCD夹角的余弦值．5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC-A1B1C1中，A1在平面ABC内的射影O在棱AC的中点处，P为棱A1B1(包含端点)上的动点．(1)求点P到平面ABC1的距离；(2)若AP⊥平面α，求直线BC1与平面α所成角的正弦值的取值范围．6(2024·重庆·模拟预测)在如图所示的四棱锥P-ABCD中，已知AB∥CD，∠BAD=90°，CD= 2AB，△PAB是正三角形，点M在侧棱PB上且使得PD⎳平面AMC．(1)证明：PM=2BM；(2)若侧面PAB⊥底面ABCD，CM与底面ABCD所成角的正切值为311，求二面角P-AC-B的余弦值．7(2024·安徽·模拟预测)2023年12月19日至20日，中央农村工作会议在北京召开，习近平主席对“三农”工作作出指示．某地区为响应习近平主席的号召，积极发展特色农业，建设蔬菜大棚．如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架，四边形ABCD是矩形，AB=8m，AD=4m，ED=CF=1m，且ED，CF都垂直于平面ABCD，GA=GB=5m，HE=HF，平面ABG⊥平面ABCD．(1)求点H到平面ABCD的距离；(2)求平面BFHG与平面AGHE所成锐二面角的余弦值．8(2024·重庆·模拟预测)如图，ACDE为菱形，AC=BC=2，∠ACB=120°，平面ACDE⊥平面ABC，点F在AB上，且AF=2FB，M，N分别在直线CD，AB上．(1)求证：CF⊥平面ACDE；(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线，若∠EAC=60°，MN为直线CD，AB的公垂线，求ANAF的值；(3)记直线BE与平面ABC所成角为α，若tanα>217，求平面BCD与平面CFD所成角余弦值的范围．9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°，使得CD 到EF 的位置，得到如图所示的几何体．(1)求证：平面ACF ⊥平面BDE ；(2)点M 为DF 上一点，若二面角C -AM -E 的余弦值为13，求∠MAD ．10(2024·安徽黄山·二模)如图，已知AB 为圆台下底面圆O 1的直径，C 是圆O 1上异于A ,B 的点，D 是圆台上底面圆O 2上的点，且平面DAC ⊥平面ABC ，DA =DC =AC =2，BC =4，E 是CD 的中点，BF =2FD ．(1)证明：DO 2⎳BC ；(2)求直线DB 与平面AEF 所成角的正弦值.11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22，A 1B 1=12AB ，M 为BC 中点，已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1 ，其中λ∈0,1 ．(1)求证D 1P ⊥AC ；(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37，当λ=23时，求直线DP 与平面AMC 1所成角的正弦值．12(2024·辽宁·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2，AB =1,BC =3，点E 为线段AC 的中点.(1)求证：AB 1∥平面BEC 1；(2)若∠A 1AC =π3，求二面角A -BE -C 1的余弦值.13(2024·广东广州·一模)如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，△DCP是等边三角形，∠DCB=∠PCB=π4，点M，N分别为DP和AB的中点.(1)求证：MN⎳平面PBC；(2)求证：平面PBC⊥平面ABCD；(3)求CM与平面PAD所成角的正弦值.14(2024·广东梅州·二模)如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，底面ABCD 为直角梯形，△PAD为等边三角形，AD⎳BC，AD⊥AB，AD=AB=2BC=2．(1)求证：AD⊥PC；(2)点N在棱PC上运动，求△ADN面积的最小值；(3)点M为PB的中点，在棱PC上找一点Q，使得AM⎳平面BDQ，求PQQC的值．15(2024·广东广州·模拟预测)如图所示，圆台O1O2的轴截面A1ACC1为等腰梯形，AC=2AA1= 2A1C1=4,B为底面圆周上异于A,C的点，且AB=BC,P是线段BC的中点.(1)求证：C1P⎳平面A1AB.(2)求平面A1AB与平面C1CB夹角的余弦值.16(2024·广东深圳·二模)如图，三棱柱ABC-A1B1C1中，侧面BB1C1C⊥底面ABC，且AB= AC，A1B=A1C．(1)证明：AA1⊥平面ABC；(2)若AA1=BC=2，∠BAC=90°，求平面A1BC与平面A1BC1夹角的余弦值．17(2024·河北保定·二模)如图，在四棱锥P -ABCD 中，平面PCD 内存在一条直线EF 与AB 平行，PA ⊥平面ABCD ，直线PC 与平面ABCD 所成的角的正切值为32，PA =BC =23，CD =2AB =4.(1)证明：四边形ABCD 是直角梯形.(2)若点E 满足PE =2ED ，求二面角P -EF -B 的正弦值.18(2024·湖南衡阳·模拟预测)如图，在圆锥PO 中，P 是圆锥的顶点，O 是圆锥底面圆的圆心，AC 是圆锥底面圆的直径，等边三角形ABD 是圆锥底面圆O 的内接三角形，E 是圆锥母线PC 的中点，PO =6,AC =4.(1)求证：平面BED ⊥平面ABD ；(2)设点M 在线段PO 上，且OM =2，求直线DM 与平面ABE 所成角的正弦值.19(2024·湖南岳阳·三模)已知四棱锥P -ABCD 的底面ABCD 是边长为4的菱形，∠DAB =60°，PA =PC ，PB =PD =210，M 是线段PC 上的点，且PC =4MC ．(1)证明：PC ⊥平面BDM ；(2)点E 在直线DM 上，求BE 与平面ABCD 所成角的最大值．20(2024·湖南·二模)如图，直四棱柱ABCD -A 1B 1C 1D 1的底面是边长为2的菱形，∠ABC =60°,BD 1⊥平面A 1C 1D .(1)求四棱柱ABCD -A 1B 1C 1D 1的体积；(2)设点D 1关于平面A 1C 1D 的对称点为E ，点E 和点C 1关于平面α对称(E 和α未在图中标出)，求平面A 1C 1D 与平面α所成锐二面角的大小.21(2024·山东济南·二模)如图，在四棱锥P-ABCD中，四边形ABCD为直角梯形，AB∥CD，∠DAB=∠PCB=60°,CD=1,AB=3,PC=23，平面PCB⊥平面ABCD，F为线段BC的中点，E为线段PF上一点.(1)证明：PF⊥AD；(2)当EF为何值时，直线BE与平面PAD夹角的正弦值为74.22(2024·山东潍坊·二模)如图1，在平行四边形ABCD中，AB=2BC=4，∠ABC=60°，E为CD 的中点，将△ADE沿AE折起，连结BD，CD，且BD=4，如图2．(1)求证：图2中的平面ADE⊥平面ABCE；(2)在图2中，若点F在棱BD上，直线AF与平面ABCE所成的角的正弦值为3010，求点F到平面DEC 的距离．23(2024·福建·模拟预测)如图，在三棱锥P-ABC中，PA⊥PB,AB⊥BC,AB=3,BC=6，已知二面角P-AB-C的大小为θ，∠PAB=θ.(1)求点P到平面ABC的距离；(2)当三棱锥P-ABC的体积取得最大值时，求：(Ⅰ)二面角P-AB-C的余弦值；(Ⅱ)直线PC与平面PAB所成角.24(2024·浙江杭州·二模)如图，在多面体ABCDPQ中，底面ABCD是平行四边形，∠DAB=60°, BC=2PQ=4AB=4,M为BC的中点，PQ∥BC,PD⊥DC,QB⊥MD．(1)证明：∠ABQ=90°；(2)若多面体ABCDPQ的体积为152，求平面PCD与平面QAB夹角的余弦值．25(2024·浙江嘉兴·二模)在如图所示的几何体中，四边形ABCD为平行四边形，PA⊥平面ABCD,PA∥QD，BC=2AB=2PA=2,∠ABC=60°.(1)证明：平面PCD⊥平面PAC；(2)若PQ=22，求平面PCQ与平面DCQ夹角的余弦值.26(2024·浙江绍兴·二模)如图，在三棱锥P-ABC中，AB=4，AC=2，∠CAB=60°，BC⊥AP.(1)证明：平面ACP⊥平面ABC；(2)若PA=2，PB=4，求二面角P-AB-C的平面角的正切值.27(2024·河北沧州·一模)如图，在正三棱锥A -BCD 中，BC =CD =BD =4，点P 满足AP=λAC ，λ∈(0,1)，过点P 作平面α分别与棱AB ，BD ，CD 交于Q ，S ，T 三点，且AD ⎳α，BC ⎳α.(1)证明：∀λ∈(0,1)，四边形PQST 总是矩形；(2)若AC =4，求四棱锥C -PQST 体积的最大值.28(2024·湖北·二模)如图1．在菱形ABCD 中，∠ABC =120°，AB =4，AE =λAD ，AF =λAB(0<λ<1)，沿EF 将△AEF 向上折起得到棱锥P -BCDEP ．如图2所示，设二面角P -EF -B 的平面角为θ．(1)当λ为何值时，三棱锥P -BCD 和四棱锥P -BDEF 的体积之比为95(2)当θ为何值时，∀λ∈0,1 ，平面PEF 与平面PFB 的夹角φ的余弦值为5529(2024·湖北·模拟预测)空间中有一个平面α和两条直线m ，n ，其中m ，n 与α的交点分别为A ，B ，AB =1，设直线m 与n 之间的夹角为π3，(1)如图1，若直线m ，n 交于点C ，求点C 到平面α距离的最大值；(2)如图2，若直线m ，n 互为异面直线，直线m 上一点P 和直线n 上一点Q 满足PQ ⎳α，PQ ⊥n 且PQ ⊥m ，(i )求直线m ，n 与平面α的夹角之和；(ii )设PQ =d 0<d <1 ，求点P 到平面α距离的最大值关于d 的函数f d ．30(2024·浙江绍兴·模拟预测)如图所示，四棱台ABCD -A 1B 1C 1D 1，底面ABCD 为一个菱形，且∠BAD =120°. 底面与顶面的对角线交点分别为O ，O 1. AB =2A 1B 1=2，BB 1=DD 1=392，AA 1与底面夹角余弦值为3737.(1)证明：OO 1⊥平面ABCD ；(2)现将顶面绕OO 1旋转θ角，旋转方向为自上而下看的逆时针方向. 此时使得底面与DC 1的夹角正弦值为64343，此时求θ的值(θ<90°)；(3)求旋转后AA 1与BB 1的夹角余弦值.大题 立体几何1(2024·黑龙江·二模)如图，已知正三棱柱ABC -A 1B 1C 1的侧棱长和底面边长均为2，M 是BC 的中点，N 是AB 1的中点，P 是B 1C 1的中点．(1)证明：MN ⎳平面A 1CP ；(2)求点P 到直线MN 的距离．【答案】(1)证明见解析(2)3【分析】(1)建立如图空间直角坐标系A -xyz ，设平面A 1CP 的一个法向量为n=(x ,y ,z )，利用空间向量法证明MN ⋅n=0即可；(2)利用空间向量法即可求解点线距.【详解】(1)由题意知，AA 1⊥平面ABC ，∠BAC =60°，而AB ⊂平面ABC ，所以AA 1⊥AB ，在平面ABC 内过点A 作y 轴，使得AB ⊥y 轴，建立如图空间直角坐标系A -xyz ，则A (0,0,0),B (2,0,0),C (1,3,0),A 1(0,0,2),B 1(2,0,2)，得M 32,32,0,N (1,0,1),P 32,32,2，所以A 1C =(1,3,-2),A 1P =32,32,0 ,MN =-12,-32,1 ，设平面A1CP 的一个法向量为n=(x ,y ,z )，则n ⋅A 1C=x +3y -2z =0n ⋅A 1P =32x +32y =0，令x =1，得y =-3,z =-1，所以n=(1,-3,-1)，所以MN ⋅n =-12×1+-32×(-3)+1×(-1)=0，又MN 不在平面A 1CP 内即MN ⎳平面A 1CP ；(2)如图，连接PM ，由(1)得PM =(0,0,-2)，则MN ⋅PM =-2，MN =2,PM =2，所以点P 到直线MN 的距离为d =PM 2-MN ⋅PMPM2= 3.2(2024·安徽合肥·二模)如图，在四棱锥P -ABCD 中，底面ABCD 是边长为2的菱形，∠BAD =60°,M 是侧棱PC 的中点，侧面PAD 为正三角形，侧面PAD ⊥底面ABCD ．(1)求三棱锥M -ABC 的体积；(2)求AM 与平面PBC 所成角的正弦值．【答案】(1)12(2)3311．【分析】(1)作出辅助线，得到线线垂直，进而得到线面垂直，由中位线得到M 到平面ABCD 的距离为32，进而由锥体体积公式求出答案；(2)证明出BO ⊥AD ，建立空间直角坐标系，求出平面的法向量，进而由法向量的夹角余弦值的绝对值求出线面角的正弦值.【详解】(1)如图所示，取AD 的中点O ，连接PO ．因为△PAD 是正三角形，所以PO ⊥AD ．又因为平面PAD ⊥底面ABCD ,PO ⊂平面PAD ，平面PAD ∩平面ABCD =AD ，所以PO ⊥平面ABCD ，且PO =3．又因为M 是PC 的中点，M 到平面ABCD 的距离为32，S △ABC =12×2×2×sin 2π3=3，所以三棱锥M -ABC 的体积为13×3×32=12．(2)连接BO ,BD ，因为∠BAD =π3，所以△ABD 为等边三角形，所以BO ⊥AD ，以O 为原点，OA ,OB ,OP 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则P 0,0,3 ,A 1,0,0 ,B 0,3,0 ,C -2,3,0 ，所以M -1,32,32 ,AM =-2,32,32,PB =0,3,-3 ,BC =-2,0,0 ．设平面PBC 的法向量为n=x ,y ,z ，则PB ⋅n =0BC ⋅n =0，即3y -3z =0-2x =0 ，解得x =0，取z =1，则y =1，所以n=0,1,1 ．设AM 与平面PBC 所成角为θ，则sin θ=cos AM ,n =AM ⋅nAM ⋅n=-2,32,32 ⋅0,1,14+34+34×1+1=3311．即AM 与平面PBC 所成角的正弦值为3311．3(2023·福建福州·模拟预测)如图，在三棱柱ABC -A 1B 1C 1中，平面AA 1C 1C ⊥平面ABC ,AB =AC =BC =AA 1=2，A 1B =6．(1)设D 为AC 中点，证明：AC ⊥平面A 1DB ；(2)求平面A 1AB 1与平面ACC 1A 1夹角的余弦值．【答案】(1)证明见解析；(2)55【分析】(1)根据等边三角形的性质得出BD ⊥AC ，根据平面ACC 1A 1⊥平面ABC 得出BD ⊥平面ACC 1A 1，BD ⊥A 1D ，利用勾股定理得出AC ⊥A 1D ，从而证明AC ⊥平面A 1DB ；(2)建立空间直角坐标系，利用坐标表示向量，求出平面A 1AB 1的法向量和平面ACC 1A 1的一个法向量，利用向量求平面A 1AB 1与平面ACC 1A 1的夹角余弦值．【详解】(1)证明：因为D 为AC 中点，且AB =AC =BC =2，所以在△ABC 中，有BD ⊥AC ，且BD =3，又平面ACC 1A 1⊥平面ABC ，且平面ACC 1A 1∩平面ABC =AC ，BD ⊂平面ABC ,所以BD ⊥平面ACC 1A 1，又A 1D ⊂平面ACC 1A 1，则BD ⊥A 1D ，由A 1B =6，BD =3，得A 1D =3，因为AD =1，AA 1=2，A 1D =3，所以由勾股定理，得AC ⊥A 1D ，又AC ⊥BD ，A 1D ∩BD =D ,A 1D ,BD ⊂平面A 1DB ，所以AC ⊥平面A 1DB ；(2)如图所示，以D 为原点，建立空间直角坐标系D -xyz ，可得A (1,0,0),A 1(0,0,3),B (0,3,0)，则AA 1 =-1,0,3 ,AB=-1,3,0 ，设平面A 1AB 1的法向量为n=(x ,y ,z )，由n ⋅AA 1=-x +3z =0n ⋅AB=-x +3y =0，令x =3，得y =1，z =1，所以n=3,1,1 ,由(1)知，BD ⊥平面ACC 1A 1，所以平面ACC 1A 1的一个法向量为BD=(0,-3,0)，记平面A 1AB 1与平面ACC 1A 1的夹角为α，则cos α=|n ⋅BD ||n ||BD |=35×3=55，所以平面A 1AB 1与平面ACC 1A 1夹角的余弦值为55．4(2024·山西晋中·三模)如图，在六面体ABCDE 中，BC =BD =6，EC ⊥ED ，且EC =ED =2，AB 平行于平面CDE ，AE 平行于平面BCD ，AE ⊥CD .(1)证明：平面ABE ⊥平面CDE ；(2)若点A 到直线CD 的距离为22，F 为棱AE 的中点，求平面BDF 与平面BCD 夹角的余弦值．【答案】(1)证明见解析(2)10535【分析】(1)设平面ABE 与直线CD 交于点M ，使用线面平行的性质，然后用面面垂直的判定定理即可；(2)证明BE ⊥平面CDE ，然后构造空间直角坐标系，直接用空间向量方法即可得出结果.【详解】(1)设平面ABE 与直线CD 交于点M ，连接ME ,MB ，则平面ABE 与平面CDE 的交线为ME ，平面ABE 与平面BCD 的交线为MB ，因为AB 平行于平面CDE ，AB ⊂平面ABE ，平面ABE 和平面CDE 的交线为ME ，所以AB ∥ME ．同理AE ∥MB ，所以四边形ABME 是平行四边形，故AE ∥MB ，AB ∥ME .因为CD ⊥AE ，AE ∥MB ，所以CD ⊥MB ，又BC =BD =6，所以M 为棱CD 的中点在△CDE 中，EC =ED ，MC =MD ，所以CD ⊥ME ，由于AB ∥ME ，故CD ⊥AB .而CD ⊥AE ，AB ∩AE =A ，AB ,AE ⊂平面ABE ，所以CD ⊥平面ABE ，又CD ⊂平面CDE ，所以平面ABE ⊥平面CDE .(2)由(1)可知，CD ⊥平面ABME ，又AM ⊂平面ABME ，所以CD ⊥AM .而点A 到直线CD 的距离为22，故AM =2 2.在等腰直角三角形CDE 中，由EC =ED =2,得CD =2,MC =MD =ME =1.在等腰三角形BCD 中，由MC =MD =1，BC =BD =6，得BM = 5.在平行四边形ABME 中，AE =BM =5，AB =EM =1，AM =22，由余弦定理得cos ∠MEA =EM 2+AE 2-AM 22EM ·AE=-55，所以cos ∠BME =55，所以BE =BM 2+EM 2-2BM ·EM cos ∠BME =2.因为BE 2+ME 2=22+12=5 2=BM 2，所以BE ⊥ME .因为平面ABME ⊥平面CDE ，平面ABME 和平面CDE 的交线为ME ，BE 在平面ABME 内.所以BE ⊥平面CDE .如图，以E 为坐标原点，EC ,ED ,EB 分别为x ,y ,z 轴正方向，建立空间直角坐标系.则E 0,0,0 ,C 2,0,0 ,D 0,2,0 ,B 0,0,2 ,A -22,-22,2 ,F -24,-24,1.所以CD =-2,2,0 ,DB =0,-2,2 ,FB =24,24,1 .设平面BCD 的法向量为m=x 1,y 1,z 1 ，则m ⋅CD=0m ⋅DB =0，即-2x 1+2y 1=0-2y 1+2z 1=0 .则可取x 1=2，得m=2,2,2 .设平面BDF 的法向量为n =x 2,y 2,z 2 ，则n ⋅FB =0n ⋅DB=0，即24x 2+24y 2+z 2=0-2y 2+2z 2=0.取z 2=1，则n=-32,2,1 ．设平面BDF 与平面BCD 的夹角为θ，则cos θ=m ⋅n m ⋅n =-3210×21=10535.所以平面BDF 与平面BCD 夹角的余弦值为10535.5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC -A 1B 1C 1中，A 1在平面ABC 内的射影O 在棱AC 的中点处，P 为棱A 1B 1(包含端点)上的动点．(1)求点P 到平面ABC 1的距离；(2)若AP ⊥平面α，求直线BC 1与平面α所成角的正弦值的取值范围．【答案】(1)23913；(2)25,104.【分析】(1)以O 为原点建立空间直角坐标系，求出平面ABC 1的法向量，再利用点到平面距离的向量求法求解即得.(2)由向量共线求出向量AP的坐标，再利用线面角的向量求法列出函数关系，并求出函数的值域即可.【详解】(1)依题意，A 1O ⊥平面ABC ，OB ⊥AC (底面为正三角形)，且A 1O =OB =3，以O 为原点，OB ,OC ,OA 1的方向分别为x ,y ,z 轴的正方向，建立空间直角坐标系，如图，则O (0,0,0),A (0,-1,0),B (3,0,0),C (0,1,0),A 1(0,0,3),C 1(0,2,3)，AC 1 =(0,3,3)，BC 1 =(-3,2,3)，AA 1 =(0,1,3)，由A 1B 1⎳AB ，A 1B 1⊄平面ABC 1，AB ⊂平面ABC 1，则A 1B 1⎳平面ABC 1，即点P 到平面ABC 1的距离等于点A 1到平面ABC 1的距离，设n =(x ,y ,z )为平面ABC 1的一个法向量，由n ⋅AC 1=3y +3z =0n ⋅BC 1=-3x +2y +3z =0，取z =3，得n=(1,-3,3)，因此点A 1到平面ABC 1的距离d =|AA 1 ⋅n||n |=2313=23913，所以点P 到平面ABC 1的距离为23913．(2)设A 1P =λA 1B 1 ，λ∈[0,1]，则AP =AA 1 +A 1P =AA 1 +λAB=(0,1,3)+λ(3,1,0)=(3λ,1+λ,3)，由AP ⊥α，得AP为平面α的一个法向量，设直线BC 1与平面α所成角为θ，则sin θ=|cos ‹BC 1 ,AP ›|=|BC 1 ⋅AP||BC 1 ||AP |=|5-λ|10⋅3λ2+(1+λ)2+3=5-λ25⋅2λ2+λ+2，令t =5-λ，则λ=5-t ，t ∈[4,5]，则sin θ=t 25⋅2(5-t )2+(5-t )+2=t25⋅2t 2-21t +57=125⋅2-21t+57t 2=125571t-7382+576，由t ∈[4,5]，得1t ∈15,14 ，于是571t -738 2+576∈225,516，25⋅571t -738 2+576∈2105,52 ，则sin θ∈25,104，所以直线BC 1与平面α所成角的正弦值的取值范围是25,104.6(2024·重庆·模拟预测)在如图所示的四棱锥P -ABCD 中，已知AB ∥CD ，∠BAD =90°，CD =2AB ，△PAB 是正三角形，点M 在侧棱PB 上且使得PD ⎳平面AMC ．(1)证明：PM =2BM ；(2)若侧面PAB ⊥底面ABCD ，CM 与底面ABCD 所成角的正切值为311，求二面角P -AC -B 的余弦值．【答案】(1)证明见解析；(2)1010．【分析】(1)连接BD 与AC 交于点E ，连接EM ，由已知得AB CD=EBED ，由线面平行的性质得PD ∥EM ，根据三角形相似可得EB ED =BM PM=12，即PM =2BM(2)设AB 的中点O ，首先由已知得PO ⊥底面ABCD ，在△PAB 中过点M 作MF ∥PO 交AB 于点F ，得MF ⊥底面ABCD ，则∠MCF 为CM 与底面ABCD 所成角，在底面ABCD 上过点O 作OG ⊥AC 于点G ，则∠PGO 是二面角P -AC -B 的平面角，根据条件求解即可【详解】(1)证明：连接BD 与AC 交于点E ，连接EM ，在△EAB 与△ECD 中，∵AB ∥CD ，∴AB CD=EBED ，由CD =2AB ，得ED =2EB ，又∵PD ⎳平面AMC ，而平面PBD ∩平面AMC =ME ，PD ⊂平面PBD ，∴PD ∥EM ，∴在△PBD 中，EB ED =BM PM=12，∴PM =2BM ；(2)设AB 的中点O ，在正△PAB 中，PO ⊥AB ，而侧面PAB ⊥底面ABCD ，侧面PAB ∩底面ABCD =AB ，且PO ⊂平面PAB ，∴PO ⊥底面ABCD ，在△PAB 中过点M 作MF ⎳PO 交AB 于点F ，∴MF ⊥底面ABCD ，∴∠MCF 为CM 与底面ABCD 所成角，∴MF CF=311，设AB =6a ，则MF=3a，∴CF=11a，BF=MF3=a，则在直角梯形ABCD中，AF=5a，而CD=12a，则AD=11a2-12a-5a2=62a，在底面ABCD上过点O作OG⊥AC于点G，则∠PGO是二面角P-AC-B的平面角，易得OA=3a，AC=66a，在梯形ABCD中，由OAOG=ACAD⇒3aOG=66a62a，得OG=3a，在Rt△POG中，PG=30a，∴cos∠PGO=OGPG=1010．7(2024·安徽·模拟预测)2023年12月19日至20日，中央农村工作会议在北京召开，习近平主席对“三农”工作作出指示．某地区为响应习近平主席的号召，积极发展特色农业，建设蔬菜大棚．如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架，四边形ABCD是矩形，AB=8m，AD=4m，ED=CF=1m，且ED，CF都垂直于平面ABCD，GA=GB=5m，HE=HF，平面ABG⊥平面ABCD．(1)求点H到平面ABCD的距离；(2)求平面BFHG与平面AGHE所成锐二面角的余弦值．【答案】(1)4(2)413【分析】(1)取AB,CD的中点M,N，证得平面ADE⎳平面MNHG，得到AE⎳GH，再由平面ABG⎳平面CDEHG，证得AG⎳EH，得到平行四边形AGHE，得到GH=AE，求得HN=4，结合HN⊥平面ABCD，即可求解；(2)以点N为原点，建立空间直角坐标系，分别求得平面BFHG和平面AGHE的法向量n =(1,3,4)和m =(1,-3,4)，结合向量的夹角公式，即可求解.【详解】(1)如图所示，取AB,CD的中点M,N，连接GM,MN,HN，因为GA=GB，可得GM⊥AB，又因为平面ABG⊥平面ABCD，且平面ABG∩平面ABCD=AB，GM⊂平面ABG，所以GM⊥平面ABCD，同理可得：HN⊥平面ABCD，因为ED⊥平面ABCD，所以ED⎳HN，又因为ED⊄平面MNHG，HN⊂平面MNHG，所以ED⎳平面MNHG，因为MN⎳AD，且AD⊄平面MNHG，MN⊂平面MNHG，所以AD⎳平面MNHG，又因为AD∩DE=D，且AD,DE⊂平面ADE，所以平面ADE⎳平面MNHG，因为平面AEHG与平面ADE和平面MNHG于AE,GH，可得AE⎳GH，又由GM⎳HN，AB⎳CD，且AB∩GM=M和CD∩HN=N，所以平面ABG⎳平面CDEHG，因为平面AEHG与平面ABG和平面CDEHF于AG,EH，所以AG⎳EH，可得四边形AGHE 为平行四边形，所以GH =AE ，因为AE =AD 2+DE 2=42+12=17，所以GH =17，在直角△AMG ，可得GM =GB 2-AB 22=52-42=3，在直角梯形GMNH 中，可得HN =3+17-42=4，因为HN ⊥平面ABCD ，所以点H 到平面ABCD 的距离为4.(2)解：以点N 为原点，以NM ,NC ,NH 所在的直线分别为x ,y ,z 轴，建立空间直角坐标系，如图所示，则E (0,-4,1),F (0,4,1),G (4,0,3),H (0,0,4)，可得HE =(0,-4,-3),HF =(0,4,-3),HG=(4,0,-1)，设平面BFHG 的法向量为n=(x ,y ,z )，则n ⋅HG=4x -z =0n ⋅HF=4y -3z =0，取z =4，可得x =1,y =3，所以n=(1,3,4)，设平面AGHE 的法向量为m=(a ,b ,c )，则m ⋅HG=4a -c =0m ⋅HE=-4b -3c =0，取c =4，可得a =1,b =-3，所以m=(1,-3,4)，则cos m ,n =m ⋅n m n=1-9+161+9+16⋅1+9+16=413，即平面BFHG 与平面AGHE 所成锐二面角的余弦值413.8(2024·重庆·模拟预测)如图，ACDE 为菱形，AC =BC =2，∠ACB =120°，平面ACDE ⊥平面ABC ，点F 在AB 上，且AF =2FB ，M ，N 分别在直线CD ，AB 上．(1)求证：CF ⊥平面ACDE ；(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线，若∠EAC =60°，MN 为直线CD ，AB 的公垂线，求ANAF的值；(3)记直线BE 与平面ABC 所成角为α，若tan α>217，求平面BCD 与平面CFD 所成角余弦值的范围．【答案】(1)证明见解析(2)AN AF=913(3)528,255 【分析】(1)先通过余弦定理及勾股定理得到CF ⊥AC ，再根据面面垂直的性质证明；(2)以C 为原点，CA 的方向为x 轴正方向，建立如图所示空间直角坐标系C -xyz ，利用向量的坐标运算根据MN ⋅CD =0MN ⋅AF =0，列方程求解即可；(3)利用向量法求面面角，然后根据tan α>217列不等式求解.【详解】(1)AB 2=AC 2+BC 2-2AC ⋅BC ⋅cos ∠ACB =12，AB =23，AF =2FB ，所以AF =433，CF=13CA +23CB ，CF 2=19CA 2+49CB 2+49CA ⋅CB =43，AC 2+CF 2=4+43=163=AF 2，则CF ⊥AC ，又因为平面ACDE ⊥平面ABC ，平面ACDE ∩平面ABC =AC ，CF ⊂面ABC ，故CF ⊥平面ACDE ；(2)以C 为原点，CA 的方向为x 轴正方向，建立如图所示空间直角坐标系C -xyz ，由∠EAC =60°，可得∠DCA =120°，DC =2，所以C 0,0,0 ,D -1,0,3 ,A 2,0,0 ,F 0,233,0 所以AF =-2,233,0 ，CD =-1,0,3 ，设AN =λAF =-2λ,233λ,0 ，则N 2-2λ,233λ,0 ，设CM =μCD ，则M -μ,0,3μ ，MN =2-2λ+μ,233λ,-3μ ，由题知，MN ⋅CD=0MN ⋅AF =0 ⇒2λ-2-μ-3μ=04λ-4-2μ+43λ=0 ，解得λ=913，μ=-213，故AN AF=913；(3)B -1,3,0 ，设∠EAC =θ，则E 2-2cos θ,0,2sin θ ，BE=3-2cos θ,-3,2sin θ ，可取平面ABC 的法向量n=0,0,1 ，则sin α=cos n ,BE=n ⋅BEn ⋅BE =2sin θ 3-2cos θ 2+3+4sin 2θ=sin θ4-3cos θ，cos α=4-3cos θ-sin 2θ4-3cos θ，则tan α=sin θ4-3cos θ-sin 2θ>217，整理得10cos 2θ-9cos θ+2<0，故cos θ∈25,12，CF =0,23,0，CD =-2cos θ,0,2sin θ ，CB =-1,3,0 ，记平面CDF 的法向量为n 1 =x ,y ,z ，则有n 1 ⋅CD =0n 1 ⋅CF =0 ⇒-2x cos θ+2z sin θ=023y =0，可得n 1=sin θ,0,cos θ ，记平面CBD 的法向量为n 2 =a ,b ,c ，则有n 2 ⋅CD=0n 2 ⋅CB =0 ⇒-2a cos θ+2c sin θ=0-a +3b =0，可得n 2=3sin θ,sin θ,3cos θ ，记平面BCD 与平面CFD 所成角为γ，则cos γ=cos n 1 ,n 2 =33+sin 2θ，cos θ∈25,12 ，所以sin 2θ∈34,2125 ，3+sin 2θ∈152,465 ，故cos γ=33+sin 2θ∈528,255 ．9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°，使得CD 到EF 的位置，得到如图所示的几何体．(1)求证：平面ACF ⊥平面BDE ；(2)点M 为DF上一点，若二面角C -AM -E 的余弦值为13，求∠MAD ．【答案】(1)证明见解析(2)∠MAD =45°【分析】(1)根据面面与线面垂直的性质可得BD ⊥AF ，结合线面、面面垂直的判定定理即可证明；(2)建立如图空间直角坐标系，设∠MAD =α，AB =1，利用空间向量法求出二面角C -AM -E 的余弦值，建立方程1-sin αcos α1+sin 2α1+cos 2α=13，结合三角恒等变换求出α即可.【详解】(1)由已知得平面ABCD ⊥平面ABEF ，AF ⊥AB ，平面ABCD ∩平面ABEF =AB ，AF ⊂平面ABEF ，所以AF ⊥平面ABCD ，又BD ⊂平面ABCD ，故BD ⊥AF ，因为ABCD 是正方形，所以BD ⊥AC ，AC ，AF ⊂平面ACF ，AC ∩AF =A ，所以BD ⊥平面ACF ，又BD ⊂平面BDE ，所以平面ACF ⊥平面BDE .(2)由(1)知AD ，AF ，AB 两两垂直，以AD ，AF ，AB 所在直线分别为x ，y ，z 轴，建立空间直角坐标系，如图.设∠MAD =α，AB =1，则A 0,0,0 ，M cos α,sin α,0 ，C 1,0,1 ，E 0,1,1 ，故AM =cos α,sin α,0 ，AC =1,0,1 ，AE =0,1,1设平面AMC 的法向量为m =x 1,y 1,z 1 ，则m ⋅AC =0，m ⋅AM=0故x 1+z 1=0x 1cos α+y 1sin α=0，取x 1=sin α，则y 1=-cos α，z 1=-sin α所以m=sin α,-cos α,-sin α设平面AME 的法向量为n =x 2,y 2,z 2 ，n ⋅AE =0，n ⋅AM=0故y 2+z 2=0x 2cos α+y 2sin α=0，取x 2=sin α，则y 2=-cos α，z 2=cos α所以n=sin α,-cos α,cos α ，所以cos m ,n =1-sin αcos α1+sin 2α1+cos 2α，由已知得1-sin αcos α1+sin 2α1+cos 2α=13，化简得：2sin 22α-9sin2α+7=0，解得sin2α=1或sin2α=72(舍去)故α=45°，即∠MAD =45°.10(2024·安徽黄山·二模)如图，已知AB 为圆台下底面圆O 1的直径，C 是圆O 1上异于A ,B 的点，D 是圆台上底面圆O 2上的点，且平面DAC ⊥平面ABC ，DA =DC =AC =2，BC =4，E 是CD 的中点，BF =2FD ．(1)证明：DO 2⎳BC ；(2)求直线DB 与平面AEF 所成角的正弦值.【答案】(1)证明见解析(2)68585【分析】(1)取AC 的中点O ，根据面面垂直的性质定理，可得DO ⊥平面ABC ，即可求证DO 2⎳OO 1，进而可证矩形，即可根据线线平行以及平行的传递性求解.(2)建系，利用向量法，求解法向量n =1,-12,3 与方向向量DB =(-1,4,-3)的夹角，即可求解．【详解】(1)证明：取AC 的中点为O ，连接DO ，OO 1，O 1O 2，∵DA =DC ，O 为AC 中点，∴DO ⊥AC ，又平面DAC ⊥平面ABC ，且平面DAC ∩平面ABC =AC ，DO ⊂平面DAC ,∴DO ⊥平面ABC ，∴DO ⎳O 1O 2，DO =O 1O 2，故四边形DOO 1O 2为矩形，∴DO 2⎳OO 1，又O ，O 1分别是AC ，AB 的中点，∴OO 1⎳BC ，∴DO 2⎳BC ；(2)∵C 是圆O 1上异于A ，B 的点，且AB 为圆O 1的直径，∴BC ⊥AC ，∴OO 1⊥AC ，∴如图以O 为原点建立空间直角坐标系，由条件知DO =3，∴A (1,0,0),B (-1,4,0),C (-1,0,0),D (0,0,3)，∴E -12,0,32 ，设F (x ,y ,z )，∴BF =(x +1,y -4,z )，FD=(-x ,-y ,3-z )，由BF =2FD ，得F -13,43,233 ，∴AF =-43,43,233 ，∴DB =(-1,4,-3)，AE =-32,0,32 ，设平面AEF 法向量为n=(x 1,y 1,z 1)，则n ⋅AE=-32x 1+32z 1=0n ⋅AF =-43x 1+43y 1+233z 1=0，取n =1,-12,3 ，设直线BD 与平面AEF 所成角为θ，则sin θ=|cos <n ,DB>|=625⋅172=68585∴直线BD 与平面AEF 所成角的正弦值为68585．11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22，A 1B 1=12AB ，M 为BC 中点，已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1，其中λ∈0,1 ．(1)求证D 1P ⊥AC ；(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37，当λ=23时，求直线DP 与平面AMC 1所成角的正弦值．【答案】(1)证明见解析(2)241391【分析】(1)方法一运用空间向量的线性运算，进行空间位置关系的向量证明即可.方法二：建立空间直角坐标系，进行空间位置关系的向量证明即可.(2)建立空间直角坐标系，利用线面角的向量求法求解即可.【详解】(1)方法一：∵A 1B 1=12AB ，∴AA 1 ⋅AB =AA 1 ⋅AD =22×22=2．∵D 1A =-12AD-AA 1∴D 1P =D 1A +AP =1-λ AB +12λ-12AD+λ-1 AA 1∴D 1P ⋅AC =1-λ AB +12λ-12AD +λ-1 AA 1 ⋅AB +AD =1-λ AB 2+12λ-12 AD2+λ-1 AB ⋅AA 1 +λ-1 AD ⋅AA 1=81-λ +812λ-12+4λ-1 =0．∴D 1P ⊥AC ，即D 1P ⊥AC ．方法二：以底面ABCD 的中心O 为原点，以OM 方向为y 轴，过O 点平行于AD 向前方向为x 轴，以过点O 垂直平面ABCD 向上方向为z 轴，建立如图所示空间直角坐标系，设正四棱台的高度为h ，则有 A 2,-2,0 ，B 2,2,0 ，C -2,2,0 ，D -2,-2,0 ，A 122,-22,h ，C 1-22,22,h ，D 1-22,-22,h ，M 0,2,0 ，AC =-22,22,0AP =1-λ 0,22,0 +12λ-22,0,0 +λ-22,22,0 =-322λ,22-322λ,λhD 1A =322,-22,-h ，D 1P =D 1A +AP =-322λ+322,-322λ+322,λh -h ．故AC ⋅D 1P=0，所以D 1P ⊥AC ．(2)设平面ABCD 的法向量为n=0,0,1 ，设平面AMC 1的法向量为m =x ,y ,z ，AM =-2,22,0 ，AC 1 =-322,322,h ，则有AM ⋅m=0AC 1 ⋅m=0 ，即-2x +22y =0-322x +322y +hz =0，令x =22h ，则m=22h ,2h ,3 ．又题意可得cos m ,n =38h 2+2h 2+9=37，可得h =2．因为λ=23，经过计算可得P 0,0,43 ，D 1-22,-22,2 ，D 1P =2,2,43．将h =2代入，可得平面AMC 1的法向量m=42,22,3 ．设直线DP 与平面AMC 1所成角的为θsin θ=cos DP ,m =8+4+42+2+16932+8+9=241391．12(2024·辽宁·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2，AB =1,BC =3，点E 为线段AC 的中点.(1)求证：AB 1∥平面BEC 1；(2)若∠A 1AC =π3，求二面角A -BE -C 1的余弦值.【答案】(1)证明见详解(2)-22【分析】(1)连接BC 1，交B 1C 于点N ，连接NE ，利用线面平行的判定定理证明；(2)由已知可知，△AA 1C 为等边三角形，故A 1E ⊥AC ，利用面面垂直的性质定理可证得A 1E ⊥底面ABC ，进而建立空间直角坐标系，利用向量法即可求二面角余弦值.【详解】(1)连接BC 1，交B 1C 于点N ，连接NE ，因为侧面BCC 1B 1是平行四边形，所以N 为B 1C 的中点，又因为点E 为线段AC 的中点，所以NE ⎳AB 1，因为AB 1⊄面BEC 1，NE ⊂面BEC 1，所以AB 1⎳面BEC 1.(2)连接A 1C ，A 1E ，因为∠A 1AC =π3，AC =AA 1=2，所以△AA 1C 为等边三角形，A 1C =2，因为点E 为线段AC 的中点，所以A 1E ⊥AC ，因为侧面ACC 1A 1⊥底面ABC ，平面ACC 1A 1∩平面ABC =AC ，A 1E ⊂平面ACC 1A 1，所以A 1E ⊥底面ABC ，过点E 在底面ABC 内作EF ⊥AC ，如图以E 为坐标原点，分布以EF ，EC ，EA 1 的方向为x ,y ,z 轴正方向建立空间直角坐标系，则E 0,0,0 ，B 32,-12,0 ，C 10,2,3 ，所以EB =32,-12,0 ，EC 1 =0,2,3 ，设平面BEC 1的法向量为m=x ,y ,z ，则m ⋅EB =32x -12y =0m ⋅EC 1=2y +3z =0，令x =1，则y =3,z =-2，所以平面BEC 1的法向量为m=1,3,-2 ，又因为平面ABE 的法向量为n=0,0,1 ，则cos m ,n =-21+3+4=-22，经观察，二面角A -BE -C 1的平面角为钝角，所以二面角A -BE -C 1的余弦值为-22.13(2024·广东广州·一模)如图，在四棱锥P -ABCD 中，底面ABCD 是边长为2的菱形，△DCP 是等边三角形，∠DCB =∠PCB =π4，点M ，N 分别为DP 和AB 的中点.(1)求证：MN ⎳平面PBC ；(2)求证：平面PBC ⊥平面ABCD ；(3)求CM 与平面PAD 所成角的正弦值.【答案】(1)证明见解析；(2)证明见解析；(3)33.【分析】(1)取PC 中点E ，由已知条件，结合线面平行的判断推理即得.(2)过P 作PQ ⊥BC 于点Q ，借助三角形全等，及线面垂直的判定、面面垂直的判定推理即得.(3)建立空间直角坐标系，利用线面角的向量求法求解即得.【详解】(1)取PC 中点E ，连接ME ,BE ，由M 为DP 中点，N 为AB 中点，得ME ⎳DC ,ME =12DC ，又BN ⎳CD ,BN =12CD ，则ME ⎳BN ,ME =BN ，因此四边形BEMN 为平行四边形，于是MN ⎳BE ，而MN ⊄平面PBC ,BE ⊂平面PBC ，所以MN ⎳平面PBC .(2)过P 作PQ ⊥BC 于点Q ，连接DQ ，由∠DCB =∠PCB =π4,CD =PC ,QC =QC ，得△QCD ≌△QCP ，则∠DQC =∠PQC =π2，即DQ ⊥BC ，而PQ =DQ =2,PQ 2+DQ 2=4=PD 2，因此PQ ⊥DQ ，又DQ ∩BC =Q ,DQ ,BC ⊂平面ABCD ，则PQ ⊥平面ABCD ，PQ ⊂平面PBC ，所以平面PBC ⊥平面ABCD .(3)由(2)知，直线QC ,QD ,QP 两两垂直，以点Q 为原点，直线QC ,QD ,QP 分别为x ,y ,z 轴建立空间直角坐标系，则C (2,0,0),P (0,0,2),D (0,2,0),M 0,22,22,A (-2,2,0)，CM =-2,22,22,AD =(2,0,0),DP =(0,-2,2)，设平面PAD 的一个法向量n =(x ,y ,z )，则n ⋅AD=2x =0n ⋅DP=-2y +2z =0，令y =1，得n=(0,1,1)，设CM 与平面PAD 所成角为θ，sin θ=|cos ‹CM ,n ›|=|CM ⋅n||CM ||n |=23⋅2=33，所以CM 与平面PAD 所成角的正弦值是33.14(2024·广东梅州·二模)如图，在四棱锥P -ABCD 中，平面PAD ⊥平面ABCD ，底面ABCD 为直角梯形，△PAD 为等边三角形，AD ⎳BC ，AD ⊥AB ，AD =AB =2BC =2．(1)求证：AD ⊥PC ；(2)点N 在棱PC 上运动，求△ADN 面积的最小值；(3)点M 为PB 的中点，在棱PC 上找一点Q ，使得AM ⎳平面BDQ ，求PQQC的值．【答案】(1)证明见解析(2)2217(3)4【分析】(1)取AD 的中点H ，连接PH ，CH ，依题意可得四边形ABCH 为矩形，即可证明CH ⊥AD ，再由PH ⊥AD ，即可证明AD ⊥平面PHC ，从而得证；(2)连接AC 交BD 于点G ，连接MC 交BQ 于点F ，连接FG ，即可得到CG AG=12，再根据线面平行的性质得到CF FM =12，在△PBC 中，过点M 作MK ⎳PC ，即可得到MKCQ=2，最后由PQ =2MK 即可得解.【详解】(1)取AD 的中点H ，连接PH ，CH ，则AH ⎳BC 且AH =BC ，又AD ⊥AB ，所以四边形ABCH 为矩形，所以CH ⊥AD ，又△PAD 为等边三角形，所以PH ⊥AD ，PH ∩CH =H ，PH ,CH ⊂平面PHC ，所以AD ⊥平面PHC ，又PC ⊂平面PHC ，所以AD ⊥PC .(2)连接HN ，由AD ⊥平面PHC ，又HN ⊂平面PHC ，所以AD ⊥HN ，所以S △ADH =12AD ⋅HN =HN ，要使△ADN 的面积最小，即要使HN 最小，当且仅当HN ⊥PC 时HN 取最小值，因为平面PAD ⊥平面ABCD ，平面PAD ∩平面ABCD =AD ，PH ⊂平面PAD ，所以PH ⊥平面ABCD ，又HC ⊂平面ABCD ，所以PH ⊥HC ，在Rt △HPC 中，CH =2，PH =3，所以PC =CH 2+PH 2=7，当HN ⊥PC 时HN =PH ⋅CH PC =237=2217，所以△ADN 面积的最小值为2217.(3)连接AC 交BD 于点G ，连接MC 交BQ 于点F ，连接FG ，因为AD ⎳BC 且AD =2BC =2，所以△CGB ∽△AGD ，所以CG AG =BC AD=12，因为AM ⎳平面BDQ ，又AM ⊂平面ACM ，平面BDQ ∩平面ACM =GF ，所以GF ⎳AM ，所以CF FM =CG AG=12，在△PBC 中，过点M 作MK ⎳PC ，则有MK CQ =MF CF=2，所以PQ =2MK ，所以PQ =2MK =4CQ ，即PQQC=415(2024·广东广州·模拟预测)如图所示，圆台O 1O 2的轴截面A 1ACC 1为等腰梯形，AC =2AA 1=2A 1C 1=4,B 为底面圆周上异于A ,C 的点，且AB =BC ,P 是线段BC 的中点.(1)求证：C 1P ⎳平面A 1AB .(2)求平面A 1AB 与平面C 1CB 夹角的余弦值.【答案】(1)证明见解析(2)17【分析】(1)取AB 的中点H ，连接A 1H ,PH ，证明四边形A 1C 1PH 为平行四边形，进而得C 1P ⎳A 1H ，即可证明；(2)建立空间直角坐标系，求两平面的法向量，利用平面夹角公式求解.【详解】(1)取AB 的中点H ，连接A1H ,PH ，如图所示，因为P 为BC 的中点，所以PH ⎳AC ,PH =12AC .在等腰梯形A 1ACC 1中，A 1C 1⎳AC ,A 1C 1=12AC ，所以HP ⎳A 1C 1,HP =A 1C 1，所以四边形A 1C 1PH 为平行四边形，所以C 1P ⎳A 1H ，又A 1H ⊂平面A 1AB ,C 1P ⊄平面A 1AB ，所以C 1P ⎳平面A 1AB .(2)因为AB =BC ,故O 2B ⊥AC ，以直线O 2A ,O 2B ，O 2O 1分别为x ,y ,z 轴，建立空间直角坐标系，如图所示，在等腰梯形A 1ACC 1中，AC =2AA 1=2A 1C 1=4，此梯形的高为h =AA 21-AC -A 1C 122= 3.因为A 1C 1=12AC ,A 1C 1⎳AC ，。